§5. Лоду 2-го порядка с постоянными коэффициентами.
Дано лоду 2-го порядка с постоянными коэффициентами (5.1), где , . Согласно предыдущему параграфу общее решение лоду 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде .
Подставляя эту функцию в уравнение (5.1), после сокращения на , получим алгебраическое уравнение, которое называется характеристическим:
(5.2)
Функция будет
решением уравнения (5.1) только при тех
значениях k,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта
. Тогда корни характеристического уравнения различны: . Решения и будут линейно независимыми, т.к. и общее решение (5.1) можно записать в виде .
. В этом случае и . В качестве второго линейно независимого решения можно взять функцию . Проверим, что эта функция удовлетворяет уравнению (5.1). Действительно, , . Подставляя эти выражения в уравнение (5.1), получим
или , т.к. и .
Частные решения и линейно независимы, т.к. . Следовательно, общее решение (5.1) имеет вид:
или .
. В этом случае корни характеристического уравнения комплексно-сопряженные: , где , . Можно проверить, что линейно независимыми решениями уравнения (5.1) будут функции и . Убедимся, что уравнению (5.1) удовлетворяет, например, функция y1. Действительно, , . Подставив эти выражения в уравнение (5.1), получим
.
Обе скобки в левой части этого равенства тождественно равны нулю. Действительно, ,
. Таким образом, функция удовлетворяет уравнению (5.1). Аналогично нетрудно убедиться в том, что и есть решение уравнения (5.1). Поскольку , то общее решение будет иметь вид:
.
§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
Теорема 1. Общее решение лнду 2-го порядка
f(x) (6.1)
представляется в виде суммы общего решения соответствующего однородного уравнения
(6.2)
и любого частного решения лнду (6.1).
Доказательство.
Докажем сначала, что будет решением уравнения (6.1). Для этого подставим в уравнение (6.1): f(x). Это равенство является тождеством, т.к. и f(x). Следовательно, есть решение уравнения (6.1).
Докажем теперь, что это решение является общим, т.е. можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида: , (6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде , где и – линейно независимые решения этого уравнения. Таким образом:
и, следовательно, начальные условия (6.3) можно записать в виде:
или
(6.4)
Произвольные постоянные и определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы = есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при , а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные и из системы уравнений (6.4) и подставив их в выражение , мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
Докажем еще одну простую теорему, которая часто используется при решении лнду.
f1(x) + f2(x). (6.5)
Доказательство.
Подставив функцию в уравнение (6.5), получим
f1 + f2. Это равенство является тождеством, т.к. f1 и f2. Теорема доказана.
studfiles.net
Лекция 4. Решение ЛОДУ и ЛНДУ второго порядка с постоянными коэффициентами
Оглавление
§ 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение ЛОДУ второго порядка с постоянными коэффициентами
Характеристическое уравнение:
Случай1. Дискриминант больше нуля
Случай2. Дискриминант равен нулю
Случай3. Дискриминант меньше нуля
Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами
§ 10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение ЛНДУ второго порядка с постоянными коэффициентами
Метод вариации постоянных
Метод решения ЛНДУ со специальной правой частью
Теорема о структуре общего решения ЛНДУ
1. Функция r (x) – многочлен степени т
2. Функция r (x) – произведение числа на показательную функцию
3. Функция r (x) – сумма тригонометрических функций
Алгоритм нахождения общего решения ЛНДУ со специальной правой частью
Приложение
§ 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение второго порядка называется линейным однородным дифференциальным уравнением (ЛОДУ) с постоянными коэффициентами, если оно имеет вид:
,
где p и q – некоторые действительные числа.
Для нахождения общего решения ЛОДУ достаточно найти два его различных частных решения и . Тогда общее решение ЛОДУ будет иметь вид
,
где С1 и С2 – произвольные независимые постоянные.
Леонард Эйлер предложил искать частные решения ЛОДУ в виде
,
где k – некоторое число.
Дифференцируя эту функцию два раза и подставляя выражения для у, у’ и у» в уравнение , получим:
,
Полученное уравнение называется характеристическим уравнением ЛОДУ. Для его составления достаточно в исходном уравнении заменить у», у’ и у соответственно на k2, k и 1:
Решив характеристическое уравнение, т.е. найдя корни k1 и k2,мы найдем и частные решения исходного ЛОДУ.
Характеристическое уравнение есть квадратное уравнение, его корни находятся через дискриминант
.
При этом возможны следующие три случая[2].
Случай 1. Дискриминант больше нуля, следовательно, корни k1 и k2 действительные и различные:
k1 ¹ k2
В этом случае общее решение ЛОДУ имеет вид:
,
где С1 и С2 – произвольные независимые постоянные.
Случай 2. Дискриминант равен нулю, следовательно, корни k1 и k2 действительные и равные:
k1 = k2 = k
В этом случае общее решение ЛОДУ имеет вид
,
где С1 и С2 – произвольные независимые постоянные.
Случай 3. Дискриминант меньше нуля. В этом случае уравнение не имеет действительных корней:
, корней нет.
В этом случае общее решение ЛОДУ имеет вид
,
где С1 и С2 – произвольные независимые постоянные,
, .
Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами сводится к нахождению корней характеристического уравнения и использованию формул общего решения уравнения (не прибегая к вычислению интегралов).
Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами:
1. Привести уравнение к виду , где p и q – некоторые действительные числа.
2. Составить характеристическое уравнение .
3. Найти дискриминант характеристического уравнения.
4. Используя формулы (см. Таблицу 1), в зависимости от знака дискриминанта записать общее решение.
Таблица 1
Таблица возможных общих решений
infopedia.su
ЛОДУ второго порядка с постоянными коэффициентами
Рассмотрим процесс нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами на примерах.
Пример 1
Решение.
Составим характеристическое уравнение:
Решаем его:
, .
Записываем общее решение данного уравнения:
,
где С1 и С2 – произвольные независимые постоянные.
Пример 2. Решить уравнение .
Решение.
Составим характеристическое уравнение:
Решаем его:
.
Записываем общее решение данного уравнения:
,
где С1 и С2 – произвольные независимые постоянные.
Пример 3. Решить уравнение .
Решение.
Составим характеристическое уравнение:
.
Дискриминант равен: .
Найдем a и b:
.
Тогда общее решение записывается в виде:
,
где С1 и С2 – произвольные независимые постоянные.
§ 10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение второго порядка называются линейным неоднородным дифференциальным уравнением (ЛНДУ) с постоянными коэффициентами, если оно имеет вид:
,
где p и q – некоторые действительные числа,
r (x) – некоторая функция.
Для каждого ЛНДУ вида можно написать соответствующее однородное уравнение: , для которого легко можно найти общее решение (см.алгоритм).
Это имеет существенное значение, т.к. общее решение ЛНДУ напрямую связано с общим решением соответствующего ЛОДУ.
Универсальным методом для нахождения общего решения ЛНДУ является метод вариации постоянных, который заключается в следующем.
Пусть мы нашли общее решение соответствующего ЛОДУ:
.
Тогда общее решение ЛНДУ находят в виде:
,
предполагая, что постоянные С1 и С2 зависят от переменной х, т.е. являются функциями. При этом функции С1(х) и С2(х) могут быть найдены поэтапно.
Сначала находят их первые производные из системы уравнений:
| С1‘ · y1 | + | С2‘ · y2 | = | |
| С1‘ · y1‘ | + | С2‘ · y2‘ | = | r (x) |
где r (x) – функция, стоящая в правой части исходного ЛНДУ.
Затем, решая дифференциальные уравнения первого порядка, находят сами функции.
В заключении найденные функции С1(х) и С2(х) подставляют в общее решение ЛОДУ.
Рассмотрим применение метода вариации постоянных на примере.
Пример. Решить уравнение .
Решение.
1. Решим соответствующее ЛОДУ:
,
2. Выпишем отдельно функции у1 и у2, найдем их производные:
,
,
3. Составим систему уравнений и решим ее:
| С1‘ · е х | + | С2‘ · е 2х | = | |||||
| С1‘ · е х | + | С2‘ · 2е 2х | = | е х | ||||
| С1‘ | + | С2‘· е х | = | |||||
| С1‘ | + | 2·С2‘·е х | = | |||||
| С2‘· е х | = – С1‘ | |||||||
| С1‘ | + | 2 ·( – С1‘) | = | |||||
| С2‘· е х | = – С1‘ | |||||||
| – С1‘ | = 1 | |||||||
Получили, что С1‘ = –1, С2‘ = 1/е х = е –х.
4. Решим дифференциальные уравнения:
5. Найденные С1 и С2 подставим в общее решение ЛОДУ, получим искомое общее решение ЛНДУ:
.
Следует отметить, что метод вариации постоянных позволяет решить любое ЛНДУ вне зависимости от r(x) – функции, стоящей в правой части исходного ЛНДУ. Однако этот метод достаточно сложен, поэтому в ряде случаев для отыскания общего решения ЛНДУ применяют второй метод – метод решения ЛНДУ со специальной правой частью.
Этот метод основан на теореме, которая определяет структуру общего решения ЛНДУ.
Теорема (Структура общего решения ЛНДУ). Общее решение ЛНДУ есть сумма общего решения соответствующего ЛОДУ и какого-либо частного решения исходного ЛНДУ:
Таким образом, нам надо найти общее решение ЛОДУ, что сделать не трудно, и отыскать какое-нибудь частное решение исходного ЛНДУ. Вид этого частного решения устанавливается по виду правой части исходного ЛНДУ, т.е. по виду функции r (x).
Рассмотрим некоторые возможные случаи.
1. Функция r (x) – многочлен степени т:
Тогда частное решение следует искать в виде
,
где k – число корней характеристического уравнения, равных нулю, т.е.
k = 0, если q ¹ 0
k = 1, если q = 0, p ¹ 0
k = 2, если q = 0, p = 0.
Пример. Найти частное решение уравнения
Решение.
Правая часть уравнения – многочлен первой степенны, следовательно, частное решение надо искать в виде
.
Определим значение параметра k: т.к. в левой части дифференциального уравнения q = 0, p = –3 ¹ 0, то k = 1, тогда частное решение имеет вид
.
Чтобы найти числа С0 и С1, найдем производные от нашего уч.н. и подставим их в исходное уравнение:
,
.
Соответствующие коэффициенты в правой и левой частях равенства должны быть равны, следовательно, можно записать систему уравнений:
Решая эту систему, получим С1 = – 1, С0 = – 1.
Теперь, зная значения коэффициентов С0 и С1, подставим их в уравнение , получим:
.
2. Функция r(x) – произведение числа на показательную функцию:
В этом случае частное решение следует искать в виде
,
где n – число корней характеристического уравнения, равных а, т.е.
п = 0, если k1 ¹ а, k2 ¹ а,
п = 1, если k1 = а, k2 ¹ а или k1 ¹ а, k2 = а
п = 2, если k1 = k2 = а
Пример. Найти частное решение уравнения
Решение.
Правая часть уравнения – это произведение числа на показательную функцию, следовательно, частное решение надо искать в виде
.
Число а = 3 по условию. Чтобы определить значение параметра п, надо найти корни характеристического уравнения:
Т.к. оба корня характеристического уравнения неравны числу а, то п = 0, тогда частное решение имеет вид:
.
Чтобы найти число С0, найдем производные от нашего уч.н. и подставим их в исходное уравнение:
,
Подставим С0 = 1 в уравнение , получим:
.
3. Функция r (x) – сумма тригонометрических функций вида:
где А, В, b – некоторые действительные числа, причем b ¹ 0.
Тогда частное решение следует искать в виде
,
где s = 1, если p = 0, q > 0,
s = 0, во всех других случаях.
Пример. Найти частное решение уравнения
Решение.
Правая часть уравнения – это тригонометрическая функций вида:
, где b = 1.
частное решение следует искать в виде
.
Параметр s = 0, т.к. не выполняется условие p = 0, q > 0, следовательно,
.
Чтобы найти числа С0 и С1, найдем производные от нашего уч.н. и подставим их в исходное уравнение:
,
.
Коэффициенты при соответствующих тригонометрических функциях в правой и левой частях равенства должны быть равны, следовательно, можно записать систему уравнений:
Решая эту систему, получим С1 = 0,1 и С0 = 0,3.
Теперь, зная значения коэффициентов С0 и С1, подставим их в уравнение , получим:
.
Подводя итог, составималгоритм нахождения общего решения ЛНДУ второго порядка с постоянными коэффициентами со специальной правой частью:
1. Привести уравнение к виду , где p и q – некоторые действительные числа, r (x) – некоторая функция.
2. Составить соответствующее однородное уравнение: .
3. Найти – общее решение этого однородного уравнения, используя Таблицу 1.
4. Используя Таблицу 2, определить общий вид частного решения ЛНДУ.
5. Найти числа Сi и записать – частное решение исходного неоднородного уравнения.
6. Записать искомое общее решение ЛНДУ по формуле:
Таблица 2
Таблица частных решений
infopedia.su
4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
Определение. Линейным однородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
,
где коэффициенты – заданные действительные числа.
Метод
решения. Согласно теореме 4.3 общим решением  на отрезке
на отрезке  линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация
линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация
– линейно независимых на том же отрезке частных решений этого уравнения .
Для их нахождения составляется и решается характеристическое уравнение
,
получаемое заменой
в исходном дифференциальном уравнении
производных
искомой функции степенями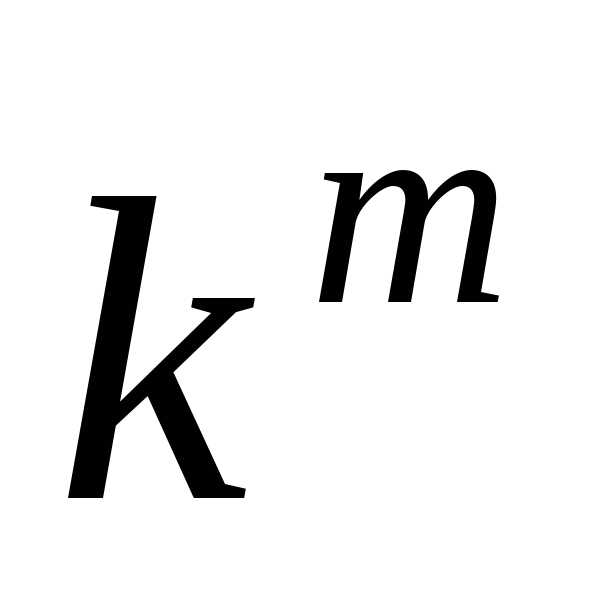 ,
причем сама функция
,
причем сама функция заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.
заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.
Каждому из n корней характеристического уравнения соответствует одно из n линейно независимых частных решений линейного однородного дифференциального уравнения, причем:
– каждому действительному простому корню k соответствует частное решение вида
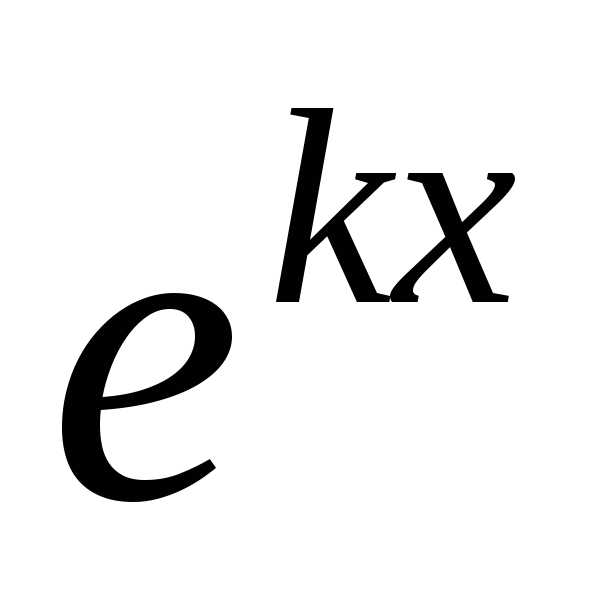 ;
;
– каждому
действительному корню k кратности  соответствуют
соответствуют частных решений вида
частных решений вида
;
– каждой паре комплексных сопряженных простых корней исоответствует два частных решения вида
;
–
каждой паре комплексных сопряженных
корней
икратности соответствуют 2
соответствуют 2 частных решений вида
частных решений вида
.
Составляя линейную комбинацию из найденных частных решений, получаем общее решение линейного однородного уравнения с постоянными коэффициентами.
Примеры
1) Найти общее решение однородного дифференциального уравнения .
Характеристическое уравнение и его решения:
–два действительных простых корня.
Частные решения однородного дифференциального уравнения:
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
2) Найти общее решение однородного дифференциального уравнения
.
Характеристическое уравнение и его решения:
–двукратный действительный корень.
Частные решения однородного дифференциального уравнения:
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
3) Найти общее решение однородного дифференциального уравнения
.
Характеристическое уравнение и его решения:
–пара комплексно сопряженных простых корней .
Частные решения однородного дифференциального уравнения:
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
4) Найти общее решение однородного дифференциального уравнения
.
Характеристическое уравнение и его решения:
–двукратные комплексно сопряженные корни .
Частные решения однородного дифференциального уравнения:
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
Определение. Линейным неоднородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
,
где коэффициенты
–
заданные действительные числа, а –
заданная функция.
–
заданная функция.
Метод решения. Согласно теореме 4.4 общим решением  на отрезке
на отрезке  линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью
линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью 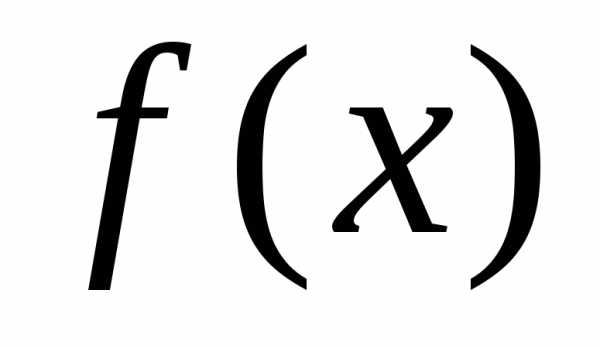 является сумма общего решения
является сумма общего решения
соответствующего однородного уравнения
и какого-нибудь
частного решения  неоднородного уравнения:
неоднородного уравнения:
.
Общее решение
однородного уравнения находить уже
умеем, поэтому остается рассмотреть
вопрос о нахождении частного решения 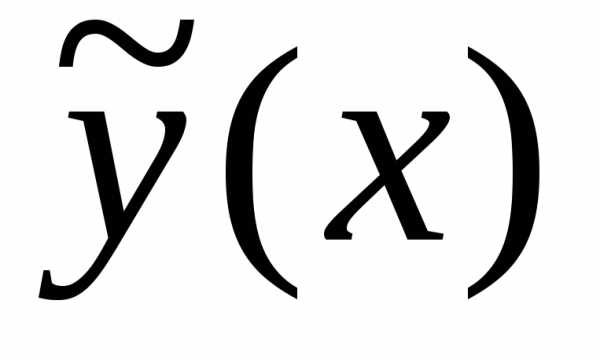 неоднородного уравнения.
неоднородного уравнения.
Если правая часть
неоднородного уравнения, т.е. функция  –
многочлен, либо показательная функция,
либо тригонометрические функции
–
многочлен, либо показательная функция,
либо тригонометрические функции 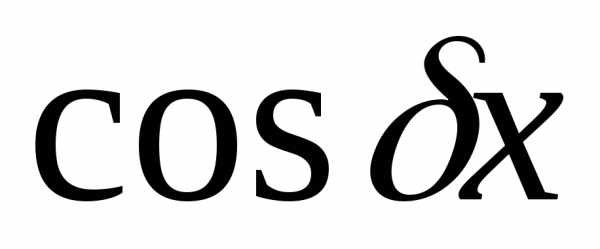 или
или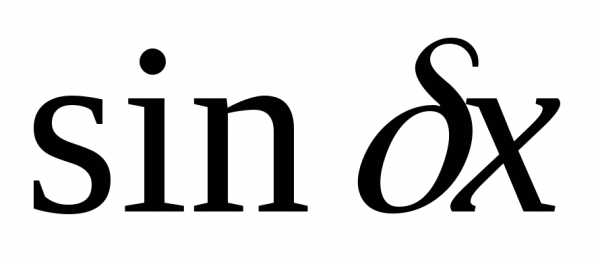 ,
либо линейная комбинация перечисленных
функций, то частное решение
,
либо линейная комбинация перечисленных
функций, то частное решение неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов.
неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов.
Если же правая
часть неоднородного уравнения есть
произвольная непрерывная функция, то
частное решение  неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных.
неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных.
Рассмотрим оба
перечисленных метода нахождения частного
решения  неоднородного уравнения.
неоднородного уравнения.
Метод неопределенных коэффициентов
Пусть правая часть неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид
,
где
и – действительные постоянные,
– действительные постоянные, и
и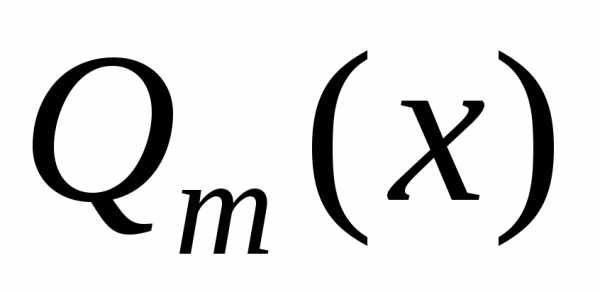 –
многочлены от x соответственно l-й
и m-й
степени.
–
многочлены от x соответственно l-й
и m-й
степени.
Тогда частное решение неоднородного уравнения ищем в виде
.
Здесь  равно показателю кратности корняв характеристическом уравнении
равно показателю кратности корняв характеристическом уравнении
.
Если характеристическое
уравнение такого корня не имеет, то
следует положить 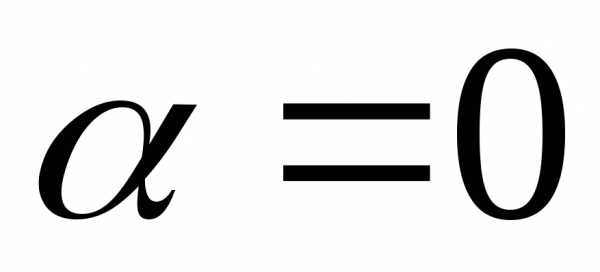 .
.
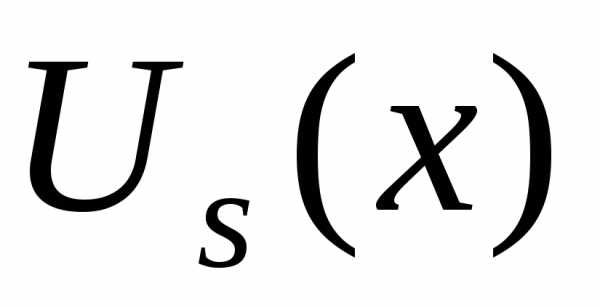 и
и –полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m:
–полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m:
Если в выражение
функции  входит хотя бы одна из функций
входит хотя бы одна из функций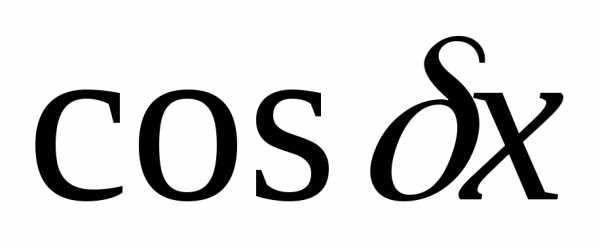 или
или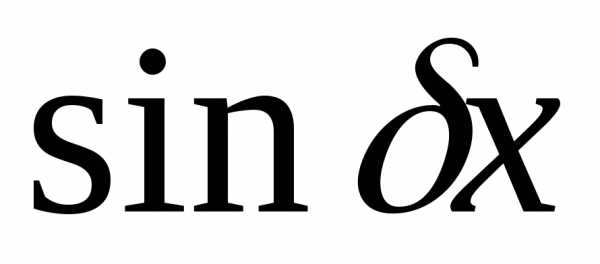 ,
то в решение
,
то в решение надо всегда вводитьобе эти функции.
надо всегда вводитьобе эти функции.
Неопределенные
коэффициенты
находятсяиз
системы линейных алгебраических
уравнений, получаемых отождествлением
коэффициентов подобных членов в правой
и левой частях исходного линейного
неоднородного дифференциального
уравнения после подстановки в него 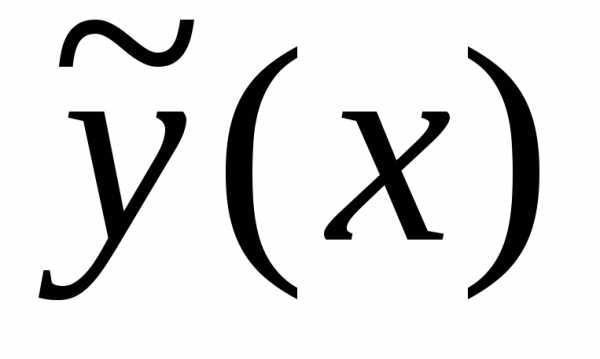 вместоy,
вместоy,  вместо
вместо ,
, вместо
вместо и т.д.
и т.д.
Если правая часть исходного дифференциального уравнения есть сумма нескольких функций рассматриваемой структуры:
,
и – соответствующие решения уравнений
,
то сумма
,
как легко установить, является частным решением исходного уравнения (принцип наложения решений).
Пример. Найти общее решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
.
Решение данного неоднородного уравнения производится в три этапа.
1) Сначала находим общее решение соответствующего однородного уравнения:
Для этого составляем и решаем характеристическое уравнение:
– два действительных простых корня.
Частные решения однородного дифференциального уравнения:
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
2) Далее ищем частное решение исходного неоднородного уравнения в виде
,
так как
характеристическое уравнение имеет
корень 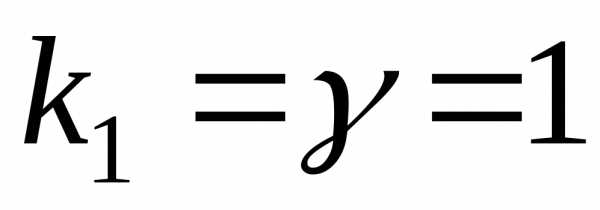
 ,
а также согласно принципу наложения
решений для правых частей.
,
а также согласно принципу наложения
решений для правых частей.
Для определения
коэффициентов  находим производные
находим производные и
и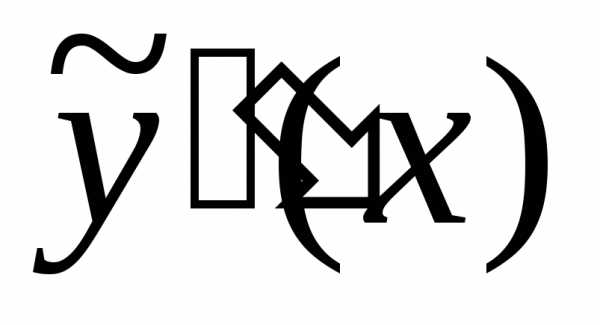 :
:
и подставляем их в исходное неоднородное уравнение:
Раскроем скобки и приведем подобные в левой части равенства:
.
Приравнивая
коэффициенты у подобных членов из обеих
частей равенства, получим систему
уравнений для определения коэффициентов  и найдем их значения:
и найдем их значения:
Таким образом, частное решение неоднородного уравнения имеет вид:
.
3) Общее решение исходного неоднородного дифференциального уравнения найдем как сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения:
.
Метод вариации произвольных постоянных (метод Лагранжа)
Частное решение линейного неоднородного дифференциального уравнения
можно найти методом вариации произвольных постоянных, если известно общее решение
соответствующего однородного уравнения
.
Именно, будем искать частное решение неоднородного уравнения в виде
,
где – неизвестные функции, для определения которых нужно составить n уравнений.
Найдем 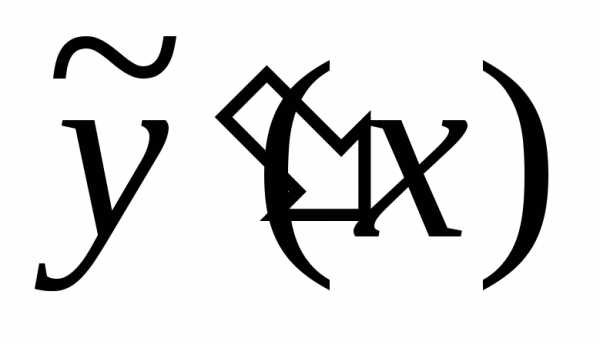 :
:
.
Положив
 ,
,
получим первое из n искомых уравнений.
Найдем 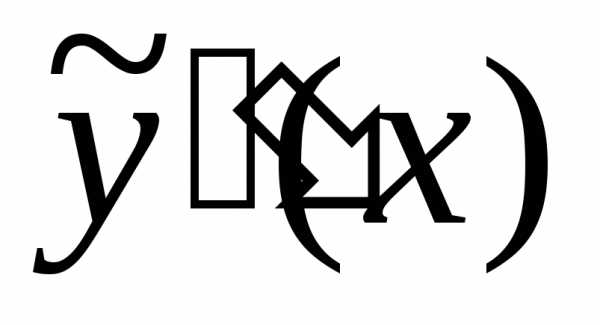 :
:
.
Положив
 ,
,
получим второе из n искомых уравнений.
Продолжая аналогичным
образом, найдем 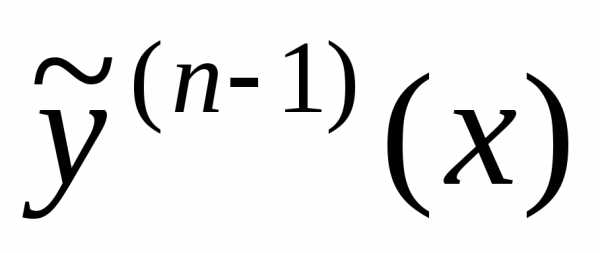 :
:
.
Положив
,
получим 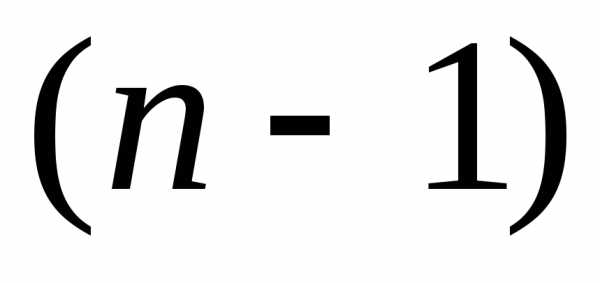 -е
изn искомых уравнений.
-е
изn искомых уравнений.
Найдем 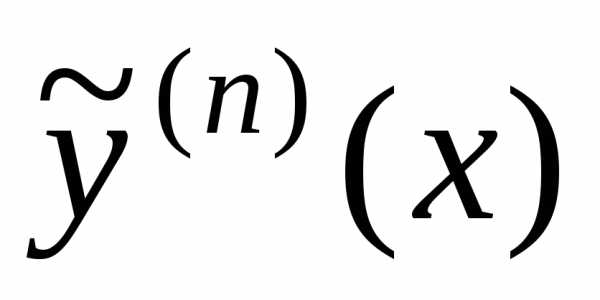 :
:
и, подставив в
исходное неоднородное уравнение  вместоy,
вместоy,  вместо
вместо  ,
, вместо
вместо ,…,
,…, вместо
вместо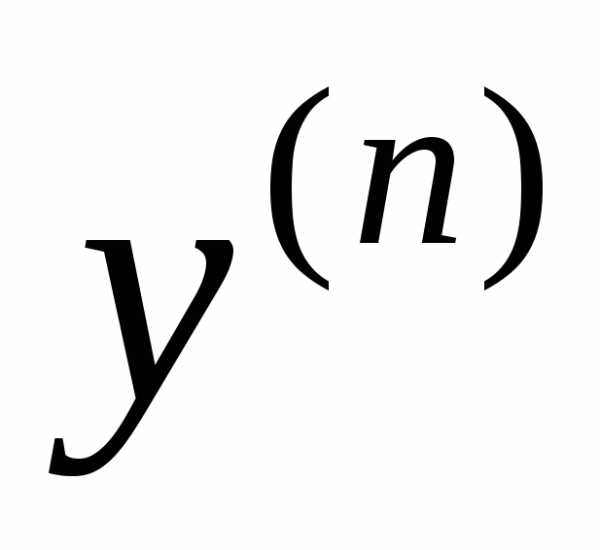 ,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций
:
,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций
:
или
,
или
,
так как – решения однородного уравнения
.
Таким образом, получили систему из n линейных неоднородных алгебраических уравнений для определения производных от n неизвестных функций :

Примем без доказательства, что определитель системы отличен от нуля. Тогда система имеет единственное решение . Определив все, после интегрирования получаем
,
Следовательно, частное решение исходного линейного неоднородного дифференциального уравнения имеет вид
,
где функции определяются полученными равенствами, а– известные линейно независимые частные решения соответствующего однородного уравнения.
Пример. Найти частное решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
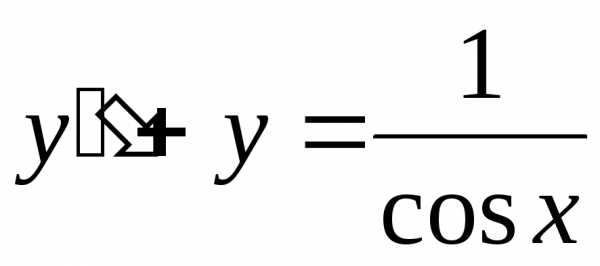 .
.
1) Сначала находим общее решение соответствующего однородного уравнения
.
Для этого составляем и решаем характеристическое уравнение:
– пара комплексно сопряженных простых корней .
Частные решения соответствующего однородного дифференциального уравнения:
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
.
2) Далее ищем частное решение исходного неоднородного дифференциального уравнения в виде
.
Составляем и
решаем систему неоднородных алгебраических
уравнений для определения  и
и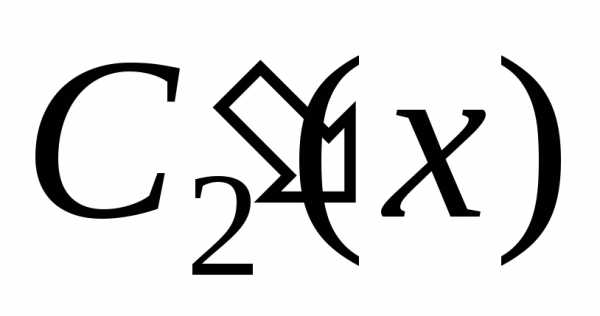 :
:
или
откуда находим
Таким образом, частное решение исходного неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами имеет вид
.
studfiles.net
11
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
1. Дифференциальные уравнения, допускающие понижение порядка.
2. Линейные дифференциальные уравнения с постоянными коэффициентами.
3. Теорема об общем решении линейных однородных дифференциальных уравнений (ЛОДУ) с постоянными коэффициентами .
4. Вид общего решения ЛОДУ с постоянными коэффициентами в зависимости от корней характеристического уравнения.
5. Теорема об общем решении линейных неоднородных дифференциальных уравнений (ЛНДУ) с постоянными коэффициентами.
6. Вид частного решения ЛНДУ с постоянными коэффициентами в зависимости от вида правой части
1. Дифференциальные уравнения, допускающие понижение порядка.
Общий вид дифференциального уравнения второго порядка или .
Общее решение .
1) Иногда решение дифференциального уравнения второго порядка может быть сведено к последовательному решению двух дифференциальных уравнений первого порядка (тогда говорят, что данное дифференциальное уравнение допускает понижение порядка).
Если дифференциальное уравнение имеет вид у«=f(х), то оно решается последовательным интегрированием.
2) Если в запись уравнения не входит искомая функция у(х), т.е. оно имеет вид F(x,y’,y»)=Q, то такое уравнение можно решить, найдя сначала вспомогательную функцию z=y‘.
2. Линейные дифференциальные уравнения с постоянными коэффициентами.
Определение. Линейным дифференциальным уравнением II порядка с постоянными коэффициентами называется уравнение вида
,
где p и q – постоянные числа, а f(x)-некоторая функция.
3. Теорема об общем решении линейных однородных дифференциальных уравнений (ЛОДУ) с постоянными коэффициентами.
Определение. Линейным однородным дифференциальным уравнением (ЛОДУ) II порядка с постоянными коэффициентами называется уравнение вида: (1)
где p и q – постоянные.
Если — решение уравнения (1), то и, где С – произвольная постоянная, также будет решением этого уравнения.
Два решения и уравнения (1) называются линейно зависимыми на некотором промежутке, если их отношение равно постоянному числу с, т.е.. В противном случае решения (функции) и линейно независимы на этом промежутке.
Если и — решения уравнения (1), то их сумма также есть решение этого уравнения.
Теорема: Если и — независимые решения уравнения (1), то
(2)
является общим решением этого уравнения.
4. Вид общего решения ЛОДУ с постоянными коэффициентами в зависимости от корней характеристического уравнения.
Уравнение (3)
называется характеристическим уравнением для уравнения (1).
Если k является корнем характеристического уравнения, то является решением уравнения (1).
1. Если характеристическое уравнение имеет два различных действительных корня и, то общее решение уравнения (1) имеет вид
(4)
2. Если характеристическое уравнение имеет два одинаковых действительных корня, то общее решение уравнения (1) имеет вид
, т.е. (5)
3. Если корни характеристического уравнения комплексные числа и, то общее решение уравнения (1 ) имеет вид: (6)
Пример. Найти общее решение уравнения.
Решение. Составим характеристическое уравнение. ; D=16-4·13<0; D= -36 = 62 i2; i =√ -1
— корни комплексные: , , , поэтому по формуле (6) имеем
-общее решение.
5. Теорема об общем решении линейного неоднородного дифференциального уравнения (ЛНДУ) с постоянными коэффициентами.
Линейным неоднородным дифференциальным уравнением (ЛНДУ) второго порядка с постоянными коэффициентами называется уравнение вида: (7)
где p и q – данные постоянные числа , f(x) – правая часть уравнения, известная функция от x.
Теорема. Общее решение неоднородного уравнения (7) равно сумме общего решения соответствующего однородного уравнения и частного решения данного неоднородного уравнения, т.е.
(8)
Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами можно найти, зная корни характеристического уравнения.
6. Вид частного решения ЛНДУ с постоянными коэффициентами в зависимости от вида правой части
Рассмотрим несколько случаев отыскания частных решений уравнения (7) методом неопределенных коэффициентов.
I. Правая часть уравнения (7) – показательная функция:
Возможны три случая:
а) m – не является корнем характеристического уравнения.
Тогда частное решение ЛНДУ (7) ищется в виде:
(9)
б) m – простой корень характеристического уравнения
, т.е. m = k 1 или m = k 2 .
В этом случае частное решение следует искать в форме
(10)
в ) m – кратный корень характеристического уравнения , т.е. m = k 1 = k 2 .
В этом случае решение следует искать в форме
(11)
Пример.;
1). — характеристическое уравнение соответствующего ЛОДУ: . , тогда имеем:
— общее решение ЛОДУ.
2). m=2 не является корнем характеристического уравнения, значит . Подставляем в данное уравнение: , ; . Значит:
— частное решение ЛНДУ.
— общее решение ЛНДУ.
II. Правая часть неоднородного уравнения (7) – полином, например, второй степени: .
Возможны два случая.
1). Если, то Z ищется в виде: (12)
2) Если, то частное решение Z следует искать в форме: (13)
Аналогично нужно поступать, если — полином какой-нибудь другой степени. Произвольные постоянные, входящие в общее решение, могут быть определены из начальных условий.
studfiles.net
6.2. Нахождение фундаментальной системы решений и общего решения ЛОДУ
Пример. Найти общее решение уравнения
y′′′−6 y′′+11y′−6 y =0 ,
если известно, | что функции | y | = ex , y | 2 | = e2x , y =e3x | являются его | ||||||||||||
решениями. |
|
|
| 1 |
|
|
| 3 |
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| Решение: | Это | ЛОДУ |
| третьего | порядка. | Покажем, что | |||||||||||
y | = ex , y | 2 | = e2x ,y = e3x образуют фундаментальную систему функций: | |||||||||||||||
1 |
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
| e x | e2x | e3x |
|
|
|
|
| 1 | 1 | 1 |
|
| |
|
|
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| W (x) = | e x | 2e2x | 3e3x |
| = e xe2xe3x |
| 1 2 | 3 |
| = | |||||
|
|
|
|
| e x | 4e2x | 9e3x |
|
|
|
|
| 1 | 4 | 9 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= e6x (18+3+ 4− 2−9−12)= 2e6 x ≠ 0.
Тогда общее решение будет
y =С1y1+С2y2+С3y3 = С1ex+С2e2x+С3e3x. Ответ:y = С1ex+С2e2x+С3e3x. ■
Линейное однородное дифференциальное уравнение (ЛОДУ) n-огопорядка с постоянными коэффициентами имеет вид:
y(n) +a1 y(n−1) +a2 y(n−2) +…… +an−1 y′+an y =0 , | (6.8) |
где все коэффициенты a1, a2, a3, …, an-1, an — числа (в частности, некоторые могут быть и нулями).
Рассмотрим уравнение второго порядка |
|
y′′+a1 y′+a2 y =0. | (6.9) |
Заметим, что в силу свойств однородных линейных уравнений нам достаточно найти два частных решений, составляющих фундаментальную систему решений уравнения (6.9), чтобы затем найти общее.
Будем искать частное решение уравнения (6.9) в виде
где k — число, которое подберем так, чтобы функция (6.10) удовлетворяла уравнению (6.9).
Дифференцируя | дважды | у, | найдем y′ = kekx ,y′′ = k 2 ekx ; | ||
подставляя в (6.9), | получим |
|
|
|
|
| k 2ekx + a k ekx + a | 2 | ekx= 0, | ||
|
| 1 |
|
| |
сокращая на ekx ≠ 0 , имеем
27
k 2 + a k+ a | 2 | = 0. | (6.11) |
1 |
|
|
Это алгебраическое квадратное уравнение относительно k , оно будет называтьсяхарактеристическим уравнением уравнения (6.9).
Итак, чтобы функция y = ekx была частным решением уравнения (6.9), нужно, чтобыk удовлетворяло уравнению (6.11).
Пусть k1 иk2 — корни характеристического уравнения (6.11), т.е.
|
|
|
|
| k | = | −a ± | a | 2 | −4a | 2 . |
|
|
|
|
|
| ||
|
|
|
|
| 1 | 1 |
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
| 1,2 |
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
Возможны случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
1. Корни k1 иk2 уравнения (6.2.4) действительные и различные, | |||||||||||||||||||
т.е. k1 ≠ k2 | (в этом случае дискриминант D = a 2 − 4a | 2 | > 0 ). | ||||||||||||||||
Тогда формула (6.10) даст два частных решения: |
| 1 |
|
|
| ||||||||||||||
|
|
|
|
|
| ||||||||||||||
|
|
|
|
| y = ek1x , y | 2 | = ek2 x. |
|
|
|
|
|
| ||||||
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| |
Эти частные решения образуют фундаментальную систему решений | |||||||||||||||||||
уравнения (6.9), так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
| y2 | = e(k2 −k1 ) x ≠C | (т.к. k≠ k | 2 | ) . |
|
|
| |||||||||
|
|
|
|
|
| ||||||||||||||
|
|
| y1 |
|
|
|
|
|
|
| 1 |
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Следовательно, общее решение уравнения (6.9) будет иметь вид | |||||||||||||||||||
|
|
|
|
|
| y = C ek1x | + C | ek2 x. |
|
|
|
|
| (6.12) | |||||
|
|
|
|
|
|
| 1 |
|
| 2 |
|
|
|
|
|
|
|
|
|
Пример. | Решить уравнение | y′′+3y′+2 y =0 . |
|
|
|
|
|
| |||||||||||
Решение. | Это ЛОДУ второго порядка. | Составим характеристическое | |||||||||||||||||
уравнение: |
|
|
|
|
| k 2 +3k +2 =0. |
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
Находим его корни: | k1=-2,k2=-1. |
|
|
|
|
|
|
|
|
|
|
|
| ||||||
Частные решения имеют вид | y = e−2x , y | 2 | = e−x . |
|
|
|
|
| |||||||||||
| y = С1e-2x+С2e-x |
| 1 |
|
|
|
|
|
|
|
|
|
|
| |||||
Тогда | будет общим решением. |
|
|
|
|
| |||||||||||||
Ответ: y = С1e-2x+С2e-x. | ■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
2.Корни характеристического уравнения (6.11) действительные и | |||||||||||||||||||
равные, т. е. | k1 =k2 =k. |
|
|
|
|
|
|
|
|
| a1 |
|
|
| |||||
В этом случае | D = a2 − 4a | = 0 и | k1 = k2 = k= − | . |
|
| |||||||||||||
|
|
| |||||||||||||||||
|
| 1 |
| 2 |
|
|
|
|
|
|
|
| 2 |
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
В данном случае формула | (6.10) дает | нам одно частное решение | |||||||||||||||||
y1 = ek x . Остается найти другое частное решениеy2, образующее вместе с решениемy1 фундаментальную систему решений уравнения (6.9).
Покажем, что таким решением будет функция вида y2 = xek x .
y = eαx (Ccos βx+ C | 2 | sin βx ) | (6.14) | |
1 |
|
|
| |
есть общее решение уравнения (6.9). |
|
|
| |
Пример. Решить уравнение | y′′+2 y′+2 y =0 . |
| ||
Решение. Это ЛОДУ второго порядка. Составим характеристическое | ||||
уравнение: |
|
|
|
|
k 2 +2k +2 =0. |
| |||
Его корни: k1 = −1 +i ,k2 = −1 −i . |
|
|
| |
В данном примере α = −1, | β =1. |
|
|
|
Пользуясь формулой (6.14), получим общее решение:
y = e−x (C1 cos x + C2 sin x). Ответ:y = e−x (C1 cos x + C2 sin x). ■
4. Рассмотрим уравнение (6.8):
y(n) +a1 y(n−1) +a2 y(n−2) +… +an−1 y′+an y =0 . |
|
|
|
|
|
|
| ||||||||||||||||||||
Составим для него характеристическое уравнение: |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
| k n + a kn−1 + a | 2 | k n−2 +….+ a | n |
| k + a | n | = 0 . |
|
| (6.15) | ||||||||||||||||
|
|
| 1 |
|
|
|
|
|
|
|
| −1 |
|
| k1,k2,k3…,kn. | ||||||||||||
Пусть уравнение (6.2.8) имеет n | различных корней |
| |||||||||||||||||||||||||
Если, кроме того, все |
| n | корней — действительные, то |
|
|
|
|
|
|
|
|
|
| ||||||||||||||
| y =C ek1x + C | 2 | ek2 x+ C ek3 x+… + C | n | ekn x |
|
| (6.16) | |||||||||||||||||||
|
|
| 1 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
| |||
есть общее решение уравнения (6.8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
Если же среди корней есть комплексный корень | k1 =α+iβ, | β ≠ 0 , | |||||||||||||||||||||||||
то уравнение | (6.15) |
| имеет |
| также сопряженный | комплексный | корень | ||||||||||||||||||||
k2 =α−iβ. | Этой паре комплексных корней соответствуют два частных | ||||||||||||||||||||||||||
решения: |
|
| = eαx cosβx |
|
|
| = eαx |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
| y |
|
| и y | 2 | sin βx . |
|
|
|
|
|
|
| ||||||||||||||
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
| k3,k4,k5…,kn | — | |||||||||||
и в этом случае (в предположении, что корни | |||||||||||||||||||||||||||
действительные и различные) общее решение уравнения (6.8) имеет вид |
| ||||||||||||||||||||||||||
y = eαx (Ccos βx+ C | 2 | sin βx)+С ek3 x + C | 4 | ek4 x +…+ C | n | xkn x. |
| ||||||||||||||||||||
| 1 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
Пусть теперь корни | k1,k2,k3…,kn — | действительные, но k1=k2=k3, | |||||||||||||||||||||||||
а числа k4, k5, k6…,kn | различны между собой и не совпадают с | k1. | В | ||||||||||||||||||||||||
этом случае, говорят, что | k1 — корень кратности 3. |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
Общее решение имеет вид |
|
|
|
|
| ek4 x+ C ek5 x |
|
|
|
|
|
| ekn x. |
|
| ||||||||||||
y = ek1x (C+ C | 2 | x + C x2 ) + C | 4 | +…+ C | n |
|
| ||||||||||||||||||||
| 1 |
| 3 |
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Рассмотрим ещё случай, когда есть кратные комплексносопряженные
корни k1 = k2 =α +iβ , | k3 = k4 =α −iβ ,β ≠ 0 , а остальные корни | ||||||||||||||||||
k5,k6…,kn | действительные и различные. Общее решение в этом случае | ||||||||||||||||||
имеет вид | y = eαx [(C+C |
| x)cos βx+ (C+C |
| x) sinβx] |
| |||||||||||||
| 2 | 4 | + | ||||||||||||||||
|
|
| 1 |
|
|
|
|
|
| 3 |
|
|
|
|
|
| |||
|
| + C ek5 x +C | ek6 x | +…+ C | ekn x. |
|
| ||||||||||||
|
|
| 5 |
|
|
|
|
| 6 |
|
| n |
|
|
|
|
|
|
|
Пример 1. | Решить уравнение | yIV −13y′′+36y = 0. |
| ||||||||||||||||
Решение. | Это | ЛОДУ четвертого порядка. Составим | |||||||||||||||||
характеристическое уравнение: |
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
| k 4 −13k 2 +36= 0. |
|
|
|
|
| |||||||||
Находим корни этого уравнения: k1 = 2 ,k2 = −2 , | k3 =3, k4 = −3. | ||||||||||||||||||
Частные решения будут иметь вид |
|
|
|
|
|
|
|
|
| ||||||||||
|
| y = e2 x , y | 2 | = e−2 x , | y = e3x | , y | 4 | = e−3x . | |||||||||||
|
| 1 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| ||
Тогда |
| y = C e2 x + C | e−2x + C e3x + C | e−3x | будет общим | ||||||||||||||
|
|
| 1 |
|
|
|
| 2 |
|
| 3 |
|
| 4 |
|
|
|
| |
решением | уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Ответ: | y = C e2 x | + C | e−2x + C e3x | + C | e−3x. |
| ■ |
|
| ||||||||||
|
| 1 | 2 |
|
|
|
|
|
| 3 | 4 |
|
|
|
|
|
|
|
|
Пример 2. Решить уравнение | y′′′+y′′−5y′+3y =0. |
| |||||||||||||||||
Решение. | Это ЛОДУ третьего порядка. Составим характеристическое | ||||||||||||||||||
уравнение: |
|
|
| k3 +k 2 −5k +3 =0 . |
|
|
|
|
|
| |||||||||
Его корни: k1 = k2 =1,k3 = −3.
Следовательно, частные решения будут иметь вид:
|
|
|
| y = ex , y | 2 | = xex , y= e−3x . |
| ||
|
|
|
|
| 1 |
| 3 |
| |
Тогда y = C ex + C | 2 | xex + C e−3x | будет общим решением уравнения. | ||||||
1 |
|
| 3 |
|
|
|
| ||
Ответ: y = C ex +C | 2 | xex +C e−3x . | ■ |
| |||||
1 |
|
| 3 |
|
|
|
| ||
Пример 3. Решить уравнение |
| yIV +8y′′+16 y =0. | |||||||
Решение. Это ЛОДУ четвертого порядка. |
| ||||||||
Составим характеристическое уравнение: k 4 +8k 2 +16 = 0 или | |||||||||
|
|
|
|
| (k 2 + 4)2 = 0. |
| |||
Найдем его корни: |
|
| k1 = k2 = 2i, | k3 =k4 = −2i . | То есть в нашем | ||||
примере α = 0, β = 2, а кратность корня равна двум. |
| ||||||||
Тогда общее решение: | +C2 x)cos 2x + (C3 +C4 x)sin 2x . | ||||||||
y = (C1 | |||||||||
Ответ: y= (C1 +C2 x)cos 2x+ (C3 +C4 x)sin 2x. | ■ | ||||||||
studfiles.net
2.4. Структура общего решения лоду 2-го порядка
Теорема. Если 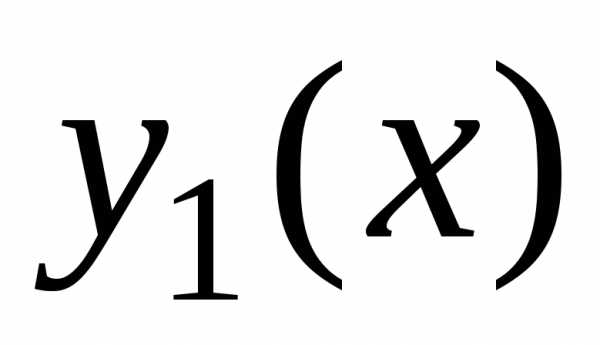 и
и –
линейно независимые решения линейного
однородного дифференциального уравнения
(2.3), то их линейная комбинация,
где
–
линейно независимые решения линейного
однородного дифференциального уравнения
(2.3), то их линейная комбинация,
где и
и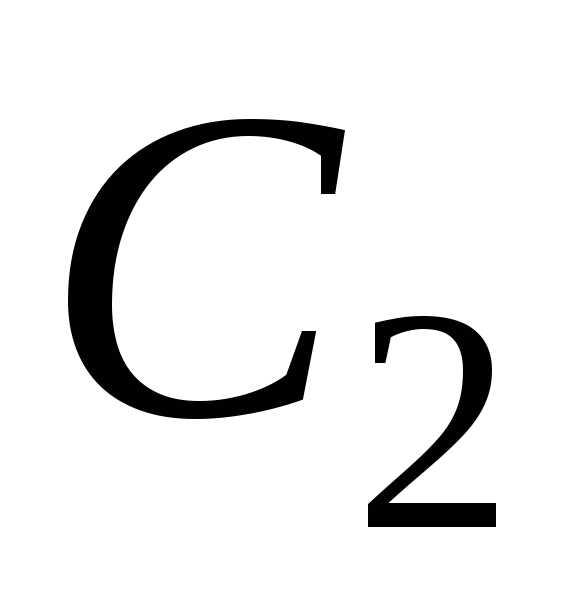 – произвольные
постоянные, является общим решением
этого уравнения.
– произвольные
постоянные, является общим решением
этого уравнения.
В данном случае
говорят, что функции  и
и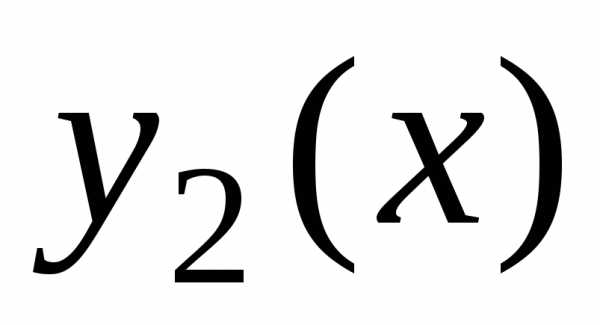 образуют фундаментальную систему решений ЛОДУ (2.3).
образуют фундаментальную систему решений ЛОДУ (2.3).
Доказательство. Первая часть
утверждения, касающаяся того, что
есть
решение уравнения (2.3), следует из теоремы
о свойствах решений ЛОДУ 2-го порядка.
Остаётся показать, что решениебудетобщим,
то есть надо показать, что при любых
начальных условиях
,можно выбрать произвольные постоянные и
и так, чтобы
удовлетворить этим условиям. Запишем
начальные условия в виде:
так, чтобы
удовлетворить этим условиям. Запишем
начальные условия в виде:
Постоянные 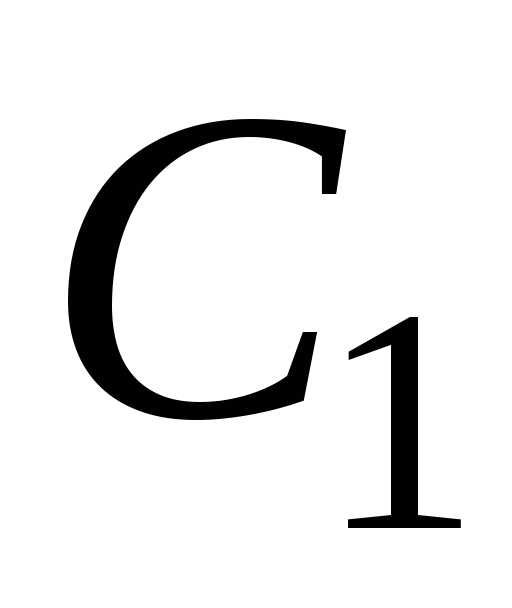 и
и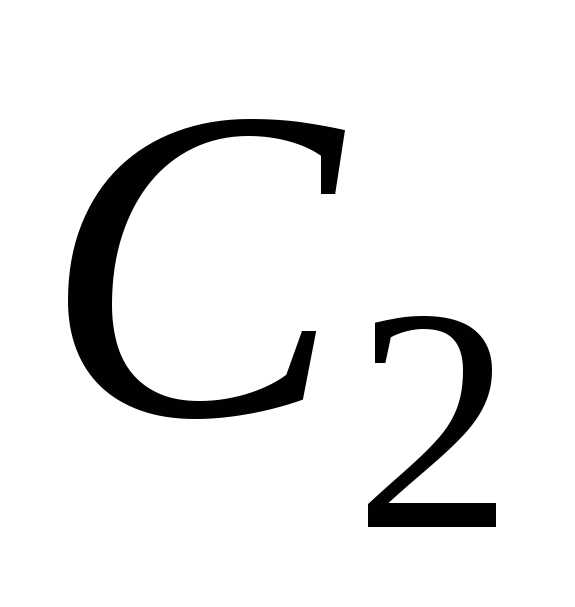 из этой
системы линейных алгебраических
уравнений определяются однозначно, так
как определитель этой системы
из этой
системы линейных алгебраических
уравнений определяются однозначно, так
как определитель этой системы  есть значение определителя Вронского
для линейно независимых решений ЛОДУ
при
есть значение определителя Вронского
для линейно независимых решений ЛОДУ
при :
:
,
а такой определитель, как было показано в предыдущем параграфе, отличен от нуля. Теорема доказана.
Пример. Доказать, что функция
,
где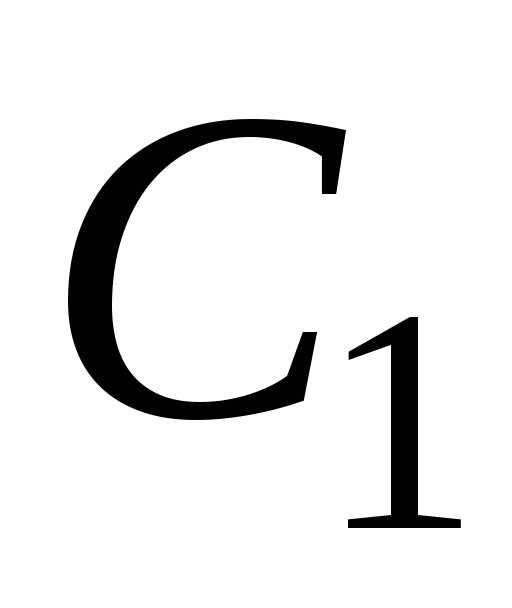 и
и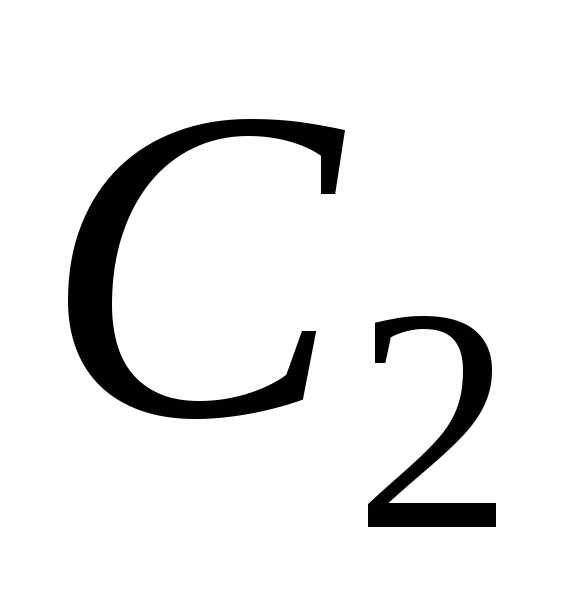 – произвольные
постоянные, является общим решением
ЛОДУ
– произвольные
постоянные, является общим решением
ЛОДУ
Решение. Легко
убедиться непосредственной подстановкой,
что функции  и удовлетворяют данному уравнению. Эти
функции являются линейно независимыми,
так как
и удовлетворяют данному уравнению. Эти
функции являются линейно независимыми,
так как .
Поэтому согласно теореме о структуре
общего решения ЛОДУ 2-го порядка функция
является общим решением данного
уравнения.
.
Поэтому согласно теореме о структуре
общего решения ЛОДУ 2-го порядка функция
является общим решением данного
уравнения.
2.5. Лоду 2-го порядка с постоянными коэффициентами
Рассмотрим ЛОДУ 2-го порядка с постоянными коэффициентами
(5.1),
где .
Согласно предыдущему
параграфу общее решение ЛОДУ 2-го порядка
легко определяется, если известны два
линейно независимых частных решения
этого уравнения. Простой метод нахождения
частных решений уравнения с постоянными
коэффициентами предложил Л. Эйлер. Это
метод, который называется методом
Эйлера,
состоит в том, что частные решения ищутся
в виде  .
Подставляя эту функцию в уравнение
(5.1), после сокращения на
.
Подставляя эту функцию в уравнение
(5.1), после сокращения на ,
получим алгебраическое уравнение,
которое называетсяхарактеристическим:
,
получим алгебраическое уравнение,
которое называетсяхарактеристическим:
(5.2)
Функция будет
решением уравнения (5.1) только при тех
значениях  ,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта
,
которые являются корнями характеристического
уравнения (5.2). В зависимости от величины
дискриминанта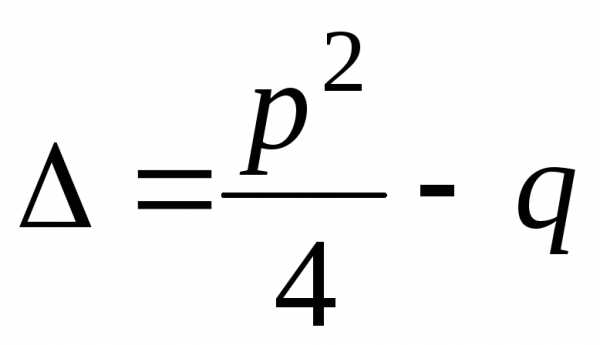 возможны три случая.
возможны три случая.
 .
Тогда корни характеристического
уравнения различны:
.
Тогда корни характеристического
уравнения различны:  .
Решения
.
Решения и
и будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
.
будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
. .
В этом случае
.
В этом случае  и
и .
В качестве второго линейно независимого
решения можно взять функцию
.
В качестве второго линейно независимого
решения можно взять функцию .
Проверим, что эта функция удовлетворяет
уравнению (5.1).
.
Проверим, что эта функция удовлетворяет
уравнению (5.1).
Действительно,
,
.
Подставляя эти выражения в уравнение (5.1), получим
или
,
так как 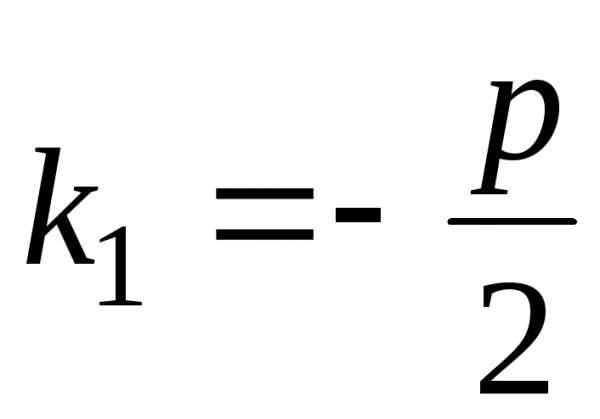 и.
и.
Частные решения 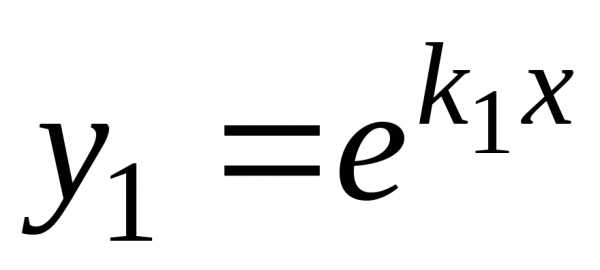 и
и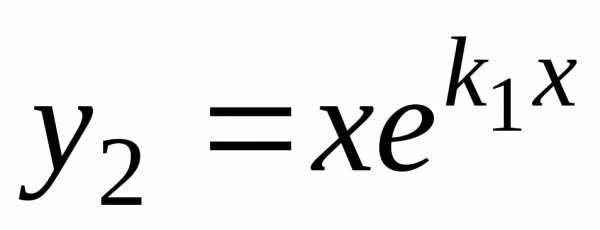 линейно независимы, так как
линейно независимы, так как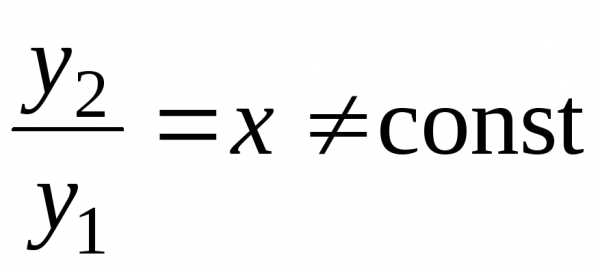 .
Следовательно, общее решение уравнения
(5.1) имеет вид:
.
Следовательно, общее решение уравнения
(5.1) имеет вид:
или .
 .
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где
.
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где ,
, .
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция
.
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция  .
.
Действительно,
,
.
Подставив эти выражения в уравнение (5.1), получим
.
Выражения в обеих скобках в левой части этого равенства тождественно равны нулю. Действительно,
,
.
Таким образом,
функция
удовлетворяет уравнению (5.1). Аналогично
нетрудно убедиться в том, что иесть решение уравнения (5.1). Поскольку ,
то общее решениебудет иметь вид:
,
то общее решениебудет иметь вид:
.
studfiles.net

 .
Тогда корни характеристического
уравнения различны:
.
Тогда корни характеристического
уравнения различны: 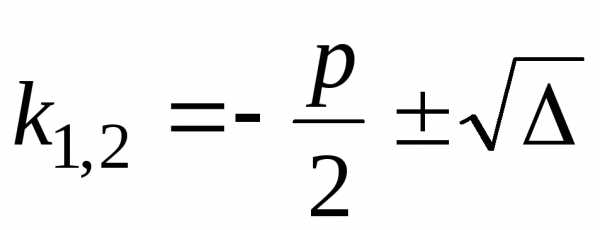 .
Решения
.
Решения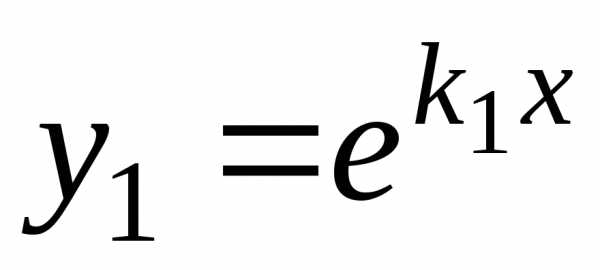 и
и будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
.
будут линейно независимыми, так как
и общее решение уравнения (5.1) можно
записать в виде
.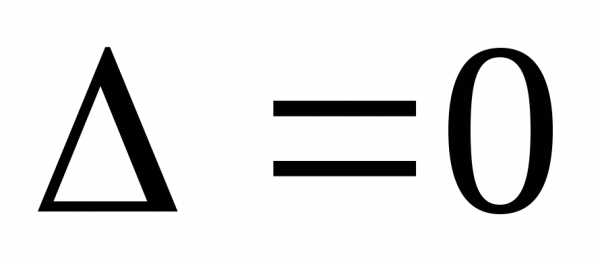 .
В этом случае
.
В этом случае 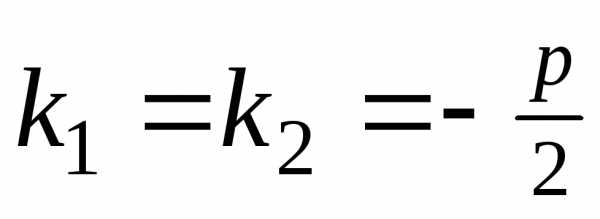 и
и .
В качестве второго линейно независимого
решения можно взять функцию
.
В качестве второго линейно независимого
решения можно взять функцию .
Проверим, что эта функция удовлетворяет
уравнению (5.1).
.
Проверим, что эта функция удовлетворяет
уравнению (5.1). .
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где
.
В данном случае корни характеристического
уравнения комплексно-сопряжены:
,
где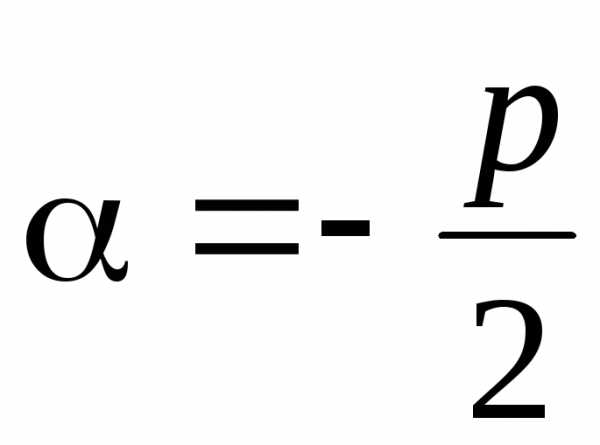 ,
,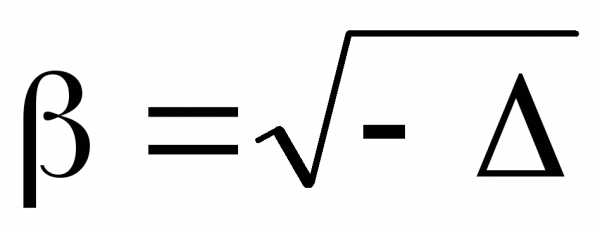 .
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция
.
Легко проверить, что линейно независимыми
решениями уравнения (5.1) будут функциии
.
Убедимся, что уравнению (5.1) удовлетворяет,
например, функция  .
.