К 1 квадратичная функция – Парабола, квадратичная функция. Как решаются квадратные уравнения?

3.3.3 Квадратичная функция, её график

Видеоурок 1: Квадратичная функция. Часть 1

Видеоурок 2: Квадратичная функция. Часть 2

Видеоурок 3: Построение графика квадратичной функции

Лекция: Квадратичная функция, её график

Квадратичная функция

Если перед Вами появилась функция вида у = ах² + bx + c, то такая функция будет иметь название квадратичной. 

Обратите внимание, функция будет квадратичной только в том случае, если коэффициент а ≠ 0.

Итак, в данной функции а, b и с — это коэффициенты:

• а — коэффициент при старшем члене,

• b — второй коэффициент,

• с — свободных член.

Любая квадратичная функция на координатной плоскости изображается в виде параболы, однако функция у = х² имеет вид:

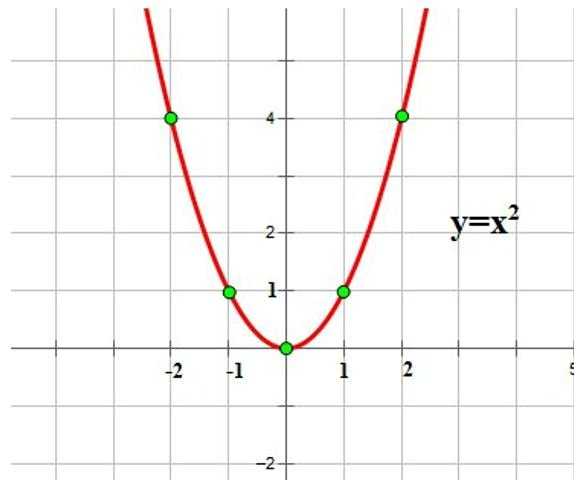
При с = 0 график всегда начинается в начале координат, а остальные 4 точки определяются самостоятельно:

Если коэффициент а < 0, то данный график будет иметь немного другой вид — ветки параболы будут направлены вниз:

Характеристика функции у = х²

1. Область значения функции — существует для всех действительных чисел.

2. Область значения функции — функция не может принимать отрицательные значения.

3. Парная функция, симметрична относительно оси ОУ.

4. Монотонно убывает на промежутке от минус бесконечности до нуля, монотонно возрастает на промежутке от нуля до бесконечности.

5. Минимум функции на все рассматриваемом промежутке в точке [0; 0].

Решение квадратного уравнения

Как мы знаем, при решении квадратного уравнения может существовать несколько случаев, которые влияют на количество корней. Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.

1. Если мы имеем уравнение вида у = ах² + bx + c, то решая его по дискриминанту, можем получить D < 0. С точки зрения графика квадратичной функции это значит, что вершина параболы находится над осью ОХ, а её ветки направлены вверх. Именно из-за того, что не существует пересечения с осью ОХ, решений данное уравнение не имеет.

2. Если дискриминант равен нулю D = 0, то это означает, что уравнение имеет один корень. Следовательно, на графике это можно показать в качестве вершины, которая лежит на оси ОХ.

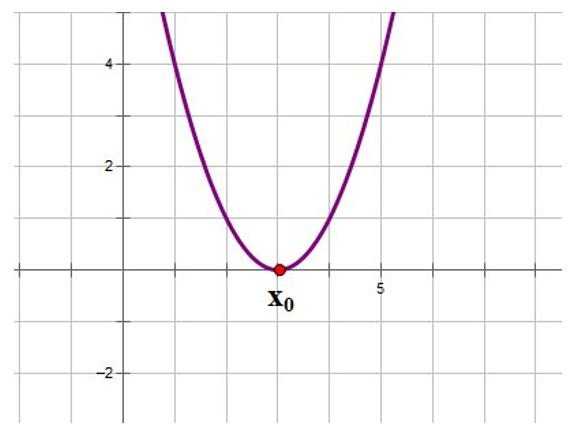
3. Если дискриминант больше нуля D > 0, это значит, что уравнение имеет два корня. На графике это можно показать, как пересечение оси ОХ ветвями параболы.

Алгоритм построения квадратичной функции

Давайте рассмотри алгоритм построение параболы по квадратичной функции на примере следующей функции: у = 2х² + 3х — 5.

1. Первым делом следует определиться с направлением ветвей параболы. Для этого необходимо обратить внимание на коэффициент, который стоит перед старшим членом. Если коэффициент положительный, то ветви параболы направлены вверх. Следовательно, 2 > 0, а значит, в нашей функции ветви параболы направлены вверх.

2. Дальше следует приравнять функцию к нулю для нахождения дискриминанта. В данном получившемся уравнении дискриминант больше нуля, а это значит, что мы будем иметь два решения, а значит, два пересечение графика с осью ОХ.

3. Теперь давайте определим, в каких точках график будет пересекать ось ОХ. Для этого необходимо решить получившееся уравнение.

В данном случае мы получили корни:

х₁ = 1, х₂ = -2,5.

4. Находим координату вершины параболы. Для этого необходимо воспользоваться формулой:

5. Еще дополнительные две симметричные точки находятся через подстановку вместо «х» нуля. В нашем уравнении мы получили, что при х = 0, у = -5.

6. А теперь нанесем вершину, точки пересечения с осью ОХ и ОУ на график. В результате этого получим:

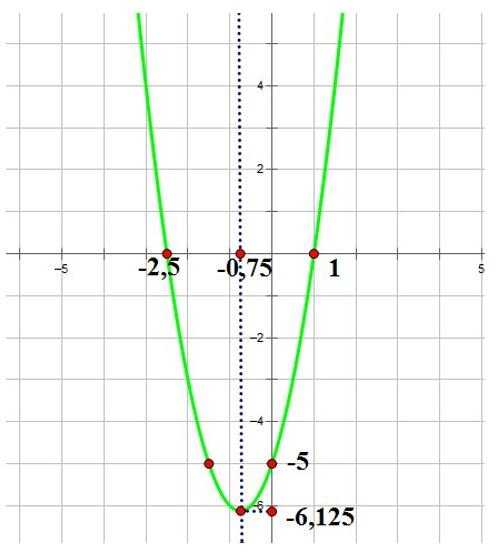
cknow.ru

Квадратичная функция

Квадратичная функция

Учитель: Иванова Ольга Николаевна

МКОУ « Горбуновская СОШ»

Свердловская область

Талицкий район

1.Построить таблицу значений .

(берём любое значение переменной Х и считаем У= Х*Х).

2. Построить на координатной плоскости точки с данными координатами

( 1;1), (2;4), (3;9), ( 4;16) (0;0), (-1;1), (-2;4),(-3;9), (-4;16).

3. Соединить полученные точки плавной линией .

Полученный график функции называется ПАРАБОЛОЙ.

х

1

у

1

2

3

4

9

4

0

16

0

-1

-2

1

4

-3

-4

9

16

0 — возрастающей . При х=0 функция принимает своё наименьшее значение . «

Основные свойства графика функции

• Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат выше оси абсцисс (Ох) – ветви параболы направлены вверх.
• График функции симметричен относительно оси ординат ( Оу) : например, у(-2) = у(2) = 4. Точку пересечения параболы с её осью симметрии называют вершиной параболы.
• При х функция является убывающей , при х 0 — возрастающей . При х=0 функция принимает своё наименьшее значение .

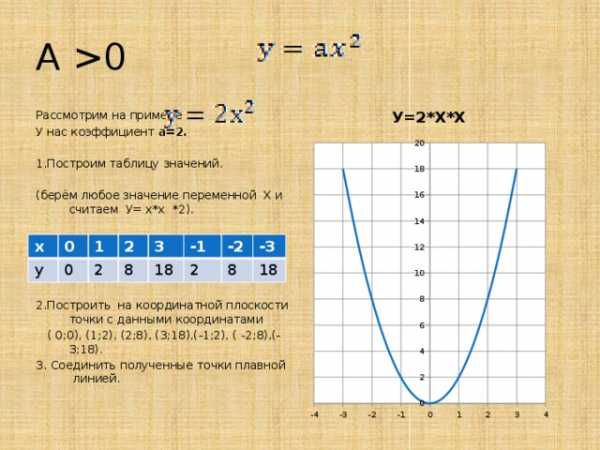0 Рассмотрим на примере У нас коэффициент а=2. 1.Построим таблицу значений. (берём любое значение переменной Х и считаем У= х*х *2). 2.Построить на координатной плоскости точки с данными координатами ( 0;0), (1;2), (2;8), (3;18),(-1;2), ( -2;8),(-3;18). 3. Соединить полученные точки плавной линией. х 0 у 1 0 2 2 3 8 18 -1 -2 2 -3 8 18 «

A 0

Рассмотрим на примере

У нас коэффициент а=2.

1.Построим таблицу значений.

(берём любое значение переменной Х и считаем У= х*х *2).

2.Построить на координатной плоскости точки с данными координатами

( 0;0), (1;2), (2;8), (3;18),(-1;2), ( -2;8),(-3;18).

3. Соединить полученные точки плавной линией.

х

0

у

1

0

2

2

3

8

18

-1

-2

2

-3

8

18

А

Рассмотрим на примере

У нас коэффициент а = — 2.

1.Построим таблицу значений.

(берём любое значение переменной Х и считаем У= х*х *( -2).

2.Построить на координатной плоскости точки с данными координатами

( 0;0), (1;-2), (2;-8), (3;-18),(-1;-2), ( -2;-8),(-3;-18).

3. Соединить полученные точки плавной линией.

х

0

у

1

0

2

-2

3

-8

-1

-18

-2

-2

-3

-8

-18

0 Графиком функции является парабола. Графиком функции является парабола. Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат ниже оси абсцисс (Ох) – ветви параболы направлены вниз . График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = -18. При х функция является возрастающей , при х 0 — . При х=0 функция принимает своё наибольшее значение ( У max). Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат выше оси абсцисс (Ох) – ветви параболы направлены вверх. График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = 18. При х функция является убывающей , при х 0 — возрастающей . При х=0 функция принимает своё наименьшее значение ( У min). Растяжение вдоль оси Оу при Сжатие к оси Ох при Растяжение вдоль оси Оу при Сжатие к оси Ох при «

Свойства функции

При а

При а 0

• Графиком функции является парабола.

• Графиком функции является парабола.

• Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат ниже оси абсцисс (Ох) – ветви параболы направлены вниз .
• График функции симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = -18.
• При х функция является возрастающей , при х 0 — . При х=0 функция принимает своё наибольшее значение ( У max).

• Парабола проходит через начало координат ( 0;0), а остальные точки параболы лежат выше оси абсцисс (Ох) – ветви параболы направлены вверх.
• График функции
  симметричен относительно оси ординат ( Оу) : например, у(-3) = у(3) = 18.
• При х функция является убывающей , при х 0 — возрастающей . При х=0 функция принимает своё наименьшее значение ( У min).

• Растяжение вдоль оси Оу при
• Сжатие к оси Ох при

• Растяжение вдоль оси Оу при
• Сжатие к оси Ох при

0, то найти корни квадратного трёхчлена по формуле 4. Найти точку пересечения параболы с осью Оу : при х=0, у = С , т.е. ( 0;С). Найти дополнительные точки параболы ( если D Все точки и им симметричные, не забываем отмечать на координатной плоскости. Соединим все отмеченные точки плавной линией — получим график квадратичной функции – параболу. «

Функция

Общая схема построения:

• Найти координаты вершины параболы ( ), где

• Отметить данную точку на координатной плоскости и провести через неё прямую, параллельную Оу – ось симметрии параболы.
• Найти точки пересечения параболы с осью Ох ( если они есть), т.е. найти D и если D 0, то найти корни квадратного трёхчлена по формуле

4. Найти точку пересечения параболы с осью Оу : при х=0, у = С , т.е. ( 0;С).

• Найти дополнительные точки параболы ( если D
• Все точки и им симметричные, не забываем отмечать на координатной плоскости.
• Соединим все отмеченные точки плавной линией — получим график квадратичной функции – параболу.

0, т.е. ( ½;0) и ( 1;0). «

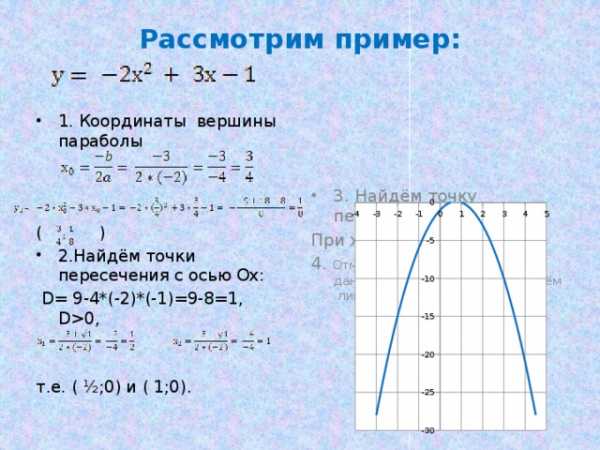
Рассмотрим пример:

• 3. Найдём точку пересечения с осью Оу:

• 1. Координаты вершины параболы

При х=0 у=-1, т.е. ( 0;-1).

4. Отметим точки симметричные данным на плоскости и проведём линию, получим параболу:

( )

• 2.Найдём точки пересечения с осью Ох:

D= 9-4*(-2)*(-1)=9-8=1, D0,

т.е. ( ½;0) и ( 1;0).

0 , то ветви параболы направлены вверх , функция принимает наименьшее значение в абсциссе вершины параболы. Если а ветви параболы направлены вниз , функция принимает наибольшее значение в абсциссе вершины параболы. Ось симметрии параболы – прямая, параллельная оси ординат ( Оу) и проходящая через вершину параболы . Область определения функции – вся числовая ось ( Ох), т.е. х – любое число. Если D = 0 , то парабола имеет с осью Ох всего одну общую точку касания – абсцисса вершины. Если D 0 , то парабола пересекает ось Ох в двух точках ( корни квадратного трёхчлена). Если D , то парабола с осью Ох не пересекается , т.е. находится выше или ниже оси, в зависимости от направления ветвей. «

Основные свойства квадратичной функции

1. Графиком функции является парабола:

Если а 0 , то ветви параболы направлены вверх , функция принимает наименьшее значение в абсциссе вершины параболы.

Если а ветви параболы направлены вниз , функция принимает наибольшее значение в абсциссе вершины параболы.

• Ось симметрии параболы – прямая, параллельная оси ординат ( Оу) и проходящая через вершину параболы .
• Область определения функции – вся числовая ось ( Ох), т.е. х – любое число.
• Если D = 0 , то парабола имеет с осью Ох всего одну общую точку касания – абсцисса вершины.
• Если D 0 , то парабола пересекает ось Ох в двух точках ( корни квадратного трёхчлена).
• Если D , то парабола с осью Ох не пересекается , т.е. находится выше или ниже оси, в зависимости от направления ветвей.

Домашнее задание

• Выучить все основные свойства квадратичной функции

• Построить графики:

№ 624, 625

любые 2 на выбор.

• с.173 – « Проверь себя!»

videouroki.net

Квадратичная функция Википедия

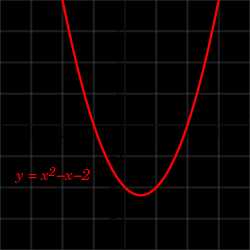График функции f(x)=x2−x−2{\displaystyle f(x)=x^{2}-x-2} Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола.

Квадратичная функция — целая рациональная функция второй степени вида f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c}, где a≠0{\displaystyle a\neq 0} и a,b,c∈R{\displaystyle a,b,c\in \mathbb {R} }. Уравнение квадратичной функции содержит квадратный трёхчлен. Графиком квадратичной функции является парабола. Многие свойства графика квадратичной функции так или иначе связаны с вершиной параболы, которая во многом определяет положение и внешний вид графика.

Содержание

• 1 Обзор основных свойств
• 2 Влияние коэффициентов на трансформацию графика
  • 2.1 Стандартная запись уравнения квадратичной функции
  • 2.2 Запись квадратичной функции через координаты вершины параболы
• 3 Нули функции
  • 3.1 Число нулей квадратичной функции
  • 3.2 Методы вычисления нулей квадратичной функции
• 4 Чётность и симметрия квадратичной функции
  • 4.1 Симметрия относительно оси ординат
  • 4.2 Осевая симметрия в общем случае
  • 4.3 Вычисление вершины параболы с помощью нулей функции
• 5 Исследование методами дифференциального и интегрального анализа
  • 5.1 Производная и первообразная
  • 5.2 Монотонность и точки экстремума
  • 5.3 Выпуклость и точки перегиба
  • 5.4 Обратимость квадратичной функции
• 6 Примеры появления на практике
• 7 Обобщение
• 8 См. также
• 9 Примечания
• 10 Литература

Обзор основных свойств[ | ]

Многие свойства квадратичной функции f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c} зависят от значения

ru-wiki.ru