Свойства квадратного корня, урок по алгебре в 8 классе, презентация, формулы и примеры
Дата публикации: .
Урок и презентация на тему:
«Свойства квадратного корня. Формулы. Примеры решений, задачи с ответами»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Свойства квадратных корней (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Интерактивное учебное пособие «Геометрия за 10 минут» для 8 класса
Свойства квадратного корня
Мы продолжаем изучать корни квадратные. Сегодня рассмотрим основные свойства корней. Все основные свойства интуитивно понятны и согласуются со всеми операциями, которые мы проводили раньше.
2$. Если квадраты двух неотрицательных чисел равны, то значит и сами числа равны, что и требовалось доказать.Из нашего свойства следует, что, например, $\sqrt{5}*\sqrt{3}=\sqrt{15}$.
Замечание 1. Свойство справедливо и для случая, когда под корнем более двух неотрицательных множителей.
Свойство 2. Если $а≥0$ и $b>0$, то справедливо следующее равенство: $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
То есть корень из частного равен частному корней.
Доказательство.
Воспользуемся таблицей и кратко докажем наше свойство.
Примеры использования свойств квадратных корней
Пример 1.
Вычислить: $\sqrt{81*25*121}$.
Решение.
Конечно, мы можем взять калькулятор, перемножить все числа под корнем и выполнить операцию извлечения корня квадратного. А если под рукой нет калькулятора, как быть тогда?
$\sqrt{81*25*121}=\sqrt{81}*\sqrt{25}*\sqrt{121}=9*5*11=495$.
Ответ: 495.
Пример 2. Вычислить: $\sqrt{11\frac{14}{25}}$.
4. Вычислить:
а) $\sqrt{128*\sqrt{8}}$;
б) $\frac{\sqrt{128}}{\sqrt{8}}$.
Действия с квадратными корнями. Модуль
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение , деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т. д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
Доказательство. Введем следующие обозначения:https://pandia.ru/text/78/290/images/image005_28.jpg» alt=»Равенство»Задание»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Интерактивное учебное пособие «Геометрия за 10 минут» для 8 класса
Образовательный комплекс «1С: Школа.
2$. Если квадраты двух неотрицательных чисел равны, то значит и сами числа равны, что и требовалось доказать.Из нашего свойства следует, что, например, $\sqrt{5}*\sqrt{3}=\sqrt{15}$.
Замечание 1. Свойство справедливо и для случая, когда под корнем более двух неотрицательных множителей.
Свойство 2. Если $а≥0$ и $b>0$, то справедливо следующее равенство: $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
То есть корень из частного равен частному корней.
Доказательство.
Воспользуемся таблицей и кратко докажем наше свойство.
Примеры использования свойств квадратных корней
Пример 1.
Вычислить: $\sqrt{81*25*121}$.
Решение.
Конечно, мы можем взять калькулятор, перемножить все числа под корнем и выполнить операцию извлечения корня квадратного. А если под рукой нет калькулятора, как быть тогда?
Ответ: 495.
Пример 2.
2}$.
4. Вычислить:
а) $\sqrt{128*\sqrt{8}}$;
б) $\frac{\sqrt{128}}{\sqrt{8}}$.
Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике.
Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению.
На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным. Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю.
Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Следующее нечетное число — это 11, остаток у нас следующий: 1
Для таких случаев существует разложение в ряд Тейлора:
√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений.
Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Квадратные корни – объяснение и примеры
В математике квадратный корень из числа x таков, что число y является квадратом x, упрощенно записывается как y 2 = x.
Например, 5 и – 5 являются квадратными корнями из 25, потому что:
5 x 5 = 25 и -5 x -5 = 25.
Квадратный корень из числа x обозначается знаком корня √x или x 1/2 . Например, квадратный корень из 16 представлен как: √16 = 4. Число, квадратный корень которого вычисляется, называется подкоренным числом. В этом выражении √16 = 4 число 16 является подкоренным числом.
Что такое квадратный корень?
Квадратный корень — это операция, обратная возведению числа в квадрат. Другими словами, квадратный корень — это операция, которая отменяет показатель степени 2.
Свойства
- Совершенное квадратное число имеет совершенный квадратный корень.
- Четное совершенное число имеет четный квадратный корень.
- Нечетное совершенное число имеет нечетный квадратный корень.
- Квадратный корень из отрицательного числа не определен.
- Только числа, заканчивающиеся четным числом нулей, имеют квадратный корень.
Как найти квадратный корень из чисел?
Есть несколько способов найти квадрат чисел.
Мы увидим несколько здесь.
Повторное вычитание
Этот метод включает успешное и многократное вычитание нечетных чисел, таких как 1, 3, 5 и 7, из числа до тех пор, пока не будет достигнут ноль. Квадрат числа равен количеству или частоте вычитания числа
Предположим, нам нужно вычислить квадрат совершенного числа, такого как 25, операция выполняется как:
| 25 -1 | = 24 |
| 24 -3 | = 21 |
| 21 -5 | = 16 |
| 16 – 7 | = 9 |
| 9 – 9 | = 0 |
Вы можете заметить, что частота вычитания равна 5, поэтому квадратный корень из 25 равен 5. последовательное деление. Простые множители группируются в пары, и вычисляется произведение каждого числа. Таким образом, произведение равно квадратному корню из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполняется как:
- 144 = 2 × 2 × 2 × 2 × 3 × 3.
- Соедините простые множители.
- Выбор одного числа из каждой пары.
- 2 × 2 × 3 = 12.
- Таким образом, √144 = 12.
Метод деления
Метод деления является подходящим методом вычисления квадрата большого числа. Ниже приведены необходимые шаги:
- Над каждой парой цифр, начиная с правой стороны, ставится черта.
- Разделить левое число на число, квадрат которого меньше или эквивалентен числам под левым концом.
- Возьмите это число как делитель и частное. Точно так же возьмите самое левое число в качестве делимого
- Разделите, чтобы получить результат
- Опустите следующее число с чертой справа от остатка
- Умножьте делитель на 2.
- Справа от этого новый делитель, найти подходящее делимое. Этот процесс повторяется до тех пор, пока мы не получим ноль в качестве остатка. Следовательно, квадрат числа равен частному.
Квадратный корень из 225 вычисляется как
- Начинайте деление с крайней левой стороны.
- В данном случае 1 — это наше число, квадрат которого меньше 2.
- Присвоение 1 в качестве делителя и частного и умножение его на 2 дает:
- Выполните шаги, чтобы получить 15 в качестве частного.
Квадратные корни (ответы на 8 часто задаваемых вопросов) – JDM Educational
Квадратные корни используются в математике, от арифметики до алгебры, исчисления и т. д. Они также используются в различных профессиях, от столярных до инженерных. Однако это все еще оставляет некоторые вопросы о квадратных корнях и их свойствах.
Итак, что вам нужно знать о квадратных корнях? Каждое ненулевое число имеет 2 квадратных корня. Каждое положительное число имеет отрицательный квадратный корень. Квадратный корень из отрицательного числа является мнимым. Квадратный корень из комплексного числа является комплексным. Некоторые квадратные корни являются рациональными или целыми числами. Мы можем складывать и умножать квадратные корни, и это может упростить нашу работу.
Конечно, есть случаи, на которые следует обратить внимание при рассмотрении вопросов о квадратных корнях.
В этой статье мы ответим на 8 распространенных вопросов о квадратных корнях. Попутно мы увидим, как квадратные корни связаны с мнимыми и комплексными числами и как их можно комбинировать с помощью сложения или умножения.
Начнем.
8 Общие вопросы о квадратных корнях
После того, как вы узнаете, как вычислять квадратные корни и что они означают, полезно знать ответы на некоторые часто возникающие вопросы.
Вычисление квадратных корней — это одно, но знание ответов на некоторые распространенные вопросы о них поможет вам легче ориентироваться в математике.Распространенный вопрос касается того, сколько ответов возможно при извлечении квадратного корня, поэтому мы начнем с него.
Имеют ли квадратные корни два ответа?
Квадратные корни имеют два ответа: главный квадратный корень и его отрицательный. Единственным исключением является число ноль, которое имеет только один квадратный корень (который равен нулю, поскольку 0 2 = 0).
Если S — главный квадратный корень из N, то N = S 2 . Также должно быть верно, что -S является квадратным корнем из N, поскольку (-S) 2 = (-S)(-S) = S 2 (произведение двух отрицательных чисел является положительным).
Пример 1: Квадратные корни из 4
Из 4 есть два квадратных корня: +2 и -2.
Главный квадратный корень из 4 равен +2. Другой квадратный корень из 4 равен -2 (противоположный или отрицательный +2).
Пример 2: Квадратные корни из 7
Из 7 есть два квадратных корня: √7 и -√7.
Главный квадратный корень из 7 равен +√7. Другой квадратный корень из 7 равен –√7 (противоположный или отрицательный +√7).
Могут ли квадратные корни быть отрицательными?
Квадратный корень из действительного числа может быть отрицательным, как мы видели в приведенных выше примерах.
Фактически, для любого положительного действительного числа существует как положительный квадратный корень (главный квадратный корень), так и отрицательный квадратный корень.
Например, один из квадратных корней из 16 равен -4, что является отрицательным значением.
Однако остается вопрос о действительных числах, которые не являются положительными.
Квадратный корень из нуля равен нулю, который не является ни положительным, ни отрицательным.
Квадратный корень из отрицательного числа не является ни положительным, ни отрицательным, и для этого требуется понятие мнимых чисел.
Имеют ли отрицательные числа квадратные корни?
Отрицательные числа имеют квадратный корень. Они называются мнимыми числами (подробнее о них можно узнать здесь).
Самое простое мнимое число — это квадратный корень из -1, который называется I (что означает «воображаемая единица»). В виде уравнения мы можем записать i = √-1 или i 2 = -1.
Мнимые числа являются подмножеством комплексных чисел и имеют действительную часть нуля.
Для отрицательного числа N мы можем переписать его как -|N|, или «отрицательное значение абсолютного значения N». Тогда квадратный корень из N:
- √N
- = √(-|N|) [N = -|N| поскольку N — отрицательное число]
- =√((-1)(|N|)) [множитель -|N| как -1 раз |N|]
- =√(-1)√(|N|) [поскольку √(ab) = √a√b]
- =i√(|N|) [так как i = √-1]
Пример: корень квадратный из -4
Квадратный корень из -4 равен i√4 или 2i. Мы можем показать это, используя i = √-1, чтобы упростить следующее:
- √-4
- =√((-1)(4)) [множитель -4 как -1 умножить на 4]
- =√(-1) √(4) [так как √(ab) = √a√b]
- =i√(4) [так как i = √-1]
- =i2 поскольку √(4) = 2]
- =2i
Все ли числа имеют квадратные корни?
Все числа имеют квадратный корень, включая все действительные числа, все мнимые числа и все комплексные числа.
Для мнимых и комплексных чисел квадратные корни будут комплексными числами. Для каждого комплексного числа, кроме нуля, есть два различных квадратных корня: главный квадратный корень и его противоположность (отрицательный).
Пример: Квадратный корень из 3 + 4i
Квадратный корень из 3 + 4i равен 2 + i. Мы можем доказать это, используя FOIL следующим образом:
- (2 + I) 2
- = (2 + I) (2 + I)
- = 4 + 2i + 2i + I 2 [Используется FOIL]
- 01013 2 =4 + 4i + i 2 [сочетание подобных членов, 2i + 2i = 4i]
- =4 + 4i – 1 [поскольку i 2 = -1]
- =3 комбинированные подобные термины, 4 – 1 = 3]
Конечно, минус 2 + i также является квадратным корнем из 3 + 4i.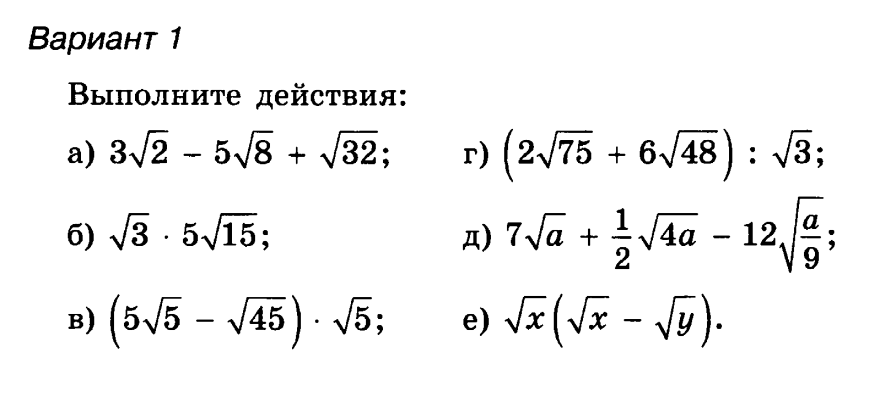
Таким образом, два квадратных корня из 3 + 4i равны 2 + i и -2 – i.
Могут ли квадратные корни быть рациональными числами?
В некоторых случаях квадратные корни могут быть рациональными числами. Нам нужно сделать несколько шагов, чтобы определить это:
- Во-первых, посмотрите на дробь под радикалом (символ квадратного корня).
- Затем максимально уменьшите дробь (это облегчит последующие шаги).
- Затем проверьте, является ли числитель полным квадратом.
- Наконец, проверьте, является ли знаменатель правильным квадратом.
Если и числитель, и знаменатель являются полными квадратами, то квадратный корень из числа рациональный. В противном случае это не так. (Важное примечание: сначала не пропускайте шаг упрощения, иначе вы придете к неправильному выводу!)
Помните, что полный квадрат получается из целого числа (целого числа) в квадрате. Например:
- 1 2 = 1
- 2 2 = 4
- 3 2 102
Давайте рассмотрим несколько примеров, чтобы прояснить эту концепцию.
Пример 1. Число с рациональным квадратным корнем
Допустим, мы хотим выяснить, рационально ли √(16/36).
Сначала возьмем дробь под корнем: 16/36.
Затем уменьшите дробь: 16/36 = 4(4)/4(9) = 4/9 (4 сокращается, так как оно появляется и в числителе, и в знаменателе).
Затем проверьте, является ли числитель полным квадратом: да, поскольку 4 = 2 2 .
Наконец, проверьте, является ли знаменатель полным квадратом: да, поскольку 9 = 3 2 .
Тогда квадратный корень из 16/36 является рациональным: его значение равно 2/3 (после максимально возможного уменьшения 4/6).
Пример 2. Число, квадратный корень которого иррационален
Допустим, мы хотим выяснить, рационально ли √(8/10).
Сначала возьмем дробь под корнем: 8/10.
Затем сократите дробь: 8/10 = 2(4)/2(5) = 4/5 (двойка сокращается, так как она появляется и в числителе, и в знаменателе).
Затем проверьте, является ли числитель полным квадратом: да, поскольку 4 = 2 2 .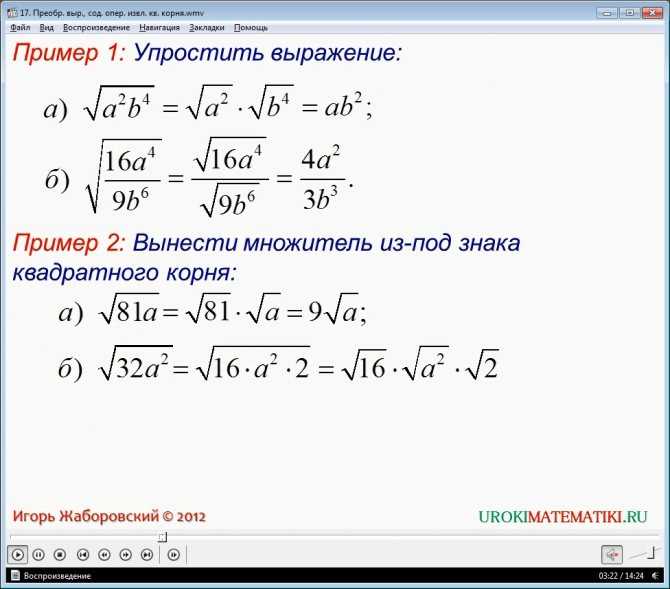
Наконец, проверьте, является ли знаменатель правильным квадратом: нет, так как 5 не является полным квадратом (оно находится между правильными квадратами 4 и 9).
Тогда квадратный корень из 8/10 иррационален. Его значение равно 2/√5 (или 2√5/5 после рационализации знаменателя).
Могут ли квадратные корни быть целыми числами?
В некоторых случаях квадратные корни могут быть целыми числами. Если число под радикалом — полный квадрат, то его квадратный корень — целое число.
Давайте рассмотрим несколько примеров, чтобы прояснить эту концепцию.
Пример 1. Число, квадратный корень которого является целым числом
Допустим, мы хотим выяснить, является ли √(81) целым числом.
Мы знаем, что 81 — полный квадрат, так как оно равно 9 2 .
Тогда его квадратный корень равен √81 = √(9 2 ) = 9, что является целым числом.
Пример 2. Число, квадратный корень которого не является целым числом
Допустим, мы хотим выяснить, является ли √(37) целым числом.
Мы знаем, что 36 — полный квадрат, так как оно равно 6 2 .
Мы знаем, что 49 — полный квадрат, так как оно равно 7 2 .
Это говорит нам о том, что квадратный корень из 37 не является целым числом, поскольку 36 < 37 < 49. Это также говорит нам о том, что квадратный корень из любого другого числа от 36 до 49 не является целым числом.
Можно ли добавлять квадратные корни?
Квадратные корни могут быть добавлены, а в некоторых случаях мы можем комбинировать их как одинаковые члены.
Пример 1. Сложение квадратных корней, похожих на члены
Допустим, мы хотим сложить 2√5 и 6√5. Поскольку оба термина имеют √5, они похожи.
Мы можем добавить их так же, как мы добавили бы другие подобные термины:
- 2 + 6 = 8
- 2x + 6x = 8x
- 2i + 6i = 8i
- 1 2? 6√5 = 8√5
Пример 2. Сложение квадратных корней, подобных слагаемым, после упрощения
Допустим, мы хотим сложить 4√3 и 2√27.
Это похоже на термины, но нам нужно немного упростить, прежде чем мы сможем это увидеть:
Мы можем переписать √8 следующим образом:
- √27
- =√((9)(3)) [множитель 27 как 9 умножить на 3]
- =√ √(ab) = √a√b]
- =3√3 [поскольку √(9) = 3]
Теперь мы видим, что у нас есть сумма подобных слагаемых, и мы можем их объединить:
- 4√3 + 2√27
- =4√3 + 2(3√3 ) [так как √27 = 3√3]
- = 4√2 4√2 + 1√2 6√2 10√3
Пример 3. Сложение квадратных корней, не похожих друг на друга
Допустим, мы хотим сложить √2 и √3. Поскольку 2 и 3 являются простыми числами и не имеют общих множителей, мы не можем их упростить или каким-либо образом переписать.
Таким образом, эти два квадратных корня можно сложить, но они не являются слагаемыми, поэтому их нельзя объединить.
Нет более простого способа записать √2 + √3, поэтому оставляем как есть.
Можно ли умножать квадратные корни?
Квадратные корни можно умножать. Основное правило задается формулой:
- (√a)(√b) = √(ab)
Это правило может помочь нам упростить произведение квадратных корней.
Пример 1. Упрощение произведения двух квадратных корней
Допустим, мы хотим умножить два квадратных корня: √2 и √3.
Чтобы упростить произведение, мы можем вычислить:
- √2*√3
- =√(2*3) [так как (√a)(√b) = √(ab)] =√6
Пример 2. Упрощение произведения двух квадратных корней
Допустим, мы хотим умножить два квадратных корня: √2 и √2.
Чтобы упростить их произведение, мы можем вычислить:
- √2*√2
- =√(2*2) [поскольку (√a)(√b) = √(ab)] 2 = √4
- = 2
Итак, для числа n мы имеем формулу:
- √n*√n = n
Заключение
Теперь ты знаешь маленький.