Решение неравенств методом математической индукции – Доказательство неравенств методом математической индукции.

Содержание

Доказательство неравенств методом математической индукции.

Доказательство методом математической индукции основано на следующей аксиоме: если предложение, в формулировку которого входит натуральное число п, истинно при п=1 и из его истинности при n=k ( где ) следует, что оно истинно и при , то оно истинно при всех натуральных значениях п.

Таким образом, доказательство по методу математической индукции проводится следующим образом:

1) доказываемое утверждение проверяется при п =1;

2) предполагая справедливость утверждения при n=k, доказывается справедливость утверждения для n=k+1.

Некоторые утверждения справедливы не для всех натуральных п, а для п, начиная с некоторого числа р. В таком случае первый шаг доказательства – это проверка справедливости утверждения для п=р .

П р и м е р. Доказать, что если , то

Доказательство. При

n=3 неравенство верно: . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что

В самом деле, имеем: . Итак, .

Но при любом натуральном значении k. Следовательно, тем более .

Согласно методу математической индукции можно сделать вывод о том, что доказываемое неравенство справедливо при всех .

Доказательство неравенств методом полной индукции.

Полная индукция – это метод рассуждений, при котором вывод делается на основании рассмотрения всех случаев, возможных по условию задачи.

П р и м е р. Доказать, что если .

Доказательство. Рассмотрим случаи:

1) . Получаем

, т.к.

Неравенство верно.

2) , т.е. .

Тогда . Неравенство справедливо.

3) т.е. .

Тогда . Неравенство справедливо.

Мы рассмотрели все возможные случаи. Значит неравенство верно для .

6. Доказательство неравенств с помощью методов математического анализа.

В этом случае доказательство неравенств сводят к исследованию соответствующих функций с помощью производных.

П р и м е р. Доказать неравенство

Доказательство. Перепишем неравенство в виде: .

Рассмотрим функцию .

Найдём производную . При , . Это значит, что при возрастает, причём . Поэтому при .

Литература

1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999

2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000

Тема: Иррациональные уравнения и неравенства.

План

1. Иррациональные уравнения, основные методы их решения.

2. Иррациональные неравенства.

Иррациональные уравнения.

Иррациональными называются уравнения и неравенства, содержащие переменную под знаком корня или под знаком возведения в дробную степень.

Все корни чётной степени, входящие в уравнение, являются арифметическими, т.е. если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то значение корня положительно.

Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.

Основные методы решения иррациональных уравнений:

1. возведение обеих частей уравнения в одну и ту же степень;

2. замена переменной;

3. умножение обеих частей уравнения на одну и ту же функцию;

4. применение свойств функций, входящих в уравнение.

Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например возведение обеих частей уравнения в чётную степень, приводят к уравнению-следствию. Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.

Возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в чётную степень.

Рассмотрим несколько примеров.

Пример 1. Решим уравнение .

Решение. Возводим обе части уравнения в квадрат, получаем:

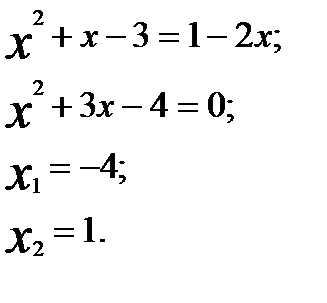
Проверка показывает, что только является корнем исходного уравнения.

Ответ: -4.

Пример 2. Решим уравнение

Решение. Выполним замену. Обозначим: заметим, что .

Тогда и .

Исходное уравнение принимает вид:

Полученное уравнение равносильно системе:

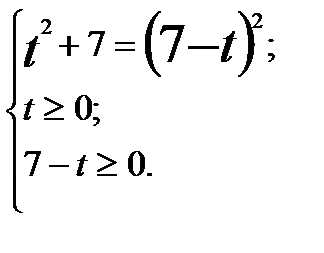
Из получившейся системы, имеем: .

Возвращаемся к подстановке, получаем:

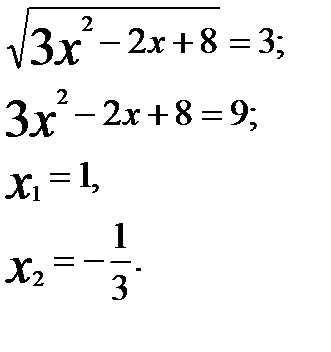
Ответ: 1; .

Пример 3. Решим уравнение .

Решение: Пусть

Тогда имеем:

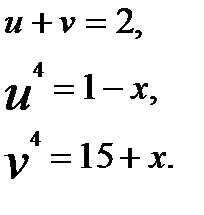
Откуда последовательно получаем:

Возвращаясь к первоначальным подстановкам, получим:

Откуда

С помощью проверки убеждаемся, что оба корня являются корнями исходного уравнения.

Ответ: 1; -15.

Пример 4. Решим уравнение .

Решение: Рассмотрим функцию .

Исходное уравнение принимает вид: .

. Функция монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что является корнем уравнения.

Ответ: 5.

Иррациональные неравенства.

Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т.д.

Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению:

1) Неравенство вида равносильно системе

2) Неравенство вида равносильно неравенству .

3) Неравенство вида равносильно совокупности систем

4) Неравенство вида равносильно системе

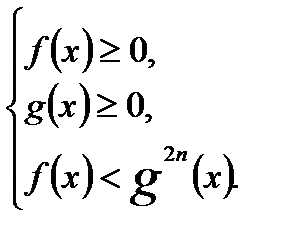
Пример 5. Решим неравенство .

Решение. Введём новую переменную . Тогда исходное неравенство принимает вид:

Решая это неравенство и возвращаясь к исходным переменным, получаем: .

Ответ: .

Пример 6. Решим неравенство .

Решение: Перепишем неравенство в виде: .

Это неравенство равносильно системе неравенств:

Откуда получаем .

Пример 6. Решим неравенство .

Решение: Рассмотрим функцию . Область определения этой функции . Функция возрастает на всей области определения, причём . Значит, неравенство решений не имеет.

Ответ: нет решений.

Литература

1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999

2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000

Текстовые задачи

План

infopedia.su

Метод математической индукции

Вступление

Основная часть

1. Полная и неполная индукция

2. Принцип математической индукции

3. Метод математической индукции

4. Решение примеров

5. Равенства

6. Деление чисел

7. Неравенства

Заключение

Список использованной литературы

Вступление

В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений — это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.

Хотя и выросла область применения метода математической индукции, в школьной программе ему отводится мало времени. Ну, скажите, что полезного человеку принесут те два-три урока, за которые он услышит пять слов теории, решит пять примитивных задач, и, в результате получит пятёрку за то, что он ничего не знает.

А ведь это так важно — уметь размышлять индуктивно.

Основная часть

По своему первоначальному смыслу слово “индукция” применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений. Простейшим методом рассуждений такого рода является полная индукция. Вот пример подобного рассуждения.

Пусть требуется установить, что каждое натуральное чётное число n в пределах 4представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.

Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).

Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.

Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:

1=1=1²

1+3=4=2²

1+3+5=9=3²

1+3+5+7=16=4²

1+3+5+7+9=25=5²

После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:

1+3+5+…+(2n-1)=n²

т.е. сумма n первых последовательных нечётных чисел равна n²

Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.

Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.

Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.

Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n (например нужно доказать, что сумма первых n нечётных чисел равна n² ). Непосредственная проверка этого утверждения для каждого значения n невозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.

+1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.

Обобщая сказанное, сформулируем следующий общий принцип.

Принцип математической индукции.

Если предложение А( n ), зависящее от натурального числа n , истинно для n =1 и из того, что оно истинно для n=k (где k -любое натуральное число), следует, что оно истинно и для следующего числа n=k+1 , то предположение А( n ) истинно для любого натурального числа n .

В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n>p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом. Если предложение А( n ) истинно при n=p и если А( k ) Þ А( k+1) для любого k>p, то предложение А( n) истинно для любого n>p.

Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n=1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n=k+1 в предположении справедливости утверждения для n=k (предположение индукции), т.е. доказывают, что А(k)ÞA(k+1).

ПРИМЕР 1

Доказать, что 1+3+5+…+(2n-1)=n² .

Решение: 1) Имеем n=1=1² . Следовательно,

утверждение верно при n=1, т.е. А(1) истинно.

2) Докажем, что А(k)ÞA(k+1).

Пусть k-любое натуральное число и пусть утверж-дение справедливо для n=k, т.е.

1+3+5+…+(2k-1)=k² .

Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что

1+3+5+…+(2k+1)=(k+1)² .

В самом деле,

1+3+5+…+(2k-1)+(2k+1)=k² +2k+1=(k+1)² .

Итак, А(k)ÞА(k+1). На основании принципа математической индукции заключаем, что предпо-ложение А(n) истинно для любого nÎN.

ПРИМЕР 2

Доказать, что

1+х+х² +х³ +…+хⁿ =(хⁿ⁺¹ -1)/(х-1), где х¹1

Решение: 1) При n=1 получаем

1+х=(х² -1)/(х-1)=(х-1)(х+1)/(х-1)=х+1

следовательно, при n=1 формула верна; А(1) ис-тинно.

2) Пусть k-любое натуральное число и пусть формула верна при n=k, т.е.

1+х+х² +х³ +…+х^k =(х^k+1 -1)/(х-1).

Докажем, что тогда выполняется равенство

1+х+х² +х³ +…+х^k +x^k+1 =(x^k+2 -1)/(х-1).

В самом деле

1+х+х² +x³ +…+х^k +x^k+1 =(1+x+x² +x³ +…+x^k )+x^k+1 =

=(x^k+1 -1)/(x-1)+x^k+1 =(x^k+2 -1)/(x-1).

Итак, А(k)ÞA(k+1). На основании принципа математической индукции заключаем, что форму-ла верна для любого натурального числа n.

ПРИМЕР 3

Доказать, что число диагоналей выпуклого n-угольника равно n(n-3)/2.

Решение: 1) При n=3 утверждение спра-

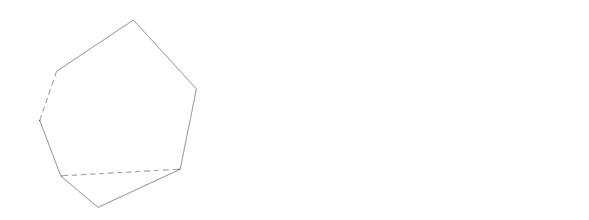А₃ ведливо, ибо в треугольнике

 А₃ =3(3-3)/2=0 диагоналей;

А₂ А(3) истинно.

2) Предположим, что во всяком

выпуклом k-угольнике имеет-

А₁ ся А_k =k(k-3)/2 диагоналей.

А_k Докажем, что тогда в выпуклом

А_k+1

(k+1)-угольнике число

диагоналей А_k+1 =(k+1)(k-2)/2.

Пусть А₁ А₂ А₃ …A_k A_k+1 -выпуклый (k+1)-уголь-ник. Проведём в нём диагональ A₁ A_k . Чтобы под-считать общее число диагоналей этого (k+1)-уголь-ника нужно подсчитать число диагоналей в k-угольнике A₁ A₂ …A_k , прибавить к полученному числу k-2, т.е. число диагоналей (k+1)-угольника, исходящих из вершины А_k+1 , и, кроме того, следует учесть диагональ А₁ А_k .

Таким образом,

_k+1 =_k +(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.

Итак, А(k)ÞA(k+1). Вследствие принципа математической индукции утверждение верно для любого выпуклого n-угольника.

ПРИМЕР 4

Доказать, что при любом n справедливо утвер-ждение:

1² +2² +3² +…+n² =n(n+1)(2n+1)/6.

Решение: 1) Пусть n=1, тогда

Х₁ =1² =1(1+1)(2+1)/6=1.

Значит, при n=1 утверждение верно.

2) Предположим, что n=k

Х_k =k² =k(k+1)(2k+1)/6.

3) Рассмотрим данное утвержде-ние при n=k+1

X_k+1 =(k+1)(k+2)(2k+3)/6.

X_k+1 =1² +2² +3² +…+k² +(k+1)² =k(k+1)(2k+1)/6+ +(k+1)² =(k(k+1)(2k+1)+6(k+1)² )/6=(k+1)(k(2k+1)+

+6(k+1))/6=(k+1)(2k² +7k+6)/6=(k+1)(2(k+3/2)(k+

+2))/6=(k+1)(k+2)(2k+3)/6.

Мы доказали справедливость равенства и при n=k+1, следовательно, в силу метода математиче-ской индукции, утверждение верно для любого на-турального n.

ПРИМЕР 5

Доказать, что для любого натурального n спра-ведливо равенство:

1³ +2³ +3³ +…+n³ =n² (n+1)² /4.

Решение: 1) Пусть n=1.

Тогда Х₁ =1³ =1² (1+1)² /4=1.

Мы видим, что при n=1 утверждение верно.

2) Предположим, что равенство верно при n=k

mirznanii.com

basics:induction [VF]

Не знаю, кто его придумал! Где-то читал, что Паскаль — для доказательства формулы бинома Ньютона1).

Этот метод применяется для доказательства утверждений, зависящих от параметра, принимающего натуральные значения; целью ставится доказать справедливость утверждения при всех значениях параметра.

Пример. Доказать справедливость формулы

при всех натуральных .

При каждом частном значении формулу можно проверить, но как совершить «переход к бесконечности» — сделать вывод о справедливости формулы для всего бесконечного набора значений ?

Для этого и используется метод математической индукции, который заключается в следующем: пусть имеется некоторое утверждение A , зависящее от параметра , принимающего значения из . Будем обозначать это утверждение А .

1. Проверяем справедливость утверждения А (этот пункт называется базисом индукции).

2. Выдвигаем предположение о справедливости утверждения А при (индукционное предположение).

3. На основании индукционного предположения доказываем утверждение А (индукционное заключение).

Если это удается осуществить, то делаем вывод, что утверждение А справедливо для всех натуральных чисел .

Проиллюстрируем работу метода на примере формулы суммы первых натуральных чисел. При она, очевидно, верна. Пусть справедлива формула

Тогда на ее основании выводим

т.е. формула остается справедливой и при . Следовательно она справедлива при всех .

Доказать справедливость формул

при .

Метод математической индукции — мощное, но не всесильное средство доказательства. Известны примеры истинных утверждений А , справедливость которых не может быть установлена этим методом.

Пример. Доказать неравенство

Решение. Справедливость для очевидна. Предположим, что оно верно для некоторого , нужно показать справедливость неравенства

Домножаем неравенство индукционного предположения на дробь , получаем:

Для того, чтобы прийти к неравенству индукционного заключения, достаточно показать, что

Это неравенство эквивалентно следующему:

возведение в квадрат приводит к:

Последнее, очевидно, неверно.

Попробуем доказать методом математической индукции более сильное утверждение

следствием которого будет доказываемое выше. Кажется, что мы должны прийти к тому же противоречию. Однако на этот раз метод осечки не дает. Для неравенство очевидно справедливо. Предположим, что оно справедливо для какого-то . Домножим его на и проверим выполнимость неравенства

Имеем:

что справедливо. ♦

Итак, исходное неравенство справедливо, но доказать его методом математической индукции не удается, хотя более сильное утверждение — удается! Такая ситуация называется парадоксом изобретателя, это название было придумано в XX веке венгерским математиком Д.Пойа2). Противоречие разрешается следующим соображением: если утверждение А слабее утверждения B , то и индукционные предположения, которые применяются в ходе доказательства, также будут находиться в том же соотношении — фактически мы получаем больший исходный ресурс для вывода индукционного заключения.

Иногда, ввиду особенности утверждения А , утверждение А не имеет смысла, тогда в качестве базиса индукции рассматривается утверждение А . В дальнейшем подобные модификации метода математической индукции будем применять без излишних комментариев.

pmpu.ru

Метод математической индукции — ПриМат

Под методом математической индукции понимают следующий способ доказательства: если требуется доказать истинность утверждения то сначала проверяют данное утверждение для некоторого натурально числа , обычно , а потом допускают истинность выражения Далее доказывают истинность утверждения

Упражнение:

Доказательство одноцветности всех лошадей — ошибочное доказательство, что все лошади одного цвета, придуманное венгерским математиком Пойа. Доказательство призвано продемонстрировать ошибки, возникающие при неправильном использовании метода математической индукции.

Доказываемое утверждение: все лошади одного цвета.

Доказательство:

Проведем доказательство по индукции.

База индукции:

Одна лошадь, очевидно, одного (одинакового) цвета.
Шаг индукции:
Пусть доказано, что любые лошадей всегда одного цвета. Рассмотрим каких-то лошадей. Уберем одну лошадь. Оставшиеся лошадей одного цвета по предположению индукции. Возвратим убранную лошадь и уберем какую-то другую. Оставшиеся лошадей снова будут одного цвета. Значит, все лошадей одного цвета.

Отсюда следует, что все лошади одного цвета. Утверждение доказано.

В чем ошибка?
Решение

Спойлер

Опровержение

Противоречие возникает из-за того, что шаг индукции не сообразуется с базой. Он верен лишь при . При (база индукции) получаемые множества оставшихся лошадей не будут пересекаться, и утверждение о равенстве цветов всех лошадей сделать нельзя.

[свернуть]

Пример:

Доказать равенство:

Пусть данное утверждение верно для

Докажем истинность утверждения для

Доказать, что для всех натуральных чисел справедливо неравенство .

Для неравенство принимает вид , т.е. оно справедливо.

Предположим, требуемое неравенство имеет место при некотором и покажем, что оно же справедливо и для .

Сложим предположение индукции с неравенством . Находим , что и требовалось доказать.

Тест «Метод математической индукции»

Лимит времени: 0

Информация

Тестовые вопросы по вышеизложенному материалу.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 3

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

С ответом
С отметкой о просмотре

Задание 1 из 3
Количество баллов: 1
С помощью теста мат.индукции можно доказать:
Правильно
Неправильно
Задание 2 из 3
Количество баллов: 1
Расположите части метода в порядке выполнения:

ib.mazurok.com

Суть метода математической индукции.

Во многих разделах арифметики, алгебры, геометрии, анализа приходится доказывать истинность предложений А(n), зависящих от натуральной переменной. Доказательство истинности предложения А(n) для всех значений переменной часто удается провести методом математической индукции, который основан на следующем принципе.

Предложение А(n) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:

Предложение А(n) истинно для n=1.
Из предположения, что А(n) истинно для n=k (где k – любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.

Этот принцип называется принципом математической индукции. Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства.

Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения А(n) для всех натуральных n, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.

Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

Метод математической индукции в решении задач на делимость.

С помощью метода математической индукции можно доказывать различные утверждения, касающиеся делимости натуральных чисел.

Следующее утверждение можно сравнительно просто доказать. Покажем, как оно получается с помощью метода математической индукции.

Пример 1. Если n – натуральное число, то число 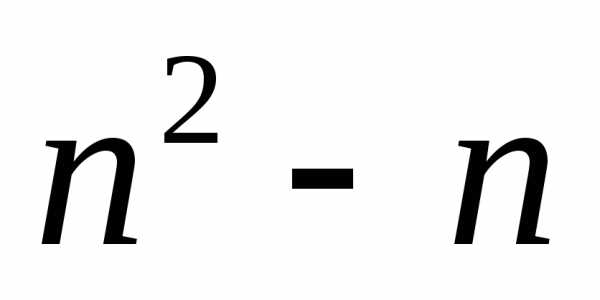четное.

При n=1 наше утверждение истинно: — четное число. Предположим, что — четное число. Так как ,a 2k – четное число, то и четное. Итак, четность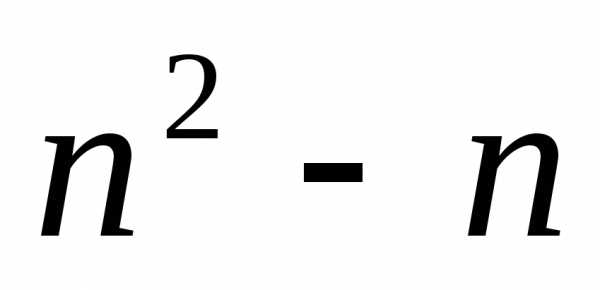доказана приn=1, из четности 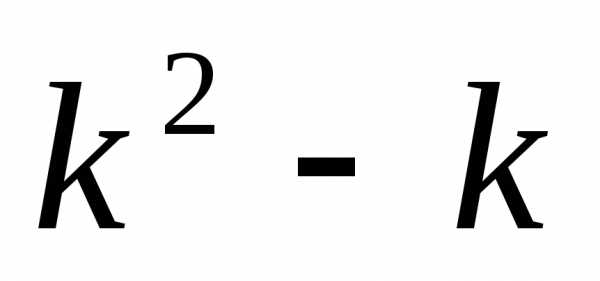выведена четность.Значит,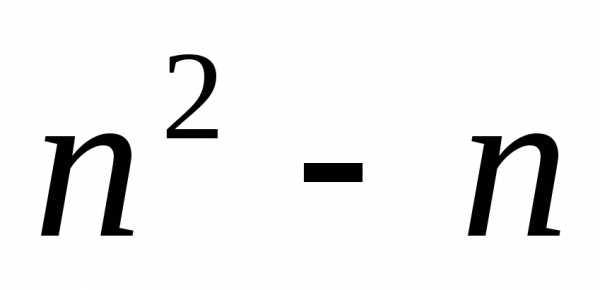четно при всех натуральных значенияхn.

Пример 2. Доказать истинность предложения

A(n)={число 5кратно 19},n – натуральное число.

Решение.

Высказывание А(1)={число кратно 19} истинно.

Предположим, что для некоторого значения n=k

А(k)={число кратно 19} истинно. Тогда, так как

, очевидно, что и A(k+1) истинно. Действительно, первое слагаемое делится на 19 в силу предположения, что A(k) истинно; второе слагаемое тоже делится на 19, потому что содержит множитель 19. Оба условия принципа математической индукции выполнены, следовательно, предложение A(n) истинно при всех значениях n.

Применение метода математической индукции к суммированию рядов.

Пример 1. Доказать формулу

, n – натуральное число.

Решение.

При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.

Предположим, что формула верна при n=k, т.е.

Прибавим к обеим частям этого равенства 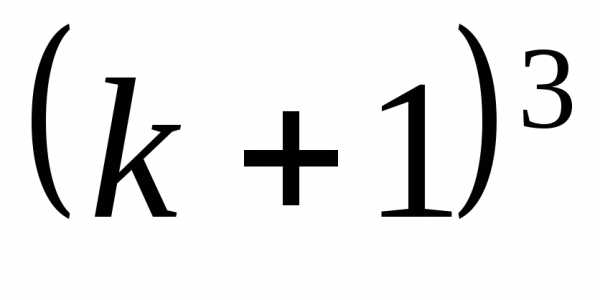и преобразуем правую часть. Тогда получим

Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1. Это утверждение справедливо при любом натуральном значении k. Итак, второе условие принципа математической индукции тоже выполнено. Формула доказана.

Пример 2. Доказать, что сумма n первых чисел натурального ряда равна .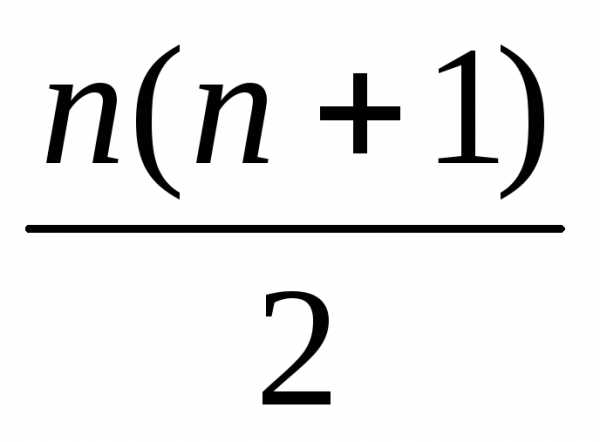

Решение.

Обозначим искомую сумму 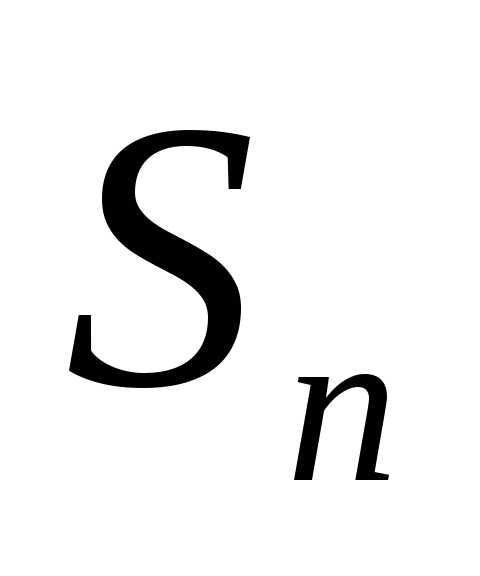, т.е..

При n=1 гипотеза верна.

Пусть . Покажем, что.

В самом деле,

Задача решена.

studfiles.net

на тему: «Метод математической индукции»

МОУ ШИЛИ

Реферат

на тему:

«Метод математической индукции»

Выполнила:

ученица 11 «А» класса

Терещенко Мария

Проверила:

Ерёмина Людмила

Александровна

Калининград

2008

Содержание:

1.Введение стр.3

2.Основная часть стр.4

-принцип математической индукции стр.6

-метод математической индукции в решении задач на делимость стр.7

-применение метода математической индукции к суммированию рядов стр.8

-пример применения метода математической индукции к доказательству неравенств стр.9

-метод математической индукции в применение к другим задачам стр.10

3.Заключение стр.11

4.Список используемой литературы стр.12

-2-

Введение

В основе всякого математического исследования лежат дедуктивный индуктивный методы. Дедуктивный метод рассуждений — это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

Например, мы каждый день наблюдаем, что Солнце восходит с востока.

Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И, тем не менее, этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.

А ведь это так важно — уметь размышлять индуктивно.

-3-

Основная часть

Пусть требуется установить, что каждое натуральное чётное число n в пределах 4< n < 20 представим в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:

1=1=1 2

1+3=4=2 2

1+3+5=9=3 2

1+3+5+7=16=4 2

1+3+5+7+9=25=5 2

-4-

После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:

1+3+5+…+(2n-1)=n 2

т.е. сумма n первых последовательных нечётных чисел равна n 2

Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.

Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n (например нужно доказать, что сумма первых n нечётных чисел равна n 2 ). Непосредственная проверка этого утверждения для каждого значения n невозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.

Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n=1. Но тогда оно справедливо и для следующего числа n=1+1=2. Из справедливости утверждения для n=2 вытекает его справедливость для n=2+1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.

Обобщая сказанное, сформулируем следующий общий принцип.

-5-

Принцип математической индукции.

Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.

Если предложение А(n) истинно при n=p и если А(k) >А(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.

-6-

Метод математической индукции в решении задач на делимость.

Пример 1

Доказать, что при любом n , 7 n -1 делится на 6 без остатка.

Решение:

1)Пусть n=1, тогда Х 1 =7 1 -1=6 делится на 6 без остатка. Значит при n=1 утвержде-ние верно. 2) Предположим, что при n=k ,7 k -1 делится на 6 без остатка. 3) Докажем, что утверждение справедливо для n=k+1.

X k+1 =7 k+1 -1=7

7 k -7+6=7(7 k -1)+6.

Первое слагаемое делится на 6, поскольку 7 k -1 делится на 6 по предположению, а вторым слага-емым является 6. Значит 7 n -1 кратно 6 при любом натуральном n. В силу метода математической индукции утверждение доказано.

Пример 2

Доказать, что 33n+3-26n-27 при произвольном натуральном n делится на 262(676) без остатка.
Решение: Предварительно докажем, что 33n+3-1 делится на 26 без остатка.
1) При n=0
33-1=26 делится на 26
2) Предположим, что при n=k
33k+3-1 делится на 26
3) Докажем, что утверждение
верно при n=k+1.
33K+6-1=27,33k+3-1=26,33k+3+(33k+3-1) -делится на 26
Теперь проведём доказательство утверждения, сформулированного в условии задачи.
1) Очевидно, что при n=1 утверждение верно
33+3-26-27=676
2) Предположим, что при n=k
выражение 33k+3-26k-27 делится на 262 без остатка.
3) Докажем, что утверждение верно при n=k+1
33k+6-26(k+1)-27=26(33k+3-1)+(33k+3-26k-27).
Оба слагаемых делятся на 262; первое делится на 262, потому что мы доказали делимость на 26 выражения, стоящего в скобках, а второе делится по предположению индукции. В силу метода математической индукции утверждение доказано

-7-

Применение метода математической индукции к суммированию рядов.

Пример 3

Доказать, что

1+х+х 2 +х 3 +…+х n =(х n+1 -1)/(х-1), где х (1)

Решение:

1) При n=1 получаем

1+х=(х 2 -1)/(х-1)=(х-1)(х+1)/(х-1)=х+1

следовательно, при n=1 формула верна; А(1) истинно.

2) Пусть k-любое натуральное число и пусть формула верна при n=k, т.е.

1+х+х 2 +х 3 +…+х k =(х k+1 -1)/(х-1).

Докажем, что тогда выполняется равенство

1+х+х 2 +х 3 +…+х k +x k+1 =(x k+2 -1)/(х-1).

В самом деле

1+х+х 2 +x 3 +…+х k +x k+1 =(1+x+x 2 +x 3 +…+x k )+x k+1 =

=(x k+1 -1)/(x-1)+x k+1 =(x k+2 -1)/(x-1).

Итак, А(k) > A(k+1).

На основании принципа математической индукции заключаем, что формула верна для любого натурального числа n.

-8-

Пример применения метода математической индукции к доказательству неравенств.

Пример 4

Доказать, что при n>2 справедливо неравенство

1+(1/2 2 )+(1/3 2 )+…+(1/n 2 )<1,7-(1/n).

Решение:

1) При n=3 неравенство верно

1+(1/2 2 )+(1/3 2 )=245/180<246/180=1,7-(1/3).

2).Предположим, что при n=k

1+(1/2 2 )+(1/3 2 )+…+(1/k 2 )=1,7-(1/k).

3) Докажем справедливость не-

равенства при n=k+1

(1+(1/2 2 )+…+(1/k 2 ))+(1/(k+1) 2 )<1,7-(1/k)+(1/(k+1) 2 ).

Докажем, что 1,7-(1/k)+(1/(k+1) 2 )<1,7-(1/k+1) U

(1/(k+1) 2 )+(1/k+1)<1/k U (k+2)/(k+1) 2 <1/k U

k(k+2)<(k+1) 2 U k 2 +2k<k 2 +2k+1.

Последнее очевидно, а поэтому

1+(1/2 2 )+(1/3 2 )+…+(1/(k+1) 2 )<1,7-(1/k+1).

В силу метода математической индукции неравенство доказано.

-9-

Метод математической индукции в применение к другим задачам.

mirznanii.com

Метод математической индукции — реферат

Калининский район

МОУ лицей № 81

Секция математики

Радько Тарас Александрович

РЕФЕРАТ

Метод математической индукции

Научный руководитель:

Ятайкина Алла Аркадьевна,

учитель математики

План

Введение

Суть метода математической индукции
Метод математической индукции в решении задач на делимость
Применение метода математической индукции к суммированию рядов
Примеры применения метода математической индукции к доказательству неравенств
Метод математической индукции в применение к другим задачам

Список использованной литературы

Введение

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.

Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И, тем не менее, этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.

Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге. Наблюдение, индукция оказываются полезными и в дальнейшем для уточнения сделанных предположений. После опытов Майкельсона по измерению скорости света в движущейся среде оказалось необходимым уточнить законы физики, создать теорию относительности.

В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство

Лежащее в основе арифметики понятие следовать за тоже появилось при наблюдениях за строем солдат, кораблей и другими упорядоченными множествами.

Не следует, однако, думать, что этим исчерпывается роль индукции в математике. Разумеется, мы не должны экспериментально проверять теоремы, логически выведенные из аксиом: если при выводе не было сделано логических ошибок, то они постольку верны, поскольку истинны принятые нами аксиомы. Но из данной системы аксиом можно вывести очень много утверждений. И отбор тех утверждений, которые надо доказывать, вновь подсказывается индукцией. Именно она позволяет отделить полезные теоремы от бесполезных, указывает, какие теоремы могут оказаться верными, и даже помогает наметить путь доказательства.

Суть метода математической индукции

Предложение А(n) истинно для n=1.
Из предположения, что А(n) истинно для n=k (где k – любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.

Метод математической индукции в решении задач на

делимость

Пример 1. Если n – натуральное число, то число четное.

При n=1 наше утверждение истинно: — четное число. Предположим, что — четное число. Так как , a 2k – четное число, то и четное. Итак, четность доказана при n=1, из четности выведена четность .Значит, четно при всех натуральных значениях n.

Пример 2. Доказать истинность предложения

A(n)={число 5 кратно 19}, n – натуральное число.

Решение.

Высказывание А(1)={число кратно 19} истинно.

Предположим, что для некоторого значения n=k

А(k)={число кратно 19} истинно. Тогда, так как

Применение метода математической индукции к

суммированию рядов

Пример 1. Доказать формулу

, n – натуральное число.

Решение.

Предположим, что формула верна при n=k, т.е.

Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим

Пример 2. Доказать, что сумма n первых чисел натурального ряда равна .

Решение.

Обозначим искомую сумму , т.е. .

При n=1 гипотеза верна.

Пусть . Покажем, что .

В самом деле,

Задача решена.

Пример 3. Доказать, что сумма квадратов n первых чисел натурального ряда равна .

Решение.

Пусть .

Предположим, что . Тогда

и окончательно .

Пример 4. Доказать, что .

Решение.

Если , то

Пример 5. Доказать, что

Решение.

При n=1 гипотеза очевидно верна.

Пусть .

Докажем, что .

Действительно,

Примеры применения метода математической индукции к

доказательству неравенств

Пример 1. Доказать, что при любом натуральном n>1

Решение.

Обозначим левую часть неравенства через .

, следовательно, при n=2 неравенство справедливо.

Пусть при некотором k. Докажем, что тогда и . Имеем , .

Сравнивая и , имеем , т.е. .

При любом натуральном k правая часть последнего равенства положительна. Поэтому . Но , значит, и .

Пример 2. Найти ошибку в рассуждении.

Утверждение. При любом натуральном n справедливо неравенство .

Доказательство.

Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.

. (1)

Докажем, что тогда неравенство справедливо и при n=k+1, т.е.

Действительно, не меньше 2 при любом натуральном k. Прибавим к левой части неравенства (1) , а к правой 2. Получим справедливое неравенство , или . Утверждение доказано.

Пример 3. Доказать, что , где >-1, , n – натуральное число, большее 1.

Решение.

При n=2 неравенство справедливо, так как .

Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.

. (1)

Покажем, что тогда неравенство справедливо и при n=k+1, т.е.

. (2)

Действительно, по условию, , поэтому справедливо неравенство

, (3)

полученное из неравенства (1) умножением каждой части его на . Перепишем неравенство (3) так: . Отбросив в правой части последнего неравенства положительное слагаемое , получим справедливое неравенство (2).

Пример 4. Доказать, что

(1)

где , , n – натуральное число, большее 1.

Решение.

При n=2 неравенство (1) принимает вид

. (2)

Так как , то справедливо неравенство

. (3)

referat911.ru

Доказательство неравенств методом математической индукции.

Метод математической индукции

basics:induction [VF]

Метод математической индукции — ПриМат

Тест «Метод математической индукции»

Информация

Суть метода математической индукции.

Применение метода математической индукции к суммированию рядов.

на тему: «Метод математической индукции»

Метод математической индукции — реферат

Добавить комментарий Отменить ответ