Примеры нахождения области определения функции – . .

Область определения функции примеры решения

Область определения функции примеры решения

Как найти область определения функции?

Рассмотрим область определения функции в математике на примерах.

Найти область определения функции примеры решений

Рассмотрим простые примеры, как находить область определения функции.

Пример нахождения области определения функции.

Найти область определения функции

y = 2 / (x + 2)

Область определения функции – это множество значений аргумента, при которых функция имеет смысл.

В данном примере область определения функции составляют все числа, кроме тех, при которых знаменатель равен нулю. Ведь на ноль делить нельзя.

Значит мы должны найти значения икс, при которых знаменатель обратится в ноль и исключить их из области определения функции.

Для решения этой задачи приравняем знаменатель к нулю:

x + 2 = 0

Решим это уравнение:

x = -2

Итак, при x = -2 знаменатель будет равен нулю. На ноль делить нельзя, а значит при этом значении икс функция теряет смысл. Теперь мы можем найти область определения функции

y = 2 / (x + 2)

Областью определения функции является вся числовая прямая, кроме числа -2.

Пример нахождения области определения функции.

Найти область определения функции

y = 2 / (4x² — 4x + 1)

Мы уже знаем, как находить область определения функции: надо указать значения аргумента, при которых она имеет смысл.

Здесь перед нами дробное выражение. Знаменатель не должен быть равен нулю.

Значит, область определения функции в данном случае – это все числа, кроме тех, которые обращают знаменатель в ноль.

Как найти такие числа? Приравнять знаменатель нулю:

4x² — 4x + 1 = 0

и решить это квадратное уравнение.

Решаем и находим, что корень уравнения x = 0,5.

Теперь можно указать область определения функции – это вся числовая прямая, кроме числа 0,5.

А что значит указать область определения функции? Это значит указать все значения аргумента (т.е. икса), при которых функция имеет смысл.

В нашем случае это все числа, кроме 0,5.

www.sbp-program.ru

Область определения функции

Остановимся на процедуре нахождения области определе­ния функции.

1. В том случае, когда функция задана в аналитическом виде (посредством формулы)

(3.1)

и никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу

f в (3.1). Эти ограничения хорошо известны: подкоренное выражение в кор­не четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком ло­гарифма должно быть только

положительным, а также неко­торые другие. Приведем здесь два примера.

Пример 1. у = log₂ (x² — 5x + 6).

Область определения этой функции находится из условия x² — 5x + 6 > 0. Поскольку x = 2 и x = 3 — корни квадратно­го трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-, 2) и (3,

). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.

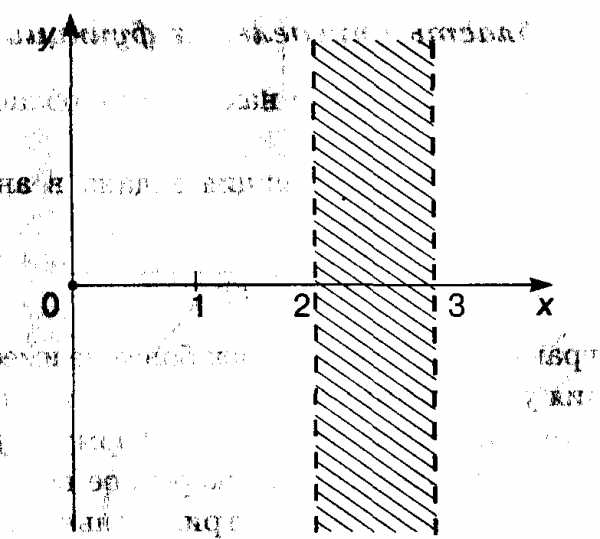
Рис. 3.4

Пример 2. у = arcsin .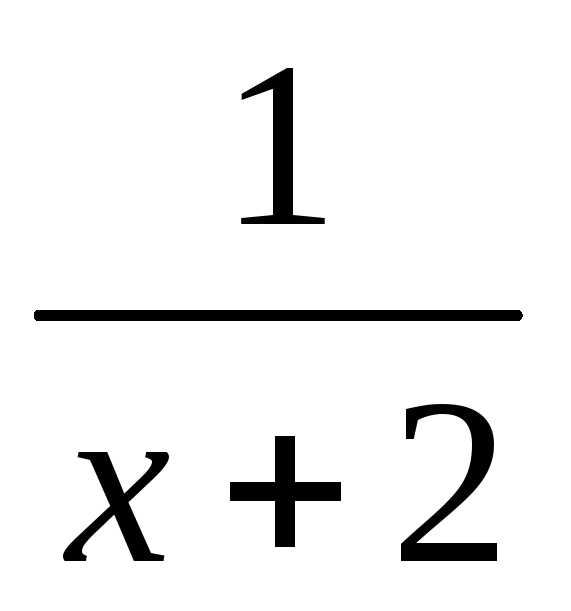

Область определения этой функции находится из совокуп­ности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не дол­жен равняться нулю, т.е.

Двойное неравенство эквивалентно двум более простым нера­венствам: х + 2 ≥ 1 и х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных проме­жутков: (-

, -3] и (-1,). Запретная точках = —2 сюда не попадает. В отличие от предыдущего примера концы полуин­тервалов входят в область определения функции.

2. Область определения функции задана вместе с функцией f(x).

Пример 3. у = 3x^—4­­^/3 + 2, 1 ≤ х ≤ 4.

3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физи­ческим смыслом).

Определение 2. Функция у = f(x) называется четной (сим­метрия относительно оси Оу), если для любых значений аргу­мента из области ее определения выполнено равенство

Определение 3. Функция у = f(x) называется нечетной (симметрия относительно начала координат О), если выпол­нено условие:

Например, функции у = х² и у = cos x являются четными, а функции у = x³ и у = sin x— нечетными.

Приложения в экономике

Приведем примеры использования функций в области эко­номики.

1. Кривые спроса и предложения. Точка равнове­сия. Рассмотрим зависимости спроса D (demand) и предложе­ния S (supply) от цены на товар Р (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от Р имеет вид ниспадаю­щей кривой (рис. 3.5, а):

(3.2)

где а < 0. В свою очередь предложение растет с увеличением цены на товар, и потому зависимость

S от Р имеет следующую характерную форму:

(3.3)

где b ≥ 1 (рис. 3.5, б). В формулах (3.2) и (3.3) с и d — так называемые экзогенные величины; они зависят от внешних причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (3.2) и (3.3), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.

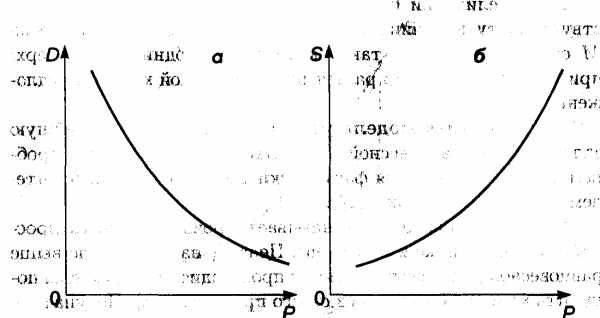
Рис. 3.5

Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие дается урав­нением

и соответствует точке пересечения кривых D и S — это так называемая точка равновесия (рис. 3.6). Цена

Ро, при которой выполнено условие (3.4), называется равновесной.

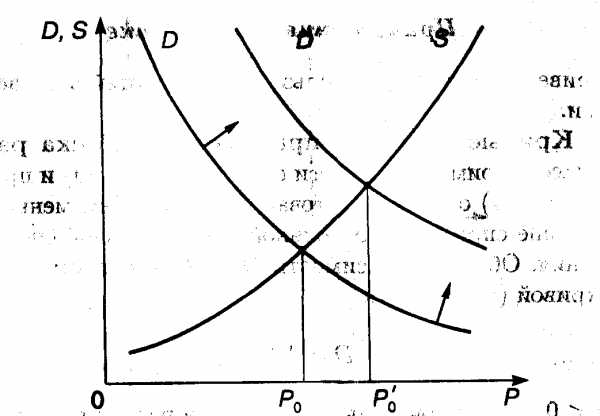
Рис. 3.6

При увеличении благосостояния населения, что соответ­ствует росту величины с в формуле (3.2), точка равновесия М смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предло­жения S.

2. Паутинная модель рынка. Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проб­лем рынка, означающая фактически торг между производите­лем и покупателем (рис. 3.7).

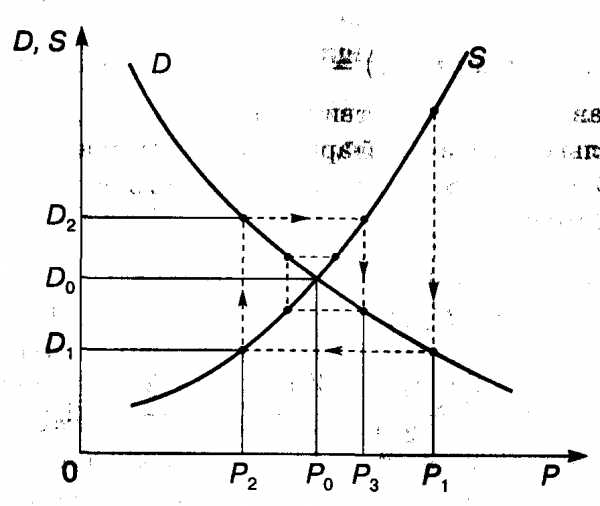
Рис. 3.7

Пусть сначала цену P

1 называет производитель (в прос­тейшей схеме он же и продавец). Цена P₁ на самом деле выше равновесной (естественно, всякий производитель стремится по­лучить максимум выгоды из своего производства). Покупатель оценивает спрос D₁ при этой цене и определяет свою цену Р₂, при которой этот спрос D₁ равен предложению. Цена Р₂ ниже равновесной (всякий покупатель стремится купить подешев­ле). В свою очередь производитель оценивает спрос D₂, соот­ветствующий цене P₂, и определяет свою цену Р₃, при которой спрос равен предложению; эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к «скручи­ванию» спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену

Р₀: P_n = P₀.

studfiles.net

Область определения функции двух переменных

Разделы: Математика

---

Цели работы:

• повторить и систематизировать нахождение области определения функции, закрепить это понятие и наглядно представить в координатной плоскости и в пространстве;
• рассмотреть аналитические и геометрические методы не изолированно друг от друга, а в тесной взаимосвязи. Это позволит облегчить переход от стандартных решений конкретных математических задач к нестандартным;
• воспитание интереса к математике и мультимедиа, активности, мобильности; восприятие компьютера, как инструмента обучения;
• использование компьютера для нахождения области определения и построения графиков с помощью графического редактора 3D Grapher 1.2, Copyright © 2000-2002 RomanLab Software и формирование информационной компетентности учащихся.

Определение функции двух переменных

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

A= – функция трех переменных.

Способы задания функций нескольких переменных

Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции. Наиболее часто функция задается аналитически — это явное задание функции или неявное задание

Например, — это явно заданная функция двух переменных; уравнение задает неявно две функции двух переменных.

Область определения функции

Непрерывное множество пар значений независимых переменных , при которых функцияопределена, называется областью определения функции.

Область определения называется замкнутой областью, если она включает в себя свою границу; открытой областью, если она не включает в себя свою границу; ограниченной областью, если может быть помещена в круг конечного радиуса.

Геометрически изобразить область определения функции можно только для функций:

• одной переменной – на прямой ,
• двух переменных – на плоскости ,
• трех переменных– в пространстве .

Геометрическое изображение самой функции возможно только для функции двух переменных.

Графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область D, которая является областью определения функции.

На рис. изображена поверхность графика функции и ее область определения.

В курсе учебного материала 9-го класса мы рассматриваем следующие задания на нахождение и построение области определения функции.

ПРИМЕРЫ

Найти область определения функции

Решение. Областью определения данной функции является вся плоскость, т.к. нет ограничений на переменные x и y.

2. Найти область определения функции .

Решение. Данная функция определена, когда xy > 0, т.е. в тех точках координатной плоскости, в которых знаки координат x и y - одинаковы. Это будут точки, лежащие в I и III координатных четвертях, т.е. множество точек, удовлетворяющих условиям:

и

3. Найти область определения функции .

Решение. Данная функция определена при условии, когда

т.е. . Это множество точек, лежащих внутри круга с центром в начале координат, радиус которого равен 2.

Изобразить на координатной плоскости Оху область определения функции .

Решение. Подкоренное выражение должно быть неотрицательно, т.е. следовательно, . Геометрическим решением неравенства служит полуплоскость, расположенная выше прямой и сама прямая.

5. Найти область определения функции и изобразить её графически.

.

Решение. Областью определения функции является множество точек плоскости, координаты которых удовлетворяют системе неравенств:

6. Изобразить на координатной плоскости Оху область определения функции

Решение. Эта функция определена, когда подкоренное выражение неотрицательно, т.е. Данным соотношениям удовлетворяют координаты всех точек, находящихся внутри кольца, образованного двумя окружностями с центрами в начале координат и радиусами R=3, R=4.

7. Изобразить на координатной плоскости Оху область определения функции

.

Решение. Учащиеся не могут найти область определения данной функции аналитически, но с помощью графического редактора 3D Grapher 1.2 это выполняется легко.

В Приложении приведено ещё несколько примеров, с решениями, для учащихся девятых классов.

Для учащихся 10-11 классов мы предлагаем систему упражнений по нахождению и построению области определения функции двух переменных. При этом отрабатываются свойства логарифмических, тригонометрических и обратных тригонометрических функций. Данные упражнения можно использовать при изучении нового материала, при повторении, при решении уравнений и неравенств.

Найти и изобразить на плоскости область определения функции

Решение. Область определения функции есть пересечение областей определения слагаемых функции. Для первой функции подкоренное выражение должно быть неотрицательным, т.е. Если значение логарифмической функции неотрицательно, то выражение, стоящее под знаком логарифма, должно быть больше или равно единице, т.е. отсюда . Это неравенство задает нам множество точек плоскости, лежащих вне окружности с центром в начале координат, радиуса 2, включая и точки данной окружности. Вторая функция определена при Следовательно, Имеем две параболы с вершиной в начале координат . Поэтому полученное неравенство задает нам часть плоскости, заключенную между этими параболами, включая границы без начала координат. Третья функция определена при

Областью определения данной функции является общая часть найденных областей определения слагаемых.

Покажите на координатной плоскости xOy область определения функции

.

Решение. Ограничения для функции имеют вид:

3. Изобразить область определения функции

Решение. Эта функция определена при , т.е.

Областью определения является часть плоскости, расположенная между двумя прямыми.

4. Найти область определения функции .

Решение. Областью определения функции является решение неравенства. Поэтому нужно решить неравенство

Решая данное неравенство, получим Это область, заключенная между двумя параболами и .

5. Построить область определения функции

Решение. Область определения данной функции определяется системой неравенств:

Первое неравенство определяет круг с центром в точке (-2;0) и радиусом равным 2 за исключением его границы:

Второе неравенство определяет I и III координатные четверти, за исключен

xn--i1abbnckbmcl9fb.xn--p1ai