Решение систем линейных уравнений методом сложения.
Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:
1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;
2) сложить почленно полученные уравнения и найти значение одной из переменных;
3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.
Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).
Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.
Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.
Найдём х и подставим его значение во 2-ое уравнение.
Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.
Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.
Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.
Ответ: (3; -5).
Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:
Сложим эти равенства почленно.
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами
):Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.
Решаем последнее уравнение системы и получаем х = -2.
Ответ: (-2; 1).
Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.
Подставим значение х=4 во 2-ое уравнение.
3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.
Ответ: (4; -3).
www.mathematics-repetition.com
Прямые методы решения систем линейных уравнений.
Цель работы – научиться решать системы линейных алгебраических уравнений, используя прямые методы решения
Задание
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.
Решить систему линейных уравнений методом прогонки для систем с трехдиагональной матрицей
Математическое описание
1. Метод Крамера
Требуется найти решение системы линейных уравнений
Ax = b, (1.1)
где 
– квадратная матрица коэффициентов
при неизвестных;
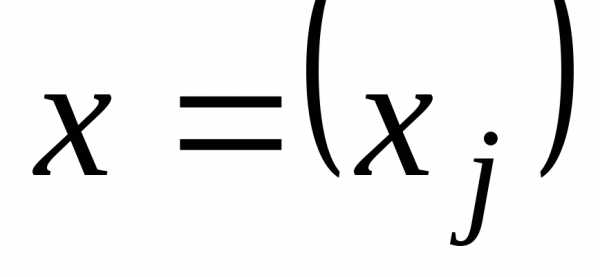
j =1, …, n. (1.2)
Здесь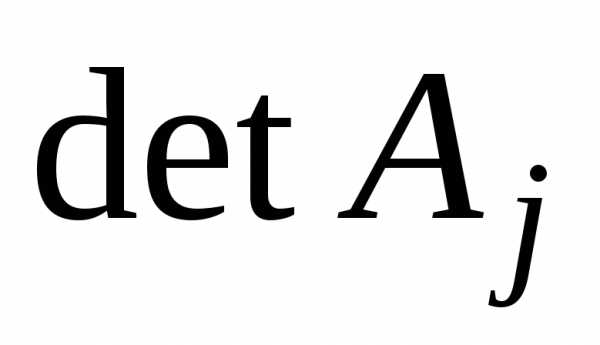 
–
определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом
правых частей.
2. Метод Гаусса
Систему уравнений (1.1) представим в виде
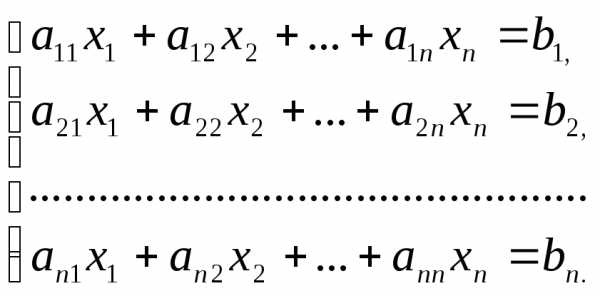(2.1)
или
i = 1,…, n.
Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее – к единичной (обратный ход).
Пусть
матрица система (2.1) – верхняя треугольная,
поэтому 
приi > j, т. е. все
элементы ниже главной диагонали равны
нулю. Тогда из последнего уравнения
сразу определяем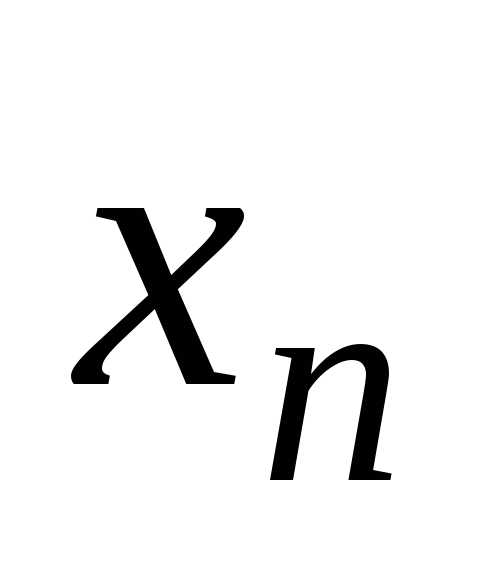 
.
Подставляя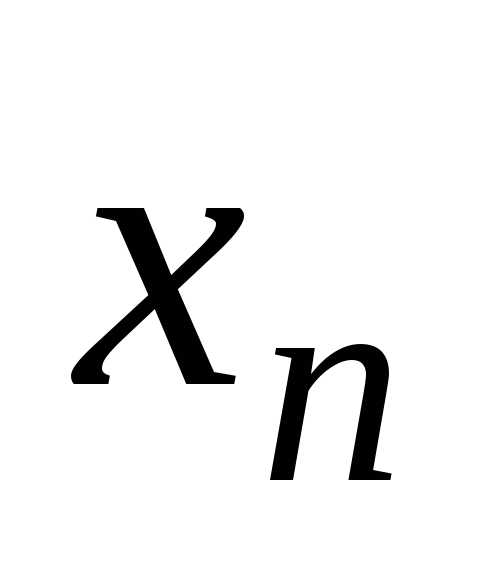
в
предпоследнее уравнение, находим 
и т. д.
Общие формулы имеют вид
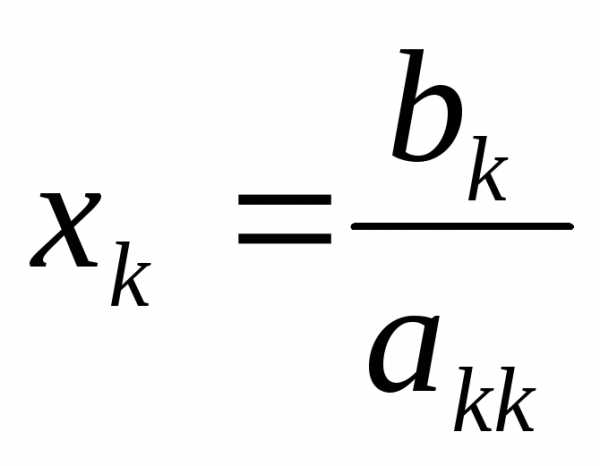при k = n (2.2)
при k = n – 1, n – 2, …, 1.
При k > l коэффициенты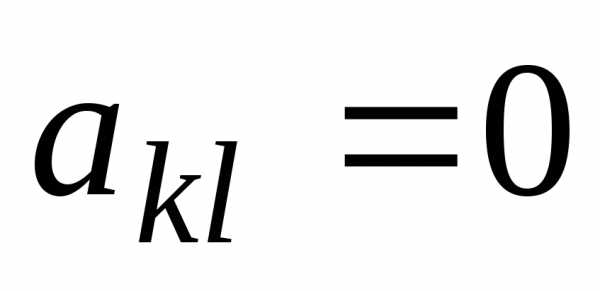 
.
Приведем
матрицу системы (1.3) к верхней треугольной.
Вычтем из второго уравнения системы
(1.3) первое, умноженное на такое число,
при котором коэффициент при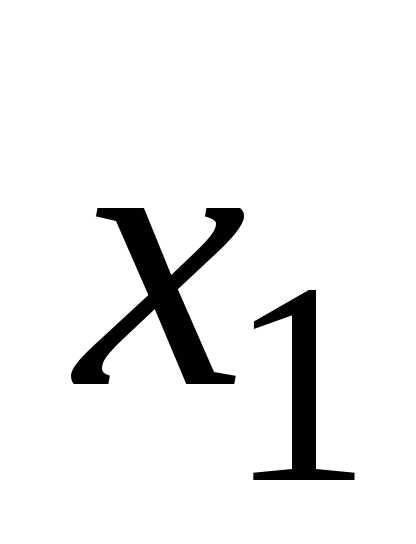 
обратится
в нуль. То же проделаем со всеми остальными
уравнениями. В результате все коэффициенты
первого столбца, лежащие ниже главной
диагонали, обратятся в нуль. Затем,
используя второе уравнение, обратим в
нуль соответствующие коэффициенты
второго столбца. Последовательно
продолжая этот процесс, приведем матрицу
систему к верхней треугольной форме.
Запишем общие формулы метода Гаусса. Пусть проведено исключение коэффициентов из (k-1)-го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:
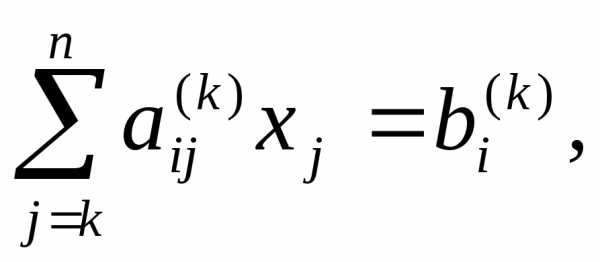
Умножим k-ю строку на
число 
m > k и вычтем из m-й строки.
Первый ненулевой элемент этой строки
обратится в нуль, а остальные изменятся
по формулам
k < m.
Весь процесс приведения называется ПРЯМЫМ ХОДОМ МЕТОДА ГАУССА. Вычисление неизвестных по формулам (1.4) называют ОБРАТНЫМ ХОДОМ метода.
3. Метод прогонки для решения систем линейных уравнений с трехдиагональной матрицей
Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы.
• Приведение трехдиагональной матрицы к верхней треугольной (прямой ход), В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное.• Запись обратного хода в виде , так как преобразованная матрица – двухдиагональная.
•Вывод
рекуррентного соотношения для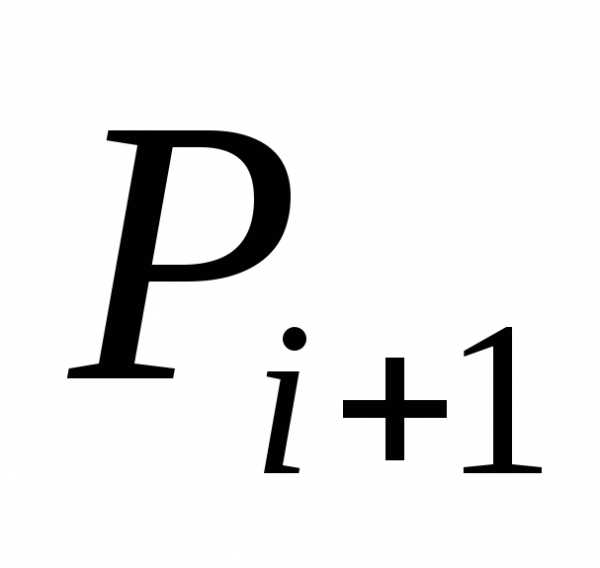 
и
через
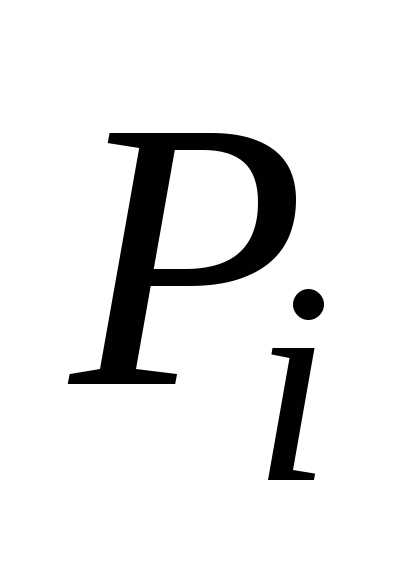и
и получение соотношения для
и
.
• Осуществление обратного хода метода прогонки и определение всех неизвестных.
Запишем систему линейных алгебраических уравнений с трехдиагональной матрицей в виде
i = 1,2,…, n, (3.1)
Матрица системы (1.6) имеет вид:
Прямой
ход метода прогонки сводится к исключению
неизвестного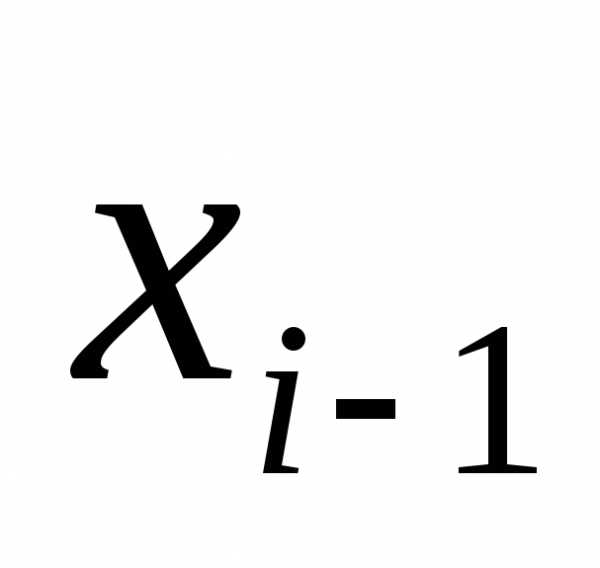 
в каждом уравнении системы. Получаемая
в результате прямого хода система
содержит в каждом уравнении только два
неизвестных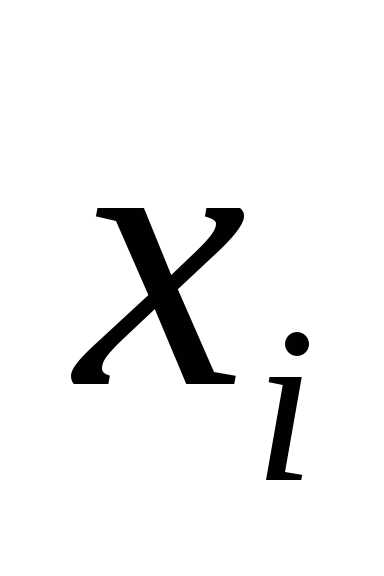
и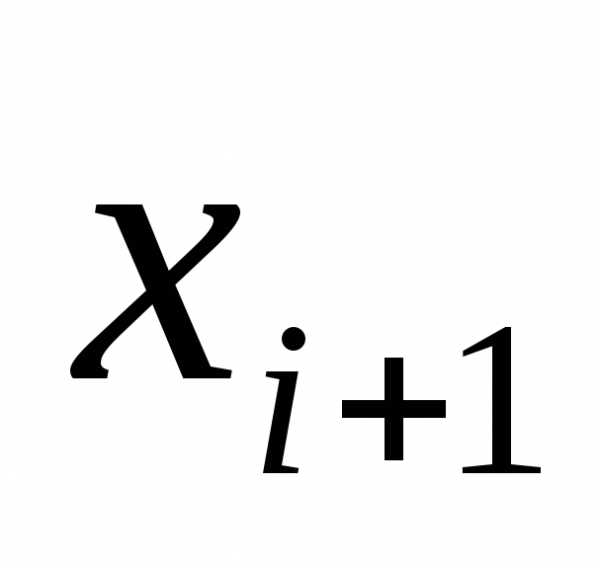
,
и матрица ее – верхняя треугольная с
двумя диагоналями. Запишемi-ю строку
преобразованной двухдиагональной
матрицы в виде
Если система (3.1) приведена к виду (3.2), то обратный ход метода Гаусса очевиден. Однако использование общих алгоритмов прямого и обратного хода нецелесообразно. Построим эффективную вычислительную схему, которая и составляет суть метода прогонки. Для этого, уменьшив в (3.2) индекс на единицу, запишем
Подставляя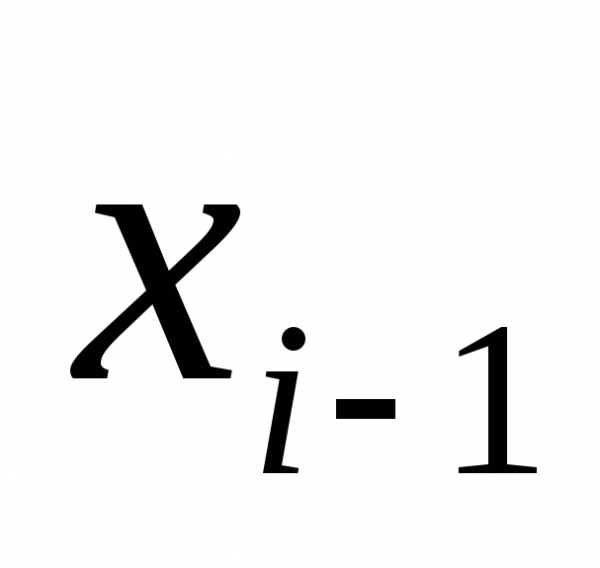 
в систему (3.1), получим соотношение
из которого нетрудно получить
Сравнивая это соотношение с (3.2), можем записать рекуррентные соотношения
(3.3)
для вычисления так называемых ПРОГОНОЧНЫХ КОЭФФИЦИЕНТОВ.
Для
начала прямого хода метода прогонки
необходимо задать начальные (стартовые)
значения прогоночных коэффициентов,
например,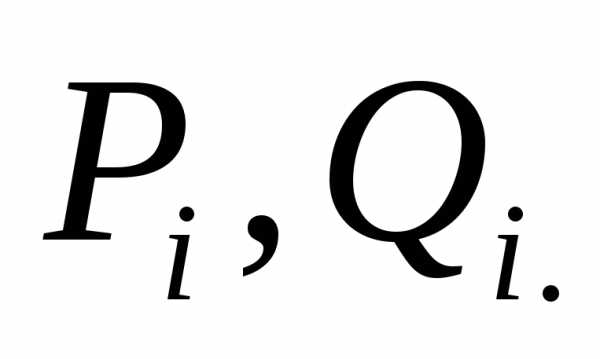
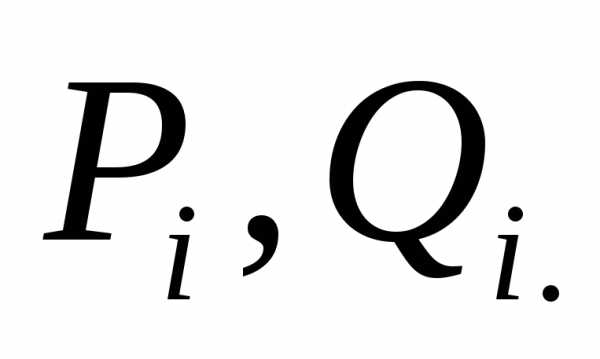в рассмотренной схеме вычислений не
требуются, так как значения коэффициентов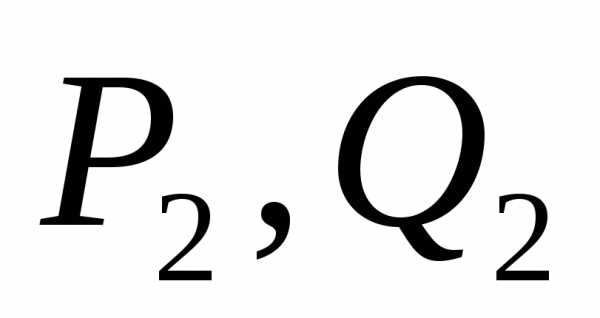
вычисляются
только через коэффициенты первого
уравнения системы (3.1): приi = 1 из (3.1)
получаем соотношение
Сравнивая это выражение с (3.2) приi =1, получаем
а значение
в обратном ходе вычисляем по соотношениюДля начала обратного хода метода прогонки
необходимо для вычислениязадать значение
.
Так как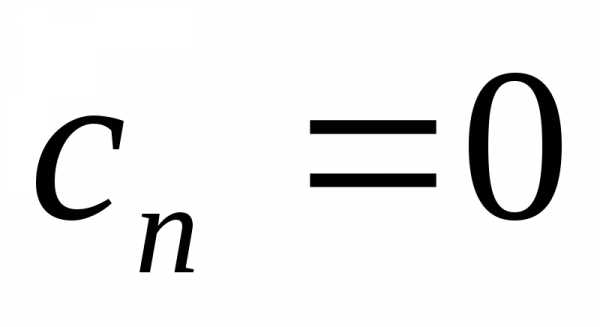
,
то из первого соотношения (3.3) вытекает,
что
и, следовательно, можно задать любое
значение для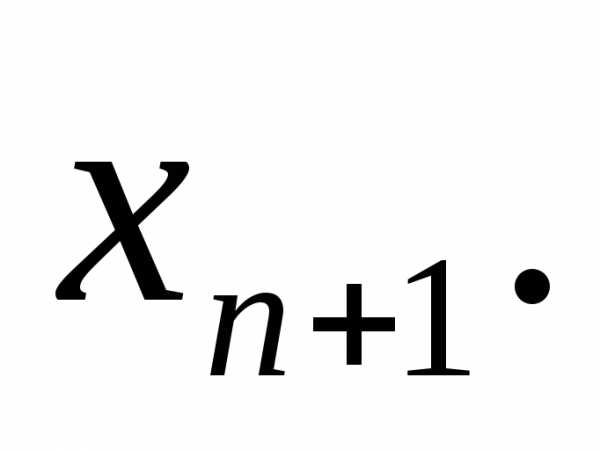
Обычно полагают 
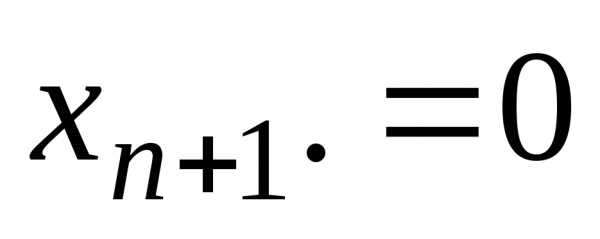,и тогда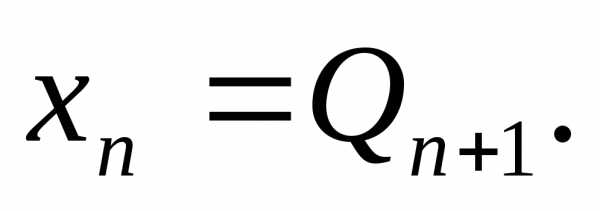 
studfiles.net
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными — это система уравнений вида
(1)
Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m — уравнений, n — количество неизвестных. x1, x2,…, xn — неизвестные, которые следует определить.
В системе (1) – фиксированные коэффициенты, b1, b2, …, bm — свободные члены — предполагаются известными.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .
Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.
Система линейных уравнений может быть представлена в матричной форме как:
или:
Ax = b
Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:
(2)
Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.
Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:
(3)
Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b1:A = A1, b=b1.
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
Имеем систему уравнений A2x = b2:
где
3 шаг.
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на
При этом получим систему A3x = b3:
(k+1)-ый шаг:
Здесь
Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
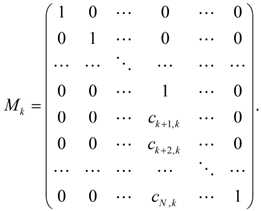
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:
и вектор
Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения
(5)
эквивалентного начальной системе линейных алгебраических уравнений.
При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
.
Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A — квадратная NxN — матрица.
Рассмотрим задачу Ax = b.
Пусть также некоторая норма в пространстве RN
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина называется числом обусловленности.
Очевидно:
- если A — диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.
Тогда справедливо следующее неравенство:
Доказательство. Имеем:
Так как
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
В начало
Содержание портала
statistica.ru