| Функция | Описание |
|---|---|
sqrt(x) | квадратный корень из xsqrt(16) = 4 |
abs(x) | абсолютное значение (модуль) xabs(-5) = 5 |
ln(x), log(x) | натуральный логарифм xln(e^2) = 2 |
log2(x) | логарифм по основанию 2 от xlog2(8) = 3 |
log3(x) | логарифм по основанию 3 от xlog3(81) = 4 |
lg(x), log10(x) | логарифм по основанию 10 от xlg(10000) = 4 |
exp(x) | возводит число Эйлера в степень xexp(2) = 7,389056 |
sin(x) | синус аргумента x, параметр x задается в радианахsin(pi/6) = 0,5 |
cos(x) | косинус аргумента x, параметр x задается в радианахcos(pi/6) = 0,866025 |
tan(x) | тангенс аргумента x, параметр tan(pi/6) = 0,57735 |
cotan(x) | котангенс аргумента x, параметр x задается в радианахcotan(pi/6) = 1,73205 |
asin(x), arcsin(x) | возвращает арксинус аргумента x в радианах |
acos(x), arccos(x) | возвращает арккосинус аргумента x в радианах |
atan(x), arctan(x) | возвращает арктангенс аргумента x в радианах |
acotan(x), arccotan(x) | возвращает арккотангенс аргумента x в радианах |
sinh(x) | гиперболический синус аргумента xsinh(x) = (exp(x) - exp(-x))/2 |
cosh(x) | гиперболический косинус аргумента xcosh(x) = (exp(x) + exp(-x))/2 |
tanh(x) | гиперболический тангенс аргумента xtanh(x) = (exp(x) - exp(-x))/(exp(x) + exp(-x)) |
asinh(x), arcsinh(x) | гиперболический арксинус аргумента x |
acosh(x), arccosh(x) | гиперболический арккосинус аргумента x |
atanh(x), arctanh(x) | гиперболический арктангенс аргумента x |
sec(x) | секанс аргумента xsec(x) = 1 / cos(x) |
cosec(x) | косеканс аргумента xcosec(x) = 1 / sin(x) |
round(x) | возвращает округленное значение xround(3,6) = 4 |
ceil(x) | округляет x в большую сторонуceil(3,6) = 4 |
floor(x) | округляет x в меньшую сторонуfloor(3,6) = 3 |
sgn(x) | «сигнум» — знак аргумента x возвращает -1 при x , |
grafikus.ru
Примеры графиков параметрических функций в пространстве
Поделиться в соцсетях:
\[ x = \cos(u)\cos(v) \\ y = \sin(u)\cos(v) \\ z = \sin(v) \\ u \in [{-\pi}; \pi], \quad v \in \Big[{-\frac{\pi}{2}}; \frac{\pi}{2}\Big] \]
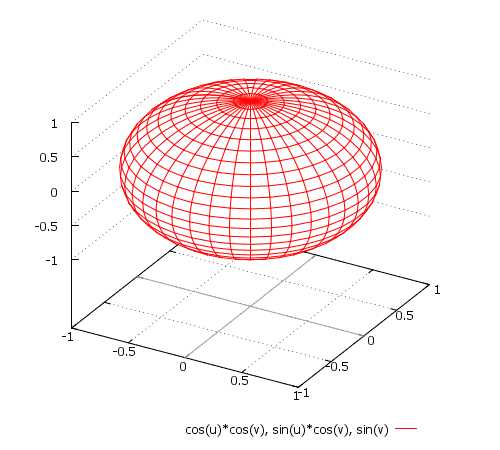
\[ x = \cos(u)\big(\cos(v) + 3\big) \\ y = \sin(u)\big(\cos(v) + 3\big) \\ z = \sin(v) \\ u \in [{-\pi}; \pi], \quad v \in [{-\pi}; \pi] \]
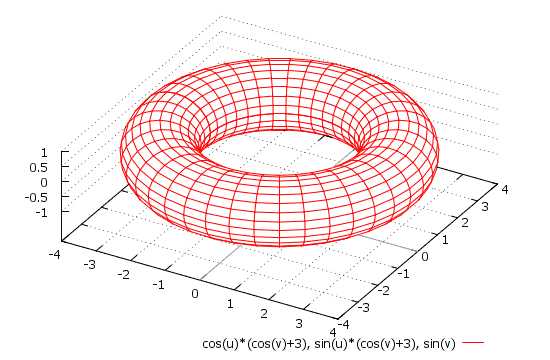
\[ x = \cos(u)\big(\cos(v) + 3\big) \\ y = \sin(u)\big(\cos(v) + 3\big) \\ z = \sin(v) + u \\ u \in [{-2\pi}; 2\pi], \quad v \in [{-\pi}; \pi] \]
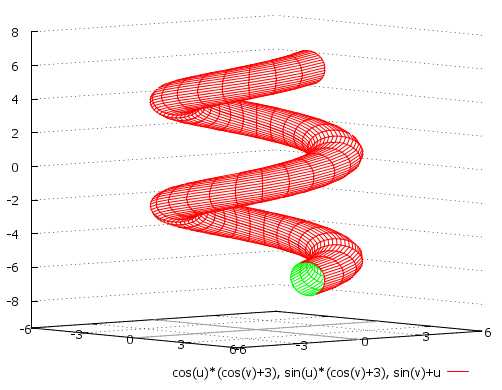
\[ x = u\cos(u)\big(\cos(v) + 1\big) \\ y = u\sin(u)\big(\cos(v) + 1\big) \\ z = u\sin(v) \\ u \in [0; 3\pi], \quad v \in [{-\pi}; \pi] \]

\[ x = u\cos(u)\big(\cos(v) + 1\big) \\ y = u\sin(u)\big(\cos(v) + 1\big) \\ z = u\sin(v) — \Big(\frac{u + 3}{8}\pi\Big)^2 — 20 \\ u \in [0; 8\pi], \quad v \in [{-\pi}; \pi] \]
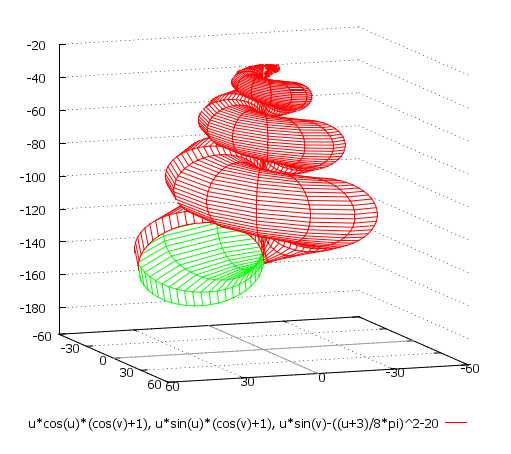
\[ x = \cos(u)\cos(v) + 3\cos(u)\Big(1,5 + \sin\frac{1,5u}{2}\Big) \\ y = \sin(u)\cos(v) + 3\sin(u)\Big(1,5 + \sin\frac{1,5u}{2}\Big) \\ z = \sin(v) + 2\cos(1,5u) \\ u \in [{-2\pi}; 2\pi], \quad v \in [{-\pi}; \pi] \]
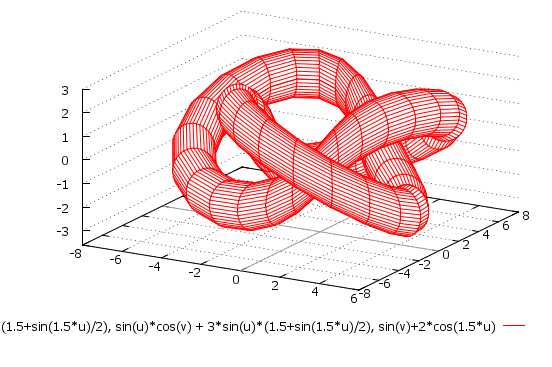
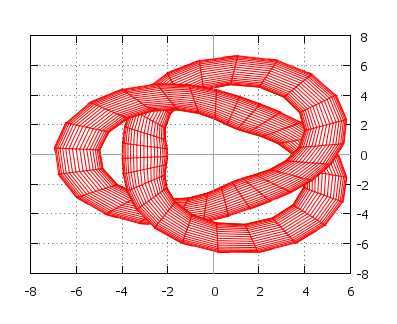
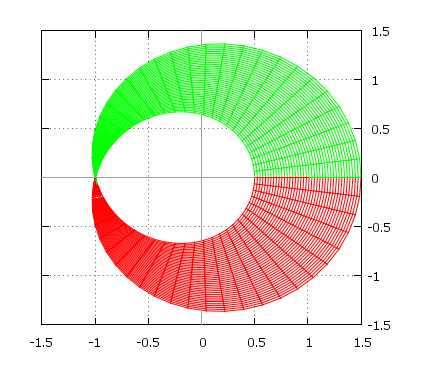
\[ x = \cos(u)\sin(v) \\ y = \sin(u)\sin(v) \\ z = \cos(v) + \lg\Big(\tan\Big(\frac{v}{2}\Big)\Big) + 0,2u — 4 \\ u \in [0; 4\pi], \quad v \in [0,001; 2] \]

\[ x = \bigg(1 + \frac{v}{2}\cos\Big(\frac{u}{2}\Big)\bigg)\cos(u) \\ y = \bigg(1 + \frac{v}{2}\cos\Big(\frac{u}{2}\Big)\bigg)\sin(u) \\ z = \frac{v}{2}\sin\Big(\frac{u}{2}\Big) \\ u \in [0; 2\pi], \quad v \in [{-1}; 1] \]

 © OddLabs, 2011-2019 |
Правильность результатов не гарантируется
© OddLabs, 2011-2019 |
Правильность результатов не гарантируетсяgrafikus.ru
Трехмерные графики функций в Excel.
Февраль 17th, 2014 Andrey K Загрузка…В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
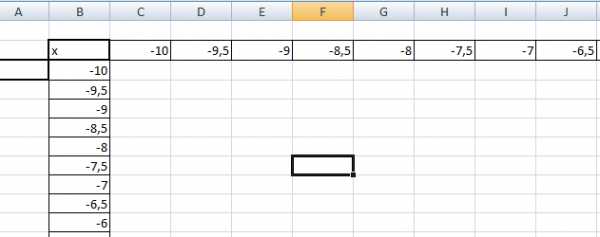
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
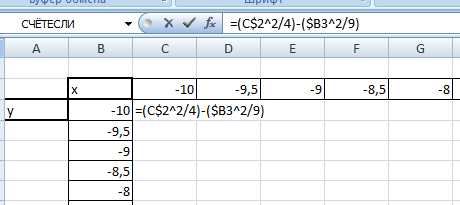
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
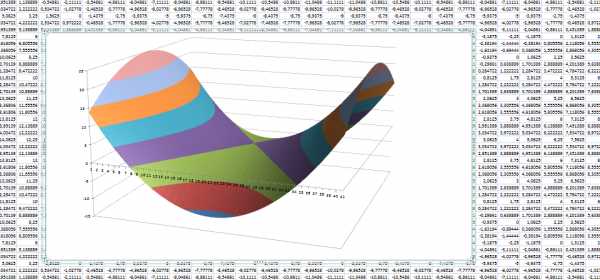
Аналогично строятся другие поверхности:
1) Эллиптический параболоид
2) Однополостный гиперболоид
3) Двухполостный гиперболоид
См. также «Построение графиков функций на плоскости в Excel»
на Ваш сайт.
krivaksin.ru
