Урок по теме «Функции y = sin x, y = cos x, их свойства и графики»
Разделы: Математика
Цели:
- Закрепление навыков построения графиков функций на основе изученного теоретического материала и перенос знаний в новую ситуацию.
- Развитие познавательного интереса к обучению.
Задачи:
- Использовать имеющиеся знания о свойствах функций в конкретных ситуациях.
- Уметь отстаивать свою точку зрения.
- Применять осознанное установление связей между аналитической и геометрической моделями тригонометрических функций.
ХОД УРОКА
I. Организационный момент
II.Опрос
Два ученика у доски выполняют задание:
Построить график функции: а) y = sin x; б)
III. Проверка домашнего задания
(Фронтальная работа. Учащиеся отвечают, а на экране демонстрируются слайды с поэтапным выполнением работы)
№ 671(в) Решите графически уравнение sin x = х + .
Ответ учащегося.
- Рассмотрим функцию y = sin x и построим ее график.
- Построим график линейной функции у = х + в этой же системе координат.
- Построенные графики пересекаются в одной точке А(–; 0), значит, заданное уравнение имеет один корень х = – .
№ 652 (б) найдите значение функции у = – sin (х +) при х =.
Решение:
Если х =, то у = – sin ( + ) = – sin (–) = sin = .
Дополнительные вопросы: Какие свойства функции здесь применили?
№ 654 (в, г) Найдите область определения функции: в) у = sin2x; г) у = .
Решение:
в) у = sin2x. D( f ) = ().
г) у = D( f ) = (), т.к. sin x +2 0 при любом значении х .
Дополнительные вопросы: Что такое область определения функции?
№ 655 (в, г) г Найдите область значений функции: в) у = sin2x; у = sin x.
Решение:
в) у = sin2x. Е( f ) = .
г) у = sin x. Е( f ) = .
Дополнительные вопросы:
1. Что такое множество значений функции?
2. Какие свойства функции еще не повторили?
IV. Ответ учащихся, работающих у доски
Дополнительные вопросы:
1. Что называется периодом функции?
2. Назовите основной период данных функций.
V. Устная работа
1. Вычислить:
2. Не выполняя построения графиков функций, определить, принадлежат ли точки графикам функции:
| а) y = sin x точка (; 1) б) y = cos x точка (2; –1). |
(Нет) (Нет) |
3. Какая функция называется периодической?
Является ли число 17 (8)
периодом функции y = sin x? y = cos x? (Нет
, да)
Назовите основной период для этих функций. (2)
4. Решите уравнение:
5. Найдите наибольшее и наименьшее значение функции на числовом промежутке:
| а) y = sin x на ; |
Ответы: 1 и –1 нет, 1 и –1 |
VI. Разминка
Учащиеся работают за партами по вариантам, 2 ученика у доски (за крыльями доски)/
Задание 1. Решите уравнение:
Взаимоконтроль (учащиеся меняются тетрадями и проверяют работу).
VII. Графическая линия
Задание 2. Построить график функции:
а) y = – sin x;
б) y = sin x +1.
в) y = – cos (
г) y = sin (x – ) + 1.
Учащиеся работают по вариантам, выбирая задания по своим силам. Представитель от группы рассказывает порядок построения графика, его ответ сопровождается соответствующими слайдами.
Задание 3. Решите графически уравнение:
| В-1 sin х = В-2 cos х = +1. |
Решение: х = х = 0 |
Учащиеся работают самостоятельно за партами.
Взаимоконтроль: учащиеся меняются тетрадями. Решение уравнений выводится на слайдах.
Задание 4. Построить график кусочной функции и перечислите ее свойства.
| В-1 f (x) = |
В-2 f (x) = |
Работа выполняется самостоятельно, желающие могут сдать тетради на проверку. Затем учащимся предлагается проверить свои работы с помощью слайдов.
VIII. Итоги урока
– На уроке мы исследовали свойства функций, научились строить графики функций и решать графически уравнения.
IX. Задание на дом: № 660 (в,г), № 671 (а,б), № 669.
22.02.2008
Поделиться страницей:urok.1sept.ru
| Найти точное значение | sin(30) | ||
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | y=sin(x) | ||
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
Внеклассный урок — Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это нечетная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках [2πn; π + 2πn] функция принимает положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Для построения графика функции y = sin x удобно применять следующие масштабы:
— на листе в клетку за единицу отрезка примем длину в две клетки.
— на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.
— на оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x:
|
0 | π | π | π | 2π | 5π | |
| | 1 | √3 | | √3 | 1 | |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. 9) Точки минимума функции: π + 2πn. наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf(x).
Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f(kx).
Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.
Причем k – любое действительное число.
При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x.
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.

Свойства функции y = tg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2, 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция на интервале (–π/2; π/2). 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция возрастает на интервале (–π/2; π/2). 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
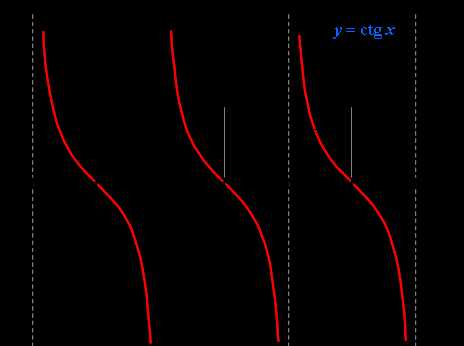
Свойства функции y = ctg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция. 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число. 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
raal100.narod.ru
