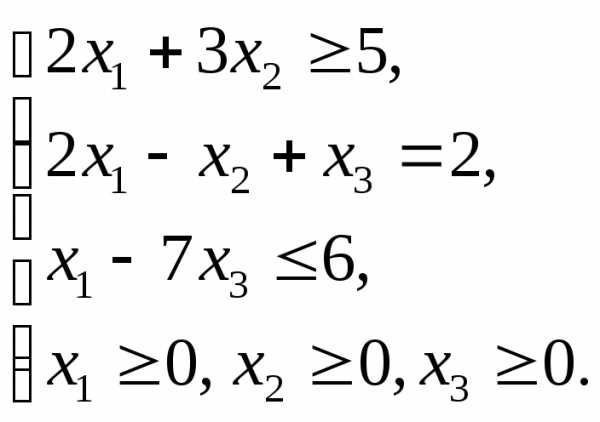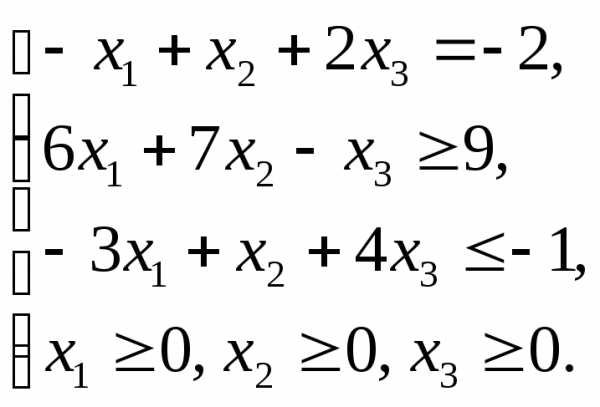Графический метод — линейное программирование
Описание метода
Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.
Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .
Построение области допустимых решений
Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.
Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).
Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.
Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.
Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.
Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).
Нахождение экстремума целевой функции
Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.
Теперь мы можем искать экстремум целевой функции
(1.1) .
Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .
Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.
Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.
Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.
Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .
Пример решения задачи линейного программирования графическим методом
Условие задачи
Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.
Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.
Решение
Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)
Тогда экономико-математическая модель задачи имеет вид:
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.
Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).
Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.
Пример 2
Условие задачи
Решить задачу линейного программирования графическим методом.
Решение
Решаем графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).
Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).
Строим прямую .
Строим прямую (ось абсцисс).
Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.
Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Решение задачи: ;
Ответ
.
Пример отсутствия решения
Условие задачи
Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.
Решение
Решаем задачу графическим методом.
Проводим оси координат и .
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).
Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).
Прямые и являются осями координат.
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.
Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .
Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.
Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:
Ответ
Максимального значения не существует.
Минимальное значение
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Графический метод решения задач линейного программирования
На этом уроке будем знакомиться с графическим методом решения задач линейного программирования, то есть, таких задач, в которых требуется найти такое решения системы линейных уравнений и (или) неравенств (системы ограничений), при котором функция цели — линейная функция — принимает оптимальное значение.
Ввиду того, что наглядность графического решения достигается лишь на плоскости, мы можем познакомиться с графическим представлением задачи только в двумерном пространстве. Это представление пригодно для системы ограничений-неравенств с двумя переменными или для систем уравнений, в которых число переменных на 2 превышает число уравнений, то есть число свободных переменных равно двум.
Поэтому графический метод имеет такие узкие рамки применения, что о нём как об особом методе решения задач линейного программирования говорить нельзя.
Однако для выработки наглядных представлений о решениях задач линейного программирования графический метод представляет определённый интерес. Кроме того, он позволяет геометрически подтвердить справедливость теорем линейного программирования.
Итак, задача линейного программирования. Требуется найти неотрицательные значения переменных и , удовлетворяющих системе неравенств
при которых линейная форма принимает оптимальное значение.
Из теории и практики решения систем линейных неравенств известно, что множество всех решений данной системы, то есть множество пар чисел и , удовлетворяющих системе, составляет многоугольник этой системы. Допустим, что это пятиугольник ABCDE (рисунок внизу).
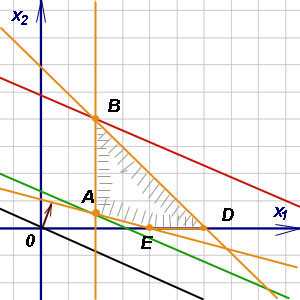Линейная форма
графически означает семейство параллельных между собой прямых. При конкретном числовом значении
F линейная форма изобразится в виде некоторой прямой. Каждую из прямых этого семейства
принято называть линией уровня. На рисунке построена линия уровня
(чёрного цвета, проходит через начало координат), соответствующая значению F =0.Если исходную линию уровня передвигать вправо, то значение F при этом возрастает. Нужное направление движения исходной линии уровня можно установить следующим образом. Коэффициенты при переменных в уравнении прямой служат координатами вектора, перпендикулярного этой прямой. Таким образом, получаем градиент — вектор (на рисунке бордового цвета). Значения функции F возрастают при перемещении исходной линии уровня в направлении вектора .
Среди прямых упомянутого семейства параллельных прямых прямые
Из основных теорем линейного программирования известно, что линейная форма достигает максимального и минимального значений в крайних точках многогранника решений. Это значит, что опорные прямые mn и MN характеризуют экстремальные значения линейной формы (функции цели), то есть в точках А и С линейная форма достигает оптимальных значений. В точке А, находящейся ближе к началу координат, функция цели достигает минимального значения, а в точке С, находящейся дальше от начала координат, — максимального значения.
1. Построить многоугольник решений системы неравенств.
3. Двигать прямую (или линейку) вдоль градиента — вектора параллельно линии равных значений в сторону многоугольника решений до соприкосновения с многоугольником решений. Если первая встреча с многоугольником решений произойдёт в крайней точке с координатами , то в этой точке функция цели достигает минимального значения. Если первая встреча произойдёт со стороной многоугольника, то данная функция цели достигает минимума во всех точках этой стороны.
4. Двигаясь дальше, придём к некоторому опорному положению, когда прямая будет иметь одну общую точку с многоугольником решений. В этой точке функция цели достигает своего максимума.
5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения — в вершине, более удалённой от начала координат.
Пример 1. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Построим многоугольник решений. Для этого начертим граничные прямые. Из первого неравенства запишем уравнение . Это уравнение первой граничной прямой. Найдём точки пересечения этой прямой с осями координат. При из уравнения получим , при получим . Это значит, что первая прямая отсекает от осей координат отрезки и .
Аналогично строим остальные граничные прямые. Вторая прямая от осей координат отсекает отрезки, равные 6. Третья прямая проходит параллельно оси , отсекая на оси отрезок, равный 2. Четвёртая прямая имеет уравнение . Она совпадает с осью .
Из рисунка ниже видно, что множество точек четырёхугольника ABDE удовлетворяет всем четырём неравенствам системы.
Следовательно, четырёхугольник ABDE является многоугольником решений системы (заштрихован вовнутрь).
Начертим линию равных значений функции цели. Приняв в равенстве F =1, получим, что эта линия отсекает отрезки 1 и 1/3 соответственно на оси и на оси . Проведём прямую через эти точки (на чертеже она чёрного цвета).
Двигая эту прямую параллельно самой себе в направлении градиента — вектора
(бордового цвета),
получим опорные прямые. Первая прямая (зелёного цвета) имеет с многоугольником общую точку
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 3. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
где .
Правильное решение и ответ.
Пример 4. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
где .
Правильное решение и ответ.
До сих пор полученные выводы были основаны на том, что множество решений задачи линейного программирования сконфигурировано так, что оптимальное решение конечно и единственно. Теперь рассмотрим примеры, когда это условие нарушается. В этих примерах многоугольник решений строится так, как показано в предыдущих примерах, остановимся же на признаках, которые отличают эти исключительные примеры.
Пример 5. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке изображены: неограниченная многогранная область решений данной системы ограничений, исходная линия уровня (чёрного цвета), вектор (бордового цвета), указывающий направление движения исходной линии уровня для нахождения максимума целевой функции.
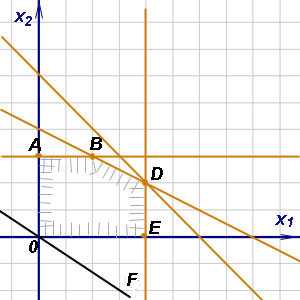
Легко заметить, что функция F может неограниченно возрастать при заданной системе ограничений, поэтому можно условно записать, что .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 6. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. Изображённая на рисунке ниже область не содержит ни одной общей точки, которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива и не может содержать ни одного решения, в том числе и оптимального.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 8. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке ниже изображены область решений системы ограничений и линия уровня (чёрного цвета). Если передвигать линию уровня параллельно исходной в направлении вектора , то она выйдет из области решений не в одной точке, как это было в предыдущих примерах, а сольётся с прямой CD, которая является граничной линией области решений.
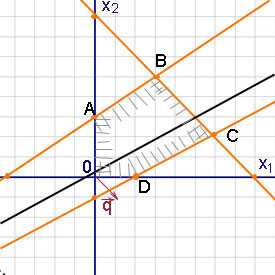
Все точки отрезка CD дают одно и то же значение функции цели, которое и служит её оптимальным значением: . Следовательно, имеется не одно, а бесчисленное множество оптимальных решений, совпадающих с точками отрезка CD, в частности, с двумя угловыми точками C и D. Этот пример показывает, что в некоторых случаях единственность оптимального решения нарушается.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Напоследок следует заметить, что строить многогранник решений можно и другим способом, отличающимся о того, который мы рассматривали. А именно: можно не искать точки пересечения прямых с осями координат, а искать точки пересечения прямых. Для этого последовательно решаются системы из двух уравнений, так, чтобы решениями были точки пересечения всех прямых. Полученные точки и будут вершинами многогранника решений. Этот способ иногда бывает удобным в случаях, когда точки пересечения прямых с осями координат — дробные числа и, неправильно отложив точку пересечения, можно получить ошибку и в поиске точек пересечения самих прямых.
Начало темы «Линейное программирование»
Поделиться с друзьями
function-x.ru
3 Графический метод решения злп
Наиболее простым и наглядным методом решения ЗЛП является графический метод. Он применяется для решения задач с двумя переменными, заданными в неканонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.
Рассмотрим задачу с двумя переменными
(1) | |
| (2) |
Графический метод основывается на возможности графического изображения области допустимых решений и нахождения среди них оптимального.
Геометрически каждое ограничение системы (2) представляет собой полуплоскость с граничной прямой. Для того, чтобы определить, какая из двух полуплоскостей является областью решения, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно верное, то областью решения является та полуплоскость, откуда взята точка, если неверное, то полуплоскость, не содержащая точку. Условия неотрицательности определяют полуплоскости с граничными прямыми. Если система (2) совместна (имеет решение), то полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы ограничений (2). Совокупность этих точек называетсямногоугольником решений.
Возможны следующие варианты области допустимых решений:
x1
а) ОДР – замкнутое множество (многоугольник) | б) ОДР – открытое множество | в) ОДР – пустое множество (Система ограничений не совместна) |
Рисунок 1 – Виды области допустимых решений (ОДР)
Многоугольник
решений также может быть и точкой, и
отрезком, и лучом. Для нахождения среди
допустимых решений оптимального решения
используют опорную прямую и линии
уровня. Линией уровня называется прямая,
на которой целевая функция принимает
постоянное значение
,
а опорная прямая – линия уровня, которая
имеет хотя бы одну общую точку с областью
допустимых решений и по отношению к
которой эта область находится в одной
из полуплоскостей. ОДР имеет не более
двух опорных прямых. Изменение значения
целевой функцииидет по направлению вектора
.
Алгоритм графического решения ЗЛП с двумя переменными:
Строят ОДР как пересечение m полуплоскостей.
Если ОДР не пустое множество, то определяют направление возрастания (убывания) целевой функции Z, т.е. строят вектор
.Строят линию уровня , перпендикулярную вектору
.Линию уровня перемещают в направлении вектора, в случае максимизации функции, или в противоположном направлении, в случае минимизации до тех пор, пока она не станет опорной прямой. Находят значение целевой функции в полученных точках или определяют, что значение целевой функции неограниченно.
.
.Рассматриваются различные расположения опорной прямой по отношению к ОДР:
x1
а) Min Z в () A Max Z в () B | б) Min Z в () A Max Z = ∞ | в) Min Z в любой () отрезка AB Max Z в () C |
Рисунок 2 – Расположение опорной прямой относительно ОДР
Пример: Решить графически ЗЛП:
Решение: Сначала проведем оси: на горизонтальной будем откладывать значения переменной x1 , а на вертикальной x2 . Далее рассмотрим условия неотрицательности переменных . Эти два ограничения показывают, что ОДР будет находиться в 1-ой четверти. Чтобы учесть оставшиеся ограничения, заменим неравенства на равенства, а затем на плоскости проведем эти прямые. Например, неравенствозаменяем на равенство, которое проходит через точки (0; 2) и (-2; 0). Обозначим эту прямую 1 . Определим полуплоскость, выбрав контрольную точку (0; 0). Так как- верное неравенство, то точки полуплоскости, содержащей (0; 0) удовлетворяют первому ограничению. Аналогично рассматриваем оставшиеся ограничения.
Рисунок 3 – Иллюстрация решения задачи
Получена
область допустимых решений – многоугольникABCDE.
Строим вектор 
и
линию уровня.
Перемещаем линию уровня вдоль вектора
до опорной прямой (обозначены пунктирными
линиями). Эта прямая проходит через
точки А и С, причем в точке А определяетсяMin
Z,
а в точке С — Max
Z.
Определим координаты точки A
как пересечение прямой 3 и прямой x2=0:
Значит,
Определим координаты точки С как пересечение прямых 2 и 4 :
Значит,
Графическим методом решаются задачи линейного программирования, записанные в каноническом виде и удовлетворяющие условию , где n – число неизвестных системы ограничений; r – ранг системы векторов условий. Если уравнения системы ограничений линейно независимы, то ранг r равен числу уравнений системы m.
Пример: Решить задачу линейного программирования
Решение: Метод применим, так как . Выпишем расширенную матрицу системы ограничений, добавив строку, содержащую коэффициенты целевой функции:
Методом Жордана — Гаусса приведем систему уравнений – ограничений к равносильной разрешенной, одновременно исключив разрешенные неизвестные из целевой функции:
Запишем задачу в преобразованном виде:
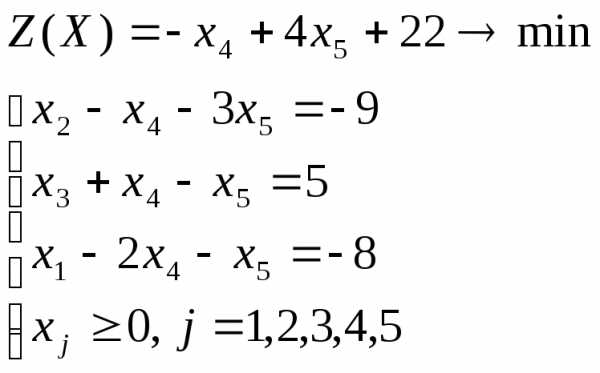
Отбросим в уравнениях неотрицательные разрешенные неизвестные х1, х2, х3 и заменим знак равенства знаками неравенства « ≤ », получим вспомогательную задачу линейного программирования с двумя переменными
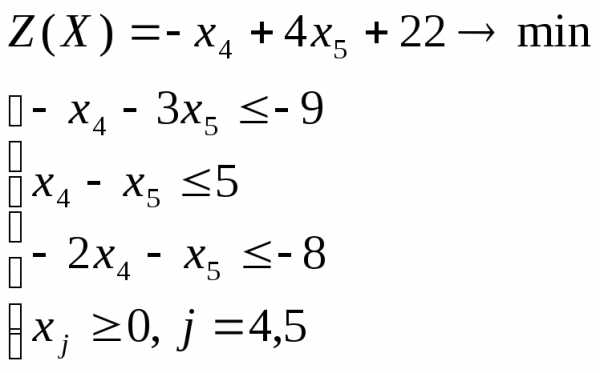
Решим задачу графическим методом. Свободный член в целевой функции 22 на отыскание оптимального решения не влияет и учитывается только при вычислении значения целевой функции.
Рисунок 4 – Графическая иллюстрация решения задачи
Находим оптимальное
решение вспомогательной задачи 
:
+
.
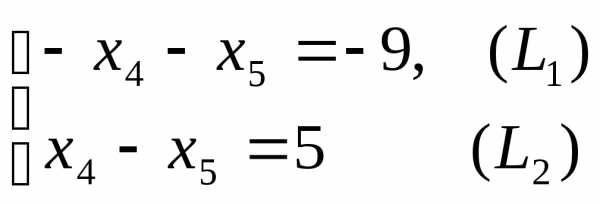Значит,
Вычисляем минимальное значение целевой функции
Находим оптимальное решение исходной задачи. Для этого используем систему ограничений в разрешенном виде:
Получаем
Ответ:
studfiles.net
1.4. Графический метод решения задач линейного программирования сnпеременными
Графическим
методом решаются ЗЛП, если в ее канонической
форме записи число переменных 
и число линейно независимых уравнений
связаны соотношением.
Алгоритм графического метода решения ЗЛП со многими переменными (n>2)
Записать каноническую форму ЗЛП.
Выбрать две свободные переменные.
Выразить все остальные переменные через свободные, т.е. решить систему ограничений заданной задачи.
Выразить целевую функцию через свободные переменные.
Полученную двухмерную задачу решить графическим методом.
Найдя координаты оптимального решения двухмерной задачи, определяем остальные координаты оптимального решения исходной задачи.
Значение целевой функции на оптимальном плане двухмерной задачи совпадает со значением целевой функции на оптимальном плане исходной задачи.
Пример 1.11
Решим графически ЗЛП, математическая модель которой составлена в примере 1.2.
;
Решение
Перейдем к эквивалентной задаче с двумя переменными.
Математическую модель задачи представим в канонической форме записи:
;
Пусть
переменные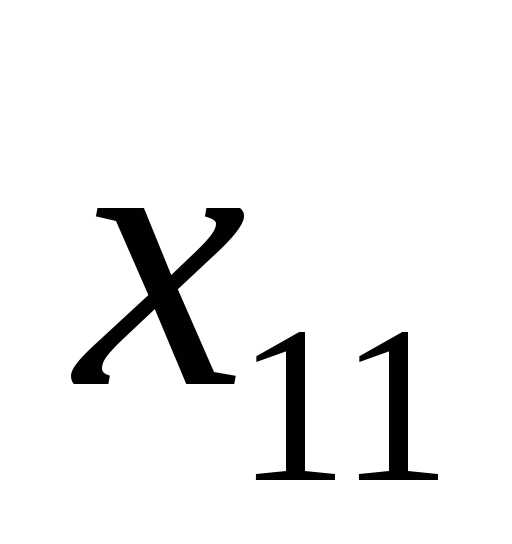 
и
будут свободными, а все остальные
переменные базисными. Выразим все
базисные переменные через свободные.
Выразим целевую функцию через свободные переменные.
Учитывая условия неотрицательности базовых переменных, получим эквивалентную задачу с двумя переменными:
или 
Полученную двухмерную задачу решим графическим методом.
Построим
ОДР задачи (Рис. 1.7). Для этого в системе
координат 
на плоскости изобразим граничные прямые:
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на данной прямой, например (0;0). Ограничения
означают, что ОДР лежит вI
четверти системы координат 
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это многоугольникABCDE.
Рис. 1.7
Строим
вектор-градиент целевой функции
=(3;6).
Оптимальное решение достигается в точке E(3;0).
Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:
Итак, решение исходной задачи: ,.
Экономический смысл полученного решения задачи:
для того, чтобы затраты были минимальными и составили 52 усл. ден. ед. необходимо, чтобы оборудование А1 выпускало 3 часа продукцию P1, оборудование А2 выпускало 4 часа продукцию P1 и 6 часов продукцию P2.
Преобразовать ЗЛП к эквивалентной двумерной ЗЛП можно и не записывая исходную задачу в канонической форме. Достаточно из ограничений-равенств системы выразить базисные переменные через выбранные две свободные и подставить это выражение всюду, где они встречаются в ограничениях-неравенствах и в целевой функции. Учитывая условия неотрицательности базисных переменных двумерная модель будет иметь то же количество ограничений, что и исходная. Таким образом, графическим методом можно решить лишь ту ЗЛП с n переменными, система ограничений которой имеет не менее n–2 линейно-независимых ограничений-равенств.
Пример 1.12
Решим графически ЗЛП:
;
Решение
Перейдем к эквивалентной задаче с двумя переменными.
Пусть
переменные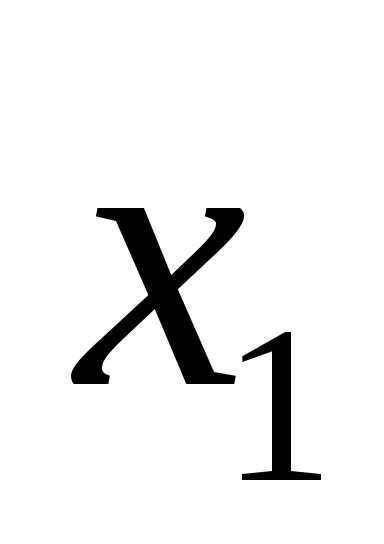 
и
будут свободными, а все остальные
переменные базисными. Выразим все
базисные переменные через свободные.
Сделаем это последовательно. Сначала
выразим, например, из второго
ограничения-равенства базисную переменную
и подставим это выражение всюду, где
она встречается в модели:
;
Раскрыв
скобки, приведя подобные и учитывая
условие неотрицательности переменной 
,
получим следующую модель от трех
переменных, эквивалентную исходной:
;
Затем
выразим, например, из первого
ограничения-равенства базисную переменную 
и подставим это выражение всюду, где
она встречается в модели:
;
Раскрыв
скобки, приведя подобные и учитывая
условие неотрицательности переменной 
,
получим следующую модель от двух
переменных, эквивалентную исходной:
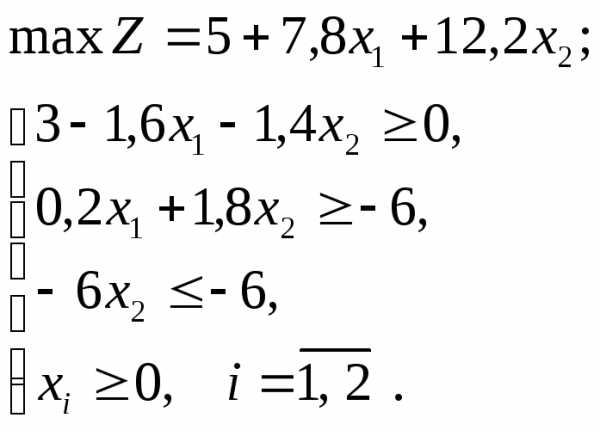или 
Полученную двухмерную задачу решим графическим методом.
Построим
ОДР задачи (Рис. 1.8). Для этого в системе
координат 
на плоскости изобразим граничные прямые:
Затем
определим, какую полуплоскость определяет
соответствующее неравенство, подставив
координаты какой-нибудь точки, не лежащей
на данной прямой, например (0;0). Ограничения
означают, что ОДР лежит вI
четверти системы координат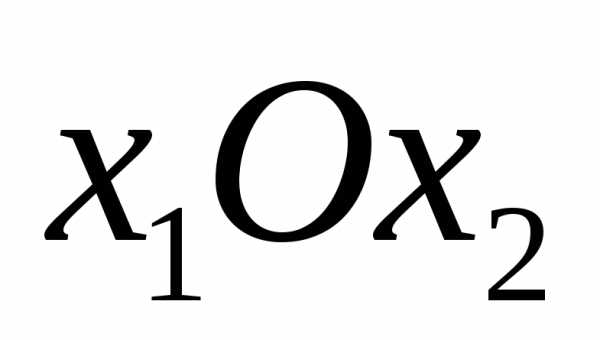 
.
Соответствующие полуплоскости на
рисунке показаны стрелками. Пересечение
указанных полуплоскостей и определяет
ОДР данной задачи – это треугольникABC.
Вектор-градиент
целевой функции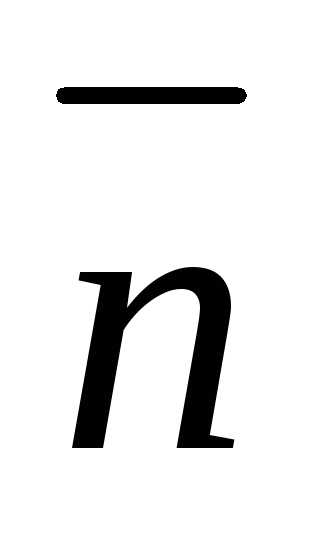
=(7,8;12,2).
Так как нас интересует направление
вектора-градиента, а не его длина, то
можно изобразить вектор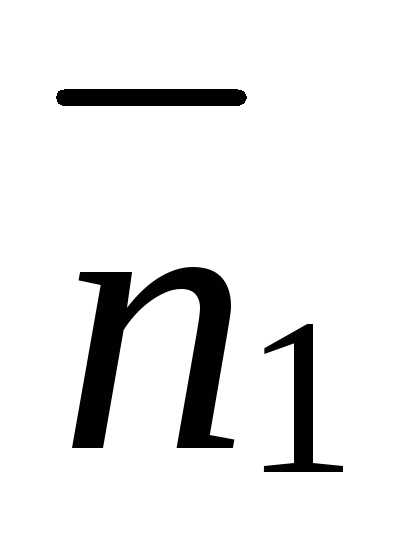
=(3,9;6,1)=0,5
,
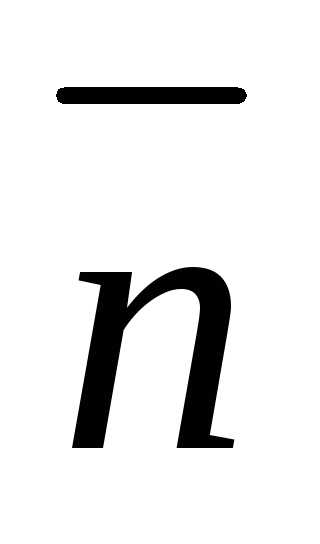который в два раза меньше вектора
градиента.
Рис. 1.8
Оптимальное
решение достигается в точке В, которая
лежит на пересечении прямой 
и оси
.
Для определения ее координат необходимо
решить систему уравнений:
Откуда
.
Таким образом,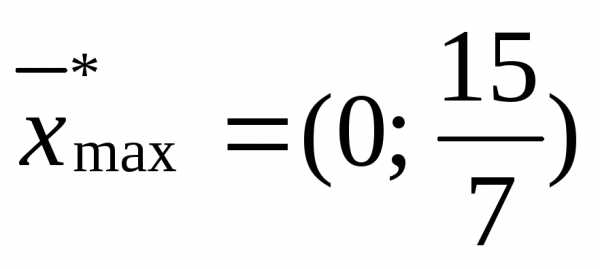
.
Подставив значение
и
в целевую функциюZ,
получаем:
.
Перейдем к решению исходной задачи. Т.е. найдем значения базисных переменных:
,
.
Итак,
решение исходной задачи: 
,.
Задачи
Решить ЗЛП графическим методом (1.4.1 – 1.4.8)
1.4.1 ; 1.4.3 ; 1.4.5 ; 1.4.7 ; | 1.4.2 ; 1.4.4 ; 1.4.6 ; 1.4.8 ; |
1.4.9 – 1.4.11
Решить задачи 1.1.4, 1.1.9, 1.1.11 (соответственно) графическим методом.
studfiles.net
05. Графический метод решения ЗЛП
Графическим методом целесообразно решать ЗЛП, содержащие не более двух переменных.
Алгоритм графического метода рассмотрим применительно к задаче:
3Х1 + 2Х2 (3.16)
При
Х1 + 2Х2 6 (а)
2Х1 + Х2 8 (б)
Р = Х1+0,8Х2 5 (в) (3.17)
-Х1 + Х2 1 (г)
Х2 2 (д)
Х1 0, Х2 0 (е)
Шаг 1. Строим область допустимых решений (3.17) – область Р, т. е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗЛП. Каждое из неравенств (а)–(д) системы ограничений (3.17) задачи геометрически определяет полуплоскость соответственно с граничными прямыми:
Х1 + 2Х2 = 6 (а)
2Х1 + Х2= 8 (б)
Х1+0,8Х2= 5 (в)
-Х1 + Х2= 1 (г)
Х2= 2 (д)
Условия неотрицательности переменных (е) ограничивают область допустимых решений первым квадратом. Области, в которых выполняются соответствующие ограничения (3.17) в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных (рис. 3.1).
Рис. 3.1
Если система неравенств (3.17) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям.
Полученная таким образом область допустимых решений Р – планов ЗЛП (см. рис. 3.1) есть многоугольник ABCDEF – замкнутое, ограниченное, выпуклое множество с шестью крайними, или угловыми, точками: A, B, C, D, E, F.
Шаг 2. Строим вектор-градиент линейной формы , указывающий направления возрастания функции .
Шаг 3. Строим прямую С1Х1 + С2Х2 = const – линию уровня функции , перпендикулярную вектору-градиенту :
3Х1 + 2Х2 = const (рис.3.2).
Рис. 3.2
Шаг 4. В случае максимизации передвигают прямую 3Х1 + 2Х2 = const в направлении вектора до тех пор, пока она не покинет область Р. Крайняя точка (или точки) области, в которой линия уровня покидает допустимую область, и является решением задачи (рис. 3.3).
Рис. 3.3
Крайняя точка С – точка максимума , С = Лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений:
Х1 + 2Х2 = 6
2Х1 + Х2 = 8.
Откуда Х*1 = 10/3; X*2 = 4/3 или = (10/3; 4/3).
Подставляя значения Х*1 и X*2 в функцию , найдем
max= = 3 . 10/3 + 2 . 4/3 = 38/3.
Замечания.
1. В случае минимизации Прямую С1Х1 + С2Х2 = const надо перемещать в направлении (-), противоположном .
2. Если допустимая область решений Р представляет собой неограниченную область и прямая при движении в направлении вектора (или противоположном ему) не покидает Р, то в этом случае Не ограничена сверху (или снизу), т. е. (или ).
Пример 3.1. Графическим способом решить ЗЛП
Max (2Х1 + Х2)
при
Х1 — Х2 2 (1)
Х1 + 3Х2 3 (2)
7Х1 — Х2 2 (3)
Х1,2 0.
Шаг 1. Строим область Р (рис. 3.4). Она является неограниченной.
Шаг 2. Строим вектор .
Шаг 3. Строим линию уровня функции = 2Х1 + Х2 = const.
Шаг 4. Передвигая линию уровня в направлении вектора , убеждаемся в неограниченном возрастании функции , то есть .
Пример 3.2. Решить графическим методом ЗЛП. Найти
Х1 + 3Х2
При ограничениях
2Х1 + 3Х2 6 (1)
Х1 + 2Х2 5 (2)
Х1 4 (3)
0 Х2 3 (4)
Рис. 3.5
Из рис. 3.5 видно, что область допустимых решений пуста (Р=).
Задача не имеет решения.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Примеры решения задач — Линейное программирование — Исследование операций — ЭММ
Условие задачи
Цех изготавливает изделия А и Б. Расход сырья, его запас и прибыль от реализации каждого изделия указаны в таблице.
| Вид сырья | Расход на изделие | Запас | |
| А | Б | ||
| 48 | 12 | 600 | |
| 24 | 21 | 840 | |
| 15 | 27 | 1350 | |
| Прибыль | 12 | 18 | |
Найти план производства изделий, обеспечивающий предприятию максимальную прибыль от их реализации. Решить задачу графическим методом.
Решение задачи
Экономико-математическая модель задачи
Через и обозначим количество выпускаемой продукции вида А и Б соответственно.
Тогда ограничения на ресурсы:
Кроме того, по смыслу задачи
Целевая функция, выражающая получаемую прибыль от реализации изделий:
Получаем следующую экономико-математическую модель:
Построение чертежа
Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые:
Найдем точки, через которые проходят прямые:
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.
Для определения полуплоскости возьмём любую точку, например точку не принадлежащую прямой (1), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:
Области решений соответствующего 1-го неравенства соответствует левая полуплоскость
Возьмём любую точку, например точку не принадлежащую прямой (2), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:
Области решений соответствующего 2-го неравенства соответствует левая полуплоскость
Для определения полуплоскости возьмём любую точку, например точку не принадлежащую прямой (3), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:
Области решений соответствующего 3-го неравенства соответствует нижняя полуплоскость
Областью допустимых решений является фигура .
Строим вектор , координаты которого пропорциональны коэффициентам целевой функции.
Перпендикулярно к построенному вектору проводим линию уровня .
Строим вектор , координаты которого пропорциональны коэффициентам целевой функции.
Перпендикулярно к построенному вектору проводим линию уровня .
Нахождение оптимального плана
Перемещаем линию уровня в направлении вектора так, чтобы она касалась области допустимых решений в крайней точке. Решением на максимум является точка D, координаты которой находим как точку пересечения прямой (2) и оси .
Таким образом, необходимо выпускать 40 ед. изделия Б. Изделие а выпускать невыгодно. При этом прибыль будет максимальной и составит 720 д.е.
mathminsk.com
Решить графически задачу — 8 Февраля 2015 — Примеры решений задач
Задача. Решить графически задачу линейного программирования, определив экстремальное значение целевой функции:
при ограничениях
Решение.
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Построим уравнение 3x1+x2 = 9 по двум точкам.
Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 9. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 3. Соединяем точку (0;9) с (3;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 3 • 0 + 1 • 0 — 9 ≤ 0, т.е. 3x1+x2 — 9≥ 0 в полуплоскости выше прямой.
Построим уравнение x1+2x2 = 8 по двум точкам.
Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 4. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 8. Соединяем точку (0;4) с (8;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 + 2 • 0 — 8 ≤ 0, т.е. x1+2x2 — 8≥ 0 в полуплоскости выше прямой.
Построим уравнение x1+x2 = 8 по двум точкам.
Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 8. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 8. Соединяем точку (0;8) с (8;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 + 1 • 0 — 8 ≤ 0, т.е. x1+x2 — 8≤ 0 в полуплоскости ниже прямой.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
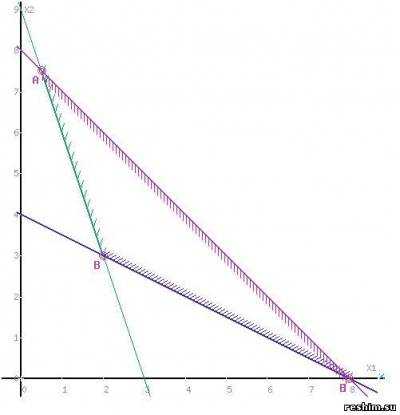
Проверить правильность построения графиков функций можно с помощью калькулятора
Рассмотрим целевую функцию задачи F = 4x1+6x2 → min.
Построим прямую, отвечающую значению функции F = 0: F = 4x1+6x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (4; 6). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
Прямая F(x) = 4x1+6x2 пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+x2=9
x1+2x2=8
Решив систему уравнений, получим: x1 = 2, x2 = 3
Откуда найдем минимальное значение целевой функции:
F(X) = 4*2 + 6*3 = 26
www.reshim.su