Вы искали интервал сходимости степенного ряда онлайн калькулятор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти интервал сходимости степенного ряда онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «интервал сходимости степенного ряда онлайн калькулятор».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как интервал сходимости степенного ряда онлайн калькулятор,найти интервал сходимости степенного ряда онлайн,найти область сходимости ряда онлайн калькулятор,найти область сходимости функционального ряда онлайн решение,область сходимости функционального ряда онлайн,онлайн калькулятор найти область сходимости ряда,онлайн калькулятор область сходимости ряда,степенные ряды онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и интервал сходимости степенного ряда онлайн калькулятор. Просто введите задачу в окошко и нажмите «решить» здесь (например, найти область сходимости ряда онлайн калькулятор).
Где можно решить любую задачу по математике, а так же интервал сходимости степенного ряда онлайн калькулятор Онлайн?
Решить задачу интервал сходимости степенного ряда онлайн калькулятор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Сходимость ряда онлайн
Проверить сходимость ряда можно несколькими способами. Во-первых можно просто найти сумму ряда. Если в результате мы получим конечное число, то такой ряд сходится. Например, поскольку
то ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.
Одним из таких методов является признак Даламбера, который записывается следующим образом:
здесь и соответственно n-ый и (n+1)-й члены ряда, а сходимость определяется значением D: Если D < 1 — ряд сходится, если D > 1 — расходится. При D = 1 — данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью признака Даламбера. Сначала запишем выражения для и . Теперь найдем соответствующий предел:
Поскольку , в соответствии с признаком Даламбера, ряд сходится.
Еще одним методом, позволяющим проверить сходимость ряда является радикальный признак Коши, который записывается следующим образом:
здесь n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением D: Если D < 1 — ряд сходится, если D > 1 — расходится. При D = 1 — данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью радикального признака Коши. Сначала запишем выражение для . Теперь найдем соответствующий предел:
Поскольку , в соответствии с радикальным признаком Коши, ряд расходится.
Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов, такие как интегральный признак Коши, признак Раабе и др.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет протестировать сходимость ряда. При этом, если калькулятор в качестве суммы ряда выдает конкретное число, то ряд сходится. В противном случае, необходимо обращать внимание на пункт «Тест сходимости ряда». Если там присутствует словосочетание «series converges», то ряд сходится. Если присутствует словосочетание «series diverges», то ряд расходится.
Ниже представлен перевод всех возможных значений пункта «Тест сходимости ряда»:
| Текст на английском языке | Текст на русском языке |
|---|---|
| By the harmonic series test, the series diverges. | При сравнении исследуемого ряда с гармоническим рядом , исходный ряд расходится. |
| The ratio test is inconclusive. | Признак Даламбера не может дать ответа о сходимости ряда. |
| The root test is inconclusive. | Радикальный признак Коши не может дать ответа о сходимости ряда. |
| By the comparison test, the series converges. | По признаку сравнения, ряд сходится |
| By the ratio test, the series converges. | По признаку Даламбера, ряд сходится |
| By the limit test, the series diverges. | На основнии того, что , или указанный предел не существует, сделан вывод о том, что ряд расходится. |
Данный калькулятор предназначен для исследования ряда на сходимость. Под числовым рядом понимается сумма членов числовой последовательности следующего вида: ∑ ∞n=1an=a1+a2+a3+…, где все a — это числа. Если говорить о функциональном ряде, то все члены последовательности являются функциями: ∑∞n=1fn(x)=f1(x)+f2(x)+f3(x)+… Ряд, членами которого являются степенные функции, называется степенным рядом: ∑∞n=1anxn. Чтобы найти сходимость числового ряда, функционального ряда или степенного ряда, необходимо знать признаки сходимости рядов. Существует необходимый признак сходимости ряда: если ряд ∑∞n=1an сходится, то (lim)┬(n→∞)an=0.
Однако данный признак не является гарантией сходимости ряда, поэтому рассматриваются также достаточные признаки сходимости. Признаки сравнения рядов заключаются в следующем. Даны два ряда ∑∞n=1an и ∑∞n=1b
converges — ряд сходится
not converges — ряд расходится.
∑ Сумма ряда онлайн
Введите данные для подчета суммы ряда
Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Сходимость ряда
Данный калькулятор умеет определять — сходится ли ряд, а также показывает — какие признаки сходимости срабатывают, а какие — нет.
Также умеет находить сходимость степенных рядов.
Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Среди функциональных рядов наиболее важное место занимают степенные ряды.
Степенным рядом называют ряд
,
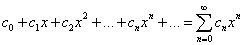члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x, а c0, c1, c2, cn — постоянные величины. Числа c1, c2, cn — коэффициенты членов ряда, c0 — свободный член. Члены степенного ряда определены на всей числовой прямой.
Вместо x могут быть различные числа.
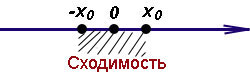
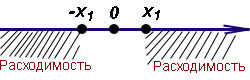
При некоторых значениях x степенные ряды могут быть сходящимися, при других значениях x — расходящимися. Обозначим через x0 некоторое значение x, при котором ряд сходится, а через x1 — значение, при котором ряд расходится. На рисунке слева показано, что интервал от −x0 до x0 является интервалом сходимости ряда, а вне этого интервала наблюдается расходимость.
Но как определить эти граничные значения x? Для этого существует вполне определённый способ. Обозначим эти граничные значения через −R и R. Находим по следующей формуле:
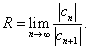
А теперь всё это в более точных формулировках, после чего перейдём к решению задач.
Множество значений переменной x, для которых ряд сходится, называется областью сходимости степенного ряда.. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox.
При подстановке в степенной ряд значения x=0 получится числовой ряд
c0+0+0+…+0+…,
который сходится.
Следовательно, при x=0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Есть степенные ряды, которые сходятся только при x=0 и расходятся при остальных значениях х. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы, которая уже была проиллюстрирована в начале этого урока.
Теорема 1 (теорема Абеля). Если степенной ряд сходится при некотором значении x = x0, отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x| < |x0|. Обратите внимание: и отправное значение «икс нулевое» и любое значение «икса», которое сравнивается с отправным, взяты по модулю — без учёта знака.
Следствие. Если степенной ряд расходится при некотором значении x = x1, то он расходится и при всех значениях |x| > |x1|.
Отсюда следует, что для любого степенного ряда имеется интервал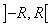 
, симметричный относительно начала координат, называемый интервалом сходимости,
в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться.
Число R называется радиусом сходимости степенного ряда.
В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x=0
и считается, что R=0) или представлять собой всю числовую прямую
(тогда ряд сходится во всех точках числовой прямой и считается, что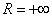 
).
Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при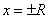 
).
Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при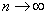 
отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, то есть
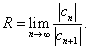(28)
Пример 1. Найти область сходимости степенного ряда
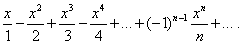
Решение. Здесь
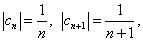
то есть
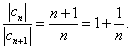
Используя формулу (28), найдём радиус сходимости данного ряда:
.
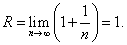Исследуем сходимость ряда на концах интервала сходимости
.
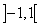Данный ряд сходится при x=1 и расходится при x=−1.
Следовательно, областью сходимости служит полуинтервал
.
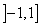Пример 2. Найти область сходимости степенного ряда
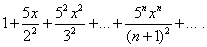
Решение. Коэффициенты ряда положительны, причём
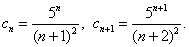
Вычисляем отношение
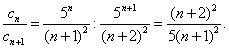
Найдём предел этого отношения, то есть радиус сходимости степенного ряда:
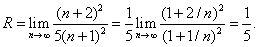
Исследуем сходимость ряда на концах интервала
.
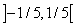Подстановка значений x=−1/5 и x=1/5
в данный ряд даёт:
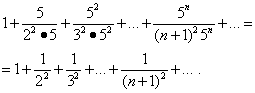
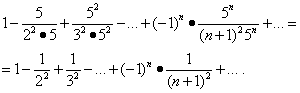
Первый из этих рядов сходится. Но тогда в силу теоремы об абсолютной сходимости
сходится и второй ряд, а область его сходимости – отрезок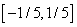 
Пример 3. Найти область сходимости степенного ряда
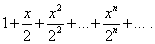
Решение. Здесь
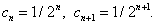
По формуле (28) находим радиус сходимости ряда:
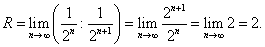
Исследуем сходимость ряда при значениях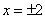 
. Подставив их в данный ряд, соответственно получим
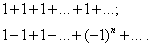
Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при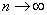 
). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал 
.
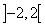Пример 4. Найти область сходимости степенного ряда
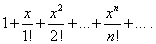
Решение. Здесь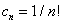 
, а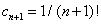 
Найдём отношение
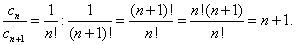
Следовательно, радиус сходимости ряда
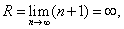
то есть ряд сходится при любом конечном значении x.
Область его сходимости – бесконечный интервал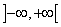 
.
Пример 5. Найти область сходимости степенного ряда
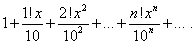
Решение. Находимо отношение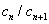 
, где 
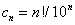, а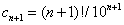 
:
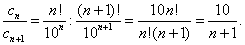
Согласно формуле (28) радиус сходимости данного ряда
,
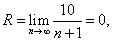то есть ряд сходится только при x=0 и расходится при остальных значениях х.
Примеры показывают, что на концах интервала сходимости ряды ведут себя различно.
Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера, или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.
Пусть для степенного ряда
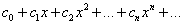(29)
радиус сходимости R > 0, т.е. этот ряд сходится на интервале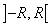 
.
Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство
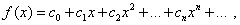(30)
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f(x) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f(x) на интервале сходимости.
Вне интервала сходимости равенство (30) не имеет смысла.
Можно доказать, что сумма степенного ряда f(x) непрерывна и дифференцируема на любом отрезке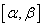 
внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.
Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.
Теорема 1. Степенной ряд (30) в интервале его сходимости можно
почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют
тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны
.
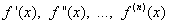Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если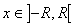 
, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
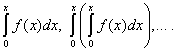
Пусть дана функция f(x), которую требуется разложить в степенной ряд, т.е. представить в виде (30):
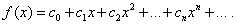
Задача состоит в определении коэффициентов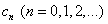 
ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:
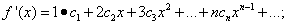
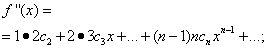
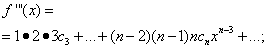
……………………………………………….. (31)
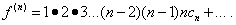
Полагая в равенствах (30) и (31) х = 0, находим
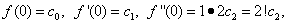
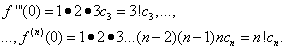
Тогда
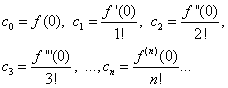
Подставляя найденные выражения в равенство (30), получим
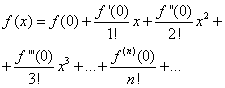(32)
Это разложение функции f(x) в ряд называется рядом Маклорена.
Найдём разложение в ряд Маклорена некоторых элементарных функций.
Пример 8. Разложить в ряд Маклорена функцию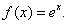 
Решение. Производные этой функции совпадают с самой функцией:
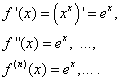
Поэтому при х=0 получаем
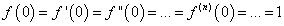
Подставляя эти значения в формулу (32), получим искомое разложение:
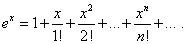(33)
Этот ряд сходится на всей числовой прямой (его радиус сходимости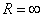 
).
Пример 9. Разложить в ряд Маклорена функции: 1) f(x)=sinx; 2) f(x)=cosx.
Решение.
1)Находим производные функции f(x)=sinx; имеем
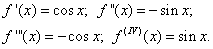
Так как производная четвёртого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдём значения функции и её производных при х = 0:
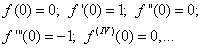
Поэтому ряд Маклорена для f(x)=sinx имеет вид
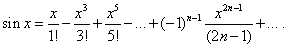(34)
2) Находим
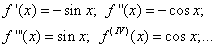
производные следующих порядков повторяются в той же последовательности. Далее, имеем
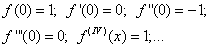
В результате получаем следующее разложение функции f(x)=cosx в ряд Маклорена:
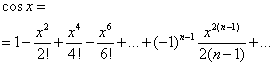
Разложить функцию в ряд Маклорена самостоятельно, а затем посмотреть решение
Пример 11. Разложить в ряд Маклорена функцию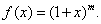 
Решение. Находим производные данной функции:
…………………………………….……..
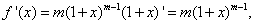
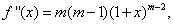
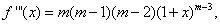
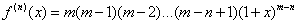
(при n<m). Необходимо различать две возможности для показателя степени m. Если m – целое положительное число, то при n=m получим
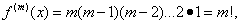
т.е. постоянную величину, а потому производные следующих порядков равны нулю. Найдём значения функции и её производных при x=0:
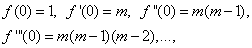
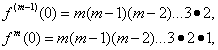
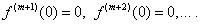
Подставляя эти значения в формулу (32), после упрощений получим
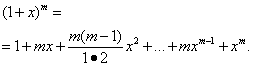
Это не ряд, а сумма, состоящая из конечного числа слагаемых и представляющая собой известное разложение бинома Ньютона.
Если же показатель m не является целым положительным числом, то производные в нуль не обратятся. Найденное выше выражение для производной
n-го порядка справедливо для любого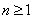 
. При х=0 получаем
Подстановка значений функции и её производных в равенство (32) в этом случае даёт
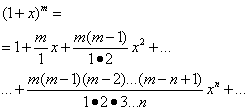(35)
Полученный ряд называется биномиальным. Найдём его интервал сходимости. Так как коэффициенты этого ряда
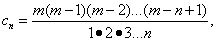
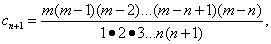
то их отношение после упрощения принимает вид
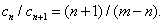
Находим предел абсолютной величины этого отношения при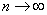 
:
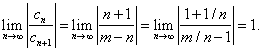
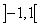— его интервал сходимости. 
Всё по теме «Ряды»
Степенные ряды. Интервал сходимости | Primer.by
, где — постоянные числа, называемые коэффициентами ряда.
Областью сходимости степенного ряда всегда является некоторый интервал.
Теорема (Абеля):
1) Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком значении х, для которого
;
2) Если ряд расходится при некотором значении , то он расходится при всяком х, для которого
Теорема:
Областью сходимости степенного ряда является интервал с цетром в начале координат.
Определение:
Интервалом сходимости степенного ряда называется интервал от –R до +R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называется радиусом сходимости степенного ряда.
На концах интервала вопрос о сходимости ряда решается индивидуально для каждого конретного ряда.
Отметим , что у некоторых рядов интервал сходимости вырождается в точку (R=0), у других охватывает всю ось ОХ (R=).
Радиус сходимости степенного ряда определяется по формуле
или
Примеры:
Пример1:
Найти область сходимости ряда
Решение.
Радиус сходимости степенного ряда можно найти по формуле: .
Т.к. и , то
.
Итак, радиус сходимости ряда . Т.о. данный степенной ряд расходится, при .
Исследуем сходимость ряда при .
Пусть. Подставим в заданный степенной ряд и получим ряд
, который сходится.
Итак, областью сходимости данного степенного ряда является значение .
Пример2:
Найти область сходимости степенного ряда .
Решение.
Радиус сходимости степенного ряда можно найти по формуле: .
Т.к. и , то
.
Итак, радиус сходимости ряда . Определим интервал сходимости данного степенного ряда:
.
– интервал сходимости степенного ряда. Исследуем сходимость ряда на концах интервала сходимости.
Пусть . Подставим в заданный степенной ряд и получим числовой ряд с положительными членами:
Получили расходящийся обобщенный гармонический ряд.
Значит, не принадлежит области сходимости степенного ряда.
Пусть. Подставим в заданный степенной ряд и получим знакочередующийся ряд
.
Для членов полученного ряда:
1)
2) , т.е.
В соответствии с признаком Лейбница данный ряд сходится и принадлежит области сходимости степенного ряда.
Итак, областью сходимости данного степенного ряда является промежуток .
Разложение в ряд — Калькулятор Онлайн
Чтобы посчитать сумму ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить ряд
- указать параметр, по которому будет считать сумма
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность)
Перейти: Найти «сумму числового ряда» →
Разложение в ряд Тейлора (степенной ряд)
Это он-лайн сервис в три шага:
- Ввести функцию, которую необходимо разложить
- Ввести точку, в окрестности которой необходимо разложить
- Указать до какого члена раскладывать
Перейти: Онлайн «Разложение функции в ряд Тейлора» →
Разложение в ряд Фурье
Это он-лайн сервис в два шага:
- Ввести функцию, которую необходимо разложить
- Ввести отрезок, на котором необходимо разложить
Перейти: Онлайн «Разложение функции в ряд Фурье» →
Чтобы посчитать произведение ряда онлайн выполните следующие действия:
- ввести выражение, для которого нужно вычислить произведение ряда
- указать параметр, по которому считать произведение
- указать значение параметра, до которого нужно подсчитать (для бесконечного ряда указываем бесконечность oo)
Перейти: Найти «произведение числового ряда» →
90000 Calculus II — Power Series 90001 Paul’s Online Notes 90002 Notes Quick Nav Download 90003 90004 90005 Go To 90006 90005 Notes 90006 90005 Practice Problems 90006 90005 Assignment Problems 90006 90005 Show / Hide 90006 90015 Show all Solutions / Steps / 90016 etc.90017 90006 90019 Hide all Solutions / Steps / 90016 etc. 90017 90006 90023 90004 90005 Sections 90006 90005 Estimating the Value of a Series 90006 90005 Power Series and Functions 90006 90005 Chapters 90006 90005 Parametric Equations and Polar Coordinates 90006 90005 Vectors 90006 90005 Classes 90006 90005 Algebra 90006 90005 Calculus I 90006 90005 Calculus II 90006 90005 Calculus III 90006 90005 Differential Equations 90006 90005 Extras 90006 90005 Algebra & Trig Review 90006 90005 Common Math Errors 90006 90005 Complex Number Primer 90006 90005 How To Study Math 90006 90005 Cheat Sheets & Tables 90006 90005 Misc 90006 90005 Contact Me 90006 90005 MathJax Help and Configuration 90006 90005 My Students 90006 90023 90004 90005 Notes Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Practice Problems Downloads 90006 90005 Complete Book — Problems Only 90006 90005 Complete Book — Solutions 90006 90085 90005 Current Chapter — Problems Only 90006 90005 Current Chapter — Solutions 90006 90085 90005 Current Section — Problems Only 90006 90005 Current Section — Solutions 90006 90005 Assignment Problems Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Other Items 90006 90005 Get URL’s for Download Items 90006 90023 90004 90005 Print Page in Current Form (Default) 90006 90005 Show all Solutions / Steps and Print Page 90006 90005 Hide all Solutions / Steps and Print Page 90006 90023 90004 90005 Home 90006 90005 Classes 90006 90005 Algebra 90004 90005 Preliminaries 90004 90005 Integer Exponents 90006 90005 Rational Exponents 90006 90005 Radicals 90006 90005 Polynomials 90006 90005 Factoring Polynomials 90006 90005 Rational Expressions 90006 90005 Complex Numbers 90006 90023 90006 90005 Solving Equations and Inequalities 90004 90005 Solutions and Solution Sets 90006 90005 Linear Equations 90006 90005 Applications of Linear Equations 90006 90005 Equations With More Than One Variable 90006 90005 Quadratic Equations — Part I 90006 90005 Quadratic Equations — Part II 90006 90005 Quadratic Equations: A Summary 90006 90005 Applications of Quadratic Equations 90006 90005 Equations Reducible to Quadratic in Form 90006 90005 Equations with Radicals 90006 90005 Linear Inequalities 90006 90005 Polynomial Inequalities 90006 90005 Rational Inequalities 90006 90005 Absolute Value Equations 90006 90005 Absolute Value Inequalities 90006 90023 90006 90023 90006 90023.90000 Calculus II — Power Series and Functions 90001 Paul’s Online Notes 90002 Notes Quick Nav Download 90003 90004 90005 Go To 90006 90005 Notes 90006 90005 Practice Problems 90006 90005 Assignment Problems 90006 90005 Show / Hide 90006 90015 Show all Solutions / Steps / 90016 etc.90017 90006 90019 Hide all Solutions / Steps / 90016 etc. 90017 90006 90023 90004 90005 Sections 90006 90005 Power Series 90006 90005 Taylor Series 90006 90005 Chapters 90006 90005 Parametric Equations and Polar Coordinates 90006 90005 Vectors 90006 90005 Classes 90006 90005 Algebra 90006 90005 Calculus I 90006 90005 Calculus II 90006 90005 Calculus III 90006 90005 Differential Equations 90006 90005 Extras 90006 90005 Algebra & Trig Review 90006 90005 Common Math Errors 90006 90005 Complex Number Primer 90006 90005 How To Study Math 90006 90005 Cheat Sheets & Tables 90006 90005 Misc 90006 90005 Contact Me 90006 90005 MathJax Help and Configuration 90006 90005 My Students 90006 90023 90004 90005 Notes Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Practice Problems Downloads 90006 90005 Complete Book — Problems Only 90006 90005 Complete Book — Solutions 90006 90085 90005 Current Chapter — Problems Only 90006 90005 Current Chapter — Solutions 90006 90085 90005 Current Section — Problems Only 90006 90005 Current Section — Solutions 90006 90005 Assignment Problems Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Other Items 90006 90005 Get URL’s for Download Items 90006 90023 90004 90005 Print Page in Current Form (Default) 90006 90005 Show all Solutions / Steps and Print Page 90006 90005 Hide all Solutions / Steps and Print Page 90006 90023 90004 90005 Home 90006 90005 Classes 90006 90005 Algebra 90004 90005 Preliminaries 90004 90005 Integer Exponents 90006 90005 Rational Exponents 90006 90005 Radicals 90006 90005 Polynomials 90006 90005 Factoring Polynomials 90006 90005 Rational Expressions 90006 90005 Complex Numbers 90006 90023 90006 90005 Solving Equations and Inequalities 90004 90005 Solutions and Solution Sets 90006 90005 Linear Equations 90006 90005 Applications of Linear Equations 90006 90005 Equations With More Than One Variable 90006 90005 Quadratic Equations — Part I 90006 90005 Quadratic Equations — Part II 90006 90005 Quadratic Equations: A Summary 90006 90005 Applications of Quadratic Equations 90006 90005 Equations Reducible to Quadratic in Form 90006 90005 Equations with Radicals 90006 90005 Linear Inequalities 90006 90005 Polynomial Inequalities 90006 90005 Rational Inequalities 90006 90005 Absolute 90006 90023 90006 90023 90006 90023.90000 Series convergence online 90001 90002 There are different ways of series convergence tesing. First of all one can just find series sum. If the value received is finite number, then the 90003 series is converged 90004. For instance, because of 90005 90002 90005 90002 the series is converged. If we was not able to find series sum, than one should use different methods for testing series convergence.90005 90002 One of these methods is the 90011 ratio test 90012, which can be written in following form: 90005 90002 90005 90002 here and is the n-th and (n + 1) series members correspondingly, and convergence of the series is determined by the value of D: if D <1 - series converged, if D> 1 — series diverged.If D = 1 — the ratio test is inconclusive and one should make additional researches. 90005 90002 As an example, test the convergence of the following series by means of ratio test. First of all write out the expressions for and . Then find corresponging limit: 90005 90002 90005 90002 Because , in concordance with ratio test, series converged.90005 90002 Another method which is able to test series convergence is the 90011 root test 90012, which can be written in the following form: 90005 90002 90005 90002 here is the n-th series member, and convergence of the series determined by the value of D in the way similar to ratio test: if D <1 - series converged, if D> 1 — series diverged.If D = 1 — the root test is inconclusive and one should make additional researches. 90005 90002 As an example, test the convergence of the following series by means of root test. First of all, write out the expression for . Then find the corresponding limit: 90005 90002 90005 90002 Because , in accordance with root test, series diverged.90005 90002 It should be noted, that along with methods listed above, there are also exist another series convergence testing methods such as integral test, Raabe test and ect. 90005 90002 Our online calculator, build on Wolfram Alpha system is able to test convergence of different series. It should be noted, that if the calculator finds sum of the series and this value is the finity number, than this series converged. In the opposite case, one should pay the attention to the «Series convergence test» pod.90005 90002 Below listed the explanation of possible values of «Series convergence test» pod: 90005 90044 90045 90046 90047 The «Series convergence test» pod value 90048 90047 Explanation 90048 90051 90052 90046 90054 By the harmonic series test, the series diverges. 90055 90054 Then the series was compared with harmonic one , initial series was recognized as diverged.90055 90051 90046 90054 The ratio test is inconclusive. 90055 90054 The application of ratio test was not able to give understanding of series convergence because the value of corresponding limit equals to 1 (see above). 90055 90051 90046 90054 The root test is inconclusive. 90055 90054 The application of root test was not able to give understanding of series convergence because the value of corresponding limit equals to 1 (see above).90055 90051 90046 90054 By the comparison test, the series converges. 90055 90054 When the comparison test was applied to the series, it was recognized as diverged one. 90055 90051 90046 90054 By the ratio test, the series converges. 90055 90054 The ratio test was able to determined the convergence of the series 90055 90051 90046 90054 By the limit test, the series diverges.90055 90054 Because of , or the mentioned limit does not exist, the series was recognized as diverged one. 90055 90051 90089 .90000 The Radius of Convergence of a Power Series 90001 90002 Recall from the Power Series page that we saw that a power series will converge at it’s center of convergence $ c $, and that it is possible that a power series can converge for all $ x \ in \ mathbb {R} $ or on some interval centered at the center of convergence. If a power series converges on some interval centered at the center of convergence, then the distance from the center of convergence to either endpoint of that interval is known as the radius of convergence which we more precisely define below.n $ is convergent only at $ x = c $, then the radius of convergence for this power series is $ R = 0 $ since the interval of convergence is $ [c — 0, c + 0] = [c, c] $ . Similarly, if the power series is convergent for all $ x \ in \ mathbb {R} $ then the radius of convergence of the power series is $ R = \ infty $ since the interval of convergence is $ (- \ infty, \ infty ) $. 90003 90002 We will now look at a technique for determining the radius of convergence of a power series using The Ratio Test for Positive Series 90003 90004 90005 90006 90007 Theorem 1: 90008 If $ \ lim_ {n \ to \ infty} \ biggr \ rvert \ frac {a_ {n + 1}} {a_n} \ biggr \ rvert = L $ where $ L $ is a positive real number or $ L = 0 $ or $ L = \ infty $, then the power series $ \ sum_ {n = 0} ^ {\ infty} a_n (x — c) ^ n $ has a radius of convergence $ R = \ frac {1} {L} $ where if $ L = 0 $ then $ R = \ infty $ and if $ L = \ infty $ then $ R = 0 $.n $. 90008 90003 90002 Once again we note that the center of convergence is $ c = 3 $. We now want to find the radius of convergence using the ratio test once again. 90003 (2) 90002 \ begin {align} \ quad L = \ lim_ {n \ to \ infty} \ biggr \ rvert \ frac {a_ {n + 1}} {a_n} \ biggr \ rvert = \ lim_ {n \ to \ infty} \ frac {a_ {n + 1}} {a_n} = \ lim_ {n \ to \ infty} \ frac {\ frac {(n + 1)} {(n + 1)!}} {\ frac {n} {n!}} = \ lim_ {n \ to \ infty} \ frac {(n + 1) n!} {n (n + 1)!} = \ lim_ {n \ to \ infty} \ frac {(n +1)!} {n (n + 1)!} = \ lim_ {n \ to \ infty} \ frac {1} {n} = 0 \ end {align} 90003 90002 Since $ L = 0 $ we get that our radius of convergence $ R = \ infty $.90003 .