Медиана в треугольнике это – Медиана треугольника – свойство, формула, определение

Содержание

Медиана треугольника | Треугольники

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника, надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.

www.treugolniki.ru

Медиана треугольника — это… Что такое Медиана треугольника?

У этого термина существуют и другие значения, см. Медиана. Треугольник и его медианы.

Медиа́на треуго́льника

(лат. mediāna — средняя) ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

Свойства

Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Большей стороне треугольника соответствует меньшая медиана.
Из векторов, образующих медианы, можно составить треугольник.
При аффинных преобразованиях медиана переходит в медиану.
Медиана треугольника делит его на две равновеликие части.

Формулы

, где m_c — медиана к стороне c; a, b, c — стороны треугольника,

поэтому сумма квадратов медиан произвольного треугольника всегда в 4/3 раза меньше суммы квадратов его сторон.

Формула стороны через медианы:

, где медианы к соответствующим сторонам треугольника, — стороны треугольника.

Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.

Медиана-обезьяна,
у которой зоркий глаз,
прыгнет точно в середину
стороны против вершины,
где находится сейчас.

Примечания

См. также

Ссылки

dic.academic.ru

Медиана треугольника, формулы и примеры

Определение и формулы медианы треугольника

Для медиан треугольника справедливы следующие утверждения:

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Медиана разбивает треугольник на два треугольника с одинаковой площадью
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

В равнобедренном треугольнике медиана, опущенная на основание, является высотой и биссектрисой.
В равностороннем треугольнике любая медиана является высотой и биссектрисой.

Формула для вычисления медианы

где – сторона треугольника, к которой проводится медиана, – две другие стороны рассматриваемого треугольника.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Все формулы медианы треугольника

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Подробности: Автор: Administrator; Опубликовано: 08 октября 2011; Обновлено: 16 мая 2017

www-formula.ru

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия

Определение. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Рис.1

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD.

Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).

Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

Рис.2

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.

Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).

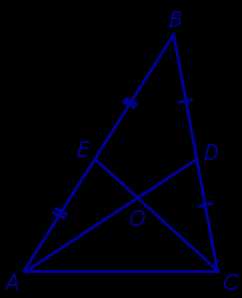
Рис.3

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

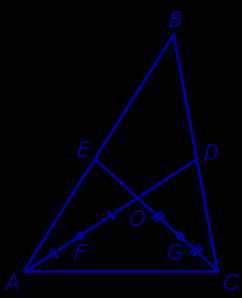
Рис.4

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

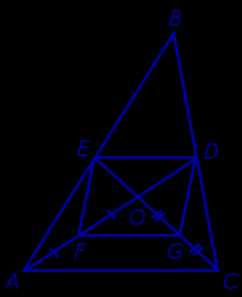
Рис.5

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,

откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны. Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).

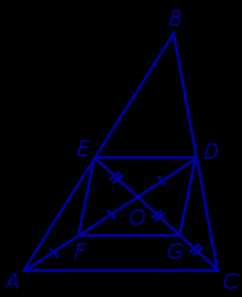
Рис.6

Таким образом,

| FO | = | OD | , | GO | = | OE | .

Следовательно,

| AF | = | FO | = | OD | , | CG | = | GO | = | OE | .

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1, считая от вершины треугольника.

Доказательство завершено.

Следствие. Все три медианы треугольника пересекаются в одной точке.

Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении 2 : 1, считая от вершины A (рис.7).

Рис.7

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение. Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

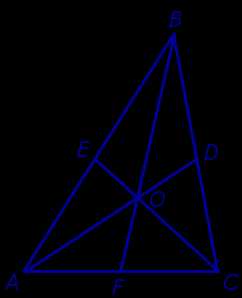
Рис.8

Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

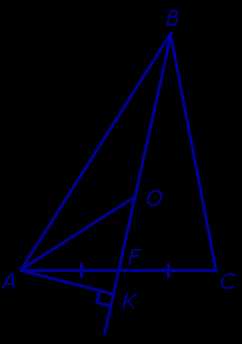
Рис.9

Тогда

В силу утверждения 1,

что и требовалось доказать.

Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:

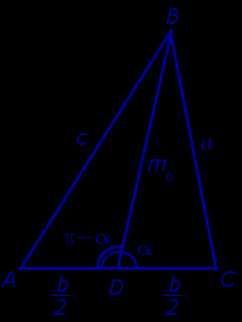
Рис.10

Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:

Складывая эти равенства, получим:
что и требовалось доказать.
Следствие. Длины медиан и длины сторон треугольника связаны формулой
Доказательство. В силу утверждения 4 справедливы равенства:
Складывая эти равенства, получим:
что и требовалось доказать.
Утверждение 5. В параллелограммепараллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.
Доказательство. Рассмотрим рисунок 11.
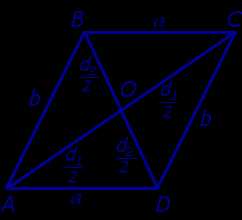
Рис.11
Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силу утверждения 4, справедливы равенства:
Следовательно,
d₁² = 2a² + 2b² – d₂²,
d₂² = 2a² + 2b² – d₁².
Складывая эти равенства, получим
что и требовалось доказать.
Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).
Рис.12
Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).
Рис.13
Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольникпрямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:
что и требовалось доказать.
Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).
Рис.14
Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.15), то будет справедливо равенство
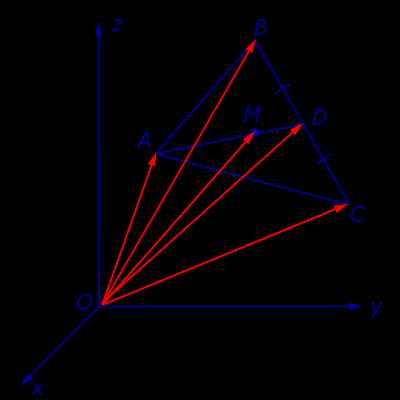
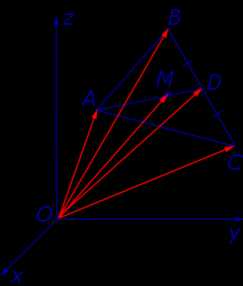
Рис.15
Доказательство. По свойствам векторов
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными».
Запись по телефону (495) 509-28-10
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Что делает медиана в треугольнике
Доброй ночи!
Вы обратились к нам с вопросом о том, что делает медиана в треугольнике. Вопрос интересно поставлен, но в нём нет ничего сложного.
Давайте вспомним с Вами, что медиана — это такой отрезок, который проведён из вершины к противоположной стороне, при этом деля её на два равных отрезка. Теперь мы можем легко использовать это свойство.
Как и у любой геометрической фигуры, у медианы есть свойства, среди которых мы можем выделить такие:

Медианы треугольника точкой их пересечения делятся в отношении , считая от вершин треугольника.
Три медианы треугольника делят треугольник на шесть равновеликих (одинаковых по площади) треугольников
Медиана делит треугольник на два равновеликих треугольника
А теперь давайте попробуем разобраться с медианой, её найти в равностороннем треугольнике, то есть в таком треугольнике, у которого все стороны, также как и углы, равны. Медиана, в таком типе треугольника, проведённая к любой стороне, является также биссектрисой и высотой.
Нам важно научится выражать медиану через сторону равностороннего треугольника. И сейчас мы будем пытаться это сделать. Нам дан треугольник , в котором — медиана, которая, учитывая теоремы, будет также и высотой. То есть при её помощи образовывается два одинаковых прямоугольных треугольника: и . Рассмотрим один из них — .
Для простоты исчисления давайте выполним замену: , а исходя из теорем .
И теперь, при помощи теоремы Пифагора мы с Вами можем выразить неизвестную медиану:

Формула выражена, но ведь это не всё. Теперь нам остаётся подставить подставить известные значения:

Ответ: см
ru.solverbook.com
Элементы треугольника. Медиана | Подготовка к ЕГЭ по математике
Категория: ПланиметрияСправочные материалы
Елена Репина 2013-04-15 2013-07-31
Определение
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны
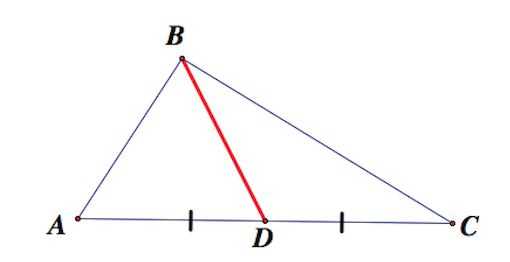
Свойства
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении
2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)
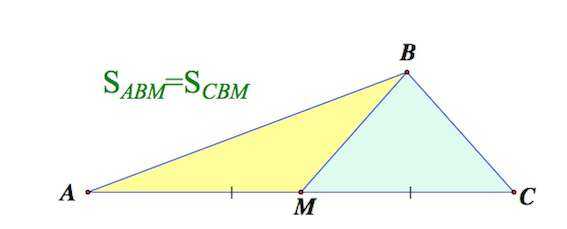
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы
5. Длина медианы треугольника вычисляется по формуле:
, где где — медиана к стороне ; — стороны треугольника
6. Длина стороны треугольника через медианы вычисляется по формуле:
, где – медианы к соответствующим сторонам треугольника, — стороны треугольника.
Автор: egeMax | Нет комментариев
egemaximum.ru
No related posts.