В арифметической прогрессии что такое n: Как найти n в арифметической прогрессии

Содержание

Арифметическая прогрессия. Учебник по ЕГЭ и ГИА

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например:
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и -ное число) всегда одно.

Число с номером называется -ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, ), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: .

В нашем случае:

Арифметическая прогрессия

Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна .
Например:

и т.д.
Такая числовая последовательность называется арифметической прогрессией.
Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность. Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается .

Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:

a)
b)
c)
d)

Разобрался? Сравним наши ответы:
Является арифметической прогрессией – b, c.
Не является арифметической прогрессией – a, d.

Вернемся к заданной прогрессии ( ) и попробуем найти значение ее -го члена. Существует два способа его нахождения.

1. Способ

Мы можем прибавлять к предыдущему значению числа прогрессии , пока не дойдем до -го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:

Итак, -ой член описанной арифметической прогрессии равен .

2. Способ

А что если нам нужно было бы найти значение -го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.
Разумеется, математики придумали способ, при котором не нужно прибавлять разность арифметической прогрессии к предыдущему значению. Присмотрись внимательно к нарисованному рисунку… Наверняка ты уже заметил некую закономерность, а именно:

Если нам нужно найти значение числа прогрессии с порядковым номером, мы прибавляем к первому члену арифметической прогрессии количество , которое на одно значение меньше порядкового номера искомого числа.

Например, посмотрим, из чего складывается значение -го члена данной арифметической прогрессии:

Иными словами:

Попробуй самостоятельно найти таким способом значение члена данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли к предыдущему значению членов арифметической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

— уравнение арифметической прогрессии.

Кстати, таким образом мы можем посчитать и -ой член данной арифметической прогрессии (да и -ый тоже можем, да и любой другой вычислить совсем несложно). Попробуй посчитать значения -го и -го членов, применив полученную формулу.

Арифметические прогрессии бывают возрастающие, а бывают убывающие.

Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.
Например:

Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.
Например:

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.
Проверим это на практике.
Нам дана арифметическая прогрессия, состоящая из следующих чисел: Проверим, какое получится -ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

Заметим, что так как арифметическая прогрессия убывающая, то значение будет отрицательным, ведь каждый последующий член меньше предыдущего.

Так как , то:

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.
Попробуй самостоятельно найти -ой и -ый члены этой арифметической прогрессии.

Сравним полученные результаты:

Свойство арифметической прогрессии

Усложним задачу — выведем свойство арифметической прогрессии.
Допустим, нам дано такое условие:
— арифметическая прогрессия, найти значение .
Легко, скажешь ты и начнешь считать по уже известной тебе формуле:

Пусть , а , тогда:

Абсолютно верно. Получается, мы сначала находим , потом прибавляем его к первому числу и получаем искомое . Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа ? Согласись, есть вероятность ошибиться в вычислениях.
А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы? Конечно да, и именно ее мы попробуем сейчас вывести.

Обозначим искомый член арифметической прогрессии как , формула его нахождения нам известна – это та самая формула, выведенная нами в начале:
, тогда:

предыдущий член прогрессии это :
последующий член прогрессии это :

Просуммируем предыдущий и последующий члены прогрессии:

Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними. Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на .

— свойство членов арифметической прогрессии.

Попробуем посчитать значение , используя выведенную формулу:

Все верно, мы получили это же число. Закрепим материал. Посчитай значение для прогрессии самостоятельно, ведь это совсем несложно.

Молодец! Ты знаешь о прогрессии почти все! Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» — Карл Гаусс…

Сумма первых n членов арифметической прогрессии

Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу: «Сосчитать сумму всех натуральных чисел от до (по другим источникам до ) включительно». Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…

Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.
Допустим, у нас есть арифметическая прогрессия, состоящая из -ти членов: Нам необходимо найти сумму данных членов арифметической прогрессии. Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму ее членов, как это искал Гаусс?

Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.

Попробовал? Что ты заметил? Правильно! Их суммы равны

А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии? Конечно, ровно половина всех чисел, то есть .
Исходя из того, что сумма двух членов арифметической прогрессии равна , а подобных равных пар , мы получаем, что общая сумма равна:
.
Таким образом, формула для суммы первых членов любой арифметической прогрессии будет такой:

, где – количество значений.

В некоторых задачах нам неизвестен -й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу -го члена.
Что у тебя получилось?

, где – количество значений.

Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма чисел, начиная от -го, и сумма чисел начиная от -го.

Сколько у тебя получилось?
У Гаусса получилось, что сумма членов равна , а сумма членов . Так ли ты решал?

На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.

Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется блочных кирпичей. Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?

В данном случае прогрессия выглядит следующим образом: .
Разность арифметической прогрессии .
Количество членов арифметической прогрессии .
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Способ 1.

Способ 2.

А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде. Сошлось? Молодец, ты освоил сумму -ных членов арифметической прогрессии.
Конечно, из блоков в основании пирамиду не построишь, а вот из ? Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – блоков:

Тренировка

Задачи:

Маша приходит в форму к лету. Ежедневно она увеличивает количество приседаний на . Сколько раз будет приседать Маша через недели, если на первой тренировке она сделала приседаний.
Какова сумма всех нечетных чисел, содержащихся в .
Лесорубы при хранении бревен укладывают их таким образом, что каждый верхний слой содержит на одно бревно меньше, чем предыдущий. Сколько бревен находится в одной кладке, если основанием кладки служат бревен.

Ответы:

Определим параметры арифметической прогрессии. В данном случае
( недели = дней).

Ответ: Через две недели Маша должна приседать раз в день.
Первое нечетное число , последнее число .
Разность арифметической прогрессии .
Количество нечетных чисел в – половина, однако, проверим этот факт, используя формулу нахождения -ного члена арифметической прогрессии:

В числах действительно содержится нечетных чисел.
Имеющиеся данные подставим в формулу:

Ответ: Сумма всех нечетных чисел, содержащихся в , равна .
Вспомним задачу про пирамиды. Для нашего случая , a , так как каждый верхний слой уменьшается на одно бревно, то всего в кучке слоев, то есть .
Подставим данные в формулу:

Ответ: В кладке находится бревен.

Подведем итоги

Арифметическая прогрессия – числовая последовательность, в которой разница между соседними числами одинакова и равна . Она бывает возрастающей и убывающей .
Формула нахождения -го члена арифметической прогрессии записывается формулой — , где – количество чисел в прогрессии.
Свойство членов арифметической прогрессии — — где – количество чисел в прогрессии.
Сумму членов арифметической прогрессии можно найти двумя способами:
, где – количество значений.
, где &n

Арифметическая прогрессия: определение, формулы, свойства

Арифметическая прогрессия – это числовая последовательность, в которой, начиная со второго числа, каждое последующее равняется предыдущему плюс постоянное слагаемое.

Общий вид арифметической прогрессии

a₁, a₁ + d, a₁ + 2d, … a₁ + (n – 1) d, …

d – шаг или разность прогрессии; это и есть постоянное слагаемое.

Члены прогрессии:

a₁
a₂ = a₁ + d
a₃ = a₂ + d = a₁ + 2d
и т.д.

Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.

Свойства и формулы арифметической прогрессии

1. Нахождение общего n-ого члена (a_n)

a_n = a_n-1 + d
a_n = a₁ + (n – 1) d
a_n = a_m – (m – n) d

2. Разность прогрессии

d = a_n – a_n-1

Также для нахождения шага используется такая формула:

3. Характеристическое свойство

Последовательность чисел a₁, a₂, a₃ … является арифметической прогрессией, если для любого ее члена выполняется следующее условие:

4. Сумма первых членов прогрессии

Чтобы найти сумму первых членов арифметической прогрессии, необходимо воспользоваться формулой:

n – количество суммируемых членов.

Если a_n заменить на a₁ + (n – 1) d, то получится:

5. Сумма членов прогрессии с n-ого по m-ный

(m – n + 1) – количество суммируемых членов.

Если a_m заменить на a_n + (m – n) d, то получим:

6. Сходимость прогрессии

Арифметическая прогрессия сходится при d = 0, во всех остальных случаях она расходится.

При этом, если:

d > 0, прогрессия называется возрастающей;
d < 0 – убывающей;
d = 0 – стационарной.

Арифметическая прогрессия. Часть 1

Прежде чем мы начнем решать задачи на арифметическую прогрессию, рассмотрим, что такое числовая последовательность, поскольку арифметическая прогрессия — это частный случай числовой последовательности.

Числовая последовательность — это числовое множество, каждый элемент которого имеет свой порядковый номер. Элементы этого множества называются членами последовательности. Порядковый номер элемента последовательности обозначается индексом:

a_1 — первый элемент последовательности;

a_5 — пятый элемент последовательности;

a_n — «энный» элемент последовательности, т.е. элемент, «стоящий в очереди» под номером n.

Между значением элемента последовательности и его порядковым номером существует зависимость. Следовательно, мы можем рассматривать последовательность как функцию, аргументом которой является порядковый номер элемента последовательности. Другими словами можно сказать, что последовательность — это функция от натурального аргумента:

Последовательность можно задать тремя способами:

1. Последовательность можно задать с помощью таблицы. В этом случае мы просто задаем значение каждого члена последовательности.

Например, Некто решил заняться личным тайм-менеджментом, и для начала посчитать в течение недели, сколько времени он проводит ВКонтакте. Записывая время в таблицу, он получит последовательность, состоящую из семи элементов:

В первой строке таблицы указан номер дня недели, во второй — время в минутах. Мы видим, что a_1=125 , то есть в понедельник Некто провел ВКонтакте 125 минут, a_4=248 , то есть в четверг — 248 минут, а a_5=15 , то есть в пятницу всего 15.

2. Последовательность можно задать с помощью формулы n-го члена.

В этом случае зависимость значения элемента последовательности от его номера выражается напрямую в виде формулы.

Например, если , то

$a_{k+1}=(k+1)^2-4*(k+1)=k^2-2k-3$

Чтобы найти значение элемента последовательности с заданным номером, мы номер элемента подставляем в формулу n-го члена.

То же самое мы делаем, если нужно найти значение функции, если известно значение аргумента. Мы значение аргумента подставляем вместо в уравнение функции:

Если, например, , то

Ещё раз замечу, что в последовательности, в отличие от произвольной числовой функции, аргументом может быть только натуральное число.

3. Последовательность можно задать с помощью формулы, выражающей зависимость значения члена последовательности с номером n от значения предыдущих членов. В этом случае нам недостаточно знать только номер члена последовательности, чтобы найти его значение. Нам нужно задать первый член или несколько первых членов последовательности.

Например, рассмотрим последовательность $b_n=2b_{n-1}+b_{n-2}$ ,

Мы можем находить значения членов последовательности один за другим, начиная с третьего:

То есть каждый раз, чтобы найти значение n-го члена последовательности, мы возвращаемся к двум предыдущим. Такой способ задания последовательности называется рекуррентным, от латинского слова recurro — возвращаться.

Теперь мы можем дать определение арифметической прогрессии. Арифметическая прогрессия — это простой частный случай числовой последовательности.

Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

Число $d=a_k-a_{k-1}$ называется разностью арифметической прогрессии. Разность арифметической прогрессии может быть положительной, отрицательной, или равной нулю.

Если d>0 d>0 , то каждый член арифметической прогрессии больше предыдущего, и прогрессия является возрастающей.

Например, 2; 5; 8; 11;… d=3

Если d<0 d>0 , то каждый член арифметической прогрессии меньше предыдущего, и прогрессия является убывающей.

Например, 2; -1; -4; -7;… d=-3

Если d=0 , то все члены прогрессии равны одному и тому же числу, и прогрессия является стационарной.

Например, 2;2;2;2;…

Основное свойство арифметической прогрессии:

Посмотрим на рисунок.

Мы видим, что

$a_k=a_{k-1}+d$ , и в то же время

$a_k=a_{k+1}-d$

Сложив эти два равенства, получим:

$2a_k=a_{k-1}+a_{k+1}$ .

Разделим обе части равенства на 2:

$a_k={a_{k-1}+a_{k+1}}/2$

Итак, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:

$a_k={a_{k-1}+a_{k+1}}/2$

Больше того, так как

$a_k=a_{k-l}+ld$ , и в то же время

$a_k=a_{k+l}-ld$ , то

$2a_k=a_{k-l}+a_{k+l}$ , и, следовательно,

$2a_k=a_{k-l}+a_{k+l}$ Каждый член арифметической прогрессии, начиная с , равен среднему арифметическому двух равноотстоящих.

Формула го члена.

Мы видим, что для членов арифметической прогрессии выполняются соотношения:

…

и, наконец, $a_n=a_{n-1}+d=a_1+d(n-1)$

Мы получили формулу n-го члена.

$a_n=a_{n-1}+d=a_1+d(n-1)$

ВАЖНО! Любой член арифметической прогрессии можно выразить через a_1 и . Зная первый член и разность арифметической прогрессии можно найти любой её член.

Сумма n членов арифметической прогрессии.

В произвольной арифметический прогрессии суммы членов, равноотстоящих от крайних равны между собой:

$a_2+a_{n-1}=a_1+d+(a_1+d(n-2))=2a_1+d(n-1)$

$a_3+a_{n-2}=a_1+2d+(a_1+d(n-3))=2a_1+d(n-1)$

Рассмотрим арифметическую прогрессию, в которой n членов. Пусть сумма n членов этой прогрессии равна S_n .

Расположим члены прогрессии сначала в порядке возрастания номеров, а затем в порядке убывания:

S_n

Сложим попарно: $(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+...+(a_n+a_1)=2S_n$

Сумма в каждой скобке равна a_1+a_n , число пар равно n.

Получаем:

$S_n={a_1+a_n}/2n={2a_1+d(n-1)}/2n$

Итак, сумму n членов арифметической прогрессии можно найти по формулам: $S_n={a_1+a_n}/2n={2a_1+d(n-1)}/2n$

Рассмотрим решение задач на арифметическую прогрессию.

1. Последовательность задана формулой n-го члена: . Докажите, что эта последовательность является арифметической прогрессией.

Докажем, что разность между двумя соседними членами последовательности равна одному и тому же числу.

$a_{n-1}=3-12{(n-1)}=15-12n$

$a_n-a_{n-1}=(3-12n)-(15-12n)=-12$

Мы получили, что разность двух соседних членов последовательности не зависит от их номера и является константой. Следовательно, по определению, эта последовательность является арифметической прогрессией.

2. Дана арифметическая прогрессия -31; -27;…

а) Найдите 31 член прогрессии.

б) Определите, входит ли в данную прогрессию число 41.

а) Мы видим, что a_1=-31 ;

Запишем формулу n-го члена для нашей прогрессии.

В общем случае

В нашем случае , поэтому

Получаем:

$a_{31}=-31+4(31-1)=89$

б) Предположим, что число 41 является членом последовательности. Найдем его номер. Для этого решим уравнение:

4n=76

n=19

Мы получили натуральное значение n, следовательно, да, число 41 является членом прогрессии. Если бы найденное значение n не было бы натуральным числом, то мы бы ответили, что число 41 НЕ является членом прогрессии.

3. а) Между числами 2 и 8 вставьте 4 числа так, чтобы они вместе с данными числами составляли арифметическую прогрессию.

б) Найдите сумму членов полученной прогрессии.

а) Вставим между числами 2 и 8 четыре числа:

n=19

Мы получили арифметическую прогрессию, в которой 6 членов.

Найдем разность этой прогрессии. Для этого воспользуемся формулой n-го члена:

Теперь легко найти значения чисел:

3,2; 4,4; 5,6; 6,8

б) $S_6={a_1+a_6}/2{6}={2+8}/2{6}=30$

Ответ: а) да; б) 30

4. Грузовик перевозит партию щебня массой 240 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено на двенадцатый день, если вся работа была выполнена за 15 дней.

По условию задачи количество щебня, которое перевозит грузовик, каждый день увеличивается на одно и то же число. Следовательно, мы имеем дело с арифметической прогрессией.

Сформулируем эту задачу в терминах арифметической прогрессии.

За первый день было перевезено 2 тонны щебня: [pmath size=14]a_1=2[/pmath].

Вся работа была выполнена за 15 дней: n=15 .

Грузовик перевозит партию щебня массой 240 тонн: $S_{15}=240$

Нам нужно найти $a_{12}$ .

Сначала найдем разность прогрессии. Воспользуемся формулой суммы n членов прогрессии.

$S_n={2a_1+d(n-1)}/2n$

В нашем случае:

$S_{15}={2*2+d(15-1)}/2{15}=240$

2+7d=16

d=2

Найдем $a_{12}$ по формуле n-го члена:

$a_{12}=a_1+11d=2+22=24$

Ответ: 24.

Продолжение статьи — решение основных типов задач на арифметическую прогрессию — читайте здесь.

И.В. Фельдман, репетитор по математике.

$a_{12}=a_1+11d=2+22=24$

Арифметическая прогрессия | umath.ru

Определение арифметической прогрессии

Определение. Числовая последовательность, каждый член которой получается из предыдущего прибавлением одного и того же числа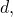

называется арифметической прогрессией. Число

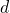называется разностью арифметической прогрессии.

То есть арифметическая прогрессия определяется рекуррентным соотношением

$a_{n+1} = a_n + d.$

Например, последовательность нечётных натуральных чисел

$1, 3, 5, 7, 9, \ldots$

является арифметической прогрессией, так как любой её член отличается от предыдущего на 2.

Общий член арифметической прогрессии 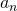задаётся формулой

$a_n = d(n - 1) + a_1.$

Например, последовательность 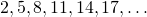$2, 5, 8, 11, 14, 17,\ldots$ образует арифметическую прогрессию с разностью 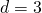d = 3 и первым членом 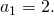Поэтому её общий член может быть задан соотношением

$a_n = 2 + 3(n-1) = 3n - 1.$

Пример 1. Найти одиннадцатый член арифметической прогрессии, если её первый член 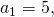а разность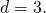 d = 3.

Решение. По формуле для общего члена арифметической прогрессии имеем

$a_{11} = 5 + 3(11 - 1) = 35.$

Теорема. Последовательность 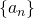$\{a_n\}$ тогда и только тогда является арифметической прогрессией, когда каждый её член, начиная со второго, равен полусумме предыдущего и последующего членов:

$a_n = \frac{a_{n - 1} + a_{n+1}}{2}.$

Доказательство. По определению арифметической прогрессии для всех 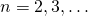$n = 2, 3, \ldots$ имеем

$d = a_n - a_{n-1} = a_{n+1} - a_n.$

Отсюда

$2a_n = a_{n-1} + a_{n+1},$

то есть

$a_n = \frac{a_{n-1} + a_{n+1}}{2}.$

Сумма первых n членов арифметической прогрессии

В качестве примера найдём сумму всех натуральных чисел от 1 до 100, то есть вычислим сумму

$S = 1 + 2 + 3 + \ldots + 99 + 100.$

Решение. Можно сидеть и долго складывать все числа по порядку. Но есть более простой способ. Запишем сумму этих чисел, а под ней — ту же сумму, но в обратной последовательности:

$\begin{array}{cccccccccc} S = & 1& + & 2& + & 3& + \ldots + &99& + &100, \\ S = &100& + &99& + &98& + \ldots + & 2& + & 1. \end{array}$

Теперь почленно сложим эти суммы:

$2S = (1 + 100) + (2 + 99) + (3 + 98) + \ldots + (100 + 1)=$

$= \underbrace{101 + 101 + \ldots + 101}_{100} = 100 \cdot 101 = 10100.$

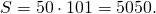
Отсюда $S = 50\cdot 101 = 5050.$

По легенде, школьный учитель математики, надеясь надолго занять детей, предложил им сосчитать эту сумму. Среди тех детей был будущий великий математик Карл Гаусс. Юный Гаусс быстро заметил, что попарные суммы членов с противоположных концов равны: 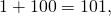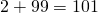и т.д, и уже через несколько минут подошёл к учителю с ответом: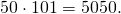 $50\cdot 101 = 5050.$

Этим же приёмом удобно воспользоваться и при вычислении суммы первых 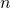членов арифметической прогрессии, если заметить, что

$a_k + a_{n+1-k} = a_1 + a_n.$

Действительно,

$a_k + a_{n+1-k} = a_1 + d(k - 1) + a_1 + d(n-k) =$

$a_1 + (a_1 + d(n-1)) = a_1 + a_n.$

Сумма первых n членов арифметической прогресиии

$S_n = a_1 + a_2 + \ldots + a_n$

равна полусумме первого и n-ного её членов, умноженной на число членов, то есть

$S_n = \frac{a_1 + a_n}{2}\cdot n.$

Доказательство. Запишем сумму 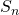S_n сначала в прямом порядке, а затем — в обратном:

$S_n = a_1 + a_2 + \ldots + a_{n-1} + a_n,$

$S_n = a_n + a_{n-1} + \ldots + a_2 + a_1.$

Сложим почленно эти два равенства и воспользуемся тем, что 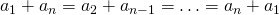$a_1 + a_n = a_2 + a_{n-1} = \ldots = a_n + a_1$ :

$2S_n = (a_1 + a_n) + (a_2 + a_{n-1}) + \ldots + (a_n + a_1) =$

$=(a_1 + a_n)n.$

Отсюда находим

$S_n = \frac{a_1 + a_n}{2}\cdot n.$

Конспект «Арифметическая прогрессия» — УчительPRO

Арифметическая прогрессия

Код ОГЭ по математике: 4.2.1. Арифметическая прогрессия. Формула общего члена арифметической прогрессии. 4.2.2. Формула суммы первых нескольких членов арифметической прогрессии

Определения и обозначения

Определение. Арифметической прогрессией называют последовательность, каждый член которой, начиная со второго, получается прибавлением к предыдущему члену одного и того же числа.

В арифметической прогрессии разность между любыми двумя соседними членами одна и та же. Эту разность называют разностью арифметической прогрессии и обозначают буквой d. Правило, по которому образуются члены арифметической прогрессии, можно записать в виде рекуррентной формулы:

а_n₊₁ – a_n = d. Или иначе: a_n₊₁ = a_n + d.

Пример 1. В арифметической прогрессии 1; 3; 5; 7; 9; 11; … разность положительна: d = 3 – 1 = 2. В этой последовательности каждый следующий член больше предыдущего; такую последовательность называют возрастающей.

Пример 2. В арифметической прогрессии 100; 90; 80; 70; 60; … разность отрицательна: d = 90 – 100 = –10. Каждый следующий член этой последовательности меньше предыдущего, и поэтому последовательность называют убывающей.

Пример 3. Последовательность 5; 5; 5; 5; 5; … , все члены которой равны между собой, тоже является арифметической прогрессией, так как разность между любыми двумя её членами одна и та же: d = 5 – 5 = 0.

Свойство арифметической прогрессии. Любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:

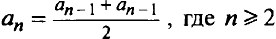
Формулы n–го члена арифметической прогрессии

Формула n–го члена арифметической прогрессии (а_n), первый член которой равен а₁ и разность равна d:

а_n = а₁ + d(n – 1).

Формула содержит четыре переменные. Если известны значения трёх из них, то можно вычислить и значение четвёртой. Убедитесь в этом, решив следующие четыре задачи (в каждом случае укажите, какие переменные известны, и получите ответ):

В арифметической прогрессии а₁ = 2 и d = 3. Найдите а₆₅. (Ответ: 194.)
В арифметической прогрессии а₈₆ = 100 и d = –4. Найдите а₁. (Ответ: 440.)
В арифметической прогрессии а₁ = 65 и а₂₁ = –55. Найдите d. (Ответ: –6.)
В арифметической прогрессии а₁ = 1 и d=4. Найдите номер члена, равного 397. (Ответ: 100.)

Пример 4. Дана арифметическая прогрессия: 1,5; 4,5; 7,5; 10,5; … . Начиная с какого номера члены этой прогрессии превосходят 1000?

В данной прогрессии а₁ = 1,5 и d = 4,5 – 1,5 = 3. Составим формулу n–го члена: а_n = 1,5 + 3(n – 1), т.е. а_n = 3_n – 1,5.

Найдём значения n, при которых выполняется условие а_n > 1000. Для этого решим неравенство 3n – 1,5 > 1000; n > 333. Таким образом, члены данной прогрессии превосходят 1000, начиная с члена, номер которого равен 334. (Для самопроверки можно вычислить а₃₃₄: имеем a₃₃₄ = 3 • 334 – 1,5 = 1000,5).

Пример 5. В арифметической прогрессии a₁₅ = 40, а₂₀ = 5. Найдём a₃₀.

Способ 1. Выразив а₁₅ и a₂₀ через а₁ и d, составим систему уравнений:

Решив её, найдём, что а₁ = 138, d = –7. (Получите этот результат самостоятельно.) Воспользовавшись формулой n–го члена, найдём a₃₀, a именно: а₃₀ = 138 – 7 • 29 = –65.

Способ 2. Выразим а₂₀ через а₁₅ и d: a₂₀ = а₁₅ + 5d. Подставив значения а₂₀ и а₁₅, получим: 5 = 40 + 5d, откуда d = –7. Теперь найдём а₃₀. Это можно сделать, например, так:
а₃₀ = а₂₀ + 10d = 5 – 7 • 10 = –65.

При решении задачи вторым способом мы воспользовались приёмом, основанным на следующим утверждении: если последовательность (а_n) – арифметическая прогрессия, то для любых натуральных n и m верно равенство:

а_n = а_m + (n – m)d.

Если вы эту формулу забудете, то в каждом конкретном случае можно выразить один член прогрессии через другой, выполнив несложные преобразования. Например, выразим а₂₀ через а₅:
а₂₀ = а₁ + 19d = (a₁ + 4d) + 15d = а₅ + 15d.

Изображение членов арифметической прогрессии
точками на координатной плоскости

Члены числовой последовательности можно изображать точками на координатной плоскости. Для этого по горизонтальной оси откладывают номер члена, a по вертикальной – соответствующий член последовательности.

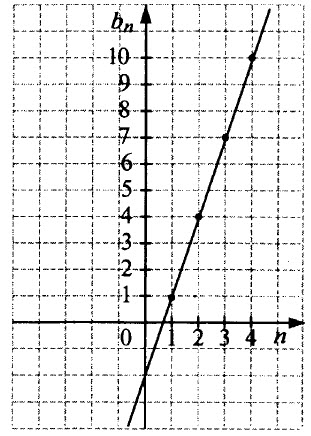
Если последовательность – арифметическая прогрессия, то точки, изображающие её члены, лежат на одной прямой. Дело в том, что зависимость n–го члена арифметической прогрессии от номера члена n является линейной. В самом деле:

a_n = a₁ + d(n – 1) = d_n + (a₁ – 1).

Например, если в арифметической прогрессии а₁ = 1 и d = 3, то а_n = 1 + 3(n – 1), т.е. а_n = 3n – 2. Значит, точки, изображающие члены этой прогрессии, лежат на прямой y = 3x – 2 (см. рис.).

Изменение членов арифметической прогрессии происходит равномерно: с каждым шагом по горизонтальной оси изображающие их точки поднимаются или опускаются на одно и то же число единиц вдоль вертикальной оси.

Формулы суммы первых n членов арифметической прогрессии

Если известны первый и последний из суммируемых членов, то удобно пользоваться формулой

Пример 6. Найдём сумму всех натуральных чисел от 1 до 1000.

Слагаемые в сумме 1 + 2 + 3 + … + 1000 образуют арифметическую прогрессию. Подставив в формулу суммы а₁ = 1, а_n= 1000, n = 1000, получим: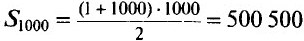

Формулу суммы первых n членов арифметической прогрессии можно записать в другом виде, выразив S_n через а₁, d и n:

Пример 7. Найдём сумму всех двузначных чисел, кратных 3.

Последовательность 12; 15; 18; … ; 99 является арифметической прогрессией, в которой а₁ = 12, а_n = 99, d= 3. Найдём номер последнего члена. Подставив в формулу а_n = а₁ + d(n – 1) указанные значения, получим уравнение 99 = 12 + 3(n – 1). Решив его, найдём, что n = 30. Теперь можно вычислить искомую сумму:

Это конспект по математике на тему «Арифметическая прогрессия». Выберите дальнейшие действия:

Арифметическая прогрессия | Онлайн калькулятор

Арифметическая прогрессия — это некая последовательность чисел, каждый следующий член которой отличается от предыдущего на одно и то же число d, называемое шаг прогрессии или разность прогрессии. Калькулятор арифметической прогрессии, используя следующие формулы, может найти первый член арифметической прогрессии , n-ный член прогрессии, найти сумму первых членов или разность.

Арифметическая прогрессия как последовательность, составленная из действительных чисел, связывает их между собой заданной закономерностью ряда. Как правило, числовой ряд начинается с того, что дан первый член арифметической прогрессии, как отправная точка. Далее каждый следующий член прогрессии получается путем прибавления к предыдущему одного и того же параметра, называемого разность арифметической прогрессии или шаг арифметической прогрессии. Если разность является положительным числом, то вся последовательность будет стремиться к плюс бесконечности, так как значения членов будут увеличиваться по мере возрастания их порядковых номеров.

Если разность арифметической прогрессии представлена отрицательным числом, каждый следующий член будет меньше предыдущего и вся последовательность будет стремиться к минус бесконечности. В некоторых случаях предел арифметической прогрессии будет конкретным числом. Это происходит, если шаг прогрессии (разность) равен нулю, тогда первый член арифметической прогрессии совпадает со всеми остальными.

Формулы арифметической прогрессии включают в себя следующие равенства:

• формула первого члена арифметической прогрессии;

• формула n-ного члена прогрессии;

• формула разности арифметической прогрессии;

• формула суммы первых членов арифметической прогрессии или суммы определенной выборки членов.

По всем формулам онлайн калькулятор рассчитывает необходимые значения, используя условия, по которым дана арифметическая прогрессия. Числа, выстроенные в симметричной последовательности, дают возможность вычислить любой член или сумму прогрессии, опираясь всего на два или три параметра в зависимости от уровня сложности задания.

{Th} `partial sum for a finite arithmetic series, a series can be written in the following way 90004 $$ S_n = a_1 + (a_1 + d) + (a_1 + 2d) + \ ldots + (a_1 + (n-1) d) $$ 90005 90008 So, 90004 $$ S_n = na_1 + [1 + 2 + 3 + \ ldots + (n-1)] d $$ 90005 90008 Since the sum of the first `(n-1)` positive integers is `\ frac {(n-1) n} {2}`, by substituting this results in the previous formula, we obtain 90004 `S_n = na_1 + \ frac {(n-1) n} {2} d` `= \ Frac {n} {2} [2a_1 + (n-1) d]` 90005 90008 When the value of the last term an is known, then using the formula for the `n ^ {th}` term of an arithmetic progression, `a_n = a_1 + (n — 1) d`, we can derive another formula for the nth partial sum of an arithmetic progression: 90004 $$ S_n = \ frac {n} {2} (a_1 + a_n) $$ 90005 Arithmetic progression calculator work with steps shows the complete step-by-step calculation for finding the `n ^ {th}` term and the `n ^ {th}` partial sum of an arithmetic progression such that there is `5` terms in the arithmetic progression, the first term is `5`, and the common difference is` 4`.For any other combinations the number of terms, the first term, and the common difference, just supply the other numbers as inputs and click on the on the 90028 «GENERATE WORK» 90029 button. The grade school students may use this arithmetic progression calculator to generate the work, verify the results or do their homework problems efficiently. 90030 90031 90032 90033 Sum of First n Numbers 90034 90035 90036 90037 90032 90039 Sum of first 100 natural numbers 90040 90039 5050 90040 90035 90032 90039 Sum of first 50 even numbers 90040 90039 2550 90040 90035 90032 90039 Sum of first 50 odd numbers 90040 90039 2500 90040 90035 90032 90039 Sum of first 50 natural numbers 90040 90039 1275 90040 90035 90032 90039 Sum of first 100 odd numbers 90040 90039 10000 90040 90035 90032 90039 Sum of first 100 even numbers 90040 90039 10100 90040 90035 90032 90039 Sum of first 10 numbers 90040 90039 55 90040 90035 90032 90039 Sum of first 10 odd numbers 90040 90039 100 90040 90035 90032 90039 Sum of first 10 even numbers 90040 90039 110 90040 90035 90032 90039 Sum of first 25 natural numbers 90040 90039 325 90040 90035 90032 90039 Sum of natual numbers from 51 to 100 90040 90039 3775 90040 90035 90032 90039 Sum of natual numbers from 50 to 100 90040 90039 3825 90040 90035 90032 90039 Sum of natual numbers from 20 to 50 90040 90039 1085 90040 90035 90116 90117 .90000 NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 90001 90002 You can opt for Chapter 5 — Arithmetic Progressions NCERT Solutions for Class 10 Maths PDF for Upcoming Exams and also You can Find the Solutions of All the Maths Chapters below. 90003 90002 NCERT Solutions for Class 10 Maths 90003 90002 Arithmetic Progression 90003 90002 Have you ever wondered why are numbers so wondrous? Ch 5 Arithmetic Progressions in NCERT Class 10 gives you the brief idea of one of the most wonderful number patterns in Mathematics.It takes you through the definition, examples and few other concepts related to the Arithmetic progressions. This chapter is divided into four sections and three exercises. 90003 90002 List of Exercises and Topics they Cover: 90003 90012 90013 90014 Exercise 5.1: Arithmetic Progression. 90003 90016 90013 90014 Exercise 5.2: nth Term Of An AP. 90003 90016 90013 90014 Exercise 5.3: Irrational Numbers 90003 90016 90013 90014 Exercise 5.4: Rational Numbers and their decimal expansions.90003 90016 90029 90002 The Fantasy of Numbers: Arithmetic Progression: 90003 90002 We come across an infinite number of patterns of Mathematics in our day to day life. Most of us just cherish at the sight of these patterns and move one while only a few wonder «WHAT IS THE MATHEMATICS BEHIND THIS PATTERN !!» One such amazing number pattern is described in Chapter 5 Maths Class 10. Arithmetic progressions is one of the most important and interesting topics in the Class 10 NCERT text book. The chapter describes the definition of arithmetic progression with examples.It also explains the general form of representing arithmetic progressions. The chapter also covers an ample number of problems which explains the steps to determine the nth term of an arithmetic sequence and the sum of the terms in an arithmetic sequence. 90003 90002 Exercise 5.1: Introduction and Arithmetic Progression 90003 90002 Exercise 5.2: Nth term of an Arithmetic Progression 90003 90002 Exercise 5.3: Sum of the terms in Arithmetic Progression 90003 90002 Exercise 5.4: Additional questions 90003 90002 Sum and Substance of Ch 5 Class 10 Maths : 90003 90012 90013 90014 Arithmetic progression is a sequence of numbers in which the difference between any two consecutive numbers is a constant when the numbers are taken in the same order.As the difference between the terms is constant throughout the sequence, it is called the common difference. 90003 90016 90013 90014 An Arithmetic progression is written in a general form as: 90003 90016 90029 90002 a, a + d, a + 2d, a + 3d, …… .., a + (n-1) d 90003 90002 In this general form, ‘a’ is the first term in the sequence, ‘d’ is the common difference and ‘n’ is the number of terms in the sequence. The first term and common difference may take up negative values. However, the number of terms in the sequence can never be a negative integer.The number of terms is always a positive whole number. 90003 90002 an = a + (n — 1) d 90003 90002 Sₙ = \ [\ frac {n} {2} \] [2a + (n-1) d] 90003 90012 90013 90014 The Arithmetic progression with ‘a’ as the first term and ‘l’ as the last term, the sum of the terms in the AP is given by product of half the number of terms in the AP and the sum of first and last terms. 90003 90016 90029 90002 Sₙ = \ [\ frac {n} {2} \] [a + l] 90003 90002 Interesting Fact About Arithmetic Progression Class 10: 90003 90002 Johann Carl Friedrich Gauss introduced the concept of Arithmetic progression.The victorious story of invention goes like this. During his schooling, the Mathematics teacher asked all the students to calculate the sum of the first 100 positive integers. He assigned this work to the students so that he can keep them engaged with work and take some rest. However, Gauss came up with the perfect answer to the question in a few moments. When asked by the teacher to explain the procedure he followed to arrive at the answer, Gauss explained it. He has arranged the first 100 integers taken in ascending order as one row and in descending order as the other row.When each corresponding element of each row was added, the sum was found to be 101. As the number of elements was hundred, he calculated the total sum as 100 x 101 = 10100. However, since he had taken the set of 100 integers twice , he divided the sum obtained by 2 and arrived at the final answer of the sum of 100 integers as 10100/2 = 5050. This formed the basis for all the further advances in the concept of arithmetic progression. 90003 90002 NCERT Solutions for Class 10 Chapter 5 PDF by Vedantu Stands out to be Unique: 90003 90012 90013 90014 The NCERT Solutions for Class 10 Chapter 5 is devised with utmost care and we at Vedantu ensure that you get the best input while referring to the solutions.90003 90016 90013 90014 Choice of words and vocabulary is also given due importance so that no incorrect problem solving methodology is conveyed due to grammatical errors. 90003 90016 90013 90014 Students and teachers are benefited with step by step solutions to the problem so 90003 90016 90029.n. Find the third term. 90008 90013 90002 90003 [2] 2020/03/20 16:04 — / — / — / — / 90004 90005 Comment / Request 90006 90007 Mallam usman deposit # 1000 in the bank for his son on each of his birthdays from the first to the twentieth inclusive. what will be the total value on the son’s twenty- first birthday? 90008 90013 90002 90003 [3] 2019/09/17 4:31 Male / 30 years old level / An engineer / — / 90004 90005 Purpose of use 90006 90007 Line design and sequencing. 90008 90005 Comment / Request 90006 90007 The sum of the first 50 terms in an arithmetic progression = 200.The sum of the next 50 terms = 2,700. What is the 10th term of the progression? 90008 90013 90002 90003 [4] 2019/03/30 6:36 Male / Under 20 years old / High-school / University / Grad student / Useful / 90004 90005 Purpose of use 90006 90007 need help 90008 90005 Comment / Request 90006 90007 help me solve this .. The first and the last term of an ap are 2 and 125 respectively. If the 5th term is 14 find the number of term in the ap 90008 90013 90002 90003 [5] 2019/01/30 1:47 Female / Under 20 years old / High-school / University / Grad student / Very / 90004 90005 Purpose of use 90006 90007 study 90008 90013 90002 90003 [6] 2018/02/24 5:57 Male / 20 years old level / High-school / University / Grad student / Very / 90004 90005 Purpose of use 90006 90007 I want to write wassce 2018 sept 90008 90013 90002 90003 [7] 2017/06/24 4:32 — / — / — / Useful / 90004 90005 Comment / Request 90006 90007 Pls solve this for me: the first term of an arithmetic progression (AP) is — 8.If the ratio of the 7th term is 5: 8, find the common difference of the AP 90008 90013 90002 90003 [8] 2012/10/29 21:27 Male / 20 years old level / High-school / University / Grad student / Very / 90004 90005 Purpose of use 90006 90007 do not know how to do it, plz help me … 90008 90005 Comment / Request 90006 90007 2 + 5 + 6 + 7 + 10 + 11 + …. nth find summation of nth term 90008 90013.90000 Arithmetic Progression — Study Material for IIT JEE 90001 90002 90003 90004 90005 90006 90007 90008 90009 Meaning of Arithmetic Progression (A.P.) 90010 90011 90004 90009 Arithmetic Progression 90010 is the sequence of numbers such that the difference between the two successive terms is always constant. And that difference is called the 90009 Common Difference 90010. It is also known as 90009 Arithmetic Sequence 90010. 90005 90004 90021 90005 90023 90024 90004 The first term of the sequence is called the 90009 Initial Term 90010 which is denoted as ‘a’. 90005 90029 90024 90004 The difference by which the consecutive numbers of the sequence increases or decreases is called the 90009 Common Difference 90010, which is denoted by’d ‘.90005 90029 90024 90004 The 90009 general term 90010 that is, the nth term of the arithmetic progression with the initial term a and the common difference d is as 90005 90029 90042 90004 90009 a 90045 n 90046 = a + (n-1) d 90010 90005 90004 90050 90009 Example 90010 90053 90005 90004 Consider the right figure- 90005 90004 90058 Here the sequence is given as 90005 90004 1, 3, 5, 7, 9, 11, 13, 15 90005 90004 Given a = 1 and d = 2 90005 90004 Let’s check the value of the 5 90065 th 90066 term using the nth term formula.90005 90004 a 90045 n 90046 = a + (n-1) d 90005 90004 a 90045 5 90046 = 1 + (5 -1) 2 90005 90004 = 1 + 8 90005 90004 = 9 90005 90004 It is given in the right figure that the 5 90065 th 90066 term is 9. 90008 90005 90007 90009 Finite and Infinite Arithmetic Progression 90010 90011 90004 The arithmetic progression with a limited number of terms is called 90009 Finite Sequence 90010. It has a last term. 90005 90004 90050 90009 Example 90010 90053 90005 90004 2, 9, 16, 23, …, 86 90005 90004 This is a finite sequence with a = 2 and d = 7 90005 90004 The arithmetic progression with unlimited number of terms is called 90009 Infinite Sequence 90010.It does not have a last term. 90005 90004 90050 90009 Example 90010 90053 90005 90004 1, 3, 5, 7, … 90005 90004 This is an infinite sequence with a = 1 and d = 2 90008 90005 90007 90009 Positive and Negative Common Difference 90010 90011 90004 It depends upon the value of the common difference that the arithmetic progression is increasing or decreasing. 90005 90023 90024 If the common difference ‘d’ is positive then the arithmetic progression will increase towards positive infinity that is, it will be an 90009 increasing sequence 90010.90029 90042 90004 If d> 0 and satisfies that a 90045 n-1 90046 a 90045 n 90046, then 90005 90004 a 90045 1 90046> a 90045 2 90046> a 90045 3 90046 … 90005 90004 90050 90009 Example 90010 90053 90005 90004 20, 10, 0, -10, -20, … 90005 90004 This is a decreasing sequence with a = 20 and d = -10. 90008 90005 90007 90009 Properties of Arithmetic Progression 90010 90011 90004 90050 90009 Example 90010 90053 90005 90004 3, 6, 9, … is an AP with a = 3 and d = 3 90005 90004 If we will add 2 to every term of the sequence then the new sequence will be 90005 90004 5, 8, 11, … with a = 5 and d = 3 90005 90004 Hence, this is also an arithmetic progression.90005 90004 90050 90009 Example 90010 90053 90005 90004 1, 2, 3, 4, … is an AP with a = 1 and d = 1 90005 90004 If we multiply the every term of the sequence with 5 then the new sequence will be 90005 90004 5, 10, 15, 20, … with a = 5 and d = 5 90005 90004 Hence, this is also an arithmetic sequence. 90008 90005 90007 90009 Graphical Representation of the Arithmetic Progression 90010 90011 90004 The Arithmetic Progression can be shown through the graphs also. It could be on number line or on the Cartesian plane.90008 90005 90225 90009 Representation on Number Line 90010 90228 90004 On the number line, the AP can be shown as follows: 90009 90010 90005 90004 90234 90005 90004 Here in the above number line, it is showing the arithmetic progression 90005 90004 1, 2, 3, 4, 5, 6, … 90005 90004 with a = 1 and d = +1 90008 90005 90225 90009 Representation on the Cartesian Plane 90010 90228 90004 90248 AP = 3, 5, 7, 9, 11 90005 90004 a = 3 and d = +2 90005 90004 Here we need the Cartesian coordinates to represent it on the Cartesian plane.90005 90004 a 90045 n 90046 is the nth term, so the corresponding Cartesian coordinates will be in the form of (n, a 90045 n 90046). 90005 90004 For the right arithmetic progression the coordinates will be as follows: 90008 90005 90007 90009 Arithmetic Series 90010 90011 90004 When we add the terms of the arithmetic progression then that sum is the arithmetic series. Like, the AP, the difference between every consecutive term is always constant. 90005 90004 The arithmetic series is in the form of 90005 90004 90009 {a + (a + d) + (a + 2d) + (a + 3d) +………} 90010 90005 90004 where a is the first term of the series and d is the difference of it which is known as the common difference of the given series. 90008 90005 90007 90009 Formula of nth term of Arithmetic Series 90010 90011 90004 If a is the first term, d is the difference and n is the total number of the terms, then the formula for nth term is given by 90005 90004 (1, 3), (2, 5), (3, 7), (4, 9), (5, 11) 90005 90004 90009 a 90045 n 90046 = a + (n — 1) d 90010 90005 90004 90050 90009 Example 90010 90053 90005 90004 What is the 10 90065 th 90066 term of the series 2 + 4 + 6 + 8 + …? 90005 90004 90009 Solution: 90010 90005 90004 In the given series a = 2 and d = 2 90005 90004 So we will put the values in the formula of nth term of the series.90005 90004 a 90045 n 90046 = a + (n — 1) d 90005 90004 Here n = 10 as we have to find the 10 90065 th 90066 term. 90005 90004 a 90045 10 90046 = 2+ (10 — 1) 2 90005 90004 = 2 + 18 90005 90004 = 20 90005 90004 So the 10 90065 th 90066 term of the series will be 20 90008 90005 90007 90009 Sum of an Arithmetic Series 90010 90011 90004 90336 90005 90004 90050 90009 Example 90010 90053 90005 90004 Find the sum of the given arithmetic progression 90005 90004 90009 2 + 5 + 8 + 11 + 14 90010 90005 90004 90009 Solution: 90010 90005 90004 Given 90005 90004 a = 2 (first term) 90005 90004 d = 3 (common difference) 90005 90004 n = 5 (as the total number of terms of the series is 5) 90005 90004 Now we will put the values in the formula 90005 90004 90365 90005 90004 90368 90005 90004 Let’s take the same example as above 90005 90004 90009 2 + 5 + 8 + 11 + 14 90010 90005 90004 Now we will find the sum of the series with a = 2 and l = 14 90009 90010 90005 90004 90381 90005 90004 Hence the sum remains the same if we calculate with the formula.90008 90005 90007 90009 Arithmetic Mean 90010 90011 90004 90009 Arithmetic Mean is basically the average of two numbers 90010. If we have two numbers n and m, then we can include a number L in between these numbers so that the three numbers will form an arithmetic sequence like n, L, m. 90005 90004 In that case the number L is the arithmetic mean of the numbers n and m. 90005 90004 According to the property of Arithmetic progression, we can say that- 90005 90004 L — n = m — L that is, the common difference of the given AP.90005 90004 90401 90005 90004 This is generally used to find the missing number of the sequence between the two given numbers. 90005 90004 90050 90009 Example 90010 90053 90005 90004 What will be the 6 90065 th 90066 number of the sequence if the 5 90065 th 90066 term is 12 and the 7 90065 th 90066 term is 24? 90005 90004 As the two numbers are given so the 6 90065 th 90066 number will be the Arithmetic mean of the two given numbers. 90005 90004 90424 90005 90004 Hence the 6 90065 th 90066 term will be 18.90005 90004 90009 We can insert two or more numbers between the two given numbers to form an Arithmetic Progression 90010. 90005 90004 Let A 90045 1 90046, A 90045 2 90046, A 90045 3 90046, …, An be n numbers between a and b such that a, A 90045 1 90046, A 90045 2 90046, A 90045 3 90046, …, An, b is an AP 90005 90004 Here, b is the (n + 2) th term, that is, b = a + [(n + 2) — 1] d = a + (n + 1) d. 90005 90004 This gives 90005 90004 90453 90005 90004 Thus, n numbers between a and b are as follows: 90005 90004 90458 90005 90004 90050 90009 Example 90010 90053 90005 90004 Insert 5 numbers between 3 and 21 such that the resulting sequence is an A.P. 90005 90004 90009 Solution: 90010 90005 90004 Let A 90045 1 90046, A 90045 2 90046, A 90045 3 90046, A 90045 4 90046 and A 90045 5 90046 be the five numbers between 3 and 21 such that 90005 90004 90009 3 90010, 90009 A 90045 1 90046 90010, 90009 A 90045 2 90046 90010, 90009 A 90045 3 90046 90010, 90009 A 90045 4 90046 90010, 90009 A 90045 5 90046 90010, 90009 21 90010 90005 90004 the sequence is in A.P. 90005 90004 Here, a = 3, b = 21, n = 7. 90005 90004 Therefore, 90005 90004 21 = 3 + (7 -1) d 90005 90004 18 = 6d 90005 90004 d = 3 90005 90004 Thus A 1 = a + d = 3 + 3 = 6; 90005 90004 A 2 = a + 2d = 3 + 2 × 3 = 9; 90005 90004 A 3 = a + 3d = 3 + 3 × 3 = 12; 90005 90004 A 4 = a + 4d = 3 + 4 × 3 = 15; 90005 90004 A5 = a + 5d = 3 + 5 × 3 = 18; 90005 90004 Hence, five numbers between 3 and 21 are 6, 9, 12, 15 and 18 90005 90004 90008 90009 More Readings 90010 90005 90004 Arithmetic Progression (A.P.) 90005 90541 90008 90225 Course Features 90228 90023 90024 731 Video Lectures 90029 90024 Revision Notes 90029 90024 Previous Year Papers 90029 90024 Mind Map 90029 90024 Study Planner 90029 90024 NCERT Solutions 90029 90024 Discussion Forum 90029 90024 Test paper with Video Solution 90029 90042 90008 .

Арифметическая прогрессия. Учебник по ЕГЭ и ГИА

Числовая последовательность

Арифметическая прогрессия

Свойство арифметической прогрессии

Сумма первых n членов арифметической прогрессии

Тренировка

Подведем итоги

Общий вид арифметической прогрессии

Свойства и формулы арифметической прогрессии

Арифметическая прогрессия. Часть 1

Арифметическая прогрессия | umath.ru

Определение арифметической прогрессии

Сумма первых n членов арифметической прогрессии

Конспект «Арифметическая прогрессия» — УчительPRO

Арифметическая прогрессия

Определения и обозначения

аn+1 – an = d. Или иначе: an+1 = an + d.

Формулы n–го члена арифметической прогрессии

аn = а1 + d(n – 1).

аn = аm + (n – m)d.

Изображение членов арифметической прогрессииточками на координатной плоскости

an = a1 + d(n – 1) = dn + (a1 – 1).

Формулы суммы первых n членов арифметической прогрессии

Арифметическая прогрессия | Онлайн калькулятор

Добавить комментарий Отменить ответ

а_n₊₁ – a_n = d. Или иначе: a_n₊₁ = a_n + d.

а_n = а₁ + d(n – 1).

а_n = а_m + (n – m)d.

Изображение членов арифметической прогрессии
точками на координатной плоскости

a_n = a₁ + d(n – 1) = d_n + (a₁ – 1).