Длина медианы треугольника
Пусть дан треугольник , длины сторон которого соответсвенно равны :
Докажем, что длину медианы , проведенной из вершины можно выразить через длины сторон треугольника с помощью такой формулы:
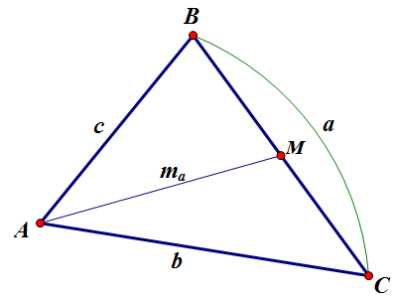
1. Достроим данный треугольник до параллелограмма.
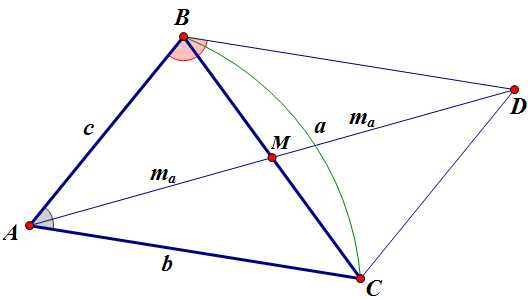
2. Из треугольника найдем косинус угла с помощью теоремы косинусов.
Отсюда (1)
3. Так как (по свойству односторонних углов),
4. Из треугольника выразим сторону :
(по свойству параллелограмма)
Подставим выражение (1) для
Утверждение доказано.
И. В. Фельдман, репетитор по математике.
ege-ok.ru
Медиана треугольника
МЕДИАНА ТРЕУГОЛЬНИКА
Слово «медиана» переводится как «равноделящая сторону». Чтобы построить медиану, надо середину стороны треугольника соединить отрезком с противолежащей вершиной треугольника. Полученный отрезок и есть медиана треугольника.
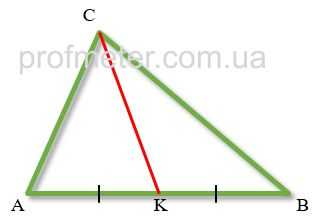
Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.
На рисунке красным цветом обозначена медиана CK. При этом она делит сторону AB треугольника пополам, AK = KB.
Свойства медианы треугольника
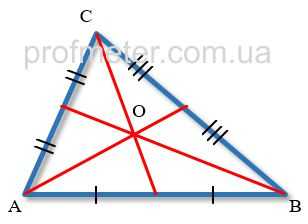
Все медианы треугольника пересекаются в одной точке, расположенной в плоскости треугольника и являющейся его центром тяжести.
-
Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1, считая от вершины треугольника. Т.е. длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины, а от точки пересечения медиан до стороны треугольника — 1/3 ее длины.
-
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
-
Треугольник делится тремя медианами на шесть равновеликих треугольников.
-
Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
-
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
-
Большей стороне треугольника соответствует меньшая медиана.
-
У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.
-
У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.
Средняя линия треугольника
Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией.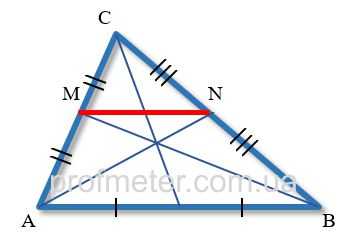
Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
Формулы медианы произвольного треугольника
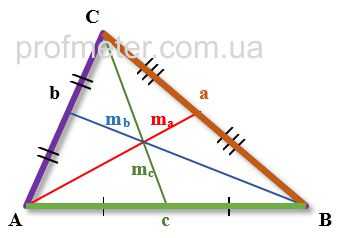
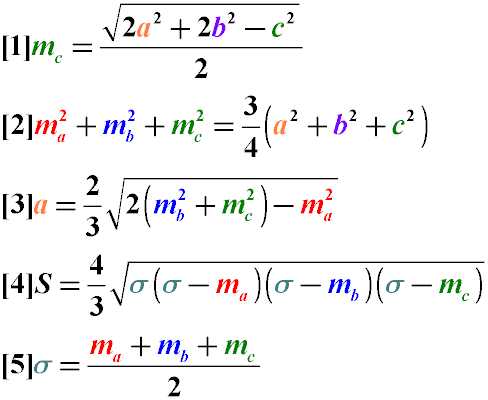
- Длина медианы, проведенной к стороне произвольного треугольника равна половине квадратного корня из удвоенной суммы квадратов двух других сторон из которой вычтен квадрат стороны, к которой проведена медиана (Формула 1)
- Сумма квадратов медиан треугольника равна 3/4 суммы квадратов его сторон (Формула 2)
- Длина стороны треугольника равна 2/3 квадратного корня из удвоенной суммы квадратов медиан, проведенных к двум другим его сторонам за вычетом квадрата медианы, проведенной к искомой стороне (Формула 3)
- Площадь треугольника можно найти через длины его медиан, используя значение полусуммы длин медиан (Формулы 4 и 5)
Площадь треугольника | Описание курса | Как найти длину медианы треугольника
profmeter.com.ua
Медиана в прямоугольном треугольнике | Треугольники
Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.
Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:
Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.
Свойства медианы, проведенной к гипотенузе:
1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.
(в следующий раз рассмотрим доказательство этого свойства)
2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.
Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.
Например:
и так далее.
www.treugolniki.ru
Медиана равностороннего треугольника | Треугольники
Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?
Теорема 1
(свойство медианы равностороннего треугольника)
В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.
Доказательство:
Пусть в треугольнике ABC AB=BC=AC.
Проведём медиану BF.
Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.
По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.
Аналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;
так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.
Что и требовалось доказать.
Теорема 2
(свойство медиан равностороннего треугольника)
Все три медианы равностороннего треугольника равны между собой.
Доказательство:
Пусть в треугольнике ABC AB=BC=AC,
AK, BF, CD — его медианы.
Тогда AF=FC=BK=CK=AD=BD.
∠BAF=∠BFC=∠ABC (как углы равностороннего треугольника).
Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон:
AK=BF=CD.
Что и требовалось доказать.
Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.
1) Выразим длину медианы равностороннего треугольника через его сторону.
Так как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.
Обозначим AB=a, BF=m, тогда AF=a/2.
По теореме Пифагора
Таким образом, формула медианы равностороннего треугольника по его стороне:
2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.
Центр правильного треугольника является центром его вписанной и описанной окружностей.
Так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:
OF=r, BO=R.
Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,
Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна
через радиус описанной окружности —
www.treugolniki.ru
Медиана в равностороннем треугольнике, все формулы
Определение и формулы медианы равностороннего треугольника
В равностороннем треугольнике любая медиана является высотой и биссектрисой
.Для медиан равностороннего треугольника справедливы следующие утверждения:
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Медиана разбивает треугольник на два равновеликих треугольника (т.е. на треугольники с одинаковой площадью).
- Весь треугольник делится своими медианами на шесть равновеликих треугольников.
- Медиана, проведенная к стороне , вычисляется по формуле:
где – сторона равностороннего треугольника.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Медиана в равнобедренном треугольнике, все формулы
Определение и формулы медианы равнобедренного треугольника
В равнобедренном треугольнике медиана, опущенная на основание, является высотой и биссектрисой.
Для медиан равнобедренного треугольника справедливы следующие утверждения:
- Медианы равнобедренного треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Медиана разбивает равнобедренный треугольник на два треугольника с одинаковой площадью.
- Весь равнобедренный треугольник делится своими медианами на шесть равновеликих (т.е. с одинаковой площадью) треугольников.
Медиана равнобедренного треугольника, проведенная к его основанию, вычисляется по формуле:
где – основание равнобедренного треугольника, – боковые стороны треугольника.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Все формулы медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
- Подробности
- Автор: Administrator
www-formula.ru
