Метод наименьших квадратов
Программа МНК
Введите данные
Данные и аппроксимация y = a + b·x
i – номер экспериментальной точки;
xi – значение фиксированного параметра в точке i;
yi – значение измеряемого параметра в точке i;
ωi – вес измерения в точке i;
yi, расч. – разница между измеренным и вычисленным по регрессии значением y в точке i;
Sxi(xi) – оценка погрешности xi при измерении y в точке i.
Кликните по графику,
чтобы добавить значения в таблицу
Данные и аппроксимация y = k·x
| i | xi | yi | ωi | yi, расч. | Δyi | Sx |
|---|
Кликните по графику,
чтобы добавить значения в таблицу
Инструкция пользователя онлайн-программы МНК.
В поле данных введите на каждой отдельной строке значения `x` и `y` в одной экспериментальной точке. Значения должны отделяться пробельным символом (пробелом или знаком табуляции).
Третьим значением может быть вес точки `w`. Если вес точки не указан, то он приравнивается единице. В подавляющем большинстве случаев веса экспериментальных точек неизвестны или не вычисляются, т.е. все экспериментальные данные считаются равнозначными. Иногда веса в исследуемом интервале значений совершенно точно не равнозначны и даже могут быть вычислены теоретически. Например, в спектрофотометрии веса можно вычислить по простым формулам, правда в основном этим все пренебрегают для уменьшения трудозатрат.
Данные можно вставить через буфер обмена из электронной таблицы офисных пакетов, например Excel из Майкрософт Офиса или Calc из Оупен Офиса. Для этого в электронной таблице выделите диапазон копируемых данных, скопируйте в буфер обмена и вставьте данные в поле данных на этой странице.
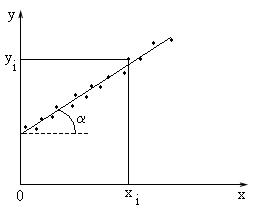
Для расчета по методу наименьших квадратов необходимо не менее двух точек для определения двух коэффициентов `b` – тангенса угла наклона прямой и `a` – значения, отсекаемого прямой на оси `y`.
Для оценки погрешности расчитываемых коэффициентов регресии нужно задать количество экспериментальных точек больше двух. Чем больше количество экспериментальных точек, тем более точна статистическая оценка коэффицинетов (за счет снижения коэффицинета Стьюдента) и тем более близка оценка к оценке генеральной выборки.
Получение значений в каждой экспериментальной точке часто сопряжено со значительными трудозатратами, поэтому часто проводят компромиссное число экспериментов, которые дает удобоваримую оценку и не привеодит к чрезмерным трудо затратам. Как правило число экспериментах точек для линейной МНК зависимости с двумя коэффицинетами выбирает в районе 5-7 точек.
Краткая теория метода наименьших квадратов для линейной зависимости
Допустим у нас имеется набор экспериментальных данных в виде пар значений [`y_i`, `x_i`], где `i` – номер одного эксперементального измерения от 1 до `n`; `y_i` – значение измеренной величины в точке `i`; `x_i` – значение задаваемого нами параметра в точке `i`.
В качестве примера можно рассмотреть действие закона Ома. Изменяя напряжение (разность потенциалов) между участками электрической цепи, мы замеряем величину тока, проходящего по этому участку. Физика нам дает зависимость, найденную экспериментально:
`I = U / R`,
где `I` – сила тока; `R` – сопротивление; `U` – напряжение.
В этом случае `y_i` у нас имеряемая величина тока, а `x_i` – значение напряжения.
В качестве другого примера рассмотрим поглощение света раствором вещества в растворе. Химия дает нам формулу:
`A = ε l C`,
где `A` – оптическая плотность раствора;
`ε` – коэффициент пропускания растворенного вещества;
`l` – длина пути при прохождении света через кювету с раствором;
`C` – концентрация растворенного вещества.
В этом случае `y_i` у нас имеряемая величина отптической плотности `A`, а `x_i` – значение концентрации вещества, которое мы задаем.
Мы будем рассматривать случай, когда относительная погрешность в задании `x_i` значительно меньше, относительной погрешности измерения `y_i`. Так же мы будем предполагать, что все измеренные величины `y_i` случайные и нормально распределенные, т.е. подчиняются нормальному закону распределения.
В случае линейной зависимости `y` от `x`, мы можем написать теоретическую зависимость:
`y = a + b x`.
С геометрической точки зрения, коэффициент `b` обозначает тангенс угла наклона линии к оси `x`, а коэффициент `a` – значение `y` в точке пересечения линии с осью `y` (при `x = 0`).
Нахождение параметров линии регресии.
В эксперименте измеренные значения `y_i` не могут точно лечь на теоеретическую прямую из-за ошибок измерения, всегда присущих реальной жизни.
Поэтому линейное уравнение, нужно представить системой уравнений:
`y_i = a + b x_i + ε_i` (1),
где `ε_i` – неизвестная ошибка измерения `y` в `i`-ом эксперименте.
Зависимость (1) так же называют регрессией, т.е. зависимостью двух величин друг от друга со статистической значимостью.
Задачей восстановления зависимости является нахождение коэффициентов `a` и `b` по экспериментальным точкам [`y_i`, `x_i`].
Для нахождения коэффициентов `a` и `b` обычно используется метод наименьших квадратов (МНК). Он является частным случаем принципа максимального правдоподобия.
Перепишем (1) в виде `ε_i = y_i — a — b x_i`.
Тогда сумма квадратов ошибок будет
`Φ = sum_(i=1)^(n) ε_i^2 = sum_(i=1)^(n) (y_i — a — b x_i)^2`. (2)
Принципом МНК (метода наименьших квадратов) является минимизация суммы (2) относительно параметров `a` и `b`.
Минимум достигается, когда частные производные от суммы (2) по коэффициентам `a` и `b` равны нулю:
`frac(partial Φ)(partial a) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial a) = 0`
`frac(partial Φ)(partial b) = frac( partial sum_(i=1)^(n) (y_i — a — b x_i)^2)(partial b) = 0`
Раскрывая производные, получаем систему из двух уравнений с двумя неизвестными:
`sum_(i=1)^(n) (2a + 2bx_i — 2y_i) = sum_(i=1)^(n) (a + bx_i — y_i) = 0`
`sum_(i=1)^(n) (2bx_i^2 + 2ax_i — 2x_iy_i) = sum_(i=1)^(n) (bx_i^2 + ax_i — x_iy_i) = 0`
Раскрываем скобки и переносим независящие от искомых коэффициентов суммы в другую половину, получим систему линейных уравнений:
`sum_(i=1)^(n) y_i = a n + b sum_(i=1)^(n) bx_i`
`sum_(i=1)^(n) x_iy_i = a sum_(i=1)^(n) x_i + b sum_(i=1)^(n) x_i^2`
Решая, полученную систему, находим формулы для коэффициентов `a` и `b`:
`a = frac(sum_(i=1)^(n) y_i sum_(i=1)^(n) x_i^2 — sum_(i=1)^(n) x_i sum_(i=1)^(n) x_iy_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.1)
`b = frac(n sum_(i=1)^(n) x_iy_i — sum_(i=1)^(n) x_i sum_(i=1)^(n) y_i) (n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2)` (3.2)
Эти формулы имеют решения, когда `n > 1` (линию можно построить не менее чем по 2-м точкам) и когда детерминант `D = n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i )^2 != 0`, т.е. когда точки `x_i` в эксперименте различаются (т.е. когда линия не вертикальна).
Оценка погрешностей коэффициентов линии регресии
Для более точной оценки погрешности вычисления коэффициентов `a` и `b` желательно большое количество экспериментальных точек. При `n = 2`, оценить погрешность коэффициентов невозможно, т.к. аппроксимирующая линия будет однозначно проходить через две точки.
Погрешность случайной величины `V` определяется законом накопления ошибок
`S_V^2 = sum_(i=1)^p (frac(partial f)(partial z_i))^2 S_(z_i)^2`,
где `p` – число параметров `z_i` с погрешностью `S_(z_i)`, которые влияют на погрешность `S_V`;
`f` – функция зависимости `V` от `z_i`.
Распишем закон накопления ошибок для погрешности коэффициентов `a` и `b`
`S_a^2 = sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial a)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial a)(partial y_i))^2 `
,`S_b^2 = sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 S_(y_i)^2 + sum_(i=1)^(n)(frac(partial b)(partial x_i))^2 S_(x_i)^2 = S_y^2 sum_(i=1)^(n)(frac(partial b)(partial y_i))^2 `
,т.к. `S_(x_i)^2 = 0` (мы ранее сделали оговорку, что погрешность `x` пренебрежительно мала).
`S_y^2 = S_(y_i)^2` – погрешность (дисперсия, квадрат стандартного отклонения) в измерении `y` в предположении, что погрешность однородна для всех значений `y`.
Подставляя в полученные выражения формулы для расчета `a` и `b` получим
`S_a^2 = S_y^2 frac(sum_(i=1)^(n) ( sum_(i=1)^(n) x_i^2 — x_i sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2) sum_(i=1)^(n) x_i^2 ) (D^2) = S_y^2 frac(sum_(i=1)^(n) x_i^2) (D)` (4.1)
`S_b^2 = S_y^2 frac(sum_(i=1)^(n) ( n x_i — sum_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac(n ( n sum_(i=1)^(n) x_i^2 — (sum_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 frac(n) (D)` (4.2)
В большинстве реальных экспериментов значение `Sy` не измеряется. Для этого нужно проводить несколько паралельных измерений (опытов) в одной или нескольких точках плана, что увеличивает время (и возможно стоимость) эксперимента. Поэтому обычно полагают, что отклонение `y` от линии регрессии можно считать случайным. Оценку дисперсии `y` в этом случае, считают по формуле.
`S_y^2 = S_(y, ост)^2 = frac(sum_(i=1)^n (y_i — a — b x_i )^2) (n-2)`
.Делитель `n-2` появляется потому, что у нас снизилось число степеней свободы из-за расчета двух коэффициентов по этой же выборке экспериментальных данных.
Такую оценку еще называют остаточной дисперсией относительно линии регрессии `S_(y, ост)^2`.
Оценка значимости коэффициентов проводится по критерию Стьюдента
`t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)`
Если рассчитанные критерии `t_a`, `t_b` меньше табличных критериев `t(P, n-2)`, то считается, что соответсвующий коэффициент не значимо отличается от нуля с заданной вероятностью `P`.
Если `t_a
Если `t_b
Для оценки качества описания линейной зависимости, можно сравнить `S_(y, ост)^2` и `S_(bar y)` относительно среднего с использованием критерия Фишера.
`S_(bar y) = frac(sum_(i=1)^n (y_i — bar y)^2) (n-1) = frac(sum_(i=1)^n (y_i — (sum_(i=1)^n y_i) /n )^2) (n-1)`
– выборочная оценка дисперсии `y` относительно среднего.
Для оценки эффективности уравнения регресии для описания зависимости расчитывают коэффициент Фишера
`F = S_(bar y) / S_(y, ост)^2`,
который сравнивают с табличным коэффициентом Фишера `F(p, n-1, n-2)`.
Если `F > F(P, n-1, n-2)`, считается статистически значимым с вероятностью `P` различие между описанием зависимости `y = f(x)` с помощью уравенения регресии и описанием с помощью среднего. Т.е. регрессия лучше описывает зависимость, чем разброс `y` относительно среднего.
| На главную | База 1 | База 2 | База 3 |
| Поиск по реквизитамПоиск по номеру документаПоиск по названию документаПоиск по тексту документа |
| Искать все виды документовДокументы неопределённого видаISOАвиационные правилаАльбомАпелляционное определениеАТКАТК-РЭАТПЭАТРВИВМРВМУВНВНиРВНКРВНМДВНПВНПБВНТМ/МЧМ СССРВНТПВНТП/МПСВНЭВОМВПНРМВППБВРДВРДСВременное положениеВременное руководствоВременные методические рекомендацииВременные нормативыВременные рекомендацииВременные указанияВременный порядокВрТЕРВрТЕРрВрТЭСНВрТЭСНрВСНВСН АСВСН ВКВСН-АПКВСПВСТПВТУВТУ МММПВТУ НКММПВУП СНЭВУППВУТПВыпускГКИНПГКИНП (ОНТА)ГНГОСТГОСТ CEN/TRГОСТ CISPRГОСТ ENГОСТ EN ISOГОСТ EN/TSГОСТ IECГОСТ IEC/PASГОСТ IEC/TRГОСТ IEC/TSГОСТ ISOГОСТ ISO GuideГОСТ ISO/DISГОСТ ISO/HL7ГОСТ ISO/IECГОСТ ISO/IEC GuideГОСТ ISO/TRГОСТ ISO/TSГОСТ OIML RГОСТ ЕНГОСТ ИСОГОСТ ИСО/МЭКГОСТ ИСО/ТОГОСТ ИСО/ТСГОСТ МЭКГОСТ РГОСТ Р ЕНГОСТ Р ЕН ИСОГОСТ Р ИСОГОСТ Р ИСО/HL7ГОСТ Р ИСО/АСТМГОСТ Р ИСО/МЭКГОСТ Р ИСО/МЭК МФСГОСТ Р ИСО/МЭК ТОГОСТ Р ИСО/ТОГОСТ Р ИСО/ТСГОСТ Р ИСО/ТУГОСТ Р МЭКГОСТ Р МЭК/ТОГОСТ Р МЭК/ТСГОСТ ЭД1ГСНГСНрГСССДГЭСНГЭСНмГЭСНмрГЭСНмтГЭСНпГЭСНПиТЕРГЭСНПиТЕРрГЭСНрГЭСНсДИДиОРДирективное письмоДоговорДополнение к ВСНДополнение к РНиПДСЕКЕНВиРЕНВиР-ПЕНиРЕСДЗемЕТКСЖНМЗаключениеЗаконЗаконопроектЗональный типовой проектИИБТВИДИКИМИНИнструктивное письмоИнструкцияИнструкция НСАМИнформационно-методическое письмоИнформационно-технический сборникИнформационное письмоИнформацияИОТИРИСОИСО/TRИТНИТОсИТПИТСИЭСНИЭСНиЕР Республика КарелияККарта трудового процессаКарта-нарядКаталогКаталог-справочникККТКОКодексКОТКПОКСИКТКТПММ-МВИМВИМВНМВРМГСНМДМДКМДСМеждународные стандартыМетодикаМетодика НСАММетодические рекомендацииМетодические рекомендации к СПМетодические указанияМетодический документМетодическое пособиеМетодическое руководствоМИМИ БГЕИМИ УЯВИМИГКМММНМОДНМонтажные чертежиМос МУМосМРМосСанПинМППБМРМРДСМРОМРРМРТУМСанПиНМСНМСПМТМУМУ ОТ РММУКМЭКННАС ГАНБ ЖТНВННГЭАНДНДПНиТУНКНормыНормы времениНПНПБНПРМНРНРБНСПНТПНТП АПКНТП ЭППНТПДНТПСНТСНЦКРНЦСОДМОДНОЕРЖОЕРЖкрОЕРЖмОЕРЖмрОЕРЖпОЕРЖрОКОМТРМОНОНДОНКОНТПОПВОПКП АЭСОПНРМСОРДОСГиСППиНОСНОСН-АПКОСПОССПЖОССЦЖОСТОСТ 1ОСТ 2ОСТ 34ОСТ 4ОСТ 5ОСТ ВКСОСТ КЗ СНКОСТ НКЗагОСТ НКЛесОСТ НКМОСТ НКММПОСТ НКППОСТ НКПП и НКВТОСТ НКСМОСТ НКТПОСТ5ОСТНОСЭМЖОТРОТТПП ССФЖТПБПБПРВПБЭ НППБЯПВ НППВКМПВСРПГВУПереченьПиН АЭПисьмоПМГПНАЭПНД ФПНД Ф СБПНД Ф ТПНСТПОПоложениеПорядокПособиеПособие в развитие СНиППособие к ВНТППособие к ВСНПособие к МГСНПособие к МРПособие к РДПособие к РТМПособие к СНПособие к СНиППособие к СППособие к СТОПособие по применению СППостановлениеПОТ РПОЭСНрППБППБ-АСППБ-СППБВППБОППРПРПР РСКПР СМНПравилаПрактическое пособие к СППРБ АСПрейскурантПриказПротоколПСРр Калининградской областиПТБПТЭПУГПУЭПЦСНПЭУРР ГазпромР НОПРИЗР НОСТРОЙР НОСТРОЙ/НОПР РСКР СМНР-НП СРО ССКРазъяснениеРаспоряжениеРАФРБРГРДРД БГЕИРД БТРД ГМРД НИИКраностроенияРД РОСЭКРД РСКРД РТМРД СМАРД СМНРД ЭОРД-АПКРДИРДМРДМУРДПРДСРДТПРегламентРекомендацииРекомендацияРешениеРешение коллегииРКРМРМГРМДРМКРНДРНиПРПРРТОП ТЭРС ГАРСНРСТ РСФСРРСТ РСФСР ЭД1РТРТМРТПРУРуководствоРУЭСТОП ГАРЭГА РФРЭСНрСАСанитарные нормыСанитарные правилаСанПиНСборникСборник НТД к СНиПСборники ПВРСборники РСН МОСборники РСН ПНРСборники РСН ССРСборники ценСБЦПСДАСДАЭСДОССерияСЗКСНСН-РФСНиПСНиРСНККСНОРСНПСОСоглашениеСПСП АССП АЭССправочникСправочное пособие к ВСНСправочное пособие к СНиПСправочное пособие к СПСправочное пособие к ТЕРСправочное пособие к ТЕРрСРПССНССЦСТ ССФЖТСТ СЭВСТ ЦКБАСТ-НП СРОСТАСТКСТМСТНСТН ЦЭСТОСТО 030 НОСТРОЙСТО АСЧМСТО БДПСТО ВНИИСТСТО ГазпромСТО Газпром РДСТО ГГИСТО ГУ ГГИСТО ДД ХМАОСТО ДОКТОР БЕТОНСТО МАДИСТО МВИСТО МИСТО НААГСТО НАКССТО НКССТО НОПСТО НОСТРОЙСТО НОСТРОЙ/НОПСТО РЖДСТО РосГеоСТО РОСТЕХЭКСПЕРТИЗАСТО САСТО СМКСТО ФЦССТО ЦКТИСТО-ГК «Трансстрой»СТО-НСОПБСТПСТП ВНИИГСТП НИИЭССтП РМПСУПСССУРСУСНСЦНПРТВТЕТелеграммаТелетайпограммаТематическая подборкаТЕРТЕР Алтайский крайТЕР Белгородская областьТЕР Калининградской областиТЕР Карачаево-Черкесская РеспубликаТЕР Краснодарского краяТЕР Мурманская областьТЕР Новосибирской областиТЕР Орловской областиТЕР Республика ДагестанТЕР Республика КарелияТЕР Ростовской областиТЕР Самарской областиТЕР Смоленской обл.ТЕР Ямало-Ненецкий автономный округТЕР Ярославской областиТЕРмТЕРм Алтайский крайТЕРм Белгородская областьТЕРм Воронежской областиТЕРм Калининградской областиТЕРм Карачаево-Черкесская РеспубликаТЕРм Мурманская областьТЕРм Республика ДагестанТЕРм Республика КарелияТЕРм Ямало-Ненецкий автономный округТЕРмрТЕРмр Алтайский крайТЕРмр Белгородская областьТЕРмр Карачаево-Черкесская РеспубликаТЕРмр Краснодарского краяТЕРмр Республика ДагестанТЕРмр Республика КарелияТЕРмр Ямало-Ненецкий автономный округТЕРпТЕРп Алтайский крайТЕРп Белгородская областьТЕРп Калининградской областиТЕРп Карачаево-Черкесская РеспубликаТЕРп Краснодарского краяТЕРп Республика КарелияТЕРп Ямало-Ненецкий автономный округТЕРп Ярославской областиТЕРрТЕРр Алтайский крайТЕРр Белгородская областьТЕРр Калининградской областиТЕРр Карачаево-Черкесская РеспубликаТЕРр Краснодарского краяТЕРр Новосибирской областиТЕРр Омской областиТЕРр Орловской областиТЕРр Республика ДагестанТЕРр Республика КарелияТЕРр Ростовской областиТЕРр Рязанской областиТЕРр Самарской областиТЕРр Смоленской областиТЕРр Удмуртской РеспубликиТЕРр Ульяновской областиТЕРр Ямало-Ненецкий автономный округТЕРррТЕРрр Ямало-Ненецкий автономный округТЕРс Ямало-Ненецкий автономный округТЕРтр Ямало-Ненецкий автономный округТехнический каталогТехнический регламентТехнический регламент Таможенного союзаТехнический циркулярТехнологическая инструкцияТехнологическая картаТехнологические картыТехнологический регламентТИТИ РТИ РОТиповая инструкцияТиповая технологическая инструкцияТиповое положениеТиповой проектТиповые конструкцииТиповые материалы для проектированияТиповые проектные решенияТКТКБЯТМД Санкт-ПетербургТНПБТОИТОИ-РДТПТПРТРТР АВОКТР ЕАЭСТР ТСТРДТСНТСН МУТСН ПМСТСН РКТСН ЭКТСН ЭОТСНэ и ТЕРэТССЦТССЦ Алтайский крайТССЦ Белгородская областьТССЦ Воронежской областиТССЦ Карачаево-Черкесская РеспубликаТССЦ Ямало-Ненецкий автономный округТССЦпгТССЦпг Белгородская областьТСЦТСЦ Белгородская областьТСЦ Краснодарского краяТСЦ Орловской областиТСЦ Республика ДагестанТСЦ Республика КарелияТСЦ Ростовской областиТСЦ Ульяновской областиТСЦмТСЦО Ямало-Ненецкий автономный округТСЦп Калининградской областиТСЦПГ Ямало-Ненецкий автономный округТСЦэ Калининградской областиТСЭМТСЭМ Алтайский крайТСЭМ Белгородская областьТСЭМ Карачаево-Черкесская РеспубликаТСЭМ Ямало-Ненецкий автономный округТТТТКТТПТУТУ-газТУКТЭСНиЕР Воронежской областиТЭСНиЕРм Воронежской областиТЭСНиЕРрТЭСНиТЕРэУУ-СТУказУказаниеУказанияУКНУНУОУРврУРкрУРррУРСНУСНУТП БГЕИФАПФедеральный законФедеральный стандарт оценкиФЕРФЕРмФЕРмрФЕРпФЕРрФормаФорма ИГАСНФРФСНФССЦФССЦпгФСЭМФТС ЖТЦВЦенникЦИРВЦиркулярЦПИШифрЭксплуатационный циркулярЭРД |
| Показать все найденные Показать действующие Показать частично действующие Показать не действующие Показать проекты Показать документы с неизвестным статусом |
| Упорядочить по номеру документаУпорядочить по дате введения |
 примерно одинаковы или неизвестны) является обычная регрессия без весов.
примерно одинаковы или неизвестны) является обычная регрессия без весов.Добавлено спустя 28 минут 18 секунд:
Забавная мысль, кажется, мысль: делаем обычный МНК, определяем 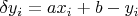 . Эти значения обычно используются для отбраковки «заведомо плохих» измерений и пересчёта параметров модели. Вот эту отбраковку можно и устроить, взяв
. Эти значения обычно используются для отбраковки «заведомо плохих» измерений и пересчёта параметров модели. Вот эту отбраковку можно и устроить, взяв 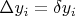 как весовые множители для следующей итерации. Получим очередной набор весов, следующую итерацию… И т.д. Сходимость, причём быстрая, интуитивно ясна. А более полная интерпретация такого алгоритма и его результата теоретиками от статистики, возможно, была бы интересной.
как весовые множители для следующей итерации. Получим очередной набор весов, следующую итерацию… И т.д. Сходимость, причём быстрая, интуитивно ясна. А более полная интерпретация такого алгоритма и его результата теоретиками от статистики, возможно, была бы интересной.
Но мне бы не хотелось уводить обсуждение в эту сторону, ибо это явно не то, чего ждёт вопрошающий (ну, если только после удовлетворения его нужд можно почесать язык об эти итерации).
Насколько я понял, вопрос автора состоит примерно в следующем. Если мы такого рода измерениями проверяем закон Ома, то какую погрешность 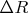 следует приписать найденному сопротивлению?
следует приписать найденному сопротивлению?
Здесь дело чуть сложнее, чем закон Ома, ибо мы фитируем два параметра. И значения 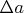 ,
, 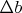
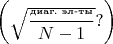 некой корреляционной матрицы. Недиагональный элемент, что-то вроде коэфф. корреляции надобно тоже проанализировать.
некой корреляционной матрицы. Недиагональный элемент, что-то вроде коэфф. корреляции надобно тоже проанализировать. Не в корреляционной ли матрице суть вопроса? Право, ARMICRON, почитайте про неё…
Добавлено спустя 11 минут 41 секунду:
Ну да, конечно.
Когда я работал на физиков, выдача ВСЕХ классических МНК-минимайзеров (Minuit, напрмер) состояла в выдаче найденных  параметров, и — непременно — их
параметров, и — непременно — их 
Метод наименьших квадратов регрессия | matematicus.ru
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
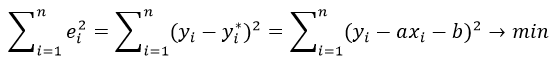
частные производные функции приравниваем к нулю
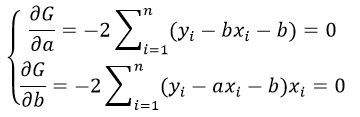
отсюда получаем систему линейных уравнений
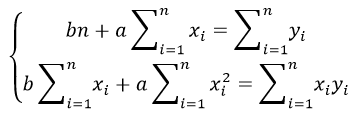
Формулы определения коэффициентов уравнения линейной регрессии:
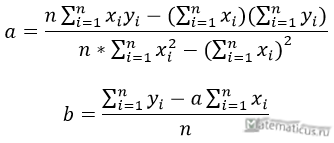
Также запишем уравнение регрессии для квадратной нелинейной функции:
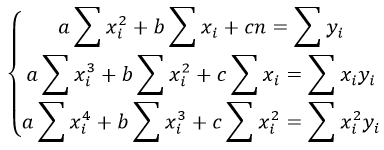
Система линейных уравнений регрессии полинома n-ого порядка:
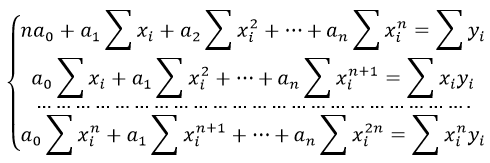
Формула коэффициента детерминации R2:
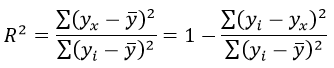
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
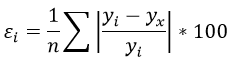
Чем меньше ε, тем лучше. Рекомендованный показатель ε<10%
Формула среднеквадратической погрешности: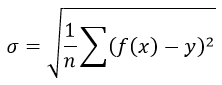
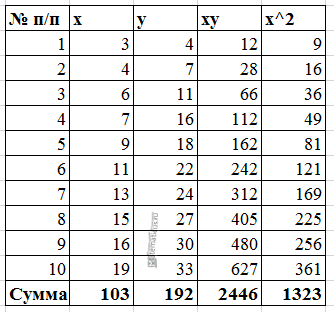
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
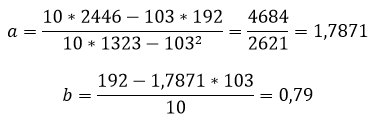
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
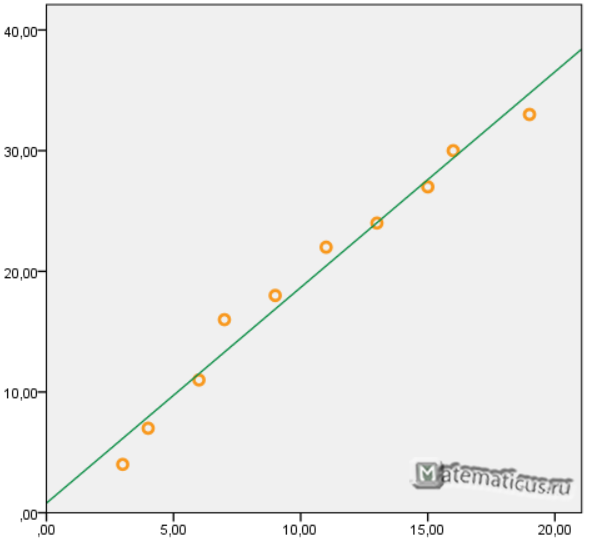
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Метод наименьших квадратов — Студопедия
Сущность метода наименьших квадратов состоит в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут такие, при которых сумма квадратов отклонений экспериментальных значений функции 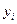 от значений самой функции
от значений самой функции 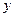 , будет наименьшей:
, будет наименьшей: 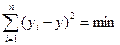 . Обычно функция
. Обычно функция 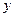 является функцией нескольких аргументов
является функцией нескольких аргументов 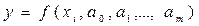 , где
, где  — неизвестные коэффициенты многочлена. Тогда на основании
— неизвестные коэффициенты многочлена. Тогда на основании 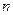 экспериментальных пар
экспериментальных пар  следует определить
следует определить  искомых аргументов аналитической зависимости, которая наилучшим образом описывает массив
искомых аргументов аналитической зависимости, которая наилучшим образом описывает массив  , т.е. в этом случае метод наименьших квадратов требует выполнения условия:
, т.е. в этом случае метод наименьших квадратов требует выполнения условия:
 .
.
Применение метода наименьших квадратов при статистической обработке результатов измерений требует учета ряда условий:
§ Значения аргументов 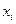 известны точно;
известны точно;
§ Результаты измерений 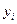 независимы и содержат лишь случайные погрешности с одинаковыми дисперсиями;
независимы и содержат лишь случайные погрешности с одинаковыми дисперсиями;
§ Погрешности измерения 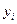 имеют нормальное распределение.
имеют нормальное распределение.
Первое условие приближенно выполняется за счет измерения значения 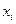 с меньшей погрешностью, чем
с меньшей погрешностью, чем 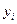 . Наличие только случайных погрешностей обеспечивается исключением из результатов измерений возможных систематических погрешностей.
. Наличие только случайных погрешностей обеспечивается исключением из результатов измерений возможных систематических погрешностей.
На основе метода наименьших квадратов можно выполнять аппроксимацию различных аналитических зависимостей, например, выражаемых такими полиномами:
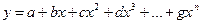 , где a, b, c, d, …, g – константы.
, где a, b, c, d, …, g – константы.
Рассмотрим случай, когда искомая зависимость имеет линейный характер вида 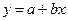 .
.
 При использовании метода наименьших квадратов необходимо по набору из
При использовании метода наименьших квадратов необходимо по набору из  экспериментальных координат (
экспериментальных координат ( 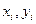 ) найти такие оценки неизвестных постоянных a и b, при которых получится прямая линия, наилучшим образом отражающая истинную анализируемую линию.
) найти такие оценки неизвестных постоянных a и b, при которых получится прямая линия, наилучшим образом отражающая истинную анализируемую линию.
График функции – прямая линия с коэффициентом b = tgα, пересекающая ось ординат в точке а.
В соответствии с методом наименьших квадратов наилучшим оценкам a и b соответствуетминимальное значение выражения 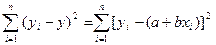 , где
, где 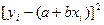 — отклонение измеренных значений
— отклонение измеренных значений  от вычисленных при
от вычисленных при  .
.
Эта величина минимальна, если ее частные производные равны нулю:
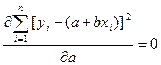 и
и 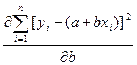 = 0.
= 0.
Решая систему этих двух уравнений, находим формулы для оценок значений a и b:


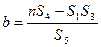
При этом:
 ;
;  ;
; 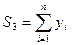 ;
; 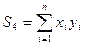 ;
; 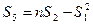 .
.
Степень приближения найденных значений a и b к истинным значениям
Этих величин оценивается с помощью их СКО 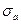 и
и  :
:
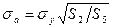 ,
, 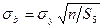 ,
,
где 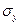 — СКО погрешности измерения величины y, значение которой можно получить из паспортных данных на средство измерения или вычислить по формуле:
— СКО погрешности измерения величины y, значение которой можно получить из паспортных данных на средство измерения или вычислить по формуле:
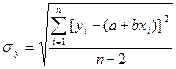 .
.
В качестве примера практического применения метода наименьших квадратов рассмотрим аппроксимацию нагрузочной характеристики одного из устройств преобразовательной техники. Для построения нагрузочной характеристики измеряют 5 … 10 пар значений выходного напряжения  и тока нагрузки
и тока нагрузки 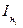 . Индекс
. Индекс 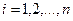 соответствует текущему измерению (n – число измерений).
соответствует текущему измерению (n – число измерений).
В данном примере было снято десять пар (n=10) экспериментальных точек  и
и 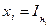 напряжения и тока соответственно.
напряжения и тока соответственно.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
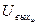 ,B ,B
| 5,35 | 5,20 | 5,11 | 4,92 | 4,76 | 4.76 | 4,50 | 4,33 | 4,30 | 4,04 |
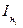 ,mA ,mA
| 105 | 110 | 129 | 148 | 154 | 181 | 190 | 206 | 225 | 241 |
По полученным экспериментальным результатам построим графическое отображение полученных пар и аппроксимируем их.
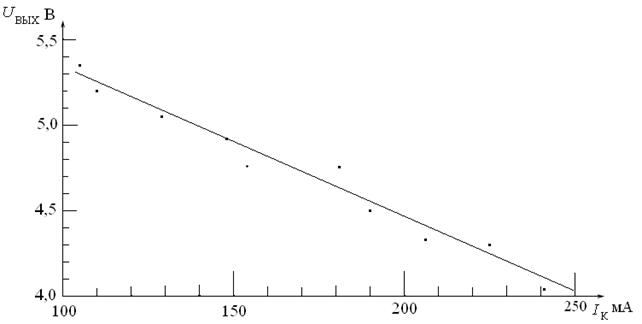
Рис. 1 Аппроксимация исследуемой зависимости методом наименьших квадратов
Из расположения экспериментальных точек видно, что аппроксимирующим уравнением может быть полином первой степени типа 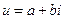 . Таким образом, на основании массива экспериментальных данных по уравнениям вычисляем коэффициенты a и b:
. Таким образом, на основании массива экспериментальных данных по уравнениям вычисляем коэффициенты a и b:
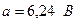 ;
;
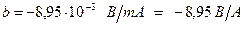
Следовательно, исследуемое устройство имеет нагрузочную характеристику, аналитически описываемую как
ПРИМЕР 2
Требуется установить реальную зависимость сопротивления металлического проводника от температуры 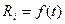 по результатам совместных измерений температуры и сопротивления. При этом теоретическая зависимость определена как
по результатам совместных измерений температуры и сопротивления. При этом теоретическая зависимость определена как 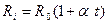 , где
, где 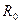 — сопротивление проводника при температуре 0 0С;
— сопротивление проводника при температуре 0 0С; 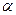 — температурный коэффициент сопротивления проводника;
— температурный коэффициент сопротивления проводника; 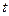 — температура в 0С.
— температура в 0С.
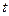 ,0С ,0С
| 10 | 15 | 20 | 25 |
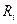 , Ом , Ом
| 10,3 | 10,9 | 11,3 | 11,6 |
Преобразуем заданную зависимость 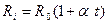 в вид
в вид 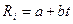 , где
, где  ,
, 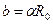 .
.
Расчеты по формулам


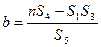
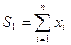 ;
;  ;
; 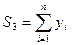 ;
; 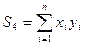 ;
; 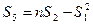
при п=4, 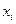 = ti,, и
= ti,, и 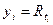 дают следующие результаты: а = 9б52 Ом, b = 0,09 Ом/градус.
дают следующие результаты: а = 9б52 Ом, b = 0,09 Ом/градус.
Пусть средство измерения имеет СКО 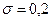 Ом. Тогда, проведя вычисления по формулам
Ом. Тогда, проведя вычисления по формулам
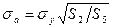 ,
, 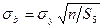 ,
,
получим: 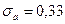 Ом,
Ом, 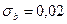 Ом/ градус.
Ом/ градус.
Окончательно получаем:
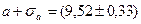 Ом.
Ом. 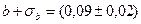 Ом/градус.
Ом/градус.
Метод наименьших квадратов.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьСущность метода наименьших квадратов заключается в отыскании параметров модели тренда, которая лучше всего описывает тенденцию развития какого-либо случайного явления во времени или в пространстве (тренд – это линия, которая и характеризует тенденцию этого развития). Задача метода наименьших квадратов (МНК) сводится к нахождению не просто какой-то модели тренда, а к нахождению лучшей или оптимальной модели. Эта модель будет оптимальной, если сумма квадратических отклонений между наблюдаемыми фактическими величинами и соответствующими им расчетными величинами тренда будет минимальной (наименьшей):
 (9.1)
(9.1)
где  — квадратичное отклонение между наблюдаемой фактической величиной
— квадратичное отклонение между наблюдаемой фактической величиной
и соответствующей ей расчетной величиной тренда,
 — фактическое (наблюдаемое) значение изучаемого явления,
— фактическое (наблюдаемое) значение изучаемого явления,
 — расчетное значение модели тренда,
— расчетное значение модели тренда,
 — число наблюдений за изучаемым явлением.
— число наблюдений за изучаемым явлением.
МНК самостоятельно применяется довольно редко. Как правило, чаще всего его используют лишь в качестве необходимого технического приема при корреляционных исследованиях. Следует помнить, что информационной основой МНК может быть только достоверный статистический ряд, причем число наблюдений не должно быть меньше 4-х, иначе, сглаживающие процедуры МНК могут потерять здравый смысл.
Инструментарий МНК сводится к следующим процедурам:
Первая процедура. Выясняется, существует ли вообще какая-либо тенденция изменения результативного признака при изменении выбранного фактора-аргумента, или другими словами, есть ли связь между «у» и «х».
Вторая процедура. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать эту тенденцию.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Пример. Допустим, мы имеем информацию о средней урожайности подсолнечника по исследуемому хозяйству (табл. 9.1).
Таблица 9.1
Номер наблюдения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Годы | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
Урожайность, ц/га | 14,2 | 15,6 | 17,5 | 14,5 | 15,3 | 17,0 | 16,6 | 17,5 | 15,0 | 17,7 |
Поскольку уровень технологии при производстве подсолнечника в нашей стране за последние 10 лет практически не изменился, значит, по всей видимости, колебания урожайности в анализируемый период очень сильно зависели от колебания погодно-климатических условий. Действительно ли это так?
Первая процедура МНК. Проверяется гипотеза о существовании тенденции изменения урожайности подсолнечника в зависимости от изменения погодно-климатических условий за анализируемые 10 лет.
В данном примере за «y» целесообразно принять урожайность подсолнечника, а за «x» – номер наблюдаемого года в анализируемом периоде. Проверку гипотезы о существовании какой-либо взаимосвязи между «x» и «y» можно выполнить двумя способами: вручную и при помощи компьютерных программ. Конечно, при наличии компьютерной техники данная проблема решается сама собой. Но, чтобы лучше понять инструментарий МНК целесообразно выполнить проверку гипотезы о существовании связи между «x» и «y» вручную, когда под рукой находятся только ручка и обыкновенный калькулятор. В таких случаях гипотезу о существовании тенденции лучше всего проверить визуальным способом по расположению графического изображения анализируемого ряда динамики — корреляционного поля:


Корреляционное поле в нашем примере расположено вокруг медленно возрастающей линии. Это уже само по себе говорит о существовании определенной тенденции в изменении урожайности подсолнечника. Нельзя говорить о наличии какой-либо тенденции лишь тогда, когда корреляционное поле похоже на круг, окружность, строго вертикальное или строго горизонтальное облако, или же состоит из хаотично разбросанных точек. Во всех остальных случаях следует подтвердить гипотезу о существовании взаимосвязи между «x» и «y», и продолжить исследования.
Вторая процедура МНК. Определяется, какая линия (траектория) способна лучше всего описать или охарактеризовать тенденцию изменения урожайности подсолнечника за анализируемый период.
При наличии компьютерной техники подбор оптимального тренда происходит автоматически. При «ручной» обработке выбор оптимальной функции осуществляется, как правило, визуальным способом – по расположению корреляционного поля. То есть, по виду графика подбирается уравнение линии, которая лучше всего подходит к эмпирическому тренду (к фактической траектории).
Как известно, в природе существует огромное разнообразие функциональных зависимостей, поэтому визуальным способом проанализировать даже незначительную их часть — крайне затруднительно. К счастью, в реальной экономической практике большинство взаимосвязей достаточно точно могут быть описаны или параболой, или гиперболой, или же прямой линией. В связи с этим, при «ручном» варианте подбора лучшей функции, можно ограничиться только этими тремя моделями.
Прямая: |
| Гипербола: |
|
|
|
Парабола второго порядка:  :
:

Нетрудно заметить, что в нашем примере лучше всего тенденцию изменения урожайности подсолнечника за анализируемые 10 лет характеризует прямая линия, поэтому уравнением регрессии будет уравнение прямой.
Третья процедура. Рассчитываются параметры регрессионного уравнения, характеризующего данную линию, или другими словами, определяется аналитическая формула, описывающая лучшую модель тренда.
Нахождение значений параметров уравнения регрессии, в нашем случае параметров  и
и  , является сердцевиной МНК. Данный процесс сводится к решению системы нормальных уравнений.
, является сердцевиной МНК. Данный процесс сводится к решению системы нормальных уравнений.
 (9.2)
(9.2)
Эта система уравнений довольно легко решается методом Гаусса. Напомним, что в результате решения, в нашем примере, находятся значения параметров  и
и  . Таким образом, найденное уравнение регрессии будет иметь следующий вид:
. Таким образом, найденное уравнение регрессии будет иметь следующий вид: 
В линейном уравнении параметр  – коэффициент регрессии указывает, на сколько единиц в среднем изменится
– коэффициент регрессии указывает, на сколько единиц в среднем изменится  с изменением
с изменением  на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи
на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи  – величина положительная, а при обратном – отрицательная. Параметр
– величина положительная, а при обратном – отрицательная. Параметр  – свободный член уравнения регрессии, то есть это значение
– свободный член уравнения регрессии, то есть это значение при
при  . Если
. Если  не получает нулевых значений, этот параметр имеет лишь расчетное назначение.
не получает нулевых значений, этот параметр имеет лишь расчетное назначение.
Приведем также системы нормальных уравнений для отыскивания параметров нелинейных уравнений.
Таблица 9.2
Форма связи | Уравнение связи | Система нормальных уравнений |
параболическая |
|
|
гиперболическая |
|
|
Следует помнить, что при изменении хотя бы одного значения входных данных (пары значений или одного из них) все коэффициенты изменят в общем случае свои значения, потому что они полностью определяются входными данными. Поэтому при повторной аппроксимации с несколькими измененными данными будет получена другая аппроксимирующая функция с другими коэффициентами.
или одного из них) все коэффициенты изменят в общем случае свои значения, потому что они полностью определяются входными данными. Поэтому при повторной аппроксимации с несколькими измененными данными будет получена другая аппроксимирующая функция с другими коэффициентами.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Аппроксимация опытных данных. Метод наименьших квадратов
Аппроксимация опытных данных – это метод, основанный на замене экспериментально полученных данных аналитической функцией наиболее близко проходящей или совпадающей в узловых точках с исходными значениями (данными полученными в ходе опыта или эксперимента). В настоящее время существует два способа определения аналитической функции:
— с помощью построения интерполяционного многочлена n-степени, который проходит непосредственно через все точки заданного массива данных. В данном случае аппроксимирующая функция представляется в виде: интерполяционного многочлена в форме Лагранжа или интерполяционного многочлена в форме Ньютона.
— с помощью построения аппроксимирующего многочлена n-степени, который проходит в ближайшей близости от точек из заданного массива данных. Таким образом, аппроксимирующая функция сглаживает все случайные помехи (или погрешности), которые могут возникать при выполнении эксперимента: измеряемые значения в ходе опыта зависят от случайных факторов, которые колеблются по своим собственным случайным законам (погрешности измерений или приборов, неточность или ошибки опыта). В данном случае аппроксимирующая функция определяется по методу наименьших квадратов.
Метод наименьших квадратов (в англоязычной литературе Ordinary Least Squares, OLS) — математический метод, основанный на определении аппроксимирующей функции, которая строится в ближайшей близости от точек из заданного массива экспериментальных данных. Близость исходной и аппроксимирующей функции F(x) определяется числовой мерой, а именно: сумма квадратов отклонений экспериментальных данных от аппроксимирующей кривой F(x) должна быть наименьшей.
Рис.1. Аппроксимирующая кривая, построенная по методу наименьших квадратов
Метод наименьших квадратов используется:
— для решения переопределенных систем уравнений, когда количество уравнений превышает количество неизвестных;
— для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений;
— для аппроксимации точечных значений некоторой аппроксимирующей функцией.
Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений расчетной аппроксимирующей функции от заданного массива экспериментальных данных. Данный критерий метода наименьших квадратов записывается в виде следующего выражения:
— значения расчетной аппроксимирующей функции в узловых точках ,
— заданный массив экспериментальных данных в узловых точках .
Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.
В зависимости от условий задачи аппроксимирующая функция представляет собой многочлен степени m
Степень аппроксимирующей функции не зависит от числа узловых точек, но ее размерность должна быть всегда меньше размерности (количества точек) заданного массива экспериментальных данных.
∙ В случае если степень аппроксимирующей функции m=1, то мы аппроксимируем табличную функцию прямой линией (линейная регрессия).
∙ В случае если степень аппроксимирующей функции m=2, то мы аппроксимируем табличную функцию квадратичной параболой (квадратичная аппроксимация).
∙ В случае если степень аппроксимирующей функции m=3, то мы аппроксимируем табличную функцию кубической параболой (кубическая аппроксимация).
В общем случае, когда требуется построить аппроксимирующий многочлен степени m для заданных табличных значений, условие минимума суммы квадратов отклонений по всем узловым точкам переписывается в следующем виде:
— координаты узловых точек таблицы;
— неизвестные коэффициенты аппроксимирующего многочлена степени m;
— количество заданных табличных значений.
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным . В результате получим следующую систему уравнений:
Преобразуем полученную линейную систему уравнений: раскроем скобки и перенесем свободные слагаемые в правую часть выражения. В результате полученная система линейных алгебраических выражений будет записываться в следующем виде:
Данная система линейных алгебраических выражений может быть переписана в матричном виде:
В результате была получена система линейных уравнений размерностью m+1, которая состоит из m+1 неизвестных. Данная система может быть решена с помощью любого метода решения линейных алгебраических уравнений (например, методом Гаусса). В результате решения будут найдены неизвестные параметры аппроксимирующей функции, обеспечивающие минимальную сумму квадратов отклонений аппроксимирующей функции от исходных данных, т.е. наилучшее возможное квадратичное приближение. Следует помнить, что при изменении даже одного значения исходных данных все коэффициенты изменят свои значения, так как они полностью определяются исходными данными.
Аппроксимация исходных данных линейной зависимостью
(линейная регрессия)
В качестве примера, рассмотрим методику определения аппроксимирующей функции, которая задана в виде линейной зависимости. В соответствии с методом наименьших квадратов условие минимума суммы квадратов отклонений записывается в следующем виде:
— координаты узловых точек таблицы;
— неизвестные коэффициенты аппроксимирующей функции, которая задана в виде линейной зависимости.
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным. В результате получаем следующую систему уравнений:
Преобразуем полученную линейную систему уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом (метод Крамера):
Данные коэффициенты обеспечивают построение линейной аппроксимирующей функции в соответствии с критерием минимизации суммы квадратов аппроксимирующей функции от заданных табличных значений (экспериментальные данные).
Алгоритм реализации метода наименьших квадратов
1. Начальные данные:
— задан массив экспериментальных данных с количеством измерений N
— задана степень аппроксимирующего многочлена (m)
2. Алгоритм вычисления:
2.1. Определяются коэффициенты для построения системы уравнений размерностью
— коэффициенты системы уравнений (левая часть уравнения)
— индекс номера строки квадратной матрицы системы уравнений
— индекс номера столбца квадратной матрицы системы уравнений
— свободные члены системы линейных уравнений (правая часть уравнения)
— индекс номера строки квадратной матрицы системы уравнений
2.2. Формирование системы линейных уравнений размерностью .
2.3. Решение системы линейных уравнений с целью определения неизвестных коэффициентов аппроксимирующего многочлена степени m.
2.4.Определение суммы квадратов отклонений аппроксимирующего многочлена от исходных значений по всем узловым точкам
Найденное значение суммы квадратов отклонений является минимально-возможным.
Аппроксимация с помощью других функций
Следует отметить, что при аппроксимации исходных данных в соответствии с методом наименьших квадратов в качестве аппроксимирующей функции иногда используют логарифмическую функцию, экспоненциальную функцию и степенную функцию.
Логарифмическая аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана логарифмической функцией вида:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Экспоненциальная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана экспоненциальной функцией вида:
Для применения метода наименьших квадратов экспоненциальная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Степенная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана степенной функцией вида:
Для применения метода наименьших квадратов степенная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Выбор наилучшей аппроксимирующей функции определяется значением среднеквадратического отклонения. В связи с этим следует по методу наименьших квадратов определить несколько аппроксимирующих функций, а затем по критерию наименьшего среднеквадратического отклонения выбрать наиболее подходящую функцию.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
90000 linux — MATLAB MCC «??? Error Using ==> mcc, return status = 1» 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 .net assembly — I have trouble using mcc compiler in MATLAB (Error using ==> mcc The output directory does not exist) 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 Error using ==> mcc — MATLAB Answers 90001 90002 I would like to make a Add in to excel — i saw it on polish webminarium. 90003 90002 I am using windows 7 professional edition, when i would like to build a add-in to excel MATLAB R2008b shows this: 90003 90002 Compiler version: 4.9 (R2008b) 90003 90002 Warning: Duplicate directory name: C: \ Users \ Kamil \ Documents \ MATLAB. 90003 90002 mcc -W ‘excel: Untitled5, Untitled5,1.0’ -d ‘C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src’ -T ‘link: lib’ -b -v ‘class {Untitled5: G: \ plotgantt.m} ‘90003 90002 Warning: Name is nonexistent or not a directory: C: \ Program 90003 90002 Files \ MATLAB \ R2008b \ toolbox \ compiler \ patch. 90003 90002 Warning: Name is nonexistent or not a directory: C: \ Program 90003 90002 Files \ MATLAB \ R2008b \ toolbox \ compiler \ patch. 90003 90002 Processing C: \ Program Files \ MATLAB \ R2008b \ toolbox \ matlab \ mcc.enc 90003 90002 Processing include files … 90003 90002 2 item (s) added. 90003 90002 Processing directories installed with MCR … 90003 90002 The file C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ mccExcludedFiles.log contains a list of functions excluded from the CTF archive. 90003 90002 2 item (s) added. 90003 90002 Generating MATLAB path for the compiled application … 90003 90002 Created 39 path items. 90003 90002 Begin validation of MEX files: Sat Apr 23 19:17:31 2011 90003 90002 End validation of MEX files: Sat Apr 23 19:17:31 2011 90003 90002 Warning: Name is nonexistent or not a directory: C: \ Program 90003 90002 Files \ MATLAB \ R2008b \ toolbox \ compiler \ patch. 90003 90002 Deleting 0 temporary MEX authorization files.90003 90002 Parsing file «G: \ plotgantt.m» 90003 90002 (Referenced from: «Compiler Command Line»). 90003 90002 Parsing file «C: \ Program Files \ MATLAB \ R2008b \ toolbox \ compiler \ deploy \ deployprint.m» 90003 90002 (Referenced from: «Compiler Command Line»). 90003 90002 Parsing file «C: \ Program Files \ MATLAB \ R2008b \ toolbox \ compiler \ deploy \ printdlg.m» 90003 90002 (Referenced from: «Compiler Command Line»). 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_idl.idl».90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_com.hpp». 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_com.cpp». 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_dll.cpp». 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5.def». 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5.rc». 90003 90002 Generating file «C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5.bas «. 90003 90002 Generating file» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ readme.txt «. 90003 90002 Generating file» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_mcc_component_data. c «. 90003 90002 Contents of temporary response file ‘C: \ Users \ Kamil \ AppData \ Local \ Temp \ mathworks_tmp_3656_28770’: 90003 90002 … 90003 90002 ‘-O -v -output» Untitled5_1_0 «-I» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src «» mwcomtypes.idl «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_idl.idl «» mclxlmain.lib «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_com.cpp «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_dll.cpp «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5.def «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5.rc «» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src \ Untitled5_mcc_component_data.c «-link dll -outdir» C: \ Users \ Kamil \ Documents \ MATLAB \ Untitled5 \ src «-regsvr ‘90003 90002 … 90003 90002 Executing command: mbuild» @C: \ Users \ Kamil \ AppData \ Local \ Temp \ mathworks_tmp_3656_28770 «90003 90002 This is mbuild Copyright 1984-2006 The MathWorks, Inc.90003 90002 -> Default options filename found in C: \ Users \ Kamil \ AppData \ Roaming \ MathWorks \ MATLAB \ R2008b 90003 90002 ———————— —————————————— 90003 90002 -> Options file = C: \ Users \ Kamil \ AppData \ Roaming \ MathWorks \ MATLAB \ R2008b \ compopts.bat 90003 90002 -> COMPILER = lcc 90003 90002 -> Compiler flags: 90003 90002 COMPFLAGS = -c -Zp8 -I «C: \ PROGRA ~ 1 \ MATLAB \ R2008b \ sys \ lcc \ include «-noregistrylookup 90003 90002 OPTIMFLAGS = -DNDEBUG 90003 90002 DEBUGFLAGS = -g4 90003 90002 arguments = -IC: \ USERS \ KAMIL \ DOCUME ~ 1 \ MATLAB \ UN3F25 ~ 1 \ SRC 90003 90002 Name switch = -Fo 90003 90002 -> Pre-linking commands = 90003 90002 -> LINKER = lcclnk 90003 90002 -> Link directives: 90003 90002 LINKFLAGS = -dll «C: \ USERS \ KAMIL \ APPDATA \ LOCAL \ TEMP \ MBUILD ~ 2 \ templib.def «-tmpdir» C: \ USERS \ KAMIL \ DOCUME ~ 1 \ MATLAB \ UN3F25 ~ 1 \ SRC \. «-L» C: \ PROGRA ~ 1 \ MATLAB \ R2008b \ sys \ lcc \ lib «-libpath» C : \ PROGRA ~ 1 \ MATLAB \ R2008b \ extern \ lib \ win32 \ lcc «C: \ USERS \ KAMIL \ APPDATA \ LOCAL \ TEMP \ MBUILD ~ 2 \ templib_stub.obj 90003 90002 LINKFLAGSPOST = mclmcrrt.lib 90003 90002 Name directive = -o «C: \ USERS \ KAMIL \ DOCUME ~ 1 \ MATLAB \ UN3F25 ~ 1 \ SRC \ Untitled5_1_0.dll» 90003 90002 File link directive = 90003 90002 Lib. link directive = 90003 90002 Rsp file indicator = @ 90003 90002 -> Resource Compiler = 90003 90002 -> Resource Linker = 90003 90002 ————————————— ————————— 90003 90002 C: \ PROGRA ~ 1 \ MATLAB \ R2008B \ BIN \ MEX.PL: Error: The chosen compiler does not support building COM objects. 90003 90002 Please see the MATLAB Builder documentation for the latest list of supported compilers. 90003 90002 Error: An error occurred while shelling out to mbuild (error code = 255). 90003 90002 Unable to build executable. 90003 90002 ??? Error using ==> mcc 90003 90002 Error executing mcc, return status = 1. 90003.90000 Steam Community :: MCC Sandbox 4 90001 90002 Showing 1-10 of 43 entries 90003 <1 2 3 4 5> 90002 Update: 27 Apr @ 1:41 pm 90003 90002 Changelog R33 hot fix: 90007 Fixed: 90007 — Ambient fire can not disable in settings 90007 — RHS campaign bug 90007 — Chance for vehicle to start a fire reduced by 50%, burning crew members will not create new fires. 90007 90003 90002 Update: 25 Apr @ 2:54 pm 90003 90002 Changelog R33: 90007 Fixed: 90007 — When opening Ship’s Spawn Menu all clients stuck on loading screen 90007 — Disable respawn and spectator script did not work 90003 90002 Added: 90007 — Main Box to all ships spawned with MCC 90007 — Force respawn dialog from MCC — under Start Location 90007 — Enable / Disable MCC respawn dialog from CBA settings 90007 — Ambient Fire to CBA settings 90007 — Ambient Birds to CBA settings 90003 90002 Update: 18 Apr @ 11:08 am 90003 90002 Fixed the ACE dependency 90003 90002 Update: 17 Apr @ 3:02 pm 90003 90002 Changelog R32: 90007 Fixed: 90007 — Getting Error «MCC_MODULE_LHD SPAWN» when load template missions.90007 — Getting Error «MCC_MODULE_RESOURCES» when load campaign missions. 90007 — Ambient Birds module did not work from Zeus. 90007 — Ambient Civilians module did not work from Zeus. 90007 — Ambient Civilians Restrict module did not work from Zeus. 90007 — Spawn Ship module did not work from Zeus. 90007 — Open Ship Dialog module did not work from Zeus. 90007 — Weapon Shop Dialog module did not work from Zeus. 90007 — Cargo Load module did not work from Zeus. 90007 — Atmosphere module did not work from Zeus.90007 — Assign AI module did not work from Zeus. 90007 — AAS Capture Point module did not work from Zeus. 90007 — AAS Spawn AI module did not work from Zeus. 90007 — Set Unconscious module did not work from Zeus. 90007 — Set Group Respawn module did not work from Zeus. 90007 — Change Pylon / Rearm module did not work from Zeus or on CUP vehicles. 90003 90002 Added: 90007 — Appropriate loadouts to CUP template missions 90007 — Ambient fire modules to Zeus and 3den 90007 — Add credit to players module to Zeus 90007 — Pressing Esc in Squad Menu or Role Selection will close the dialog 90003 90002 Update: 12 Jun, 2019 @ 1:22 pm 90003 90002 Changelog R31: 90007 — Added Load to cargo module to 3den: load objects to vehicles using ACE or MCC cargo system.90007 — Added: MCC logistics to helicopters and planes, can now loda vehicles and objects to them. 90007 — Added: Automatically spawn parachute when unloading objects using helicopters or planes. 90003 90002 Fixed — Ambient Civilians module: Civilians spawn infron of players 90007 Fixed — Advance and secure resistance faction did not bleed tickets on death 90007 Fixed — UAV icon always shown on map 90007 Fixed — Name tags shown when using MCC medical HUD 90003 90002 Changed Zeus: 90003 90002 Object editing: 90007 — Added change unit behavior 90007 — Added Edit unit names 90007 — Added vehicles’s turn lights on / off 90007 — Added vehicles’s turn engine on / off 90007 — Added BI Garage to vehicles — customized components and colors .90007 — Added Unload ACE or MCC cargo from vehicles and objects. 90007 — Reworked — Payload interface, change aircragt pylons and armaments. 90003 90002 Modules: 90007 — Reworked icons, description and categories. 90007 — Added Load to cargo module to 3den: load objects to vehicles using ACE or MCC cargo system. 90007 — Added Create Zone module to Zeus & 3den — creates MCC zone from Zeus or 3den 90007 — Added Assign to MCC zone — assign units / groups to MCC zones from Zeus or 3den 90003 90002 Update: 11 Jan, 2019 @ 7:58 am 90003 90002 R30 — Hotfix 90003 90002 fixed — MCC campaign does not generate missions 90003 90002 Update: 11 Jan, 2019 @ 7:26 am 90003 90002 R30 Hotfix.90003 90002 MCC campaign was broken 90003 90002 Update: 11 Jan, 2019 @ 12:48 am 90003 90002 Changelog r30: 90007 — Fixed: Mission Generator to a specific zone 90007 — Fixed: Conflict with CBA addon settings and MCC modules settings caused unpredictable behavior 90007 — Fixed: Role’s icon did not show on template missions 90007 — Fixed: Disarming an IED did not completed generated mission 90007 — Added: MCC template to CUP Chernarus winter 90007 — Added: 3 MCC campaigns to CUP Chernarus winter 90007 — Changed: Generate mission to a zone will work much better and allows the selection of a specific zone.90003 90002 Update: 1 Jan, 2019 @ 12:57 pm 90003 90002 Changelog r29: 90007 — Fix: Spawning artillery was called on each client and not only on the server 90007 — Fixed: MCC bugging warlords and high command 90007 90003 90002 Update: 24 Dec, 2018 @ 2:12 pm 90003 90002 Changelog r28: 90007 — Added: Mission Generator objectives will clear area of terrain objects before spawning in objectives 90007 — Added: While using ACE a player can now use MCC action only to halt AI or quickly open doors 90007 — Added: MCC ammo crate , fuel crate and supply crate will be shown in Zeus 90007 — Added: Withdraw and deposite ammo / fuel / material boxes from any FOB or HQ (from the main box) 90007 — Added: Sleep interval so modules will overwrite CBA settings if placed in a mission 90007 — Added: MCC direct CAS — should work for all vehicles but resaults may vary depends on the addon vehicle.90007 — Removed: Enable role selection from CBA settings 90007 — Changed: Clear area objective’s area reduced by 50% 90007 — Changed: The way the campaign determine if a mission is done — for more accurate results 90007 — Fixed: MCC CAS did not work 90007 — Fixed: Can not generate mission to a specific zone 90007 — Fixed: Restrict vehicles to roles was on by default 90007 — Fixed: Campaign stops after first mission 90007 — Fixed: MCC interaction did not open / close door on non vanila maps 90007 — Fixed: MCC medics healing dead bodies and not willing to heal after player respawn 90007 — Fixed: MCC AI medics did not regroup after healing 90007 — Fixed: Wrong class names in Mission Wizard objectives — destroy cache spawned helicopters and destroy fuel tanks spawns radio towers 90007 — Fixed: Video probe was upside down when mirroring under a door using ACE 90007 — Fixed: MCC interaction pop up while using ACE 90007 — Fixed: Can not open HQ vault from ACE 90007 — Fixed: systemchat when unit respa wned 90003 .





