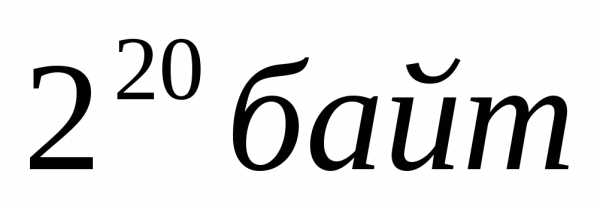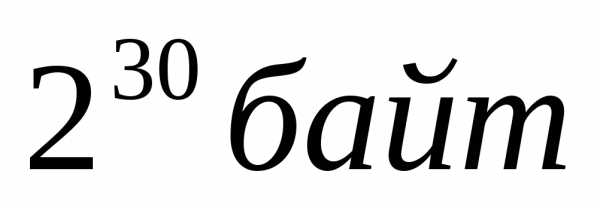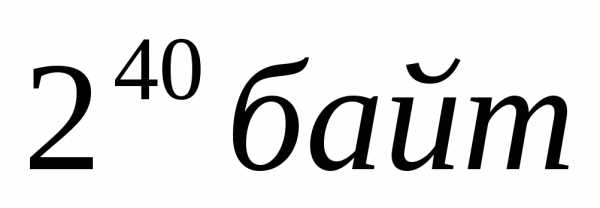«Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций. Практическая работа №1. Кодирование информации»
Тема урока: «Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций.
Практическая работа №1. Кодирование информации»
Цели: сформировать у учащихся понимание процесса обмена информацией; показать различные виды кодирования информации; выявить преимущества двоичного кодирования различных видов информации.
Требования к знаниям и умениям:
Учащиеся должны знать:
что такое «код», «кодирование», «двоичное кодирование», бит;
почему в вычислительной технике используется двоичное кодирование информации;
как кодируются различные виды информации в вычислительной технике.
Учащиеся должны уметь:
— кодировать информацию;
— восстанавливать информацию по ее кодовому представлению.
Ход урока
Орг. Момент
Актуализация
Визуальная проверка выполнения домашнего задания.
Опрос по теме знаковая система
Заполнить таблицы
Естественные языки (носят национальный характер): речь и письменность | Формальные языки (интернациональны, понятны всем) | |||||
Примеры | -русский язык; — английский язык; -и т.д. | — язык математики; — язык химии; — языки программирования — командные языки опера — и т.д. | ||||
Алфавит — набор основных символов, различимых по их начертанию | — кириллица — 33 буквы; — латиница — 26 букв; — иероглифы и др | Алфавит жестко зафиксирован. — арабские цифры; — ноты; — дорожные знаки; — точки и тире; — изображения элементов | ||||
Синтаксис — правила для образования предложений языка | Формируется из большого числа правил, из которых существуют исключения | Наличие строгих правил | ||||
Грамматика — правила правописания | ||||||
Физическая природа знаков | Изображения на бумаге, звуки (фонемы), электрические импульсы и т.д. | |||||
Информация | Естественный язык | Формальный язык | ||||
Нахождение площади прямоугольника | ||||||
Правило дорожного движения | ||||||
Призыв о помощи | ||||||
3. Изложение нового материала
1. Кодирование информации
Когда человек или какой-либо другой живой организм или какое-то устройство участвуют в информационном процессе, то все они представляют информацию в той или иной форме. При выполнении домашнего задания вы также представляли информацию в различных формах.
Когда мы представляем информацию в разных формах или преобразуем ее из одной формы в другую, мы информацию кодируем.
Код — это система условных знаков для представления информации.
Кодирование — это операция преобразования символов или группы символов одного кода в символы или группы символов другого кода.
Человек кодирует информацию с помощью языка.
Язык — это знаковая форма представления информации.
В процессе обмена информацией кроме кодирования информации происходит и ее декодирование.
Теоретически и экспериментально было показано, что с технической точки зрения самым удобным и эффективным является использование двоичного кода, то есть набора символов, алфавита, состоящего из пары чисел {0,1}. Поскольку двоичный код используется для хранения информации в вычислительных машинах, его еще называют машинным кодом.
Цифры 0 и 1, образующие набор {0,1}, обычно называют двоичными цифрами, потому что они используются как алфавит в так называемой двоичной системе счисления. Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Элементарное устройство памяти компьютера, которое применяется для изображения одной двоичной цифры, называется двоичным разрядом или битом.
Слово «бит» произошло от английского термина bit, представляющего собой сокращение словосочетания Binary digit – двоичная цифра.
1 бит кодирует 2 понятия или сообщения (0 или 1).
2 бита — 4 разных сообщения (11 или 00 или 01 или 10).
3 бита — 8 разных сообщений.
4 бита — 16 сообщений и т.д.
Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 — есть сигнал, 0 — нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Как разные виды информации кодируются в компьютере?
2. Кодирование чисел
В двоичной системе счисления для записи чисел используется всего две цифры — 1 и 0. С их помощью можно записать любое число. Во всем остальном эта система счисления не отличается от привычной для вас десятичной системы. Она обладает всеми теми же свойствами, в ней соблюдаются все основные законы выполнения арифметических операций.
3. Кодирование текстовой информации
Для кодирования текстовой информации в компьютере также применяется двоичное кодирование, т.е. представление текста в виде последовательности 0 и 1. Каждому символу алфавита сопоставили определенное целое число, которое и принято считать кодом этого символа.
Бит – это очень маленькая порция информации. Поэтому, так же как и при записи десятичных чисел, используется несколько десятичных разрядов – разряд единиц, разряд десятков, сотен и т.д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
Для хранения двоичных чисел в компьютере используется устройство, которое принято называть ячейкой памяти. / Память компьютера можно образно представить себе как автоматическую камеру хранения, состоящую из отдельных ячеек, в каждую из которых можно положить некоторое число./
Ячейки образуются из нескольких битов, так же как двоичные числа образуются из двоичных разрядов. В общем случае ячейки различных компьютеров могут состоять из различного количества битов. Поэтому, начиная с машин третьего поколения, стандартными являются те ячейки, которые состоят из восьми битов.
Элемент памяти компьютера, состоящий из восьми битов, называется байтом.
а) б)Сколько же бит необходимо для кодирования символов?
Чтобы ответить на этот вопрос, нужно определить их количество. Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Запись двоичного кода легко спутать с аналогичным по записи десятичным числом. В таких случаях справа от двоичного числа записывают индекс 2, а около десятичного числа указывают индекс 10. Например: 101100112 – двоичное число, 1011001110 – десятичное.
Так как байт состоит из восьми двоичных разрядов, то количество различных кодов, различных комбинаций из восьми нулей и единиц, записываемых в один байт, равно 28=256. (00000001, 00000010,…, 11111111).
С помощью 1 байта можно закодировать 256 различных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Система счисления | Основание | Алфавит цифр |
Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Двоичная | 2 | 0, 1 |
Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.
Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.
Переведем десятичное число 20 в двоичную систем счисления (основание системы счисления p=2).
В итоге получили 2010 = 10100
Обратный перевод осуществляется операцией умножение. Умножаем на p в n-1 степени
1*24+0*23+1*22+0*21+0*20=20
4. Закрепление пройденного
1. Каким образом информация добирается от источника информации до приемника
2. Как информация кодируется в компьютере. Почему?
Практическая работа №1. Кодирование информации
Перевести
ИЗ 10-ной в 2-ную
27, 48, 64, 115, 57
ИЗ 2-ной в 10-ную
1011, 11011,1111, 10000
5. Итоги урока
Выставление оценок.
Беседа: что понятно, что – нет, что нового…
Домашнее задание
Уровень знания: выучить, что такое код, кодирование, бит, байт и формулу, связывающую количество разных сообщений и количество бит.
§ 1.5 чит.
Уровень понимания:
Перевести
ИЗ 10-ной в 2-ную
47, 28, 92, 18, 103
ИЗ 2-ной в 10-ную
1001, 111,1100, 1110
multiurok.ru
Бинарная азбука Морзе онлайн
Простое кодирование и декодирование азбуки Морзе, используя двоичный код
Здесь можно легко и просто закодировать текст в Азбуку Морзе, да не просто в обычные точки и тире, а ещё и в бинарный код!Правила кодирования
Кодирование азбуки Морзе в бинарный код — это просто замена точек и тире на единицы и нули, но по определённым правилам:
- «Точка» кодируется цифрой 1
- «Тире» кодируется тремя единицами (ведь тире по длительности равно трём точкам)
- Между точкой и тире используется разделитель: цифра 0
- Между каждым символом используется два нуля, так можно будет отличить, что начался следующий символ
Как пользоваться
Исходный текст нужно набрать или вставить в верхнем поле, затем нажать кнопку «Закодировать», чтобы получить в
нижнем поле закодированный текст. Режим кодирования (бинарный или обычный) можно выбрать в выпадающем списке.
Чтобы раскодировать, нужно опять же, вставить или набрать текст в верхнем поле и нажать «Раскодировать». Тогда внизу появится раскодированный текст.
Для удобства существует кнопка «Поменять местами», которая меняет содержимое полей местами, что избавляет от ручного
копирования и вставки текста, если вдруг для проверки захочется раскодировать то, что было только что закодировано или если захочется ещё раз закодировать уже закодированное сообщение (а это возможно, да!).
Также имеются некоторые настройки, а именно:
- Выбор режима кодирования и декодирования. Можно и в обычную азбуку Морзе, и в бинарную
- Выбор алфавита: кириллические символы или латинские. Если при расшифровки послания получился какой-то дикий транслит, возможно, стоит поменять алфавит
- Выбор регистра букв. Имеет смысл, как и предыдущий пункт, только при расшифровке. Выбор между БОЛЬШИМИ СТРАШНЫМИ И ВЫЗЫВАЮЩИМИ ПАНИКУ или тихими и спокойными строчными буквами
Выбор определённого алфавита не отключает полностью другой. Поэтому, если попадутся символы, которых нет в указанном алфавите, то они поищутся ещё и в другом. Знаки препинания, цифры и другие символы находятся отдельно, поэтому выбор алфавита на них никак не влияет.
Примечание. Если попытаться раскодировать в бинарном режиме обычную азбуку Морзе, то, скорее всего, ничего не получится.
Символы, которые не удалось закодировать или раскодировать, будут помечены вопросительным знаком.
Полностью бесплатно
Данный сервис можно использовать совершенно бесплатно. Не нужно скачивать никакого дополнительного программного обеспечения для пользования этим сервисом.
Используемые алфавиты для кодирования и декодирования
Таблицы взяты из wikipedia, они же и используются для кодирования, но некоторые символы измененыБуквы
| Кириллица | Латиница | Код Морзе |
|---|---|---|
| А | A | .- |
| Б | B | -… |
| В | W | .— |
| Г | G | —. |
| Д | D | -.. |
| Е, Ё | E | . |
| Ж | V | …- |
| З | Z | —.. |
| И | I | .. |
| Й | J | .— |
| К | K | -.- |
| Л | L | .-.. |
| М | M | — |
| Н | N | -. |
| О | O | — |
| П | P | .—. |
| Р | R | .-. |
| С | S | … |
| Т | T | — |
| У | U | ..- |
| Ф | F | ..-. |
| Х | H | …. |
| Ц | C | -.-. |
| Ч | CH | —. |
| Ш | SH | —- |
| Щ | Q | —.- |
| Ъ | Ñ | —.— |
| Ы | Y | -.— |
| Ь, Ъ | X | -..- |
| Э | É | ..-.. |
| Ю | Ü | ..— |
| Я | Ä | .-.- |
Цифры и символы
| Символ | Код |
|---|---|
| 1 | .—- |
| 2 | ..— |
| 3 | …— |
| 4 | ….- |
| 5 | ….. |
| 6 | -…. |
| 7 | —… |
| 8 | —.. |
| 9 | —-. |
| 0 | —— |
| . (точка) | …… |
| , (запятая) | .-.-.- |
| : (двоеточие) | —… |
| ; (точка с запятой) | -.-.-. |
| ( | -.—.- |
| ) | -.—.. |
| ‘ (Апостроф) | .—-. |
| » (кавычки) | .-..-. |
| — (тире) | -….- |
| / (слеш) | -..-. |
| ? (знак вопроса) | ..—.. |
| ! (восклицательный знак) | —..— |
| (знак раздела, пробел) | -…- |
| @ | .—.-. |
| \n (перевод строки) | -.-.. |
| \r (перевод каретки) | -.-..- |
| [END] (конец связи) | ..-.- |
Примечание. Дизайн сайта был честно подсмотрен на аналогичном сервисе, который кодирует base64.
Анектод в тему:
Немцы копали на глубине, соответствующей 18 веку и нашли медные провода. Значит, в Германии уже была телефонная
связь.
Американцы копали на глубине 15 века и обнаружили стеклянные фрагменты. Значит, в Америке уже была
оптоволоконная связь.
Русские копнули на глубине 11 века и ничего не нашли. Значит, уже в те времена в России пользовались
беспроводной связью.
Время выполнения: 0.0018 сек.
morsebin.karamush.ru
Разбор задачи A13 (демо ЕГЭ 2006)
Решение:Построим графы для быстрого поиска в двоичной строке букв:
На графе розовым цветом выделены коды иcпользуемых букв.
Начнем с варианта 1:
Анализ строки 110100000100110011 происходит так:
1) берем первый символ. Он равен «1», поэтому смотрим граф с вершиной, равной «1»:
Видно, что в этом графе есть коды: 10 и 11.
2) берем второй символ. Он равен «1», поэтому идем по правой ветке: 1→11. кодом «11» закодирована буква К.
После того как нашли символ, анализ снова начинаем с вершины графа.
3) берем следующий третий символ. Он равен «0», поэтому смотрим граф с вершиной, равной «0»:
Видно, что в этом графе есть коды: 01, 000 и 001.
5)берем четвертый символ. Он равен «1», поэтому идем по правой ветке: 0→01. кодом «01» закодирована буква A.и т.д. для остальных символов закодированной строки.
В таблицах ниже описан полный анализ всех строк:
Вариант1
| Двоичная строка | 11 01 000 001 001 10 01 1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Путь в графе до кода буквы | 1→11 | 0→01 | 0→00→000 | 0→00→001 | 0→00→001 | 1→10 | 0→01 | 1 |
| Двоичная строка, разбитая на коды букв | 11 | 01 | 000 | 001 | 001 | 10 | 01 | 1 |
| Буква | К | А | В | Р | Р | Д | А | — |
Вариант2
| Двоичная строка | 11 10 10 000 01 001 001 1 | |||||||
|---|---|---|---|---|---|---|---|---|
| Путь в графе до кода буквы | 1→11 | 1→10 | 1→10 | 0→00→000 | 0→01 | 0→00→001 | 0→00→001 | 1 |
| Двоичная строка, разбитая на коды букв | 11 | 10 | 10 | 000 | 01 | 001 | 001 | 1 |
| Буква | К | Д | Д | В | А | Р | Р | — |
Вариант3
| Двоичная строка | 11 01 000 01 001 10 01 11 | |||||||
|---|---|---|---|---|---|---|---|---|
| Путь в графе до кода буквы | 1→11 | 0→01 | 0→00→000 | 0→01 | 0→00→001 | 1→10 | 0→01 | 1→11 |
| Двоичная строка, разбитая на коды букв | 11 | 01 | 000 | 01 | 001 | 10 | 01 | 11 |
| Буква | К | А | В | А | Р | Д | А | К |
Вариант4
| Двоичная строка | 11 01 10 000 10 01 10 01 0 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Путь в графе до кода буквы | 1→11 | 0→01 | 1→10 | 0→00→000 | 1→10 | 0→01 | 1→10 | 0→01 | 0 |
| Двоичная строка, разбитая на коды букв | 11 | 01 | 10 | 000 | 10 | 01 | 10 | 01 | 0 |
| Буква | К | А | Д | В | Д | А | Д | А | — |
Сообщения вариантов 1, 2, 4 оканчиваются кодом, которым не закодирована ни одна буква:
вариант 1 — «1»,
вариант 2 — «0»,
вариант 4 — «1».
Сообщение варианта 3 может быть корректно декодировано.
Получили: 110100001001100111.
infoegehelp.ru
2. Символизация (кодирование) информации.
Как мы выяснили из первой главы информация – это нематериальная составляющая окружающего нас мира. Для ее материализации (однозначного отображения и передачи) используется символизация информации, то есть определение количества и качества (значения) информации. Для символизации информации люди используют различные языки. Различают естественные и искусственные(формальные) языки.Естественные языкиразвивались веками и используются для общения людей между собой.Формальные языкиразрабатываются для специального применения. Примером формальных языков могу служить языки программирования, языки кодирования информации для ее передачи, хранения и т.п.
Каждый язык имеет свой алфавит. Под алфавитом языка понимают набор символов. То есть символизация информации – это описание объектов или явлений с помощью символов того или иного алфавита. Подмощностью алфавитапонимают количество символов, составляющий данный алфавит, что в свою очередь определяет количество возможных комбинаций (слов) которые можно составить из символов данного алфавита в соответствии с определенными правилами.
Кодомназывают совокупность знаков (символов), предназначенных для представления той или иной информации в соответствии с определенными правилами. Символизацию информации (представление в виде символов) называюткодированием. Кодируют информацию с целью ее передачи или хранения.
Для примера кодирования возьмем предмет мебели стол. Для кодирования информации об этом предмете на русском языке нам понадобиться записать последовательность символов «СТОЛ», а кодирования информации об этом предмете на английском «TABLE».
Естественные языки очень часто имеют одинаковый код для определения различных объектов. Так например слово «коса» может означать девичью косу, речную отмель и инструмент для скашивания травы. В формальных языках такое кодирование недопустимо. Это определяется тем, что естественные языки оперируют контекстом (набором слов) при анализе и классификации информации, а формальные непосредственно словами.
Количество и графическое отображение символов в алфавитах естественных языков сложилось исторически и характеризуется особенностями языка (произносимыми звуками). Например русский алфавит имеет 33 символа, латинский – 26, китайский несколько тысяч.
Минимальное количество знаков алфавита равно единице. Допустим, что алфавит имеет один знак и пусть это будет * (звездочка). Тогда цвета радуги будут кодироваться как: * — красный, ** — оранжевый, *** — желтый, **** — зеленый, ***** — голубой, ****** — синий, ******* — фиолетовый.
2.1. Двоичный алфавит.
В информатике и вычислительной технике широко используется алфавит, имеющий два знака, например «1» и «0». Этими символами в логике и технике приводят в соответствие понятия «да» и «нет», «есть сигнал» и «нет сигнала», «истина» и «ложь». Такой алфавит называют двоичнымилибинарным(binary) в соответствии с этим вводится наименьшая единица информациибит (bit).
Одного бита информации достаточно для кодирования текущего состояния объекта, имеющего два статических состояния, например лампочки «0» — выключено, «1» — включено. То есть одноклавишный выключатель является носителем одного бита информации, которого нам достаточно для определения состояния лампочки.
В реальной жизни крайне редко встречаются объекты состояние которых можно закодировать одним битом информации и нет объектов, которые можно описать одним битом. Для кодирования от трех до четырех состояний или признаков объекта требуется уже два бита информации. Для кодирования от четырех до девяти состояний объекта уже требуется три бита. 9-16 состояний 4 бита, 17-32 состояний 5 бит. В общем случае количество бит, необходимых для кодирования Nсостояний или диапазона значений свойств объектов или явлений определяется по формуле 1:
(1) |
где
N– количество состояний или диапазон значений свойств объектов,
q– количество бит информации необходимых для кодирования требуемого количества состояний или диапазона свойств объектов.
Было принято, что следующей базовой единицей информации будет являться байт– это последовательность бит длина которой равна 8 битам. Одним байтом можно закодировать от 1 до 256 различных объектов, например символов.
На практике используются более объемные единицы измерения информации, приведенные в таблице 1.
Таблица 1.
1 байт | =8 бит |
1 слово | =2 байта = 16бит |
1 двойное с слово | =2 слова = 4байта=32бита |
1 килобайт (Кб) | =1024 байт |
1 мегабайт (Мб) | =1024 килобайт = |
1 гигабайт (Гб) | =1024 мегабайт= |
1 терабайт (Тб) | =1024 гигабайт= |
Пример 1.
Подсчитаем объем памяти, требуемый для хранения книги объемом 100 страниц, при учете, что в среднем на каждой странице по 40 строк, а в каждой строке в среднем по 60 символов.
studfiles.net
Урок №2. Тексты. Кодирование
Май 10 2013
Как решать некоторые задачи разделов A и B экзамена по информатике
Урок №2. Тексты. Кодирование
В основе каждого текста лежит алфавит – конечное множество символов. В основе текстов на русском языке лежит алфавит, называемый кириллицей, состоящий из 33 строчных и 33 заглавных букв алфавита. Тексты английского языка построены на основе латиницы – алфавита, содержащего 26 строчных и 26 заглавных букв. Конечно алфавит, на основе которого строятся тексты на естественных языках, содержит не только буквы, но и цифры, знаки операций и множество других специальных символов.
Пусть задан алфавит T, содержащий m символов:
T = { t1, t2, …tm}
Словом S в алфавите T называют любую последовательность символов алфавита:
S = s1s2…sk,
где si – это символы алфавита. Число символов в слове – k называют длиной слова.
Справедливо утверждение:
Число различных слов длины k, которые можно построить в алфавите из m символов, равно: N = mk
Справедливость утверждения легко доказывается по индукции.
Базис индукции: при k = 1, утверждение справедливо, поскольку словами длины 1 являются m символов алфавита.
Шаг индукции: Пусть утверждение справедливо при некотором k. Это означает, что построено mk слов длины k. Из каждого слова можно построить m новых слов длины k +1, приписывая к слову поочерёдно m символов алфавита. Таким образом, слов длины k + 1 будет:
N = mk * m = mk+1
Это простое, но важное утверждение, которое в том или ином виде используется при решении различных задач.
Алфавит компьютера
Тексты, которые хранятся в памяти компьютера, используют один из самых примитивных алфавитов, состоящий всего из двух символов:
T2 = {0, 1}
С другой стороны мы знаем, что в памяти компьютера можно хранить не только тексты на различных естественных языках, но и графику, музыку и другую информацию различного вида. Как такое возможно? Разберемся с текстами. Пусть есть два алфавита – T, состоящий из m символов и алфавит T2. Представление текстов в алфавите T текстами в алфавите T2 называется кодированием. Простейший способ кодирования состоит в том, чтобы символы алфавита T кодировать словами конечной длины алфавита T2. Умея кодировать каждый символ, можно кодировать любой текст символ за символом.
Какова должна быть минимальная длина слов в алфавите T2, чтобы было возможно этими словами закодировать алфавит из m символов? Очевидно, что длина может быть определена из условия:
2k >= m
Если, например, m = 30, то наименьшее возможное значение k равно 5.
Долгое время при работе с текстами, сохраняемыми в компьютере, использовался код ASCII, в котором каждый символ алфавита кодировался словом из 8 бит (одним байтом). Такой алфавит, содержащий 256 различных символов, мог включать латиницу и кириллицу, цифры, знаки операций, знаки препинания, скобки и другие символы. Но все-таки этого алфавита явно недостаточно, чтобы можно было хранить в памяти компьютера тексты на любых естественных языках. Чтобы такое было возможно, необходимо, чтобы алфавит включал алфавиты всех известных естественных языков, в том числе алфавит украинского языка, готику, греческий алфавит, алфавит языка иврит, арабского языка, китайские и японские иероглифы.
В сегодняшних компьютерах для хранения текстов используется кодировка из двух байтов, называемая UNICODE кодировкой, позволяющая словами из 16 битов кодировать алфавит, содержащий 216 — 65536 символов. Для большинства существующих естественных языков такого алфавита хватает для представления текстов, записанных на этих языках.
Задача 9:
Автомобильный номер состоит из 7 символов. В качестве символов используются 30 букв и 10 цифр. Символ кодируется минимально возможным набором битов. Номер представляется целым числом байтов. Какую память требуется иметь для хранения 1000 номеров.
Ответ: Примерно 6 Кб.
Решение: Алфавит для записи текстов, представляющих номера автомобилей, содержит 40 символов (30 букв и 10 цифр). Для кодировки такого алфавита потребуются двоичные слова длины 6 (26 > 40). Для кодировки всего номера потребуется 6*7 = 42 бита. Округляя в большую сторону до целого числа байтов, получим, что для хранения одного номера потребуется 6 байтов. Для хранения 1000 номеров достаточно 6 Кб.
Задача 10:
В командной олимпиаде по информатике участвуют ученики из школ, номера которых заданы двузначными цифрами. В команде может быть не более 7 учеников. Какой минимальный объем памяти потребуется для хранения 500 номеров участников олимпиады, если каждый номер представляется целым числом байтов?
Ответ: Достаточно 1 Кб.
Решение: Номер участника может состоять из номера школы и номера участника в данной школе. Для 100 номеров школ достаточно 7-и битов (27 > 100). Для номера участника в школе достаточно 3-х битов (23 > 7). Поэтому для хранения номера участника достаточно 10 битов. Округляя в большую сторону до целого числа байтов, получим, что 2-х байтов достаточно для хранения номера. Для хранения 500 номеров достаточно одного килобайта.
Задача 11:
Алфавит состоит из 4-х букв {М, У, Х, А} Слова длины 5 перечисляются в лексикографическом порядке. Нумерация слов начинается с единицы. Какое слово в этом перечислении стоит под номером 1016, под номером 365?
Ответ: ХХХМХ; ММУХА
Решение: Число различных слов длины 5 в 4-х буквенном алфавите равно 45 = 210 = 1024. При перечислении их в алфавитном (лексикографическом) порядке под номером 1 стоит слово ААААА, под номером 1024 – слово ХХХХХ. В задачах экзамена ЕГЭ обычно требуется указать слово, стоящее близко к концу перечисления, что имеет место в нашей задаче, в которой требуется назвать слово под номером 1016, стоящее в первом десятке с конца перечисления. Поэтому для решения задачи достаточно выписать десять слов в обратном лексикографическом порядке, что и дает слово ХХХМХ.
Для ответа на второй вопрос, где требуется найти слово, стоящее в середине перечисления, такой явный способ выписывания слов не подходит. В этом случае следует применять более общий подход, применимый для всех случаев. Для его понимания нужно вспомнить системы счисления.
Поставим в соответствие буквам алфавита цифры (А – 0, М – 1, У – 2, Х -3). При задании этого соответствия учитывается принятый порядок следования букв в алфавите. Число букв задает число используемых цифр, а тем самым задает основание системы счисления. Введенное соответствие букв и цифр порождает соответствие между словами в алфавите и числами в соответствующей системе счисления, в нашем случае – четверичной системе счисления. При лексикографическом перечислении слов длины k слову, стоящему под номером N, соответствует число N-1 в четверичной системе счисления, содержащее k цифр, включая незначащие нули. Так, слову под номером 1, состоящему из 5 букв, соответствует число 0, записанное как 00000, или, после замены цифр буквами, — ААААА. Поэтому для решения задачи, зная N, достаточно получить запись числа N-1 в четверичной системе, а затем заменить цифры буквами.
Получим решение задачи этим способом для N = 1016 и N = 365.
N — 1 = 1015 = 3* 44 + 3* 43 +3* 42 + 1* 41 + 3 = 333134 = ХХХМХ
N -1 = 364 = 1* 44 + 1* 43 +2* 42 +3* 41 + 0 = 112304 = ММУХА
Задача 12:
Алфавит состоит из 3-х букв {А,М, П} Слова длины 4 перечисляются в лексикографическом порядке. Нумерация слов начинается с единицы. Под каким номером стоит слово МАМА, слово — ПАПА?
Ответ: 31; 61
Решение: В троичной системе слову МАМА соответствует число 10103 = 33 + 3 = 30. В перечислении, где нумерация начинается с 1, номер этого слова равен 31.
Слову ПАПА соответствует число 20203 = 60.
Кодирование словами переменной длины
Кодировка символов алфавита T словами алфавита Т2 фиксированной длины k имеет то преимущество, что закодированный текст легко поддается расшифровке – декодированию. Действительно, достаточно закодированный текст разбить на группы длины k, и каждой группе поставить в соответствие символ алфавита. Недостатком такого способа является некоторая неэффективность процедуры кодирования, — каждому символу алфавита всегда соответствует k битов алфавита Т2. Память компьютера достаточно дешевая, поэтому жертвуют неэффективностью использования памяти ради удобства декодирования.
В других ситуациях эффективность важнее удобства декодирования. Примерами являются азбука Брайля, азбука Морзе. В азбуке Морзе, где для передачи информации используется алфавит из двух символов – точки и тире, для однозначного декодирования вводится третий символ – пауза. При передаче данных по телеграфу, использующему азбуку Морзе, точке, тире и паузе соответствуют сигналы разной длительности.
Рассмотрим пример неоднозначного кодирования. Пусть у нас есть алфавит из 3-х символов – А, М, П. Введем следующую кодировку: А – 0, М – 1, П – 10. Рассмотрим закодированный текст: 1010. Этому тексту соответствуют два слова – МАМА и ПП. Как видите, введенная кодировка не обеспечивает однозначное декодирование.
Можно ли при использования кодировки словами переменной длины наложить ограничения на способ кодирования, чтобы декодирование было однозначным? Ответ положителен. Если при кодировании выполняется условие Фано, то декодирование однозначно. Кодирование называется префиксным, если при кодировании существует пара символов, такая, что код одного символа является префиксом кода другого символа. В нашем примере кодирование является префиксным, поскольку для символов М и П код символа М является префиксом (началом) кода символа П. Условие Фано выполняется, если кодирование не является префиксным. Условие Фано является достаточным условием для однозначного декодирования. Оно не является необходимым условием.
Рассмотрим несколько задач, решение которых предполагает использование условия Фано.
Задача 13:
Для трехбуквенного алфавита {А, М, П} используется кодировка А – 01, М – 10, П – 001. Какой код минимальной длины следует задать для кодировки буквы Т, добавляемой в алфавит?
Ответ: Т – 11.
Решение: Используемая кодировка удовлетворяет условию Фано, — ни один код не является префиксом другого кода, что гарантирует однозначность декодирования. Для нового символа, добавляемого в алфавит, нельзя использовать код, состоящий из одного символа, поскольку будет нарушено условие Фано. Для кода, состоящего из двух символов, возможен только один вариант, удовлетворяющий условию Фано, — Т – 11.
Задача 14:
Для четырехбуквенного алфавита {А, М, П, Т} используется кодировка А – 01, М – 10, П – 001, Т — 11. Можно ли уменьшить длину кода одного из символов, сохраняя однозначность декодирования?
Ответ: Можно. П – 00.
Решение: Используемая кодировка удовлетворяет условию Фано, — ни один код не является префиксом другого кода, что гарантирует однозначность декодирования. Не нарушая условия Фано, для кодирования буквы П можно использовать код 00. Заметьте, в этом случае все символы кодируются словами постоянной длины. Для такой кодировки условие Фано выполняется автоматически, поскольку все слова различны и имеют одинаковую длину, так что ни одно из них не может быть префиксом другого слова.
10 задач для самостоятельной работы
- Представьте в кодировке Unicode следующий текст: «Иван да Марья».
Напомню правила кодировки:
- За исключением буквы «ё» кодировка алфавита кириллицы плотная. Это означает, что код буквы, следующей в алфавите, на единицу больше кода предшествующей буквы.
- Кодировка больших букв предшествует кодировке малых букв.
- Кодировка ASCII (первые 128 символов) является подмножеством кодировки Unicode. В обеих кодировках код пробела равен 20 в шестнадцатеричной системе (32 в десятичной системе).
- Код первой буквы алфавита кириллицы в кодировке Unicode равен 410 в шестнадцатеричной системе.
- Определите способ шифрования и декодируйте следующий текст: «молымушамалымамам».
- Декодируйте текст, зашифрованный кодом Цезаря:
«цщччропеднареоуъфцтёшорёетёшктёшорё».
Исходный текст содержал пробелы и символы алфавита кириллицы. При шифровании заглавные и строчные буквы не различались. Символ «пробела» считался предшествующим символам алфавита. - Кодом Грея называется код, в котором коды каждых двух соседних символов отличаются только в одном разряде. Первый и последний символы считаются соседними. Предложите код Грея для кодирования цифр шестнадцатеричной системы счисления.
- В алфавите из четырех букв {А, У, М, П} частоты вхождения символов алфавита в тексты различны и составляют соответственно {0,5; 0,25; 0,125; 0,125}. Постройте неравномерный двоичный код, соблюдая условие Фано.
- В биоинформатике генетический код рассматривается как последовательность слов, называемых кодонами или триплетами. Каждый триплет представляет слово длины 3 в алфавите из четырех букв { А, Ц, Г, Т}. Содержательно, каждый символ алфавита соответствует одному из четырех нуклеотидов {аденин, цитозин, гуанин, тимин}. Содержательно, каждый триплет однозначно задает одну из двадцати стандартных аминокислот, из которых синтезируются белки. Поскольку различных аминокислот 20, а триплетов 64, то возникает избыточность, — разные триплеты могут задавать одну и ту же аминокислоту. Какая кислота имеет максимальную степень избыточности и сколько триплетов задают эту кислоту? Найдите эту информацию в интернете.
- Для идентификации автомобилей использовались семизначные цифровые номера. Две последние цифры задавали номер региона, пять первых цифр задавали номер автомобиля в данном регионе. В связи с ростом автомобильного парка номеров стало не хватать, и было принято решение изменить нумерацию, добавив буквенные символы. Все старые номера автомобилей сохранялись. Два последних символа по-прежнему задавали номер региона. Пять первых символов могли быть буквенными. Для благозвучности номера и его лучшего запоминания нечетные символы номера составлялись из 20 согласных букв, четные символы номера – второй и четвертый – могли быть одной из 7 гласных букв. Во сколько раз такая реформа увеличивала число номеров?
- Все старые номера автомобилей (смотри задачу 7) хранились в памяти компьютера. Сколько памяти требуется отвести для хранения новых номеров, если для каждого номера отводится целое число байтов, а каждый символ номера с учетом его специфики кодируется минимально возможным числом битов?
- В алфавите из пяти символов {Д, Е, И, Л, Р} слова выписаны в лексикографическом порядке. Какие слова стоят под номерами 334 и 2134?
- Память фотоаппарата составляет 512 Мб. Вы хотите хранить в памяти 1000 снимков. Какое возможное разрешение следует установить для снимков (1024 * 1024, 1024 * 512, 512 * 512, 512 * 256, 256 * 256, 128* 128)? Для хранения цвета одной точки используется схема RGB, где каждый оттенок красного, зеленого и голубого цвета задается числом в пределах от 0 до 255.
Ответы к задачам
- 41843243043D204344302041C43044044C44F
- Текст: «Мама мыла Машу мылом». При кодировании пробелы игнорируются. Порядок слов меняется на обратный. Заглавные и строчные буквы не различаются. Порядок букв в каждом слове меняется на обратный.
- Текст: «Русский язык информатика математика». Константа кода Цезаря, определяющая сдвиг по алфавиту, равна 6.
- 0 → 0000; 1 → 0001; 2 → 0011; 3 → 0010; 4 → 0110; 5 → 0111; 6 → 0101; 7 → 0100; 8 → 1100; 9 → 1101; A → 1111; B → 1110; C → 1010; D → 1011;
E → 1001; F → 1000; - Чаще встречаемые символы кодируются короткими кодовыми словами. Код, удовлетворяющий условию Фано, может быть следующим:
А → 0; У → 10; М → 110; П → 111; - Такой кислотой является, например, серин, задаваемый 6-ю различными кодонами.
- Почти в пять раз, k = (203 *72 +105) /105.
- Примерно 160 Мб. (4 байта на номер).
- ДИЛЕР и ЛИДЕР
- 512 * 256
Скачать урок №2 можно здесь.
Автор: bivant • Информатика, ЕГЭ. • 0
edu.cps.tver.ru
Информатика — Кодирование
1. Основные понятия
Закодировать текст – значит сопоставить ему другой текст. Кодирование применяется при передаче данных – для того, чтобы зашифровать текст от посторонних, чтобы сделать передачу данных более надежной, потому что канал передачи данных может передавать только ограниченный набор символов (например, — только два символа, 0 и 1) и по другим причинам.
При кодировании заранее определяют алфавит, в котором записаны исходные тексты (исходный алфавит) и алфавит, в котором записаны закодированные тексты (коды), этот алфавит называется кодовым алфавитом. В качестве кодового алфавита часто используют двоичный алфавит, состоящий из двух символов (битов) 0 и 1. Слова в двоичном алфавите иногда называют битовыми последовательностями.
2. Побуквенное кодирование
Наиболее простой способ кодирования – побуквенный. При побуквенном кодировании каждому символу из исходного алфавита сопоставляется кодовое слово – слово в кодовом алфавите. Иногда вместо «кодовое слово буквы» говорят просто «код буквы». При побуквенном кодировании текста коды всех символов записываются подряд, без разделителей.
Пример 1. Исходный алфавит – алфавит русских букв, строчные и прописные буквы не различаются. Размер алфавита – 33 символа.
Кодовый алфавит – алфавит десятичных цифр. Размер алфавита — 10 символов.
Применяется побуквенное кодирование по следующему правилу: буква кодируется ее номером в алфавите: код буквы А – 1; буквы Я – 33 и т.д.
Тогда код слова АББА – это 1221.
Внимание: Последовательность 1221 может означать не только АББА, но и КУ (К – 12-я буква в алфавите, а У – 21-я буква). Про такой код говорят, что он НЕ допускает однозначного декодирования
Пример 2. Исходный и кодовый алфавиты – те же, что в примере 1. Каждая буква также кодируется своим номером в алфавите, НО номер всегда записывается двумя цифрами: к записи однозначных чисел слева добавляется 0. Например, код А – 01, код Б – 02 и т.д.
В этом случае кодом текста АББА будет 01020201. И расшифровать этот код можно только одним способом. Для расшифровки достаточно разбить кодовый текст 01020201 на двойки: 01 02 02 01 и для каждой двойки определить соответствующую ей букву.
Такой способ кодирования называется равномерным. Равномерное кодирование всегда допускает однозначное декодирование.
Далее рассматривается только побуквенное кодирование
3. Неравномерное кодирование
Равномерное кодирование удобно для декодирования. Однако часто применяют и неравномерные коды, т.е. коды с различной длиной кодовых слов. Это полезно, когда в исходном тексте разные буквы встречаются с разной частотой. Тогда часто встречающиеся символы стоит кодировать более короткими словами, а редкие – более длинными. Из примера 1 видно, что (в отличие от равномерных кодов!) не все неравномерные коды допускают однозначное декодирование.
Есть простое условие, при выполнении которого неравномерный код допускает однозначное декодирование.
Код называется префиксным, если в нем нет ни одного кодового слова, которое было бы началом (по-научному, — префиксом) другого кодового слова.
Код из примера 1 – НЕ префиксный, так как, например, код буквы А (т.е. кодовое слово 1) – префикс кода буквы К (т.е. кодового слова 12, префикс выделен жирным шрифтом).
Код из примера 2 (и любой другой равномерный код) – префиксный: никакое слово не может быть началом слова той же длины.
Пример 3. Пусть исходный алфавит включает 9 символов: А, Л, М, О, П, Р, У, Ы, -. Кодовый алфавит – двоичный. Кодовые слова:
А: 00 М: 01 -: 100 Л: 101 У: 1100 Ы: 1101 Р: 1110 О: 11110 П: 11111Кодовые слова выписаны в алфавитном порядке. Видно, что ни одно из них не является началом другого. Это можно проиллюстрировать рисунком
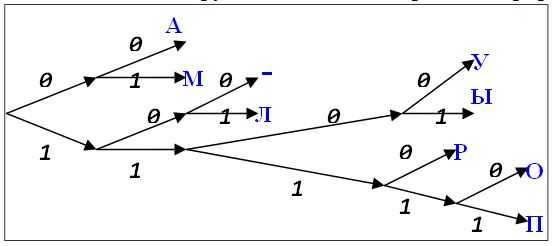На рисунке изображено бинарное дерево. Его корень расположен слева. Из каждого внутреннего узла выходит два ребра. Верхнее ребро имеет пометку 0, нижнее – пометку 1. Таким образом, каждому узлу соответствует слово в двоичном алфавите. Если слово X является началом (префиксом) слова Y, то узел, соответствующий слову X, находится на пути из корня в узел, соответствующий слову Y. Наши кодовые слова находятся в листьях дерева. Поэтому ни одно из них не является началом другого.
Теорема (условие Фано). Любой префиксный код (а не только равномерный) допускает однозначное декодирование.
Разбор примера (вместо доказательства). Рассмотрим закодированный текст, полученный с помощью кода из примера 3:
0100010010001110110100100111000011100
Будем его декодировать таким способом. Двигаемся слева направо, пока не обнаружим код какой-то буквы. 0 – не кодовое слово, а 01 – код буквы М.
0100010010001110110100100111000011100
Значит, исходный текст начинается с буквы М: код никакой другой буквы не начинается с 01! «Отложим» начальные 01 в сторону и продолжим.
01 00010010001110110100100111000011100 МДалее таким же образом находим следующее кодовое слово 00 – код буквы А.
01 00010010001110110100100111000011100 М АДоведите расшифровку текста до конца самостоятельно. Убедитесь, что он расшифровывается (декодируется) однозначно.
Замечание. В расшифрованном тексте 14 букв. Т.к. в алфавите 9 букв, то при равномерном двоичном кодировании пришлось бы использовать кодовые слова длины 4. Таким образом, при равномерном кодировании закодированный текст имел бы длину 56 символов – в полтора раза больше, чем в нашем примере (у нас 37 символов).
4. Как все это повторять. Задачи на понимание
Знание приведенного выше материала достаточно для решения задачи 5 из демо-варианта и близких к ней (см. здесь). Повторять (учить) этот материал стоит в том порядке, в котором он изложен. При этом нужно решать простые задачи – до тех пор, пока не будет достигнуто полное понимание. Ниже приведены возможные типы таких задач. Опытные учителя легко придумают (или подберут) конкретные задачи таких типов. Если будут вопросы – пишите.
1) Понятие побуквенного кодирования.
Дан алфавит Ф и кодовые слова для всех слов в алфавите Ф. Закодировать заданный текст в алфавите Ф. Коды могут быть с использованием разных кодовых алфавитов, равномерные и неравномерные.
2) Префиксные неравномерные коды.
2.1) Дан алфавит Ф и двоичный префиксный код для этого алфавита. Построить дерево кода (см. рис.1) и убедиться, что код – префиксный.
2.2) Дан алфавит Ф и двоичный префиксный код для этого алфавита. Декодировать (анализом слева направо) данный текст в кодовом алфавите.
2.3) Дан алфавит Ф и кодовые слова для всех слов в алфавите Ф. Определить, является ли данный код префиксным, или нет. В качестве примеров полезно приводить:
— Равномерный код. — Неравномерный префиксный код (полезно нарисовать депево этого кода как на рис.1). — Различные пополнения данного неравномерного префиксного кода с помощью кода еще одной буквы так, чтобы полученный код либо оставался префиксным, либо переставал им быть. При анализе дополнительной буквы полезно использовать дерево исходного кода. Полезно рассмотреть различные варианты «потери префиксности»: (а) новый код – начало одного из старых; (б) один из старых кодов – начало нового.2.4) Решать задачи для самостоятельного решения, например, отсюда
ege-go.ru
Если в обычном (естественном) языке, на котором люди общаются, слова сосоят из букв, то в формальных языках слова состоят из символов и если символы принимают значения «0» или «1», то это и есть буквы двоичного слова. Последовательность символов ( нулей и единиц) называют двоичным словом. Двоичные слова являются словами формального языка, который разрабатывается для специальных применений. Примером формальных языков могут служить языки программирования, языки кодирования информации для ее передачи, хранения и т.п.
До недавнего времени байта было достаточно, чтобы закодировать все символы текста в русском и латинском алфавите: буквы, цифры, знаки препинания, управляющие сигналы — все то, что передавалось компьютеру с клавиатуры. Для этого использовался код ASCII (American Standard Coding for Information Interchange — Американский Стандартный Код для Обмена Информацией). С развитием информатики байт начал сдерживать возможность увеличения количества используемых символов. В настоящее время завершается переход на двухбайтовое кодирование символов с использованием кода Unicode. 16-битовое двоичное слово позволяет закодировать 65536 символов и команд. |
www.reshim.su