Формулы площади трапеции
Задачи на площадь трапеции решают в школьном курсе планиметрии. Расчеты не слишком сложны в изучении этой темы, однако с течением времени забывается и теоретический материал и формулы для вычисления площади трапеции. Из данного материала Вы научитесь находить площадь трапеции и ознакомитесь с распространенными для вычислений формулами.
Формулы площади трапеции
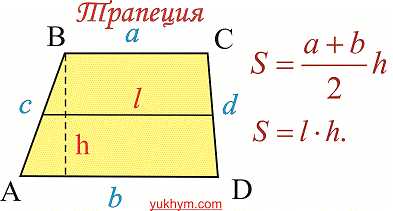
1. Площадь трапеции равна произведению полусуммы основ на высоту:
Средняя линия трапеции равна полусумме оснований, таким образом предыдущую формулу площади можно записать в виде
Ниже на рисунке приведены соответствующие формулы и обозначения
2. Если задано диагонали трапеции и угол между ними (смотрите рисунок )
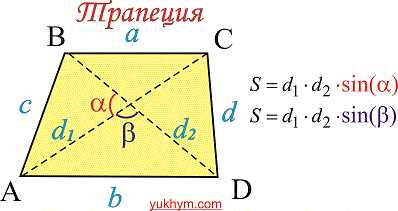
то площадь трапеции находят по формуле
Данная формула, как и предыдущая, достаточно проста в вычислениях.
Следующая формула требует большего количества расчетов.
3. Бывают сложные примеры на трапецию когда задано все четыре ее стороны. В таких случаях используют первую формулу площади трапеции
или вторую
При применении формулы следует помнит, что между сторонами должны выполняться условия b>a и c>d.
4. Если в задании известно что трапеция равнобедренная (боковые стороны равны ) то для того, чтобы найти площадь трапеции кроме выше приведенных формул используют следующие:
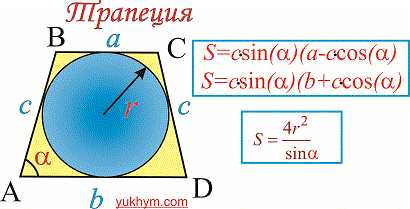
- если задано основу, боковую сторону и угол между ними
- если известен радиус вписанной окружности и угол при основании
Здесь r – радиус окружности, alpha – угол при основании, c – боковая сторона равнобокой трапеции.
Если радиус вписанной окружности и нужен угол не известны в условии задания — пользуйтесь выше приведенным формулам площади трапеции.
Теперь Вы знаете как найти площадь трапеции – используйте приведенные формулы на практике и не питайте проблем в обучении.
Посмотреть материалы:
yukhym.com
формулы площади, доказательства. Трапеция на занятиях с репетитоом по математике — Колпаков Александр Николаевич
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве, подготовка к ЕГЭ в Строгино.
ankolpakov.ru
Как найти площадь трапеции | Треугольники
Как найти площадь трапеции? Для этого в зависимости от данных условия можно использовать несколько формул.
1. Площадь трапеции равна произведению полусуммы её оснований на высоту.
Для трапеции ABCD, AD ∥ BC, с высотой BF площадь равна
Если AD=a, BC=b, BF=h, формула для нахождения площади трапеции
2. Площадь трапеции равна произведению её средней линии на высоту.
Если MN=m, BF=h, формула для нахождения площади трапеции через среднюю линию и высоту
3. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.
или, так как sin∠BOC=sin(180º-∠COD)=sin∠COD,
Если AC=d1, BD=d2, ∠COD=φ, то формула для нахождения площади трапеции через диагонали —
Если диагонали трапеции перпендикулярны,
так как sin 90º=1,
то формула площади трапеции
4. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.
Так как в трапецию можно вписать окружность, если суммы ее противолежащих сторон равны, то AB+CD=AD+BC. Следовательно, полупериметр трапеции равен сумме её оснований: p=AD+BC или p=a+b.
Таким образом, получаем еще одну формулу для нахождения площади трапеции через радиус вписанной окружности:
(Так как радиус вписанной в трапецию окружности равен половине высоты трапеции:
то эта формула может быть получена непосредственно из формулы из пункта 1).
www.treugolniki.ru
Нахождение площади трапеции
С такими геометрическими фигурами, как трапеции, все мы очень часто встречаемся в жизни. Чаще других с ними приходится иметь дело инженерам-проектировщикам, разрабатывающим различные детали. При этом им практически всегда нужно определять площадь трапеции, форму которой будет иметь то или иное изделие.
На мебельных предприятиях часто изготавливаются столы с трапецеидальными столешницами, которые отличаются не только оригинальным дизайном, но еще и очень удобны в небольших и стесненных помещениях. Для того чтобы точно рассчитать расход материала, требуемого для изготовления этих изделий, их разработчики всегда используют формулу, по которой производится нахождение площади трапеции.
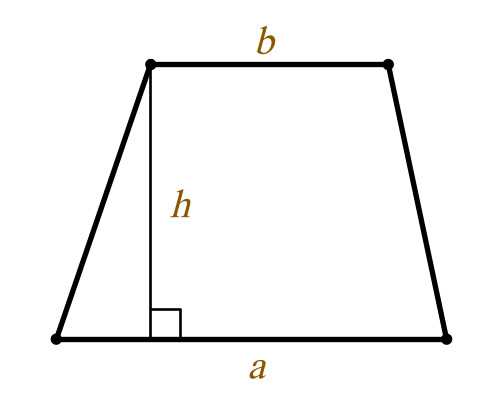
Вычисление площади трапеции
a – нижнее основание
b – верхнее основание
h – высота трапеции
S – площадь
Многие современные здания (причем как в городах, так и за их пределами) проектируются таким образом, чтобы их окна имели нестандартную и запоминающуюся форму, в том числе и трапецеидальную. Само собой разумеется, что при их разработке для тех, кто будет их, в конечном итоге, изготавливать, нужно точно определить не только длину нижнего и верхнего основания, а также размеры всех углов, и площадь самой сборки. При этом также применяется формула, на основании которой происходит
Детали трапецеидальной формы наличествуют практически в каждом современном автомобиле. К ним, к примеру, относятся почти все стекла, устанавливаемые в дверях. Поэтому при конструировании машин специалистам приходится пользоваться формулами, по которым происходит вычисление площади трапеции.
В последние годы многие наши соотечественники обзаводятся загородными домами, коттеджами и дачами, причем многие из этих строений имеют так называемые вальмовые крыши. Они представляют собой кровельные конструкции, состоящие из четырех скатов, два из которых, являющиеся торцевыми, имеют фору треугольников, а два других – трапеций. На таких крышах практически никогда не задерживается снег, что очень важно в российских условиях. Перед тем, как производить кровельные работы, необходимо определить, какое количество материала для этого потребуется, а это значит, что нужно производить вычисление площади трапеции.
Отправляясь на какой-нибудь морской курорт, где отдыхающие не только проводят время на пляжах, но еще и активно занимаются водными видами спорта, то неподалеку о берега можно увидеть небольшие яхты, некоторые паруса которых изготовлены в форме трапеций.
simple-math.ru
Площадь трапеции
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз ))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
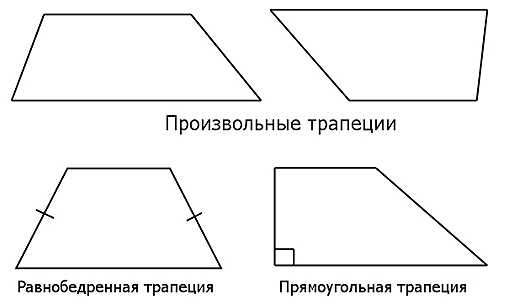
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l, и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
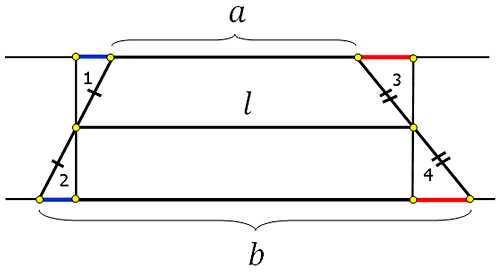
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
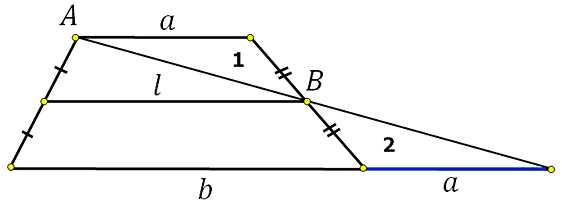
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что средняя линия треугольника равна половине параллельного ей основания, то есть:
Всё!
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
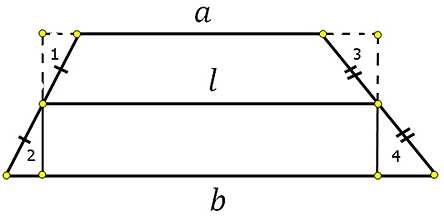
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Делитесь информацией в социальных сетях.
matematikalegko.ru
Как найти площадь трапеции формула
Трапеция – это одна из фигур, которая часто используется в геометрии. Трапеция – это выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Те стороны, что параллельны, называются основаниями, а те, что не параллельны — боковыми сторонами.
Отрезок, который соединяет середины боковых сторон, называется средней линией. Все эти термины служат помощниками в определении площади трапеции. Для её нахождения существует несколько формул.
Первая формула
Первая формула использует основания и высоту трапеции. Для того, чтобы найти площадь (S) по такому принципу, вам необходимо пройти следующие этапы:
Шаг 1
Найти длину первого основания, которую мы обозначим как а.
Шаг 2
Найти длину второго основания, которую мы обозначим, как b.
Шаг 3
Провести высоту.

Шаг 4
Измерить высоту и обозначить её как h.
Шаг 5
Сложить длины оснований (а+ b).
Шаг 6
Разделить полученную сумму на 2 ((а+ b):2).
Шаг 7
Умножить полученный результат на длину высоты (½ (a+b) * h).
Формула для нахождения площади выглядит следующим образом: S = ½ (a+b) * h. Или другими словами полусумма оснований, умноженная на высоту.

Вторая формула
Вторая формула заключает в себе величину средней линии и высоты. Для того, чтобы найти площадь (S) по такому принципу, вам необходимо пройти следующие этапы:
Шаг 1
Найти величину высоты (h).
Шаг 2
Провести среднюю линию, соединив середины боковых сторон между собой (m).
Шаг 3
Умножить высоту на среднюю линию (h* m).
Формула для нахождения площади выглядит следующим образом: S = h * m. Или другими словами высота, умноженная на среднюю линию.
Существуют и другие варианты того, как найти площадь трапеции, но они являются более сложными, а следовательно и не такими частыми в использовании.
Приведенные выше формулы просты и удобны в использовании. Неотступно выполняя один пункт инструкции за другим, вы сможете безошибочно определить площадь трапеции.
kakumno.ru
Формула площади трапеции
В статье понятно и доступно разберем формулу площади трапеции, но для начала отработаем основные понятия!
Трапеция это геометрическая четырехугольная фигура, состоящая из двух параллельных линий называющихся основанием и двух боковых линии не являющиеся параллельными, называющиеся боковые стороны. Линия которая соединяет стороны как основные так и боковые посередине, называется — средней линией, высота выводится под углом 900.
Площадью трапеции называется участок на плоскости, который ограничен данной фигурой, обозначается в единицах квадратных.
В случае если мы знаем величину средней линии k, формула меняется на более легкую, она приравнивается к половине суммы длины основных линий
В случае когда мы знаем длину всех сторон, можно рассчитать площадь используя данную формулу
Если разобрать данную формулу на примере, то мы получим следующее:
Рассмотрим для ясности: трапеция с длиной боковых линий х = 5 см, g = 4 см, основные линии y = 3 см, z = 7 см. Требуется найти S = ?.
Трапеция бывает однобокой, ещё ее называют равнобедренной — так как диагонали равны между собой. Для нее формула может складываться через радиус вписанной в нее окружности, диагонали и углы прилегающие к основанию.
В случае когда мы знаем длину диагоналей и угол находящийся между ними:
В том случае когда выводим формулу с помощью боковых сторон и углов прилегающих к основанию. Формула будет выглядеть так:
S = x * sin ?(y — x * cos ?)S = x * sin ?(z + x * cos ?)
Вывод: Если нам известно одно основание из двух и величины углов принадлежащие этому основанию, мы без труда сможем узнать площадь трапеции.
Трапеция бывает криволинейной — это тогда, когда трапеция находится на оси координат, ограничена графиком продолжительной функции.
В случае когда основание трапеции находится на оси х и ограничено точками x1 = z, x2 = y. Вычислить площадь трапеции помогут интегралы
где F (z) — значение в точке z
F (y) — значение в точке y
Разберем для наглядности: Криволинейная трапеция, ограниченная функцией y = f(x). Функция F(x) = — x3 — 27×2 — 240x — 8. Нужно найти S = ?. Фигура ограничивается: графиком сверху y = f(x)., снизу ОХ осью, слева х = (-10), справа х = (-8).
Пользуемся данной формулой, получаем:
В условиях задачи дана функция. С помощью нее найдем значения точек.
1) F(-8) = -(-8)3 — 27 х (-8)2 — 240 х (-8) — 8 = 24-1728+1920 — 8 = 696
2) F(-10) = -(-10)3 — 27 х (-10)2 — 240 х (-10) — 8 = 1000-2700+240 — 8 = 692
3) F(-8) — F (-10) = 696 — 692 = 4
Ответ: S = 4
Вот собственно и всё по формулам площади для разных видов трапеций. Если у вас появились какие то вопросы, обязательно пишите их в комментариях. Успехов в учебе.
vamsochinenie.ru — база сочинений на самые разные темы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
