Как считать корни в алгебре – . . ? .

методы умножения, примеры с объяснением

Известно, что знак корня  является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.

Yandex.RTB R-A-339285-1

Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:

• без множителей;
• с множителями;
• с разными показателями.

Метод умножения корней без множителей

Алгоритм действий:

Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Пример

Пример 1: 18×2=?

Пример 2: 10×5=?

Пример 3: 33×93=?

Далее необходимо перемножить числа под корнем.

 

Пример

Пример 1: 18×2=36

Пример 2: 10×5=50

Пример 3: 33×93=273

Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:

Пример

Пример 1: 36=6. 36 — квадратный корень из шести (6×6=36).

Пример 2: 50=(25×2)=(5×5)×2=52. Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.

Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.

Метод умножения показателей с множителями

Алгоритм действий:

Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:

Пример

Пример 1: 32×10=3?3×

zaochnik.com

правила, методы, примеры как делить квадратные корни

Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.

Единственное, что необходимо все время держать в голове —  подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.

Yandex.RTB R-A-339285-1

 

Метод 1. Деление подкоренных выражений

Алгоритм действий:

Записать дробь

Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.

Пример 1

144÷36, это выражение следует переписать так: 14436

Использовать один знак корня

В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.

Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.

Пример 2

14436. Это выражение следует записать так: 14436

Разделить подкоренные выражения

Просто разделите одно выражение на другое, а результат запишите под знаком корня.

Пример 3

14436=4, запишем это выражение так: 14436=4

Упростить подкоренное выражение (если необходимо)

Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.

Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.

Пример 4

4 — полный квадрат, потому что 2×2=4. Из этого следует:

4=2×2=2. Поэтому 14436=4=2.

Метод 2. Разложение подкоренного выражения на множители

Алгоритм действий:

Записать дробь

Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители. 

Пример 5

8÷36, переписываем так 836

Разложить на множители каждое из подкоренных выражений

Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.

Пример 6

Упростить числитель и знаменатель дроби

Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.

Пример 7

2266×62×2×2, из этого следует: 836=226

Рационализировать знаменатель (избавиться от корня)

В математике существую

zaochnik.com

Умножение корней

19 января 2017

Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.

Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)

Вы ведь тоже ещё не вкурили?

Урок получился довольно большим, поэтому я разделил его на две части:

1. Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
2. Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.

Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.

Основное правило умножения

Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:

Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:

\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]

Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.

Примеры. Рассмотрим сразу четыре примера с числами:

\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]

Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу.

Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.

Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.

Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:

Примеры.

\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]

И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.

Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.

Случай произвольного показателя

Итак, с квадратными корнями разобрались. А что делать с кубическими? Или вообще с корнями произвольной степени $n$? Да всё то же самое. Правило остаётся прежним:

Чтобы перемножить два корня степени $n$, достаточно перемножить их подкоренные выражения, после чего результат записать под одним радикалом.

В общем, ничего сложного. Разве что объём вычислений может оказаться больше. Разберём парочку примеров:

Примеры. Вычислить произведения:

\[\begin{align} & \sqrt[4]{20}\cdot \sqrt[4]{\frac{125}{4}}=\sqrt[4]{20\cdot \frac{125}{4}}=\sqrt[4]{625}=5; \\ & \sqrt[3]{\frac{16}{625}}\cdot \sqrt[3]{0,16}=\sqrt[3]{\frac{16}{625}\cdot \frac{16}{100}}=\sqrt[3]{\frac{64}{{{25}^{2}}\cdot 25}}= \\ & =\sqrt[3]{\frac{{{4}^{3}}}{{{25}^{3}}}}=\sqrt[3]{{{\left( \frac{4}{25} \right)}^{3}}}=\frac{4}{25}. \\ \end{align}\]

И вновь внимание второе выражение. Мы перемножаем кубические корни, избавляемся от десятичной дроби и в итоге получаем в знаменателе произведение чисел 625 и 25. Это довольно большое число — лично я с ходу не посчитаю, чему оно равно.

Поэтому мы просто выделили точный куб в числителе и знаменателе, а затем воспользовались одним из ключевых свойств (или, если угодно — определением) корня $n$-й степени:

\[\begin{align} & \sqrt[2n+1]{{{a}^{2n+1}}}=a; \\ & \sqrt[2n]{{{a}^{2n}}}=\left| a \right|. \\ \end{align}\]

Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:

Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?

При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)

Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.

Умножение корней с разными показателями

Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt[7]{23}$? Можно ли вообще это делать?

Да конечно можно. Всё делается вот по этой формуле:

Правило умножения корней. Чтобы умножить $\sqrt[n]{a}$ на $\sqrt[p]{b}$, достаточно выполнить вот такое преобразование:

\[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\]

Однако эта формула работает только при условии, что подкоренные выражения неотрицательны. Это очень важное замечание, к которому мы вернёмся чуть позже.

А пока рассмотрим парочку примеров:

\[\begin{align} & \sqrt[3]{3}\cdot \sqrt[4]{2}=\sqrt[3\cdot 4]{{{3}^{4}}\cdot {{2}^{3}}}=\sqrt[12]{81\cdot 8}=\sqrt[12]{648}; \\ & \sqrt{2}\cdot \sqrt[5]{7}=\sqrt[2\cdot 5]{{{2}^{5}}\cdot {{7}^{2}}}=\sqrt[10]{32\cdot 49}=\sqrt[10]{1568}; \\ & \sqrt{5}\cdot \sqrt[4]{3}=\sqrt[2\cdot 4]{{{5}^{4}}\cdot {{3}^{2}}}=\sqrt[8]{625\cdot 9}=\sqrt[8]{5625}. \\ \end{align}\]

Как видите, ничего сложного. Теперь давайте разберёмся, откуда взялось требование неотрицательности, и что будет, если мы его нарушим.:)

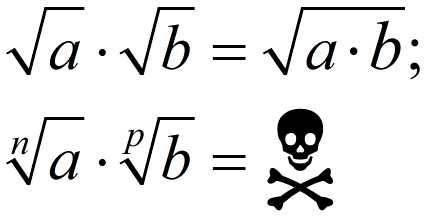Умножать корни несложно

Почему подкоренные выражения должны быть неотрицательными?

Конечно, можно уподобиться школьным учителям и с умным видом процитировать учебник:

Требование неотрицательности связано с разными определениями корней чётной и нечётной степени (соответственно, области определения у них тоже разные).

Ну что, стало понятнее? Лично я, когда читал этот бред в 8-м классе, понял для себя примерно следующее: «Требование неотрицательности связано с *#&^@(*#@^#)~%» — короче, я нихрена в тот раз не понял.:)

Поэтому сейчас объясню всё по-нормальному.

Сначала выясним, откуда вообще берётся формула умножения, приведённая выше. Для этого напомню одно важное свойство корня:

\[\sqrt[n]{a}=\sqrt[n\cdot k]{{{a}^{k}}}\]

Другими словами, мы можем спокойно возводить подкоренное выражение в любую натуральную степень $k$ — при этом показатель корня придётся умножить на эту же степень. Следовательно, мы легко сведём любые корни к общему показателю, после чего перемножим. Отсюда и берётся формула умножения:

\[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}}\cdot \sqrt[p\cdot n]{{{b}^{n}}}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\]

Но есть одна проблема, которая резко ограничивает применение всех этих формул. Рассмотрим вот такое число:

\[\sqrt[3]{-5}\]

Согласно только что приведённой формуле мы можем добавить любую степень. Попробуем добавить $k=2$:

\[\sqrt[3]{-5}=\sqrt[3\cdot 2]{{{\left( -5 \right)}^{2}}}=\sqrt[6]{{{5}^{2}}}\]

Минус мы убрали как раз потому, что квадрат сжигает минус (как и любая другая чётная степень). А теперь выполним обратное преобразование: «сократим» двойку в показателе и степени. Ведь любое равенство можно читать как слева-направо, так и справа-налево:

\[\begin{align} & \sqrt[n]{a}=\sqrt[n\cdot k]{{{a}^{k}}}\Rightarrow \sqrt[n\cdot k]{{{a}^{k}}}=\sqrt[n]{a}; \\ & \sqrt[n\cdot k]{{{a}^{k}}}=\sqrt[n]{a}\Rightarrow \sqrt[6]{{{5}^{2}}}=\sqrt[3\cdot 2]{{{5}^{2}}}=\sqrt[3]{5}. \\ \end{align}\]

Но тогда получается какая-то хрень:

\[\sqrt[3]{-5}=\sqrt[3]{5}\]

Этого не может быть, потому что $\sqrt[3]{-5} \lt 0$, а $\sqrt[3]{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:

1. Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
2. Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.

В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)

Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.

Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:

Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.

Пример. В числе $\sqrt[3]{-5}$ можно вынести минус из-под знака корня — тогда всё будет норм:

\[\begin{align} & \sqrt[3]{-5}=-\sqrt[3]{5} \lt 0\Rightarrow \\ & \sqrt[3]{-5}=-\sqrt[3\cdot 2]{{{5}^{2}}}=-\sqrt[6]{25}=-\sqrt[3\cdot 2]{{{5}^{2}}}=-\sqrt[3]{5} \lt 0 \\ \end{align}\]

Чувствуете разницу? Если оставить минус под корнем, то при возведении подкоренного выражения в квадрат он исчезнет, и начнётся хрень. А если сначала вынести минус, то можно хоть до посинения возводить/убирать квадрат — число останется отрицательным.:)

Таким образом, самый правильный и самый надёжный способ умножения корней следующий:

1. Убрать все минусы из-под радикалов. Минусы бывают только в корнях нечётной кратности — их можно поставить перед корнем и при необходимости сократить (например, если этих минусов окажется два).
2. Выполнить умножение согласно правилам, рассмотренным выше в сегодняшнем уроке. Если показатели корней одинаковые, просто перемножаем подкоренные выражения. А если разные — используем злобную формулу \[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\].
3. 3.Наслаждаемся результатом и хорошими оценками.:)

Ну что? Потренируемся?

Пример 1. Упростите выражение:

\[\begin{align} & \sqrt[3]{48}\cdot \sqrt[3]{-\frac{4}{3}}=\sqrt[3]{48}\cdot \left( -\sqrt[3]{\frac{4}{3}} \right)=-\sqrt[3]{48}\cdot \sqrt[3]{\frac{4}{3}}= \\ & =-\sqrt[3]{48\cdot \frac{4}{3}}=-\sqrt[3]{64}=-4; \end{align}\]

Это самое простой вариант: показатели корней одинаковы и нечётны, проблема лишь в минусе у второго множителя. Выносим этот минус нафиг, после чего всё легко считается.

Пример 2. Упростите выражение:

\[\begin{align} & \sqrt[4]{32}\cdot \sqrt[3]{4}=\sqrt[4]{{{2}^{5}}}\cdot \sqrt[3]{{{2}^{2}}}=\sqrt[4\cdot 3]{{{\left( {{2}^{5}} \right)}^{3}}\cdot {{\left( {{2}^{2}} \right)}^{4}}}= \\ & =\sqrt[12]{{{2}^{15}}\cdot {{2}^{8}}}=\sqrt[12]{{{2}^{23}}} \\ \end{align}\]

Здесь многих смутило бы то, что на выходе получилось иррациональное число. Да, так бывает: мы не смогли полностью избавиться от корня, но по крайней мере существенно упростили выражение.

Пример 3. Упростите выражение:

\[\begin{align} & \sqrt[6]{a}\cdot \sqrt[3]{{{a}^{4}}}=\sqrt[6\cdot 3]{{{a}^{3}}\cdot {{\left( {{a}^{4}} \right)}^{6}}}=\sqrt[18]{{{a}^{3}}\cdot {{a}^{24}}}= \\ & =\sqrt[18]{{{a}^{27}}}=\sqrt[2\cdot 9]{{{a}^{3\cdot 9}}}=\sqrt{{{a}^{3}}} \end{align}\]

Вот на это задание хотел бы обратить ваше внимание. Тут сразу два момента:

1. Под корнем стоит не конкретное число или степень, а переменная $a$. На первый взгляд, это немного непривычно, но в действительности при решении математических задач чаще всего придётся иметь дело именно с переменными.
2. В конце мы умудрились «сократить» показатель корня и степень в подкоренном выражении. Такое случается довольно часто. И это означает, что можно было существенно упростить вычисления, если не пользоваться основной формулой.

Например, можно было поступить так:

\[\begin{align} & \sqrt[6]{a}\cdot \sqrt[3]{{{a}^{4}}}=\sqrt[6]{a}\cdot \sqrt[3\cdot 2]{{{\left( {{a}^{4}} \right)}^{2}}}=\sqrt[6]{a}\cdot \sqrt[6]{{{a}^{8}}} \\ & =\sqrt[6]{a\cdot {{a}^{8}}}=\sqrt[6]{{{a}^{9}}}=\sqrt[2\cdot 3]{{{a}^{3\cdot 3}}}=\sqrt{{{a}^{3}}} \\ \end{align}\]

По сути, все преобразования выполнялись лишь со вторым радикалом. И если не расписывать детально все промежуточные шаги, то в итоге объём вычислений существенно снизится.

На самом деле мы уже сталкивались с подобным задание выше, когда решали пример $\sqrt{5}\cdot \sqrt[4]{3}$. Теперь его можно расписать намного проще:

\[\begin{align} & \sqrt{5}\cdot \sqrt[4]{3}=\sqrt[2\cdot 4]{{{5}^{4}}\cdot {{3}^{2}}}=\sqrt[2\cdot 4]{{{\left( {{5}^{2}}\cdot 3 \right)}^{2}}}= \\ & =\sqrt[4\cdot 2]{{{\left( 75 \right)}^{2}}}=\sqrt[4]{75}. \end{align}\]

Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?

Смотрите также:

1. Что такое корень натуральной степени $n$
2. Сложные иррациональные уравнения — что с ними делать и как их решать?
3. Пробный ЕГЭ 2012. Вариант 2 (без логарифмов)
4. Что такое ЕГЭ по математике 2012
5. Наибольшее и наименьшее значение
6. Задача 7: касательная к графику функции — 2

www.berdov.com

Счет, степени, корни — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений

К оглавлению…

При выполнении численных вычислений с большим количеством операций и дробей желательно выполнять следующие рекомендации:

• Переводите десятичные дроби в обыкновенные, т.е. такие у которых есть числитель и знаменатель.
• Не старайтесь посчитать сразу все выражение. Выполняйте вычисления по одному действию, пошагово. При этом учтите, что:
  • сначала выполняют операции в скобках;
  • затем считают произведения и/или деления;
  • потом суммируют или вычитают;
  • и в последнюю очередь, если это была многоэтажная дробь, делят уже полностью упрощенный числитель на тоже полностью упрощенный знаменатель;
  • причем выполняя в первую очередь операции в скобках также соблюдают ту же последовательность, сначала произведения или деления внутри скобок, потом суммирование или вычитание в скобках, а если внутри скобки есть другая скобка то действия в ней выполняются прежде всего.
• Не спешите умножать и делить «страшные числа». Скорее всего, в одном из следующих действий что-то сократится. Чтобы проще было сократить можно числа раскладывать на простые множители.
• При сложении и вычитании выделяйте в дробях целую часть (если это возможно). При умножении и делении, наоборот, приводите дробь к виду без целой части.

От корней в знаменателе принято избавляться. Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (a — b) является выражение (a + b) и наоборот).

При преобразовании или упрощении алгебраических выражений последовательность действий такова:

• Разложить на множители все, что можно разложить на множители.
• Сократить все, что можно сократить.
• И только потом приводить к общему знаменателю. Ни в коем случае не пытайтесь сразу сломя голову приводить к общему знаменателю. Пример будет становиться чем дальше, тем страшнее.
• Снова разложить на множители и сократить.

Для того чтобы перевести десятичную периодическую дробь в обыкновенную (с числителем и знаменателем) необходимо:

• Из числа, стоящего до второго периода в исходной периодической дроби вычесть число, стоящее до первого периода в этой же дроби и записать полученную разность в числитель будущей обыкновенной дроби.
• В знаменателе же записать столько девяток, сколько цифр в периоде исходной дроби, и столько нулей, сколько цифр между запятой и первым периодом.
• Не забыть про целую часть, если она есть.

При решении задач из данной темы также необходимо помнить много сведений из предыдущих тем. Приведём далее основные из них.

 

Формулы сокращенного умножения

К оглавлению…

При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения:

Последние две формулы также часто удобно использовать в виде:

 

Квадратный трехчлен и теорема Виета

К оглавлению…

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:

Итак, еще раз о теореме Виета:

• Если D < 0 (дискриминант отрицателен), то уравнение корней не имеет и теорему Виета применять нельзя.
• Если D > 0 (дискриминант положителен), то уравнение имеет два корня и теорема Виета прекрасно работает.
• Если D = 0, то уравнение имеет единственный корень, для которого бессмысленно вводить понятие суммы или произведения корней, поэтому теорему Виета тоже не применяем.

 

Основные свойства степеней

К оглавлению…

У математических степеней есть несколько важных свойств, перечислим их:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

 

Основные свойства математических корней

К оглавлению…

Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:

Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):

Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:

Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение. Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:

 

Основные свойства квадратного корня

К оглавлению…

Квадратным корнем называется математический корень второй степени:

Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:

Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:

Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:

educon.by

Извлечение корня из большого числа

А у вас есть зависимость от калькулятора? Или вы считаете, что кроме как с калькулятором или при помощи таблицы квадратов очень сложно вычислить, например, .

Случается, школьники привязаны к калькулятору и даже 0,7 на 0,5 умножают, нажимая на заветные кнопочки. Говорят, ну я все равно знаю как посчитать, а сейчас сэкономлю время… Вот будет  экзамен… тогда и напрягусь…

Так дело в том, что на экзамене и так будет предостаточно «напряжных моментов»… Как говорится, вода камень точит. Вот и на экзамене мелочи, если их много, способны подкосить…

Давайте минимизируем количество возможных неприятностей.

Извлекаем квадратный корень из большого числа

Мы будем говорить сейчас только о случае, когда результат извлечения корня квадратного – целое число.

Случай 1.

Итак, пусть нам во что-бы то ни стало (например,  при вычислении дискриминанта) нужно вычислить корень квадратный из 86436.

Мы будем раскладывать число 86436 на простые множители. Делим на 2, – получаем 43218; снова делим на 2, – получаем 21609. На 2 больше нацело число не делится. Но так как сумма цифр делится на 3, то и само число делится на 3 (вообще говоря, видно, что оно и на 9 делится). . Еще раз делим на 3, – получаем  2401. 2401 на 3 нацело не делится. На пять не делится (не оканчивается цифрой 0 или 5).

Подозреваем делимость на 7. Действительно,  а ,

Итак, Полный порядок!

Поэтому

Случай 2.

Пусть нам нужно вычислить . Действовать так же, как описано выше, неудобно. Пытаемся разложить на простые множители…

На 2 число 1849 нацело не делится (не является четным)…

На 3 нацело не делится (сумма цифр не кратна 3)…

На 5 нацело не делится (последняя цифра – не 5 и не 0)…

На 7 нацело не делится, на 11 не делится, на 13 не делится… Ну и долго нам так перебирать все простые числа?

Будем рассуждать несколько иначе.

Мы понимаем, что

,

то есть

или

Мы сузили круг поиска. Теперь перебираем числа от 41 до 49. Причем ясно, что раз последняя цифра числа – 9, то останавливаться стоит на вариантах 43 или 47, – только эти  числа при возведении в квадрат дадут последнюю цифру 9.

Ну и тут уже, конечно, мы останавливаемся на 43. Действительно,

P.S. А как, ксатати, мы умножаем 0,7 на 0,5?

Следует умножить 5 на 7, не обращая внимание на нули и знаки, а потом отделить, идя справа налево, два знака запятой. Получаем 0,35.

Смотрите также «Отдельные случаи вычисления дискриминанта».

egemaximum.ru

Свойства квадратных корней. Решение задач. Видеоурок. Алгебра 8 Класс

На этом уроке мы систематизируем те знания о квадратных корнях, которые мы получили на предыдущих уроках. Вначале мы вспомним определение квадратного корня, основные свойства корней, а затем закрепим знание теории на решении практических задач с корнями.

Вначале повторим основную теорию.

Определение. Квадратным корнем из неотрицательного числа  называется такое неотрицательное число , квадрат которого равен .

.

Из определения следует тождество  при .

Пример 1. Вычислить значения корней:

а) ;

б) ;

в) ;

г) ;

д) .

Основные свойства квадратного корня:

а)

б)  (аналогично верно и для любого количества множителей)

в)

г)

Пример 2. Вычислите а) ; б) .

Решение. а) Преобразуем десятичную дробь к виду обыкновенной дроби .

б) Внесем частное корней под один корень и выполним сокращение: .

Ответ. 1,5; 30.

Пример 3. Вычислить .

Решение. Для вычисления корней из больших чисел удобно использовать их разложение на простые множители, что можно сделать согласно основной теореме арифметики.

. Из полученного разложения можно записать: .

Ответ. 28.

Пример 4. Вычислить .

Решение. Для выполнения умножения дробей и извлечения из них квадратного корня необходимо привести их к виду неправильных дробей.

 и . Подставим полученные дроби под знак корня:

.

Ответ..

Пример 5. Вычислить .

Решение. Этот пример демонстрирует, что в некоторых случаях для преобразования численных выражений удобно пользоваться формулами сокращенного умножения, в данном случае это формула разности квадратов.

.

Ответ..

Пример 6. Дано: . Доказать: .

Доказательство. Отметим, что указанная функция имеет область определения  из определения квадратного корня. Выпишем, чему равны левая и правая часть доказываемого тождества:

, что и требовалось доказать.

Доказано.

На следующем уроке мы начнем рассмотрение преобразований выражений с корнями.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал для всей семьи (Источник).

2. Подготовка к единому государственному экзамену по математике (Источник).

3. Фестиваль педагогических идей «Открытый урок» (Источник).

 

Домашнее задание

1. №323, 326, 334, 346. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Вычислите: а) , б) , в) , г) .

3. Используя свойства квадратных корней, найдите значение числового выражения: а) , б) , в) .

4. Вычислите: а) , б) .

interneturok.ru

Как складывать квадратные корни

Квадратным корнем из числа X называется число A, которое в процессе умножения самого на себя (A * A) может дать число X. 
Т.е. A * A = A² = X, и √X = A.

Над квадратными корнями (√x), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9. Первое число 4 является квадратом числа 2. Второе число 9 является квадратом числа 3. Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5. 
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54.

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3,
54 = 2 * 3 * 3 * 3.

В числе 24 мы имеем множитель 4, его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9.

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6.

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней – это знаменатель дроби, например, A / (√a + √b).
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b.

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a – b.

Аналогично, если в знаменателе имеется разность корней: √a — √b, числитель и знаменатель дроби умножаем на выражение √a + √b.

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ( (√3 + √5) * (√3 — √5) ) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5).
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5.

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5.

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89.

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

imdiv.com