Що таке медіана трикутника – Медіана трикутника — Вікіпедія

МЕДІАНА ТРИКУТНИКА ТА Її ВЛАСТИВОСТІ.

МЕДІАНА  ТРИКУТНИКА ТА Її ВЛАСТИВОСТІ.

 Медіана трикутника.

Медіаною трикутника називають відрізок, що сполучає вершину трикутника із серединою протилежної сторони.

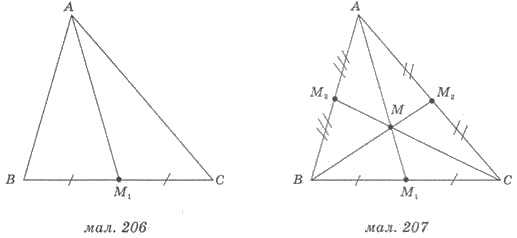
На малюнку 206 відрізок АМ₁ — медіані трикутника АВС. Точку М₁ називають основою медіани. Будь-який трикутник має три медіани. На малюнку 208 відрізки АМ₁, ВМ₂ і СМ₃ — медіани трикутника АВС.

  Медіана трикутника – це відрізок, що з’єднує вершину трикутника та середину протилежної сторони. Трикутник має три медіани, які прийнято позначати m_а, m_b, m_с. Запам’ятаємо, що з вершини А виходить медіана m_а, з вершини В виходить медіана m_b, з вершини С виходить медіана m_с..      Зауваження.  Правильність побудови трьох медіан в трикутнику можна перевірити за їх властивістю перетину в одній точці, яка знаходиться всередині трикутника. Властивості медіан: 1.Кожна медіана трикутника лежить всередині трикутника, а в точці перетину медіан  ділиться на частини рахуючи від вершини, як  2:1. тобто довша частинка медіани вдвічі більша , ніж коротша частинка, яка  становить третю частинку від усієї довжини  медіани.

2. Завжди  можна відновити трикутник за трьома його медіанами.
3. Якщо відомі довжини трьох сторін трикутника, то можна  знайти довжини трьох медіан цього трикутника за такими формулами.                       

4. Точку перетину медіан трикутника називають іноді центр маси трикутника. 5.Якщо з’єднати точку перетину медіан трикутника з вершинами, то трикутник розбивається на три рівновеликі трикутники, тобто у цих трикутників рівні площі. 6. Медіана прямокутного трикутника, що проведена до найдовшої сторони, рівна половині цієї сторони та розділяє прямокутний трикутник на два рівнобедрені трикутники. 7.Кожна медіана трикутника розрізає його на два рівновеликих трикутника. 8. Площа трикутника, що складений з медіан даного трикутника, рівна три чверті площі даного трикутника. 9.Сума трьох векторів, що виходять з точки перетину медіан до вершин трикутника , рівна нулю. 10.Точка перетину медіан при проектуванні трикутника на площину переходить в точку перетину медіан спроектованого трикутника. Зазначимо, що такою властивістю не володіють точки перетину бісектрис та висот. 11.Завжди існує трикутник, сторони якого рівні та паралельні медіанам даного трикутника. 

Властивість медіан трикутника:

У будь-якому трикутнику медіани перетинаються в одній точці (вона називається центроїдом трикутника) і в цій точці поділяються у відношенні 2:1, починаючи від вершини.

На малюнку 207 точка М — центроїд трикутника.

Тоді 

Довжину медіани трикутника m_а проведену до сторони а, можна знайти за формулою:

де b і с — сторони трикутника, між якими проходить медіана.

Приклад. Основа рівнобедреного трикутника дорівнює 4 см, а медіана, що проведена до бічної сторони — 5 см. Знайдіть довжини бічних сторін. Розв’язання. За умовою основа а = 4 см, m_а = 5 см. Позначимо бічні сторони b = с = х. Тоді маємо:  х = 6 (враховуючи х > 0 ). Отже, довжина бічної сторони 6 см. 

geom7klass.blogspot.com

Медіана трикутника

Слово «медіана» перекладається як «рівноподіляюча сторону». Щоб побудувати медіану, треба середину сторони трикутника з’єднати відрізком з протилежною вершиною трикутника. Отриманий відрізок і є медіана трикутника.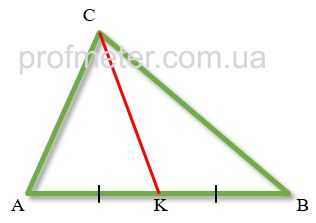
Медіана трикутника — відрізок, проведений з вершини трикутника, що з’єднує цю вершину з серединою протилежної сторони трикутника.

На малюнку червоним кольором позначена медіана CK

. При цьому вона ділить сторону AB трикутника навпіл, AK = KB.

Властивості медіани

Всі медіани трикутника перетинаються в одній точці, розташованій в площині трикутника і що є його центром ваги.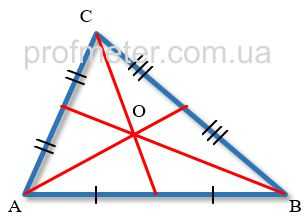

Для визначення цієї точки досить побудувати дві медіани трикутника, і точка їх перетину належатиме третьої медіані цього трикутника.

• Точкою перетину медіан трикутника кожна медіана ділиться у відношенні 2:1, рахуючи від вершини трикутника. Тобто довжина відрізка медіани від вершини трикутника до точки перетину медіан становить 2/3 всієї її довжини, а від точки перетину медіан до сторони трикутника — 1/3 її довжини.
• Медіана розбиває трикутник на два рівновеликих (по площі) трикутника.
• Трикутник ділиться трьома медианами на шість рівновеликих трикутників.
• З сегментів, які формують медіани, можна скласти трикутник, площа якого буде дорівнює 3/4 від всього трикутника. Довжини медіан задовольняють нерівності трикутника.
• У прямокутному трикутнику медіана, проведена з вершини з прямим кутом, дорівнює половині гіпотенузи.
• Більшій стороні трикутника відповідає менша медіана.
• У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються.
• У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються.

Середня лінія трикутника

Відрізок, проведений через основи двох будь-яких медіан трикутника, є його середньою лінією.

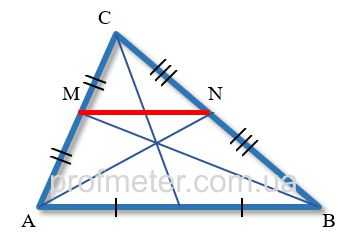
Середня лінія трикутника з’єднує дві точки решт медіан, що лежать на сторонах трикутника

Середня лінія трикутника завжди паралельна тій стороні трикутника, з якої вона не має спільних точок.
Середня лінія трикутника дорівнює половині довжини того боку трикутника, якої вона паралельна.

profmeter.com.ua

Медіана трикутника

Медіана і висота трикутника — це одна з найбільш захоплюючих і цікавих тем геометрії. Термін «Медіана» означає пряму або відрізок, який з’єднує вершину трикутника з його протилежною стороною. Іншими словами, медіана — це лінія, яка проходить з середини однієї сторони трикутника в протилежну вершину цього ж трикутника. Оскільки у трикутника тільки три вершини і три сторони, значить і медіани може бути тільки три.

Властивості медіани трикутника

1. Все медіани трикутника перетинаються в одній точці і розділяються цією точкою в співвідношенні 2: 1, рахуючи від вершини. Таким чином, якщо намалювати в трикутнику всі три медіани, то точка їх перетину буде ділити їх на дві частини. Частина, яка розташовується ближче до вершини, становитиме 2/3 всієї лінії, а частина, яка розташовується ближче до сторони трикутника — 1/3 лінії. Перетинаються медіани в одній точці.
2. Три медіани, проведені в одному трикутнику, ділять цей трикутник на 6 маленьких трикутників, чия площа буде дорівнює.
3. Чим більше сторона трикутника, від якої виходить медіана , тим менше ця медіана. І навпаки, найкоротша сторона має найдовшу медіану.
4. Медіана в прямокутному трикутнику має ряд власних характеристик. Наприклад, якщо навколо такого трикутника описати коло, яка проходитиме через усі вершини, то медіана прямого кута, проведена до гіпотенузи, стане радіусом описаного кола (тобто її довжина становитиме відстань від будь-якої точки окружності до її центру).

Рівняння довжини медіани трикутника

Формула медіани виходить з теореми Стюарта і говорить, що медіана — це квадратний корінь з відносини квадратів суми сторін трикутника, які утворюють вершину, за вирахуванням квадрата сторони, до якої проведена медіана до чотирьох. Іншими словами, щоб дізнатися довжину медіани потрібно звести в квадрат показники довжини кожної сторони трикутника, а потім записати це у вигляді дробу, в чисельнику якого буде сума квадратів сторін, які утворюють кут, звідки виходить медіана, мінус квадрат третьої сторони.

В якості знаменника тут виступає цифра 4. Потім з даннойдробі потрібно витягти корінь квадратний, і тоді ми отримаємо довжину медіани.

Точка перетину медіан трикутника

Як ми писали вище, всім медіани одного трикутника перетинаються в одній точці. Цю точку називають центром трикутника. Він ділить кожну медіану на дві частини, довжина яких співвідноситься як 2: 1. При цьому центр трикутника є і центром описаної навколо нього кола. А інші геометричні фігури мають власні центри.

Координати точки перетину медіан трикутника

Щоб знайти координати перетину медіан одного трикутника, скористаємося властивістю центроїда, згідно з яким він ділить кожну медіану на відрізки 2: 1. Позначаємо вершини як як A (x1; y1), B (x2; y2), C (x3; y3),

і обчислюємо координати центру трикутника за формулою: x0 = (x1 + x2 + x3)/3; y0 = (y1 + y2 + y3)/3.

Площа трикутника через медіану

Всі медіани одного трикутника ділять цей трикутник на 6 рівних трикутників, а центр трикутника ділить кожну медіану у співвідношенні 2: 1. Тому якщо відомі параметри кожної медіани, можна обчислити і площа трикутника через площу одного з маленьких трикутників, а потім збільшити цей показник у 6 разів.

У випадку з прямокутним трикутником чинимо так. Навколо трикутника описуємо коло, а ще одну вписуємо в нього. Пам’ятаємо, що площа трикутника дорівнює сумі квадрата радіуса внутрішньої окружності і подвійного добутку радіуса описаної і вписаного кола. При цьому, радіус описаної дорівнює довжині медіани, яка йде до середини гіпотенузи. А радіус вписаного обчислюємо через властивість центру трикутника ділити кожну медіану на дві частини у співвідношенні 2: 1. Всі отримані значення вставляємо в формулу і отримуємо площа прямокутного трикутника.

olympica.com.ua

Медіана трикутника

Трикутник і його медіани.

Медіана трикутника ( лат. mediāna — Середня) — відрізок усередині трикутника, що з’єднує вершину трикутника з серединою протилежної сторони, а також пряма, що містить цей відрізок.

1. Властивості

• Медіани трикутника перетинаються в одній точці, яка називається центроїдів, і діляться цією точкою на дві частини у відношенні 2:1, рахуючи від вершини.
• Трикутник ділиться трьома медианами на шість рівновеликих трикутників.
• Більшій стороні трикутника відповідає менша медіана.
• З векторів, що утворюють медіани, можна скласти трикутник.
• При афінних перетвореннях медіана переходить в медіану.
• Медіана трикутника ділить його на дві рівновеликі частини.
• Медіана трикутника є чевіаной

2. Формули

, Де m _c — медіана до сторони c; a, b, c — сторони трикутника,

тому сума квадратів медиан довільного трикутника завжди в 4 / 3 рази менше суми квадратів його сторін.

• Формула боку через медіани:

, Де m _a, m _b, m _c медіани до відповідних сторонам трикутника, a, b, c — Сторони трикутника.

Якщо дві медіани перпендикулярні, то сума квадратів сторін, на які вони опущені, в 5 разів більше квадрата третьої сторони.

Медіана, це така мавпа, яка опускається на бік і ділить її порівну

МЕДІА — мавпа
У якій гостре око,
Стрибне точно в середину
Сторони проти вершини,
Де знаходиться зараз.

Полегшує запам’ятовування формулювання. Найчастіше вживається дітьми.

Примітки

znaimo.com.ua

Медіана трикутника — Howling Pixel

Медіа́на — в геометрії, відрізок, який з’єднує вершину трикутника з серединою протилежної сторони

Властивості

• Медіани трикутника перетинаються в точці, яка є його центром мас.
• Медіана поділяє трикутник на два трикутники з рівними площами, а три проведені медіани — на шість рівновеликих.
• В точці перетину медіани трикутника діляться у відношенні 2:1.
• Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи.
• При афінному перетворенні площини медіана трикутника переходить в медіану.
• Якщо дві медіани трикутника перпендикулярні, то сума квадратів сторін, на які вони опущені, у п’ять разів більша за квадрат третьої сторони, тобто, якщо mb⊥mc{\displaystyle m_{b}\perp m_{c}}, то b2+c2=5a2{\displaystyle b^{2}+c^{2}=5a^{2}}.

Формули

Див. також

Джерела

• Бевз Г. П. Геометрія трикутника. — Київ: Генеза, 2005. — 120 с. ISBN 966-504-431-1
• Бевз Г. П., Бевз В. Г., Владімірова Н. Г. Геометрія: Підручник для 7-9 кл. — Київ: Вежа, 2004. — 309 с. ISBN 966-7091-66-Х
• Кушнір І. А. Трикутник і тетраедр в задачах: кн. для вчителя / І. А. Кушнір. — К. : Радянська школа, 1991. — 208 с. — ISBN 5-330-02081-6
• Кушнір І. А. Повернення втраченої геометрії / І. Кушнір. — Київ: Факт, 2000. 280 с. ISBN 966-7274-75-5

Висота трикутника

Висота́ трику́тника — відрізок, проведений з вершини трикутника до прямої, яка містить сторону протилежну вершині та перпендикулярний до неї. Висотою також називають довжину висоти трикутника, тобто відстань від вершини до протилежної сторони. Основою висоти називається точка перетину висоти та прямої, яка містить протилежну сторону.

Висоту використовують для обчислення площі трикутника. Вона дорівнює половині добутку довжини висоти на довжину основи, тобто протилежної сторони:

S=12ah,{\displaystyle S={\frac {1}{2}}ah,}

де a,h{\displaystyle a,\,h} — відповідно довжина сторони та висота трикутника (h{\displaystyle h} від англ. height), опущена на цю сторону. Отже, найдовша висота трикутника буде лежати навпроти найкоротшої сторони трикутника. Висота пов’язана з довжинами сторін трикутника тригонометричними функціями.

У рівнобедреному трикутнику (трикутнику, в якому дві сторони конгруентні), висота, проведена до неконгруентної сторони, потрапляє у середню точку цієї сторони. Також, ця висота буде бісектрисою кута трикутника, з вершини якого вона проведена.

В прямокутному трикутнику висота, опущена на гіпотенузу ділить її на два відрізки довжини m і n. Якщо довжину висоти позначити через hc{\displaystyle h_{c}}, то отримаємо співвідношення:

hc=mn{\displaystyle h_{c}={\sqrt {mn}}}  (середнє геометричне)

В гострокутному трикутнику всі три висоти лежать всередині трикутника. В тупокутному трикутнику дві висоти опускаються на продовження сторін та лежать поза межами трикутника. В прямокутному трикутнику дві висоти збігаються з катетами цього трикутника.

Три висоти або їх продовження, перетинаються в одній точці, яка називається ортоцентром трикутника. Ортоцентр буде лежати всередині трикутника (і відповідно всі основи перпендикулярів лежать в трикутнику) тоді і тільки тоді, якщо трикутник не тупокутний (в ньому жоден з внутрішніх кутів не більший за прямий кут).

Ортоцентр

Ортоцентр (від грец. ορθοξ — прямий) — точка перетину висот трикутника або їх продовжень. Інакше: ортоцентром називається точка перетину прямих, що містять висоти трикутника. Зазвичай ортоцентр позначають великою латинською літерою H{\displaystyle H}.

В гострокутному трикутнику ортоцентр лежить всередині трикутника. В тупокутному — поза межами трикутника. В прямокутному трикутнику ортоцентр збігається з вершиною прямого кута.

Трикутник

Трику́тник у евклідовій геометрії — геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що їх сполучають. Трикутник з вершинами A, B, і C позначається ABC. Трикутник є многокутником і 2-симплексом. В евклідовій геометрії трикутник однозначно задає площину. Всі трикутники двовимірні.

Основні відомості про трикутники були наведені Евклідом в його праці «Елементи» біля 300 до н. е.

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com

Медiана прямокутного трикутника

Примітка. У даному уроці викладено теоретичні матеріали і рішення завдань з геометрії на тему «медіана у прямокутному трикутнику». Якщо Вам необхідно вирішити завдання з геометрії, якої тут немає — пишіть про це у форумі. Майже напевно курс буде доповнено.

См. также этот урок на русском языке.

Властивості медіани прямокутного трикутника 

Визначення медiани

Медіаною трикутника називається відрізок, що з’єднує один з кутів трикутника з серединою протилежної йому сторони. (медіаною також називають пряму, що містить даний відрізок)

• Медіани трикутника перетинаються в одній точці і діляться цією точкою на дві частини у відношенні 2:1, рахуючи від вершини кута. Точка їх перетину називається центром тяжіння трикутника (відносно рідко у завданнях для позначення цієї точки використовується термін «центроїд»)
• Медіана розбиває трикутник на два рівновеликих трикутника
• Трикутник ділиться трьома медианами на шість рівновеликих трикутників
• Більшої сторони трикутника відповідає менша медіана.

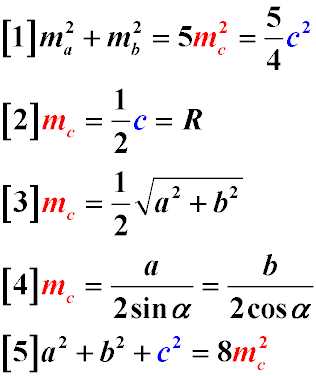
Задачі з геометрії, пропоновані для вирішення, в основному, використовують наступні властивості медіани прямокутного трикутника:

• Сума квадратів медіан, опущених на катети прямокутного трикутника дорівнює п’яти квадратах медіани, опущеною на гіпотенузу (формула 1)
• Медіана, опущена на гіпотенузу прямокутного трикутника дорівнює половині гіпотенузи (формула 2)
• Медіана, опущена на гіпотенузу прямокутного трикутника, дорівнює радіусу кола, описаного навколо прямокутного трикутника (формула 3)
• Медіана, опущена на гіпотенузу, дорівнює половині квадратного кореня з суми квадратів катетів (формула 4)
• Медіана, опущена на гіпотенузу, дорівнює частці від ділення довжини катета на два синуса противолежащего катету гострого кута (формула 5)
• Медіана, опущена на гіпотенузу, дорівнює частці від ділення довжини катета на два косинуса прилеглого катету гострого кута (формула 6)
• Сума квадратів сторін прямокутного трикутника дорівнює восьми квадратах медіани, опущеною на його гіпотенузу (формула 7)

Позначення в формулах:
a, b — катети прямокутного трикутника
c — гіпотенуза прямокутного трикутника
Якщо позначити трикутник, як ABC, то

ВС = а

AC = b

AB = c

(тобто сторони a,b,c — є протилежними відповідним кутам)

m_a — медіана, проведена до катету а 

m_b — медіана, проведена до катету b

m_c — медіана прямокутного трикутника, проведена до гіпотенузи с

α (альфа) — кут CAB, протилежний стороні а

Задача про медіану у прямокутному трикутнику

Медіани прямокутного трикутника, проведені до катетам, дорівнюють, відповідно, 3 см і 4 див. Знайдіть гіпотенузу трикутника.

Рішення. 

Перш ніж розпочати вирішення завдання, звернемо увагу на співвідношення довжини гіпотенузи прямокутного трикутника і медіани, яка опущена на неї. Для цього звернемося до формулами 2, 4, 5 властивостей медіани в прямокутному трикутнику. В цих формулах явно вказано співвідношення гіпотенузи і медіани, яка на неї опущена як 1 до 2. Тому,для зручності майбутніх обчислень (що ніяк не вплине на правильність рішення, але зробить його більш зручним), позначимо довжини катетів AC і BC через змінні x та y як 2x і 2y (а не x і y). 

Розглянемо прямокутний трикутник ADC. Кут C у нього прямий за умовою задачі, катет AC — загальний з трикутником ABC, а катет CD дорівнює половині BC згідно властивостям медіани. Тоді, по теоремі Піфагора  

AC² + CD² = AD²

Оскільки AC = 2x, CD = y (так як медіана ділить катет на дві рівні частини), то
4x² + y² = 9 

Одночасно, розглянемо прямокутний трикутник EBC. У нього також кут З прямою за умовою задачі, катет BC є спільним з катетом BC вихідного трикутника ABC, а катет EC за властивістю медіани дорівнює половині катета AC вихідного трикутника ABC.
По теоремі Піфагора:
EC² + BC²  = BE²

Оскільки EC = x (медіана ділить катет навпіл), BC = 2y, то
x² + 4y²  = 16

Так як трикутники ABC, EBC і ADC пов’язані між собою загальними сторонами, то обидва отриманих рівняння також пов’язані між собою.
Розв’яжемо отриману систему рівнянь.
4x² + y² = 9
x² + 4y²  = 16 

Складемо обидва рівняння (втім, можна було вибрати і будь-який інший спосіб рішення).
5x² + 5y² = 25  
5( x² + y² ) = 25
x² + y² = 5 

Звернемося до вихідного трикутника ABC. За теоремою Піфагора
AC² + BC²  = AB²

Так як довжина кожного з катетів нам «відома», ми прийняли, що їх довжина дорівнює 2x і 2y, тобто
4x² + 4y² = AB²
Так як обидва доданки мають спільний множник 4, винесемо його за дужки    
4 ( x² + y² ) = AB²  
Чому дорівнює  x² + y² ми вже знаємо (див. вище x² + y² = 5), тому просто підставимо значення замість  x² + y² 

AB² = 4 х 5
AB² = 20
AB = √20 = 2√5  

Відповідь: довжина гіпотенузи дорівнює 2√5     

profmeter.com.ua

Перетин медіан трикутника

07.07.2015

Існує теорема про те, що медіани трикутника перетинаються в одній точці, і ця точка ділить кожну медіану в співвідношенні 2:1, де 2 відповідає відрізку від вершини, з якої проведена медіана, до точки перетину медіан, а 1 відповідає відрізку від точки перетину медіан до середини сторони, до якої проведена медіана.

Щоб довести цю теорему, розглянемо трикутник ABC з медіанами AE, BF, CD. Тобто точки D, E, F ділять навпіл сторони AB, BC, CA відповідно.

Нам не відомо, чи перетинаються всі медіани в одній точці (це ще потрібно довести). Однак будь-які дві медіани перетнуться в одній точці, тому що не можуть бути паралельні. Нехай медіани AE і BF перетинаються в точці O.

Перетин двох медіан трикутника

Медіана BF ділить медіану AE на два відрізки AO і EO. Проведемо через точку E пряму, паралельну BF. Ця пряма перетне сторону AC в якійсь точці L. Також проведемо через середину відрізка AB (точку D) ще одну паралельну до BF пряму. Вона перетне AC в точці K.

Згідно з теоремою Фалеса, якщо на одній стороні кута від його вершини відкласти послідовно рівні відрізки і провести через кінці цих відрізків паралельні прямі, які перетинають іншу сторону кута, то ці паралельні прямі відсічуть на другій стороні кута також рівні між собою відрізки.

Подивимося на кут BCA даного трикутника. Відрізки BE і EC рівні між собою, прямі BF і EL паралельні один одному. Тоді згідно теоремі Фалеса CL = LF.
Якщо ж подивитися на кут BAC, так як AD = BD і DK || BF, то AK = KF.

Так як відрізки AF і CF рівні між собою (так як Їх утворює медіана) і кожен з них ділиться на два рівних відрізка, то всі чотири відрізка боку AC рівні між собою: AK = KF = FL = LC.

Розглянемо кут EAC. Через кінці трьох рівних відрізків боку AC проведені паралельні прямі. Отже, вони відсікають на стороні AE рівні між собою відрізки. Відрізок AO містить в собі два таких відрізка, а EO тільки один. Таким чином, ми довели, що як мінімум одна медіана трикутника точкою перетину з іншою медіаною ділиться на два відрізки, довжини яких співвідносяться як 2:1.

Тепер розглянемо перетин медіани AE з медіаною CD. Нехай вони перетинаються в точці P.

Аналогічно попередньому, доводиться, що паралельні прямі FM, CD, EN ділять сторону AB на рівні відрізки. У свою чергу вони ж ділять AE на три рівних відрізка. Причому від вершини A до перетину медіан два таких відрізка, а після – один.

Один і той же відрізок можна розділити на три рівні частини так, щоб при одному варіанті поділу вони були одного розміру, а при іншому – іншого. Тому точки O і P повинні збігатися. Це означає, що всі три медіани трикутника перетинаються в одній точці.

Щоб довести, що дві інші медіани діляться точкою перетину у співвідношенні 2:1, можна аналогічно попередньому провести паралельні прямі до сторін AB і BC.

« Перетин висот трикутника Симетричні фігури »

moyaosvita.com.ua