Матрица тема по математике – умножение, сложение, вычитание. Как решать, с чего начать

Проект по математике.Тема :»Нумерология.Матрица Пифагора»

Описание слайда:

Человек с числом судьбы 1 обладает задатками лидерства в любой сфере. Он честолюбив и решителен, обладает хорошими организаторскими способностями. Люди с числом судьбы 1 редко бывают подчиненными или исполнителями чужой воли, им больше нравится самим руководить другими людьми. Негативной стороной характера таких людей является сверхчувствительность, они с трудом переносят критику, бывают, склонны к унынию и тщеславию. /Манукян А., Якушева Е./ Дипломатия и тактичность – вот основные качества человека с числом судьбы 2. Благодаря прирожденной дружелюбности, умению сосредотачиваться на главном, такие люди часто успешно продвигаются по служебной лестнице. К негативу характера человека с числом судьбы 2 можно отнести частую перемену настроения и излишнюю чувствительность /Абдурашидова Н, Дычко А, Егорова Н, Тафизова Д/. Люди с числом судьбы 4 напоминают чем — то квадрат с его надежными четырьмя углами и равными сторонами. Расчетливость, практичность и целеустремленность – вот на чем основывается жизнь таких людей. Другой стороной характера человека с числом судьбы 4 может являться его чрезмерная мелочность, чувство ответственности и консерватизм, которые способны тормозить продвижение в делах, а также создавать проблемы в семейной жизни./Кенджаев Р, Марюшкина А, Сибирякова А, Ядгаров Ф/ Людям с числом судьбы 5 характерно прирожденное чувство свободы, которое зовет их на всевозможные приключения, а врожденный ум и неуемная энергия являются залогом того, что они будут происходить постоянно. Их ирония, юмор, а также повышенная чувствительность способны подчинять окружающих людей. Люди с числом судьбы 5 наделены незаурядным умом и изобретательностью, что позволяет им выполнять несколько занятий одновременно. Негативной стороной характера человека с таким числом является его непостоянство, ревность, склонность к унынию и злобность /Сухарев Д/ В нумерологии число судьбы 6 связано неразрывно с умением приспосабливаться, мудростью и дипломатией. Люди с таким числом бескорыстны в своих стремлениях и являются большими ценителями красоты. Гармония во всем — в доме и профессиональной деятельности – вот их кредо. К немногочисленным недостаткам человека с числом судьбы 6 относятся экстравагантность, навязчивое покровительство и, отчасти, мнительность./Прозоров в, Стрельцова А, Якушева К/ Для людей с числом судьбы 7 открыт внутренний мир как ни для кого другого. Они прирожденные философы и мыслители. Многие из них становятся хорошими учителями и писателями. Такие люди часто медлительны и у них находится много времени для отдыха и размышлений. А еще число 7 является мистическим числом, поэтому, люди с таким числом судьбы обладают хорошей интуицией. Их недостатками является склонность к угрюмости, отчужденности и скрытности. /Щёлокова И/ Число судьбы 8 обещает своему обладателю власть, достаток и процветание. Прирожденные организаторские способности помогают таким людям и их семье добиться материального и духовного благополучия. Они очень проницательны, дисциплинированны и хорошо разбираются в людях. Часто становятся борцами за справедливость, так как не терпят ущемления прав других людей. Обратной стороной характера таких людей является их увлечение властью и деньгами. /Волкова А, Джолматов И, Фомина Е, Чурик А/ Судьба человека с числом 9 представляет собой сумму судеб, определяемых всеми другими числами. Поэтому, такие люди наделены всеми присущими другим числам положительными и отрицательными свойствами, что делает их чрезвычайно могущественной личностью в любом смысле слова./Клоус З, Краснов К, Осипова Д, Хачатрян Н, Шарипова У/ Число судьбы.

infourok.ru

Матрицы. Линейные операции над матрицами.

Тема 1.1. Лекция 1. Занятие 1.

Тема: Матрицы. Линейные операции над матрицами.

Матрицейназывается прямоугольная таблица, составленная из чисел или каких-либо других объектов. У матрицы различают элементы, строки и столбцы. В общем виде:

Первый индекс указывает номер строки, а второй номер столбца. Иногда коротко пишут: т.е. I меняется от 1 до m, а j от 1 до n.

Пара чисел называется размерностью матрицы.

Если число строк равно числу столбцов, то матрица называется квадратной, тогда говорят о ее порядке.

Матрица, у которой всего один столбец называется столбцевой, или числовым вектором.

Матрица, у которой всего одна строка называется строчной.

Матрица, у которой все элементы равны нулю, называется нулевой. И обозначается 0.

Квадратная матрица, у которой равны нулю все элементы, кроме, быть может, стоящих на главной диагонали, называется

диагональной.

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной

Иногда применяется транспонирование матрицы А, т.е. перемена ролями ее строк и столбцов, полученную матрицу обозначим .

 

Действия над матрицами.

 

1. Матрицы одинакового размера можно складывать по формуле:

(1)

 

 

2. Матрицы можно умножать на число по формуле:

(2)

 

3. Если число столбцов в первой матрице равно числу строк во второй, то матрицы можно перемножать друг на друга по правилу:

(3)

— получается путем умножения элементов I-той строки первой матрицы на элементы j-того столбца второй и результаты складываются.

Схема умножения матриц: r

 

n

n

m

 

Квадратная матрица имеет определитель, который будем обозначать detА или .

 

Тема 1.1 Лекция 2. Занятие 2

Тема: Определители второго и третьего порядка. Вычисление определителей с применением их свойств.

Выражение называется определителем ( детерминантом) второго порядка и записывается в виде: , (4)

где вертикальные черточки – знак определителя.

Аналогично определитель матрицы третьего порядка: (5)

Это выражение называется определителем третьего порядка .

Данный определитель можно вычислить по правилу треугольника:

 

Главная диагональ и треугольники с основаниями, параллельными главной диагонали со знаком плюс.

побочная диагональ и треугольники с основаниями, параллельными побочной диагонали со знаком минус.

 

 

Определитель третьего порядка имеет три строки (горизонтальные ряды), три столбца

(вертикальные ряды), девять элементов ( числа .

Свойства определителей:

1. Если переставить два параллельных ряда , т.е. две строки или два столбца, то определитель умножится на –1.

2. Если определитель имеет два одинаковых ряда, то он равен нулю.

3. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя.

4. Определитель, имеющий нулевой ряд, равен нулю.

5. Если к каждому из элементов какого-либо ряда прибавить числа, пропорциональные соответствующим элементам какого-нибудь другого ряда, параллельному первому, то значение определителя не изменится.

6. Определитель не меняется, если заменить его строки столбцами и обратно. Это называется транспонированием определителя.

 

Разложение определителя по элементам ряда:

Алгебраическим дополнением к элементу называется определитель, полученный из данного вычеркиванием строки и столбца, в которых находится данный элемент. Но этот определитель надо взять со знаком «+» или «-« , в зависимости от положения данного элемента в исходном определителе: если сумма индексов элемента четна, то берется со знаком «+», если нечетно, то «-«. Обозначается

В определителе (5 ) алгебраическое дополнение элемента равно ,

алгебраическое дополнение элемента равно и т.д.

Имеет место следующее свойство определителей: определитель равен сумме произведений элементов какого-нибудь из рядов на алгебраические дополнения этих элементов.

Например: Разложение определителя по элементам первой строки:

(6)

Обратная матрица.

Обратной к матрице А называется матрица , такая, что .

Квадратная матрица, для которой , называется вырожденной. Вырожденная матрица не имеет обратной, а всякая невырожденная матрица имеет обратную.

Возьмем невырожденную матрицу , тогда обратная будет (7),

где большими буквами А₁……С₃ – обозначены алгебраические дополнения соответствующих элементов в матрице А.

Ранг матрицы.

Вычеркнем из матрицы А несколько строк и столбцов так, чтобы количество оставшихся строк равнялось количеству оставшихся столбцов. Если после этого заменить знак матрицы на знак определителя, то полученный определитель называется минором матрицы АМатрица имеет много миноров, причем некоторые из них могут равняться нулю, а другие отличны от нуля. Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы А

.

Ранг нулевой матрицы, у которой все миноры равны нулю, принимается равным нулю.

Ранг матрицы равен максимально возможному числу ее линейно независимых строк. Матрицу А с помощью элементарных преобразований сводят к ступенчатому виду и посчитают количество строк. Это и будет ранг матрицы.

Элементарные преобразования:

1. меняем местами строки.

2. прибавляем к одной строке другую, умноженную на какое либо число.

3. Отбрасываем нулевые строки.

 

Тема: Векторы на плоскости и в пространстве. Основные понятия.

Векторы на плоскости

Если началом вектора является точка А( ), а концом В( ) , то имеет координаты: = (1)

Над векторами, заданными своими координатами можно производить следующие действия: если и , то (2)

(3)

, где (4)

Вектор

коллинеаренвектору , если их координаты пропорциональны: .

Расстояние между точками и равно (5)

Следовательно длина вектора вычисляется по формуле (6)

Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: ; ; (7)

Если λ=1, то получим формулы для середины отрезка: ; (8)

Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле (10)

Косинус угла между векторами находится по формуле: (11)

Условие перпендикулярности двух векторов:

 

Векторы в пространстве

Если началом вектора является точка А( ), а концом В( ) , то имеет координаты: = (12)

Над векторами, заданными своими координатами можно производить следующие действия: если и , то (13)

(14)

, где (15)

Вектор коллинеаренвектору , если их координаты пропорциональны: .

Расстояние между точками и равно (16)

Следовательно длина вектора вычисляется по формуле (17)

Если отрезок АВ разделен точкой С в отношении АС:СВ=λ. То координаты точки С находятся по формулам: ; ; (18)

Если λ=1, то получим формулы для середины отрезка: ; ; (19) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями координат.

; ; (20)

(21)

Скалярное произведение векторов, заданными своими координатами в пространстве вычисляется по формуле (22)

Косинус угла между векторами находится по формуле: (23)

Условие перпендикулярности двух векторов:

Прямая на плоскости.

Способы задания прямой основаны на аксиомах и теоремах школьного курса. Из школьного же курса известно общее уравнение прямой: .

1. Задание прямой проходящей через точку и имеющую данный угловой коэффициент.

 

Угловым коэффициентом прямойназывается число, равное отношению второй координаты ее направляющего вектора к первой координате

Замечание: Геометрический смысл углового коэффициента имеет смысл только в

ортонормированном базисе: ,

1. Задание прямой проходящей через точку и имеющую данный нормальный вектор.

Всякий вектор, перпендикулярный прямой, называется нормальным вектором прямой.

Если прямая задана общим уравнением , то за нормальный вектор можно принять .

Дано: : .

1. Задание прямой через точку, принадлежащую этой прямой, и направляющий вектор.

Направляющим вектором прямой называется всякий вектор, параллельный этой прямой или лежащий на ней. Если прямая задана общим уравнением , то направляющим вектором является или .

Дано: || каноническое уравнение прямой будет:

— . (13)

4. Задание прямой проходящей через две различные точки.

Дано: .

Условие перпендикулярности прямых:

Угол между пересекающимися прямыми вычисляется по формуле:

Условие параллельности прямых:

Понятие функции

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.

Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу хÎ X сопоставляет один и только один элемент уÎ Y, называется функцией и записывается у=ƒ(х), хÎ X или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.

Например, соответствия ƒ и g, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г — нет. В случае в — не каждому элементу хÎX соответствует элемент уÎY. В случае г не соблюдается условие однозначности.

Множество X называется областью определения функции ƒ и обозначается D(f). Множество всех уÎY называется множеством значений функции ƒ и обозначается Е(ƒ).

Числовые функции. График функции. Способы задания функций

Пусть задана функция ƒ : X→Y.

Если элементами множеств X и Y являются действительные числа (т. е. XÌ R и YÌ R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).

Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.

Частное значение функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х²-3, то ƒ(0)=-3, ƒ(2)=5.

Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.

Например, графиком функции у=√(1-х²) является верхняя полуокружность радиуса R=1 с центром в О(0;0) (см. рис. 99).

Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции у= √(1-х2)является отрезок [-1; 1].

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).

Графический способ: задается график функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.

Преимуществом графического задания является его наглядность, недостатком — его неточность.

Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.

Обратная функция

Пусть задана функция у=ƒ(х) с областью определения D и множеством значений Е. Если каждому значению уєЕ соответствует единственное значение хєD, то определена функция х=φ(у) с областью определения Е и множеством значений D (см. рис. 102).

Такая функция φ(у) называется обратной к функции ƒ(х) и записывается в следующем виде: х=j(y)=f^-1(y).Про функции у=ƒ(х) и х=φ(у) говорят, что они являются взаимно обратными. Чтобы найти функцию х=φ(у), обратную к функции у=ƒ (х), достаточно решить уравнение ƒ(х)=у относительно х (если это возможно).

Примеры:

1. Для функции у=2х обратной функцией является функция х=у/2;

2.Для функции у=х2 хє[0;1] обратной функцией является х=√у;заметим, что для функции у=х², заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению у соответствует два значения х (так, если у=1/4, то х1=1/2, х2=-1/2).

Из определения обратной функции вытекает, что функция у=ƒ(х) имеет обратную тогда и только тогда, когда функция ƒ(х) задает взаимно однозначное соответствие между множествами D и Е. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

Заметим, что функция у=ƒ(х) и обратная ей х=φ(у) изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у=ƒ(х) запишется в виде у=φ(х).

Это означает, что точка M₁(x_o;y_o) кривой у=ƒ(х) становится точкой М₂(у_о;х_о) кривой у=φ(х). Но точки M₁ и М₂ симметричны относительно прямой у=х (см. рис. 103). Поэтому графики взаимно обратных функции у=ƒ(х) и у=φ(х) симметричны относительно биссектрисы первого и третьего координатных углов.

Сложная функция

Пусть функция у=ƒ(u) определена на множестве D, а функция u= φ(х) на множестве D₁, причем для » xÎ D₁ соответствующее значение u=φ(х) є D. Тогда на множестве D ₁ определена функция u=ƒ(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).

Переменную u=φ(х) называют промежуточным аргументом сложной функции.

Например, функция у=sin2x есть суперпозиция двух функций у=sinu и u=2х. Сложная функция может иметь несколько промежуточных аргументов.

Интегрирование по частям

Теорема: Пусть даны две функции и , дифференцируемы на промежутке . Если существует интеграл , следовательно, существует интеграл .

Условно интегралы, берущиеся по частям, можно разбить на группы.

1.

за обозначают то что в скобках, а за все остальное.

2.

за обозначают , а за все остальное.

3. берутся с помощью повторного интегрирования (за u берем ,

за все остальное)

 

 

X

при условии, что сохраняет знак на отрезке

 

Площадь криволинейной трапеции, ограниченной двумя кривыми

и двумя прямыми вычисляется по формуле

 

 

y x=a x=b

0 a b x

Задача вычисления пути.

Материальная точка движется прямолинейно с некоторой мгновенной скоростью . Требуется найти путь, который пройдет тело за промежуток времени от до

Если , то .

Если — функция, то путь , пройденный телом, определяется из равенства

при и при

 

Тема 1.1. Лекция 1. Занятие 1.

Тема: Матрицы. Линейные операции над матрицами.

Матрицейназывается прямоугольная таблица, составленная из чисел или каких-либо других объектов. У матрицы различают элементы, строки и столбцы. В общем виде:

Первый индекс указывает номер строки, а второй номер столбца. Иногда коротко пишут: т.е. I меняется от 1 до m, а j от 1 до n.

Пара чисел называется размерностью матрицы.

Если число строк равно числу столбцов, то матрица называется квадратной, тогда говорят о ее порядке.

Матрица, у которой всего один столбец называется столбцевой, или числовым вектором.

Матрица, у которой всего одна строка называется строчной.

Матрица, у которой все элементы равны нулю, называется нулевой. И обозначается 0.

Квадратная матрица, у которой равны нулю все элементы, кроме, быть может, стоящих на главной диагонали, называется диагональной.

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной

Иногда применяется транспонирование матрицы А, т.е. перемена ролями ее строк и столбцов, полученную матрицу обозначим .

 

Действия над матрицами.

 

1. Матрицы одинакового размера можно складывать по формуле:

(1)

 

 

2. Матрицы можно умножать на число по формуле:

(2)

 

3. Если число столбцов в первой матрице равно числу строк во второй, то матрицы можно перемножать друг на друга по правилу:

(3)

— получается путем умножения элементов I-той строки первой матрицы на элементы j-того столбца второй и результаты складываются.

Схема умножения матриц: r

 

n

n

m

 

Квадратная матрица имеет определитель, который будем обозначать detА или .

 

Тема 1.1 Лекция 2. Занятие 2

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Теоретический материал по математике на тему: «Матрицы»

ЕН.01 Элементы высшей математики Шаповалова Н.В.

МАТРИЦЫ (определение).

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством  n  столбцов. Числа  m  и  n  называются  порядками  или  размерами матрицы.

Матрица порядка m × n записывается в форме =>

или , (i=1,2,…m; j=1,2,…n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

ВИДЫ МАТРИЦ.

Матрица строка: Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой.

Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом.

Нулевая матрица

Если все элементы матрицы равны нулю, то матрица называется нулевой матрицей.

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы.

Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E ⁿ, где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

Главная диагональ матрицы

Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами.

Элементы расположенные на местах a₁₁, a₂₂ ,…, a_nn образуют главную диагональ матрицы.

В случае m×n -матриц элементы

a_ii ( i=1,2,…,min(m,n)) также образуют

главную диагональ.

Побочная диагональ матрицы

Элементы расположенные на местах a_1n, a_2n-1 ,…, a_n1 образуют

побочную диагональ матрицы.

Диагональная

матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю.

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A.

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0.Очевидно, что в качестве матрицы -A следует взять матрицу

(-1)A, элементы которой отличаются от элементов A знаком.

Верхняя треугольная матрица

Квадратная матрица  порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j .

Нижняя треугольная матрица

Квадратная матрица  порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i. Например:

Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(A^T).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) илиN(A).

Кососимметричная

(Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

A^T=−A.

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Транспонирование матрицы — это операция над матрицей, при которой ее строки и столбцы меняются местами:

Интернет-ресурсы:

http://mathprofi.ru/deistviya_s_matricami.html

http://mathprofi.ru/kak_naiti_obratnuyu_matricu.html

http://alik-abdulin.narod.ru/matrixes/matrixes.html

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Умножение матрицы на число

Сложение матриц

Вычитание матриц

Примеры:

Умножение матриц

Транспонирование матриц

Симметричные и антисимметричные матрицы

Степень матрицы

Пусть  квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

A⁰=E, где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1. ДЕЙСТВИЯ НАД МАТРИЦАМИ.

Задание 1: Даны матрицы А и В. Найдите А+В, А-В, ( — А), ( — В), 3А, 15В, А*В, В*А.

Задание 2: Выполните действия над матрицами.

1

4

2

5

3

6

Интернет-ресурсы:

http://oplib.ru/svyaz/view/912715_tema_3_teoriya_predelov

infourok.ru

«Матрицы и действия с ними»

Дисциплина – «Математика»

Курс -2

Семестр -3

Практическая работа №1

Тема: «Матрицы и действия с ними»

Цель: сформировать умение выполнять арифметические действия с матрицами.

Методические указания и теоретические сведения к практической работе

Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:

.

Для обозначения матрицы используют заглавные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись «матрица B имеет размер mxn» означает, что речь идет о матрице, состоящей из m строк и n столбцов.

Например, матрица имеет размер 2x3. Далее, b_ij — обозначение элемента, стоящего на пересечении i-й строки и j—го столбца данной матрицы (в примере b₂₃=5).

При ссылке на i-ю строку матрицы A используют обозначение A_i, при ссылке на j-й столбец – обозначение A_j.

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера nxn называют матрицей n-го порядка. Элементы a₁₁ , a₂₂ ,…, a_nn квадратной матрицы A (размера nxn) образуют главную диагональ.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.

Например, — единичная матрица 4-го порядка.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали треугольной. Например, среди квадратных матриц размера 3x3

, , ,

матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.

Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.

Действия над матрицами.

1. Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):

Пример 1. + =

2. Умножение на число

Чтобы умножить матрицу A на отличное от нуля действительное число k, необходимо каждый элемент матрицы умножить на это число:

.

Пример 2. Найти 2A—B, если , .

Решение. Сначала умножаем матрицу A на число 2, затем матрицу B на число -1, и, наконец, находим сумму полученных матриц:

3. Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А_mxn=(a_ij) на матрицу В_nxp=(b_jk) называется матрица С_mxp=(c_ik) такая, что элемент i-ой строки и k-ого столбца произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-ого столбца матрицы В.

Если матрицы А и В квадратные одного размера, то произведение АВ и ВА всегда существует.

Пример 3. Найти произведение матриц и .

Решение. Размер матрицы A 3x2, матрицы — В 2х2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем:

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается A^T .

Так, если , то .

Если , то .

Пример 4. Найти АВ+С^Т , если

Решение. Воспользовавшись вычислениями примера 3, также правилами умножения матрицы на число и сложения матриц, получим:

АВ+С^Т =.

Практическая работа №1

Тема: «Матрицы и действия с ними»

Содержание практической работы

Вариант 1.

1. Найти сумму и разность матриц А и В, где

2. _{Найти С}^Т_{, где}

3. Найти матрицы:

а) 2А;

б) 8В^Т;

в) 2А+5В;

г) -3А-7,5В, где

4. Найти произведения матриц АВ и ВА, где

5. Найти А³ , где

6. Найти значение матричного многочлена 2А²+3А+5Е, где

7. Доказать равенство (AB)C=A(BC) для матриц:

1) , , ;

2) , , .

Дополнительные задания

8. Выполнить арифметические действия с матрицами:

1) ; 2) ;

3) ; 4) ;

5) ;

6);

7)

_{9. Доказать равенство для матриц (АВ)С=А(ВС)}

, , ;

10. Найти: 1) ; 2) ; 3) .

infourok.ru

Методические рекомендации по математике на тему «Матрицы. Действия с матрицами» для 2 курса

Практическая работа № 1. Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел — матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин «матрица» появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m — строк и n — столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,…, a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц — поэлементная операция

2. Вычитание матриц — поэлементная операция

3. Произведение матрицы на число — поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

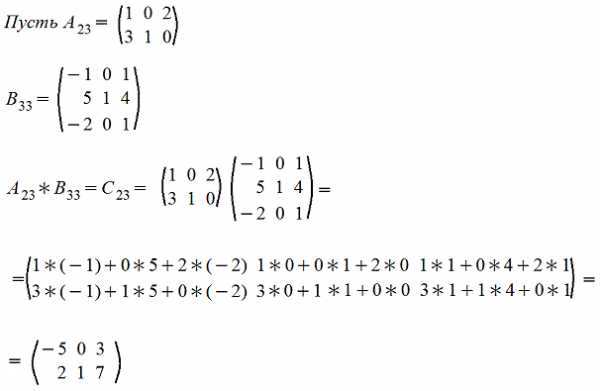
5. Возведение в степень

m>1 целое положительное число. А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A’

Строки и столбцы поменялись местами

Пример

Свойства операций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A’)’=A

(λA)’=λ(A)’

(A+B)’=A’+B’

(AB)’=B’A’

Виды матриц

1. Прямоугольные: m и n — произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) — во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A’=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

Ясно, A’=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji — комплексно — сопряженное к a_ji, т.е. если A=3+2i, то комплексно — сопряженное Ã=3-2i)

Пример

infourok.ru

Готовый кроссворд по математике — на тему «Матрицы»

По горизонтали
3. Есть операция вычисления матрицы c, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго
8. Матрица, полученная из исходной матрицы с заменой строк на столбцы
13. В вычислительной математике матрица, содержащая много нулей. Организовав подходящую структуру данных, вычисления с разреженными матрицами можно проводить очень быстро. Антоним: заполненная
14. Математический объект, записываемый в виде прямоугольной таблицы элементов
16. Как называется данное действие Сложения (a+b)+c=a+(b+c)
21. Если умножить матрицу на неё, то получится единичная матрица
23. Что означает это действие c=a-b
По вертикали
1. Какая матрица прибавление к которой A не изменяет A
2. Метод вычисления детерминанта матрицы 3-го порядка
4. Матрица, при умножении на которую любая матрица остаётся неизменной
5. Что означает это действие сложения a+b=b+a
6. Операция, при которой матрица отражается относительно главной диагонали
7. В вычислительной математике матрица, которая практически не содержит нулей. Такую матрицу приходится хранить в памяти целиком. Антоним: разреженная
8. Матрица, полученная из исходной матрицы с заменой строк на столбцы
9. Назовите вид матрицы по данному действию ab=-ab
10. Многочлен от элементов квадратной матрицы
11. Матрица второго порядка
12. Кому принадлежит фундаментальные результаты в теории матриц
15. Квадратная матрица, все элементы которой кроме диагональных-нулевые
17. Одно из основных понятий линейной алгебры
18. Что означает это действие c=a+b
19. Метод решения линейных уровнений
20. Часть матрицы,находящаяся в вертикальном положении
22. Назовите вид матрицы для решения задач синтеза законов управления. :
23. Матрицы также называют…

spisok-literaturi.ru

Реферат по математике на тему Матрица читать бесплатно

Матрица

Матрицы уже давно стали неотъемлемой частью решения множества математических задач и вопросов. Они представляют собой прямоугольную или квадратную таблицу чисел, в зависимости от количества строк и столбцов в ней. Общепринятое обозначение количества строк в матрице – латинская буква m, и количество столбцов, в свою очередь, обозначается n. Таким образом, если в матрице m=n, значит это квадратная матрица порядка n. С матрицами можно выполнять стандартные алгебраические операции: сложение, вычитание, умножение, деление. Подразумевается как сложение, умножение, вычитание матрицы с одним числом, отличным от нуля и так же все эти операции между двумя матрицами. Однако их можно проделывать не с любыми матрицами, а лишь теми, что соразмерны друг другу. Все эти сведения общеизвестны и широко применяемы. Но существуют так же и другие операции, специфические именно для матриц. Прежде, чем рассказать о них, обратимся к истории и узнаем некоторые факты о возникновении матриц.

История возникновения матриц.

Первые упоминания о матрицах дошли до нас ещё из Древнего Китая, а так же и из работ древних арабских математиков. В те давние времена матрицы называли «волшебными квадратами», и уже тогда стали зарождаться правила сложения двух и более матриц. Уже некоторое время спустя в XXVII в, когда появилась теория определетилей, выдающийся математик Габриэль Крамер опубликовал свое, по сей день известное и используемое «Правило Крамера». Приблизительно в этот же период появился не менее популярный «Метод Гауса». Ну а непосредственно введение самого термина «матрица» — заслуга Джеймса Сильвестра. Термин появился в 1850 году.

Определитель матрицы.
Сущeствует опрeделитель лишь для квадратной матрицы, т е для матрицы, в которой количество строк соответствует количеству столбцов (m=n). Матрицы в математике обозначаются заглавными латинскими буквами (A, B, C), а определители, в свою очередь обозначаются как (det A, det B, det C)

Пример матрицы:

Пример опредeлителя матрицы:

Данное выражение является формулой, по которой вычисляется определитель:

Помимо простых алгебраических операции, над матрицами выполняются и другие специфические действия, для приведения матрицы к наиболее удобному виду для выполнения последующих операций над ней. Рас смотрим некоторые из них.

Транспонирование матриц.
При произведении этой операции матрица меняется таким образом, что первая ее строка заменяется первым столбцом, вторая строка вторым столбцом и так далее. В результате мы получаем, так называемую, транспонированную матрицу, которая обозначается так же, как и обычная матрица, только добавляется индекс T.

Обратная матрица.
Обратная матрица для матрицы А обозначается как А в степени -1. A^-1 При умножении матрицы на обратную ей получается единичная матрица (E), то есть матрица, все элементы которой нули, кроме чисел на главной диагонали (от верхнего левого угла до нижнего правого), которые равны 1.

см. также: Все рефераты по математике

www.sdamna5.ru