Лабораторная работа №4. Реализация пошагового алгоритма решения задачи линейного программирования табличным симплекс-методом средствами Excel при выполнении всех условийЗадание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП. Задача. Решить задачу табличным симплекс-методом [8]. при ограничениях Порядок выполнения работы: I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом в чистом виде.
II. Оформление исходных данных.
Шапка таблицы: столбец базисных переменных (B), столбец свободных членов, имеющиеся переменные. Следующая строка таблицы соответствует первому ограничению. Базисная переменная, найденная в первом ограничении, свободный член, коэффициенты при переменных соответствующего ограничения. Аналогичным образом заполняются 2 и 3 строки. Последняя строка – это строка целевой функции, которая заполняется следующим образом, свободный член без изменения знака, а коэффициенты при переменных с противоположным (рис. 26). Рис. 26. Исходная симплекс таблица.
Рис. 27. Значение целевой функции и начальный опорный план. III. Нахождение оптимального плана и оптимального значения целевой функции.
Рис. 28. Выбор ведущего столбца.
Рис. 29. Составление отношений.
Рис. 30. Результат отношений.
Рис. 31. Выбор ведущей строки.
Рис. 32. Ведущий элемент.
Рис. 33. Новый базис.
Для получения 1 в ячейке С13 необходимо каждый элемент ведущей строки поделить на ведущий элемент. В ячейку С13 запишите формулу = С5/2 (рис 34), нажмите Enter. Рис. 34. Получение 1 в ячейке С13. Рис. 35. Первая строка второй симплексной таблицы. Для этого во второй симплексной таблице 1 (ячейка С13) умножьте на элемент предыдущей таблицы, соответствующий элементу ячейки С14, взятый с противоположным знаком и сложите с этим же элементом. Так как элемент, соответствующий элементу ячейки С14 равен 1 (ячейка С6), то это означает, что все элементы первой строки второй симплексной таблицы умножаются на (-1) и складывается с соответствующими элементами первой симплексной ьаблицы. Запишите в ячейку С14 формулу =C13*(-1)+C6 (рис. 36). Рис. 36. Элемент С14 второй симплексной таблицы. Рис. 37. Элемент С15 второй симплексной таблицы. Рис. 38. Элемент С16 второй симплексной таблицы.
Рис. 39. Первая и вторая симплексные таблицы.
Рис. 40. Значение целевой функции и опорного плана второй симплексной таблицы.
Рис. 41. Первая, вторая и третья симплексные таблицы.
Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad. |
topuch.ru
Алгоритм Симплекс-метода:
1. Преобразовываем неравенства в равенства
2. Находим начальное допустимое базисное решение
3. На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, то процесс закончен.
4. На основе условия допустимости выбираем исключаемая переменная
5. Вычисляем элементы новой ведущей строки
новая ведущая строка = текущая строка/ведущий элемент
6. Вычисляем элементы остальных строк, включая z-строку
новая строка = текущая строка – ее коэффициенты в ведущем столбце * новую ведущую строку
Переходим к шагу 3.
Для удобства записи итерационного процесса все значения записываем в Симплекс-таблицу.
2. Пример решения задачи лп с использованием пакета ms excel
Для многих задач оптимизации удобно применять модель линейного программирования. Суть задачи заключается в составлении системы неравенств, описывающих соответствующие ограничения задачи и задания функции оптимизации.
Для нахождения решения в подобных моделях, можно использовать средство MS EXCEL – ПОИСК РЕШЕНИЯ.
Рассмотрим, как составить модель линейного программирования и найти ее решение на примере.
2.1. Постановка задачи
На трех станках обрабатываются детали двух видов (А и Б), причем каждая деталь проходит обработку на всех станках. Известно время обработки деталей на каждом станке, время работы станков в течение одного цикла производства и прибыль от продажи одной детали каждого вида (данные в таблице). Составить план производства, обеспечивающий наибольшую прибыль.
станки | Время обработки деталей (час) | Время работы станка за цикл производства (час) | |
А | Б | ||
I | 1 | 2 | 16 |
II | 1 | 1 | 10 |
III | 3 | 1 | 24 |
Прибыль на одну деталь (тыс. р) | 4 | 2 | |
2.2. Построение математической модели
Обозначим
через х1 и х2 количество единиц деталей видов А и Б,
планируемое к выпуску. Тогда время
обработки х
х1 +2*х2<=16;
Аналогично для станков II и III получаем неравенства соответственно:
х1 + х2<=10;
3*х1 + х2<=24;
Кроме того, по смыслу определения веденных величин х1 и х2 , должны выполняться условия: х1>=0; х2>=0;
Таким образом, получаем систему неравенств, называемую системой ограничений задачи:
Любое решение (х1; х2) системы ограничений называется планом выпуска продукции или допустимым планом задачи.
Прибыль от реализации х1 единиц деталей вида А равна 4.х1, а прибыль от реализации х2 единиц деталей вида Б равна 2х2. Суммарная прибыль от реализации продукции, выпущенной согласно плану (х1; х2) равна:
F(х1; х2)=4х1+2х2(тыс. руб).
Линейная функция F(х1; х2) называется целевой функцией задачи.
По условию задачи требуется найти такой план (х1; х2) при котором прибыль была бы максимальной.
Таким образом, построена математическая модель задачи как задачи линейного программирования:
F(х1; х2)=4х1+2х2→max
studfiles.net
Лабораторная работа №4. Реализация пошагового алгоритма решения задачи линейного программирования табличным симплекс-методом средствами Excel при выполнении всех условий
Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП.
Поясним последовательность действий при решения задачи ЛП табличным симплекс-методом на примере.
Задача. Решить задачу табличным симплекс-методом [8].
при ограничениях

Порядок выполнения работы:
I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом в чистом виде.
 .
.Задача каноническая.
В каждом ограничении есть базисная переменная:
 — в первом,
— в первом, — во втором,
— во втором, — в третьем.
— в третьем.В целевой функции нет базисных переменных.
II. Оформление исходных данных.
Откройте табличный процессор Excel и введите заголовок Табличный способ решения задач линейного программирования.
Заполните начальную симплекс-таблицу.
Шапка таблицы: столбец базисных переменных (B), столбец свободных членов, имеющиеся переменные.
Следующая строка таблицы соответствует первому ограничению. Базисная переменная, найденная в первом ограничении, свободный член, коэффициенты при переменных соответствующего ограничения. Аналогичным образом заполняются 2 и 3 строки.
Последняя строка – это строка целевой функции, которая заполняется следующим образом, свободный член без изменения знака, а коэффициенты при переменных с противоположным (рис. 26).

Рис. 26. Исходная симплекс таблица.
Проконтролируйте правильность заполнения таблицы. Так как
(5 строка) с ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении
 (столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с  (столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,
(столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с  (столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули.
(столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули.
Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 27).

III. Нахождение оптимального плана и оптимального значения целевой функции.
Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.
Среди отрицательных элементов индексной строки выберите наибольший по модулю элемент. Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 28).

Рис. 28. Выбор ведущего столбца.
Теперь необходимо определить какую переменную исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов (
). Например, в ячейку I5 введите формулу =B5/C5. Растяните формулы для ячеек I6, I7, исключая ячейку индексной строки (рис. 29). )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца (

Рис. 29. Составление отношений.
Определите результат отношений (таблица 5), учитывая, что в результате может получиться число, отличное от нуля, 0 или бесконечность (рис. 30).

Рис. 30. Результат отношений.
Выберите наименьшее из отношений. Строку, в которой получился наименьший результат, назовите ведущей (рис. 31). Данная строка показывает, какую переменную необходимо исключить из базиса.
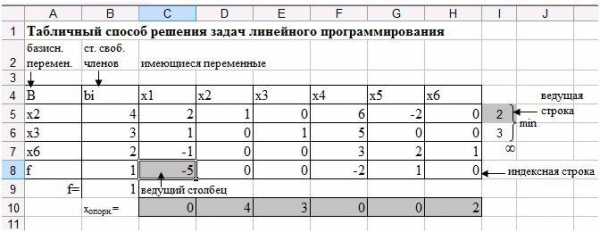
Рис. 31. Выбор ведущей строки.
На пересечении ведущей строки и ведущего столбца получается ведущий элемент (рис. 32).
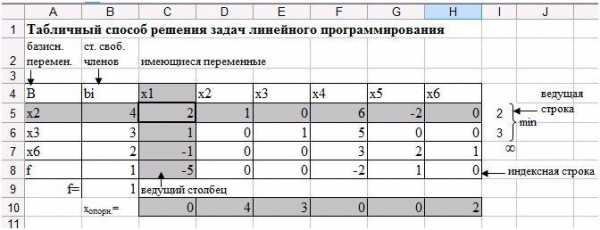
Рис. 32. Ведущий элемент.
Постройте новую симплексную таблицу. Выведите переменную
 из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная .
.

Рис. 33. Новый базис.
Так как теперь
 — базисная переменная, то на пересечении
— базисная переменная, то на пересечении (13
строка)
с
(13
строка)
с  (столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным.
(столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным.
Для получения 1 в ячейке С13 необходимо каждый элемент ведущей строки поделить на ведущий элемент.
В ячейку С13 запишите формулу = С5/2 (рис 34), нажмите Enter.
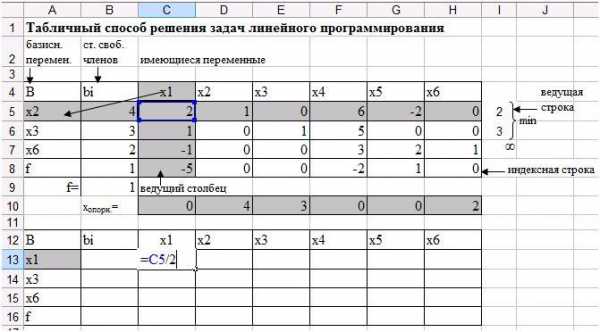
Рис. 34. Получение 1 в ячейке С13.
Растяните формулу (рис. 35).

Рис. 35. Первая строка второй симплексной таблицы.
Затем получите нуль в ячейке С14.
Для этого во второй симплексной таблице 1 (ячейка С13) умножьте на элемент предыдущей таблицы, соответствующий элементу ячейки С14, взятый с противоположным знаком и сложите с этим же элементом.
Так как элемент, соответствующий элементу ячейки С14 равен 1 (ячейка С6), то это означает, что все элементы первой строки второй симплексной таблицы умножаются на (-1) и складывается с соответствующими элементами первой симплексной ьаблицы. Запишите в ячейку С14 формулу =C13*(-1)+C6 (рис. 36).
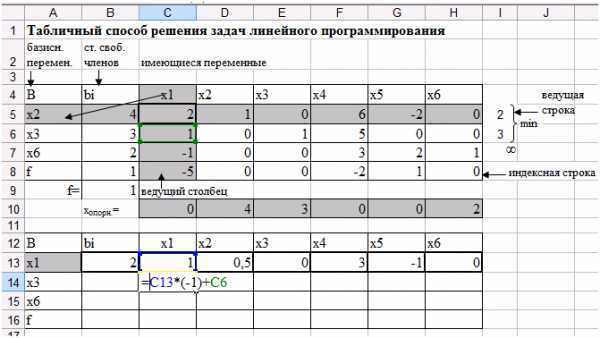
Рис. 36. Элемент С14 второй симплексной таблицы.
Аналогичным образом получите остальные элементы базисного столбца (рис. 37 и рис. 38).

Рис. 37. Элемент С15 второй симплексной таблицы.

Рис. 38. Элемент С16 второй симплексной таблицы.
Растяните формулы базисного столбца по строкам, получите вторую симплексную таблицу (рис. 39).

Рис. 39. Первая и вторая симплексные таблицы.
Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным.
Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 40). Проконтролируйте, что значение целевой функции максимизируется.
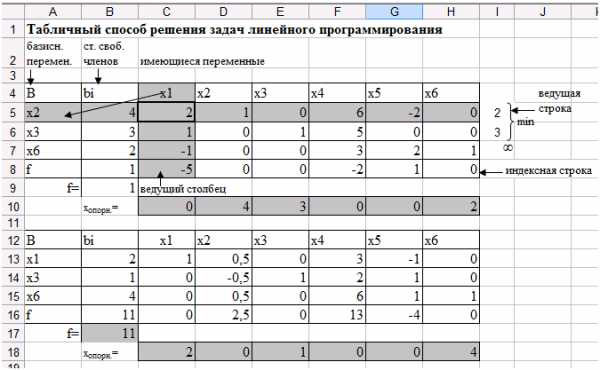
Рис. 40. Значение целевой функции и опорного плана второй симплексной таблицы.
Организуйте процесс улучшения плана, выполнив предложенные шаги, начиная с пункта 5, до тех пор пока не будет выполняться какой-нибудь из критериев остановки. Получите третью симплексную таблицу (рис. 41).

Рис. 41. Первая, вторая и третья симплексные таблицы.
В индексной строке нет отрицательных элементов, поэтому план оптимален,
 .
.
Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.
studfiles.net
Решение задачи линейного программирования графическим методом, симплекс-методом и через «Поиск решения» в Excel ЗАДАНИЕ. кг сырья первого типа, a
Лабораторная работа 1
Лабораторная работа 1 Решение задач линейного программирования графическим методом с использованием MS Excel Цель работы решить задачу линейного программирования графическим методом, с использованием надстройки
ПодробнееЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Исследование операций Определение Операция — мероприятие, направленное на достижение некоторой цели, допускающее несколько возможностей и их управление Определение Исследование операций совокупность математических
ПодробнееЛинейное программирование
Линейное программирование Задача 1… 2 Задача 2… 3 Задача 3… 5 Задача 4… 7 Задача 5… 10 Задача 6… 12 Задача 7… 15 Задача 8… 19 Задача 9… 21 Задача 10… 24 Задача 11… 27 Задача 1. Составить
ПодробнееЭкономико-математические методы и модели.
ИНСТИТУТ МИРОВОЙ ЭКОНОМИКИ И ИНФОРМАТИЗАЦИИ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Экономико-математические методы и модели. МОСКВА — 00 Практические задания
ПодробнееПрактическая работа 5.4.
Практическая работа 5.4. Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры «Поиск решения» Microsoft Excel Цель работы. Выполнив эту работу, Вы научитесь:
ПодробнееИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Краткая теория для выполнения контрольной работы по дисциплине ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ Составление штатного расписания Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей,
ПодробнееГрафическое решение задачи
На приобретение машин для участка выделены 30 т.р. Производственная площадь участка — 70 м 2. Можно закупить машины двух видов: стоимостью 3 т.р. и 5 т.р. олее дорогая машина требует для установки 12 м
ПодробнееГрафическое решение задачи
Решить задачу линейного программирования, где 3x12x2 8 x14x2 10 x1 0 x 2 0 LX3x14x2 max а) геометрическим способом, б) перебором базисных решений, в) симплекс-методом. Графическое решение задачи L X 3×14
Подробнееопределяется матрицей A.
Задание.Мебельная фабрика планирует выпуск двух видов продукции А и Б. Спрос на продукцию не определен, однако можно предполагать, что он может принимать одно из трех состояний (I, II и III). В зависимости
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Ижевский государственный технический университет кафедра САПР МЕТОДИЧЕСКИЕ УКАЗАНИЯ к проведению практических занятий по дисциплине «Системный анализ» на тему
Подробнееизделия j-го вида i 1,
Лабораторная работа 4 Тема работы: Решение задачи об оптимальном распределении ресурсов при выпуске продукции с использованием процедуры Поиск решения Microsoft Excel. Цель работы: Научиться использовать
ПодробнееМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Учреждение образования «Полоцкий государственный университет» МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к практической подготовке по дисциплине «Высшая математика: Математическое программирование» для студентов заочного
ПодробнееКонтрольная работа. F=6*x 1 +3*х 2, (3)
Контрольная работа Задача 5 На предприятии имеется сырье видов 1, 2, 3 Из него можно изготавливать изделия типов А и В Пусть запасы видов сырья на предприятии составляют b 1, b 2, b 3 ед соответственно,
ПодробнееАдрес: г. Воронеж ул. Мичурина, 1, ауд. 124
Министерство сельского хозяйства РФ Воронежский государственный аграрный университет им. К.Д. Глинки Кафедра информационного обеспечения и моделирования агроэкономических систем Контактная информация:
ПодробнееРешение задач исследования операций
Федеральное агентство по образованию Белгородский государственный технологический университет им. В. Г. Шухова Г. Л. Окунева, А. В. Борзенков, С. В. Рябцева Решение задач исследования операций Учебное
ПодробнееМАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ КЕМЕРОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ Г.С. Ветрова, Л.А. Яковлева МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ Учебное пособие для студентов экономических
ПодробнееГУМРФ им. адмирала С.О. Макарова. х х
Постановка задачи Для перевозки изделий, состоящи из дву контейнеров А и В, у компании «Транзит» имеются три транспортны средства разны типов, возможности которы приведены в таблице. Перевозка дву различны
ПодробнееАЛГОРИТМ СИМПЛЕКС-МЕТОДА
АЛГОРИТМ СИМПЛЕКС-МЕТОДА Прежде всего нужно знать, что симплекс-метод является универсальным методом решения задач линейного программирования (ЗЛП) в том смысле, что он позволяет решать ЗЛП с любым количеством
ПодробнееЛинейная алгебра
Линейная алгебра 08.12.2012 Линейные модели в экономике Линейное программирование Линейная алгебра (лекция 13) 08.12.2012 2 / 25 Задача линейного программирования: F (x 1, x 2,…, x n ) = n c j x j max(min),
ПодробнееНелинейная задача оптимизации.
Нелинейная задача оптимизации. Кольцов С.Н 2014 www.linis.ru Задача безусловной оптимизации Задача оптимизации формулируется следующим образом: заданы множество Х (допустимое множество задачи) и функция
Подробнее1.1. Инструмент подбор параметра
Excel 2007. Анализ «что-если» 1. Подбор параметра 1.1. Инструмент подбор параметра 2. Создание сценариев для анализов «что-если» 2.1. Создание сценария 2.2. Просмотр сценария 2.3. Создание итогового отчета
ПодробнееЛабораторная работа 8. Анализ «Что-Если»
1 Лабораторная работа 8. Анализ «Что-Если» Цель работы: освоить начальные навыки экономического анализа данных с помощью специальных инструментов Excel. Задание 1. Рассчитать ежемесячную выплату при изменяющейся
Подробнееdocplayer.ru
Решение симплекс методом задачи ЛП: пример и алгоритм
Симплекс метод — это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений.
Перед тем, как перейти к алгоритму симплекс метода, несколько определений.
Всякое неотрицательное решение системы ограничений называется допустимым решением.
Пусть имеется система m ограничений с n переменными (m n).
Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и n — m неосновных. (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю, основные же переменные, как правило, отличны от нуля, то есть являются положительными числами.
Любые m переменных системы m линейных уравнений с n переменными называются основными, если определитель из коэффициентов при них отличен от нуля. Тогда остальные n — m переменных называются неосновными (или свободными).
Алгоритм симплекс метода
- Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на — 1) и в каждое ограничение ввести дополнительные переменные (со знаком «плюс», если в исходном неравенстве знак «меньше или равно», и со знаком «минус», если «больше или равно»).
- Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
- Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
- Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2.
Важные условия
- Если допустимое базисное решение даёт оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение — не единственное.
- Если в выражении линейной формы имеется неосновная переменная с отрицательным коэффициентом в случае её максимизации (с положительным — в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит также с отрицательными коэффициентами или отсутствует, то линейная форма не ограничена при данной системе ограничений. В этом случае её максимальное (минимальное) значение записывают в виде .
Путём построения симплексных таблиц решить задачу линейного программирования намного проще, чем путём алгебраических преобразований, который показан в следующем параграфе. Симплексные таблицы очень наглядны. Существует несколько разновидностей правил работы с симплексными таблицами. Мы разберём правило, которое чаще всего называется правилом ведущего столбца и ведущей строки.
Будет нелишним открыть в новом окне пособие Действия с дробями: их, дробей в задачах на симплекс-метод, мягко говоря, хватает.
Пример. Найти максимум функции при ограничениях
Решение.
Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Это было сделано с соблюдением следующего правила: если в первоначальном ограничении знак «меньше или равно», то добавочную переменную нужно прибавлять, а если «больше или равно», то добавочную переменную нужно отнимать.
Введённые добавочные переменные принимаем за основные (базисные). Тогда и — неосновные (свободные) переменные.
Выразив основные (базисные) переменные через неосновные (свободные), получим
Функцию цели также выразим через неосновные (свободные) переменные:
Из коэффициентов при переменных (неизвестных) построим первую симплексную таблицу.
| Таблица 1 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Последнюю строку таблицы, в которой записаны функция цели и коэффициенты при свободных переменных в ней, будем называть в индексной строкой.
Полученное решение не оптимально, так как в индексной строке коэффициенты при свободных переменных отрицательны. То есть оптимальным будет то решение, в котором коэффициенты при свободных переменных в индексной строке будут больше или равны нулю.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей таблице найдём наибольшее (по модулю) из чисел и . Это число 2. Поэтому ведущий столбец — тот столбец, в котором записано
Для определения ведущей строки находим минимум отношений свободных членов к элементам ведущего столбца, причём если в числителе положительное число, а в знаменателе отрицательное, отношение считается равным бесконечности.
Итак,
.
Поэтому ведущая строка — та, в которой записано
Ведущим элементом, таким образом, является -2.
Составляем вторую симплексную таблицу.
Новый базисный элемент вписываем первой строкой, а столбец, в котором стояло , вписываем новую свободную переменную
Заполняем первую строку. Для этого все числа, стоящие в ведущей строке таблицы 1, делим на ведущий элемент и записываем в соответствующий столбец первой строки таблицы 2, кроме числа, стоящего в ведущем столбце, куда записывается величина, обратная ведущему элементу (то есть, единица, делённая на ведущий элемент).
Заполняем столбец вспомогательных коэффициентов. Для этого числа ведущего столбца таблицы 1, кроме ведущего элемента, записываем с противоположными знаками в графу вспомогательных коэффициентов таблицы 2.
| Таблица 2 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Кто ещё не открыл в новом окне пособие Действия с дробями, может сделать это сейчас, поскольку самое время.
Для получения остальных строк таблицы 2 числа, уже стоящие в первой строке этой таблицы, умножаем на вспомогательный коэффициент, стоящий в заполняемой строке, и к результату прибавляем число из таблицы 1, стоящее в той же строке при соответствующей переменной.
Например, для получения свободного члена второй строки число 1 умножаем на 1 и прибавляем из таблицы 1 число -4. Получаем -3. Коэффициент при во второй строке находим так же: . Так как в предыдущей таблице отсутствует столбец с новой свободной переменной , то коэффициент второй строки в столбце новой свободной переменной будет (то есть из таблицы 1 прибавляем 0, так как в таблице 1 столбец с отсутствует).
Так же заполняется и индексная строка:
Полученное таким образом решение вновь не оптимально, так как в индексной строке коэффициенты при свободных переменных вновь отрицательны.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей симплексной таблице найдём наибольшее (по модулю) из чисел и , то есть, модулей коэффициентов в индексной строке. Это число 2. Поэтому ведущий столбец — тот столбец, в котором записано .
Для поиска ведущей строки найдём минимум отношений свободных членов к элементам ведущей строки. Получаем:
.
Следовательно, ведущая строка — та, в которой записано , а ведущим элементом является -3/2.
Составляем третью симплексную таблицу
Новую базисную переменную записываем первой строкой. В столбец, в котором было , вписываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
| Таблица 3 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | -1/2 |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |
Вычисление остальных строк на примере второй строки:
Полученное решение вновь не оптимальное, поскольку коэффициенты при свободных неизвестных в индексной строке вновь отрицательные.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к четвёртой симплексной таблице найдём наибольшее из чисел и . Это число .
Следовательно, ведущий столбец — тот, в котором записано .
Для нахождения ведущей строки найдём минимум модулей отношений свободных членов к элементам ведущего столбца:
.
Поэтому ведущая строка — та, в которой записано , а ведущий элемент 1/3.
В четвёртой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Вычисление остальных строк на примере второй строки:
Полученное решение так же не оптимально, но оно уже лучше предыдущих, так как один из коэффициентов при свободных переменных в индексной строке неотрицателено.
Для улучшения плана перейдём к следующей симплексной таблице.
Найдём наибольшее из чисел 4 и . Это число 4. Следовательно, ведущий столбец .
Для нахождения ведущей строки найдём
.
Следовательно, ведущая строка — та, в которой записано . Но и уже были вместе среди свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой ведущий столбец — тот, в котором записано .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для нахождения ведущей строки найдём
.
Следовательно, ключевая строка — та, в которой записано , а ведущий элемент 1.
В пятой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Попробуем сразу узнать, не является ли решение оптимальным. Поэтому для остальных строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Свободные члены:
— во второй строке ;
— в третьей строке ;
— в четвёртой строке .
Индексная строка:
Смотрим в симплексную таблицу 5. Видим, что получено оптимальное решение, так как коэффициенты при свободных неизвестных в индексной строке неотрицательны.
Ответ:
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс методом.
Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе. Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию цели в виде , так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий оптимальности, будет модифицирован следующим образом.
Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.
Пример. Найти максимум функции при ограничениях
Решение.
Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и — неосновные переменные.
Выразив основные переменные через неосновные, получим
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.
Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести и , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).
Попробуем перевести в основные переменную . Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при . Имеем . Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную , которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.
Если же перевести в основные переменную , то наименьшее отношение свободных членов к коэффициентам при составит . Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг II.
Основные переменные , неосновные переменные .
Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим
Следовательно, имеем новое базисное решение , которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).
От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевести и . Переведём в основные переменные . Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при . Имеем . Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.
В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции — бесконечность и когда система не имеет ни одного решения.
Шаг III.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Новое базисное решение имеет вид . Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим . Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при переменная и поэтому перейдёт в число неосновных.
В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение — не единственное.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг IV.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через те же неосновные переменные, примет вид . Продолжим перебор для поиска максимума.
Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная является основной. Находим . Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная и переходит в число неосновных.
Шаг V.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение является оптимальным, а максимум линейной формы
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Начало темы «Линейное программирование»
Продолжение темы «Линейное программирование»
Поделиться с друзьями
function-x.ru
Симплекс-метод, примеры решения задач
Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. Первая задача содержит знаки неравенства только » ≤ » (задача с начальным базисом), вторая может содержить знаки » ≥ «, » ≤ » или » = » (задача с искусственным базисом), они решаются по разному.
Симплекс-метод, решение задачи с начальным базисом
1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений » ≤ «).
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является системой с базисом (базис s1, s2, s3, каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 — свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: -система ограничений должна быть системой уравнений с базисом; -свободные члены всех уравнений в системе должны быть неотрицательны.
Полученная система — система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь «БП» означает столбец базисных переменных, «Решение» — столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.
симплекс-метод итерация 0
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | -6 | 0 | 0 | 0 | 0 | — |
s1 | 2 | 1 | 1 | 0 | 0 | 64 | 64/1=64 |
s2 | 1 | 3 | 0 | 1 | 0 | 72 | 72/3=24 |
s3 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Для улучшения решения перейдем к следующей итерации симплекс-метода, получим следующую симплекс-таблицу. Для этого надо выбрать разрешающий столбец, т.е. переменную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x2 (коэффициент -6).
Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца «Решение» к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 20).
Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следовательно, на следующей итерации симплекс-метода переменная x2 заменит в базисе s1. Заметим, что в z-строке отношение не ищется, там ставится прочерк » — «. В случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.
Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований — превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).
1)Вычисление строки х2 таблицы «Итерация 1». Сначала делим все члены разрешающей строки s3 таблицы «Итерация 0» на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x2 в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s3 таблицы «Итерация 0» будет совпадать со строкой х2 таблицы «Итерация 1». Строку x2 таблицы «Итерации 1» мы получили 0 1 0 0 1 20, остальные строки таблицы «Итерация 1» будут получены из этой строки и строк таблицы «Итерация 0» следующим образом:
2) Вычисление z-строки таблицы «Итерация 1». На месте -6 в первой строке (z-строке) в столбце х2 таблицы «Итерация 0» должен быть 0 в первой строке таблицы «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на 6, получим 0 6 0 0 6 120 и сложим эту строку с первой строкой (z — строкой) таблицы «Итерация 0» -4 -6 0 0 0 0, получим -4 0 0 0 6 120. В столбце x2 появился ноль 0, цель достигнута. Элементы разрешающего столбца х2 выделены красным цветом.
3) Вычисление строки s1 таблицы «Итерация 1». На месте 1 в s1 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.
4) Вычисление строки s2 таблицы «Итерация 1». На месте 3 в s2 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -3, получим 0 -3 0 0 -3 -60 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 1 3 0 1 0 72, получим строку 1 0 0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице «Итерация 1» стал единичным, он содержит одну 1 и остальные 0.
Строки таблицы «Итерация 1» получаем по следующему правилу:
Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).
Например для z-строки имеем:
Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).
Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.
симплекс-метод итерация 1
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | 0 | 0 | 0 | 6 | 120 | — |
s1 | 2 | 0 | 1 | 0 | -1 | 44 | 44/2=22 |
s2 | 1 | 0 | 0 | 1 | -3 | 12 | 12/1=12 |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | — |
Разрешающий столбец х1, разрешающая строка s2, s2 выходит из базиса, х1 входит в базис. Совершенно аналогично получим остальные симплекс-таблицы, пока не будет получена таблица со всеми положительными коэффициентами в z-строке. Это признак оптимальной таблицы.
симплекс-метод итерация 2
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 0 | 4 | -6 | 168 | — |
s1 | 0 | 0 | 1 | -2 | 5 | 20 | 20/5=4 |
x1 | 1 | 0 | 0 | 1 | -3 | 12 | — |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Разрешающий столбец s3, разрешающая строка s1, s1 выходит из базиса, s3 входит в базис.
симплекс-метод итерация 3
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 6/5 | 8/5 | 0 | 192 | — |
s3 | 0 | 0 | 1/5 | -2/5 | 1 | 4 | — |
x1 | 1 | 0 | 3/5 | -1/5 | 0 | 24 | — |
x2 | 0 | 1 | -1/5 | 2/5 | 0 | 16 | — |
В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1 = 24, x2 = 16, zmax = 192.
studfiles.net
Лабораторная работа №5. Реализация пошагового алгоритма решения задачи линейного программирование методом искусственного базиса (м-методом) средствами Excel
Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП табличным симплекс-методом, применяя метод искусственного базиса.
Поясним последовательность действий при решения задачи ЛП методом искусственного базиса (М-методом) на примере.
Задача. Решить задачу табличным симплекс-методом [8].
при ограничениях

Порядок выполнения работы:
I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом.
 .
.Задача не является канонической, приведите ее к канонической форме.
Переведите исходную функцию на максимум.
Избавьтесь от неравенств во втором и третьем ограничении способом, указанным в 2.1.
В ограничениях 1 и 2 есть базисные переменные:
 — в первом,
— в первом, — во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод.
— во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод.
Составьте расширенную задачу, добавив искусственные переменные к тем ограничениям, где нет базисных переменных.
Расширенная задача:
,
В целевой функции расширенной задачи есть базисные переменные. Выполните условие, выразив базисные переменные
 и
и через небазисные. Подставьте выражения
в целевую функцию.
через небазисные. Подставьте выражения
в целевую функцию.
,
.
Таким образом, получите задачу линейного программирования, для которой выполняются все 4 условия.
,
II. Оформление исходных данных.
Откройте табличный процессор Excel и введите заголовок Метод искусственного базиса.
Заполните начальную симплекс-таблицу, таким же образом как в лабораторной работе №4, добавив в нее столбец для переменной
 и
и -строку
(рис. 42).
-строку
(рис. 42).
Рис. 42. Исходная симплекс таблица.
Проконтролируйте правильность заполнения таблицы. Так как
 ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении (5
строка)
с
(5
строка)
с  (столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с  (столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,
(столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с  (столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули.
(столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули.
Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 43).
Рис. 43. Значение целевой функции и начальный опорный план.
III. Нахождение оптимального плана и оптимального значения целевой функции.
Так в индексной строке есть отрицательный коэффициент при переменной, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.
В индексной строке найдите отрицательные элементы. Составьте выражения, учитывая
 -строку.
Получите.
-строку.
Получите.
В данном случае
один отрицательный элемент – это
выражение
,
которое соответствует переменной .
.
Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 44).
Рис. 44. Ведущий столбец.
Определите какую переменную необходимо исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов (
 )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца ( ).
Найдите ведущую строку и ведущий элемент
(рис. 45).
).
Найдите ведущую строку и ведущий элемент
(рис. 45).
Рис. 45. Ведущая строка и ведущий столбец.
Постройте новую симплексную таблицу. Выведите переменную
 из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной .
Значения столбца
.
Значения столбца можно удалить, так как переменная вышла
из базиса (рис. 46).
можно удалить, так как переменная вышла
из базиса (рис. 46).

Рис. 46. Первая и вторая симплексные таблицы.
Так как в
 -строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция
-строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция (рис. 47).
(рис. 47).
Рис. 47. Симплексная таблица.
В индексной строке есть отрицательные коэффициенты при переменных, опорный план не является оптимальным.
Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 48). Проконтролируйте, что значение целевой функции максимизируется.
Организуйте процесс улучшения плана, выполнив те же шаги, до тех пор, пока не будет выполняться какой-нибудь из критериев остановки, получите новую таблицу (рис. 48).

Рис. 48. Симплексные таблицы.
В индексной строке нет отрицательных элементов, поэтому план оптимален,
 .
Так как в исходной задаче функция
стремится к минимуму, то
.
Так как в исходной задаче функция
стремится к минимуму, то
Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.
studfiles.net

 .
.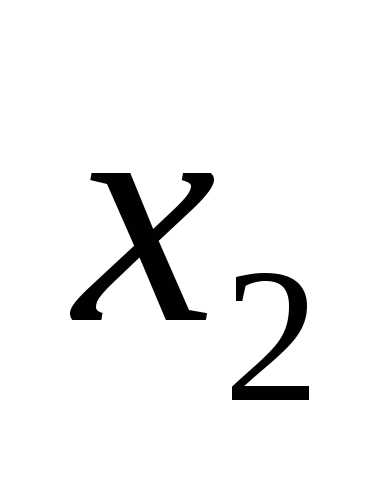 — в первом,
— в первом, — во втором,
— во втором, — в третьем.
— в третьем. ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении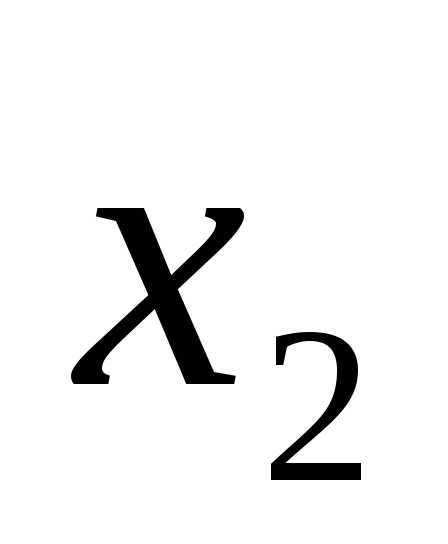
 (столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с  (столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,
(столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с  (столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули.
(столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули. )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца (
 из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная .
. — базисная переменная, то на пересечении
— базисная переменная, то на пересечении (13
строка)
с
(13
строка)
с  (столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным.
(столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным. .
. .
. — в первом,
— в первом, — во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод.
— во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод. и
и через небазисные. Подставьте выражения
в целевую функцию.
через небазисные. Подставьте выражения
в целевую функцию. и
и -строку
(рис. 42).
-строку
(рис. 42). ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении (5
строка)
с
(5
строка)
с  (столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с 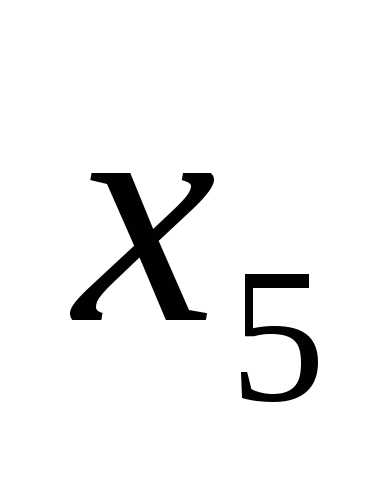 (столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,
(столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с 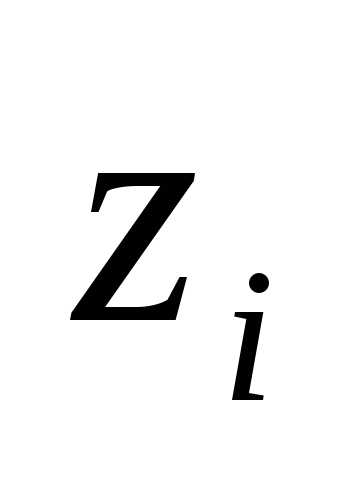 (столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули.
(столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули. -строку.
Получите.
-строку.
Получите. )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца ( ).
Найдите ведущую строку и ведущий элемент
(рис. 45).
).
Найдите ведущую строку и ведущий элемент
(рис. 45). из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной .
Значения столбца
.
Значения столбца можно удалить, так как переменная вышла
из базиса (рис. 46).
можно удалить, так как переменная вышла
из базиса (рис. 46). -строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция
-строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция (рис. 47).
(рис. 47). .
Так как в исходной задаче функция
стремится к минимуму, то
.
Так как в исходной задаче функция
стремится к минимуму, то