Сложение числа и матрицы – умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Сложение матриц онлайн

умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Сложение и вычитание матриц

Сложение и вычитание матриц, умножение матриц на число в MS EXCEL. Примеры и методы

Билет 2. Сложение матриц и умножение матрицы на число, свойства этих операций.

Глава 2.2. Матрицы и определители §2.2.1. Сложение матриц и умножение матрицы на число

умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Сложение матриц онлайн

умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Сложение и вычитание матриц

Сложение и вычитание матриц, умножение матриц на число в MS EXCEL. Примеры и методы

Билет 2. Сложение матриц и умножение матрицы на число, свойства этих операций.

Глава 2.2. Матрицы и определители §2.2.1. Сложение матриц и умножение матрицы на число

2. Определители 2-го и 3-го порядков. Свойства определителей.

Сложение матриц

2. Определители 2-го и 3-го порядков. Свойства определителей.

Умножение матрицы на число

Умножение матриц

Умножение матриц на число

Свойства операций сложения матриц и умножения на число:

Билет 3. Умножение матриц, свойства умножения (доказать ассоциативность).

Свойства умножения матриц:

§2.2.2 Умножение матриц

2. Определители 2-го и 3-го порядков. Свойства определителей.

Сложение матриц

2. Определители 2-го и 3-го порядков. Свойства определителей.

Умножение матрицы на число

Умножение матриц

Умножение матриц на число

Свойства операций сложения матриц и умножения на число:

Билет 3. Умножение матриц, свойства умножения (доказать ассоциативность).

Свойства умножения матриц:

§2.2.2 Умножение матриц

Добавить комментарий Отменить ответ

Свойства сложения матриц:

Свойства сложения матриц:

Вы также можете

Вы также можете

Содержание

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В c_ij = a_ij + b_ij Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется

матрица В, такая что

b_ij = k × a_ij. В = k × A b_ij = k × a_ij. Матрица — А = (-1) × А называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А — А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С — матрицы, α и β — числа.

Умножение матриц (Произведение матриц):

ik = a_i1 × b_1k + a_i2 × b_2k + … + a_in × b_nk, т. е. находиться сумма произведений элементов i — ой строки матрицы А на соответствующие элементы j — ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е — единичная матрица того же размера.

Свойства умножения матриц:

Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких — либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой

матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)^Т = В^ТА^Т; 7. (АВС)^Т = С^ТВ^ТА^Т; 8. (А + В)^Т = А^Т + В^Т;

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца

матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда

определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы:

studfiles.net

Сложение матриц А и В – это нахождение такой матрицы С, все элементы которой представляют собой сложенные попарно соответствующие элементы исходных матриц А и В. Складывать допускается только матрицы одинаковой размерности (допустим m × n), т.е. имеющие равное количество строк и равное количество столбцов.

Таким образом, математически сумма матриц выглядит так:

А_m×n + B_m×n = C_m×n

Каждый элемент искомой матрицы равен сумме соответствующих элементов заданных матриц:

c_ij = a_ij + b_ij,

где i принимает значение от 1 до m, j имеет значения от 1 до n.

Рассмотрим пример сложения двух матриц размера 2 × 3.
Даны две матрицы:

Найти сумму матриц А и В.
Решение:

Коммутативность – переместительный математический закон, согласно которому результат сложения матриц не зависит от их перестановки.
A + В = В + А
Ассоциативность – сочетательный математический закон, согласно которому результат сложения матриц не зависит от последовательности расстановки скобок.
А + (В + С) = (А + В) + С
Сложение с нулевой матрицей – для любой матрицы существует нейтральный элемент, которым является нулевая матрица, сложение с которым не изменяет исходную матрицу.
Нулевая матрица O – матрица, все элементы которой имеют нулевое значение.
А + О = А
Существование противоположной матрицы – для ненулевой матрицы А всегда существует матрица –А, суммой которых является нулевая матрица.
А + (-А) = О

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x

(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.

www.yotx.ru

Сложение матриц:

Умножение матрицы на число:

b_ij = k × a_ij. В = k × A b_ij = k × a_ij. Матрица — А = (-1) × А называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А_m×n на матрицу В_n×p, называется матрица С_m×p такая, что с_ik = a_i1 × b_1k + a_i2 × b_2k + … + a_in × b_nk, т. е. находиться сумма произведений элементов i — ой строки матрицы А на соответствующие элементы j — ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е — единичная матрица того же размера.

Свойства умножения матриц:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Следствие:

Свойство № 2:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Свойство № 5:

Свойство № 6:

Свойство № 7:

Пример применения свойств для вычисления определителя матрицы:

studfiles.net

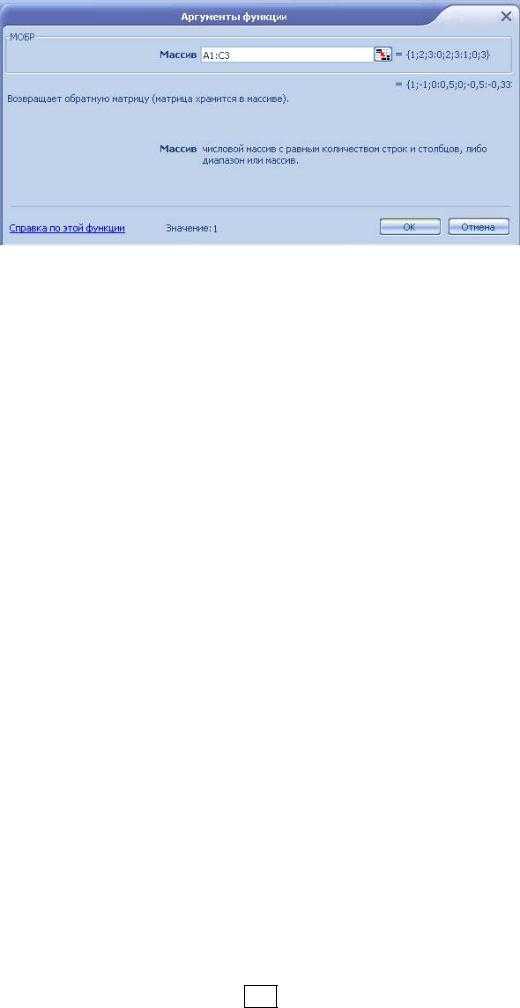
Рис П1.4. Пример заполнения диалогового окна МОБР

5.Если обратная матрица не появилась в диапазоне А5:С7, то следует щелкнуть указателем мыши в строке формул и повторить нажатие

CTRL+SHIFT+ENTER.

Врезультате в диапазоне А5:С7 появится обратная матрица:

1	-1	0
0,5	0	-0,5

-0,33333	0,33333	0,33333

Складывать (вычитать) можно только матрицы одного размера. Суммой
матриц A = (aij )	и B= (bij )	размера m ×n называется матрицаC = A + B , эле-
менты которой	cij= aij+ bij	для i= 1,2,…,m;			j = 1,2,…,n		(то есть матрицы
складываются поэлементно). Например, если:
		1	2	7
		A =	− 1	13	;
		9	− 1	13
		0	− 4	− 3
		B =	19
то C= A+ B:		5	19	31
то C= A+ B:	1 + 0	2 − 4 7− 3		1		− 2	4
	1 + 0	2 − 4 7− 3		1		− 2	4
C =		− 1 +19	13 + 31	=		18
	9 + 5	− 1 +19	13 + 31		14	18	44

В частном случае A + 0 = A .

Аналогично определяется разность двух матриц C = A − B .

В MS Excel для выполнения операций суммирования и вычитания матриц могут быть использованы формулы, вводимые в соответствующие ячейки.

Пример 4. Пусть матрицаA из рассмотренного примера, введена в диапазонА1:С2, а матрицаB – в диапазонА4:С5. Необходимо найти матрицуC , являющуюся их суммой.

Решение

1.Табличный курсор установите в левый верхний угол результирующей матрицы, например в А7.

2.Введите формулу для вычисления первого элемента результирующей матрицы =А1 + А4 (предварительно установив английскую раскладку клавиатуры).

3.Скопируйте введенную формулу в остальные ячейки результирующей матрицы: установите табличный курсор в ячейку А7; наведите указатель мыши на точку в правом нижнем углу ячейки, так чтобы указатель мыши принял вид тонкого крестика; при нажатой левой кнопке мыши протяните указатель до ячейкиС7; затем так же протяните указатель мыши до ячейкиС8.

Врезультате в ячейках А7:С8 появится матрица, равная сумме исходных матриц.

Подобным же образом вычисляется разность матриц, только в формуле для вычисления первого элемента вместо знака + ставится знак-.

C = A+ B=		1	− 2	4
C = A+ B=		14	18
		14	18	44
1			6	10
C = A− B=	4		− 20	− 18
	4		− 20	− 18

Произведением матрицы A на числоk называется матрицаB = k A, элементы которойbij = k aij дляi = 1,2,…,m ;j = 1,2,…,n . Иначе говоря, при ум-

ножении матрицы на постоянную каждый элемент этой матрицы умножается на эту постоянную: k Aij = (k aij ).

Например, для матриц A иB из предыдущего параграфа:

	1	0,5		1	3,5
		A =				;
2				− 0,5	6,5
		4,5
			0	8	6
−2 B=			−10	− 38	− 62

Вчастности, произведение матрицы A на число0 есть нулевая матрица, то есть0 A = 0 .

ВMS Excel для выполнения операции умножения матрицы на число могут быть использованы формулы, вводимые в соответствующие ячейки.

Пример 5. Пусть, как и в предыдущем параграфе (пример 4) матрицаA введена в диапазоныА1:С2. Необходимо получить матрицуC = 3 × A.

Решение

1.Табличный курсор поставьте в левый верхний угол результирующей матрицы, например в Е1.

2.Введите формулу для вычисления первого элемента результирующей матрицы =3*А1 (предварительно установив английскую раскладку клавиатуры).

3.Скопируйте введенную формулу в остальные ячейки результирующей матрицы: поставьте табличный курсор в ячейку Е1; наведите указатель мыши на точку в правом нижнем углу ячейки, так чтобы указатель мыши принял вид тонкого крестика; при нажатой левой кнопке мыши протяните указатель до ячейкиG1; таким же образом протяните указатель мыши до ячейкиG2.

Врезультате в ячейках E1:G2 появится матрица, равная исходной матрице, умноженной на постоянную –3.

	3	6	21
3 A =	27	− 3	39

Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй.

Пусть A = (aij )m ×n ,B = (bij )n × p , тогда размерность произведенияA× B равнаm × p .

При этом матрица C (размераm × p ) называется произведением матрицA иB , если каждый ее элементcij равен сумме произведений элементовi -йстроки матрицыA на соответствующие элементыj -гостолбца матрицыB :

cij= ai 1b1 j+ ai 2	b2 j+ …+ aipbpj= ∑p		aikbkj;		i = 1,2,…,m;	j = 1,2,…,n.
		k=1
Таким образом, перемножение матриц осуществляется по следующему
правилу:
1 стр 1 стб		1 стр 2 стб		L	1 стр p стб
	2 стр 1 стб	2 стр 2 стб		L	2 стр p стб
C = A B=	2 стр 1 стб	2 стр 2 стб		L	2 стр p стб
	L	L		L	L
		m стр 1 стб
m стр 1 стб		m стр 1 стб		L m стр p стб

Пусть, например,

	1		3	4	2	1	3
						2	2
C = A B=		3 2 0			−1			=
						10	0
		0	1	−1 2
						12	−1

Многие свойства, присущие операциям над числами, справедливы и для операций умножения матриц (что следует из определений этих операций).

Для матриц верны общие свойства операции умножения:

1.A (B C )= (A B) C – ассоциативность.

2.A (B + C )= A B + A C – дистрибутивность.

3.(A+ B) C= A C+ B C.

4.(α A) B = A (α B)=α (A B),α – константа.

Однако имеются и специфические свойства операций умножения матриц.

5.Умножение матриц не коммутативно – A B ≠ B A.

Вчастном случае коммутативным законом обладает произведение любой квадратной матрицы A n-гопорядка на единичную матрицуE того же порядка, причем это произведение равноA .

6.Если E – единичная матрица, тоE A = A;B E = B .

Таким образом, единичная матрица играет при умножении ту же роль, что и число 1 при умножении чисел.

7. Из того, что A B = 0 , не следует, чтоA = 0 илиB = 0 .

В алгебре матриц нет действия деления. Выражение A / B не имеет смысла. Его заменяют два различных выраженияB−1 A иA B−1 если существуетB−1 . Для квадратных матриц возможна операция возведения в степень. По определению полагают, чтоA0 = E иA1 = A . Целой положительной степеньюAm (m > 1) квадратной матрицыA называется произведениеm матриц, равныхA , то есть:

Am = A A … A

14243

m раз

Для нахождения произведения двух матриц в Excel используется функция МУМНОЖ, которая вычисляет произведение матриц (матрицы хранятся в массивах).

Функция имеет вид МУМН0Ж(массив1;массив2). Здесь массив1и мас-

сив2 – это перемножаемые массивы. При этом количество столбцов аргументамассив1 должно быть таким же, как количество строк аргументамассив2, и оба массива должны содержать только числа. Результатом является массив с таким же числом строк, какмассив1 и с таким же числом столбцов, какмассив2.

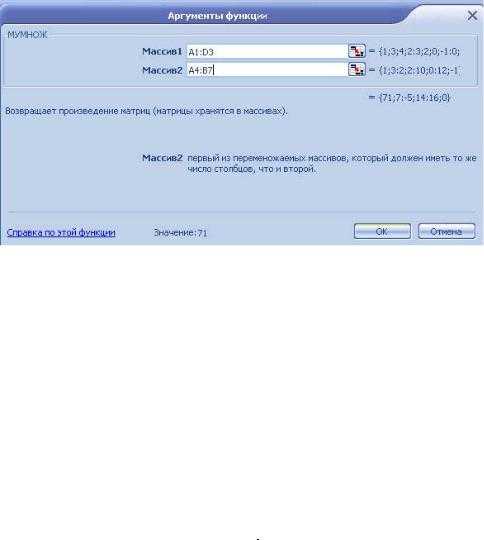
Массив C , который является произведением двух массивовA иB , определяется следующим образом:C = (∑aij bij ), гдеi – номер строки, aj – но-

мер столбца.

Пример 6. Пусть матрицаA из рассмотренного примера введена в диапазонA1:D3, а матрицаB – в диапазонА4:В7. Необходимо найти произведение этих матрицC .

Решение:

1.Выделите блок ячеек под результирующую матрицу. Для этого требуется найти размер матрицы-произведения.Ее размерность будетm × p , в данном примере3 × 2 . Например, выделите блок ячеекF1:G3 (указателем мыши при нажатой левой кнопке).

2.Нажмите на панели инструментов Стандартная кнопкуВставка функ-

ции.

3.В появившемся диалоговом окне Мастер функций в полеКатегория вы-

берите Математические, а в полеФункция – имя функцииМУМНОЖ.

После этого щелкните на кнопке ОК.

4.Появившееся диалоговое окно МУМНОЖ мышью отодвиньте в сторону от исходных матриц и введите диапазон исходной матрицыA –A1:D3 в рабочее полеМассив1 (указателем мыши при нажатой левой кнопке), а диапазон матрицыB –А4:В7 введите в рабочее полеМассив2 (рис. П1.5). После этого нажмите сочетание клавишCTRL+SHIFT+ENTER.

Рис. П1.5. Пример заполнения рабочих полей диалогового окна МУМНОЖ

5.Если произведение матриц A× B не появилось в диапазонеF1:G3, то следует щелкнуть указателем мыши в строке формул и еще раз нажать комби-

нацию клавиш CTRL+SHIFT+ENTER.

Врезультате в диапазоне F1:G3 появится произведение матриц:

	71		7
		−5 14
C = A B=		−5 14		.
		16	1
		16	1

	67

studfiles.net

В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.

Операция сложения определена только для матриц одного порядка. Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.

Сумма двух матриц А и В — это матрица, элементы которой равны сумме соответствующих элементов матриц А и В.

В MS EXCEL операцию сложения матриц реализовать элементарно.

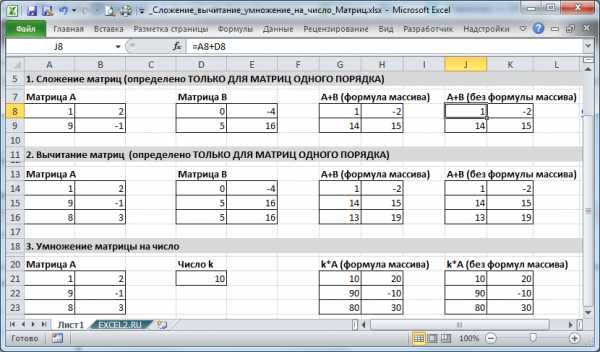
Поместив матрицу А размерности 2х2 в диапазон А8:В9, а матрицу B той же размерности 2х2 в диапазон D8:E9, в ячейке J8 введем формулу =A8+D8. Скопировав формулу в нужные ячейки, например, с помощью Маркера заполнения, получим матрицу А+В.

Аналогичного результата можно добиться с использованием формулы массива. Выделив диапазон G8:H9 в Строке формул введите формулу =A8:B9+D8:E9 и нажмите CTRL+SHIFT+ENTER. Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно Невозможно удалить часть массива).

Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см. файл примера).

Операция умножения матрицы на число определена для матриц любого порядка.

Произведение матрицы А и числа k — это матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.

В MS EXCEL это реализовано с помощью формулы =A21*$D$21 (предполагается, что матрица находится в диапазоне А21:В23, а число в ячейке D21). Обратите внимание, что в формуле использована абсолютная адресация на ячейку с числом. Это позволяет при копировании формулы (для отображения всех элементов матрицы k*А) ссылаться на одну и ту же ячейку с числом.

excel2.ru

Определение 5. Две матрицы , , , и , , , будем называть равными, если .

Краткая запись: .

Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.

Определение 6. Суммой двух матриц , , , и , , , называется такая матрица , , , что .

Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.

Пример 8. Найти сумму матриц

и .

В соответствии с определением 6 найдем

Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.

Определение 7. Произведением матрицы , , , на вещественное число называется такая матрица, , , для которой .

Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.

Пример 9. Найти линейную комбинациюматриц

и .

Пользуясь определением 7, получаем

, ,

далее привлекаем определение суммы матриц (определение 6):

1. Сложение коммутативно: .

2. Сложение ассоциативно:.

3. Существует нулевая матрица , удовлетворяющая условиюдля всехА.

4. Для любой матрицы А существует противоположная матрица В, удовлетворяющая условию .

Для любых матриц А и В и любых действительных чисел имеют место равенства:

5. .

6. .

7. .

8. .

Проверим свойство 1. Обозначим ,. Пусть,,. Имеем

и так как равенство доказано для произвольного элемента, в соответствии с определением 5 . Свойство 1 доказано.

Аналогично доказывается свойство 2.

В качестве матрицы возьмем матрицу порядка, все элементы которой равны нулю.

Сложив с любой матрицейпо правилу, данному в определении 6, мы матрицуне изменим, и свойство 3 справедливо.

Проверим свойство 4. Пусть . Положим. Тогда, следовательно, свойство 4 справедливо.

Проверку свойств 5 — 8 опустим.

Определение 8. Произведением матрицы , , , на матрицу , , , называется матрица , , , с элементами .

Краткая запись: .

Пример 10. Найти произведение матриц

и .

В соответствии с определением 8 найдем

Пример 11. Перемножить матрицы

и .

Имеем

Замечание 1. Число элементов в строке матрицы равно числу элементов в столбце матрицы(число столбцов матрицыравно числу строк матрицы).

Замечание 2. В матрице строк столько же, сколько в матрице, а столбцов столько же, сколько в.

Замечание 3. Вообще говоря, (умножение матриц некоммутативно).

Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.

Пример 12. Перемножим в обратном порядке матрицы ииз примера 10.

таким образом, в общем случае .

Отметим, что в частном случае равенство возможно.

Матрицы и, для которых выполняется равенство, называютсяперестановочными, или коммутирующими.

Умножение дистрибутивно:

, .

2. Умножение ассоциативно: .

Докажем свойство 1. Пусть ,,,,,,,,.

Обозначим ,,,,,,,.

Имеем

и, таким образом, в соответствии с определением 6 , или, возвращаясь к старым обозначениям,. Свойство 1 доказано.

Так как умножение матриц некоммутативно, следовало бы доказать и правую дистрибутивность: . Опустим доказательство, так как оно аналогично приведенному доказательству левой дистрибутивности.

Докажем свойство 2. Пусть ,,,,,,,,.

Обозначим ,,,,,,,,,,,.

Имеем

таким образом, .

Вернемся к старым обозначениям и получим: , т.е. свойство 2 доказано.

Для квадратных матриц справедливо следующее утверждение, которое приведем без доказательства.

Теорема 2. Для любых двух квадратных матриц и

Приведем пример, иллюстрирующий утверждение теоремы 2.

Пример 13. Даны матрицы

и .

Вычислить .

Воспользуемся теоремой 2: .

Найдем произведение непосредственно:

. Следовательно, результаты совпадают.

studfiles.net

Матрицей называется прямоугольная таблица чисел

Можно рассматривать матрицы, элементами которых являются не только числа. Мы ограничиваемся здесь числовыми матрицами для простоты. Элементы матрицы зачитываются так: аодин один,аодин два и т.д. Как видим, элементы матриц располагаются по строчкам и столбцам. Если в матрице m строчек и n столбцов, то будем говорить, что матрица А имеетстроение m x n.Если число строчек и столбцов равно одному и тому же числу n, то матрица называетсяквадратной порядка n. Матрица вида

называется матрицей-строчкой или просто строчкой. Матрица вида

называется матрицей-столбцом или просто столбцом.Две матрицы А и В одного строения

называются равными, если у них все соответствующие элементы равны, т.е.

Возьмем две матрицы А и В одного строения. Матрица С, имеющая такое же строение, называется их суммой, если ее элементы равны суммам соответствующих элементов матриц А и В. Проще говоря, для того, чтобы сложить матрицы, надо сложить их соответствующие элементы

Пример.

Тот факт, что складывать можно только матрицы одного строения, изобразим схематически

Свойства сложения матриц:

А+В = В+А (закон коммутативности сложения),
(А+В)+С = А + (В+С) (закон ассоциативности сложения),
если 0 – нулевая матрица, все элементы которой равны нулю, того же строения, что и строение матрицы А, то А+0=А, 0 +А=А (существование нейтрального элемента относительно сложения).

Разностью В-Аматриц В и А одинакового строения называется матрица С, которую надо прибавить к А, чтобы получить В:

А + С = В, С = В – А.

Разность 0–А обозначается -А, т.е. А + (-А) = О.

Матрица -А называется противоположной матрице А.

Из свойств ассоциативности сложения матриц следует, что имеет смысл сумма трех матриц А₁+ А₂+ А₃= (А₁+ А₂) + А₃и сумма любого конечного числа матриц одного строения А₁+…+ А_n= (А₁+…+А_n-1) +А_n.

Произведением матрицы А на число называется матрица, получающаяся из А умножением всех ее элементов на.

При умножении матрицы на число получается матрица того же строения.

Свойства умножения матрицы на число:

()А =(А),
(+)А =А +А,
(А+В) = А +В,
1А = А,
0А = О,
(-1)А = -А.

Упражнения и задачи

Проверить сформулированные свойства на примерах. Доказать их.
Матрица А^Tназываетсятранспонированной для матрицы А, если ее строчки – это столбцы матрицы А. Доказать, что

(А+В)^T= А^T+В^T, (А)^T=(А)^T.

Произведением строчки на столбецназывается сумма произведений соответствующих элементов

Перемножать можно только строчку на столбец, если они имеют одно и то же число элементов.

Пусть даны две матрицы

причем число столбцов матрицы А равно числу строчек матрицы В.

Произведением матрицы А на матрицу В называется матрица С, у которой на пересечении строчкиi и столбца j находится произведениеi-той строчки матрицы А на j-тый столбец матрицы В, т.е.

Чтобы перемножить две матрицы надо каждую строчку матрицы А умножить на каждый столбец матрицы В. В этом заключается правило: строчка на столбец. Схематически это правило можно изобразить так

Строения перемножаемых матриц связаны условием: число столбцов первого сомножителя равно числу строчек второго. Тогда число строчек произведения равно числу столбцов второго сомножителя. Изобразим это схематически:

Пример.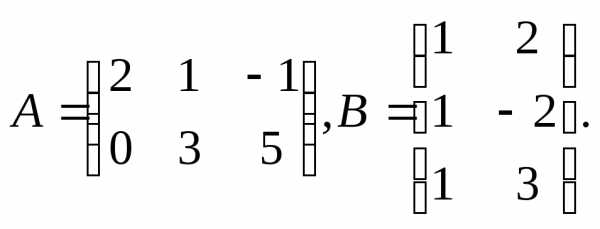

Тогда

Свойства умножения матриц:

Умножение матриц некоммутативно, т.е. существуют матрицы, для которых АВВА.
Если имеют смысл произведения матриц АВ и ВС, то также имеют смысл произведения (АВ)С и А(ВС) и (АВ)С = А(ВС) (закон ассоциативности умножения матриц).
Если имеют смысл АВ, ВС и АВ+АС, то имеет смысл и произведение А(В+С), причем А(В+С) = АВ +АС (закон дистрибутивности умножения матриц относительно сложения слева). Имеет место также и аналогичный закон справа.
(АВ) = (А)В,(АВ) = А(В).
Е_mА = А, АЕ_n= А, где Е_mи Е_n– квадратные матрицы соответственно порядковm иn, у которых на главных диагоналях расположены единицы, а на остальных местах нули.
(АВ)^Т= В^ТА^Т,
А^kА^l= А^k⁺^l, где А⁰= Е, А¹= А, А²= АА, А^k= А^k^-1А.

studfiles.net

1 1 + 3 2+ 4 10+ 2 12

1 3 + 3 2+ 4 0+ 2(−1)

3 1 + 2 2+ 0 10− 1 12

3 1 + 2 2+ 0 10− 1 12

3 3 + 2 2+ 0 0− 1(−1)

0 1 + 1 2− 1 10+ 2 12 0 3+ 1 2− 1 0+ 2(−1)