Запоминание через понимание. Визуализация синуса
Запоминание через понимание
Смотрим определение синуса в учебнике геометрии. «Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе».
Дает ли это определение понимание синуса? Нет, не дает. Определение не полное. Потому что оно рассматривает только частный случай треугольника — прямоугольный треугольник.
Смотрим определение синуса в учебнике алгебры. «Ордината точки Р, полученной при повороте точки Р (1;0) вокруг начала координат на угол а-радиан, называется синусом числа а, а абсцисса этой точки — косинусом».
Это определение вообще из области математической абстракции, так как вводит отрицательные значения синуса и косинуса. И с пониманием синуса по этому определению ещё больше сложностей.
Есть простой тест на понимание синуса и косинуса. Попросите школьника нарисовать линию косинуса для произвольного треугольника (не прямоугольного). Если он этого сделать не может — он не понимает, что такое синус и косинус.
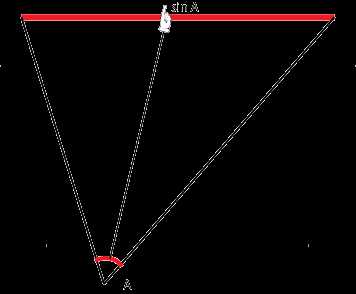
Иллюстрация 1. Тест на понимание. Где линия косинуса?
(Предполагается описанная окружность с единичным диаметром)
Итак, школьные учебники не дают информации для понимания понятий «синус» и «косинус». Основное понятие тригонометрии (и элементарное понятие) «засекретили», спрятали в частных случаях и в математических абстракциях.
При возникновении проблем с пониманием сейчас можно обратиться к поисковым системам и найти в них недостающую информацию. Чтобы визуализировать синус и косинус, нужно вернуться к истокам тригонометрии, понять, откуда эти понятия появились, и для каких целей.
Изначально синус не связан с треугольником. Синус появился из окружности и вписанного в окружность угла.
В окружности с единичным диаметром синус — это хорда, на которую опирается вписанный угол. А косинус — это перпендикулярная хорде-синусу хорда. На иллюстрации видно, что для любого вписанного угла в окружности имеется две линии синуса и две линии косинуса, которые образуют прямоугольник.
Вот эту иллюстрацию и следует использовать для запоминания понятий «синус» и «косинус». По этой иллюстрации можно дать определение синусу своими словами.
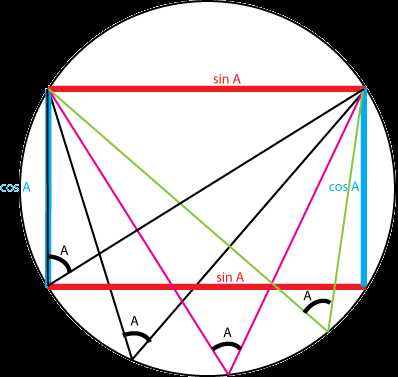
Иллюстрация 2. В окружности с единичным диаметром линии синуса и косинуса (для вписанного угла)
образуют прямоугольник.
На картинке виден частный случай — прямоугольный треугольник,
в котором линия косинуса совпадает с катетом.
Связан ли синус (длина хорды) с противолежащим углом? Ведь мы привыкли говорить «синус угла». Связь длины хорды с углом очень не простая… Скорее, можно говорить о табличном соответствии длины хорды и величины вписанного в окружность угла.
Синус напрямую связан с другим элементом в окружности — с её диаметром. Если мы рассмотрим окружность с произвольным диаметром и вписанный в эту окружность произвольный треугольник (не прямоугольный), то синус получается путем деления стороны треугольника на диаметр этой окружности. То есть, синус — это коэффициент пропорциональности стороны вписанного в окружность треугольника. Понятие «синус» напрямую связано со стороной треугольника. Но традиции есть традции — принято говорить «синус угла».
Как получаются синусы сторон треугольника видно на иллюстрации ниже. Мы можем вычислить синусы всех сторон (или синусы всех углов, как принято говорить), измерив точной линейкой стороны треугольника и диаметр описанной окружности, и разделив каждую сторону на диаметр. Величины углов нам для этого не нужны.
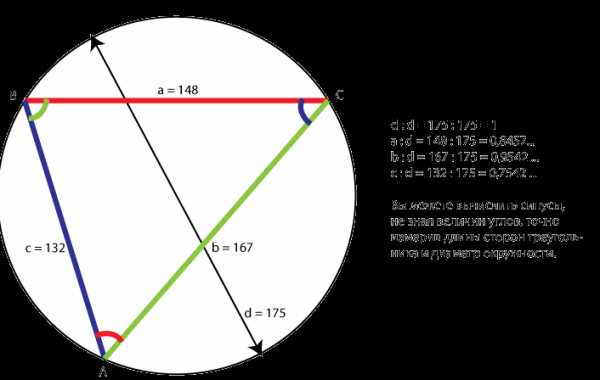
Иллюстрация 3. Опишем вокруг треугольника окружность
и точно измерим стороны треугольника и диаметр окружности
В результате мы получим пропорционально уменьшенный треугольник, вписанный в окружность с единичным диаметром, стороны которого и будут синусами сторон исходного треугольника.
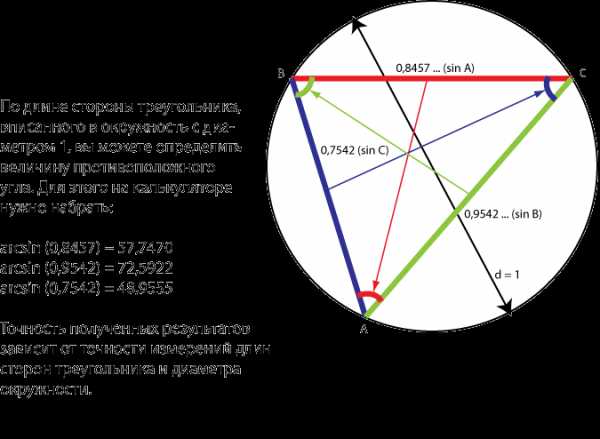
Иллюстрация 4. Стороны треугольника стали синусами,
когда мы уменьшили окружность до единичного диаметра
Усвоив понятие синуса, визуализировав его у себя в воображении, поняв, откуда оно появилось, можно переходить к частным случаям синуса и косинуса, изложенным в учебниках. Легко заметить, что в прямоугольном треугольнике одна из сторон (гипотенуза) одновременно является и диаметром описанной окружности. Теперь становится более понятным определение из учебника геометрии, по которому синус угла — это отношение катета к гипотенузе (т.е., к диаметру окружности). На иллюстрации 2 видно, что косинус совпадает со стороной треугольника только в прямоугольном треугольнике. В любом другом треугольнике линия косинуса находится вне треугольника. В учебнике алгебры, где синус рассматриваются как проекция точки окружности на ось координат, переходят на половины углов и полухорды, и с единичного диаметра на единичный радиус. Для чего? Чтобы ввести отрицательные значения тригонометрических функций.
На иллюстрации 3 и 4 видна теорема синусов. Теорема синусов является очевидной и не нуждается в доказательстве. Если синусы сторон (углов) изначально получены нами путем деления каждой стороны треугольника на диаметр описанной окружности, то отношение любой стороны треугольника к синусу стороны (синусу угла) будет одной и той же величиной, равной диаметру окружности. Это и есть теорема синусов.
a/sinA = b/sinB = c/sinC = d
(sin A — коэффициент пропорциональности стороны «a»)
————————————————-
А как же все таки угол связан со своим синусом?
Ведь для решения задач удобно находить синус угла по значению самого угла. Сейчас это не проблема. На любом калькуляторе вы можете набрать sin (вставить угол) и получить результат с заданной точностью.
Изменение значения синуса при равномерном изменении величины угла визуально похоже на перемещение с равноускоренным движением (представьте падающий на землю шарик и его ускорение в каждую секунду). И очень приблизительные значения синуса (по углу) можно вычислить по формуле перемещения с равноускоренным движением. Но четкой функциональной зависимости значения синуса от величины угла нет. С заданной точностью синус вычисляется по формуле:
В.Козаренко
Дата размещения материала на сайте: 17 марта 2011 года
mnemotexnika.narod.ru
Интегрирование тригонометрических функций: методы и примеры
(1)
Воспользовавшись известными тригонометрическими формулами
(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам
(5)
и
(6)
Пример 1. Найти интеграл от тригонометрической функцииРешение. По формуле (2) при
имеем
Поэтому
Применяя далее формулу (5), получим
Пример 2. Найти интеграл от тригонометрической функцииРешение. По формуле (3) при получаем следующее преобразование подынтегрального выражения:
Поэтому
Применяя далее формулу (6), получим
Пример 3. Найти интеграл от тригонометрической функцииРешение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:
Применяя формулу (6), получим
Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.
(7)
В частных случаях один из показателей (m или n) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен — sin x dx).
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 — нечётный. Тогда, учитывая, что
получим
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t. Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cos x и полагая t = cos x. Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей — нечётный. Всё дело в том, что частное степеней синуса и косинуса — это частный случай их произведения: когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень — отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени — только чётные. О них — следующем абзаце.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше.
Поэтому интегрирование следует продолжать по той же схеме.
Пример 4. Найти интеграл от тригонометрической функции
Решение. Показатель степени косинуса – нечётный. Поэтому представим
в виде
и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим
Возвращаясь к старой переменной, окончательно найдём
Пример 5. Найти интеграл от тригонометрической функции
.
Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим
в виде
и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим
Раскроем скобки
и получим
Возвращаясь к старой переменной, получаем решение
Пример 6. Найти интеграл от тригонометрической функции
Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:
Тогда получим
Во втором интеграле произведём замену переменной, полагая t = sin2x. Тогда (1/2)dt = cos2x dx. Следовательно,
а
Окончательно получаем
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус — в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t, но и tgx = t и ctgx = t.
Пример 8. Найти интеграл от тригонометрической функции
.
Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
Пример 9. Найти интеграл от тригонометрической функции
.
Решение. Преобразуем тангенс в отношение синуса и косинуса:
.
Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Пример 10. Найти интеграл от тригонометрической функции
.
Решение. Произведём замену переменной: , тогда .
Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :
Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:
где .
Тогда .
Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.
Пример 12. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.
Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда
Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 2. Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:
.
Пример 13. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.
Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда
.
Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 3. Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:
.
Пример 14. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
Используем метод неопределённых коэффициентов. Получим следующее подынтегральное выражение:
Чтобы найти коэффициенты, решим систему уравнений:
Теперь получаем:
Используем подведение под знак дифференциала:
К последнему слагаемому применяем замену переменной , тогда . Получаем:
Преобразуем и вернём на место первоначальную переменную и окончательно получим решение:
Начало темы «Интеграл»
Продолжение темы «Интеграл»
function-x.ru
Внеклассный урок — Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Простейшие тригонометрические уравнения: обобщения, таблицы значений x, примеры
Уравнение sin x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения sin x = a:
x = (-1)n · arcsin α + πn где n – любое целое число (n ∈ Z). |
Частные случаи, когда уравнение sin x = а имеет более простое решение:
| |
|
|
|
|
|
|
Остальные значения x в уравнении sin x = а:
| | |
1 | π | 5π |
1 | π | 5π |
√2 | π | 3π |
√2 | π | 3π |
√3 | π | 2π |
√3 | π | 2π |
Уравнение cos x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения cos x = a:
x = ± arccos α + 2πk где k – любое целое число (k ∈ Z). |
Частные случаи, когда уравнение cos x = а имеет более простое решение:
| |
| π |
| |
| |
Остальные значения x в уравнении cos x = а:
|
| |
1 | π | π |
1 | 2π | 2π |
√2 | π | π |
√2 | 3π | 3π |
√3 | π | π |
√3 | 5π | 5π |
Уравнения tg x = a и ctg x = a.
Формула решения уравнения tg x = a:
x = arctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Формула решения уравнения ctg x = a:
x = arcctg a + πk где a – любое действительное число (a ∈ R), k – любое целое число (k ∈ Z). |
Значения x в уравнениях tg x = а и ctg x = а:
|
| |
| | |
√3 | | π |
√3 | | π |
| | π |
| | π |
| √3 | π |
| √3 | π |
| | π |
Примеры.
1) Решим уравнение
√2
sin 3x = ——
2
Решение.
Для простоты заменим переменную 3x обобщенной переменной t. Итак:
3x = t .
Тогда наше уравнение принимает привычный вид:
√2
sin t = ——
2
Применяем формулу:
√2
t = (–1)n arcsin —— + πn
2
Находим значение арксинуса:
√2 π
arcsin —— = —
2 4
Подставляем это значение арксинуса:
π
t = (–1)n — + πn
4
Теперь вместо t вновь подставляем переменную 3x:
π
3x = (–1)n — + πn
4
Находим значение переменной, применяя правило деления дробей:
π π 1 πn π πn
x = (–1)n — : 3 + πn : 3 = (–1)n — ∙ — + —— = (–1)n —— + ——
4 4 3 3 12 3
Ответ:
π πn
x = (–1)n —— + ——
12 3
2) Решим уравнение
1
cos 2x = – —
2
Решение.
Напомним: решать пример будем по формуле
x = ± arccos a + 2πn.
Для простоты можем заменить 2x на t. Тогда наша формула примет вид t = ± arccos a + 2πn. Но в данном случае можем обойтись и без этого.
Итак, вычисляем значение арккосинуса:
1 2π
2x = ± arccos (– —) + 2πn = ± —— + 2πn
2 3
Находим значение x, применяя правило деления дробей:
2π 2π 1 2π π
x = ± —— : 2 + 2πn : 2 = ± —— ∙ — + πn = ± —— + πn = ± — + πn
3 3 2 6 3
Ответ:
π
x = ± — + πn
3
3) Решим уравнение
π √3
tg (4x – —) = ——
6 3
Решение.
Напомним: здесь мы применяем формулу
x = arctg a + πn.
Чтобы не запутаться при следующем шаге, заменим в формуле переменную x на переменную t:
t = arctg a + πn.
Далее отмечаем, что:
π
t = (4x – —).
6
Тогда наше уравнение принимает следующий вид:
π √3
4x – — = arctg —— + πn.
6 3
Находим значение арктангенса:
√3 π
arctg —— = —
3 6
Подставляем значение арктангенса в нашу формулу:
π π
4x – — = — + πn.
6 6
Находим значение 4x:
π π 2π π
4x = — + — + πn = —— + πn = — + πn
6 6 6 3
Осталось найти значение x, применяя правило деления дробей:
π π 1 πn π πn
x = — : 4 + πn : 4 = — ∙ — + —— = —— + ——
3 3 4 4 12 4
Ответ:
π πn
x = —— + ——, n ∈ Z
12 4
raal100.narod.ru
