Синус и косинус это – Cинус, косинус, тангенс и котангенс

Содержание

Что такое синус и косинус в тригонометрии? :: SYL.ru

Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.

Школьный предмет

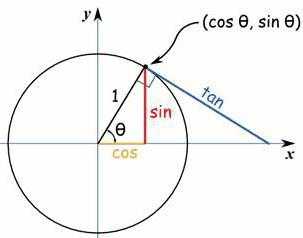
Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.

Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.

Использование

Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?

Определения

Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус – прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?

На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.

Что нужно запомнить

Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.

Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.

Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.

Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.

Теоремы

В базовой тригонометрии существует две основные теоремы: синусов и косинусов.

Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая – что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.

Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать – две рассмотренные теоремы существенно упростят решение задачи.

Цели и задачи

Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации – это может быть величина одного угла и длины двух сторон или, например, три стороны.

Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.

Нестыковки при изучении тригонометрии

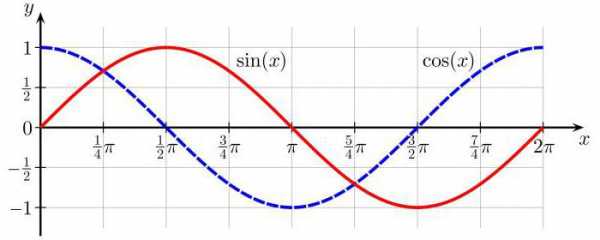
Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.

Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?

Единицы измерения

Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга – 2 сантиметра, длина окружности составит 3,14*2, или 6,28.

Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.

Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева – «Пи». Это угловая величина, измеренная в радианах, ведь полукруг – это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.

Заглянем в будущее

Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая – это прямая.

Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.

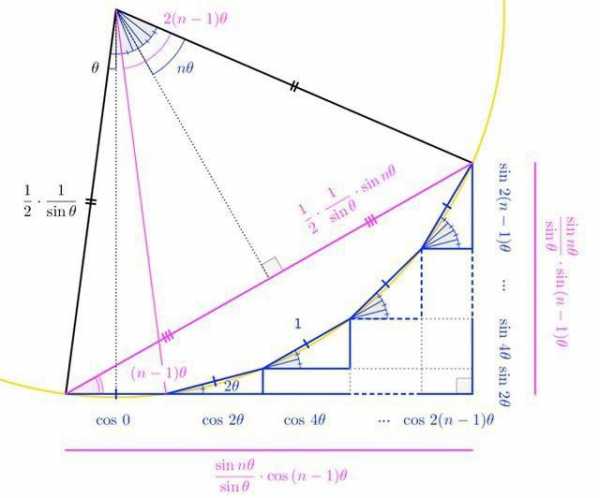
Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.

Тригонометрические функции в жизни

Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь – здесь приходится использовать более сложные формулы.

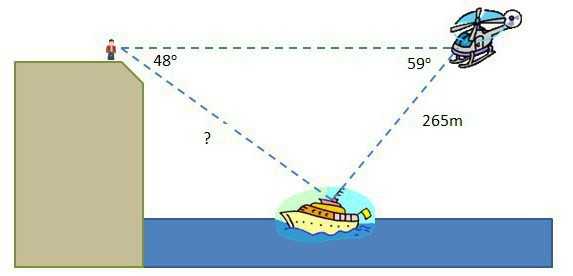
Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.

В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.

Заключение

Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться – стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия – это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.

Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.

В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.

www.syl.ru

Синус. Что это такое?

Тригонометрия является разделом математики, изучающим тригонометрические функции, а также их использование на практике. К таким функциям относятся синус, косинус, тангенс и котангенс.

Синус – это тригонометрическая функция, отношение величины противолежащего катета к величине гипотенузы.

Синус в тригонометрии.

Как уже сказано выше, синус имеет непосредственное отношение к тригонометрии и тригонометрическим функциям. Его функция определяется тем, чтобы

помогать высчитать угол, при условии известности величин сторон треугольника;
помогать высчитать величины стороны треугольника, при условии известности угла.

Необходимо помнить, что величина синуса будет всегда одинакова для любых размеров треугольника, поскольку синус – это не измерение, а соотношение.

Следовательно, для того чтобы не высчитывать эту постоянную величину при каждом решении той или иной задачи, были созданы специальные тригонометрические таблицы. В них величины синусов, косинусов, тангенсов и котангенсов уже просчитаны и закреплены. Обычно эти таблицы приводятся на форзаце учебников по алгебре и геометрии. Также их можно найти в Интернете.

Синус в геометрии.

Геометрия требует наглядности, поэтому, чтобы понять на практике, что такое синус угла, нужно нарисовать треугольник с прямым углом.

Допустим, что стороны, образующие прямой угол, названы а, в, противоположный им угол – х.

Обычно в заданиях указана длина сторон. Допустим, а=3, в=4. В таком случае соотношение сторон будет выглядеть как ¾. При этом если удлинить стороны треугольника, прилегающие к острому углу х, то увеличатся и стороны а и в, и гипотенуза – третья сторона прямоугольного треугольника, лежащая не под прямым углом к основанию. Теперь стороны треугольника можно назвать иначе, допустим:

m, n, k.

При этом видоизменении сработал закон тригонометрии: длины сторон треугольника изменились, а их отношение – нет.

Тот факт, что при изменении длины сторон треугольника во сколько угодно раз и при сохранении величины угла х, соотношение между его сторонами всё равно останется неизменным, заметили ещё древние ученые. В нашем случае длина сторон могла измениться так: а/в = ¾, при удлинении стороны а до 6 см, а в – до 8 см получаем: m/n = 6/8 = 3/4.

Соотношения сторон в прямоугольном треугольнике в связи с этим получили названия:

синус угла х – это отношение противолежащего катета к гипотенузе: sinx = а/с;
косинус угла х – это отношение прилежащего катета к гипотенузе: сosx = в/с;
тангенс угла х – это отношение противолежащего катета к прилежащему: tgx = а/в;
котангенс угла х – это отношение прилежащего катета к противолежащему: ctgx = в/а.

КОСИНУС — это… Что такое КОСИНУС?

КОСИНУС — (ново лат. cosinus, вместо complementi sinus дополнение синуса). Синус угла дополнения: в прямоугольном треугольнике косинус угла есть частное от деления прилежащего катета на гипотенузу. Словарь иностранных слов, вошедших в состав русского языка … Словарь иностранных слов русского языка

КОСИНУС — (cosine) В прямоугольном треугольнике отношение катета и гипотенузы, образующих угол. Косинус угла х записывается как cos х. Если начертить окружность радиусом, равным единице, то при измерении величины угла против часовой стрелки, начиная с… … Экономический словарь

КОСИНУС — КОСИНУС, в ТРИГОНОМЕТРИИ отношение длины стороны, прилежащей к острому углу, к длине ГИПОТЕНУЗЫ в прямоугольном треугольнике. Сокращенно косинус угла А обозначают как cos A … Научно-технический энциклопедический словарь

КОСИНУС — (новолат. cosinus от complementi sinus синус дополнения), одна из тригонометрических функций … Большой Энциклопедический словарь

КОСИНУС ФИ — (cos ?) для синусоидального тока, то же, что коэффициент мощности … Большой Энциклопедический словарь

КОСИНУС — КОСИНУС, а, муж. (спец.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношению к гипотенузе катета, прилежащего к данному острому углу. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

КОСИНУС ФИ — (cos j), для синусоидального тока, то же, что коэффициент мощности (см. КОЭФФИЦИЕНТ МОЩНОСТИ) … Энциклопедический словарь

косинус — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

косинус — косинусоидальный косинусный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы косинусоидальныйкосинусный EN cosine … Справочник технического переводчика

косинус — синус дополнения лат.: cosinus, complementi sinus новолат. лат … Словарь сокращений и аббревиатур

dic.academic.ru

Что такое синус?

Кто из нас не кричал в школе, что математика ему никогда не пригодиться. Всем нам казалось, что все эти заумные формулы, громоздкие уравнения и сложные названия не имеют никакого отношения к реальной жизни. Но рано или поздно все знания, полученные нами в школе, находят свое применение. И знание того, что такое синус, косинус или тангенс может спасти вашу репутацию.

Немного школьной геометрии

Итак, синус — это соотношение сторон в прямоугольном треугольнике. Вспомним, из чего состоит прямоугольный треугольник.

Углы. Сумма углов в треугольнике — 180^о. Прямой угол равен 90^о. Значит, остальные два в сумме тоже должны давать 90^о. То есть, у нас один прямой угол и два острых.

Стороны. Прямоугольный треугольник состоит из гипотенузы и двух катетов. Два катета составляют собой прямой угол, а гипотенуза лежит напротив него.

Что такое синус угла? Как уже было сказано, это соотношение сторон. Но каких? Синусом острого угла является отношение катета, который лежит напротив этого угла, к гипотенузе. Рассмотрим на примере:

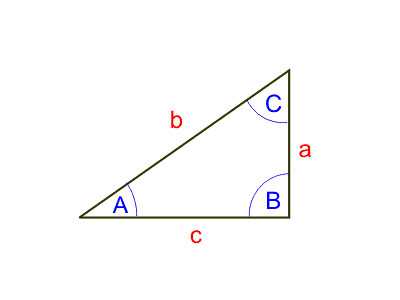
Синусом угла А будет отношение стороны а (противолежащего катета) к стороне b (гипотенузе).

Синусом угла С будет отношение стороны с (катет лежит напротив стороны С) к стороне b (гипотенузе).

То есть, если стороны равны a=3, с=4, b=5, то синусом угла А будет 3/5, а синусом угла С будет 4/5.

Что нам это даёт? Пока что ничего, но давайте рассмотрим другой пример. Увеличим треугольник, продлив стороны. Теперь у нас получилось вот что:

Как видно по рисунку, длины сторон увеличились, а вот углы – нет. Но что самое интересное – соотношения тоже не поменялись!

Допустим, d=6, k=8, m=10. Тогда Синусом угла А будет соотношение d/m = 6/10. Сокращаем на два обе стороны уравнения и получаем те же 3/5, как и в первом случае! И как бы вы ни меняли, удлиняли или укорачивали стороны, отношение сторон всё равно будет одинаковым.

Поэтому ясно, что синус – величина постоянная.

А теперь — тригонометрия

Древние греки заметили это давно. Они вычислили синусы основных углов и записали их, чтобы дальше пользоваться уже готовыми величинами, а не выдумывать новые.

Помимо синуса, у угла также есть косинус (отношение прилежащего катета к гипотенузе), тангенс (отношение противолежащего катета к прилежащему) и котангенс (отношение прилежащего катета к противолежащему). Все эти величины называются тригонометрическими функциями угла, и используются для расчетов и решения задач.

Загадочные таблицы Брадиса

Каждый раз вычислять синус не нужно. Существуют специально составленные таблицы Брадиса, в которых уже записаны все синусы, косинусы, т

elhow.ru

косинус — это… Что такое косинус?

КОСИНУС — КОСИНУС, косинуса, муж. (лат. cosinus) (мат.). Синус дополнительного угла, функция угла, выражаемая отношением прилегающего к углу катета к гипотенузе. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

косинус — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

sokrasheniya.academic.ru

СИНУС — это… Что такое СИНУС?

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (sine) Соотношение в прямоугольном треугольнике между стороной, противоположной углу, и гипотенузой. Синус угла х пишется как sin x. Если описывается круг единичного радиуса, измерение углов начинается с востока против часовой стрелки; sin x –… … Экономический словарь

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона