Синусы и косинусы углов все – , , .

Таблица синусов и косинусов

Таблица синусов и косинусов может пригодится учащимся, студентам и инженерам для произведения тригонометрических расчетов. Она позволяет найти синус и косинус любого целого угла от 0 до 360 градусов.

Пользоваться таблицей очень просто — найдите нужный угол и в той же строке увидите синус и косинус этого угла. Для примера возьмем угол, равный 30 градусам. Найдя его в таблице мы увидим, что Cos(30) = 0,866025404, а Sin(30) = 0,5.

Угол (градусы)	Косинус (Cos)	Синус (Sin)
0°	1	0
1°	0,999847695	0,017452406
2°	0,999390827	0,034899497
3°	0,998629535	0,052335956
4°	0,99756405	0,069756474
5°	0,996194698	0,087155743
6°	0,994521895	0,104528463
7°	0,992546152	0,121869343
8°	0,990268069	0,139173101
9°	0,987688341	0,156434465
10°	0,984807753	0,173648178
11°	0,981627183	0,190808995
12°	0,978147601	0,207911691
13°	0,974370065	0,224951054
14°	0,970295726	0,241921896
15°	0,965925826	0,258819045
16°	0,961261696	0,275637356
17°	0,956304756	0,292371705
18°	0,951056516	0,309016994
19°	0,945518576	0,325568154
20°	0,939692621	0,342020143
21°	0,933580426	0,35836795
22°	0,927183855	0,374606593
23°	0,920504853	0,390731128
24°	0,913545458	0,406736643
25°	0,906307787	0,422618262
26°	0,898794046	0,438371147
27°	0,891006524	0,4539905
28°	0,882947593	0,469471563
29°	0,874619707	0,48480962
30°	0,866025404	0,5
31°	0,857167301	0,515038075
32°	0,848048096	0,529919264
33°	0,838670568	0,544639035
34°	0,829037573	0,559192903
35°	0,819152044	0,573576436
36°	0,809016994	0,587785252
37°	0,79863551	0,601815023
38°	0,788010754	0,615661475
39°	0,777145961	0,629320391
40°	0,766044443	0,64278761
41°	0,75470958	0,656059029
42°	0,743144825	0,669130606
43°	0,731353702	0,68199836
44°	0,7193398	0,69465837
45°	0,707106781	0,707106781
46°	0,69465837	0,7193398
47°	0,68199836	0,731353702
48°	0,669130606	0,743144825
49°	0,656059029	0,75470958
50°	0,64278761	0,766044443
51°	0,629320391	0,777145961
52°	0,615661475	0,788010754
53°	0,601815023	0,79863551
54°	0,587785252	0,809016994
55°	0,573576436	0,819152044
56°	0,559192903	0,829037573
57°	0,544639035	0,838670568
58°	0,529919264	0,848048096
59°	0,515038075	0,857167301
60°	0,5	0,866025404
61°	0,48480962	0,874619707
62°	0,469471563	0,882947593
63°	0,4539905	0,891006524
64°	0,438371147	0,898794046
65°	0,422618262	0,906307787
66°	0,406736643	0,913545458
67°	0,390731128	0,920504853
68°	0,374606593	0,927183855
69°	0,35836795	0,933580426
70°	0,342020143	0,939692621
71°	0,325568154	0,945518576
72°	0,309016994	0,951056516
73°	0,292371705	0,956304756
74°	0,275637356	0,961261696
75°	0,258819045	0,965925826
76°	0,241921896	0,970295726
77°	0,224951054	0,974370065
78°	0,207911691	0,978147601
79°	0,190808995	0,981627183
80°	0,173648178	0,984807753
81°	0,156434465	0,987688341
82°	0,139173101	0,990268069
83°	0,121869343	0,992546152
84°	0,104528463	0,994521895
85°	0,087155743	0,996194698
86°	0,069756474	0,99756405
87°	0,052335956	0,998629535
88°	0,034899497	0,999390827
89°	0,017452406	0,999847695
90°	0	1
91°	-0,017452406	0,999847695
92°	-0,034899497	0,999390827
93°	-0,052335956	0,998629535
94°	-0,069756474	0,99756405
95°	-0,087155743	0,996194698
96°	-0,104528463	0,994521895
97°	-0,121869343	0,992546152
98°	-0,139173101	0,990268069
99°	-0,156434465	0,987688341
100°	-0,173648178	0,984807753
101°	-0,190808995	0,981627183
102°	-0,207911691	0,978147601
103°	-0,224951054	0,974370065
104°	-0,241921896	0,970295726
105°	-0,258819045	0,965925826
106°	-0,275637356	0,961261696
107°	-0,292371705	0,956304756
108°	-0,309016994	0,951056516
109°	-0,325568154	0,945518576
110°	-0,342020143	0,939692621
111°	-0,35836795	0,933580426
112°	-0,374606593	0,927183855
113°	-0,390731128	0,920504853
114°	-0,406736643	0,913545458
115°	-0,422618262	0,906307787
116°	-0,438371147	0,898794046
117°	-0,4539905	0,891006524
118°	-0,469471563	0,882947593
119°	-0,48480962	0,874619707
120°	-0,5	0,866025404
121°	-0,515038075	0,857167301
122°	-0,529919264	0,848048096
123°	-0,544639035	0,838670568
124°	-0,559192903	0,829037573
125°	-0,573576436	0,819152044
126°	-0,587785252	0,809016994
127°	-0,601815023	0,79863551
128°	-0,615661475	0,788010754
129°	-0,629320391	0,777145961
130°	-0,64278761	0,766044443
131°	-0,656059029	0,75470958
132°	-0,669130606	0,743144825
133°	-0,68199836	0,731353702
134°	-0,69465837	0,7193398
135°	-0,707106781	0,707106781
136°	-0,7193398	0,69465837
137°	-0,731353702	0,68199836
138°	-0,743144825	0,669130606
139°	-0,75470958	0,656059029
140°	-0,766044443	0,64278761
141°	-0,777145961	0,629320391
142°	-0,788010754	0,615661475
143°	-0,79863551	0,601815023
144°	-0,809016994	0,587785252
145°	-0,819152044	0,573576436
146°	-0,829037573	0,559192903
147°	-0,838670568	0,544639035
148°	-0,848048096	0,529919264
149°	-0,857167301	0,515038075
150°	-0,866025404	0,5
151°	-0,874619707	0,48480962
152°	-0,882947593	0,469471563
153°	-0,891006524	0,4539905
154°	-0,898794046	0,438371147
155°	-0,906307787	0,422618262
156°	-0,913545458	0,406736643
157°	-0,920504853	0,390731128
158°	-0,927183855	0,374606593
159°	-0,933580426	0,35836795
160°	-0,939692621	0,342020143
161°	-0,945518576	0,325568154
162°	-0,951056516	0,309016994
163°	-0,956304756	0,292371705
164°	-0,961261696	0,275637356
165°	-0,965925826	0,258819045
166°	-0,970295726	0,241921896
167°	-0,974370065	0,224951054
168°	-0,978147601	0,207911691
169°	-0,981627183	0,190808995
170°	-0,984807753	0,173648178
171°	-0,987688341	0,156434465
172°	-0,990268069	0,139173101
173°	-0,992546152	0,121869343
174°	-0,994521895	0,104528463
175°	-0,996194698	0,087155743
176°	-0,99756405	0,069756474
177°	-0,998629535	0,052335956
178°	-0,999390827	0,034899497
179°	-0,999847695	0,017452406
180°	-1	1,22515E-16
181°	-0,999847695	-0,017452406
182°	-0,999390827	-0,034899497
183°	-0,998629535	-0,052335956
184°	-0,99756405	-0,069756474
185°	-0,996194698	-0,087155743
186°	-0,994521895	-0,104528463
187°	-0,992546152	-0,121869343
188°	-0,990268069	-0,139173101
189°	-0,987688341	-0,156434465
190°	-0,984807753	-0,173648178
191°	-0,981627183	-0,190808995
192°	-0,978147601	-0,207911691
193°	-0,974370065	-0,224951054
194°	-0,970295726	-0,241921896
195°	-0,965925826	-0,258819045
196°	-0,961261696	-0,275637356
197°	-0,956304756	-0,292371705
198°	-0,951056516	-0,309016994
199°	-0,945518576	-0,325568154
200°	-0,939692621	-0,342020143
201°	-0,933580426	-0,35836795
202°	-0,927183855	-0,374606593
203°	-0,920504853	-0,390731128
204°	-0,913545458	-0,406736643
205°	-0,906307787	-0,422618262
206°	-0,898794046	-0,438371147
207°	-0,891006524	-0,4539905
208°	-0,882947593	-0,469471563
209°	-0,874619707	-0,48480962
210°	-0,866025404	-0,5
211°	-0,857167301	-0,515038075
212°	-0,848048096	-0,529919264
213°	-0,838670568	-0,544639035
214°	-0,829037573	-0,559192903
215°	-0,819152044	-0,573576436
216°	-0,809016994	-0,587785252
217°	-0,79863551	-0,601815023
218°	-0,788010754	-0,615661475
219°	-0,777145961	-0,629320391
220°	-0,766044443	-0,64278761
221°	-0,75470958	-0,656059029
222°	-0,743144825	-0,669130606
223°	-0,731353702	-0,68199836
224°	-0,7193398	-0,69465837
225°	-0,707106781	-0,707106781
226°	-0,69465837	-0,7193398
227°	-0,68199836	-0,731353702
228°	-0,669130606	-0,743144825
229°	-0,656059029	-0,75470958
230°	-0,64278761	-0,766044443
231°	-0,629320391	-0,777145961
232°	-0,615661475	-0,788010754
233°	-0,601815023	-0,79863551
234°	-0,587785252	-0,809016994
235°	-0,573576436	-0,819152044
236°	-0,559192903	-0,829037573
237°	-0,544639035	-0,838670568
238°	-0,529919264	-0,848048096
239°	-0,515038075	-0,857167301
240°	-0,5	-0,866025404
241°	-0,48480962	-0,874619707
242°	-0,469471563	-0,882947593
243°	-0,4539905	-0,891006524
244°	-0,438371147	-0,898794046
245°	-0,422618262	-0,906307787
246°	-0,406736643	-0,913545458
247°	-0,390731128	-0,920504853
248°	-0,374606593	-0,927183855
249°	-0,35836795	-0,933580426
250°	-0,342020143	-0,939692621
251°	-0,325568154	-0,945518576
252°	-0,309016994	-0,951056516
253°	-0,292371705	-0,956304756
254°	-0,275637356	-0,961261696
255°	-0,258819045	-0,965925826
256°	-0,241921896	-0,970295726
257°	-0,224951054	-0,974370065
258°	-0,207911691	-0,978147601
259°	-0,190808995	-0,981627183
260°	-0,173648178	-0,984807753
261°	-0,156434465	-0,987688341
262°	-0,139173101	-0,990268069
263°	-0,121869343	-0,992546152
264°	-0,104528463	-0,994521895
265°	-0,087155743	-0,996194698
266°	-0,069756474	-0,99756405
267°	-0,052335956	-0,998629535
268°	-0,034899497	-0,999390827
269°	-0,017452406	-0,999847695
270°	-1,83772E-16	-1
271°	0,017452406	-0,999847695
272°	0,034899497	-0,999390827
273°	0,052335956	-0,998629535
274°	0,069756474	-0,99756405
275°	0,087155743	-0,996194698
276°	0,104528463	-0,994521895
277°	0,121869343	-0,992546152
278°	0,139173101	-0,990268069
279°	0,156434465	-0,987688341
280°	0,173648178	-0,984807753
281°	0,190808995	-0,981627183
282°	0,207911691	-0,978147601
283°	0,224951054	-0,974370065
284°	0,241921896	-0,970295726
285°	0,258819045	-0,965925826
286°	0,275637356	-0,961261696
287°	0,292371705	-0,956304756
288°	0,309016994	-0,951056516
289°	0,325568154	-0,945518576
290°	0,342020143	-0,939692621
291°	0,35836795	-0,933580426
292°	0,374606593	-0,927183855
293°	0,390731128	-0,920504853
294°	0,406736643	-0,913545458
295°	0,422618262	-0,906307787
296°	0,438371147	-0,898794046
297°	0,4539905	-0,891006524
298°	0,469471563	-0,882947593
299°	0,48480962	-0,874619707
300°	0,5	-0,866025404
301°	0,515038075	-0,857167301
302°	0,529919264	-0,848048096
303°	0,544639035	-0,838670568
304°	0,559192903	-0,829037573
305°	0,573576436	-0,819152044
306°	0,587785252	-0,809016994
307°	0,601815023	-0,79863551
308°	0,615661475	-0,788010754
309°	0,629320391	-0,777145961
310°	0,64278761	-0,766044443
311°	0,656059029	-0,75470958
312°	0,669130606	-0,743144825
313°	0,68199836	-0,731353702
314°	0,69465837	-0,7193398
315°	0,707106781	-0,707106781
316°	0,7193398	-0,69465837
317°	0,731353702	-0,68199836
318°	0,743144825	-0,669130606
319°	0,75470958	-0,656059029
320°	0,766044443	-0,64278761
321°	0,777145961	-0,629320391
322°	0,788010754	-0,615661475
323°	0,79863551	-0,601815023
324°	0,809016994	-0,587785252
325°	0,819152044	-0,573576436
326°	0,829037573	-0,559192903
327°	0,838670568	-0,544639035
328°	0,848048096	-0,529919264
329°	0,857167301	-0,515038075
330°	0,866025404	-0,5
331°	0,874619707	-0,48480962
332°	0,882947593	-0,469471563
333°	0,891006524	-0,4539905
334°	0,898794046	-0,438371147
335°	0,906307787	-0,422618262
336°	0,913545458	-0,406736643
337°	0,920504853	-0,390731128
338°	0,927183855	-0,374606593
339°	0,933580426	-0,35836795
340°	0,939692621	-0,342020143
341°	0,945518576	-0,325568154
342°	0,951056516	-0,309016994
343°	0,956304756	-0,292371705
344°	0,961261696	-0,275637356
345°	0,965925826	-0,258819045
346°	0,970295726	-0,241921896
347°	0,974370065	-0,224951054
348°	0,978147601	-0,207911691
349°	0,981627183	-0,190808995
350°	0,984807753	-0,173648178
351°	0,987688341	-0,156434465
352°	0,990268069	-0,139173101
353°	0,992546152	-0,121869343
354°	0,994521895	-0,104528463
355°	0,996194698	-0,087155743
356°	0,99756405	-0,069756474
357°	0,998629535	-0,052335956
358°	0,999390827	-0,034899497
359°	0,999847695	-0,017452406
360°	1	0

Часто используемые значения косинуса

Косинус 0 градусов = 1

Косинус 30 градусов = 0,866025404 = {\frac {\sqrt{3}}{2}}

Косинус 45 градусов = 0,707106781 = {\frac {\sqrt{2}}{2}}

Косинус 60 градусов = 0,5 = {\frac {1}{2}}

Косинус 90 градусов = 0

Косинус 120 градусов = -0,5 = {-\frac {1}{2}}

Косинус 135 градусов = -0,707106781 = {-\frac {\sqrt{3}}{2}}

Косинус 180 градусов = -1

Просмотров страницы: 89 987

mnogoformul.ru

Таблица СИНУСОВ для углов от 0° до 360° градусов

---

СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.

Малая таблица значений тригонометрических функций (в радианах и градусах)

α (радианы)	0	π/6	π/4	π/3	π/2	π	√3π/2	2π
α (градусы)	0°	30°	45°	60°	90°	180°	270°	360°
SIN α (СИНУС)	0	1/2	√2/2	√3/2	1	0	-1	0

…

Полная таблица синусов для углов от 0° до  360° с шагом всего в 1° 

Угол в градусах	Sin (Синус)
0°	0
1°	0.0175
2°	0.0349
3°	0.0523
4°	0.0698
5°	0.0872
6°	0.1045
7°	0.1219
8°	0.1392
9°	0.1564
10°	0.1736
11°	0.1908
12°	0.2079
13°	0.225
14°	0.2419
15°	0.2588
16°	0.2756
17°	0.2924
18°	0.309
19°	0.3256
20°	0.342
21°	0.3584
22°	0.3746
23°	0.3907
24°	0.4067
25°	0.4226
26°	0.4384
27°	0.454
28°	0.4695
29°	0.4848
30°	0.5
31°	0.515
32°	0.5299
33°	0.5446
34°	0.5592
35°	0.5736
36°	0.5878
37°	0.6018
38°	0.6157
39°	0.6293
40°	0.6428
41°	0.6561
42°	0.6691
43°	0.682
44°	0.6947
45°	0.7071
46°	0.7193
47°	0.7314
48°	0.7431
49°	0.7547
50°	0.766
51°	0.7771
52°	0.788
53°	0.7986
54°	0.809
55°	0.8192
56°	0.829
57°	0.8387
58°	0.848
59°	0.8572
60°	0.866
61°	0.8746
62°	0.8829
63°	0.891
64°	0.8988
65°	0.9063
66°	0.9135
67°	0.9205
68°	0.9272
69°	0.9336
70°	0.9397
71°	0.9455
72°	0.9511
73°	0.9563
74°	0.9613
75°	0.9659
76°	0.9703
77°	0.9744
78°	0.9781
79°	0.9816
80°	0.9848
81°	0.9877
82°	0.9903
83°	0.9925
84°	0.9945
85°	0.9962
86°	0.9976
87°	0.9986
88°	0.9994
89°	0.9998
90°	1

…

Полная таблица синусов для углов от 91° до 180°

Угол в градусах	Sin (Синус)
91°	0.9998
92°	0.9994
93°	0.9986
94°	0.9976
95°	0.9962
96°	0.9945
97°	0.9925
98°	0.9903
99°	0.9877
100°	0.9848
101°	0.9816
102°	0.9781
103°	0.9744
104°	0.9703
105°	0.9659
106°	0.9613
107°	0.9563
108°	0.9511
109°	0.9455
110°	0.9397
111°	0.9336
112°	0.9272
113°	0.9205
114°	0.9135
115°	0.9063
116°	0.8988
117°	0.891
118°	0.8829
119°	0.8746
120°	0.866
121°	0.8572
122°	0.848
123°	0.8387
124°	0.829
125°	0.8192
126°	0.809
127°	0.7986
128°	0.788
129°	0.7771
130°	0.766
131°	0.7547
132°	0.7431
133°	0.7314
134°	0.7193
135°	0.7071
136°	0.6947
137°	0.682
138°	0.6691
139°	0.6561
140°	0.6428
141°	0.6293
142°	0.6157
143°	0.6018
144°	0.5878
145°	0.5736
146°	0.5592
147°	0.5446
148°	0.5299
149°	0.515
150°	0.5
151°	0.4848
152°	0.4695
153°	0.454
154°	0.4384
155°	0.4226
156°	0.4067
157°	0.3907
158°	0.3746
159°	0.3584
160°	0.342
161°	0.3256
162°	0.309
163°	0.2924
164°	0.2756
165°	0.2588
166°	0.2419
167°	0.225
168°	0.2079
169°	0.1908
170°	0.1736
171°	0.1564
172°	0.1392
173°	0.1219
174°	0.1045
175°	0.0872
176°	0.0698
177°	0.0523
178°	0.0349
179°	0.0175
180°	0

…

Таблица синусов для углов  181° — 270°

Угол	Sin (Синус)
181°	-0.0175
182°	-0.0349
183°	-0.0523
184°	-0.0698
185°	-0.0872
186°	-0.1045
187°	-0.1219
188°	-0.1392
189°	-0.1564
190°	-0.1736
191°	-0.1908
192°	-0.2079
193°	-0.225
194°	-0.2419
195°	-0.2588
196°	-0.2756
197°	-0.2924
198°	-0.309
199°	-0.3256
200°	-0.342
201°	-0.3584
202°	-0.3746
203°	-0.3907
204°	-0.4067
205°	-0.4226
206°	-0.4384
207°	-0.454
208°	-0.4695
209°	-0.4848
210°	-0.5
211°	-0.515
212°	-0.5299
213°	-0.5446
214°	-0.5592
215°	-0.5736
216°	-0.5878
217°	-0.6018
218°	-0.6157
219°	-0.6293
220°	-0.6428
221°	-0.6561
222°	-0.6691
223°	-0.682
224°	-0.6947
225°	-0.7071
226°	-0.7193
227°	-0.7314
228°	-0.7431
229°	-0.7547
230°	-0.766
231°	-0.7771
232°	-0.788
233°	-0.7986
234°	-0.809
235°	-0.8192
236°	-0.829
237°	-0.8387
238°	-0.848
239°	-0.8572
240°	-0.866
241°	-0.8746
242°	-0.8829
243°	-0.891
244°	-0.8988
245°	-0.9063
246°	-0.9135
247°	-0.9205
248°	-0.9272
249°	-0.9336
250°	-0.9397
251°	-0.9455
252°	-0.9511
253°	-0.9563
254°	-0.9613
255°	-0.9659
256°	-0.9703
257°	-0.9744
258°	-0.9781
259°	-0.9816
260°	-0.9848
261°	-0.9877
262°	-0.9903
263°	-0.9925
264°	-0.9945
265°	-0.9962
266°	-0.9976
267°	-0.9986
268°	-0.9994
269°	-0.9998
270°	-1

…

Таблица синусов для углов от 271° до 360°

Угол	Sin (Синус)
271°	-0.9998
272°	-0.9994
273°	-0.9986
274°	-0.9976
275°	-0.9962
276°	-0.9945
277°	-0.9925
278°	-0.9903
279°	-0.9877
280°	-0.9848
281°	-0.9816
282°	-0.9781
283°	-0.9744
284°	-0.9703
285°	-0.9659
286°	-0.9613
287°	-0.9563
288°	-0.9511
289°	-0.9455
290°	-0.9397
291°	-0.9336
292°	-0.9272
293°	-0.9205
294°	-0.9135
295°	-0.9063
296°	-0.8988
297°	-0.891
298°	-0.8829
299°	-0.8746
300°	-0.866
301°	-0.8572
302°	-0.848
303°	-0.8387
304°	-0.829
305°	-0.8192
306°	-0.809
307°	-0.7986
308°	-0.788
309°	-0.7771
310°	-0.766
311°	-0.7547
312°	-0.7431
313°	-0.7314
314°	-0.7193
315°	-0.7071
316°	-0.6947
317°	-0.682
318°	-0.6691
319°	-0.6561
320°	-0.6428
321°	-0.6293
322°	-0.6157
323°	-0.6018
324°	-0.5878
325°	-0.5736
326°	-0.5592
327°	-0.5446
328°	-0.5299
329°	-0.515
330°	-0.5
331°	-0.4848
332°	-0.4695
333°	-0.454
334°	-0.4384
335°	-0.4226
336°	-0.4067
337°	-0.3907
338°	-0.3746
339°	-0.3584
340°	-0.342
341°	-0.3256
342°	-0.309
343°	-0.2924
344°	-0.2756
345°	-0.2588
346°	-0.2419
347°	-0.225
348°	-0.2079
349°	-0.1908
350°	-0.1736
351°	-0.1564
352°	-0.1392
353°	-0.1219
354°	-0.1045
355°	-0.0872
356°	-0.0698
357°	-0.0523
358°	-0.0349
359°	-0.0175
360°	0

…

Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.

Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».

Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.

Пример

Чему равен синус 45? …

— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071

---

Автор: Bill4iam

---

kvn201.com.ua

Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов.

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов. Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Вариант для печати. sin(0°)=sin(360°)=0; точная, но чуть более сложная таблица ( с точностью до 1″) здесь. Углы 1° — 90° Углы 91° — 180° Углы 181° — 270° Углы 271° — 360° Угол Sin 1° sin= 0.0175 2° sin= 0.0349 3° sin= 0.0523 4° sin= 0.0698 5° sin= 0.0872 6° sin= 0.1045 7° sin= 0.1219 8° sin= 0.1392 9° sin= 0.1564 10° sin= 0.1736 11° sin= 0.1908 12° sin= 0.2079 13° sin= 0.225 14° sin= 0.2419 15° sin= 0.2588 16° sin= 0.2756 17° sin= 0.2924 18° sin= 0.309 19° sin= 0.3256 20° sin= 0.342 21° sin= 0.3584 22° sin= 0.3746 23° sin= 0.3907 24° sin= 0.4067 25° sin= 0.4226 26° sin= 0.4384 27° sin= 0.454 28° sin= 0.4695 29° sin= 0.4848 30° sin= 0.5 31° sin= 0.515 32° sin= 0.5299 33° sin= 0.5446 34° sin= 0.5592 35° sin= 0.5736 36° sin= 0.5878 37° sin= 0.6018 38° sin= 0.6157 39° sin= 0.6293 40° sin= 0.6428 41° sin= 0.6561 42° sin= 0.6691 43° sin= 0.682 44° sin= 0.6947 45° sin= 0.7071 46° sin= 0.7193 47° sin= 0.7314 48° sin= 0.7431 49° sin= 0.7547 50° sin= 0.766 51° sin= 0.7771 52° sin= 0.788

dpva.ru

Тригонометрическая таблица

В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:

sin 0⁰=0, cos 0⁰ = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 90⁰ = 1, cos 90⁰ =0, ctg90⁰ = 0,тангенс от 90⁰ будет неопределенным

Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:

sin 30⁰ = 1/2, cos 30⁰ = √3/2, tg 30⁰ = √3/3, ctg 30⁰ = √3
sin 45⁰ = √2/2, cos 45⁰ = √2/2, tg 45⁰= 1, ctg 45⁰ = 1
sin 60⁰ = √3/2, cos 60⁰ = 1/2, tg 60⁰ =√3 , ctg 60⁰ = √3/3

Изобразим все полученные значения в виде тригонометрической таблицы:

Таблица синусов, косинусов, тангенсов и котангенсов!

Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

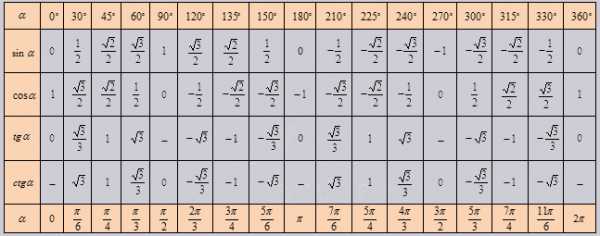
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0⁰+360⁰*z …. 330⁰+360⁰*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

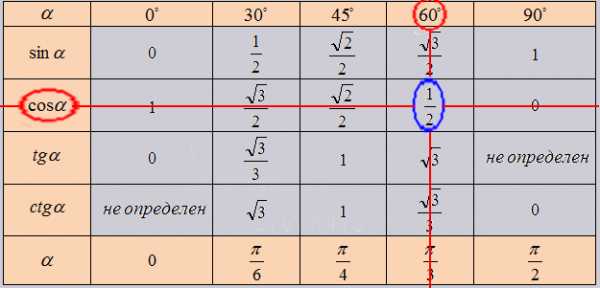
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020⁰ = 300⁰+360⁰*2. Найдем по таблице.

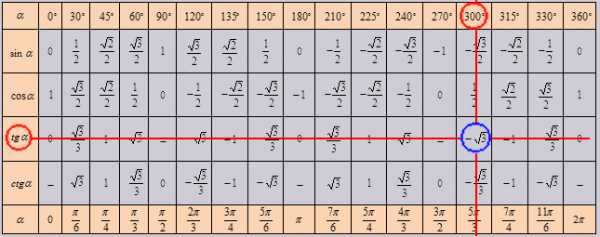
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.

Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

Синус и косинус

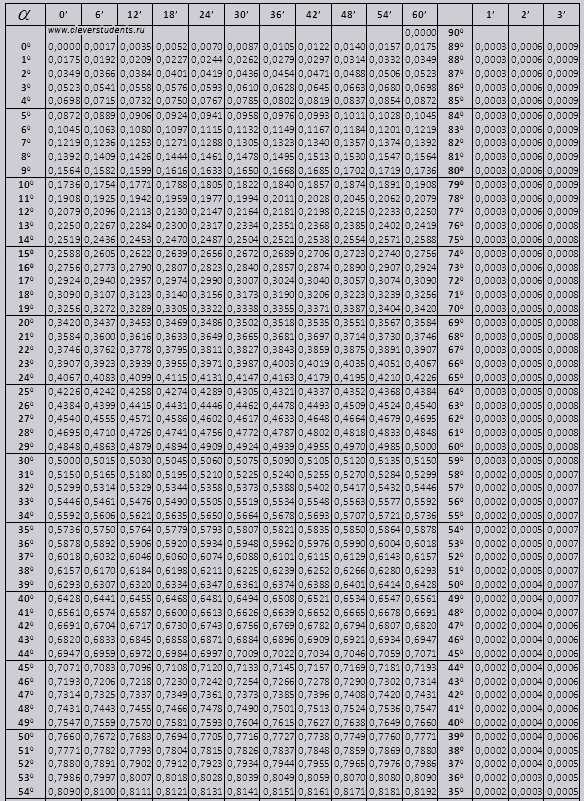
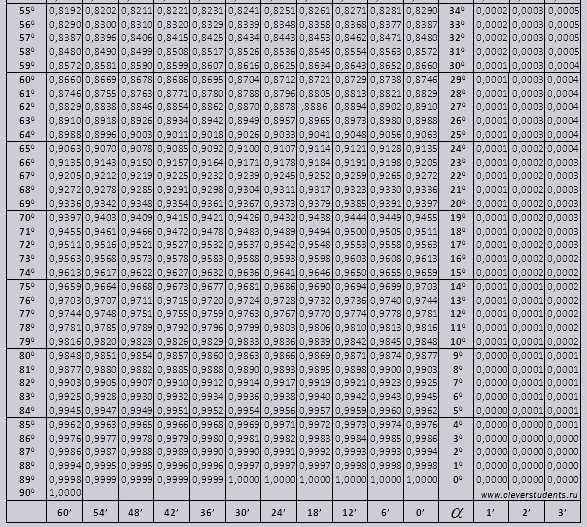
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.

tg до 900 и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.

Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20⁰ = 0.9397

Значения tg угла до 90⁰ и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78⁰ 37мин = 4,967

а ctg 20⁰ 13мин = 25,83

Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!

Заметка: Стеновые отбойники — отбойная доска для защиты стен. Перейдите по ссылке настенные отбойники бескаркасные (http://www.spi-polymer.ru/otboyniki/) и узнайте подробнее.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

reshit.ru

Основные формулы тригонометрии | umath.ru

1. Определения синуса, косинуса, тангенса и котангенса угла.

Синус угла  (обозначается ) – ордината точки , полученной поворотом точки вокруг начала координат на угол .

Косинус угла (обозначается ) – абсцисса точки , полученной поворотом точки вокруг начала координат на угол .

Тангенс угла (обозначается ) – отношение синуса угла к его косинусу, т.е.

Котангенс угла (обозначается ) – отношение косинуса угла к его синусу, т.е.
2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.

Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :

Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом функции:Число является наименьшим положительным периодом синуса и косинуса, а число – наименьшим положительным периодом тангенса и котангенса.
Для любого целого справедливы равенства
5. Формулы сложения:
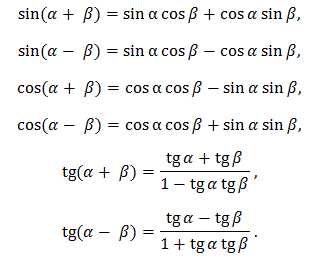
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10. Формулы суммы и разности косинусов:
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:

umath.ru

синусы и косинусы, тангенсы, котангенсы

Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах. На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов.

Пользоваться таблицами просто. Пример: найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5. Те цифры, что находятся вверху и внизу таблицы (со штрихами: ‘) это минуты. Если в задаче они тоже даны, то это лишь конкретизирует значения градусов, они необязательны для нахождения. Возможно, вам также будет интересна полная таблица синусов и таблица производных.

https://uchim.org/matematika/tablica-bradisa — uchim.org

Синусы и косинусы

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	cos	1′	2′	3′
											0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85°	3	6	9
5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80°	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75°	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70°	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65°	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60°	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55°	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50°	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45°	2	4	6
45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40°	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35°	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829

uchim.org

Синус косинус и тангенс — материалы для подготовки к ЕГЭ по Математике

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол обозначается соответствующей греческой буквой .

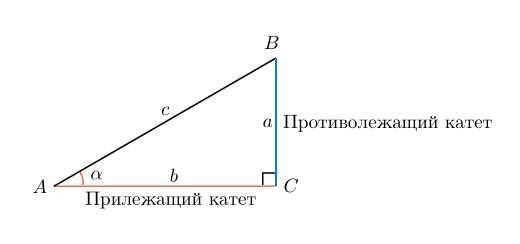
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

Давайте докажем некоторые из них.

1. Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
2. С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла  катет а будет прилежащим.Получаем, что . Иными словами, .
3. Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
4. Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

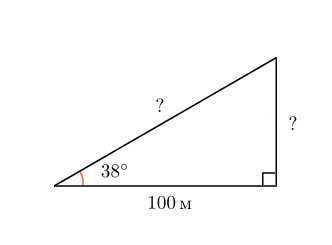
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от  до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

Ты нашел то, что искал? Поделись с друзьями!

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол  равен , . Найдите .

Задача решается за четыре секунды.

Поскольку , .

2. В треугольнике угол  равен , , . Найдите .

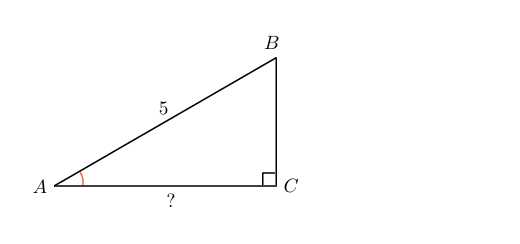
Имеем:

Отсюда

Найдем  по теореме Пифагора.

Задача решена.

Часто в задачах встречаются треугольники с углами  и  или с углами  и . Основные соотношения для них запоминайте наизусть!

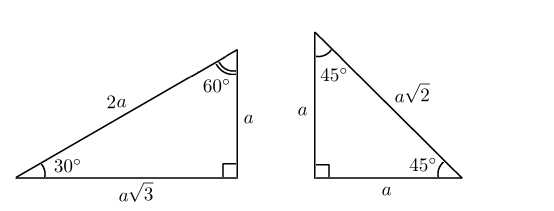
Для треугольника с углами  и  катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами  и  — равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru