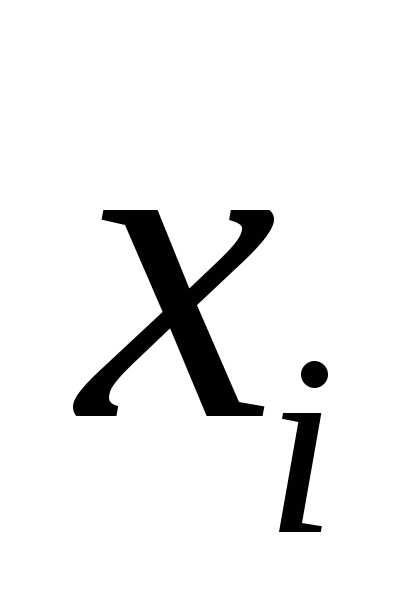Дискретные случайные величины. Пример решения задачи на Викиматик
Случайной величиной называют переменную величину, которая в результате каждого испытания принимает одно заранее неизвестное значение, зависящее от случайных причин. Случайные величины обозначают заглавными латинскими буквами: $X,\ Y,\ Z,\ \dots $ По своему типу случайные величины могут быть дискретными и непрерывными.
Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.
Пример 1. Приведем примеры дискретных случайных величин:
а) число попаданий в мишень при $n$ выстрелах, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
б) число выпавших гербов при подкидывании монеты, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
в) число прибывших кораблей на борт (счетное множество значений).
г) число вызовов, поступающих на АТС (счетное множество значений).
1. Закон распределения вероятностей дискретной случайной величины.
Дискретная случайная величина $X$ может принимать значения $x_1,\dots ,\ x_n$ с вероятностями $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Соответствие между этими значениями и их вероятностями называется законом распределения дискретной случайной величины. Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.
$\begin{array}{|c|c|}
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end{array}$
Пример 2. Пусть случайная величина $X$ — число выпавших очков при подбрасывании игрального кубика. Такая случайная величина $X$ может принимать следующие значения $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятности всех этих значений равны $1/6$. Тогда закон распределения вероятностей случайной величины $X$:
$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$
Замечание. Поскольку в законе распределения дискретной случайной величины $X$ события $1,\ 2,\ \dots ,\ 6$ образуют полную группу событий, то в сумме вероятности должны быть равны единице, то есть $\sum{p_i}=1$.
2. Математическое ожидание дискретной случайной величины.
Математическое ожидание случайной величины задает ее «центральное» значение. Для дискретной случайной величины математическое ожидание вычисляется как сумма произведений значений $x_1,\dots ,\ x_n$ на соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$, то есть: $M\left(X\right)=\sum^n_{i=1}{p_ix_i}$. В англоязычной литературе используют другое обозначение $E\left(X\right)$.
Свойства математического ожидания $M\left(X\right)$:
- $M\left(X\right)$ заключено между наименьшим и наибольшим значениями случайной величины $X$.
- Математическое ожидание от константы равно самой константе, т.е. $M\left(C\right)=C$.
- Постоянный множитель можно выносить за знак математического ожидания: $M\left(CX\right)=CM\left(X\right)$.
- Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
- Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.
Пример 3. Найдем математическое ожидание случайной величины $X$ из примера $2$.
$$M\left(X\right)=\sum^n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$
Можем заметить, что $M\left(X\right)$ заключено между наименьшим ($1$) и наибольшим ($6$) значениями случайной величины $X$.
Пример 4. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=2$. Найти математическое ожидание случайной величины $3X+5$.
Используя вышеуказанные свойства, получаем $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2+5=11$.
Пример 5. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=4$. Найти математическое ожидание случайной величины $2X-9$.
Используя вышеуказанные свойства, получаем $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4-9=-1$.
3. Дисперсия дискретной случайной величины.
Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия.
Дисперсия дискретной случайной величины $X$ равна:
$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}.\ $$
В англоязычной литературе используются обозначения $V\left(X\right),\ Var\left(X\right)$. Очень часто дисперсию $D\left(X\right)$ вычисляют по формуле $D\left(X\right)=\sum^n_{i=1}{p_ix^2_i}-{\left(M\left(X\right)\right)}^2$.
Свойства дисперсии $D\left(X\right)$:
- Дисперсия всегда больше или равна нулю, т.е. $D\left(X\right)\ge 0$.
- Дисперсия от константы равна нулю, т.е. $D\left(C\right)=0$.
- Постоянный множитель можно выносить за знак дисперсии при условии возведения его в квадрат, т.е. $D\left(CX\right)=C^2D\left(X\right)$.
- Дисперсия суммы независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
- Дисперсия разности независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.
Пример 6. Вычислим дисперсию случайной величины $X$ из примера $2$.
$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}={{1}\over {6}}\cdot {\left(1-3,5\right)}^2+{{1}\over {6}}\cdot {\left(2-3,5\right)}^2+\dots +{{1}\over {6}}\cdot {\left(6-3,5\right)}^2={{35}\over {12}}\approx 2,92.$$
Пример 7. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=2$. Найти дисперсию случайной величины $4X+1$.
Используя вышеуказанные свойства, находим $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\left(X\right)=16\cdot 2=32$.
Пример 8. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=3$. Найти дисперсию случайной величины $3-2X$.
Используя вышеуказанные свойства, находим $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.
4. Функция распределения дискретной случайной величины.
Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.
Функцией распределения случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X < x\right)$
Свойства функции распределения:
- $0\le F\left(x\right)\le 1$.
- Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha < X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
- $F\left(x\right)$ — неубывающая.
- ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.
Пример 9. Найдем функцию распределения $F\left(x\right)$ для закона распределения дискретной случайной величины $X$ из примера $2$.
$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$
Если $x\le 1$, то, очевидно, $F\left(x\right)=0$ (в том числе и при $x=1$ $F\left(1\right)=P\left(X < 1\right)=0$).
Если $1 < x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.
Если $2 < x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.
Если $3 < x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.
Если $4 < x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.
Если $5 < x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.
Если $x > 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+1/6+1/6=1$.
Итак, $F(x)=\left\{\begin{matrix}
0,\ при\ x\le 1,\\
1/6,при\ 1 < x\le 2,\\
1/3,\ при\ 2 < x\le 3,\\
1/2,при\ 3 < x\le 4,\\
2/3,\ при\ 4 < x\le 5,\\
5/6,\ при\ 4 < x\le 5,\\
1,\ при\ x > 6.
\end{matrix}\right.$
График функции распределения $F\left(x\right)$:

wikimatik.ru
Дискретная случайная величина и ее числовые характеристики. Примеры решения задач
Дискретная случайная величина и ее числовые характеристики
Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
Закон распределения
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Функцией распределения дискретной случайной величины называют функцию:
,
определяющую для каждого значения аргумента x вероятность того, что случайная величина X примет значение, меньшее этого x.
Математическое ожидание дискретной случайной величины
,
где — значение дискретной случайной величины; — вероятности принятия случайной величиной X значений .
Если случайная величина принимает счетное множество возможных значений, то:
Математическое ожидание числа наступлений события в n независимых испытаниях:
,
где p — вероятность наступления события.
Дисперсия и среднеквадратическое отклонение дискретной случайной величины
Дисперсия дискретной случайной величины:
или .
Дисперсия числа наступлений события в n независимых испытаниях
,
где p — вероятность наступления события.
Среднеквадратическое отклонение дискретной случайной величины:
.
Пример 1
Составьте закон распределения вероятностей дискретной случайной величины (д.с.в.) X – числа k выпадений хотя бы одной «шестерки» в n = 8 бросаниях пары игральных кубиков. Постройте многоугольник распределения. Найдите числовые характеристики распределения (моду распределения, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение s(X)). Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз». Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу». P(Ā) = q = = .
Соответственно,
P(A) = p = 1 – P(Ā) = .
Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X – число k выпадений хотя одной шестерки при бросании двух кубиков подчиняется биномиальному закону распределения вероятностей:
где = – число сочетаний из n по k.
Проведенные для данной задачи расчеты удобно оформить в виде таблицы:
Распределение вероятностей д.с.в. X º k (n = 8; p = ; q
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Сумма |
8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
| ||
Pn(k) | 0,0541 | 0,1904 | 0,2932 | 0,258 | 0,1419 | 0,05 | 0,011 | 0,0013 | 0,0001 | 1 |
Полигон (многоугольник) распределения вероятностей дискретной случайной величины X представлен на рис.:
Рис. Полигон распределения вероятностей д.с.в. X=k.
Вертикальной линией показано математическое ожидание распределения M(X).
Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P8(2) = 0,2932 максимально). Математическое ожидание по определению равно:
где xk = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:
D(X) = = 4,8097.
Среднее квадратическое отклонение (СКО):
s(X) = = 2,1931.
Пример2
Дискретная случайная величинаX задана законом распределения
Найти функцию распределения F(x) и построить ее график.Решение. Если , то (третье свойство).
Если , то . Действительно, X может принять значение 1 с вероятностью 0,3.
Если , то . Действительно, если удовлетворяет неравенству
, то равно вероятности события , которое может быть осуществлено, когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события равна сумме вероятностей 0,3 + 0,1=0,4. Если , то . Действительно, событие достоверно, следовательно, его вероятность равна единице. Итак, функция распределения аналитически может быть записана так:
График этой функции:
Пример3
В магазине куплено 3 электроприбора: чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них соответственно равны . Составить закон распределения случайной величины X – числа приборов, вышедших из строя в течение гарантийного срока.Решение. X – число приборов, вышедших из строя, имеет следующие возможные значения:
— все три прибора не выйдут из строя в течении гарантийного срока;
— один прибор выйдет из строя;
— два прибора выйдут из строя;
— три прибора выйдут из строя.
Найдем соответствующие этим значениям вероятности. По условию, вероятности выхода из строя приборов равны: тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны:
Закон распределения имеет вид:
0 | 1 | 2 | 3 | |
0,684 | 0,283 | 0,032 | 0,001 |
Проверка: 1.
www.matem96.ru
Дискретные и непрерывные случайные величины.
По своей физической природе случайные величины могут быть детерминированными и случайными.
Дискретной называют случайную величину, отдельные значения которой можно перенумеровать (число изделий, количество деталей – бракованных и годных и т.п.).
Непрерывной называют случайную величину, возможные значения которой заполняют некоторый промежуток (отклонение размера изготовленной детали от номинала, погрешность измерения, величина отклонения формы детали, высота микронеровностей и т.п.).
Случайная величина не может характеризоваться каким-то одним значением. Для неё необходимо указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.
В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом x > X. Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
| F (х) = Р(Х < х ). |
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение σ(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
Случайная величина характеризуется в теории вероятностей законом ее распределения. Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины — дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.
Дифференциальный закон распределенияхарактеризуетсяплотностью распределения вероятностей f(x) случайной величиных. Вероятность Р попадания случайной величины в интервал от х1 до х2при этом дается формулой:
Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х1 до х2 к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.
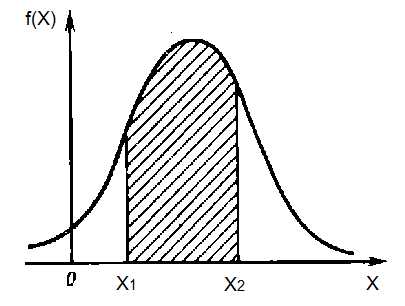
В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.
Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой
Вероятность, что случайная величина будет меньше х1 дается значением функции F(х) при х = х1 :
Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений. К ним относятся моменты слу-чайных величин: начальные и центральные, которые представляют собой некоторые средние значения. При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.
Начальный момент k-го порядка определяется формулой:
Наибольший практический интерес представляет начальный момент первого порядка — математическое ожидание случайной величины m1 (k=1):
Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.
Центральный момент k-го порядка определяется формулой:
Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных значений этой величины:
На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:
Дрейф нуля в усилителях постоянного тока (УПТ). Самопроизвольное изменение напряжения на выходе при отсутствии напряжения на входе – входного сигнала.
Похожие статьи:
poznayka.org
ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ — КиберПедия
ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Одним из важнейших понятий теории вероятностей является понятие случайной величины.
Случайной величиной называется переменная, которая в результате испытания принимает одно и только одно возможное значение, но какое именно – заранее не известно.
Примеры случайных величин:
— количество студентов на лекции;
— количество больных в городе;
— число родившихся в течение суток в г. Кемерово;
— продолжительность человеческой жизни.
Случайные величины принято обозначать прописными латинскими буквами X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z,…
Вероятности случайных величин обозначают буквами с соответствующими индексами — запись показывает вероятность того, что случайная величина принимает значение .
Случайные величины разделяют на дискретные и непрерывные.
Дискретной называют случайную величину, принимающую отдельные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.
Например,
— количество мальчиков, родившихся в каком-либо месяце;
— количество рецептов, поступивших в аптеку в течение дня;
— число ударов пульса больного в минуту;
— количество осложнений после операций в данной больнице.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Число возможных значений непрерывной случайной величины бесконечно.
Например,
— температура воздуха в течение дня;
— продолжительность человеческой жизни;
— время инкубационного периода заболевания.
ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.
Для непрерывной случайной величины можно дать еще одно определение:
Случайная величина называется непрерывной, если ее функция распределения непрерывно в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Непрерывную случайную величину можно задать не только с помощью функции распределения , но и с помощью плотности вероятности.
Плотностью вероятности (плотностью распределения) непрерывной случайной величины называется производная ее функции распределения
Иногда функцию называют дифференциальной функцией распределения или дифференциальным законом распределения.
График плотности вероятности называют кривой распределения. Кривая распределения лежит не ниже оси абсцисс, и площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Свойства плотности вероятности непрерывной случайной величины
1. Плотность вероятности – неотрицательная функция
.
2. Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от ее плотности вероятности в пределах от до
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле
.
ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Одним из важнейших понятий теории вероятностей является понятие случайной величины.
Случайной величиной называется переменная, которая в результате испытания принимает одно и только одно возможное значение, но какое именно – заранее не известно.
Примеры случайных величин:
— количество студентов на лекции;
— количество больных в городе;
— число родившихся в течение суток в г. Кемерово;
— продолжительность человеческой жизни.
Случайные величины принято обозначать прописными латинскими буквами X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z,…
Вероятности случайных величин обозначают буквами с соответствующими индексами — запись показывает вероятность того, что случайная величина принимает значение .
Случайные величины разделяют на дискретные и непрерывные.
Дискретной называют случайную величину, принимающую отдельные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.
Например,
— количество мальчиков, родившихся в каком-либо месяце;
— количество рецептов, поступивших в аптеку в течение дня;
— число ударов пульса больного в минуту;
— количество осложнений после операций в данной больнице.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Число возможных значений непрерывной случайной величины бесконечно.
Например,
— температура воздуха в течение дня;
— продолжительность человеческой жизни;
— время инкубационного периода заболевания.
cyberpedia.su
Законы распределения дискретных случайных величин
Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:
- Биномиальный закон распределения
- Пуассоновский закон распределения
- Геометрический закон распределения
- Гипергеометрический закон распределения
Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.
1. Биномиальный закон распределения.
Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$. Фактически, случайная величина $X$ — это число появлений события $A$ в $n$ независимых испытаний Бернулли. Закон распределения вероятностей случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.
Пример. В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ — числа мальчиков в семье.
Пусть случайная величина $\xi $ — число мальчиков в семье. Значения, которые может принимать $\xi :\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$, где $n=2$ — число независимых испытаний, $p=0,5$ — вероятность появления события в серии из $n$ испытаний. Получаем:
$P\left(\xi =0\right)=C^0_2\cdot {0,5}^0\cdot {\left(1-0,5\right)}^{2-0}={0,5}^2=0,25;$
$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot {\left(1-0,5\right)}^{2-1}=2\cdot 0,5\cdot 0,5=0,5;$
$P\left(\xi =2\right)=C^2_2\cdot {0,5}^2\cdot {\left(1-0,5\right)}^{2-2}={0,5}^2=0,25.$
Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:
$\begin{array}{|c|c|}
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi ) & 0,25 & 0,5 & 0,25 \\
\hline
\end{array}$
Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _{i=1}^{n}P(\xi _{{\rm i}} )=0,25+0,5+0,25=1 $.
Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt{D\left(\xi \right)}=\sqrt{0,5}\approx 0,707$.
2. Закон распределения Пуассона.
Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.
Замечание. Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.
Пример. Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.
Пример. Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.
Пусть дискретная случайная величина $X$ — число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.
$P\left(X=0\right)={{1^0}\over {0!}}\cdot e^{-1}=0,368;$
$P\left(X=1\right)={{1^1}\over {1!}}\cdot e^{-1}=0,368;$
$P\left(X=2\right)={{1^2}\over {2!}}\cdot e^{-1}=0,184;$
$P\left(X=3\right)={{1^3}\over {3!}}\cdot e^{-1}=0,061;$
$P\left(X=4\right)={{1^4}\over {4!}}\cdot e^{-1}=0,015;$
$P\left(X=5\right)={{1^5}\over {5!}}\cdot e^{-1}=0,003;$
$P\left(X=6\right)={{1^6}\over {6!}}\cdot e^{-1}=0,001;$
…
$P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$
Закон распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & … & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & … & {{{\lambda }^k}\over {k!}}\cdot e^{-\lambda } \\
\hline
\end{array}$
Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.
3. Геометрический закон распределения.
Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p{\left(1-p\right)}^{k-1},\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.
Пример. Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.
Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.
Пример. На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.
Пусть случайная величина $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^{k-1}$, где: $p=2/5$ — вероятность задержания рыбы через шлюз, $q=1-p=3/5$ — вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.
$P\left(X=1\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^0={{2}\over {5}}=0,4;$
$P\left(X=2\right)={{2}\over {5}}\cdot {{3}\over {5}}={{6}\over {25}}=0,24;$
$P\left(X=3\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^2={{2}\over {5}}\cdot {{9}\over {25}}={{18}\over {125}}=0,144;$
$P\left(X=4\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^3+{\left({{3}\over {5}}\right)}^4={{27}\over {125}}=0,216.$
Тогда ряд распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end{array}$
Математическое ожидание:
$M\left(X\right)=\sum^n_{i=1}{x_ip_i}=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$
Дисперсия:
$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2=}0,4\cdot {\left(1-2,176\right)}^2+0,24\cdot {\left(2-2,176\right)}^2+0,144\cdot {\left(3-2,176\right)}^2+$
$+\ 0,216\cdot {\left(4-2,176\right)}^2\approx 1,377.$
Среднее квадратическое отклонение:
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{1,377}\approx 1,173.$
4. Гипергеометрический закон распределения.
Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ — число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:
$P\left(X=k\right)={{C^k_mC^{n-k}_{N-m}}\over {C^n_N}}$
Замечание. Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.
$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК. Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.
Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}$.
Пример. В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.
а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;
б) Найдите числовые характеристики этого распределения.
Пусть случайная величина $X$ — число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ — размер совокупности, $m=5$ — число успехов в совокупности, $n=3$ — размер выборки, $k=0,\ 1,\ 2,\ 3$ — число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)={C_{m}^{k} \cdot C_{N-m}^{n-k} \over C_{N}^{n} } $. Имеем:
$P\left(X=0\right)={{C^0_5\cdot C^3_3}\over {C^3_8}}={{1}\over {56}}\approx 0,018;$
$P\left(X=1\right)={{C^1_5\cdot C^2_3}\over {C^3_8}}={{15}\over {56}}\approx 0,268;$
$P\left(X=2\right)={{C^2_5\cdot C^1_3}\over {C^3_8}}={{15}\over {28}}\approx 0,536;$
$P\left(X=3\right)={{C^3_5\cdot C^0_3}\over {C^3_8}}={{5}\over {28}}\approx 0,179.$
Тогда ряд распределения случайной величины $X$:
$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end{array}$
Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.
$M\left(X\right)={{nm}\over {N}}={{3\cdot 5}\over {8}}={{15}\over {8}}=1,875.$
$D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}={{3\cdot 5\cdot \left(1-{{5}\over {8}}\right)\cdot \left(1-{{3}\over {8}}\right)}\over {8-1}}={{225}\over {448}}\approx 0,502.$
$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{0,502}\approx 0,7085.$
wikimatik.ru
Дискретные и непрерывные случайные величины
Как правило, при изготовлении продукции на процесс её производства оказывает влияние множество различных факторов, в результате чего наблюдается разброс значений показателей качества продукцию. Таким образом, показатели качества изготовляемой продукции или оказываемых услуг следует рассматривать как случайные величины.
Случайной величиной называется такая величина, которая в результате испытаний в границах определенного интервала может принимать различные числовые значения (согласно СТБ ГОСТ Р 50779.10 случайная величина — переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей).
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные значения и не могут принимать значения промежуточные между ними. Например, количество негодных деталей в партии может быть только целым положительным числом 1, 2, 3 и т.д., но не может быть 1,3; 1,7 и т.п.
Непрерывной случайной величинойназывается такая величина, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.
Например, действительные размеры деталей, обработанных на станке, являются случайными величинами непрерывного типа, так как они могут принять любое численное значение в определенных границах.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей.
Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей для каждого из значений, называется распределением случайных величин(согласно СТБ ГОСТ Р 50779.10 распределение – это функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений).
Распределение случайной величины можно представить в табличном, графическом виде и при помощи статистических оценок.
При представлении распределения случайной величины в табличном виде каждому номеру исследуемой единицы продукции (номеру измерения) соответствует значение показателя качества для данной единицы продукции (результат измерения).
При представлении распределения случайной величины в графическом виде строят график распределения в координатах значение случайной величины – вероятность (частота, частость) значения случайной величины.
На рисунке ниже показаны графики распределения дискретной и непрерывной случайных величин.
Рисунок — График распределения дискретной случайной величины
Рисунок — График распределения непрерывной случайной величины
Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате испытаний.
Следовательно, эмпирическим распределением случайной величиныназывается совокупность экспериментальных ее значений, расположенных в порядке возрастания, с указанием частот или частостей для каждого из значений(согласно СТБ ГОСТ Р 50779.10 распределение частот – это эмпирическое отношение между значениями признака и его частотами или его относительными частотами).
Таблица. Пример табличного представления теоретического распределения дискретной случайной величины
X | X1 | X2 | X3 | X4 | X5 | |
P(X) | P(X1) | P(X2) | P(X3) | P(X4) | P(X5) | P(Xi)=1 |
Таблица. Пример табличного представления эмпирического распределения дискретной случайной величины
X | X1 | X2 | X3 | X4 | X5 | |
mx | 1/30 | 3/30 | 15/30 | 6/30 | 5/30 | mxi=1 |
Графически эмпирическое распределение дискретной случайной величины можно представить в виде столбиковой диаграммы, образуемой набором столбцов равной ширины, высоты которых пропорциональны частотам дискретных значений случайной величины.
Рисунок — Столбиковая диаграмма дискретной случайной величины.
Если случайная величина является непрерывной, то возникают некоторые сложности с представлением ее распределения в виде таблицы или графика. Поэтому на практике при изучении случайных величин непрерывного типа полученные значения разбивают на равные интервалы с таким расчетом, чтобы значение интервала было несколько больше погрешности измерения исследуемой величины. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь следующий вид.
Таблица. Эмпирическое распределение случайной величины непрерывного типа.
Интервал значений Х | Среднее арифметическое значение | Частота fi | Частость mi |
160,031 — 160,033 | 160,032 | 3 | 0,03 |
160,033 — 160,035 | 160,034 | 3 | 0,03 |
160,035 — 160,037 | 160,036 | 5 | 0,05 |
160,037 — 160,039 | 160,038 | 26 | 0,26 |
160,039 — 160,041 | 160,040 | 31 | 0,31 |
160,041 — 160,043 | 160,042 | 19 | 0,19 |
160,043 — 160,045 | 160,044 | 8 | 0,08 |
160,045 — 160,047 | 160,046 | 5 | 0,05 |
fi= 100 | mi = 1 |
Эмпирическое распределение случайной непрерывной величины графически может быть представлено в виде гистограммы распределения, полигона частот или полигона кумулятивных частот.
Гистограмма распределения представляет собой совокупность соприкасающихся прямоугольников, основания которых равны интервалам разбиения непрерывной случайной величины, а площади пропорциональны частотам, с которыми значения случайной величины попадают в эти интервалы (согласно СТБ ГОСТ Р 50779.10 гистограмма (распределения) – это графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов).
Рисунок — Гистограмма распределения случайной непрерывной величины.
Полигон частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны серединам интервалов разбиения, а ординаты – соответствующим частотам.
Рисунок — Полигон частот случайной непрерывной величины.
Полигон кумулятивных частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам интервалов разбиения, а ординаты – либо кумулятивным частотам, либо кумулятивным частостям (кумулятивным относительным частотам).
Рисунок — Полигон кумулятивных частот случайной непрерывной величины.
При теоретических описаниях случайных величин непрерывного типа используется функция распределения. Теоретическое распределение случайной непрерывной величины графически может быть представлено в виде интегральной, обратной интегральной, дифференциальной функций распределения и функции интенсивности.
Пусть Х — случайная величина, а х — какое-либо действительное число (при этом Х < х). Событию Х < х отвечает вероятность Р(Х < х), которая является функцией F(х), т.е.
Р(Х < х) = F(х)
F(Х) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения.
Для дискретной случайной величины интегральная функция распределения F(Х) легко определяется по таблице или графику.
Таким образом, для приведенного выше примера распределения дискретной случайной величины (при Х < 4):
F(X) = Р(Х<4) = P(Х=1) + P(Х=2) + P(Х=3) = 1/30 + 4/30 +15/30 = 19/30
График интегральной функции распределения дискретной случайной величины будет иметь вид ступенчатой кривой. Ординаты кривой для любого значения Х будут представлять сумму вероятностей предшествующих значений.
Рисунок — Интегральная функция распределения дискретной случайной величины
Вероятность того, что случайная величина при испытаниях окажется в границах двух заданных значений х1 и х2 (х2 > х1) равна приращению интегральной функции на этом участке, т.е.
Р(х1 ≤ Х ≤ х2) = Р(Х < х2) — Р(Х < х1) = F(Х2) — F(Х1)
Если обратиться к выше приведенному примеру распределения дискретной случайной величины, то при х1= 2 и х2 = 3:
Р(2≤Х≤3) = Р(Х < 3) — Р(Х < 2)= F(Х2) — F(Х1)= 4/30—1/30 = 3/30
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид монотонно возрастающей кривой. На практике с помощью интегральной функции распределения определяют теоретические частоты распределения.
Рисунок — Интегральная функция распределения
непрерывной случайной величины
Обратная интегральная функция распределения равна разности между единицей и интегральной функции распределения.
Плотностью распределения (дифференциальной функцией распределения) случайной величины называют первую производную от интегральной функции распределения:
Для аналитического описания непрерывной случайной величины в теории надежности используют функцию интенсивности, равную отношению дифференциальной функции распределения к обратной интегральной функции распределения:
Рисунок — Функция интенсивности непрерывной случайной величины.
studfiles.net
Примеры распределений дискретных случайных величин
 Биномиальное
распределение
Биномиальное
распределение
,,,
, .
 Распределение
Пуассона
Распределение
Пуассона
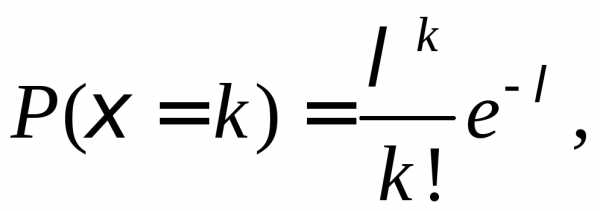
 ,,
,,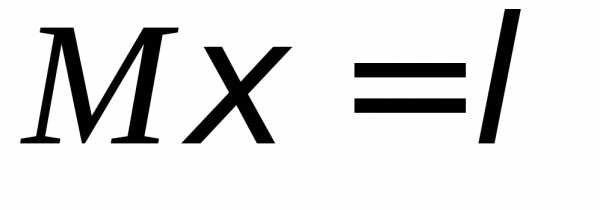 ,
,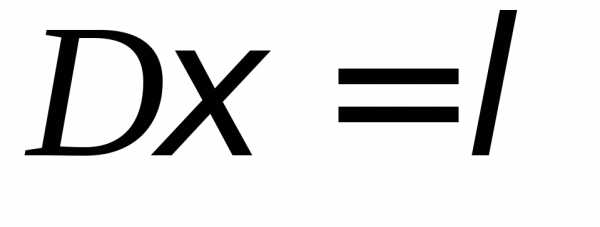 .
.
Примеры распределений непрерывных случайных величин
 Равномерное
распределение
Равномерное
распределение
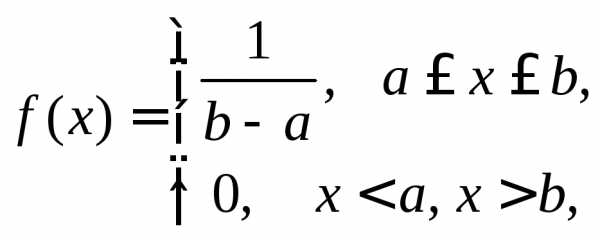
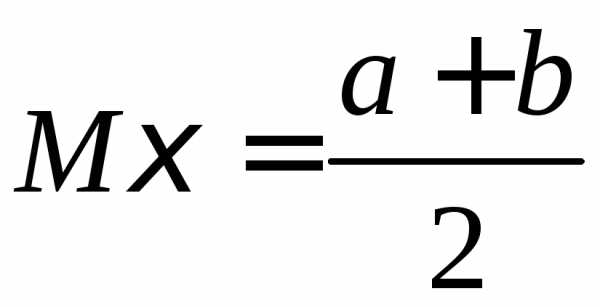 ,
, 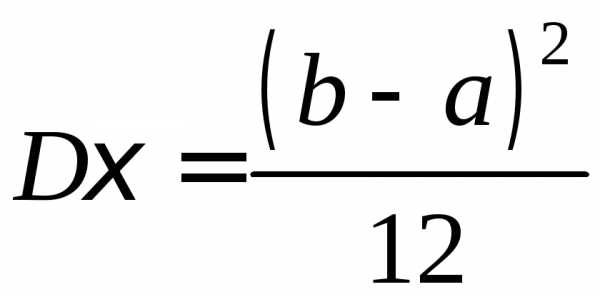 .
.
 Нормальное
распределение (с параметрами
Нормальное
распределение (с параметрами 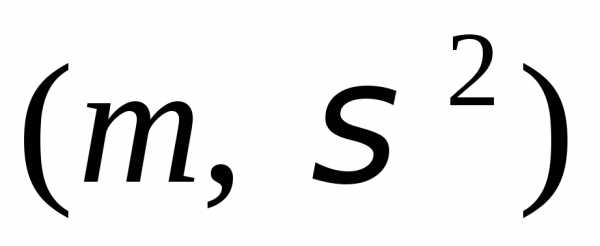 )
)
 ,
, 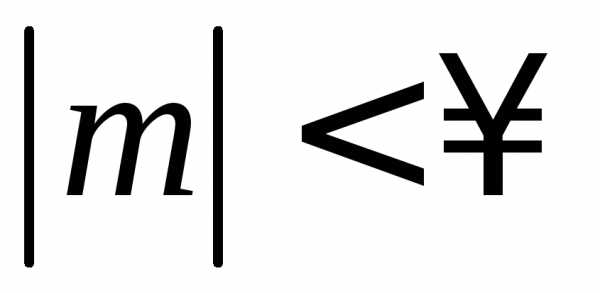 ,
, ,
,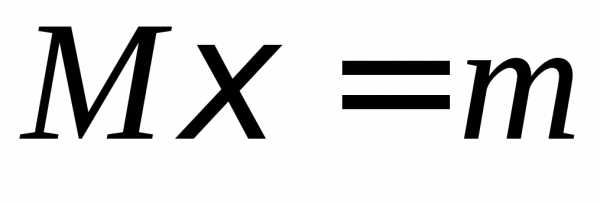 ,
,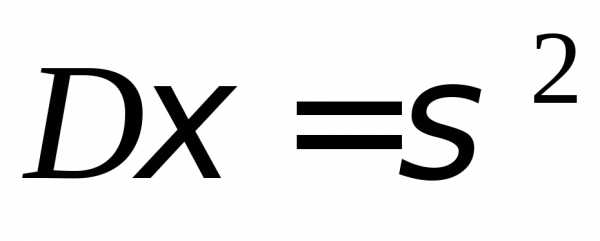 .
.
Запись
означает, что случайная величина распределена нормально с параметрами
распределена нормально с параметрами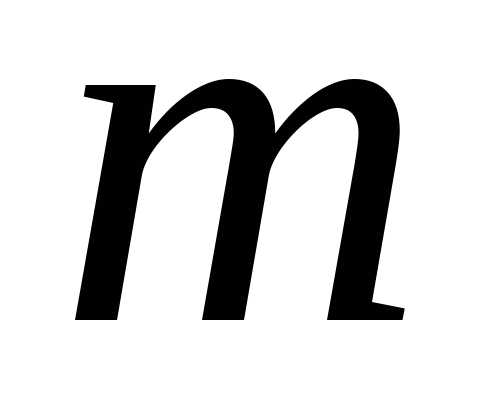 и
и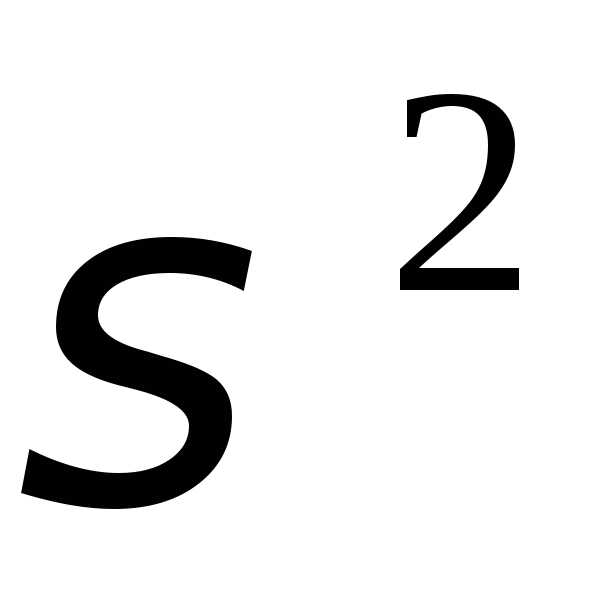 .
.
 Показательное
распределение
Показательное
распределение
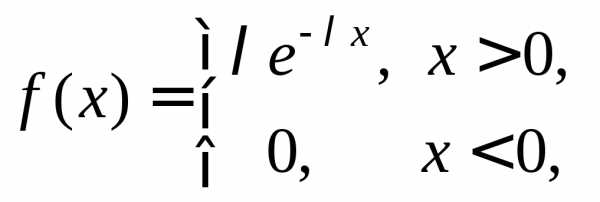
 ,
, 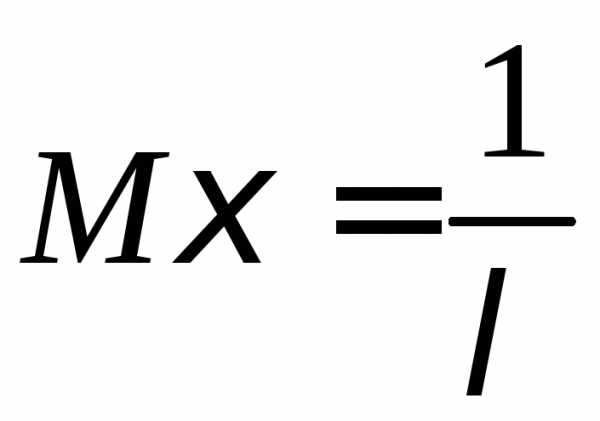 ,
,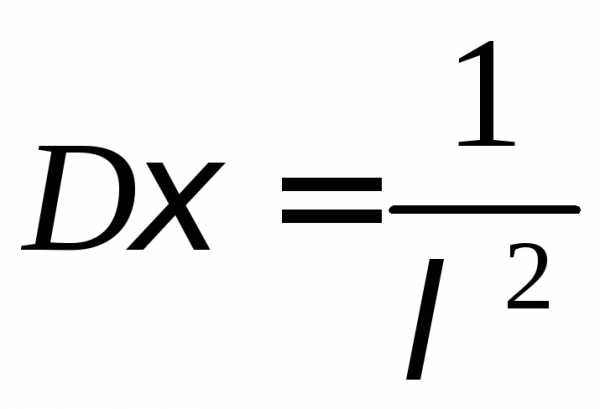 .
.
 Распределение
Релея
Распределение
Релея 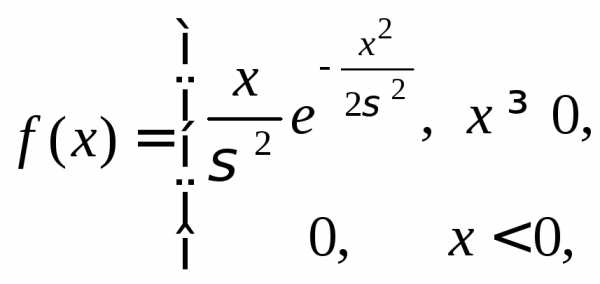
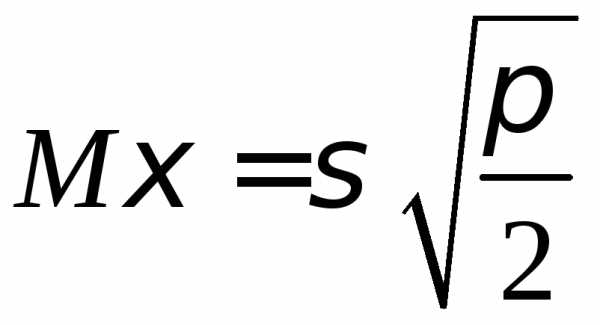 ,
,  .
.
 Гамма-распределение
с параметрами
Гамма-распределение
с параметрами  ,
,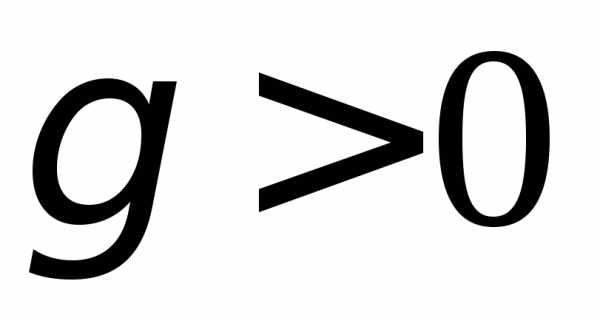
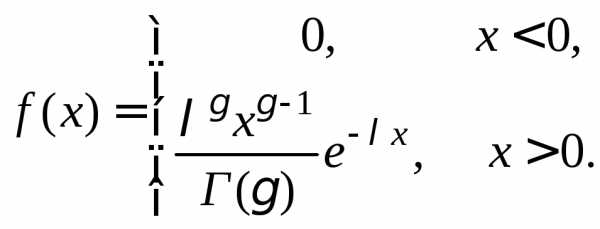
Здесь 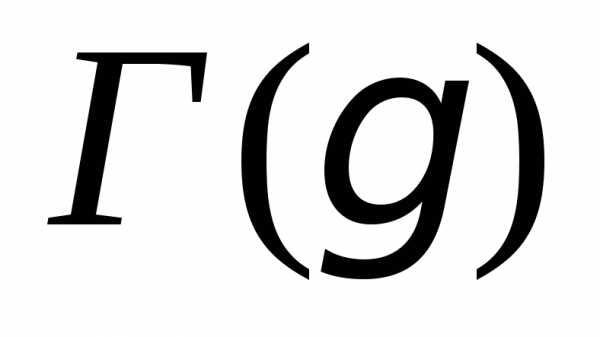 –
гамма-функция:
–
гамма-функция: 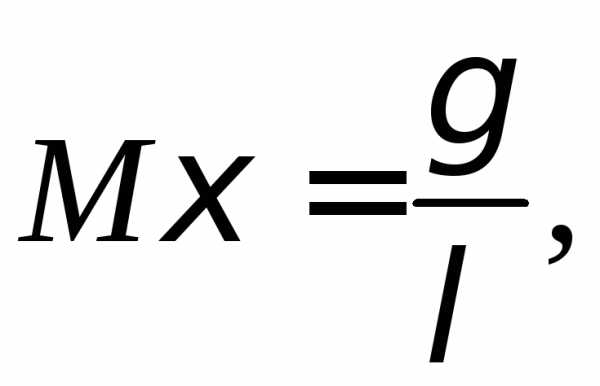
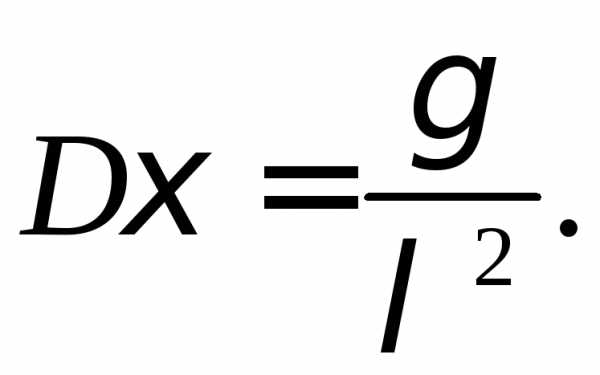
Пример 1. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытания, равны 0,8. Испытания заканчиваются после первого же изделия, не выдержавшего испытания.
1.
Найти закон распределения вероятностей
(ряд распределения) для числа испытаний
(случайной величины  ).
).
2. Построить многоугольник распределения.
3. Найти функцию распределения и построить её график.
4.
Найти: а) 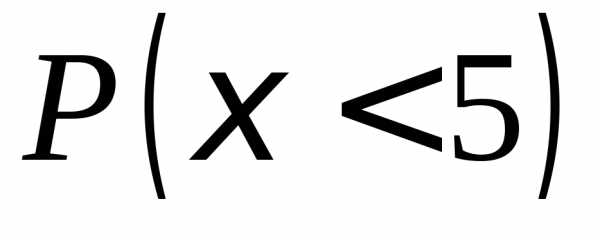 ,
б)
,
б)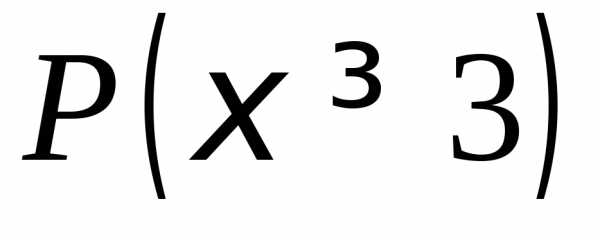 ,
в).
,
в).
Решение. Введем в
рассмотрение случайную величину 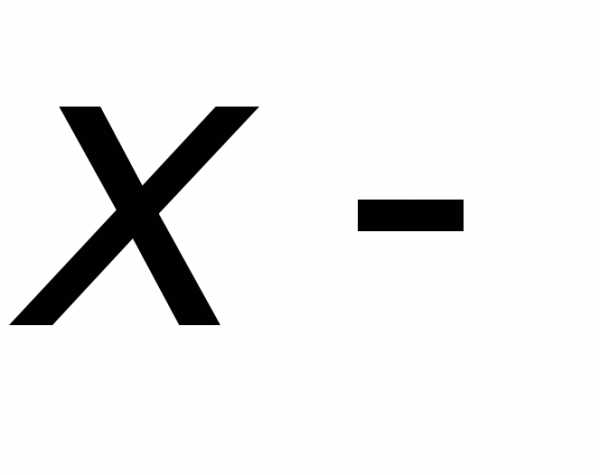 число
изделий, прошедших испытания. Очевидно,
что случайная величина
число
изделий, прошедших испытания. Очевидно,
что случайная величина  может принимать значения от 1 и,
теоретически, до бесконечности.
может принимать значения от 1 и,
теоретически, до бесконечности.
Случайная
величина  примет значение равное
примет значение равное ,
если осуществится событие, состоящее
в том, что
,
если осуществится событие, состоящее
в том, что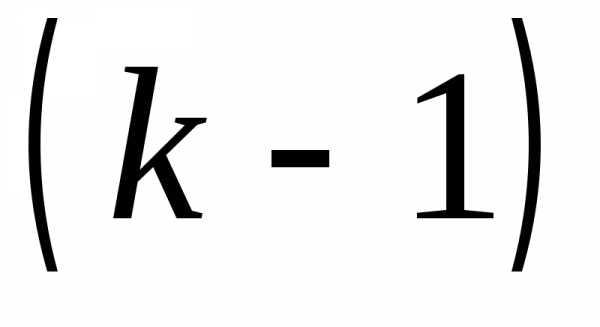 изделия пройдут испытания, а
изделия пройдут испытания, а –е
изделие не пройдет. Если
–е
изделие не пройдет. Если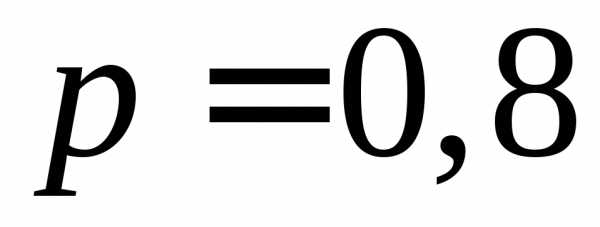 – вероятность того, что изделие пройдет
испытание, а– вероятность того, что изделие не
пройдет испытание, то по теореме умножения
вероятностей случайных событий,,
где.
– вероятность того, что изделие пройдет
испытание, а– вероятность того, что изделие не
пройдет испытание, то по теореме умножения
вероятностей случайных событий,,
где.
Закон распределения вероятностей будет иметь вид
Для
построения многоугольника распределения
в декартовой прямоугольной системе
координат построим точки 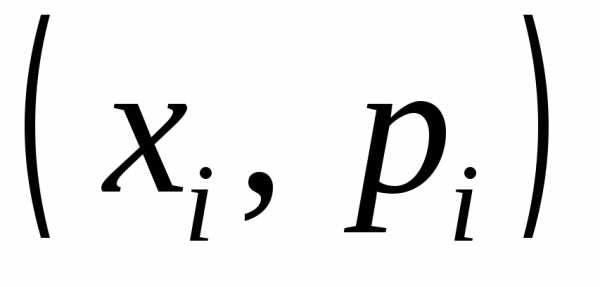 и соединим их ломаной.
и соединим их ломаной.
3. Функция распределения
Для
решаемой задачи 
Строим график функции распределения
4. а)
.
б) ,
в) .
Пример 2. Дискретная
случайная величина  может принимать три значения
может принимать три значения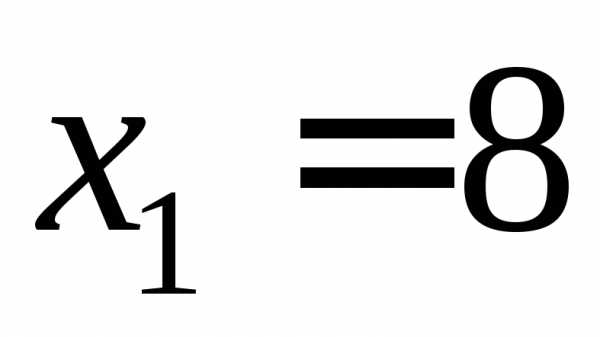 ,
, ,
,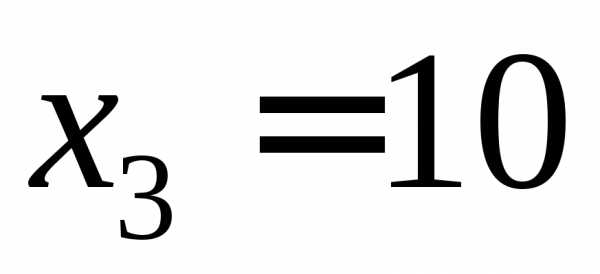 .
Вероятности этих значений соответственно
равны
.
Вероятности этих значений соответственно
равны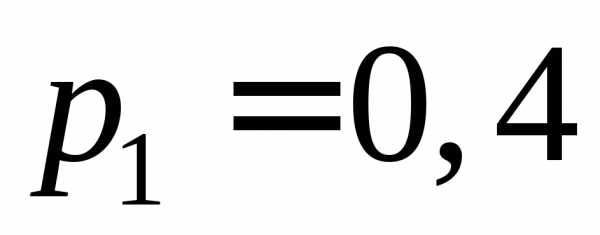 ,
, ,
,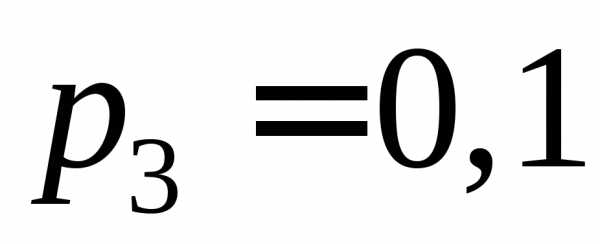 .
Найти математическое ожидание
.
Найти математическое ожидание ,
дисперсию
,
дисперсию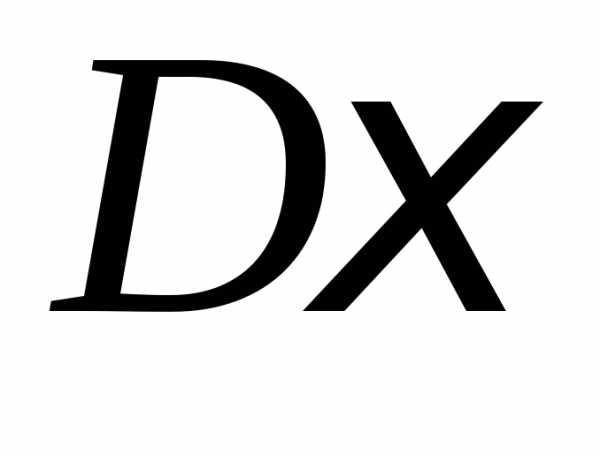 и среднее квадратическое отклонение
и среднее квадратическое отклонение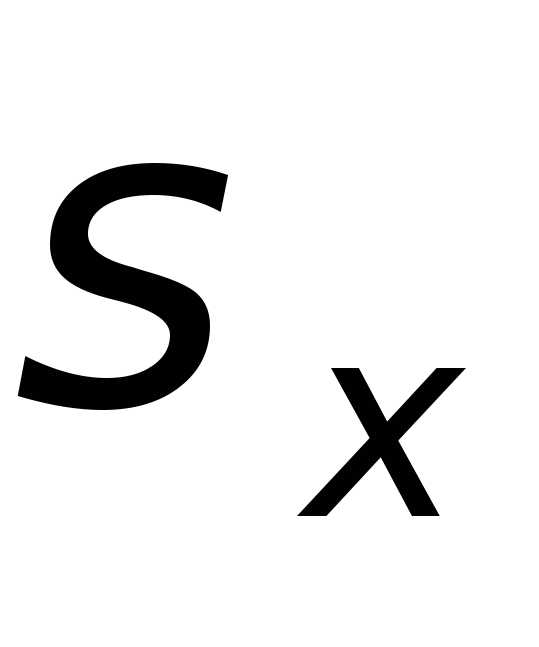 .
.
Решение. Для дискретной случайной величины .
В данном случае .
.
.
Пример
3. Дискретная
случайная величина  может принимать три значения, два из
которых известны
может принимать три значения, два из
которых известны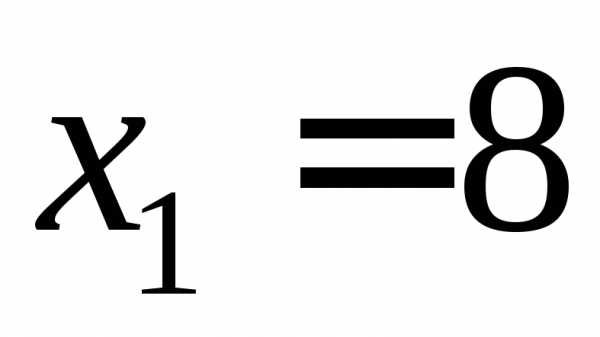 ,
,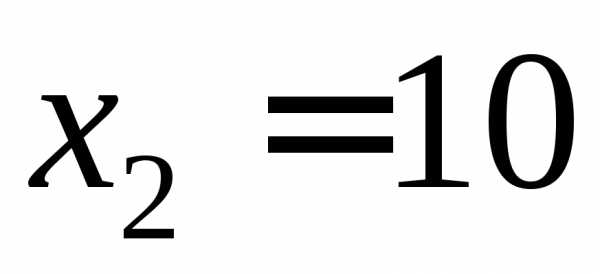 .
Вероятности этих значений соответственно
равны,
.
Вероятности этих значений соответственно
равны,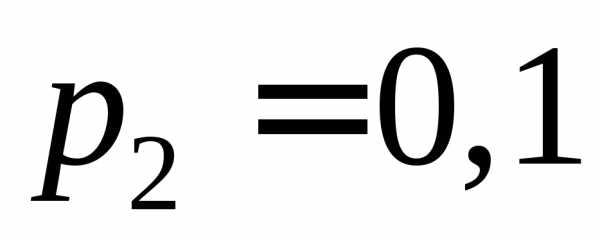 .
Найти закон распределения случайной
величины
.
Найти закон распределения случайной
величины ,
если известно её математическое ожидание.
,
если известно её математическое ожидание.
Решение. Обозначим третье возможное значение
случайной величины через 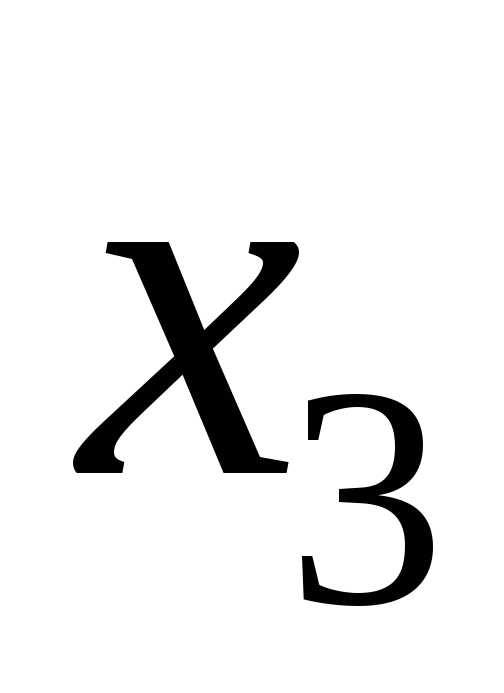 .
Так как для дискретной случайной величины
.
Так как для дискретной случайной величины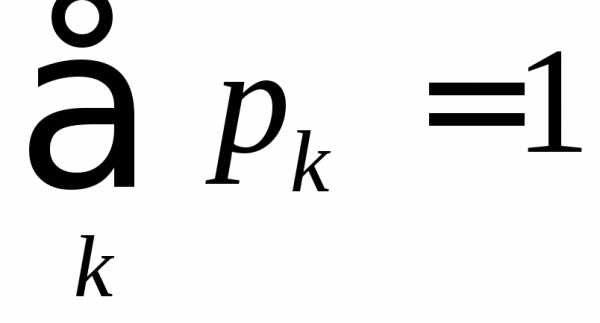 ,
то.
Значение
,
то.
Значение найдем из условия,
то есть из уравнения.
Решив уравнение, найдем
найдем из условия,
то есть из уравнения.
Решив уравнение, найдем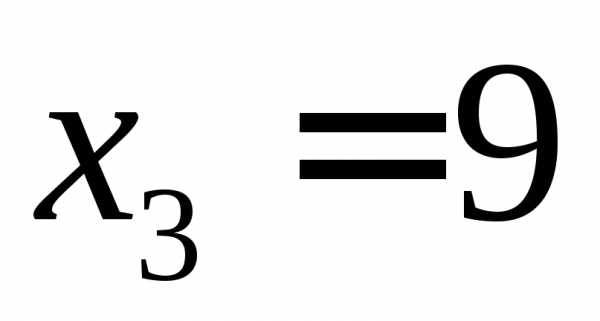 .
Составим закон распределения
.
Составим закон распределения
| 8 | 9 | 10 |
| 0,4 | 0,5 | 0,1 |
Пример
4. Плотность
распределения вероятностей случайной
величины  задается соотношением
задается соотношением
Найти
параметр  ,
функцию распределения вероятностей
случайной величины
,
функцию распределения вероятностей
случайной величины ,
,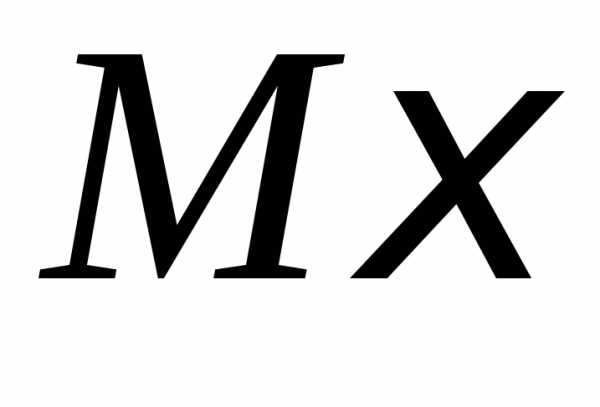 ,
,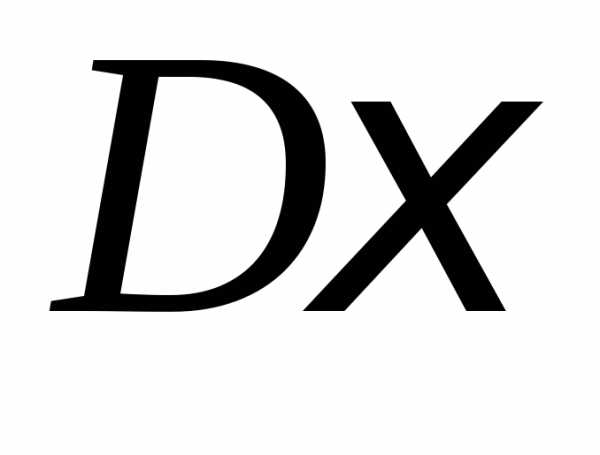 ,
,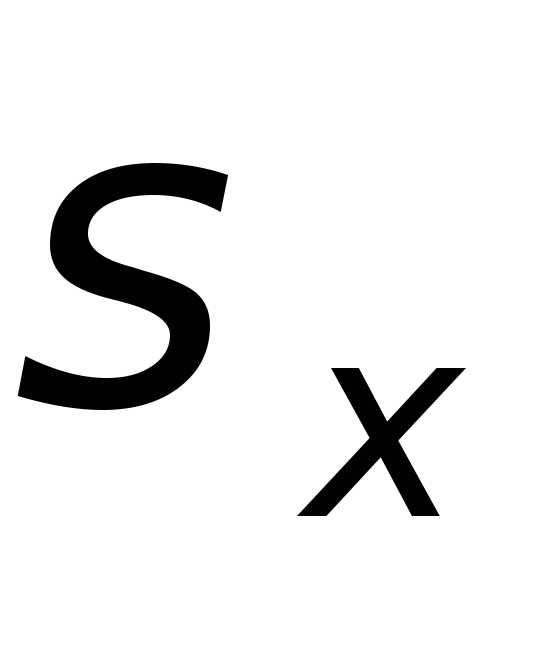 и
и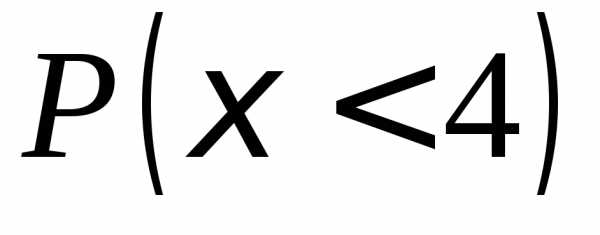 .
.
Решение. Значение параметра  найдем из условия нормировки
найдем из условия нормировки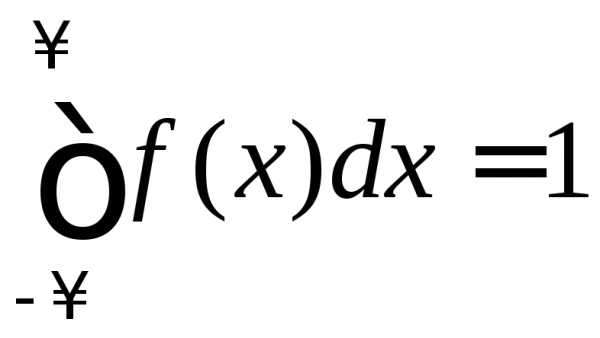 .
Для заданной
.
Для заданной это условие примет вид.
Интегрируя, получим
это условие примет вид.
Интегрируя, получим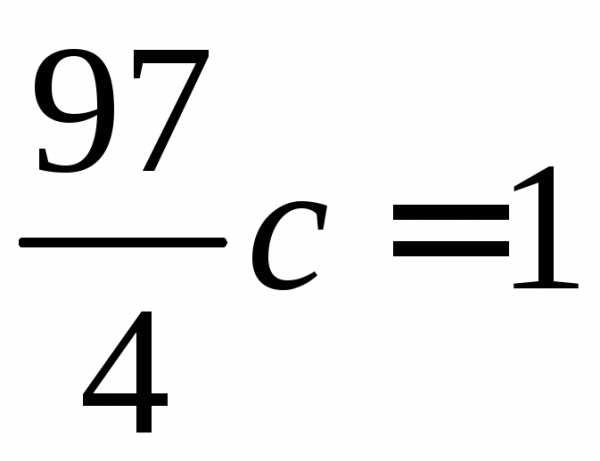 ,
откуда
,
откуда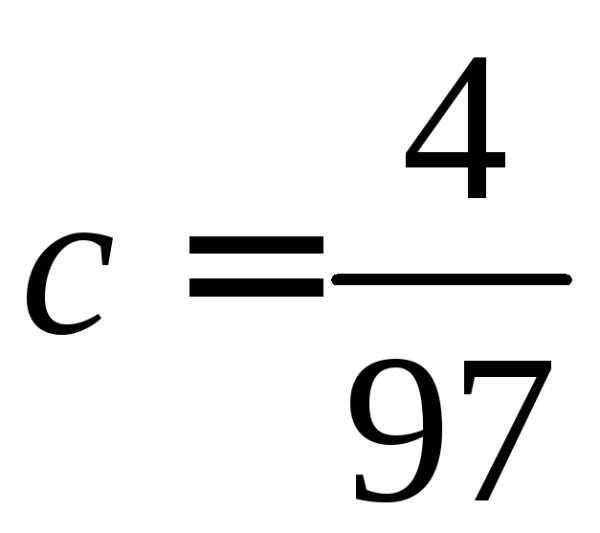 .
Следовательно
.
Следовательно
.
.
.
.
Пример 5. Поток заявок, поступающих на телефонную станцию, представляет собой простейший поток. Математическое ожидание числа вызовов за час равно 30. Найти вероятность того, что за минуту поступит не менее двух вызовов.
Решение. Так как поток заявок представляет собой простейший поток, то число заявок, поступающих на телефонную станцию, распределено по закону Пуассона
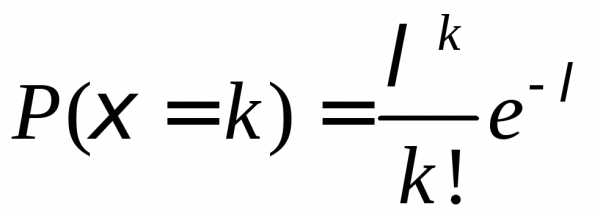
 ,,
,,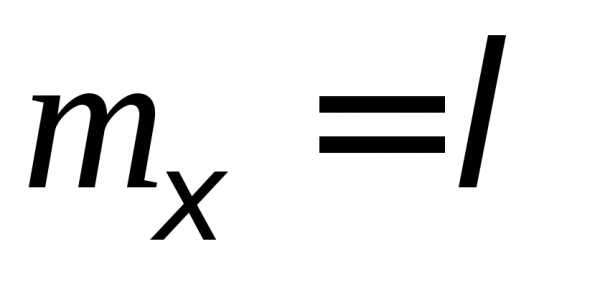 ,
,
с
математическим ожиданием 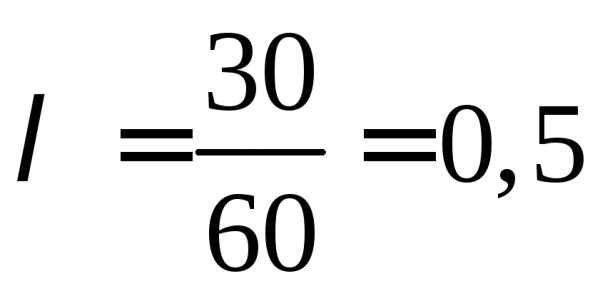 .
.
Следовательно, для решаемой задачи
Обозначим
через 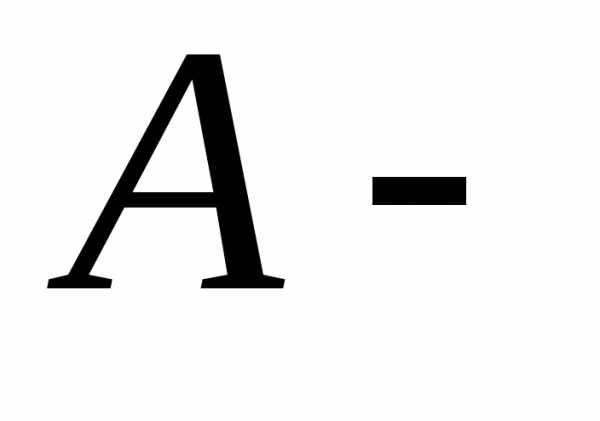 событие, состоящее в том, что за минуту
поступит не менее двух вызовов. Тогда
событие, состоящее в том, что за минуту
поступит не менее двух вызовов. Тогда
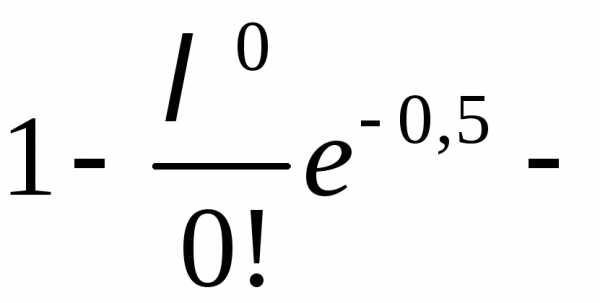
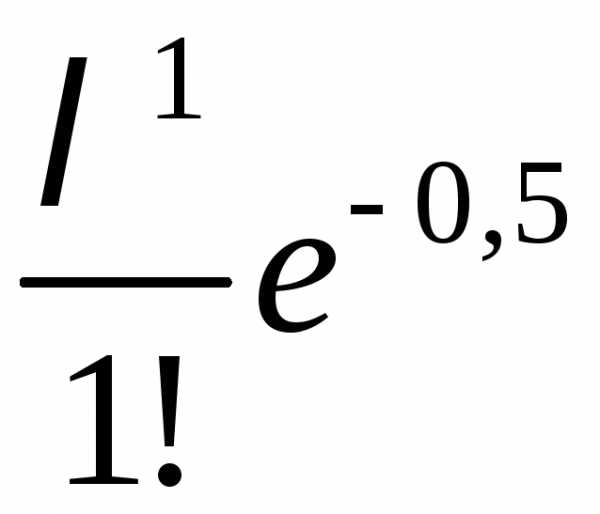 =
=
=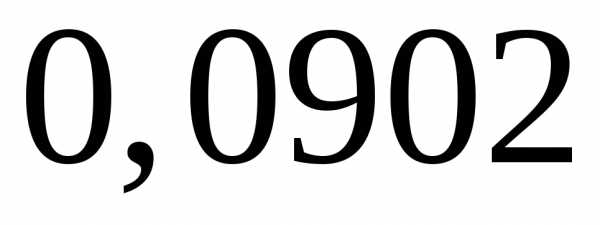 .
.
Пример 6. Случайная
величина  имеет пуассоновское распределение и
известно, что ее математическое ожидание
имеет пуассоновское распределение и
известно, что ее математическое ожидание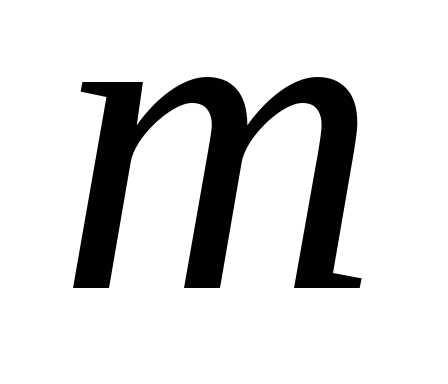 и дисперсия
и дисперсия связаны соотношением.
связаны соотношением.
Найти
вероятность 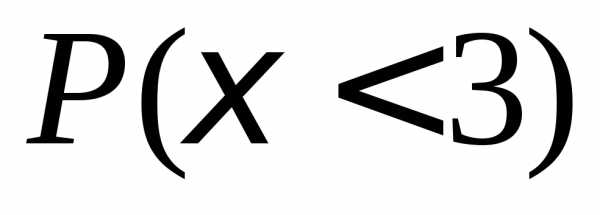 ,
,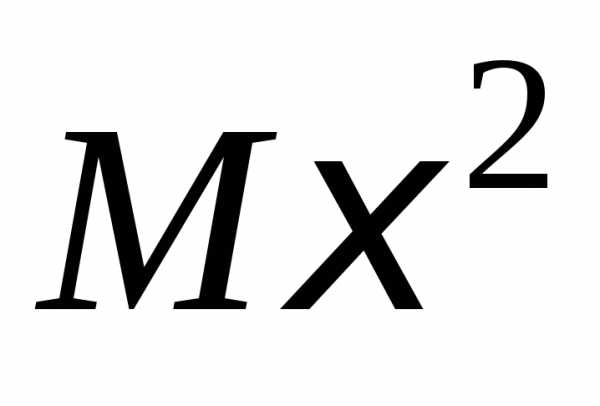 .
.
Решение. Известно,
что математическое ожидание и дисперсия
пуассоновского распределения совпадают
и равны значению его пара-метра 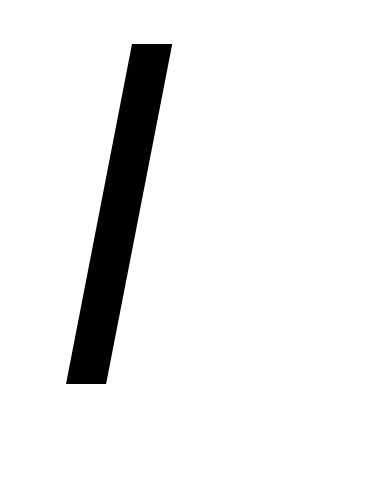 .
Условие задачи приводит к уравнению
относительно
.
Условие задачи приводит к уравнению
относительно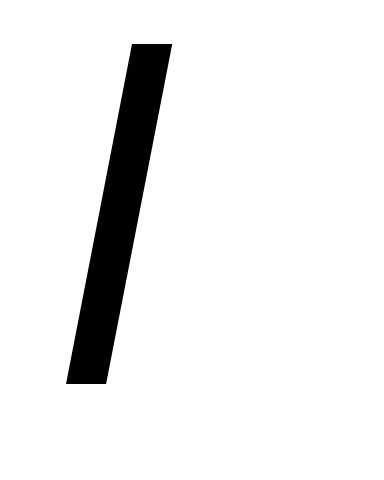 :
:
,
решениями
которого являются числа 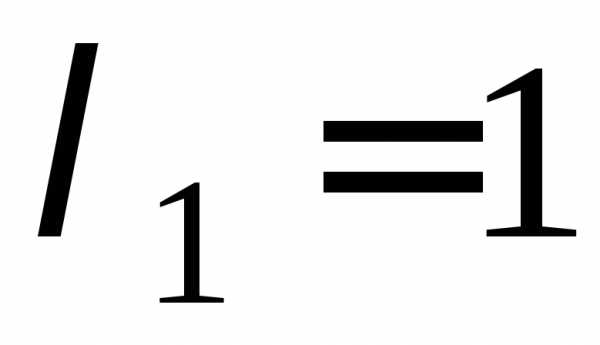 ,
,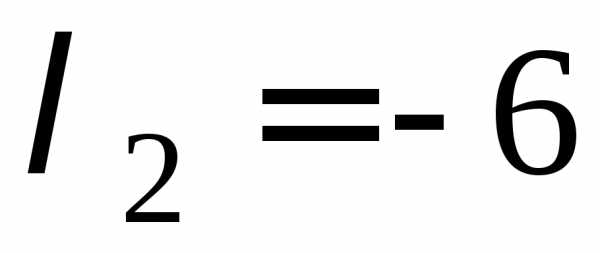 .
Последнее значение не может быть
параметром пуассоновского распределения
в силу положительности параметра. Таким
образом, случайная величина
.
Последнее значение не может быть
параметром пуассоновского распределения
в силу положительности параметра. Таким
образом, случайная величина имеет ряд распределения
имеет ряд распределения
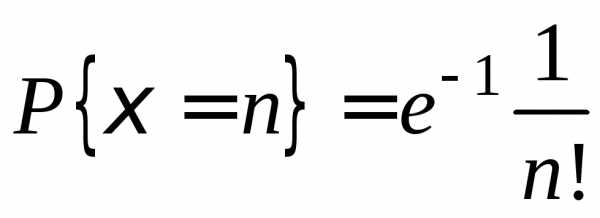 ,
.
,
.
Для искомой вероятности получаем
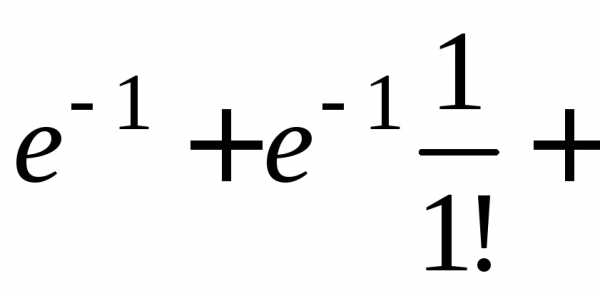
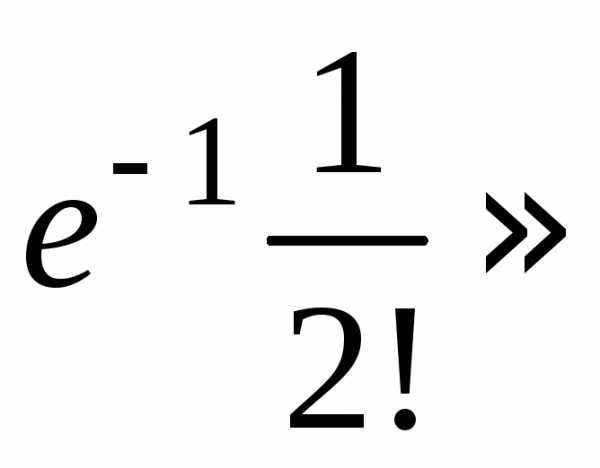
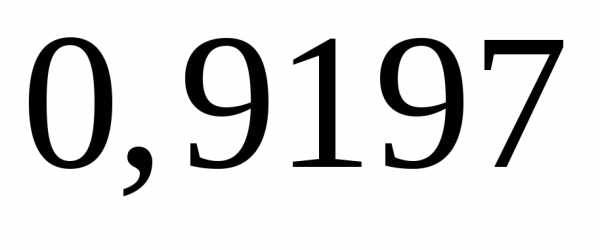 .
.
Известно, что . Из этого равенства. Для заданной случайной величины,. Следовательно,.
Пример
7. Время
безотказной работы некоторого узла
сложного агрегата – экспоненциальная
случайная величина со средним 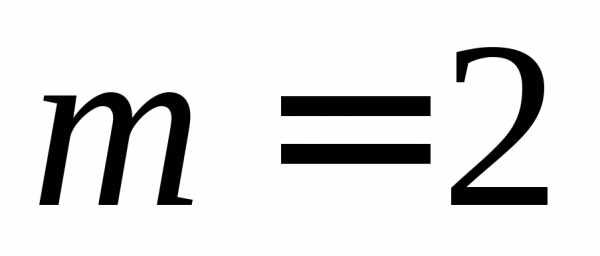 .
Для увеличения надежности агрегата
узел дублируется – ставят параллельно
несколько одинаковых, но функционирующих
независимо узлов. Сколько узлов следует
запараллелить, чтобы с вероятностью,
не меньшей чем 0,9, по крайней мере один
из них не вышел из строя за 10 часов
работы?
.
Для увеличения надежности агрегата
узел дублируется – ставят параллельно
несколько одинаковых, но функционирующих
независимо узлов. Сколько узлов следует
запараллелить, чтобы с вероятностью,
не меньшей чем 0,9, по крайней мере один
из них не вышел из строя за 10 часов
работы?
Решение. По
условию задачи  –
случайное время безотказной работы
узла – имеет экспоненциальное
(показательное) распределение. Это
означает, что
–
случайное время безотказной работы
узла – имеет экспоненциальное
(показательное) распределение. Это
означает, что
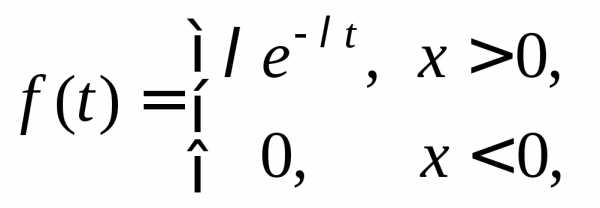
 ,
,
Известно,
что математическое ожидание экспоненциальной
случайной величины есть величина,
обратная параметру: 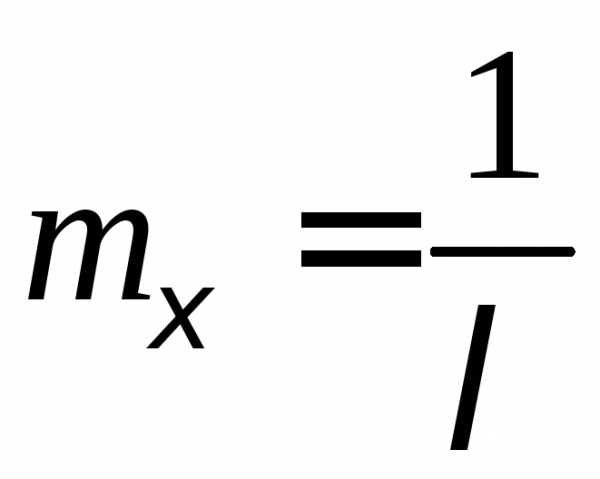 .
По условию задачи
.
По условию задачи ,
следовательно,
,
следовательно,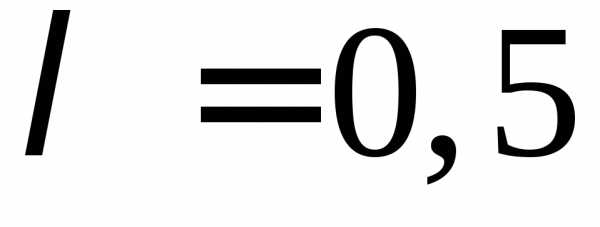 .
.
Таким
образом, вероятность отказа узла в
течение 10 часов будет равна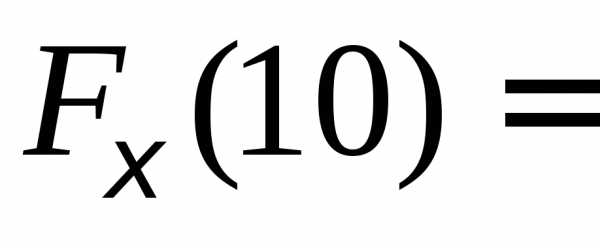 .
.
Если
запараллелено  идентичных узлов, то событие
идентичных узлов, то событие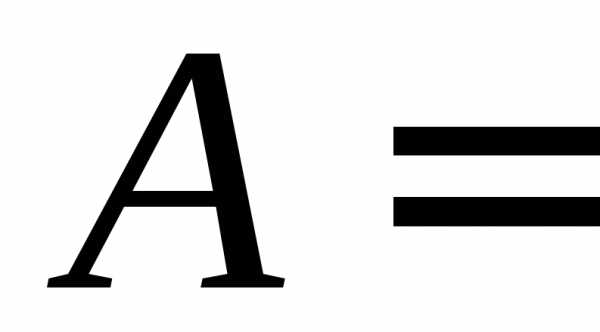 {по
крайней мере один из узлов не выйдет из
строя за 10 часов} является противоположным
событию
{по
крайней мере один из узлов не выйдет из
строя за 10 часов} является противоположным
событию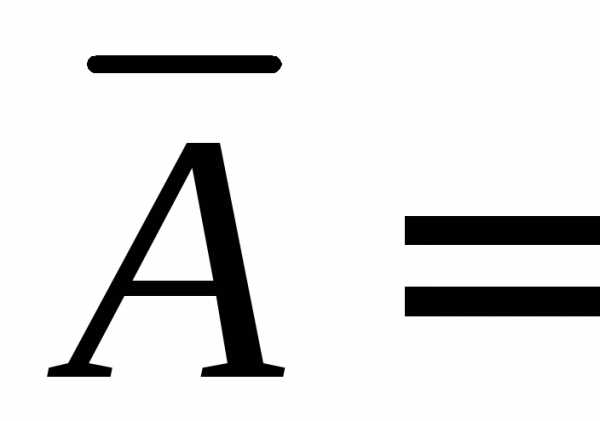 {все
узлы выйдут из строя за 10 часов}. Поэтому,.
Узлы работают независимо, поэтому по
теореме умножения вероятностей
независимых событий
{все
узлы выйдут из строя за 10 часов}. Поэтому,.
Узлы работают независимо, поэтому по
теореме умножения вероятностей
независимых событий
.
Искомое
значение  может быть найдено как наименьшее целое
решение неравенства
может быть найдено как наименьшее целое
решение неравенства
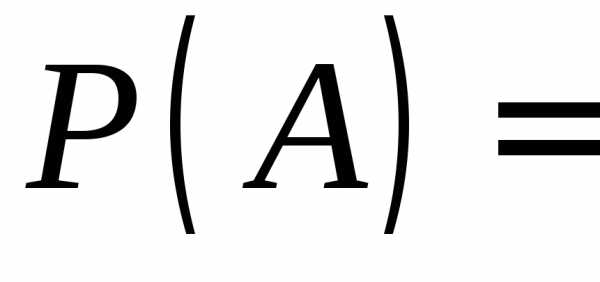
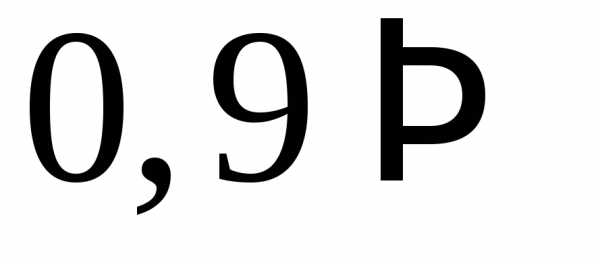 .
.
studfiles.net