Синуса разложение в ряд – .

alexxlab / / Школьная жизнь

Содержание

Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.

Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2

sin2x+b3sin3x+…,

где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

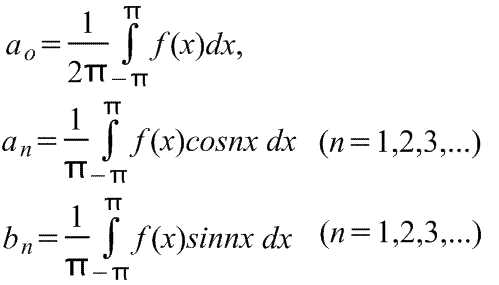
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)

Где ao — константа, с 1=(a1

2+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.

Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x)

четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a

o и an

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

 

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

Где коэффициенты ряда Фурье, 

Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

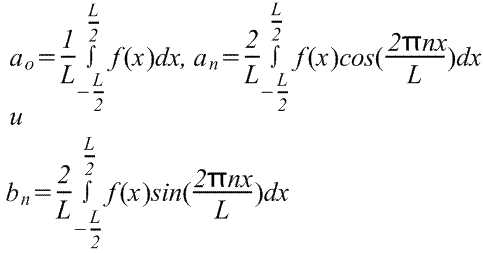
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

tehtab.ru

Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.

Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.  

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,

где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

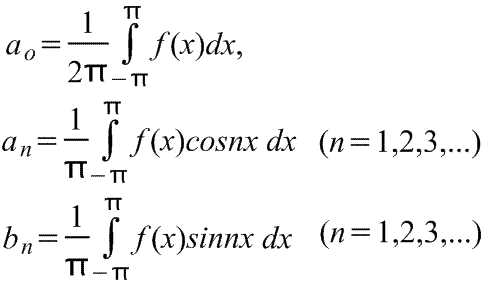
Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)

Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.

Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1

) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций в ряд Фурье.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

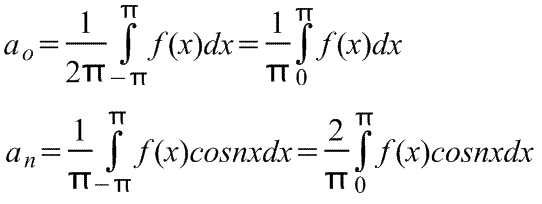
Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x)

dpva.ru

Разложение в ряд Тейлора

Введите функцию, которую будете раскладывать в ряд Тейлора

Выполним разложение функции f(x) в ряд Тейлора в точки x0 до n-го члена

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)
Абсолютное значение x
(модуль x или |x|)
arccos(x)
Функция — арккосинус от x
arccosh(x)
Арккосинус гиперболический от x
arcsin(x)
Арксинус от x
arcsinh(x)
Арксинус гиперболический от x
arctg(x)
Функция — арктангенс от x
arctgh(x)
Арктангенс гиперболический от x
e
e число, которое примерно равно 2.7
exp(x)
Функция — экспонента от x (что и e^x)
log(x) or ln(x)
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi
Число — «Пи», которое примерно равно 3.14
sin(x)
Функция — Синус от x
cos(x)
Функция — Косинус от x
sinh(x)
Функция — Синус гиперболический от x
cosh(x)
Функция — Косинус гиперболический от x
sqrt(x)
Функция — квадратный корень из x
sqr(x) или x^2
Функция — Квадрат x
tg(x)
Функция — Тангенс от x
tgh(x)
Функция — Тангенс гиперболический от x
cbrt(x)
Функция — кубический корень из x
floor(x)
Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x)
Функция — Знак x
erf(x)
Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа
вводить в виде 7.5, не 7,5
2*x
— умножение
3/x
— деление
x^3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание

www.kontrolnaya-rabota.ru

Разложение функции синуса в ряд

Первое, что необходимо сделать при вычислении какой-либо функции по ее разложению в ряд, это уменьшить, если возможно, диапазон значений аргумента, для которых требуется это вычисление. Это может значительно уменьшить ошибку округления. «Математическое» определение синуса через его разложение в степенной ряд пригодно для всех значений аргу­мента, но при этом подразумевается, что вычисление синуса необхо­димо производить с бесконечно большим количеством значащих цифр. На прак­тике при вычислениях с помощью ЭВМ степенной ряд для синуса стано­вится совершенно бесполезным при больших значениях аргументах и дает совершенно бессмысленные результаты.

В случае синуса задача решается весьма просто:

,

Таким образом, отнимая некоторое число, кратное , мы сводим задачу нахождения синуса произвольного угла к задаче нахождения угла, лежащего между — /2 и /2.

На практике уменьшение аргумента не производится последовательным вычитанием. Вместо этого первоначальный угол делится на , причем деление организовано так, что частное получается целым. Остаток от деления будет определять собой некоторый угол, заключенный между 0 и . Если остаток больше /2, то еще одно вычитание дает угол между — /2 и /2. Целое частное от деления исходного угла на используется для того, чтобы определить, следует ли изменить знак окончательного результата (при нечетном частном).

Практическая часть

Алгоритм расчета функции синуса

В данной работе используется арифметика c фиксированной запятой, следовательно, требуется, чтобы все числа были представлены по абсолютному значению меньше единицы.

Для преставления функции синуса воспользуемся формулами приведения и двойного угла:

(1)

для случая, когда аргумент лежит в интервале и

(2)

для случая, когда аргумент лежит в интервале .

Рассмотрение двух случаев обусловлено тем, что невозможно использовать лишь одно соотношение (1), так как при расчетах будут возникать числа большие единицы.

В итоговых формулах расчета функции синуса (1) и (2) присутствует умножение на 2, которое будет заменено на сложение величины самой с собой.

Таким образом, число, поступающее на вход нашей машины, не будет превышать единицы по модулю, так как максимально возможный аргумент равен , либо .

Для представления формул (1) и (2) в виде общего ряда используем стандартный ряд Тейлора для синуса в диапазоне ≤ x ≤ :

 

 

Для аргумента синуса равного разложение в ряд Тейлора будет иметь следующий вид:

Далее, общий ряд для вычисления функции sin(x) по формуле (1):

(3)

Разложение в ряд Тейлора для аргумента синуса, равного , будет иметь следующий вид:

И общий ряд для вычисления sin(x) по формуле (2):

 

(4)

 

 

Будем рассматривать два случая:

1. В вычислительной машине реализована функция умножения. Алгоритм вычисления показан на Схеме 2.

2. В вычислительной машине не реализована функция умножения. При этом алгоритм процедуры умножения реализован отдельно и показан на Схеме 1. Алгоритм вычисления показан на Схеме 3.

 

 

Сдвиг res на 1 разряд вправо
Сдвиг res на 1 разряд вправо  
Схема 1. Блок-схема процедуры умножения
n – разрядность сетки  
Схема 2. Функция умножения в вычислительной машине реализована  
Схема 2. Функция умножения в вычислительной машине реализована  
Схема 3. Функция умножения в вычислительной машине не реализована  
xpow:=mult(xpow, a)    
xpow:=mult(xpow, a)    

Оценка погрешностей




infopedia.su

ряд Тейлора | C++ для приматов

Задача

Вычислите с точностью [latex]\varepsilon[/latex] значение функции [latex]f\left( x \right) = \ln \left( 1-x^2 \right)[/latex] . При вычислениях допустимо использовать только арифметические операции.

Входные данные

В одной строке заданы значение переменной [latex]x[/latex] и точность вычислений [latex]\varepsilon[/latex].
[latex]\left | x \right |< 1[/latex]

Выходные данные

Значение функции в точке [latex]x[/latex] .

Тесты

[latex]\varepsilon[/latex][latex]x[/latex] [latex]ln(1-x^2)[/latex]Результат
0.0010.5[latex]ln(0.75)[/latex]-0.287435
0.00010.5[latex]ln(0.75)[/latex]-0.287671
0.010.1[latex]ln(0.99)[/latex]-0.01005
0.001-0.1[latex]ln(0.99)[/latex]-0.01005
0.10[latex]ln(1.00)[/latex]0
0.010[latex]ln(1.00)[/latex]0

 

Код программы

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

#include <iostream>

#include <cmath>

using namespace std;

 

int main() {

    double E, logarithm = 0, ai = 1, p = 1, x;

    int i = 1;

    cin >> x >> E;

    while(ai > E){

        p *= x*x;  // вычисление числителя члена ряда

        ai = p / i; // вычисление члена ряда

        logarithm -= ai;

        i++;

    }

    cout <<  logarithm;

return 0;

}

ideone.com

 

Решение

Функцию [latex]f\left( x \right) = \ln \left( 1-x^2 \right)[/latex] можно представить в виде:
[latex]ln\left ( 1-x^2 \right )= ln\left ( 1-x \right )\left ( 1+x \right ) = ln\left ( 1-x \right )+ln\left ( 1+x \right )[/latex] (по свойствам логарифма).

Для решения задачи необходимо воспользоваться формулой Тейлора  для натурального логарифма с опорной точкой [latex]x_{0}=0[/latex] (ряд Маклорена). Для функции [latex]ln\left (1+x\right )[/latex] она имеет следующий вид:

[latex]ln\left (1+x\right )=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\cdots+\frac{\left ( -1 \right )^{n-1}}{n}x^{n}=\sum_{n=1}^{\infty}\frac{\left (-1\right )^{n-1}}{n}x^{n}[/latex]

Подставив в формулу [latex]-x[/latex] вместо [latex]x[/latex] , получим:

[latex]ln\left (1-x\right )=-x-\frac{x^{2}}{2}-\frac{x^{3}}{3}-\cdots -\frac{x^{n}}{n}=-\sum_{n=1}^{\infty}\frac{x^{n}}{n}[/latex]

Тогда,

[latex]ln\left (1+x\right )+ln\left (1-x\right )=\sum_{n=1}^{\infty}\frac{\left (-1\right )^{n-1}}{n}x^{n}-\sum_{n=1}^{\infty}\frac{x^{n}}{n}=[/latex]

[latex]=\sum_{n=1}^{\infty }\left[\frac{\left (-1\right )^{n-1}}{n}x^{n}-\frac{x^{n}}{n}\right]=\sum_{n=1}^{\infty }\frac{x^{n}\left (\left (-1\right )^{n-1}-1\right )}{n}=[/latex][latex]=-x^{2}+0-\frac{x^{4}}{2}+0-\frac{x^{6}}{3}+0-\cdots[/latex]

Так как при нечетном [latex]n[/latex] члены данного ряда обращаются в ноль, его можно записать в виде:

[latex]-\sum_{0}^{\infty}\frac{x^{2n+2}}{n+1}=-x^{2}-\frac{x^{4}}{2}-\frac{x^{6}}{3}-\cdots-\frac{x^{2n+2}}{n+1}[/latex]

Далее необходимо найти рекуррентную формулу для членов данного ряда.

[latex]\frac{a_{n}}{a_{n-1}}=\frac{x^{2n+2}}{n+1}\cdot\frac{n-1+1}{x^{2\left ( n-1 \right )+2}}=\frac{x^{2}\cdot n }{n+1}[/latex]

Затем необходимо суммировать до тех пор пока очередное слагаемое не будет меньше заданной точности.

cpp.mazurok.com

Ряды Тейлора, Бином, Степенные ряды

Ряд Тейлора функции одной переменной

$f(x)=f(a)+f'(a)(x-a)+\frac{f»(a)(x-a)^2}{2!}+\cdots+\frac{f^{(n-1)}(a)(x-a)^{n-1}}{(n-1)!}+R_n$ где $R_n$, остаточный член после n слагаемых, может быть записан в одной из следующих форм:

Форма Лагранжа $R_n=\frac{f^{(n)}(x-a)^n}{n!}$

Форма Коши $R_n=\frac{f^{(n)}(\xi)(x-\xi)^{n-1}(x-a)}{(n-1)!}$

Величина $\xi$, которая может отличаться для двух форм, лежит в промежутке между $a$ и $x$. Результат справедлив, если $f(x)$ имеет непрерывные производные до порядка $n$ как минимум.

Если $\lim_{n\rightarrow\infty} R_n=0$, полученный бесконечный ряд называется рядом Тейлора функции $f(x)$ в окрестности $x = a$. Если $a = 0$, такое разложение часто называют рядом Маклорена. Эти ряды, часто называемые степенными рядами, обычно сходятся для всех значений $x$ из некоторого интервала, который называется интервалом сходимости, и расходятся для всех $x$ вне этого интервала.

Возведение в степень двучленов

$(a+x)^n=a^n+na^{n-1}x+\frac{n(n-1)}{2!}a^{n-2}x^2+\frac{n(n-1)(n-2)}{3!}a^{n-3}x^3+\cdots=$
$= a^n+\binom{n}{1}a^{n-1}x+\binom{n}{2}a^{n-2}x^2+\binom{n}{3}a^{n-3}x^3+\cdots$

Особо стоит выделить следующие разложения

$(a+x)^2=a^2+2ax+x^2$

$(a+x)^3=a^3+3a^2x+3ax^2+x^3$

$(a+x)^4=a^4+4a^3x+6a^2x^2+4ax^3+x^4$

$(1+x)^{-1}=1-x+x^2-x^3+x^4-\cdots,$     $-1

$(1+x)^{-2}=1-2x+3x^2-4x^3+5x^4-\cdots,$     $-1

$(1+x)^{-3}=1-3x+6x^2-10x^3+15x^4-\cdots$     $-1

$(1+x)^{-\frac{1}{2}}=1-\frac{1}{2}x+\frac{1\cdot3}{2\cdot4}x^2-\frac{1\cdot3\cdot5}{2\cdot4\cdot6}x^3+\cdots$     $-1

$(1+x)^{\frac{1}{2}}=1+\frac{1}{2}x-\frac{1}{2\cdot4}x^2+\frac{1\cdot3}{2\cdot4\cdot6}x^3-\cdots$     $-1

$(1+x)^{-\frac{1}{3}}=1-\frac{1}{3}x+\frac{1\cdot4}{3\cdot6}x^2-\frac{1\cdot4\cdot7}{3\cdot6\cdot9}x^3+\cdots$     $-1

$(1+x)^{\frac{1}{3}}=1+\frac{1}{3}x+\frac{2}{3\cdot6}x^2-\frac{2\cdot5}{3\cdot6\cdot9}x^3-\cdots$     $-1

Разложение в ряд показательной и логарифмической функций

$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$     $-\infty

$a^x=e^{x\ln x}=1+x\ln a+\frac{(x\ln a)^2}{2!}+\frac{(x\ln a)^3}{3!}+\cdots$     $ -\infty

$\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots$    $-1

$\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)=x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\cdots$    $-1

$\ln x=2\left\{\left(\frac{x-1}{x+1}\right)+\frac{1}{3}\left(\frac{x-1}{x+1}\right)^3+\frac{1}{5}\left(\frac{x-1}{x+1}\right)^5+\cdots\right\}$     $x>0$

$\ln x=\left(\frac{x-1}{x}\right)+\frac{1}{2}\left(\frac{x-1}{x}\right)^2+\frac{1}{3}\left(\frac{x-1}{x}\right)^3+\cdots$     $x\geq\frac{1}{2}$

Разложение в ряд тригонометрических функций

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$     $-\infty

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$     $-\infty

$tg x=x+\frac{x^3}{3}+\frac{2x^5}{15}+\frac{17x^7}{315}+\cdots+\frac{2^{2n}(2^{2n}-1)B_nx^{2n-1}}{(2n)!}+\cdots$     $|x|

$\text{ctg} x=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\frac{2x^5}{945}-\cdots-\frac{2^{2n}B_nx^{2n-1}}{(2n)!}-\cdots$     $0

$\sec x=1+\frac{x^2}{2}+\frac{5x^4}{24}+\frac{61x^6}{720}+\cdots+\frac{E_nx^{2n}}{(2n)!}+\cdots$     $|x|

$\csc x=\frac{1}{x}+\frac{x}{6}+\frac{7x^3}{360}+\frac{31x^5}{15,120}+\cdots+\frac{2(2^{2n-1}-1)B_nx^{2n-1}}{(2n)!}+\cdots$     $0

$\sin^{-1}x=x+\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot3}{2\cdot4}\frac{x^5}{5}+\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\frac{x^7}{7}+\cdots$     $|x|

$\cos^{-1}x=\frac{\pi}{2}-\sin^{-1}x=\frac{\pi}{2}-\left(x+\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot3}{2\cdot4}\frac{x^5}{5}+\cdots\right)$     $|x|

$\text{tg}^{-1}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$, когда $|x| $\text{tg}^{-1}x=\pm\frac{\pi}{2}-\frac{1}{x}+\frac{1}{3x^3}-\frac{1}{5x^5}+\cdots$     $[+\ \text{если}\ x\geq1, -\ \text{если}\ x\leq-1]$

$\text{ctg}^{-1}x=\frac{\pi}{2}-\text{tg}^{-1}x =\frac{\pi}{2}-\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)$, когда $|x| $\text{ctg}^{-1}x=\frac{\pi}{2}-\text{tg}^{-1}x =p\pi+\frac{1}{x}-\frac{1}{3x^3}+\frac{1}{5x^5}-\cdots$, когда [p=0 если x>1, p=1 если x

$\sec^{-1}x=\cos^{-1}\left(\frac{1}{x}\right)=\frac{\pi}{2}-\left(\frac{1}{x}+\frac{1}{2\cdot3x^3}+\frac{1\cdot3}{2\cdot4\cdot5x^5}+\cdots\right)$     $|x|>1$

$\csc^{-1}x=\sin^{-1}\left(\frac{1}{x}\right)=\frac{1}{x}+\frac{1}{2\cdot3x^3}+\frac{1\cdot3}{2\cdot4\cdot5x^5}+\cdots$     $|x|>1$

Разложение в ряд гиперболических функций

$\text{sh} x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\cdots$     $-\infty

$\text{ch} x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots$     $-\infty

$\text{th} x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots+\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_nx^{2n-1}}{(2n)!}+\cdots$     $|x|

$\text{cth} x=\frac{1}{x}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\cdots+\frac{(-1)^{n-1}2^{2n}B_nx^{2n-1}}{(2n)!}+\cdots$     $0

$\sec\text{h}x=1-\frac{x^2}{2}+\frac{5x^4}{24}-\frac{61x^6}{720}+\cdots+\frac{(-1)^nE_nx^{2n}}{(2n)!}+\cdots$    $|x|

$\csc\text{h}x=\frac{1}{x}-\frac{x}{6}+\frac{7x^3}{360}-\frac{31x^5}{15,120}+\cdots+\frac{(-1)^n2(2^{2n-1}-1)B_nx^{2n-1}}{(2n)!}+\cdots$     $0

$\text{sh}^{-1}x= x-\frac{x^3}{2\cdot3}+\frac{1\cdot3x^5}{2\cdot4\cdot5}-\frac{1\cdot3\cdot5x^7}{2\cdot4\cdot6\cdot7}+\cdots$   $|x|

$\text{sh}^{-1}x=\pm\left(\ln|2x|+\frac{1}{2\cdot2x^2}-\frac{1\cdot3}{2\cdot4\cdot4x^4}+\frac{1\cdot3\cdot5}{2\cdot4\cdot6\cdot6x^6}-\cdots\right)$     [+ если $x\geq 1$ — если $x\leq-1$]

$\text{ch}^{-1}x=\pm\left\{\ln(2x)-\left(\frac{1}{2\cdot2x^2}+\frac{1\cdot3}{2\cdot4\cdot4x^4}-\frac{1\cdot3\cdot5}{2\cdot4\cdot6\cdot6x^6}+\cdots\right)\right\}$   [+ если $\text{ch}^{-1}x>0, x\geq1$   — если $\text{ch}^{-1}x

$\text{th}^{-1}x=x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\cdots$     $|x|

$\text{cth}^{-1}x=\frac{1}{x}+\frac{1}{3x^3}+\frac{1}{5x^5}+\frac{1}{7x^7}+\cdots$     $|x|>1$

Различные разложения

$e^{\sin x}=1+x+\frac{x^2}{2}-\frac{x^4}{8}-\frac{x^5}{15}+\cdots$     $-\infty

$e^{\cos x}=e\left(1-\frac{x^2}{2}+\frac{x^4}{6}-\frac{31x^6}{720}+\cdots\right)$     $-\infty

$e^{\text{tg} x}=1+x+\frac{x^2}{2}+\frac{x^3}{2}-\frac{3x^4}{8}+\cdots$     $|x|

$e^x\sin x=x+x^2+\frac{2x^3}{3}-\frac{x^5}{30}-\frac{x^6}{90}+\cdots+\frac{2^\frac{n}{2}\sin\left(\frac{n\pi}{4}\right)x^n}{n!}+\cdots$     $-\infty

$e^x\cos x=1+x-\frac{x^3}{3}-\frac{x^4}{6}+\cdots+\frac{2^\frac{n}{2}\cos\left(\frac{n\pi}{4}\right)x^n}{n!}+\cdots$     $-\infty

$\ln|\sin x|=\ln|x|-\frac{x^2}{6}-\frac{x^4}{180}-\frac{x^6}{2835}-\cdots-\frac{2^{2n-1}B_nx^{2n}}{n(2n)!}+\cdots \qquad 0

www.math10.com

Разложение f(x) = sin x в ряд Маклорена

(30.6.2.) Обозначим этапы осуществления разложения заданной функции в ряд Маклорена: определим производные, запишем ряд Маклорена для этой функции, обозначим интервал сходимости, применяя признак Даламбера.


1) Определяем производные

 

 

иначе выражаясь,

 

 

запишем ряд Маклорена для функции

 

(30.12)

 

2) Находим интервал сходимости, используя признак Даламбера к:

 

 

для ряда характерна сходимость на промежутке.

3) Представим запись:

 

 

Применив неравенство.

 

 

Сюжеты Математика

(38.4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.

3074 0

(38.3.) Большинство графов, которые используются в приложениях (например, графы сортировок, классификаций) предполагают наличие диаграмм, именуемых деревьями. Связный неориентированный граф без циклов, в частности, предполагающий отсутствие петель и кратных ребер, именуют деревом. Несвязный неориентированный граф без цикла — лес, его связные компоненты являются деревьями.

8283 0

(38.2.) В рамках обозначенной темы рассмотрим случай определения связного неориентированного мультиграфа в качестве эйлерова и гамильтонова графа.

11246 0

Комментарии ()

Вы должны авторизоваться, чтобы оставлять комментарии.

radiomaster.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *