Задания В11. Логарифмические выражения | Подготовка к ЕГЭ по математике
Часть 4.
Здесь смотрим части 1, 2, 3, 5
При решении задач, что мы сегодня рассматриваем, нам понадобятся свойства логарифмов.
Числовые логарифмические выражения
Задание 1.
Найдите значение выражения .
Решение: + показать
Задание 2.
Найдите значение выражения .
Решение: + показать Представим как и далее воспользуемся следующим свойством логарифмов: при : А теперь применяем основное логарифмическое тождество: Ответ: 49.
Задание 3.
Найдите значение выражения .
Решение: + показать
Задание 4.
Найдите значение выражения .
Решение: + показать
Задание 5.
Найдите значение выражения .
Решение: + показать Ответ: 12.
Задание 6.
Найдите значение выражения .
Решение: + показать Складывать логарифмы не имеем право, у них разные основания.
Тогда
Ответ: 1,5.
Задание 7.
Найдите значение выражения .
Решение: + показать
Задание 8.
Найдите значение выражения .
Решение: + показать Ответ: 2.
Задание 9.
Найдите значение выражения .
Решение: + показать
Задание 10.
Найдите значение выражения .
Решение: + показать Ответ: 9.
Задание 11.
Найдите значение выражения .
Решение: + показать Ответ: 1.
Задание 12.
Найдите значение выражения .
Решение: + показать Ответ: 9.
Задание 13.
Найдите значение выражения .
Решение: + показать Ответ: 0.
Задание 14.
Вычислите значение выражения: .
Решение: + показать В самом конце мы применили основное логарифмическое тождество, а до этого – следствие из свойства 7 логарифмов. Ответ: 2.
Задание 15.
Найдите значение выражения .
Решение: + показать Обратите внимание, это не произведение логарифмов. У логарифма по основанию подлогарифмным выражением является . Ответ: 0,25.
Буквенные логарифмические выражения
Задание 1.
Найдите , если .
Решение: + показать При имеем: Ответ: -32.
Задание 2.
Найдите значение выражения , если .
Решение: + показать
🙂 После плодотворной работы не помешало бы и отдохнуть немного… –>+ показать
Жизнь полна неожиданностей, неправда ли?

Вы можете пройти обучающий тест по теме «Преобразование логарифмических выражений».
Логарифмы, примеры решений
Теория про логарифмы
Логарифм по основанию 10 называется десятичным логарифмом и обозначается :
а логарифм по основанию называют натуральным и обозначают :
Примеры
ПРИМЕР 3| Задание | Вычислить значение выражения
|
| Решение | Перейдем в каждом из слагаемых к логарифму по основанию 18, используя формулу перехода . Получим:
Так как сумма логарифмов равна логарифму произведения, последняя сумма перепишется в виде:
Число 324 можно представить как степень 18, получим
далее выносим степень как коэффициент перед знаком логарифма:
Учитывая, что , окончательно будем иметь:
|
| Ответ |
| Задание | Вычислить |
| Решение | Перейдем во всех логарифмах к основанию 2, используя формулу перехода к новому основанию:
получим
Представим 4 и 8 в виде степени двойки и вынесем полученные степени за знак логарифма как коэффициент:
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Логарифмические выражения
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
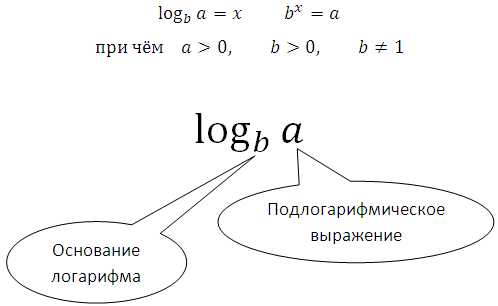
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
При возведении в степень произведения в эту же степень возводится каждый множитель.
Так же необходимо знать следующее свойство:
Рассмотрим примеры:
*Данный контент (более 20 подробно решённых примеров) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Решение логарифмических уравнений. 10-й класс
Разделы: Математика
Класс: 10.
Предмет: Алгебра и начала анализа.
Цели:
- обеспечить повторение, обобщение, систематизацию материала по теме. Создать условия контроля, самоконтроля усвоения знаний и умений;
- способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора;
- содействовать воспитанию интереса, математической активности, умению общаться, общей культуры.
Тип занятия: систематизация и обобщение знаний.
Оборудование: учебники, медиапроектор, пособия по математике, листы учета знаний.
Литература:- Алгебра и начала анализа. Учебник под редакцией А.Б. Жижченко 10 класс
- Алимов Ш.А. Алгебра и начала анализа, 10-11. — М., 2005.
- Глейзер Г.И. История математики в школе. — М., 1982.
- Шабунин М.И. Алгебра и начала анализа. Дидактические материалы для 10-11 классов. — М., 1998.
- Лысенко Ф.Ф. Математика ЕГЭ-2009. Легион, 2009.
- Клово А.Г. Математика ЕГЭ-2010 М., 2010.
Ход урока
Потому-то, словно пена
Опадают наши рифмы
И величие степенно
Отступает в логарифмы
Борис Слуцкий
I. Подготовка учащихся к работе. (Ознакомление с темой урока)
Вступительное слово учителя. Поистине безграничны приложения логарифмов и логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Более трех столетий прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. Они помогали астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняя жизнь вычислителям». Известный физик Эйхенвальд вспоминал: «Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах…» И действительно, так называемые ступени темперированной хроматической гаммы (12-звуковой) частот звуковых колебаний представляют собой логарифмы. Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях -взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем, каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали. Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития.
II. Математический диктант по основным понятиям необходимым для решения уравнений.
(Проверка на слайде)
- Равенство двух алгебраических выражений называется (уравнением)
- Значение переменной, при котором уравнение обращается в верное числовое равенство называется (корнем уравнения)
- Показатель степени, в которую надо возвести положительное и отличное от единицы число а, чтобы получить число в называется (логарифмом)
- Десятичным логарифмом называют логарифм с основанием равным (10)
- Натуральный логарифм, это логарифм с основанием (е)
- Логарифм единицы по основанию а равен (0)
- Логарифм а по основанию а равен (1)
III. Систематизация теоретического материала.
1) На доске записаны уравнения, решите их и сопоставьте им правильный ответ.
2) Данные уравнения расположить согласно способам и приемам решения.
| Решение по определению | Применение свойств логарифмов | Переход к одному основанию | Логарифмирование обеих частей | Графическое решение уравнения |
| № | № | № | № | № |
3) Найти ошибку в записи и прокомментировать ее (устные комментарии)
-2х=26
Х=-13
Ответ: -13.
4) Тестовое задание на нахождение идеи решения уравнения. Необходимо сопоставить уравнение, прием и формулу необходимую для решения уравнения.
Ответ:
| 1 | в | * |
| 2 | г | • |
| 3 | а | ** |
| 4 | б | Δ |
IV. Практическая работа.
1) Работа по вариантам, с программированными заданиями. Необходимо решить уравнение и выбрать правильный ответ. У доски работаю четверо учащихся, в итоге появляется определенный набор цифр.
Ответ: 09. 05. 1945 года.
2) Решить систему уравнений у доски с комментариями.
V. Самостоятельная работа по уровням.
Учащимся предлагается оценить свои возможности и выбрать уровень заданий.
| 1 уровень (1б) | 2 уровень (2б) | 3 уровень (3б) |
VI. Подведение итогов урока.
- подсчет баллов набранных за урок (работа с листами учета знаний)
- определение результативности работы учащихся
- выставление оценок.
VII. Домашнее задание:
Подготовится к контрольной работе.
Приложение.
21.06.2011
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Решебник Примеры для самостоятельного решения Тест Логарифмы Логарифм числа и его преобразование
Все вопросы и замечания просьба направлять по адресу [email protected]Решебник
Примеры для самостоятельного решения
Тест
Логарифмы
Логарифм числа и его преобразование
Определение. Логарифмом числа по основанию называется показатель степени , в которую надо возвести основание a, чтобы получить данное число .
— любое действительное число,
> 0– логарифмируемое число,
— основание логарифма, > 0 , 1
При любом > 0 , 1 и любых > 0, > 0 верны следующие равенства:
1.
2.
3.
4. для любого kR
5. для любого
6.
7.
8. (формула перехода к новому основанию)
9. , b 1
10. , b 1.
Замечание. Отметим важную особенность формул 1, 2, 3, 4, 5. Их правые и левые части, взятые по отдельности, определены на разных множествах значений переменных и . В формуле 1 левая часть определена лишь при > 0, а правая – для всех R. В формулах 2 и 3 левые части определены для всех пар значений и одного знака (то есть при ), а правые – лишь для > 0 и > 0. В формуле 4 при k = 2n, где nN, n 0, левая часть определена для всех 0, правая же – только для > 0. В формуле 5 при k = 2n левая часть определена для всех и , а правая для . Отличие множеств определения следует учитывать при применении этих формул для преобразования уравнений. Оно может привести как к потере решений, так и к появлению посторонних значений неизвестных. При решении примеров на это следует обращать внимание.
Решебник
Теория
Примеры для самостоятельного решения
Тест
| Пример1. Вычислить: а) ; б) ; в) |
Решение.
| Пример 2. Вычислить: а) ; б) ; в) ; г) . |
Решение.
| Пример 3. Вычислить: а) ; б) ; в) . |
Решение.
| Пример 4. Вычислить: а) ; б) ; в) . |
Решение:
| Пример 5. Вычислить: а) ; б) ; в) . |
Решение.
| Пример 6. Вычислить: а) ; б) ; в) . |
Решение:
| Пример 7. Вычислить: а) ; б) ; |
Решение:
| Пример 8. Вычислить: а) ; б) . |
Решение.
| Пример 9. Вычислить: а) ; б) . |
Решение.
| Пример 10. Вычислить: . |
Решение.
| Пример 11. Вычислить: . |
Решение:
| Пример 12. Вычислить: . |
Решение:
| Пример 13. Вычислить: . |
Решение:
| Пример 14. Вычислить: . |
Решение.
| Пример 15. Вычислить: . |
Решение:
| Пример 16. Выразить через логарифмы по основанию 2: а) ; б) ; в) . |
Решение.
| Пример 17. Вычислить: . |
Решение.
| . | для любого kR (формула перехода к новому основанию) |
| Пример 18. Вычислить: а) ; б) . |
Решение:
| Пример 19. Вычислить: . |
Решение:
| Пример 20. Вычислить: . |
Решение.
| . | , b 1 для любого kR |
| Пример 21. Вычислить: . |
Решение.
| Пример 22. Вычислить: . |
Решение.
| . | , b 1 |
| Пример 23.Вычислить выражение при условии . |
Решение.
Для закрепления пройденного материала рекомендуем пройти следующий тест.
Примеры для самостоятельного решения
Теория
Решебник
Тест
Вычислить:
1. а) ,
б) ,
в) .
Решение.
Ответ.
2. а) ,
б) ,
в) .
Решение.
Ответ.
3. а) ,
б) ,
в) .
Решение.
Ответ.
4. а) ,
б) ,
в) .
Решение.
Ответ.
5. а) ,
б) ,
в) .
Решение.
Ответ.
6. а) ,
б) ,
в) .
Решение.
Ответ.
7. а) ,
б) .
Решение.
Ответ.
8. а) ,
б) .
Решение.
Ответ.
9. а) ,
б) .
Решение.
Ответ.
10. .
Решение.
Ответ.
11. Выразить через логарифмы по основанию 3:
а) ,
б) ,
в) ,
г) .
Решение.
Ответ.
Вычислить:
12. а) ,
б) .
Решение.
Ответ.
13. .
Решение.
Ответ.
14. .
Решение.
Ответ.
15. .
Решение.
Ответ.
16. .
Решение.
Ответ.
17. .
Решение.
Ответ.
18. .
Решение.
Ответ.
19. .
Решение.
Ответ.
20. .
Решение.
Ответ.
21. .
Решение.
Ответ.
Теория
Решебник
Примеры для самостоятельного решения
Тест
Решение
Теория
Решебник
Примеры для самостоятельного решения
Тест
1. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
2. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
3. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
4. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
5. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
6. а) .
б) .
в) .
назад к условию задачи для самостоятельного решения
7. а).
б) .
назад к условию задачи для самостоятельного решения
8. а).
б) .
назад к условию задачи для самостоятельного решения
9.а) .
б) .
назад к условию задачи для самостоятельного решения
10. .
назад к условию задачи для самостоятельного решения
11.а) .
б) .
в) .
г) .
назад к условию задачи для самостоятельного решения
12. а) .
б) .
назад к условию задачи для самостоятельного решения
13.
.
назад к условию задачи для самостоятельного решения
14. .
назад к условию задачи для самостоятельного решения
15. .
назад к условию задачи для самостоятельного решения
16. .
назад к условию задачи для самостоятельного решения
17. .
назад к условию задачи для самостоятельного решения
18. .
назад к условию задачи для самостоятельного решения
19. .
.
назад к условию задачи для самостоятельного решения
20. .
.
назад к условию задачи для самостоятельного решения
21. .
назад к условию задачи для самостоятельного решения
Теория
Решебник
Примеры для самостоятельного решения
Тест
Ответы
| 1. а) 6, б) 4, в) –2. назад 2. а) –1, б) –9, в) -4. назад 3. а) 2, б) , в) 1,5. назад 4. а) 9, б)25, в) 9. назад 5. а) 9, б) 49, в) . назад 6. а) , б) 3,5, в). назад 7. а) 1, б) 0. назад 8. а) 1, б) 2. назад 9. а) 2, б) 2. назад 10. 1. назад | 11. а) , б) , в) , г) . назад 12. а) 5, б)2. назад 13. 890. назад 14. 24, назад 15. . назад 16. 2. назад 17. 5. назад 18. . назад 19. 4,5 назад 20. . назад 21. 0. назад |
Теория
Решебник
Примеры для самостоятельного решения
Тест
mognovse.ru
Формулы логарифмов. Логарифмы примеры решения.
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения.
Ранее мы уже познакомились с понятием логарифма. А также рассмотрели основные свойства и примеры решения.
Формулы логарифмов сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.
Примеры решения логарифмов на основании формул.
Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.
Логарифмы, примеры:
log28 = 3, т.к. 23 = 8
log749 = 2, т.к. 72 = 49
log51/5 = -1, т.к. 5-1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
lg100 = 2
log10100 = 2, т.к. 102 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
- Основное логарифмическое тождество
a logab = bПример.
82log83 = (82log83)2 = 32 = 9
- Логарифм произведения равен сумме логарифмов
loga (bc) = logab + logacПример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
- Логарифм частного равен разности логарифмов
loga (b/c) = logab — logacПример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
- Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.
log49 = log223 2 = log23
- Переход к новому основанию
logab = logcb/logca,если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: «Решение логарифмических уравнений. Как решать, на примерах». Не пропустите!
Если у вас остались вопросы по решению, пишите их в комментариях к статье.
Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Логарифм. Примеры
Логарифмом числа b по основанию a обозначают выражение . Вычислить логарифм значит найти такой степень x (),при котором выполняется равенство
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x).
Из записи видно, что основы в записи не пишут. Для примера
Натуральный логарифм – это логарифм у которого за основу экспонента ( обозначают ln(x)).
Экспонента равна 2,718281828…. Чтобы запомнить экспоненту можете изучить правило: экспонента равна 2,7 и два раза год рождения Льва Николаевича Толстого. Зная это правило будете знать и точное значение экспоненты, и дату рождения Льва Толстого.
И еще один важный логарифм по основанию два обозначают
Производная от логарифм функции равна единице разделенной на переменную
Интеграл или первообразная логарифма определяется зависимостью
Приведенного материала Вам достаточно, чтобы решать широкий класс задач связанных с логарифмами и логарифмирования. Для усвоения материала приведу лишь несколько распространенных примеров из школьной программы и ВУЗов.
Примеры на логарифмы
Прологарифмировать выражения
Пример 1.
а). х=10ас^2 (а>0,с>0).
По свойствам 3,5 вычисляем
2.
По свойству разницы логарифмов имеем
3.
Используя свойства 3,5 находим
4. где .
На вид сложное выражение с использованием ряда правил упрощается к виду
——————————————
Нахождение значений логарифмов
Пример 2. Найти х, если
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
Подставляем в запись и скорбим
Поскольку основания равные, то приравниваем выражения
——————————————
Пример 3. Пусть задано значение логарифмов
Вычислить log[a](x), если
Решение: Прологарифмируем переменную, чтобы расписать логарифм через сумму слагаемых
——————————————
На этом знакомство с логарифмами и их свойствами только начинается. Упражняйтесь в вычислениях, обогащайте практические навыки — полученные знания Вам скоро понадобятся для решения логарифмических уравнений. Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме — логарифмические неравенства …
yukhym.com
