Скалярное произведение векторов примеры – свойства, примеры вычисления, физический смысл

Скалярное произведение векторов

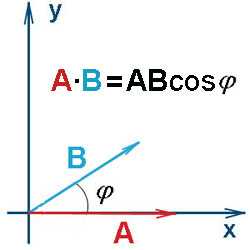
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a

y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; … ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =

= 5 |a|² + 12 a · b — 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ — 9 · 2² = 45 +36 -36 = 45.

Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.

Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:

a = i + 2j
b = 4i — 8j

Тогда используя свойства ортов (i² = 1, j² = 1, i·j = 0)

(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i² — 30i·j + 12j·i — 20j² = 12 — 0 + 0 — 20 = -8

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.

ru.onlinemschool.com

Скалярное произведение векторов: теория и решения задач

Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 1:    (1)

Можно встретить и другое название этой операции: внутреннее произведение.

Скалярное произведение вектора на себя называется скалярным квадратом.

Сформулируем другое определение, эквивалентное определению 1.

Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:

   (2)

или

   (3)

На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора. Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория.

Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:

Пример 1. Даны векторы . Найти скалярное произведение векторов , если их длины и угол между ними представлены следующими значениями:

Решение:

Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.

На плоскости

Если два вектора и на плоскости определены своими двумя декартовыми прямоугольными координатами

и

,

то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:

.

В пространстве

Если два вектора и в пространстве определены своими тремя декартовыми прямоугольными координатами

и

,

то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:

.

Геометрические свойства

В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.

На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла — φ1 и φ2. Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения. Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит

π, то есть 180 градусов. На рисунке этот угол обозначен как φ1.

1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю:

.

Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.

2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.

3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше

π/2) тогда и только тогда, когда их скалярное произведение отрицательно.

---

Пример 3. Даны длины двух векторов и угол между ними:

.

Определить, при каком значении числа векторы и ортогональны (перпендикулярны).

Решение. Перемножим векторы по правилу умножения многочленов:

.

Теперь вычислим каждое слагаемое:

.

Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:

Ответ: мы получили значение λ = 1,8, при котором векторы ортогональны.

---

Пример 4. В координатах даны векторы:

.

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Решение. Вычислять будем путём сложения произведений соответствующих координат.

.

Получили отрицательное число, поэтому векторы образуют тупой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили нуль, поэтому векторы образуют прямой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

Решить задачу самостоятельно, а затем посмотреть решение

Иногда выигрышным для наглядности является представление двух перемножаемых векторов в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:

Тогда скалярное произведение векторов будет произведением этих матриц:

Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.

В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.

Пример 6. Найти скалярные произведения пар векторов

и

,

используя матричное представление.

Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй — в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:

Аналогично представляем вторую пару и находим:

Как видим, результаты получились те же, что и у тех же пар из примера 4.

---

Чтобы выразить скалярное произведение векторов

                              (1)

в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:

То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины. Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:

Так как векторы

попарно перпендикулярны, то попарные произведения ортов будут равны нулю:

Теперь выполним умножение векторных многочленов:

 

Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:

Получаем формулу косинуса угла между двумя векторами:

---

Пример 7. Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).

Найти угол .

Решение. Находим координаты векторов:

,

.

По формуле косинуса угла получаем:

Следовательно, .

---

Пример 8. Даны два вектора

и

Найти сумму, разность, длину, скалярное произведение и угол между ними.

Решение.

1.Сумма

2.Разность

3.Длина

4.Скалярное произведение

5.Угол между и :

Решить задачи самостоятельно, а затем посмотреть решения

---

Пример 12. Среди векторов

Найти а) коллинеарные; б) ортогональные.

Решение.

а) проверим пропорциональность соответствующих координат векторов — условие коллинеарности (повторение материала предыдущей части темы «Векторы»).

Для векторов и :

 

Равенство не выполняется.

Для векторов и :

Равенство выполняется.

Для векторов и :

Равенство не выполняется.

Наше исследование показало, что коллинеарны векторы и .

б) найдём скалярные произведения векторов.

Наше исследование показало, что ортогональны векторы и и и .

Расчёт работы постоянной силы

Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная точка перемещается прямолинейно из начала координат в конец вектора B под действием постоянной силы F = A, образующей угол с перемещением S = A. Из физики известно, что работа силы F при перемещении S равна . Таким образом, работа постоянной силы при прямолинейном перемещении её точки приложения равна скалярному произведению вектора силы F = B на вектор перемещения S = A.

Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно часто встречается в последующих разделах математики, особенно, аналитической геометрии. Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?

Экономический смысл скалярного произведения векторов

В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение

выражает суммарную стоимость всех товаров x.

Поделиться с друзьями

Начало темы «Векторы»

Продолжение темы «Векторы»

function-x.ru

Скалярное произведение векторов, формула и примеры

Определение и формула скалярного произведения векторов

Если векторы заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:

   

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:

   

Выражение называется скалярным квадратом вектора .

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

   

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

   

4. Операция скалярного умножения коммуникативна:

   

5. Если скалярное произведение двух ненулевых векторов равно нулю, то эти вектора ортогональны (перпендикулярны):

   

6. .

7. Операция скалярного умножения дистрибутивна:

   

8. Если угол между векторами острый, то скалярное произведение этих векторов будет положительным числом (так как косинус острого угла – положительное число). Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла есть величина отрицательная). Имеют место и обратные утверждения.

9. Если векторы сонаправлены, то угол между ними будет равен , а скалярное произведение будет положительным. Угол между противоположно направленными векторами равен и их скалярное произведение отрицательно.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Скалярное произведение векторов — урок. Геометрия, 9 класс.

Скалярным произведением двух векторов a→ и b→ будет скалярная величина (число), равная произведению модулей этих векторов, умноженное на косинус угла между ними:

a→⋅b→=a→⋅b→⋅cosα

 

Очень важно правильно определить угол между векторами. Если векторы не имеют общей начальной точки, необходимо представить, какой угол бы образовался, если их переместить к общей начальной точке.

 

Угол между векторами обозначают a→b→ˆ=α.

 

1. Если векторы сонаправлены, то a→b→ˆ=0°:

 

Обрати внимание!

Так как косинус угла в \(0\) градусов равен \(1\), то скалярное произведение сонаправленных векторов является произведением их длин.

Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.

2. Если векторы противополжно направлены, то a→b→ˆ=180°:

 

Обрати внимание!

Так как косинус угла в \(180\)градусов равен \(-1\), то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.

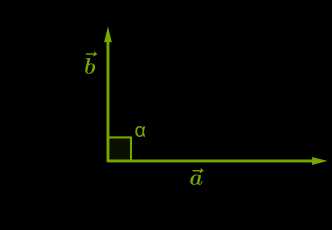
3. Векторы называют перпендикулярными, если a→b→ˆ=90°:

 

Обрати внимание!

Так как косинус прямого угла равен \(0\), то скалярное произведение перпендикулярных векторов равно \(0\).

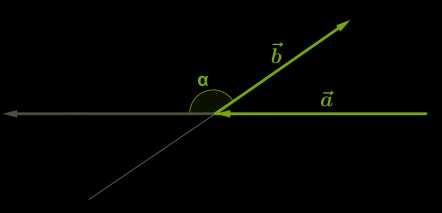
4. Внимательно необходимо рассмотреть ситуации, когда векторы образуют тупой угол:

 

 

Обрати внимание!

Так как косинус тупого угла отрицательный, то скалярное произведение таких векторов, которые образуют тупой угол, является отрицательным.

Скалярное произведение векторов, заданных координатами

Если a→xa;ya и b→xb;yb, то a→⋅b→=xa⋅xb+ya⋅yb.

 

Так как в координатах a→=xa2+ya2 иb→=xb2+yb2, то можно определить косинус угла между векторами и, следовательно, величину угла.

 

cosα=a→⋅b→a→⋅b→cosα=xa⋅xb+ya⋅ybxa2+ya2⋅xb2+yb2

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нулю. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору.

 

a→⋅a→>0;0→⋅0→=0

2. Скалярное произведение вектора самого на себя равно квадрату его модуля:

a→⋅a→=a→2

 

3. Для скалярного произведения в силе переместительный закон:

a→⋅b→=b→⋅a→

 

4. Для скалярного произведения в силе распределительный закон:

 

a→+b→⋅c→=a→⋅c→+b→⋅c→

 

5.  Для скалярного произведения в силе сочетательный закон:

 

k⋅a→⋅b→=k⋅a→⋅b→

 

6. Если скалярное произведение двух не нулевых векторов равно нулю, то эти векторы перпендикулярны.

www.yaklass.ru

Скалярное произведение векторов

Угол между векторами

Рассмотрим два данных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$. Отложим от произвольно выбранной точки $O$ векторы $\overrightarrow{a}=\overrightarrow{OA}$ и $\overrightarrow{b}=\overrightarrow{OB}$, тогда угол $AOB$ называется углом между векторами $\overrightarrow{a}$ и $\overrightarrow{b}$ (рис. 1).

Рисунок 1.

Отметим здесь, что если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены или один из них является нулевым вектором, тогда угол между векторами равен $0^0$.

Обозначение: $\widehat{\overrightarrow{a},\overrightarrow{b}}$

Понятие скалярного произведения векторов

Определение 1

Скалярное произведение двух векторов – это скаляр (число), равный произведению длин двух векторов на косинус угла между этими векторами.

Математически это определение можно записать следующим образом:

Скалярное произведение может равняться нулю в двух случаях:

1. Если один из векторов будет нулевым вектором (Так как тогда его длина равна нулю).

2. Если векторы будут взаимно перпендикулярны (то есть $cos{90}^0=0$).

Отметим также, что скалярное произведение больше нуля, если угол между этими векторами острый (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ } >0$), и меньше нуля, если угол между этими векторами тупой (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ }

С понятием скалярного произведения связано понятие скалярного квадрата.

Определение 2

Скалярным квадратом вектора $\overrightarrow{a}$ называется скалярное произведение этого вектора самого на себя.

Получаем, что скалярный квадрат равен

\[\overrightarrow{a}\overrightarrow{a}=\left|\overrightarrow{a}\right|\left|\overrightarrow{a}\right|{cos 0^0\ }=\left|\overrightarrow{a}\right|\left|\overrightarrow{a}\right|={\left|\overrightarrow{a}\right|}^2\]

Вычисление скалярного произведения по координатам векторов

Помимо стандартного способа нахождения значения скалярного произведения, который вытекает из определения, существует еще один способ.

Рассмотрим его.

Пусть векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ имеют координаты $\left(a_1,b_1\right)$ и $\left(a_2,b_2\right)$, соответственно.

Теорема 1

Скалярное произведение векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ равно сумме произведений соответствующих координат.

Математически это можно записать следующим образом

\[\overrightarrow{a}\overrightarrow{b}=a_1a_2+b_1b_2\]

Доказательство.

1. Пусть один из векторов будет нулевым вектором. К примеру, $\overrightarrow{a}=(0,0)$.

   Тогда $\overrightarrow{a}\overrightarrow{b}=0$. С другой стороны $a_1a_2+b_1b_2=0\cdot a_2+0\cdot b_2=0$, значит

   \[\overrightarrow{a}\overrightarrow{b}=a_1a_2+b_1b_2\]

2. Оба вектора не будут нулевыми векторами.

   Отложим от произвольной точки $O$ векторы $\overrightarrow{OA}$ и $\overrightarrow{OB}$ (рис. 2).

   Рисунок 2. Иллюстрация теоремы 1

   По теореме косинусов, получим:

   \[{AB}^2={OA}^2+{OB}^2-2OA\cdot OBcosO\]

   Так как $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$, получим

   \[{|\overrightarrow{OB}-\overrightarrow{OA}|}^2={|\overrightarrow{OA}|}^2+{|\overrightarrow{OB}|}^2-2\left|\overrightarrow{OA}\right||\overrightarrow{OB}|\] \[\overrightarrow{OA}\overrightarrow{OB}=\frac{1}{2}\left({|\overrightarrow{OA}|}^2+{|\overrightarrow{OB}|}^2-{|\overrightarrow{OB}-\overrightarrow{OA}|}^2\right)\]

   Так как векторы $\overrightarrow{OA}$ и $\overrightarrow{OB}$ имеют координаты $\left(a_1,b_1\right)$ и $\left(a_2,b_2\right)$, соответственно, то $\overrightarrow{OB}-\overrightarrow{OA}=\left(a_2-a_1,b_2-b_1\right)$. Тогда равенство примет вид

   \[\overrightarrow{OA}\overrightarrow{OB}=\frac{1}{2}\left(a^2_1+b^2_1+a^2_2+b^2_2-{(a_2-a_1)}^2-{(b_2-b_1)}^2\right)=a_1a_2+b_1b_2\]

Теорема доказана.

Эта теорема имеет несколько следствий:

Следствие 1: Векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ перпендикулярны тогда и только тогда, когда $a_1a_2+b_1b_2=0$

Следствие 2: Косинус угла между векторами равен $cos\alpha =\frac{a_1a_2+b_1b_2}{\sqrt{a^2_1+b^2_1}\cdot \sqrt{a^2_2+b^2_2}}$

Свойства скалярного произведения векторов

Для любых трех векторов и действительного числа $k$ справедливо:

1. ${\overrightarrow{a}}^2\ge 0$

   Данное свойство следует из определения скалярного квадрата (определение 2).

2. Переместительный закон: $\overrightarrow{a}\overrightarrow{b}=\overrightarrow{b}\overrightarrow{a}$.

   Данное свойство следует из определения скалярного произведения (определение 1).

3. Распределительный закон:

   $\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}$. \end{enumerate}

   По теореме 1, имеем:

   \[\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+b_1b_3+b_2b_3==\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}\]

4. Сочетательный закон: $\left(k\overrightarrow{a}\right)\overrightarrow{b}=k(\overrightarrow{a}\overrightarrow{b})$. \end{enumerate}

   По теореме 1, имеем:

   \[\left(k\overrightarrow{a}\right)\overrightarrow{b}=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow{a}\overrightarrow{b})\]

Пример задачи на вычисление скалярного произведения векторов

Пример 1

Найти скалярное произведение векторов $\overrightarrow{a}$ и $\overrightarrow{b}$, если $\left|\overrightarrow{a}\right|=3$ и $\left|\overrightarrow{b}\right|=2$, а угол между ними равен ${{30}^0,\ 45}^0,\ {90}^0,\ {135}^0$.

Решение.

Используя определение 1, получаем

Для ${30}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({30}^0\right)\ }=6\cdot \frac{\sqrt{3}}{2}=3\sqrt{3}\]

Для ${45}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({45}^0\right)\ }=6\cdot \frac{\sqrt{2}}{2}=3\sqrt{2}\]

Для ${90}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({90}^0\right)\ }=6\cdot 0=0\]

Для ${135}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({135}^0\right)\ }=6\cdot \left(-\frac{\sqrt{2}}{2}\right)=-3\sqrt{2}\]

spravochnick.ru

Скалярное произведение векторов.

Навигация по странице:

Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; … ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:

   a · a ≥ 0

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

   a · a = 0   <=>   a = 0

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

   a · a = |a|²

4. Операция скалярного умножения коммуникативна:

   a · b = b · a

5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

   a ≠ 0, b ≠ 0, a · b = 0   <=>   a ┴ b

6. (αa) · b = α(a · b)

7. Операция скалярного умножения дистрибутивна:

   (a + b) · c = a · c + b · c

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =

= 5 |a|² + 12 a · b — 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ — 9 · 2² = 45 +36 -36 = 45.

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 4. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Скалярное произведение векторов

Для начала вспомним, какие действия над векторами вам известны.

Итак, это сложение двух векторов по правилу треугольника или параллелограмма и нескольких векторов по правилу многоугольника. Вектор разности векторов  мы получали как вектор суммы векторов .

Также вам знакомо правило умножение вектора на число.

Сегодня вы познакомитесь с ещё одним действием над векторами — скалярным умножением векторов.

Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Скалярное произведение векторов  обозначают так .

Или возможна запись без знака умножения.

Оно равно произведению длин данных векторов на косинус угла между ними.

Стоит вспомнить, что угол между векторами получают, откладывая данные векторы от одной точки. При этом выбирают угол меньший 180°

Обратите внимание, ранее, при выполнении сложения, вычитания векторов и умножения вектора на число, результатом каждого из этих действий мы получали некоторый вектор.

Результатом же скалярного произведения векторов является число.

Сейчас подробнее рассмотрим случай, когда скалярное произведение векторов равно 0.

Понятно, что для этого хотя бы один из множителей должен быть равен нулю.

Такими будут случаи, когда хотя бы один из векторов в произведении является нулевым.

Если же векторы  ненулевые, то косинус угла между ними должен быть равен 0.

Среди возможных значений градусной меры угла между двумя векторами только лишь косинус угла в 90° равен 0.

Отсюда получаем, что векторы  перпендикулярны.

Подытожим. Скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым.

Ну, а скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Из формулы скалярного произведения также можно заметить, что, если векторы  не нулевые, то их длины всегда больше нуля, поэтому их произведение тоже положительно. А вот значение косинуса угла между ними может принимать как положительные, так и отрицательные значения.

Можно сказать, что скалярное произведение двух ненулевых векторов больше нуля, если угол между векторами острый. Равно нулю, если угол между ним прямой. И меньше нуля, если угол между данными векторами тупой. Ещё раз обратим внимание на то, что эти заключения верны для ненулевых векторов .

Задача. Найти скалярное произведение векторов  и , пользуясь данными рисунков.

Решение.

а)

б)

в)

г)

Мы рассмотрели примеры применения формулы скалярного произведения двух векторов и убедились, что скалярное произведение ненулевых векторов больше нуля, если угол между ними является острым, равно нулю — если векторы перпендикулярны, и меньше нуля — если угол между векторами тупой.

А сейчас рассмотрим сонаправленные векторы  и . Запишем формулу их скалярного произведения.

Вы должны помнить с прошлых уроков, что угол между сонаправленными векторами равен нулю. А косинус угла в 0° равен 1. Тогда получаем, что скалярное произведение сонаправленных векторов равно произведению их длин.

Говоря о противоположно направленных векторах, можно вспомнить, что угол между ними равен 180°. Значит, косинус равен -1.

Тогда скалярное произведение противоположно направленных векторов равно .

Что касается, скалярного произведения вектора на самого себя, то его называют скалярным квадратом вектора. Этот случай можно рассматривать в контексте сонаправленных векторов. Действительно, ведь векторы равны, а значит, и сонаправлены. Такое произведение равно произведению длин данного вектора.

Тогда получаем, что скалярный квадрат вектора равен квадрату его длины.

Задача. Найдём скалярные квадраты векторов , ,  и .

Решение.

 

 

 

 

Скалярное произведение векторов применяется не только в математике. Например, из курса механики известно, что работа постоянной силы F при перемещении из точки М в точку Н равна .

Тем самым получаем, что работа силы F равна скалярному произведению вектора силы  и вектора перемещения .

Вернёмся к скалярному произведению в математике и решим несколько задач.

Задача. К одной и той же точке приложены  и , действующие под углом в  друг к другу. , . Найти величину равнодействующей силы .

Решение.

1 способ

 

 

 

 

 

,

2 способ

 

 

 

 

 

,

Ответ: .

Задача. В ,где , проведена высота . Вычислить , , , .

Решение

 

 

, так как

 

 

Подведём итоги нашего урока.

Сегодня вы познакомились с новым действием над векторами — скалярным умножением векторов.

Скалярным произведением двух векторов называют произведение длин данных векторов на косинус угла между ними.

Проанализировав эту формулу, мы заметили, что скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым. Ну, а скалярное произведение ненулевых векторов рано нулю, тогда и только тогда, когда данные векторы перпендикулярны.

Также, пользуясь знаниями об углах между сонаправленными и противоположно направленными векторами, мы выяснили, что скалярное произведение сонаправленных векторов равно произведению их длин, а скалярное произведение противоположно направленных векторов противоположно произведению их длин.

Введя понятия скалярного квадрата вектора, мы получили, что он равен квадрату длины данного вектора.

Знания о скалярном произведении векторов можно применять не только на уроках математики. Так же они широко используются в физике.

videouroki.net