Сообщение на тему замечательные пределы – Реферат Замечательные пределы

Замечательные пределы, формулы и доказательства

Первый замечательный предел:

   

Следствия:

   

   

   

   

Подробнее про первый замечательный предел читайте в отдельной теме.

Примеры решений с первым замечательным пределом

Второй замечательный предел

   

здесь – постоянная Эйлера

Следствия:

   

   

   

   

   

Подробнее про второй замечательный предел читайте в отдельной теме.

Примеры решений со вторым замечательным пределом

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Тема 21 первый замечательный предел. Второй замечательный предел

КОНСПЕКТ 21

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.

21.1 ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

Рассмотрим следующий предел: Согласно правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида, которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

– тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра может выступать не только переменная, но и элементарная функция, сложная функция.Важно лишь, чтобы она стремилась к нулю.

Примеры: ,,,

Здесь ,,,, и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.

Пример 1

Найти предел

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида , ееобязательно указываемв оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится, а в знаменателе.

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить». А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания. Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:Теперь только осталось избавиться от трехэтажности дроби:Готово. Окончательный ответ:

21.2 ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка:  – это иррациональное число.

В качестве параметра может выступать не только переменная, но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 2

Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 

Нетрудно заметить, что при основание степени, а показатель – , то есть имеется, неопределенность вида:

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать. Для этого возводим основание в степень, и, чтобы выражение не изменилось – возводим в степень:

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву:

При этом сам значок предела перемещаем в показатель.

 

ПРАКТИКУМ 21

ЗАДАНИЕ N 1Тема: Первый замечательный предел…

Решение:Чтобы воспользоваться первым замечательным пределомнеобходимо, используя соотношениевынести множительза знак предела. Тогда:

ЗАДАНИЕ N 2Тема: Первый замечательный предел…

Решение:Чтобы воспользоваться первым замечательным пределомнеобходимо, используя соотношениевынести множительза знак предела. Тогда:

ЗАДАНИЕ N 3Тема: Второй замечательный пределПусть. Тогдаравен …

Решение:Обращаем внимание, что функциюнужно преобразовать так, чтобы использовать второй замечательный предел – формулу. Для этого числитель и знаменатель дроби необходимо разделить на число, получаетсяДалее нужно выполнить замену переменной, полагая. Тогда если, то,и, следовательно,Получаем

ЗАДАНИЕ N 4Тема: Второй замечательный пределПусть. Тогдаравен …

Решение:Обращаем внимание, что функциюнужно преобразовать так, чтобы использовать второй замечательный предел – формулу. Для этого числитель и знаменатель дроби необходимо разделить на число, получаетсяДалее нужно выполнить замену переменной, полагая. Тогда если, то,и, следовательно,Получаем

САМОСТОЯТЕЛЬНАЯ РАБОТА 21

ЗАДАНИЕ N 1Тема: Первый замечательный предел

…

 ЗАДАНИЕ N 2Тема: Первый замечательный предел…

ЗАДАНИЕ N 3Тема: Первый замечательный предел…

 ЗАДАНИЕ N 4Тема: Второй замечательный пределПусть. Тогдаравен …

ЗАДАНИЕ N 5Тема: Второй замечательный пределПусть. Тогдаравен …

 ЗАДАНИЕ N 6Тема: Второй замечательный пределПусть. Тогдаравен …

ЗАДАНИЕ N 7

Тема: Второй замечательный пределПусть. Тогдаравен …

ЗАДАНИЕ N 8Тема: Второй замечательный пределПусть. Тогдаравен …

0

studfiles.net

44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.

Как показывает приведённый выше пример 2.36, пределы отношения бесконечно малых можно упрощать, откидывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные бесконечно малые. Для того, чтобы этот способ вычисления пределов (точнее, раскрытия неопределённостей вида) можно было применять к возможно большему числу примеров, мы должны иметь достаточно большой запас известных пар эквивалентных бесконечно малых величин. Для наиболее употребительной базысоздадим такой запас в виде таблицы «стандартных» эквивалентных бесконечно малых.

Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи обозначение этой базы будем пропускать и писать знаквместо.

1) . Эту формулу мы уже доказали и использовали в примерах. Эквивалентностьиприозначает в точности, что первый замечательный предел равен 1.

2) . Эта эквивалентность тоже была доказана выше в одном из примеров.

3) . Докажем эту эквивалентность:

4) . Докажите это в качестве упражнения, сделав заменуи применив предыдущую табличную формулу.

5) . Для доказательства воспользуемся формулой. Далее, имеем:

Это означает, что доказываемая эквивалентность имеет место.

6) (). Для доказательства этой эквивалентности сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

и мы доказали формулу 6.

В частном случае, при , получаем эквивалентность

) .

7) (). Для доказательства сделаем заменуи выразимчерез:. Согласно формуле 6,при, откуда. Из непрерывности логарифма следует, чтои, значит,при. В этой формуле осталось лишь сменить обозначение переменногона, чтобы получить формулу 7.

В частном случае, при , получаем эквивалентность

) .

Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней .

1)	.
2)	.
3)	.
4)	.
5)	.
6)	().
)	.
7)	().
)	.

Приведём примеры применения табличных формул для раскрытия неопределённостей вида .

Замеча́тельные преде́лы— термин, использующийся в советских и российских учебниках поматематическому анализудля обозначения некоторых широко известныхматематических тождествсо взятиемпредела. Особенно известны:

Содержание

Первый замечательный предел

Доказательство

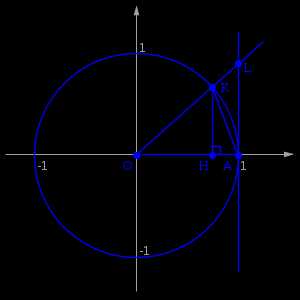
Рассмотрим односторонние пределыии докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

Точка K— точка пересечения луча с окружностью, а точкаL— с касательной к единичной окружности в точке. ТочкаH— проекция точкиKна осьOX.

Очевидно, что:

(1)

(где — площадь сектора)

(из 🙂

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

Доказательство следствий  [показать]

Второй замечательный предел

или

Доказательство второго замечательного предела:

Доказательство для натуральных значений x  [показать]

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами:, где— это целая часть x.

Отсюда следует: , поэтому

.

Если , то. Поэтому, согласно пределу, имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку, тогда

.

Из двух этих случаев вытекает, что для вещественного x.

Следствия

5. для,

studfiles.net

Первый и второй замечательный предел

Найти замечательные пределы трудно не только многим студентам первого, второго курса обучения которые изучают теорию пределов, но и некоторым преподавателям.

Формула первого замечательного предела

Следствия первого замечательного предела запишем формулами
1. 2. 3. 4. Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.

Пример 1. Найти предел функции sin(7*x)/(5*x)
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7

Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал.
Также, если есть обратный вид функции — это также первый замечательный предел. А все потому, что замечательный предел равен единице

Это же правило касается и следствий 1 замечательного предела. Поэтому если Вас спросят «Чему равен первый замечательный предел?» Вы без колебаний должны ответить, что это — единица.

Пример 2. Найти предел функции sin(6x)/tan(11x)
Решение: Для понимания конечного результата распишем функцию в виде

Чтобы применить правила замечательного предела умножим и разделим на множители

Далее предел произведения функций распишем через произведение пределов

Без сложных формул мы нашли предел часки тригонометрических функций. Для усвоения простых формул попробуйте придумать и найти предел на 2 и 4 формулу следствия 1 замечательного предела. Мы рассмотрим более сложные задачи.

Пример 3. Вычислить предел (1-cos(x))/x^2
Решение: При проверке подстановкой получим неопределенность 0/0. Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу

При этом предел преобразится к понятному виду

Нам удалось свести функцию к квадрату замечательного предела.

Пример 4. Найти предел
Решение: При подстановке получим знакомую особенность 0/0. Однако переменная стремится к Pi, а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х, чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y

Таким образом использовав тригонометрическую формулу, которая приведена в предыдущем задании, пример сведен к 1 замечательному пределу.

Пример 5. Вычислить предел
Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле

После этого получим нужную неопределенность 0/0. Далее выполняем замену переменных в пределе, и используем периодичность котангенса

Последние замены позволяют использовать следствие 1 замечательного предела.

Второй замечательный предел равен экспоненте

Это классика к которой в реальных задачах на пределы не всегда легко прийти.
В вычислениях Вам понадобятся пределы — следствия второго замечательного предела:
1. 2. 3. 4.
Благодаря второму замечательному пределу и его последствиям можно исследовать неопределенности типа ноль разделить на ноль, единица в степени бесконечность, и бесконечность разделить на бесконечность, да еще и в таком же степени

Начнем для ознакомления с простых примеров.

Пример 6. Найти предел функции
Решение: Напрямую применить 2 замечательный пределу не получится. Сначала следует превратить показатель, чтобы он имел вид обратный к слагаемому в скобках

Это и есть техника сведения к 2 замечательному пределу и по сути — вывода 2 формулы следствия предела.

Пример 7. Найти предел функции
Решение: Имеем задания на 3 формулу следствия 2 замечательного предела. Подстановка нуля дает особенность вида 0/0. Для возведения предела под правило превратим знаменатель, чтоб при переменной был тот же коэффициент что и в логарифм

Это также легко понять и выполнить на экзамене. Трудности у студентов при исчислении пределов начинаются с следующих задач.

Пример 8. Вычислить предел функции [(x+7)/(x-3)]^(x-2)
Решение: Имеем особенность типа 1 в степени бесконечность. Если не верите, можете везде вместо «икс» подставить бесконечность и убедиться в этом. Для возведения под правило поделим в скобках числитель на знаменатель, для этого предварительно выполним манипуляции

Подставим выражение в предел и превратим к 2 замечательному пределу

Предел равен экспоненте в 10 степени. Константы, которые являются слагаемыми при переменной как в скобках так и степени никакой «погоды» не вносят — об этом следует помнить. А если Вас спросят преподаватели — «Почему не превращаете показатель?» (Для этого примера в x-3), то скажите что «Когда переменная стремится к бесконечности то к ней хоть добавляй 100 хоть отнимай 1000, а предел останется такой как и был!».
Есть и второй способ вычислять пределы такого типа. О нем расскажем в следующем задании.

Пример 9. Найти предел
Решение: Теперь вынесем переменную в числителе и знаменателе и превратим оду особенность на другую. Для получения конечного значения используем формулу следствия 2 замечательного предела

Пример 10. Найти предел функции
Решение: Заданный предел найти под силу не каждому. Для возведения под 2 предел представим, что sin (3x) это переменная, а нужно превратить показатель

Далее показатель запишем как степень в степени

В скобках описаны промежуточные рассуждения. В результате использования первого и второго замечательного предела получили экспоненту в кубе.

Пример 11. Вычислить предел функции sin(2*x)/ln(3*x+1)
Решение: Имеем неопределенность вида 0/0. Кроме этого видим, что функцию следует превращать к использованию обеих замечательных пределов. Выполним предыдущие математические преобразования

Далее без труда предел примет значение

Вот так свободно Вы будете чувствовать себя на контрольных работах, тестах, модулях если научитесь быстро расписывать функции и сводить под первый или второй замечательный предел. Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас.
Для этого заполните форму, укажите данные и вложите файл с примерами. Мы помогли многим студентам — сможем помочь и Вам!

yukhym.com

Лекция 13. Замечательные пределы

Лекция 13. Замечательные пределы.

13.1. Первый замечательный предел.

♦ Теорема 13.1 (о пределе промежуточной функции). Если в некоторой окрестности точки 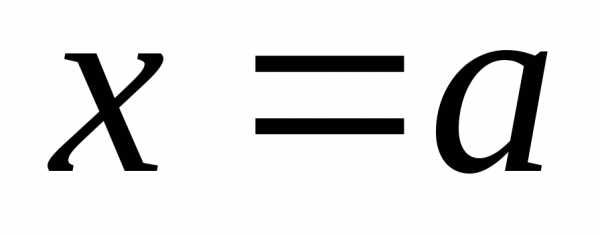(или при достаточно больших значенияхx) функция 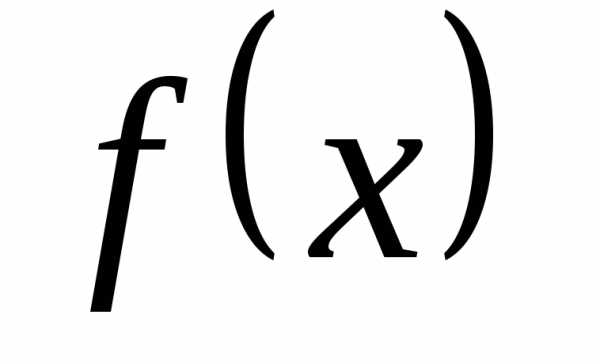заключена между двумя функциям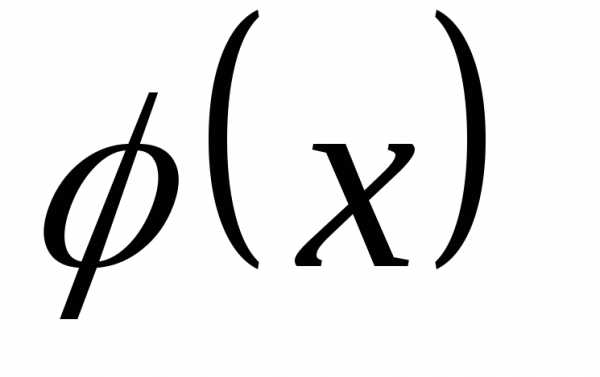ии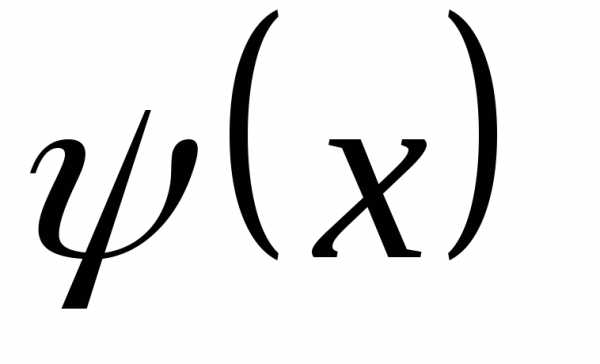, имеющими одинаковый пределA при 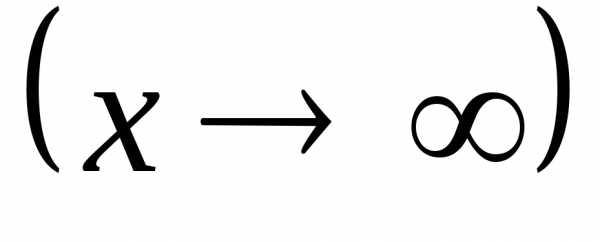, то функция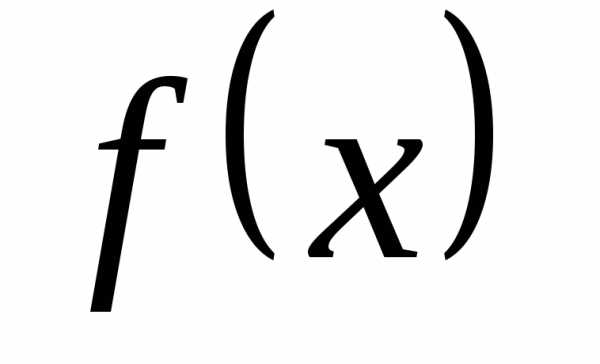имеет тот же пределA.

Доказательство. Пусть при 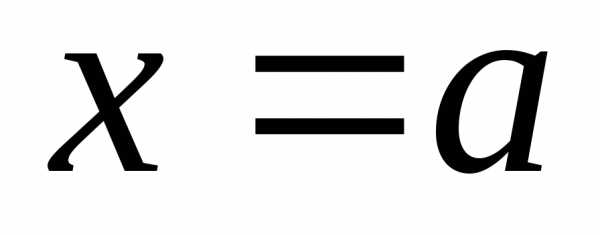. Это означает, что для любого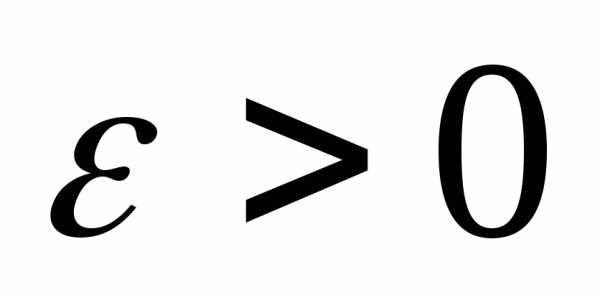найдётся число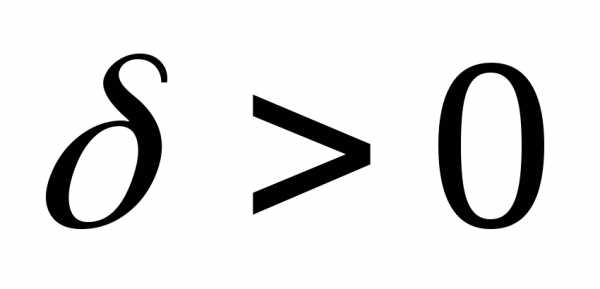такое, что для всех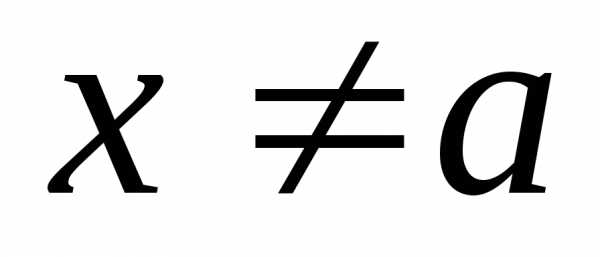и удовлетворяющих условию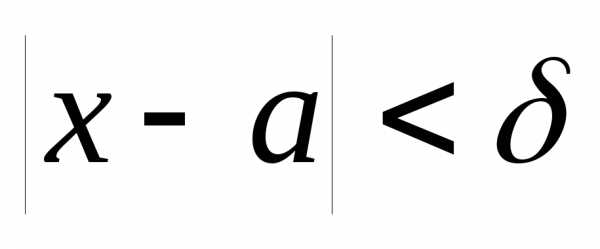будут верны одновременно неравенстваиили,. Так как по условию, то, то естьи это означает, что. ■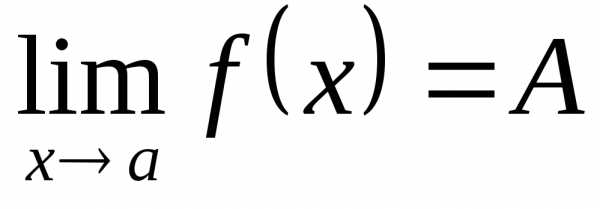

♦ Теорема 13.2 (первый замечательный предел).

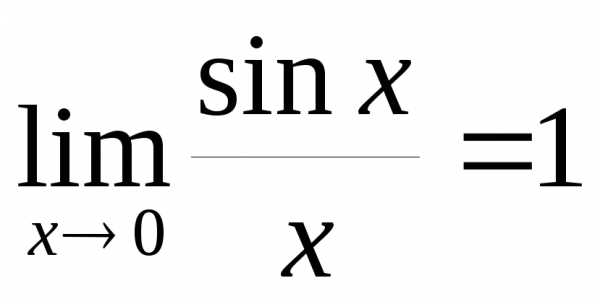. (13.1)

Доказательство. Рассмотрим круг радиуса R с центром в точке O (рис. 13.1). Пусть OB – подвижный радиус, образующий угол x 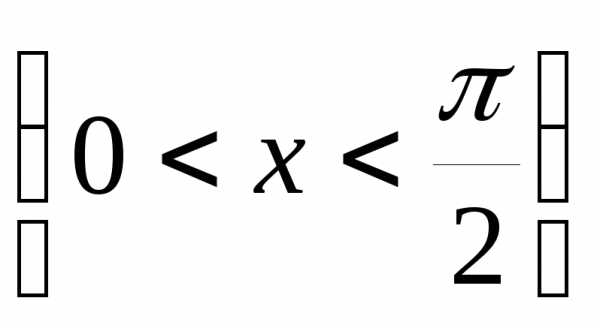с осьюOA. Площадь треугольника AOB меньше площади сектора AOB, которая в свою очередь меньше площади треугольника AOC, то есть

.

Таким образом,

.

Функции и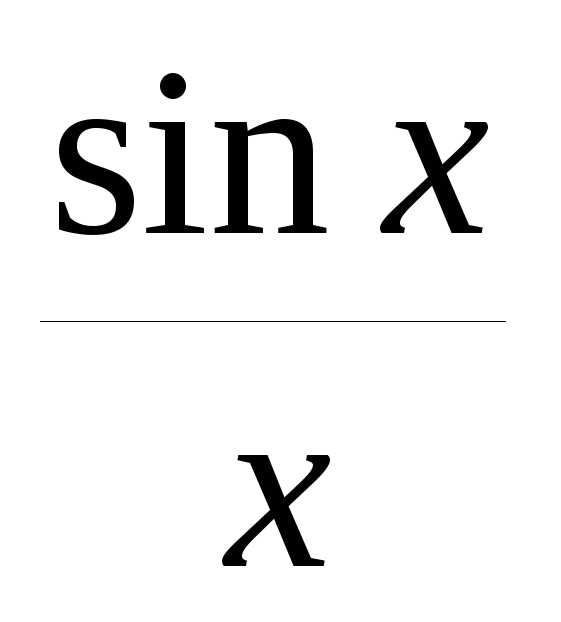чётные, поэтому полученные неравенства справедливы и при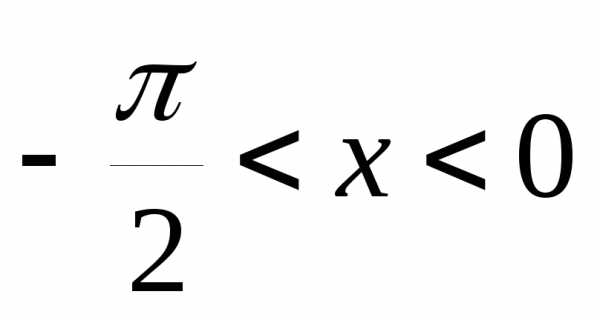. При переходе к пределу приполучим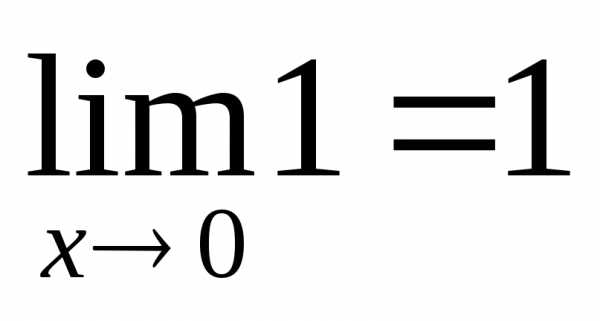,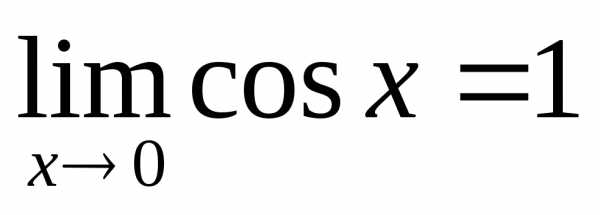и на основании теоремы 13.1 предел промежуточной функции. ■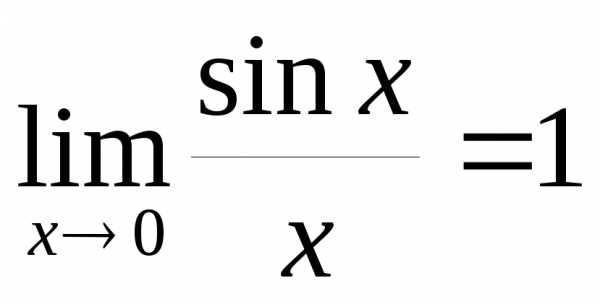

 Пример 13.1. 1) .

2) .

13.2. Второй замечательный предел.

Функция 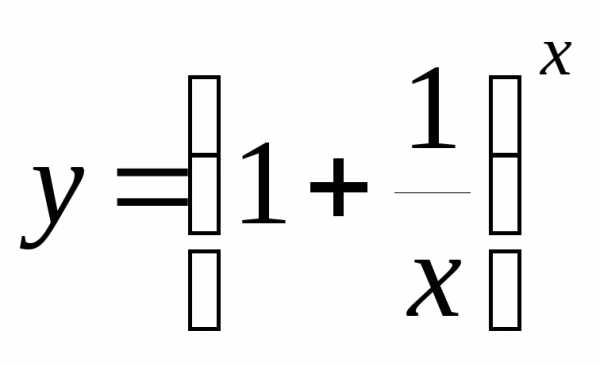прии(гдех в отличие от натурального n «пробегает» все значения числовой оси) имеет предел, равный числу е:

.

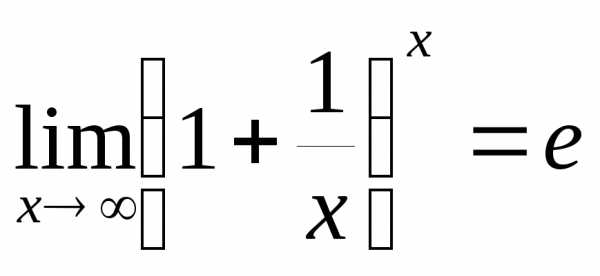Этот предел называется вторым замечательным пределом.

Если положить 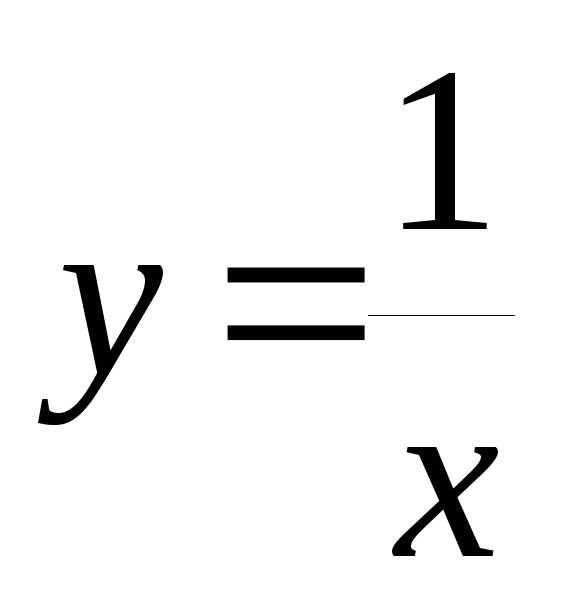, тогда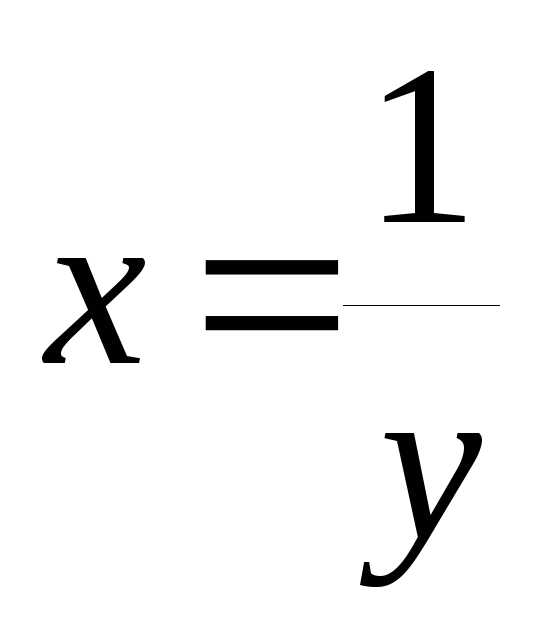. При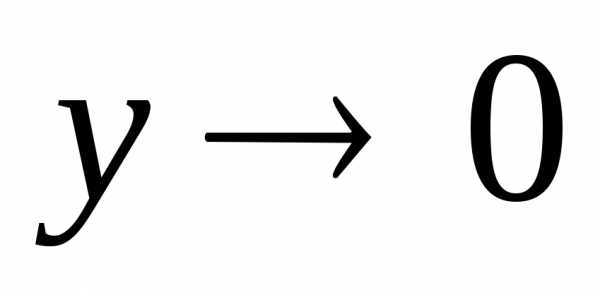и получаем

.

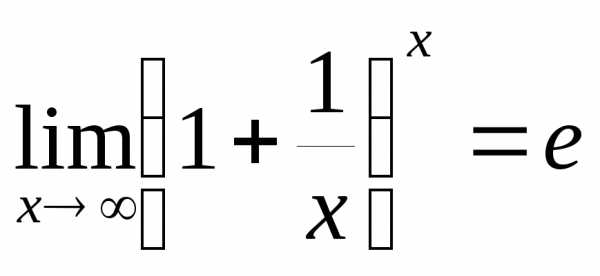
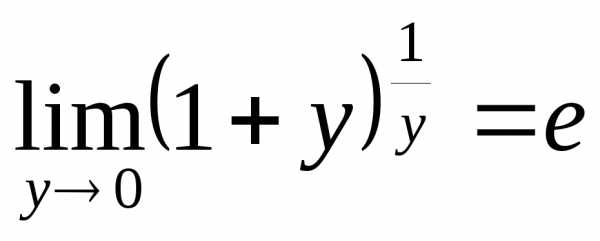Число е называется числом Эйлера или неперовым числом, график функции 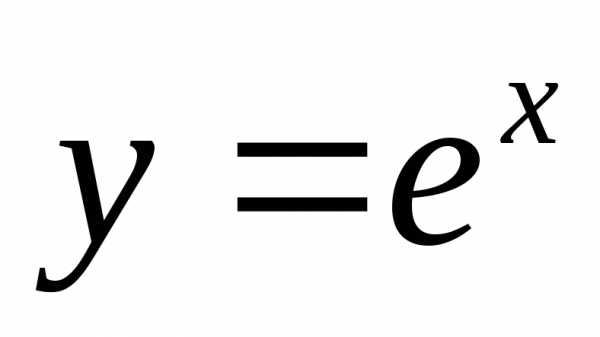получил названиеэкспоненты (рис. 13.2). Логарифмы по основанию е называются натуральными логарифмами, обозначаются . К числуе приводят решения многих прикладных задач статистики, физики, биологии, химии, анализ таких процессов, как распад радия, размножение бактерий и т.п.

Рис. 13.2.

13.3. Нахождение пределов с помощью эквивалентных бесконечно малых функций.

Эквивалентные бесконечно малые функции используются при вычислении пределов отношений двух бесконечно малых для раскрытия неопределенностей вида .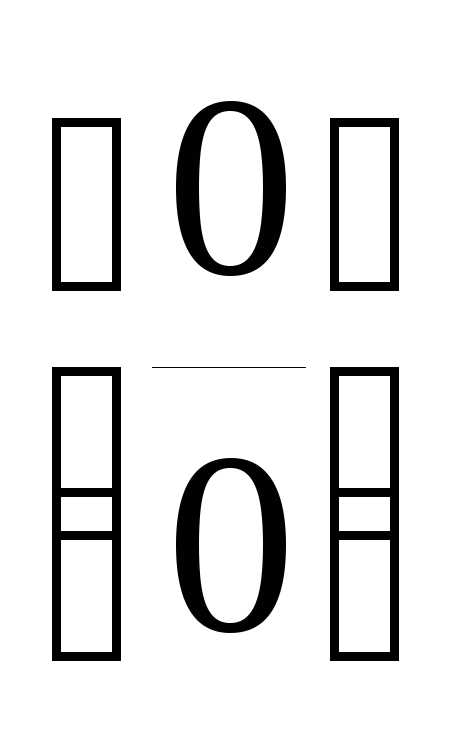

Запишем следствия из 1-го и 2-го замечательных пределов в виде таблицы эквивалентных бесконечно малых. При

 Пример 13.2. 1) Найти .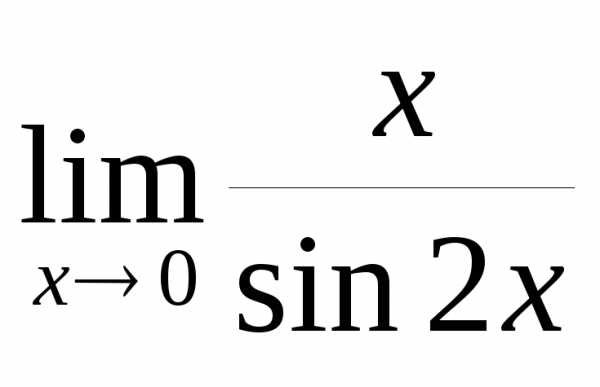

При 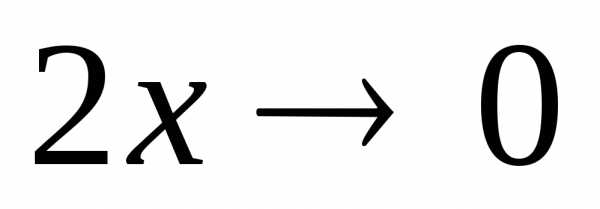и, значит,. Заменяя знаменатель на эквивалентную бесконечно малую, получаем.

2) Найти .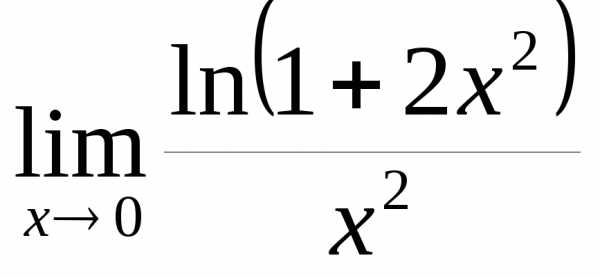

.

3) Найти .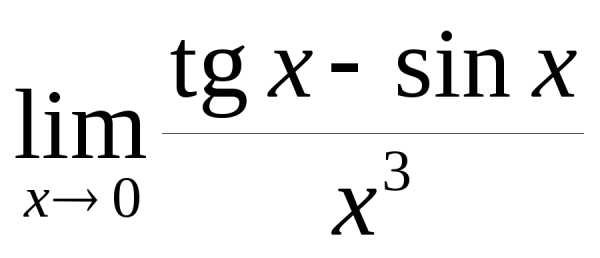

. 

60

studfiles.net

Замечательные пределы — Пределы и способы их решения

Замечательные пределы.
Примеры решений

Продолжаем наш разговор на тему Пределы и способы их решения. Перед изучением материалов данной страницы настоятельно рекомендую ознакомиться со статьей Пределы. Примеры решений. Из вышеуказанной статьи Вы сможете узнать, что же такое предел, и с чем его едят – это ОЧЕНЬ важно. Почему? Можно не понимать, что такое определители и успешно их решать, можно совершенно не понимать, что такое производная и находить их на «пятёрку». Но вот если Вы не понимаете, что такое предел, то с решением практических заданий придется туго. Также не лишним будет ознакомиться с образцами оформления решений и моими рекомендациями по оформлению. Вся информация изложена в простой и доступной форме.

А для целей данного урока нам потребуются следующие методические материалы: Замечательные пределы и Тригонометрические формулы. Их можно найти на странице Математические формулы, таблицы и справочные материалы. Лучше всего методички распечатать – это значительно удобнее, к тому же к ним часто придется обращаться в оффлайне.

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.

Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел, Второй замечательный предел. Следует отметить, что это исторически сложившиеся названия, и, когда, например, говорят о «первом замечательном пределе», то подразумевают под этим вполне определенную вещь, а не какой-то случайный, взятый с потолка предел.

Начнем.

Первый замечательный предел

Рассмотрим следующий предел:  (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

 – тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра  может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры:
, , ,

Здесь , , , , и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

Почему? Потому-что многочлен  не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.

На практике не все так гладко, почти никогда студенту не предложат решить халявный предел  и получить лёгкий зачет. Хммм… Пишу эти строки и пришла в голову очень важная мысль – все-таки «халявные» математические определения и формулы вроде   лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, а нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

Теперь только осталось избавиться от трехэтажности дроби:

Готово. Окончательный ответ:

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“

Используем первый замечательный предел

“

Пример 2

Найти предел

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:

Действительно, у нас неопределенность  и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :

Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

Собственно, ответ готов:

В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Пример 3

Найти предел

Подставляем ноль в выражение под знаком передела:

Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле  (кстати, с котангенсом делают примерно то же самое, см. методический материал Горячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).

 В данном случае:

Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел

Пробуем подставить ноль в числитель и знаменатель:

Получена неопределенность  (косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

Постоянные множители вынесем за значок предела:

 

Организуем первый замечательный предел:

Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

Избавимся от трехэтажности:

Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

Пример 5

Найти предел

Этот пример сложнее, попробуйте разобраться самостоятельно:

 

Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка:  – это иррациональное число.

В качестве параметра  может выступать не только переменная , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение  , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при  основание степени , а показатель – , то есть имеется, неопределенность вида :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать  . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель.

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :

Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел .
Легко заметить, что в данном примере . Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :

Наконец-то долгожданное  устроено, с чистой совестью превращаем его в букву :

Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово.

А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

Пример 8

Найти предел

Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:

В результате получена знакомая неопределенность . Очевидно, что в данном примере . С помощью знакомого искусственного приема организуем в показателе степени конструкцию :

Выражение  со спокойной душой превращаем в букву :

Еще не всё, в показателе у нас появилась неопределенность вида . Раскладываем тангенс на синус и косинус (ничего не напоминает?):

Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

А что такое  и к чему оно стремится, нужно уже знать, иначе «двойка»!

Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов.

В 90-95% на зачете, экзамене Вам встретится первый замечательный предел или второй замечательный предел. Как быть, если попался «экзотический» замечательный предел? (со списком всех замечательных пределов можно ознакомиться в соответствующей методичке). Ничего страшного, практически все выкладки, приёмы решения для первого замечательного предела справедливы и для остальных замечательных пределов. Нужно решать их по аналогии.

Да, так чему же равен предел ?

Если у Вас получился ответ , значит в понимании высшей математики не всё так безнадежно = ).

Желаю успехов!

lablek.ru

Тема 2. Предел функции. замечательные пределы — Студопедия.Нет

Министерство образования и науки Российской Федерации

 

ФГБОУ ВПО «Сибирский государственный технологический университет»

 

 

О. А. Шушерина

 

Математика

Сборник задач к практическим занятиям

Направление подготовки 080200.62 Менеджмент

Профиль подготовки Производственный менеджмент (по отраслям)

Направление подготовки 080400.62 Управление персоналом

Профиль подготовки Контроллинг и аудит персонала

Квалификация (степень) выпускника Бакалавр Очная форма обучения

 

Содержание

Введение

Модуль 1. Дифференциальное исчисление функций одной переменной

Тема 1. Функции одной переменной, свойства и графики.

Тема 2. Предел функции. Замечательные пределы.

Тема 3. Непрерывные функции.

Тема 4. Производные функции одной переменной.

Тема 5. Экстремум, наибольшее и наименьшее значения функции.

Контрольная работа № 1 «Дифференциальное исчисление функции одной переменной»

Модуль 2. Дифференциальное исчисление функций

Нескольких переменных

Тема 1. Функции двух переменных, линии уровня. Частные производные.

Тема 2. Экстремум функции двух переменных (безусловный и условный).

Тема 3. Наибольшее и наименьшее значения функции двух переменных в области. Градиент функции.

Контрольная работа № 2 «Дифференциальное исчисление функции нескольких переменных»

Модуль 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.

Тема 1. Методы нахождения неопределенного интеграла.

Тема 2. Интегрирование рациональных функций.

Тема 3. Вычисление определенного интеграла (формула Ньютона-Лейбница, метод подстановки).

Тема 4. Вычисление площадей плоских фигур. Несобственные интегралы.

Контрольная работа № 3 «Неопределенный и определенный интегралы»

Вопросы к зачету (1-й семестр)

Библиографический список

 

ВВЕДЕНИЕ

Учебно-практическое пособие «Математика. Сборник задач к практическим занятиям» является компонентом учебно-методического комплекса дисциплины. Его цель – помочь студентам в организации самостоятельной деятельности и овладении практическими навыками уверенного решения задач.

 

Для приобретения профессиональных, культурных и математических компетенций в процессе решения задач предлагаем следующий порядок работы:

§ проработать теоретический материал по разделу (учебному модулю) – усвоить язык дисциплины, осмыслить базовые понятия, формулы, теоремы;

§ прорешать задачи по изучаемому разделу – сначала общие для всех студентов, а затем из индивидуального задания иовладеть методами их решения;

§ ответить на контрольные вопросы.

 

Это поможет освоить весь объем задач, который следует решить по данной теме и сформировать общекультурные компетенции: владение методами количественного анализа и моделирования, теоретического и экспериментального исследования.

 

В Сборник задач (1-й семестр) включены учебно-методические материалы по учебным модулям:

1. Дифференциальное исчисление функции одной переменной.

2. Дифференциальное исчисление функции нескольких переменных.

3. Интегральное исчисление функции одной переменной.

 

Каждая тема учебного модуля содержит задачи для решения на практическом занятии и дома.

Предлагаются задачи студентам с различным уровнем математической подготовки. Студент видит весь объем задач, которые следует решить, и в случае, если он работает быстрее, чем остальные, то ему не нужно терять время на ожидание новой задачи и проверки правильности решенной задачи. Если студент справился с задачами практического занятия, то он начинает решать задачи для домашнего задания.

Приведены примерные варианты контрольных работ по учебным модулям.

 

Желаем успехов!

 

Модуль 1. дифференциальное исчисление функции одной переменной

 

Тема 1. функции одной переменной, свойства и графики

Область определения и свойства функции

1.1.Найти и построить область определения функций одной переменной.

1) ; 2) ;             3) ;

4) ;    5) ; 6) .

1.2.Установить, является ли функция четной или нечетной.

1) ; 2) ;     3) ; 

4) ;     5) ; 6) .

1.3.По заданным функциям  и  построить сложную функцию

Построение графиков функций

1.4.Построить графики функций с помощью геометрических преобразований графиков основных элементарных функций (сдвиг, растяжение и сжатие по осям).

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

 

8) ;

9) ;

10) ;

11) ;

12) ;

13) .

.

 

Тема 2. Предел функции. замечательные пределы

 

Вычисление предела

2.1. Вычислить пределы функций при .

1) ; 2) ; 3) ;

4) ; 5) ; 6) ; 7) .

2.2. Вычислить пределы функций при .

1) ; 2) ;

3) ; 4) .

Первый замечательный предел

2.3. Используя первый замечательный предел, вычислить пределы.

ж) ;       з) ;               и) .

Второй замечательный предел

2.4. Используя второй замечательный предел, вычислить пределы.

1) ;     2) ;     3) ;

4) ;      5) ;  6) .

 

 

Тема 3. Непрерывные функции

 

Точки разрыва функции

3.1.Найти точки разрыва функции

studopedia.net