Сравнение дробей
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Сравнение дробей с одинаковыми знаменателями
Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
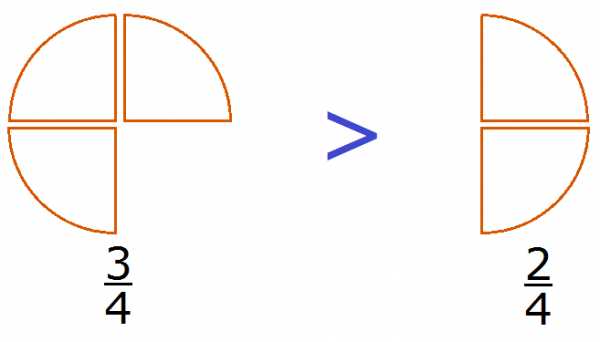
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Например, сравнить дроби и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
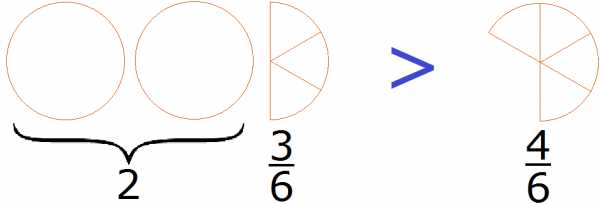
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10−8=2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь
А это значит, что и уменьшаемое меньше, чем вычитаемое
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его, когда изучим отрицательные числа.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Сравнение чисел
Давайте попробуем сделать Сравнение чисел до 10. Это очень легко например: 23 и 56, 37 и 98, 90 и 98.На первый взгляд все легко. Но что если сравнить вот эти числа:
177364 и 774857, 887375 и 975858, 7475638 и 7474665. Спорим ты не сравнишь их так быстро как предыдущие числа.Но есть один способ как быстро сравнивать такие большие числа как: 4563873586 и 4748575657. Представим что одноименные разряды соревнуются — еденицы с еденицами, десятки с десятками, сотни с сотнями и т. д.
у чисел 2566 и 2758 в старшем разряде тысяч числа одинаковые тогда мы смотрим на следующее число. У разряда сотен в числе 2566 равно 5 а в числе 2758 в разряде сотен будет 7 тем самым мы узнаем что число 2566 меньше числа 2758 потому, что 5 меньше 7. Точно так же мы делаем и с десятками, и с единицами. Числа с одинаковым количеством цифр сравнивают поразрядно, начиная со старшего разряда. Теперь ты сможешь с легкостью сравнить эти большие числа. Результат сравнения чисел записываю с помощью 3 знаков: > (больше), < (меньше), = (равно).Например: 243<748, 27957397=27957397, 87465>858465. Но бывают случаи как 22224 и 222224 в этих случаях больше то число в котором больше цифр. В данном случае больше число 222224 потому , что в этом числе 6 цифр а в числе 22224 всего 4 цифры.
Теперь что такое кратное сравнение . это тоже самое сравнение, только здесь мы делим числа друг на друга и узнаем во сколько раз одно число меньше или больше другого. Например: 28 и 3 — 28 : 3 =7 (р.). Почему р. потому, что раз- во сколько раз и поэтому мы обязательно пишем р. или раз.
Теперь разностное сравнение. Это тоже самое что и кратное, только вместо деления у нас вычитание . например 476 и 333 — 476кг.-333кг.=143(кг.).
Еще есть сравнения дробей . Например:2/33>24\33 ( если эти числа от одного чила например числа 7364)

uchik.ru
Сравнения 1 степени. Теория чисел.
В теории чисел, которая занимается изучением целочисленных значений, есть еще одна задача, которую мы попытаемся решить.
если нам известны A,B,C то при каком значении x это равенство будет верным?
Как пример
Решение подобных задач, неразрывно связано с функцией Эйлера. Хотя конечно есть и альтернативный метод решения (по Евклиду), но мы его рассмаотривать не будем.
Как же решать подобные уравнения. Вспомним, что по формуле Ферма-Эйлера есть следующая зависимость. Если a и m — взаимно простые числа ( то есть не имеющие общих делителей), то
С учетом того, что функция Эйлера от простого числа m равна m-1, получаем знаменитую формулу для любого простого числа
где как уже сказано a должно быть взаимно простым с m.
Способ Эйлера, позволяющий решать подобные сравнения в формулах выглядит так
Тогда, решая уравнение
узнаем чему же равен x
Попробуем решить наш первый пример.
функция Эйлера для числа 47 равна 46
и окончательная формула равна
Если считать «влоб» получится огромное число, но нам надо узнать всего лишь
Для решения подобной задачи мы воспользуемся материалом Остаток числа в степени по модулю и узнаем что наше решение
равно
проверим подставив полученное значение
делится нацело, а значит наше решение верное.
Как можете заметить, мы можем решать еще попутно аналогичную задачу, которая называется обратное значение по модулю для класса вычетов и которая выражается формулой
Удачных расчетов!
- Средние величины данных в поле комплексных чисел >>
abakbot.ru
