Степень на степень деление – Как делить степени | Алгебра

Как делить степени | Алгебра

Как делить степени? При каких условиях деление степеней возможно?

В алгебре найти частное степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

Чтобы разделить степени с одинаковыми основаниями, надо основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя (или коротко: при делении степеней показатели вычитают):

   

или

   

или

   

(последнюю формулу удобно использовать, если показатель степени в знаменателе больше показателя степени в числителе).

При делении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

   

Рассмотрим, как делить степени, на конкретных примерах.

   

Единицу в показателе степени не пишут, но при делении степеней ее следует учесть:

   

При делении степеней с одинаковыми основаниями и одинаковыми показателями получаем единицу:

   

   

   

   

Вынесение общего показателя при делении степеней позволяет упростить вычисления:

   

   

В выражениях возведение в степень выполняется в первую очередь.

Если нужно число разделить на степень либо степень разделить на число, сначала следует выполнить возведение в степень, а затем — деление:

   

   

www.algebraclass.ru

Как делить степени | Сделай все сам

Математические действия со степенями дозволено исполнять только в том случае, когда основания показателей степени идентичны, и когда между ними стоят знаки умножения либо деления. Основание показателя степени – это число, которое возводится в степень.

Инструкция

1.

Если числа со степенями делятся друг на друга (см рисунок 1), то у основания (в данном примере – это число 3) возникает новая степень, которая образуется из вычитания показателей степени. Причем, это действие проводится впрямую: из первого показателя вычитается 2-й. Пример 1. Введем обозначение: (а)в, где в скобках – а – основание, за скобками – в – показатель степени. (6)5 : (6)3 = (6)5-3 = (6) 2 = 6*6 = 36.Если в результате получается число в негативной степени, то такое число преобразуется в обычную дробь, в числителе которой стоит единица, а в знаменателе основание с полученным при разности показателем степени, только в позитивном виде (со знаком плюс). Пример 2. (2) 4 : (2)6 = (2) 4-6 = (2) -2 = 1/(2)2 = ?. Деление степеней может быть записано в ином виде, через знак дроби, а не как указано в этом шаге через знак «:». От этого тезис решения не меняется, все производится верно также, только запись будет вестись со знаком горизонтальной (либо косой) дроби, взамен двоеточия.Пример 3. (2) 4 /(2)6 = (2) 4-6 = (2) -2 = 1/(2)2 = ?.

2. При умножении идентичных оснований, имеющих степени, производится сложение степеней. Пример 4. (5) 2* (5)3 = (5)2+3 =(5)5 = 3125.Если показатели степеней имеют различные знаки, то их сложение проводится согласно математическим законам.Пример 5. (2)1* (2)-3 = (2) 1+(-3) = (2) -2 = 1/(2)2 = ?.

3. Если основания показателей степени различаются, то скорое каждого их дозволено привести к одному и тому же виду, путем математического реформирования. Пример 6. Пускай нужно обнаружить значение выражения: (4)2 : (2)3. Зная, что число четыре дозволено представить как два в квадрате, решается данный пример так:(4)2 : (2)3 = (2*2)2 : (2)3. Дальше при возведении в степень числа. Теснее имеющего степень, показатели степеней умножаются друг на друга: ((2)2)2 : (2)3 = (2)4 : (2)3 = (2) 4-3 = (2)1 = 2.

Слог – минимальная фонетическая единица. В нем соединяются различные по степени звучности звуки. Особенно громкие исполняют слогообразующую функцию. В состав единицы должен входить гласный звук. Без гласных звуков не может быть слога. В устной речи звуки группируются в

слоги по дальнейшим правилам.

Инструкция

1. Не смешивайте деление слова на слоги и перенос слова, это различные категории. Слоги — принадлежность устной речи, а перенос — это письменная речь, грамматика. Сравните: идея — в звучании три слога, и-де-я. А переносить слово невозможно. Посмотрите: цветастый – 2 слога, а перенести дозволено по-различному: пе–стрый, пес-трый.

2. Деля слова на слоги, рассматривайте закон восходящей звучности: предисловие неначального (не первого в слове) слога строится от слабо звучащего. Если в слове есть сочетание согласных между гласными, то слоговая граница должна пройти так, дабы дальнейший слог начинался с менее громкого согласного. Скажем, произнесите слово «каска» [ка – ска].

3. Деление на слоги изготавливаете по фонетическому звучанию, а не по тому, как вы пишете. Если слог является открытым, то есть заканчивается гласным звуком, то деление на слог будет проходить позже гласного. Скажем: собака – со-ба-ка. копна – ко-пна. Граница слога будет проходить на стыке сонорного согласного и громкого. Скажем, парта [пар-та].

4. Слогораздел пройдет позже Й, если за ним будет стоять всякий согласный. Майка [май-ка].

5. Запомните: удвоенные согласные (между гласными) переходят в дальнейший слог. Скажем, ка-сса, дро-жжи, га-мма. НО, при переносе слов с двойными согласными, одну букву оставляйте на строке, а иную переносите: ван-на, длин-ный, искус-ство.

6. Закон восходящей звучности не соблюдается в последних слогах слова: [цвиэ-то’к], [л’иэ-жы’т], [го’-лъс] и т.д.

7. Почаще каждого, при переносе слова применяется деление на слоги, но есть масса исключений из этого правила. Не оставляйте на строке исключительную букву. Ъ, Ь, Й – эти буквы не отделяйте от предыдущих. Скажем: объ-езд, фоль-гой, зай-ка. Не отрывайте от приставки финальную согласную букву, если корень слова тоже начинается с согласной. Положительный перенос: раз-лив, под-писать. Не забирайте у корня стоящую первой согласную букву. Положительно переносить: при-крепить.

Разделять дробь на дробь несложно – необходимо каждого лишь умножить первую дробь на “опрокинутую” вторую. Впрочем, тут имеются свои нюансы, рассматривать которые все-таки надобно.

Инструкция

1. При делении обычных дробей, нужно умножить первую дробь (делимое) на опрокинутую вторую дробь (делитель). Такая

дробь , где числитель и знаменатель поменялись местами называют обратной (к начальной).При делении дробей нужно проконтролировать, дабы вторая дробь и знаменатели обеих дробей не равнялась нулю (либо не принимали нулевых значений при определенных значениях параметров/переменных/неизвестных). Порой, из-за массивного вида дроби, это крайне неочевидно. Все значения переменных (параметров), обращающих в нуль делитель (вторую дробь ) либо знаменатели дробей нужно указать в результате.Пример 1: поделить 1/2 на 2/31/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4, илиПример 2: поделить а/с на х/са/с : х/с = а/с * с/х = (а*с)/(с*х) = а/х, где с ? 0, х ? 0.

2. Дабы поделить смешанные дроби, надобно привести их к обычному виду. Дальше действуем как в п. 1.Для реформирования смешанной дроби к обычному виду необходимо ее целую часть умножить на знаменатель, а после этого прибавить это произведение к числителю.Пример 3: преобразовать смешанную

дробь 2 2/3 в обычную:2 2/3=(2 + 2*3)/3=8/3Пример 4: поделить дробь 3 4/5 на 3/10:3 4/5 : 3/10 = (3*5+4)/5 :3/10 = 19/5 : 3/10 = 19/5 * 10/3 = (19*10)/(5*3)=38/3=12 2/3

3. При делении дробей различных типов (смешанных, десятичных, обычных), все дроби заранее приводятся к обычному виду. Дальше – согласно п. 1. Десятичная дробь переводится в обычную дюже примитивно: в числитель записывается десятичная дробь без запятой, а в знаменатель – порядок дроби (десять для десятых, сто для сотых и т.д.).Пример 5: привести десятичную дробь 3,457 к обычному виду:потому что в дроби присутствуют «тысячные» (457 тысячных), то и знаменатель полученной дроби будет равняться 1000:3,457=3457/1000Пример 6: поделить десятичную

дробь 1,5 на смешанную 1 1/2:1,5 : 1 1/2 = 15/10 : 3/2 = 15/10 * 2/3 = (15*2)/(10*3) = 30/30 = 1.

4. При делении 2-х десятичных дробей обе дроби заранее умножаются на 10 в такой степени, дабы делитель стал целым числом. Позже чего производится деление десятичной дроби «нацело».Пример 7: 2,48/12,4=24,8/124=0,2.При необходимости (исходя из условий задачи) дозволено подобрать такое значение множителя, дабы целыми стали как делитель, так и делимое. Тогда задача деления десятичных дробей сведется к делению целых чисел.Пример 8: 2,48/12,4=248/1240=0,2

Видео по теме

Полезный совет
Помните, если данное основание кажется непохожим на второе основание, нужно искать математический выход. Примитивно так различные числа не даются. Разве, что в учебнике наборщиком сделана опечатка.

jprosto.ru

как умножить или разделить степени с разными показателями и основаниями? пожалуйста, очень срочно нужно!

Приводят все основания к одному и действуют по правилам. Если к одному основанию свести нельзя, то считают каждую степень по отдельности.

Если основания одинаковы, то при умножении основание остается прежним, показатели складываются (при делении вычитаются) . Степень с разными основаниями нельзя умножать или делить, пока эти основания не приравнять друг к другу. Показатели тут роли не играют.

<img src=»//otvet.imgsmail.ru/download/222734490_f86420b81e20f3cb351d6808990639dc_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/222734490_f86420b81e20f3cb351d6808990639dc_120x120.jpg» data-big=»1″>

представь 14^2 как 2^2*7^2 и тогда все получится

touch.otvet.mail.ru

Правило деление степеней — Aiki-group.ru

Правило деления степеней

Правило деления степеней. При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:

Слайд 11 из презентации «Деление и умножение степеней» к урокам алгебры на тему «Степень»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке алгебры, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Деление и умножение степеней.ppt» можно в zip-архиве размером 1313 КБ.

«Деление и умножение степеней» — a2 a3 = a2+3 = a5. a3 = a · a · a. Найдем произведение a2 и a3. 100. 2+3. 5 раз. 64 = 144 = 1 0000 =. Умножение и деление степеней. 3 раза. a2 a3 =.

«Степени двойки» — 1024+. Правила перевода из одной системы счисления в другую. Гусельникова Е.В. Школа №130. Содержание. Таблица степеней двойки. Переведём число 1998 из десятичной в двоичную систему. Кислых В.Н. 11Э Зинько К.О. 11Э. Преподаватель: Выполнили: Рассмотрим схему преобразования на примере.

«Степень с отрицательным показателем» — Степень с отрицательным показателем. 5 12?3 (27?3 ). -2. -1. Вычислите: -3.

«Степень с рациональным показателем» — по теме: «Степень с рациональным показателем». Цели урока: I. Организационная часть. Проверка домашнего задания 1.Математический диктант 2. Взаимопроверка III.Самостоятельная работа IV. Обобщающий урок. Ход урока. Подготовка к контрольной работе V. Подведение итогов урока VI. II.

«Степень с целым показателем» — Представьте выражение в виде степени. X-12. Расположите в порядке убывания. Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен. Вычислите. Упростите.

«Свойства степени» — Обобщение знаний и умений по применению свойств степени с натуральным показателем. Вычислительная пауза. Свойства степени с натуральным показателем. Проверь себя! Применение знаний для решения различных по сложности задач. Тест. Физминутка. Развитие настойчивости, мыслительной активности и творческой деятельности.

900igr.net

Правило деление степеней

1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):

(abc…) n = a n b n c n …

Пример 1. (7•2•10) 2 = 7 2 •2 2 •10 2 = 49•4•100 = 19600. Пример 2. (x 2 –a 2 ) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3

Практически более важно обратное преобразование:

a n b n c n … = (abc…) n

т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.

Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2 ) 2 =[(a +b)(a 2 – ab +b 2 )] 2 =(a 3 +b 3 ) 2

2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:

Пример 5. Пример 6.

Обратное преобразование:. Пример 7.. Пример 8..

3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:

Пример 9.2 2 •2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .

4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого

Пример 11. 12 5 :12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3 :(x-y) 2 =x-y.

5. При возведении степени в степень показатели степеней перемножаются:

Пример 13. (2 3 ) 2 =2 6 =64. Пример 14.

maths.yfa1.ru

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:
2a 4 — (-6a 4 ) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3 ) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные.

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2 : то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2 )⋅(a 2 + y 2 ) = a 4 — y 4 .
(a 4 — y 4 )⋅(a 4 + y 4 ) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.

Таким образом a 3 b 2 делённое на b 2 , равно a 3 .

Запись a 5 , делённого на a 3 , выглядит как $\frac$. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел.

При делении степеней с одинаковым основанием их показатели вычитаются..

Так, y 3 :y 2 = y 3-2 = y 1 . То есть, $\frac= y$.

И a n+1 :a = a n+1-1 = a n . То есть $\frac = a^n$.

Или:
y 2m : y m = y m
8a n+m : 4a m = 2a n
12(b + y) n : 3(b + y) 3 = 4(b +y) n-3

Правило также справедливо и для чисел с отрицательными значениями степеней.
Результат деления a -5 на a -3 , равен a -2 .
Также, $\frac : \frac = \frac.\frac= \frac= \frac$.

h 2 :h -1 = h 2+1 = h 3 или $h^2:\frac = h^2.\frac= h^3$

Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac$ Ответ: $\frac$.

2. Уменьшите показатели степеней в $\frac$. Ответ: $\frac$ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

www.math20.com

Алгебра – 7 класс. Умножение и деление степеней

Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Умножение и деление степеней

Цель урока: научится производить действия со степенями числа.

Для начала вспомним понятие «степень числа». Выражение вида $\underbrace_$ можно представить, как $a^n$.

Справедливо также обратное: $a^n= \underbrace_$.

Это равенство называется «запись степени в виде произведения». Оно поможет нам определить, каким образом умножать и делить степени.
Запомните:
a – основание степени.
n – показатель степени.
Если n = 1, значит, число а взяли один раз и соответственно: $a^n= 1$.
Если n= 0, то $a^0= 1$.

Почему так происходит, мы сможем выяснить, когда познакомимся с правилами умножения и деления степеней.

Правила умножения

a) Если умножаются степени с одинаковым основанием.
Чтобы $a^n * a^m$, запишем степени в виде произведения: $\underbrace_ * \underbrace_$.
На рисунке видно, что число а взяли n+m раз, тогда $a^n * a^m = a^$.

Пример.
$2^3 * 2^2 = 2^5 = 32$.

Это свойство удобно использовать, что бы упростить работу при возведении числа в большую степень.
Пример.
$2^7= 2^3 * 2^4 = 8 * 16 = 128$.

б) Если умножаются степени с разным основанием, но одинаковым показателем.
Чтобы $a^n * b^n$, запишем степени в виде произведения: $\underbrace_ * \underbrace_$.
Если поменять местами множители и посчитать получившиеся пары, получим: $\underbrace_$.

Значит, $a^n * b^n= (a * b)^n$.

Пример.
$3^2 * 2^2 = (3 * 2)^2 = 6^2= 36$.

Правила деления

a) Основание степени одинаковое, показатели разные.
Рассмотрим деление степени с большим показателем на деление степени с меньшим показателем.

Запишем степени в виде дроби:

Для удобства деление запишем в виде простой дроби.

Теперь сократим дробь.

Получается: $\underbrace_= a^$.
Значит, $\frac=a^$.

Это свойство поможет объяснить ситуацию с возведением числа в нулевую степень. Допустим, что n=m, тогда $a^0= a^=\frac =1$.

б) Основания степени разные, показатели одинаковые.
Допустим, необходимо $\frac$. Запишем степени чисел в виде дроби:

Для удобства представим.

Используя свойство дробей, разобьем большую дробь на произведение маленьких, получим.
$\underbrace* \frac * \ldots * \frac >_$.
Соответственно: $\frac=( \frac)^n$.

mathematics-tests.com

Степени и корни

Операции со степенями и корнями. Степень с отрицательным ,

нулевым и дробным показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются :

a m · a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели вычитаются .

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

( a / b ) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р . ( 2 · 3 · 5 / 15 ) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:

Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .

Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5 ) 0 = 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :

О выражениях, не имеющих смысла. Есть несколько таких выражений.

где a ≠ 0 , не существует .

В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0

— любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.

Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то

0 0 — любое число.

Р е ш е н и е . Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,

что x – любое число; но принимая во внимание, что в

нашем случае x > 0 , ответом является x > 0 ;

www.bymath.net

Это интересно:

• Правила безопасности с утюгом Правила техники безопасности при работе утюгом Правила техники безопасности при работе утюгом. 1.Перед включением утюга в электросеть нужно проверить изоляцию шнура и положение утюга на подставке. 2.Включение и […]
• Проблемы водного налога Проблемы водного налога Состояние, анализ и проблемы совершенствования водного налога При заборе воды сверх установленных квартальных (годовых) лимитов водопользования налоговые ставки в части такого превышения […]
• Этапы исполнения приказа как составить приказ о переходе с 223фз на 44 фз Сергей Антонов 30 Ответ написан год назад Профессор 455 Ответ написан год назад Например: приказ об отмене применения положения о закупках. Оценка ответа: 0 Добавить […]
• Правило на умножение и деление положительных и отрицательных чисел Деление отрицательных чисел Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению. Если « a » и « b » положительные числа, то разделить число « a » на число « […]
• Разрешением 960h Разрешения D1, 960Н, 720Р, 960Р, 1080Р Системы видеонаблюдения получают все большее распространение по всему миру. Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […]
• Виды собственности по конституций Конституционное право Российской Федерации. Баглай М.В. 6-е изд., изм. и доп. — М.: Норма, 200 7 . — 7 84 с. Настоящий учебник, представляющий собой шестое, измененное и дополненное, издание, написан известным […]

aiki-group.ru

Деление многочлена на многочлен столбиком

РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ

Деление многочлена на многочлен столбиком

Для решения уравнение вида Р(х)=0, где Р(х) — многочлен степени n>2, часто применяют метод понижения степени. Он основывается на таком факте: если число x=b является корнем многочлена P(x), то есть P(b)=0, то многочлен P(x) делится без остатка на двучлен x-b.

После того, как мы разделим многочлен P(x) степени n на двучлен x-b, то мы получим многочлен степени n-1, то есть на единицу меньшей исходного. И  дальше процедуру можно повторить.

Если старший коэффициент многочлена P(x) равен 1, то корни многочлена P(x) мы ищем среди делителей свободного члена.

Решим уравнение

Свободный член многочлена в левой части уравнения равен 10.

Делители числа 10: 1; 2; 5; 10.

Проверим, является ли какое-либо из этих чисел корнем многочлена. Для этого последовательно подставим эти значения  вместо х в  многочлен.

является корнями многочлена , и он делится на  двучлены и без остатка.

Разделим многочлен  на двучлен x-2 столбиком:

 

Таким образом, корни исходного уравнения:

х=2; х=1; х=-5.

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Правила возведения в степень

---

a— основание степени, действительное число ( aϵ R )

n — показатель степени, натуральное число ( n ϵ N )

 

 

 

Произведение степеней с одинаковым основанием:

 

Деление степеней с одинаковым основанием:

если  n > m

 

если  n = m

 

если  n < m

 

Возведение степени в степень:

 

Произведение в степени:

 

Деление в степени:

---

Подробности

Автор: Administrator

Опубликовано: 24 августа 2012

Обновлено: 24 мая 2017

www-formula.ru

Деление степеней с одинаковыми основаниями

Пусть надо a⁹ ÷ a³; здесь, согласно смыслу деления, дано произведение = a⁹ и дан один множитель = a³. Надо найти другой множитель. Напишем данное произведение (a⁹) подробнее

a · a · a · a · a · a · a · a · a

и отделим, например, подчеркивая, данный множитель, т. е. a³ или a · a · a. Тогда мы увидим, каков другой множитель, а именно осталось неподчеркнутым

a · a · a · a · a · a,

что = a⁶. Итак,

a⁹ ÷ a³ = a⁶.

Пусть надо b⁴⁷ ÷ b¹⁸. Данное произведение есть b⁴⁷ или такое произведение, где b повторяется множителем 47 раз; отделим один данный множитель, b¹⁸, или произведение, где b повторяется 18 раз множителем. Тогда мы сообразим, что искомым множителем является произведение, где b повторяется 29 раз множителем, т. е. b²⁹. Итак, b⁴⁷ ÷ b¹⁸ = b²⁹.

Также

x¹⁵ ÷ x⁵ = x¹⁰
(a + b)⁷ ÷ (a + b) = (a + b)⁶
3²³ ÷ 3²⁰ = 3³ = 27 и т. д.

Вообще

a^m ÷ aⁿ = a^m-n (если m > n)

или словами: при делении степеней с одинаковыми основаниями основание степени остается без изменения, а показатель делителя вычитается из показателя делимого (если показатель делимого больше показателя делителя).

Пусть теперь надо

20a⁵b⁴c²d ÷ 5a³b³c².

Здесь дано произведение (20a⁵b⁴c²d) и один множитель 5a³b³c²; надо найти другой множитель. У произведения коэффициент (+20), он получился от умножения коэффициента данного множителя (+5) на коэффициент искомого множителя. Чтобы найти этот коэффициент, надо (+20) ÷ (+5), получим +4. В данном произведении a взято множителем 5 раз, в данном множителе a входит множителем 3 раза. Поэтому в искомом множителе a должно входить множителем 2 раза, т. е. в искомом множителе должно быть a². В данном произведении b берется множителем 4 раза, а в данном множителе – 3 раза; следовательно, в искомом множителе b должно входить множителем лишь 1 раз. В данном произведении имеем c² (c берется множителем 2 раза) и в данном множителе имеем c². Поэтому в искомом множителе c не должно вовсе входить. В данном произведении имеется множитель d, а в данном множителе d вовсе нет; поэтому d должно иметься в искомом множителе. Итак,

20a⁵b⁴c²d ÷ 5a³b³c² = 4a²bd.

Еще примеры:

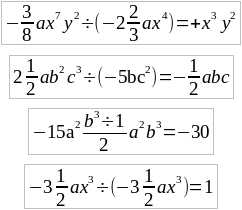
В предыдущем встречались деления, вроде c² ÷ c²; a ÷ a; b³ ÷ b³; и т. д. Здесь уместно заметить, что частное от деления какого-либо числа на самое себя всегда равно 1.

maths-public.ru

No related posts.