Точечные оценки
Замечание. Термин «точечная» связан с тем, что в качестве заменителя неизвестного параметра предлагается конкретное число. Это «хорошо», поскольку позволяет поставить конкретное значение в формулу распределения и тем самым полностью его восстановить, и «плохо», поскольку мы не знаем, насколько хорошо наше приближение. Соответствующие формулы являются асимптотическими и является ли наше (точное) n (точно) достаточным для такого вывода неочевидно. Более того (как будет показано далее) существует непреодолимый «зазор» между оценкой и истинным значением параметра (информационное неравенство) о-
Итак, оценка — это функция от нашей выборки. Но функций от выборки можно придумать великое множество. Очевидно, что эта функция должна еще «хорошо приближать» оцениваемый параметр. Поэтому оценка должна удовлетворять нескольким условиям:
Определения.
Оценка  (Х1…
,Хn ) называется состоятельной оценкой параметра θ,
если
(Х1…
,Хn ) называется состоятельной оценкой параметра θ,
если
 (Х1…
,Хn )→ θ по вероятности при n→∞
(Х1…
,Хn )→ θ по вероятности при n→∞
Кроме того,
желательно, чтобы, пользуясь величиной  вместоθ,
мы по крайней мере не делали систематической
ошибки в сторону завышения или занижения,
т. е. чтобы выполнялось условие
вместоθ,
мы по крайней мере не делали систематической
ошибки в сторону завышения или занижения,
т. е. чтобы выполнялось условие
Оценка  (Х1…
,Хn )называется несмещенной,
если
(Х1…
,Хn )называется несмещенной,
если
Е (
Наконец, желательно, чтобы выбранная несмещенная оценка обладала по сравнению с другими «хорошими» оценками наименьшей дисперсией, т. е.
D[ ]
= min .
]
= min .
Оценка, обладающая таким свойством, называется эффективной.
Замечание. На практике не всегда удается удовлетворить всем этим требованиям. Например, может оказаться, что, даже если эффективная оценка существует, формулы для ее вычисления оказываются слишком сложными, и приходится удовлетворяться другой оценкой, дисперсия которой несколько больше. Иногда применяются — в интересах простоты расчетов — незначительно смещенные оценки (см., например, описание выборочной дисперсии). Таким образом, выбор оценки всегда предваряется рассмотрением соответствия ее указанным требованиям и ее эффективности.
Определение. Выборочное
среднее 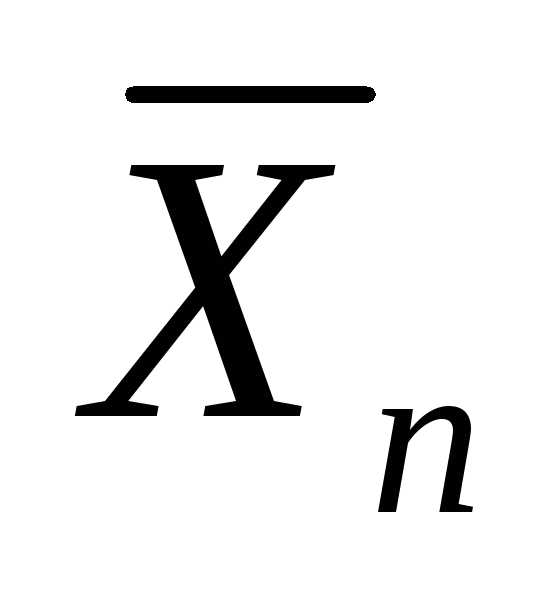 =
=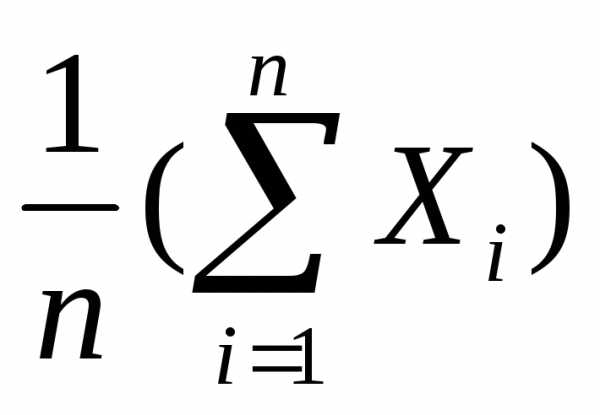 .
Выборочное среднее является средним
значением (математическим ожиданием)
для эмпирической функции распределения.
.
Выборочное среднее является средним
значением (математическим ожиданием)
для эмпирической функции распределения.
Пример. Выборочное среднее является несмещенной состоятельной оценкой для математического ожидания.
Определение. Выборочная дисперсия . Выборочная дисперсия характеризует среднеквадратичное отклонение выборочных величин от выборочного среднего.
Замечание.
В определении выборочной дисперсии
должен бы использоваться множитель 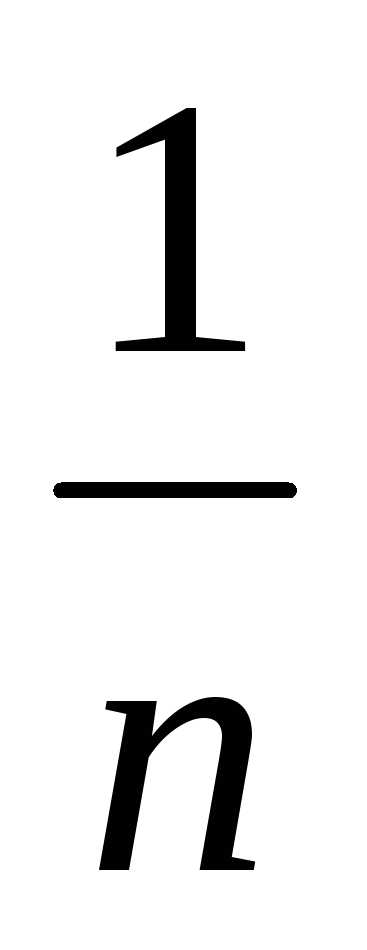
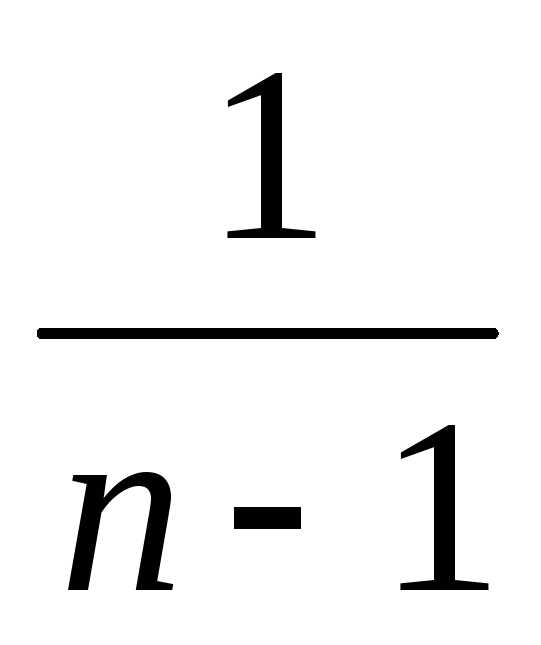 ,
но тогда не соблюдается условие
несмещенности. Выборочную дисперсию с
множителем
,
но тогда не соблюдается условие
несмещенности. Выборочную дисперсию с
множителем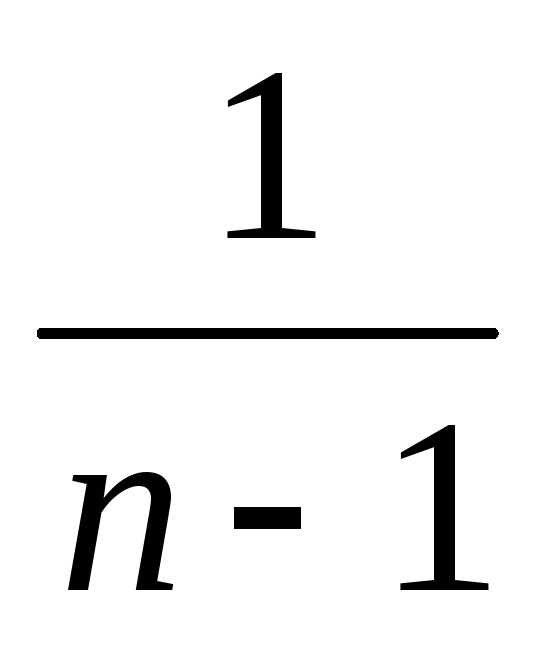 называют
еще исправленнойвыборочной
дисперсией.
называют
еще исправленнойвыборочной
дисперсией.Пример. Выборочная дисперсия является несмещенной состоятельной оценкой для дисперсии
Замечание. Так же как и для дисперсии (см. свойства дисперсии) для выборочной дисперсии для удобства вычислений нередко пользуются таким равенством :
Пример. Дана выборка 92, 94, 103, 105, 106. Найти оценки для математического ожидания и (несмещенную) дисперсии.
Выборочное среднее:

 .
Выборочный момент является моментом
порядка k
для эмпирической функции распределения.
.
Выборочный момент является моментом
порядка k
для эмпирической функции распределения.
Пример. Выборочный момент порядка k является несмещенной состоятельной оценкой начального момента k-го порядка.
Замечание. Аналогично случаю начальных моментов случайной величины Х, выборочное среднее (выборочное математическое ожидание) является выборочным начальным моментом 1 порядка
Определение. Выборочный (центральный) момент порядка k
Пример. Выборочный центральный момент k-го порядка является состоятельной оценкой центрального момента k-го порядка.
Замечание. Аналогично случаю центральных моментов случайной величины Х, выборочная дисперсия является выборочным центральным моментом 2
порядка
Определение. Случайной выборкой объема n, отвечающей паре случайных величин (X,Y) называется набор n независимых, одинаково распределенных пар случайных величин (X1 , Y1 ), (X2 , Y2 ), … (Xn , Yn ), каждая из которых имеет такое же совместное распределение как и пара величин (X,Y)
Определение. Выборочная ковариация
Определение. Выборочный коэффициент корреляции
Пример. Выборочная ковариация является несмещенной состоятельной оценкой ковариации
Пример. Выборочный коэффициент корреляции является состоятельной оценкой коэффициента корреляции
Вернемся к
рассмотрению эффективной
оценки
Рассмотренные выше оценки являются наиболее эффективными (в своих классах).
Замечание. Иногда вместо термина „эффективная оценка» говорят „несмещенная оценка с минимальной дисперсией», „оптимальная оценка».
Итак, дисперсия оценки – часто используемая мера качества оценки. Чем она меньше, тем оценка лучше. Однако, при определенных условиях существует нижняя граница для величины этой дисперсии, которую уже нельзя улучшить. То есть, даже самая лучшая оценка будет иметь дисперсию не меньшую некоторой величины. Соответствующее утверждение носит название Неравенства Рао-Крамера.
D  (Х1…
,Хn ) 1 / nI(),
где
—
количество информации по Фишеру
(информация Фишера) – частная производная
логарифма плотности (в случае непрерывной
модели, или вероятности – дискретной)
по параметру, а
(Х1…
,Хn ) 1 / nI(),
где
—
количество информации по Фишеру
(информация Фишера) – частная производная
логарифма плотности (в случае непрерывной
модели, или вероятности – дискретной)
по параметру, а (Х1…
,Хn ) — несмещенная оценка неизвестного
параметра θ.
(Х1…
,Хn ) — несмещенная оценка неизвестного
параметра θ.
Определение.
Оценка  (Х1…
,Хn ) называется асимптотически
нормальной с дисперсией Δ2,
если
(Х1…
,Хn ) называется асимптотически
нормальной с дисперсией Δ2,
если
( – ) сходится
при n →∞ по
распределению к стандартному нормальному
закону (нормальное распределение при
нулевом математическом ожидании и
дисперсии, равной 1)
– ) сходится
при n →∞ по
распределению к стандартному нормальному
закону (нормальное распределение при
нулевом математическом ожидании и
дисперсии, равной 1)
Точечные оценки параметров случайной величины
Точечными оценкамипараметров называют такие оценки, которые выражаются каким-то одним числом (точкой).
Таким
числом могут быть, например, параметры  и
и нормального распределения или параметр
нормального распределения или параметр закона Пуассона. Не все переменные могут
быть оценками.
закона Пуассона. Не все переменные могут
быть оценками.
Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, самостоятельности и эффективности.
1. Несмещенность. Оценка не должна содержать систематической ошибки. Это означает, что математическое ожидание оценки некоторого параметра, взятое по всем возможным выборкам, должно быть равно действительному значению параметра.
Если
действительное значение оцениваемого
параметра обозначить  ,
а его оценку
,
а его оценку ,
то требование несмещенности запишется
в виде
,
то требование несмещенности запишется
в виде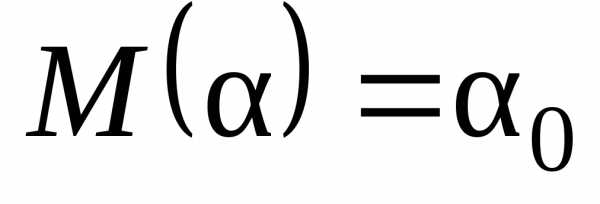 .
.
2. Состоятельность. Оценка  должна приближаться
к
должна приближаться
к 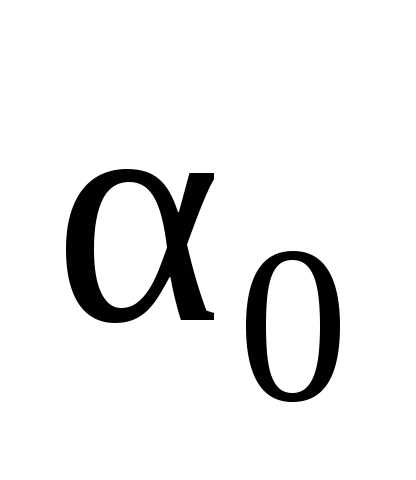 по мере увеличения объема выборки. Но
ввиду того, что оценка
по мере увеличения объема выборки. Но
ввиду того, что оценка является случайной величиной, об этом
приближении можно говорить только
в вероятностном смысле.
является случайной величиной, об этом
приближении можно говорить только
в вероятностном смысле.
Для
состоятельности оценки  ,
получаемой при выборке объема
,
получаемой при выборке объема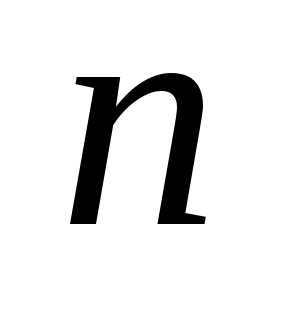
 к
к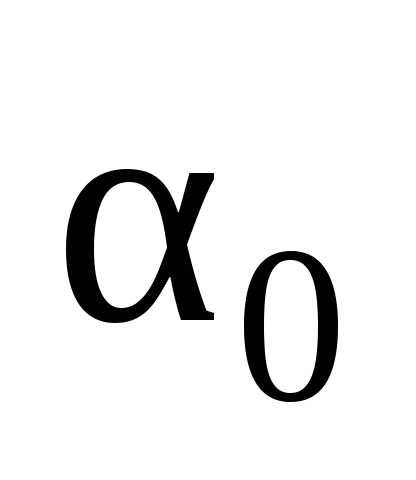 ,
т.е..
,
т.е..Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются!).
3. Эффективность. Несмещенная оценка  параметра
параметра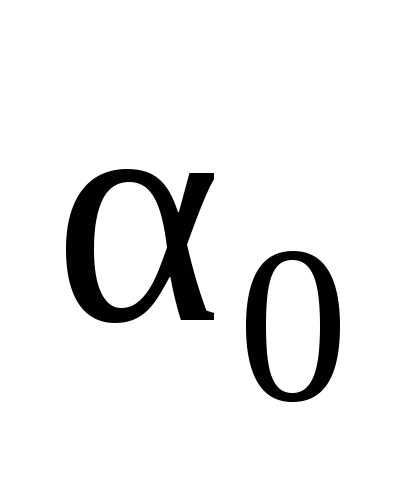 называется эффективной, если она имеет
наименьшую дисперсию среди всех возможных
несмещенных оценок
называется эффективной, если она имеет
наименьшую дисперсию среди всех возможных
несмещенных оценок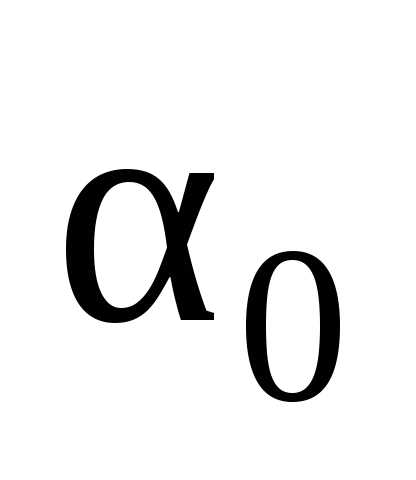 ,
то есть оценка
,
то есть оценка эффективна,
если ее дисперсия минимальна.
эффективна,
если ее дисперсия минимальна.
Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям, и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами.
Рассмотрим
несмещенные точечные оценки параметров
распределения. Запишем в виде таблицы
полученные в результате изучения
выборки значения признака 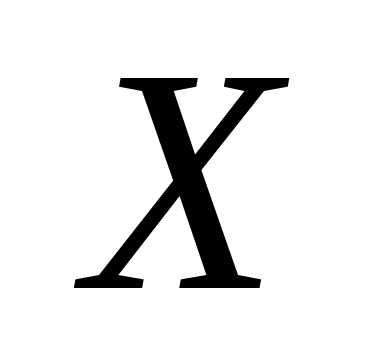 в неубывающем
порядке . Такая последовательность
называется вариационным
рядом, а сами значения
вариантами. Если
среди вариантов есть одинаковые, то
вариационный ряд записывают в виде
таблицы.
в неубывающем
порядке . Такая последовательность
называется вариационным
рядом, а сами значения
вариантами. Если
среди вариантов есть одинаковые, то
вариационный ряд записывают в виде
таблицы.
Варианты, | | | … | |
Частоты, | | | … | |
При этом сумма частот равна объёму выборки, т.е.
. (1.1)
Величины 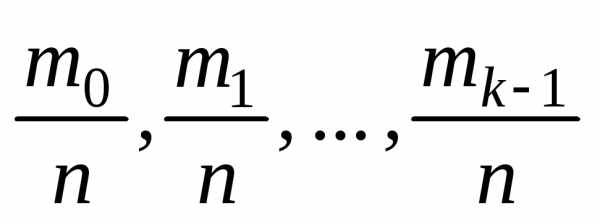 называются относительными частотами
или частостями. Из (1.1) следует
называются относительными частотами
или частостями. Из (1.1) следует
.
Часто вариационный ряд, записанный в виде такой таблицы, называют статистическим рядом распределения.
Если во второй строке статистического ряда распределения вместо частот записать частости, то полученная таблица будет иметь большое сходство с рядом распределения дискретной случайной величины.
Тогда для указанной выборки можно построить полигон распределения и выборочную (эмпирическую) функцию распределения аналогично тому, как это делалось для дискретной случайной величины .
Если значения признака изменяются непрерывно в некотором промежутке, то строят интервальный ряд, имеющий вид:
Интервалы | | | … | |
Частоты | | | … | |
Графическим представлением интервального ряда является гистограмма, пример которой изображен на рис. 1.1.
Поскольку
точные значения параметров распределения
признака  в генеральной
совокупности
в генеральной
совокупности  и
и 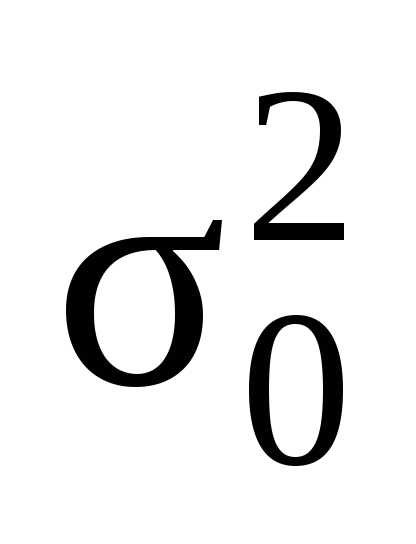 в большинстве случаев определить не
представляется возможным, то эти
параметры следует оценить, используя
соответствующие параметры выборки.
в большинстве случаев определить не
представляется возможным, то эти
параметры следует оценить, используя
соответствующие параметры выборки.
Выборочная
средняя  представляет собой
среднее значение признака
представляет собой
среднее значение признака 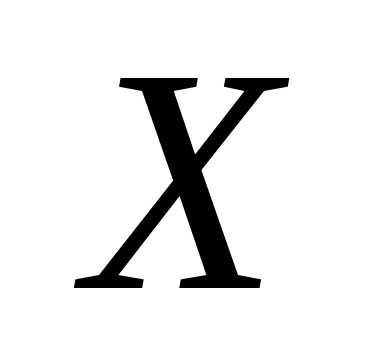 в выборке и определяется по формуле
в выборке и определяется по формуле
.

Рис. 1.1. Пример гистограммы интервального ряда для 6 интервалов
Если используется интервальный ряд, то за варианты принимаются, как правило, середины интервалов.
Выборочная
дисперсия 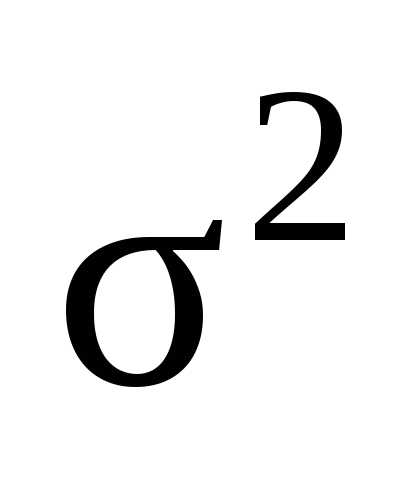 определяется по формуле
определяется по формуле
,
или по упрощенной формуле
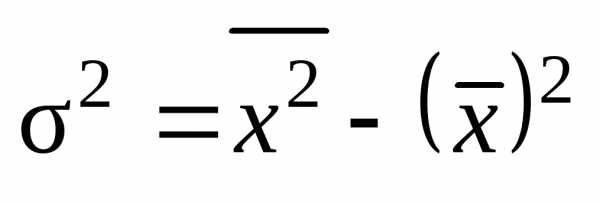 ,
,
где 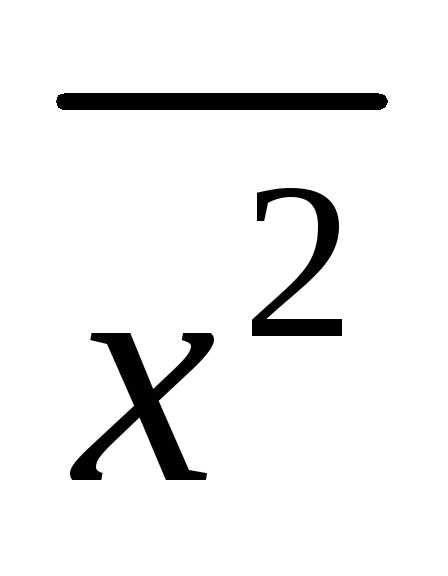 определяется по формуле
определяется по формуле
.
Выборочное
среднее квадратическое отклонение  определяется как квадратный корень
из
определяется как квадратный корень
из 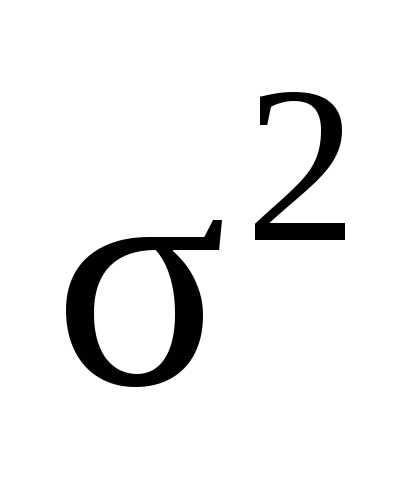 .
В качестве точечной оценки параметров
генеральной совокупности может
приниматься соответствующий параметр
выборки. Можно доказать следующее.
.
В качестве точечной оценки параметров
генеральной совокупности может
приниматься соответствующий параметр
выборки. Можно доказать следующее.
1. 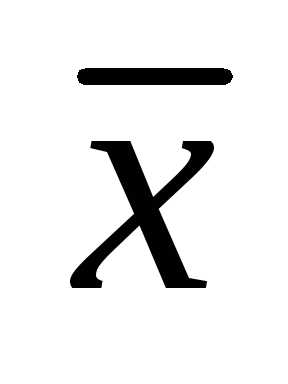 является несмещенной
точечной оценкой
является несмещенной
точечной оценкой 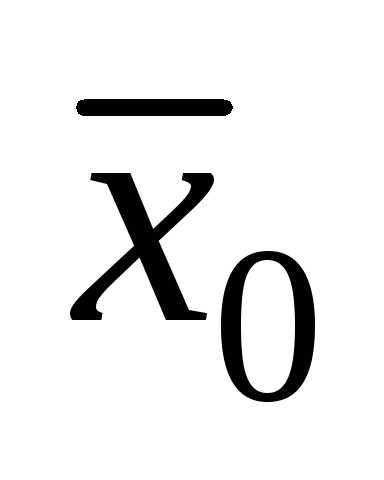 ,
т.е.
,
т.е.
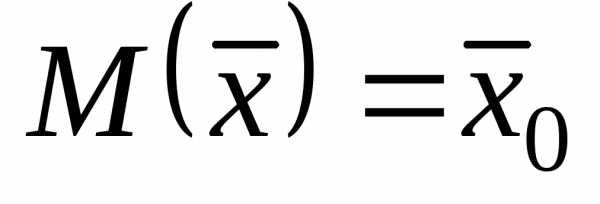 .
.
2.
Оценка 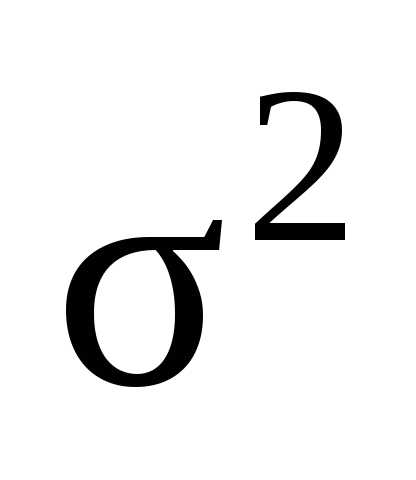 для генеральной дисперсии
для генеральной дисперсии 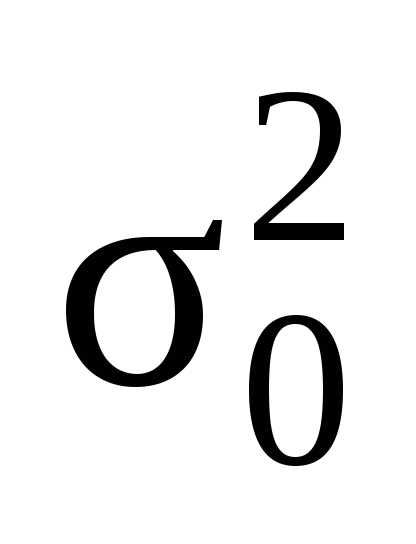 является состоятельной, нонесмещенной.
Поэтому вводят величину
является состоятельной, нонесмещенной.
Поэтому вводят величину
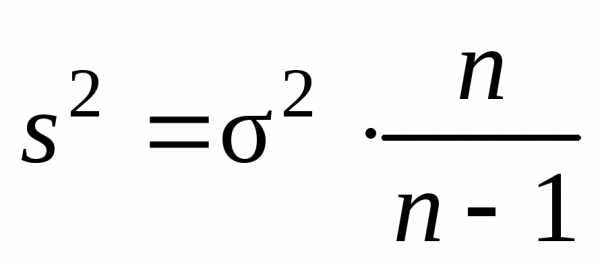 ,
,
которая называется исправленной статистической выборочной дисперсией. Эта величина является несмещенной оценкой генеральной дисперсии , т.е.
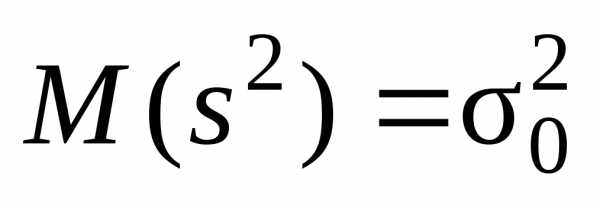 .
.
Величина 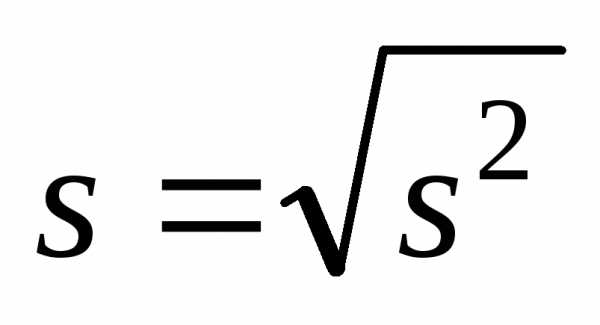 называется
исправленным выборочным средним
квадратическим отклонением и является
несмещенной точечной оценкой генерального
среднего квадратического отклонения
называется
исправленным выборочным средним
квадратическим отклонением и является
несмещенной точечной оценкой генерального
среднего квадратического отклонения 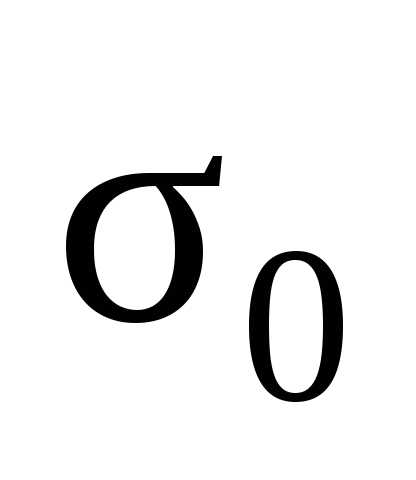 ,
т.е.
,
т.е.
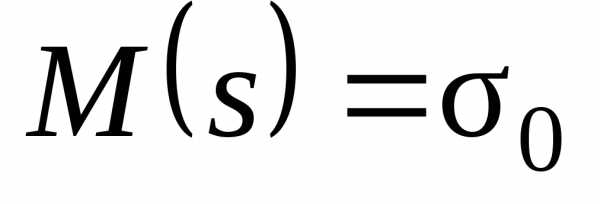 .
.
Для решения статистических задач используются специальные распределения случайных величин, сконструированных на основе нормального распределения. Рассмотрим частные случаи этого вида распределения.
Распределение
«хи квадрат» 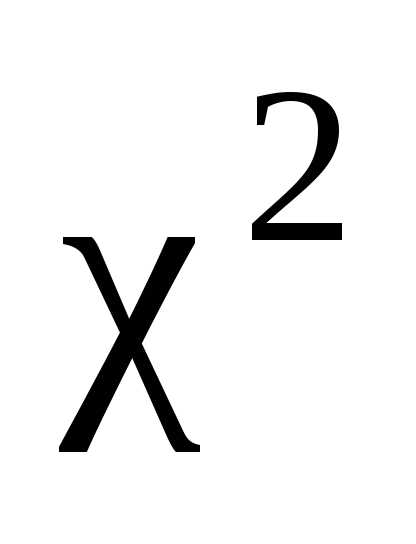
Важным
частным случаем нормального распределения
является так называемое распределение 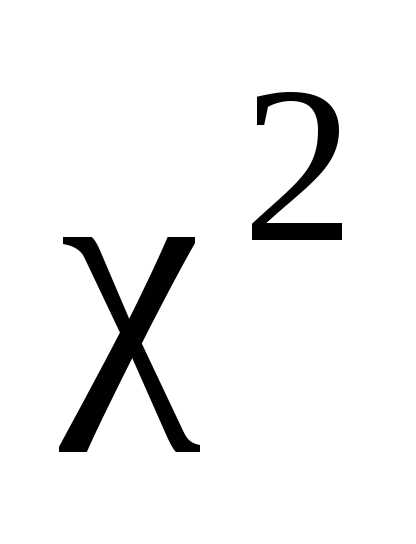 .
Это распределение является
двухпараметрическим и описывает
случайные величины, распределенные на
полуинтервале
.
Это распределение является
двухпараметрическим и описывает
случайные величины, распределенные на
полуинтервале 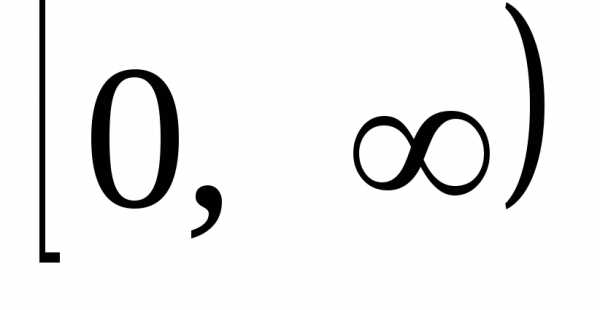 .
.
Пусть
имеется 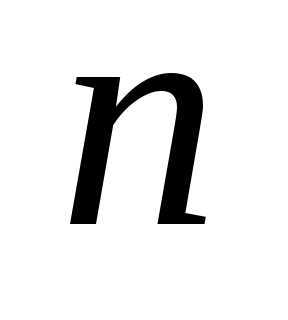 независимых случайных величин
,
распределенных по нормальному закону
с математическим ожиданием, равным
нулю, и дисперсией, равной единице. Тогда
случайная величина
независимых случайных величин
,
распределенных по нормальному закону
с математическим ожиданием, равным
нулю, и дисперсией, равной единице. Тогда
случайная величина
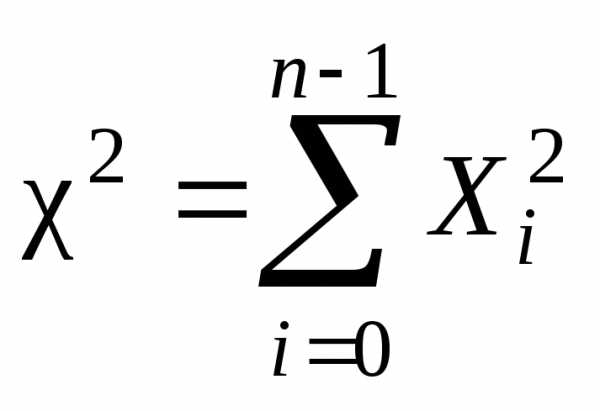
распределена
по закону Пирсона или 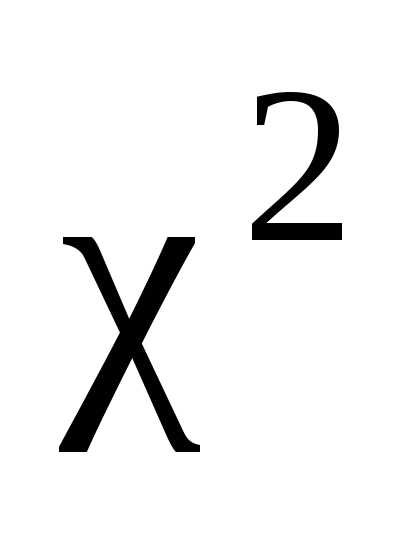 – «хи квадрат», с характеристиками
– «хи квадрат», с характеристиками 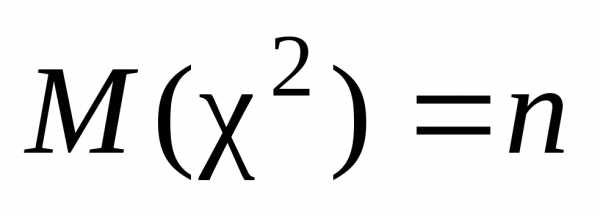 ,
, 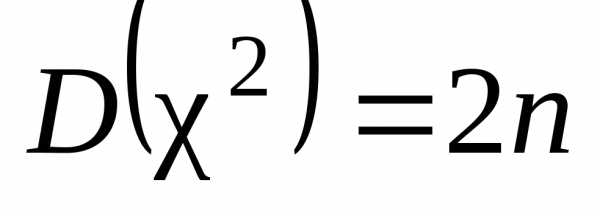 .
.
Распределением 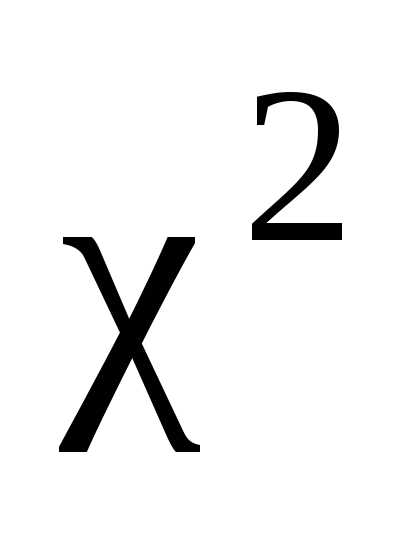 с
с 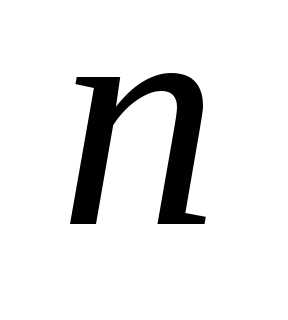 степенями свободы
называется распределение суммы квадратов
степенями свободы
называется распределение суммы квадратов 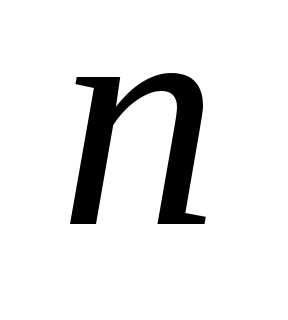 независимых случайных
величин, каждая из которых подчинена
нормальному закону с математическим
ожиданием, равным нулю, и дисперсией,
равной единице.
независимых случайных
величин, каждая из которых подчинена
нормальному закону с математическим
ожиданием, равным нулю, и дисперсией,
равной единице.
Очевидно,
что  может принимать лишь неотрицательные
значения. График плотности распределения
случайной величины
может принимать лишь неотрицательные
значения. График плотности распределения
случайной величины 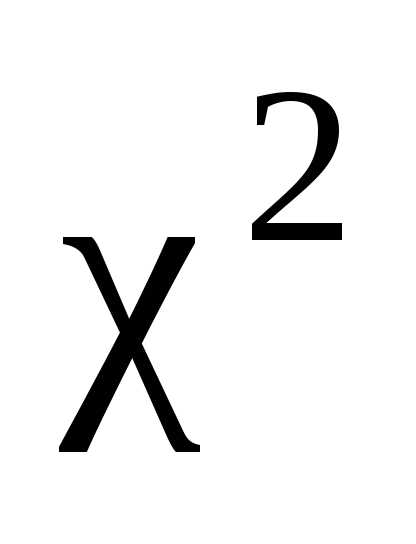 представляет собой
кривую, изображенную на рис. 1.2.
представляет собой
кривую, изображенную на рис. 1.2.

Рис.
1.2. Кривая плотности распределения 
Для
того чтобы определить вероятность
попадания случайной величины 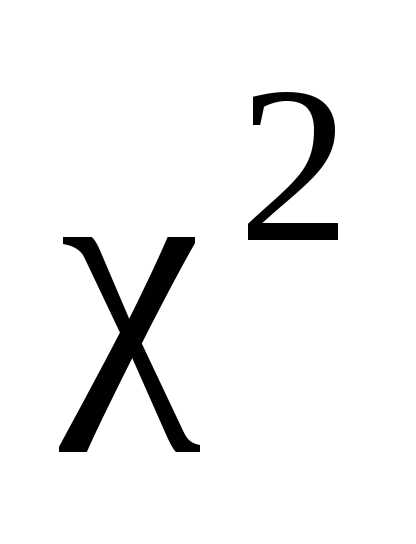 в какой-либо промежуток из множества
положительных чисел, пользуются таблицей
распределения
в какой-либо промежуток из множества
положительных чисел, пользуются таблицей
распределения (прил. 2).
(прил. 2).
Обычно
такая таблица позволяет по заданной
вероятности  и по числу степеней
свободы
и по числу степеней
свободы  определить так
называемый квантиль
определить так
называемый квантиль 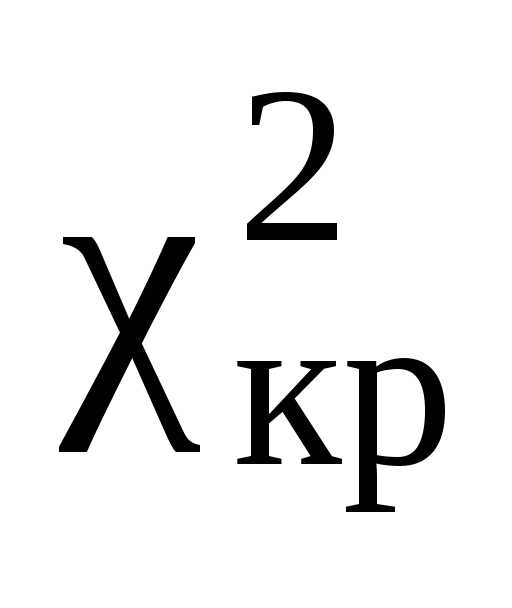 – критическое
значение
,
если
– критическое
значение
,
если и
и 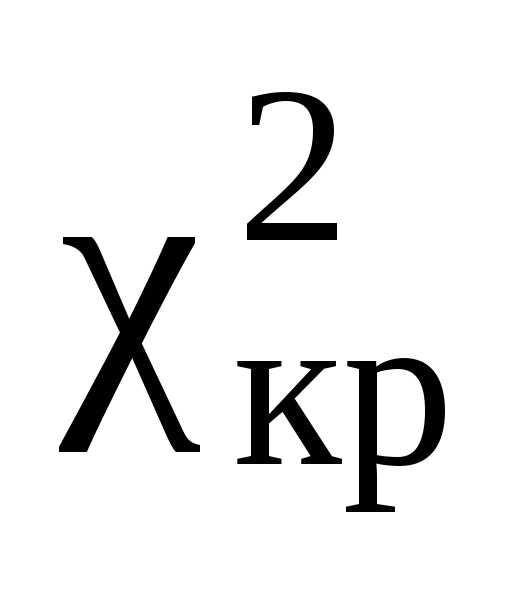 связаны соотношением:
связаны соотношением:
.
Эта
формула означает: вероятность того, что
случайная величина 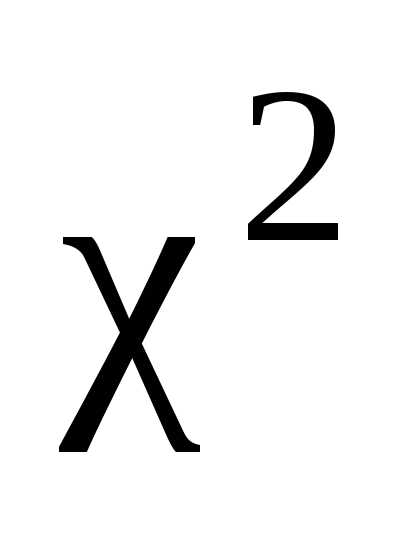 примет значение большее, чем табличное
значение
примет значение большее, чем табличное
значение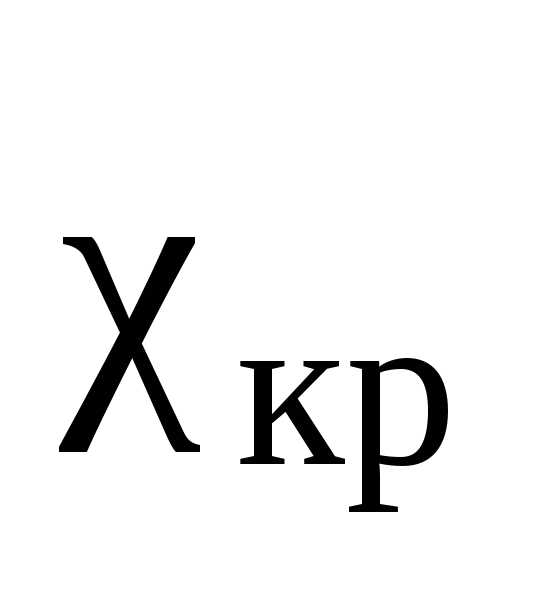 ,
равна
,
равна .
Из таблицы (прил. 2) очевидно, что случайная
величина
.
Из таблицы (прил. 2) очевидно, что случайная
величина с 10 степенями свободы с вероятностью
с 10 степенями свободы с вероятностью при-нимает значение, равное 3,94.
при-нимает значение, равное 3,94.
Распределение Стьюдента (или t-распределение)
Другим важным случаем нормального распределения является однопараметрическое распределение Стьюдента (рис. 1.3). Ему подчиняется случайная величина, распределенная на всей числовой оси. Пусть – независимые стандартные нормальные случайные величины . Тогда случайная величина
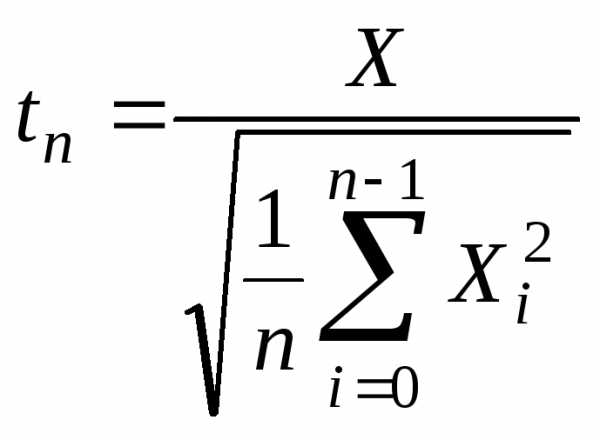
имеет
распределение Стьюдента с 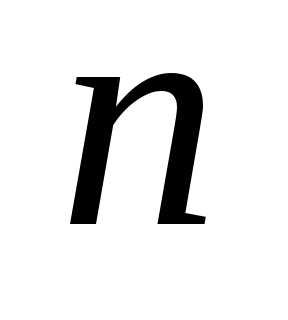 степенями свободы.
степенями свободы.
Если
число степеней свободы 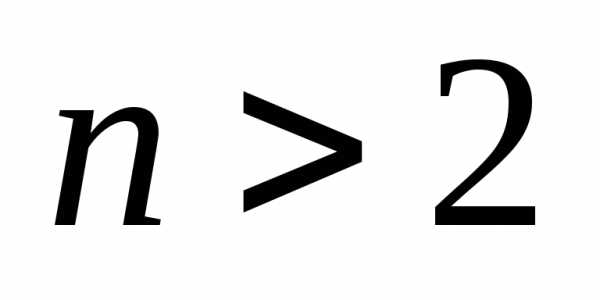 ,
то
,
то
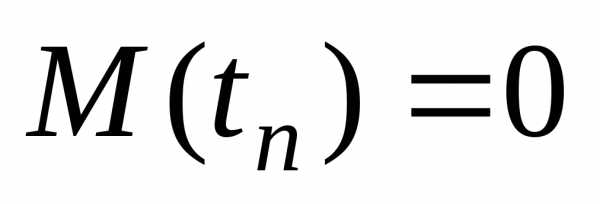 ,
, 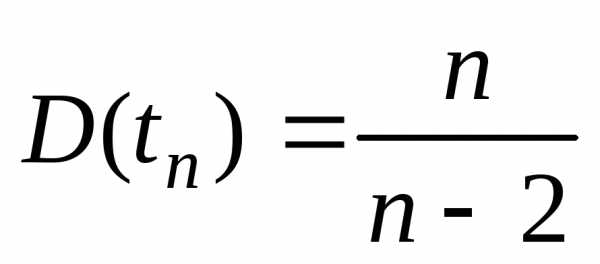 .
.

Рис. 1.3. Стандартное нормальное распределение (1) и распределение Стьюдента (2)
При распределение Стьюдента стремится к
нормальному с математическим ожиданием
0 и дисперсией 1.
Уже при 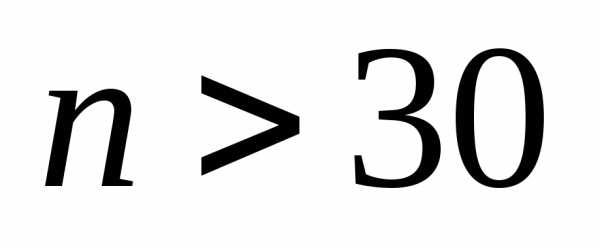 распределение Стьюдента можно приближенно
заменить на стандартное нормальное.
распределение Стьюдента можно приближенно
заменить на стандартное нормальное.
Распределение Фишера
Пусть
независимые
случайные величины, где 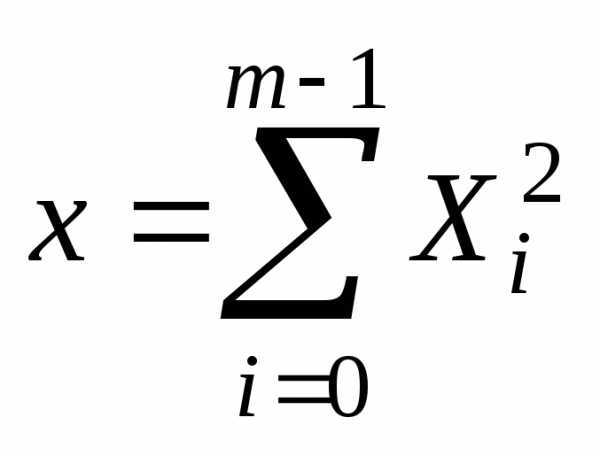 и
и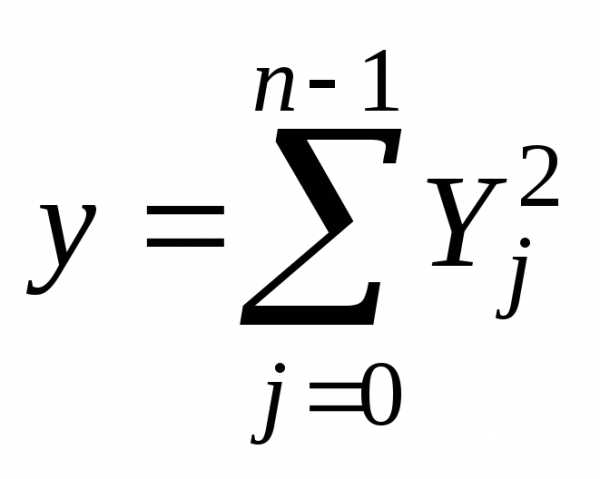 .
Тогда случайная величина
.
Тогда случайная величина
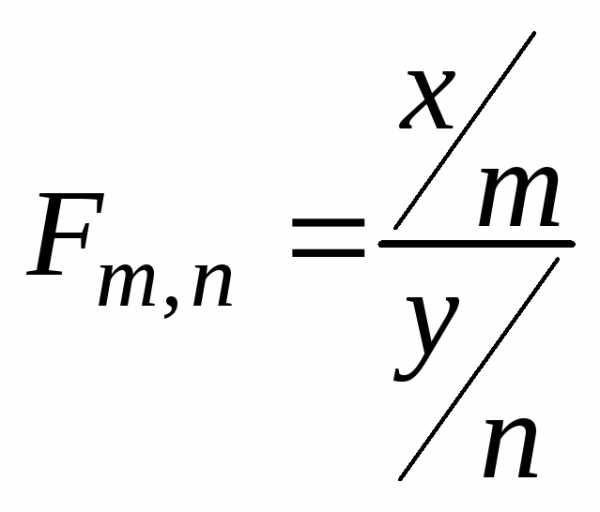
распределена
по закону Фишера со степенями свободы 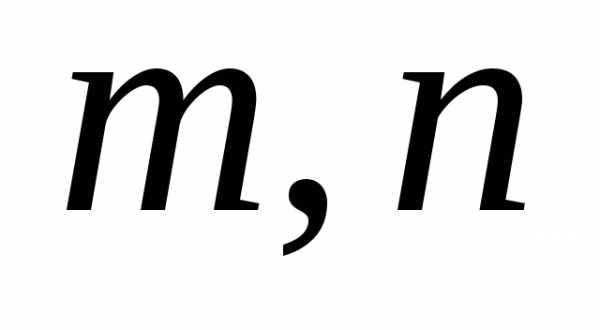 с математическим ожиданием (если
с математическим ожиданием (если )
)
 и
,
если
и
,
если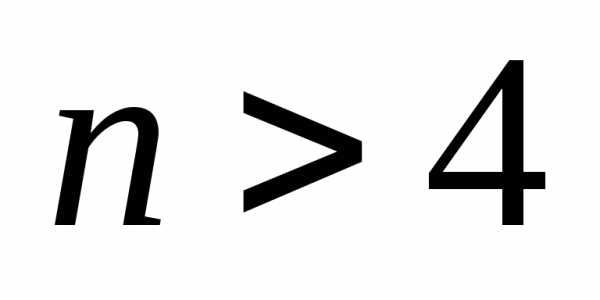 .
.
При
заданных числах 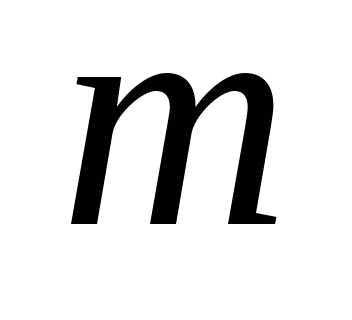 и
и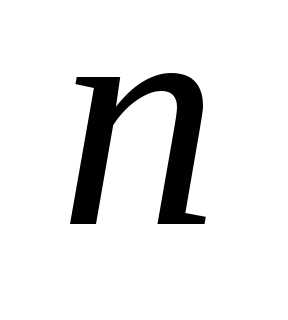 ,
вероятности
,
вероятности по прил. 6 определяется значение
по прил. 6 определяется значение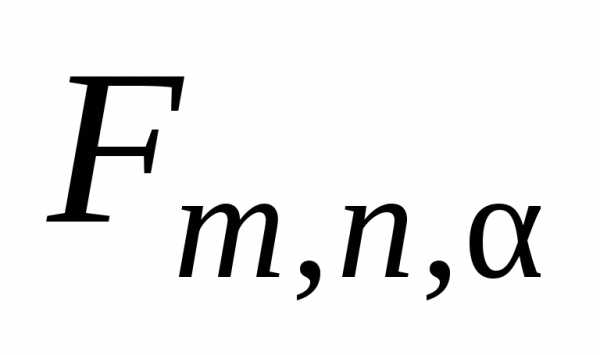 такое,
что
такое,
что
.
Обычно
таблицы составляются для значений  ,
равных 0,05 или 0,01, а иногда для обоих этих
значений. В таблицах значений закона
Фишера иногда вместо обозначений
,
равных 0,05 или 0,01, а иногда для обоих этих
значений. В таблицах значений закона
Фишера иногда вместо обозначений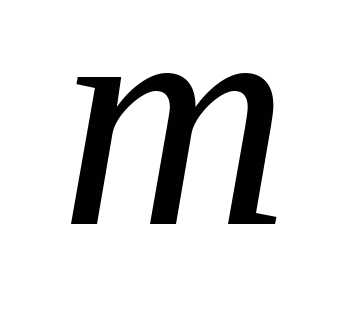 и
и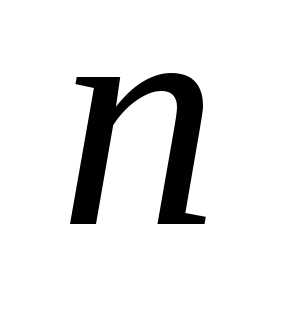 используются
используются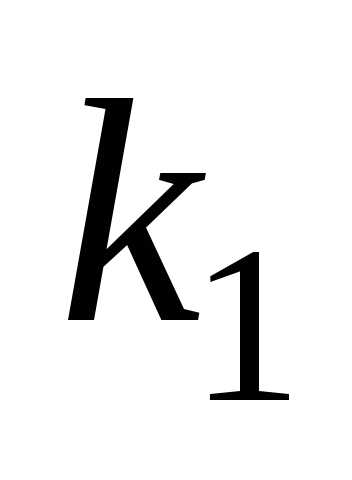 и
и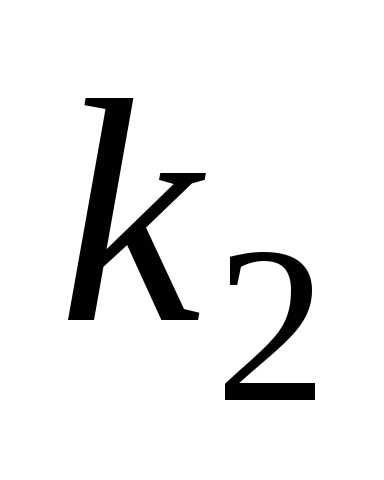 соответственно. Пример плотности
распределения случайной величины
соответственно. Пример плотности
распределения случайной величины  приведён на рис.
1.4.
приведён на рис.
1.4.

Рис.
1.4. Плотность распределения случайной
величины 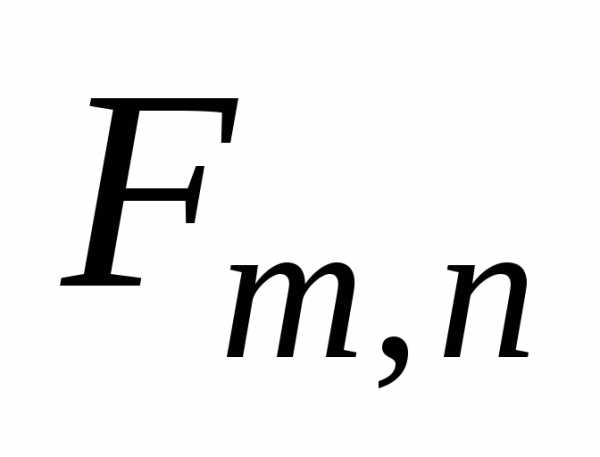 при
при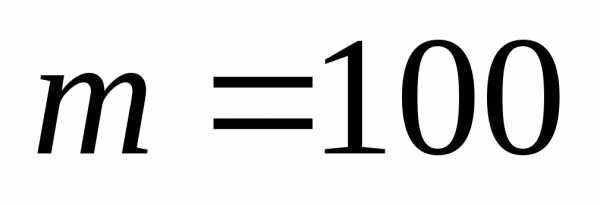 и
и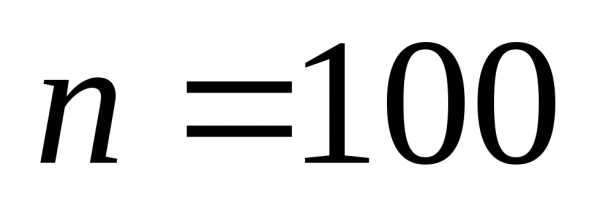
studfiles.net
Точечные оценки параметров распределения.
Пусть неизвестен
параметр распределения ,
любая функцияна выборке
,
любая функцияна выборке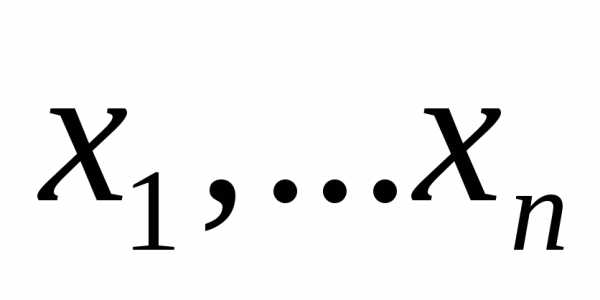 называетсяточечной оценкой
называетсяточечной оценкой  .
Оценки тоже являются случайными
величинами.
.
Оценки тоже являются случайными
величинами.
Требования к оценкам.
Несмещенность

Состоятельность
Эффективность (по сравнению с другими оценками) – если дисперсия оценки меньше дисперсий других оценок.
Можно показать, что несмещенная оценка состоятельна, если ее выборочная дисперсия стремится к нулю при .
Оценки ищут различными методами: методом моментов, методом максимального правдоподобия, методом наименьших квадратов и др.
Оценка среднего
значения ГС (математического ожидания)
– выборочное среднее. 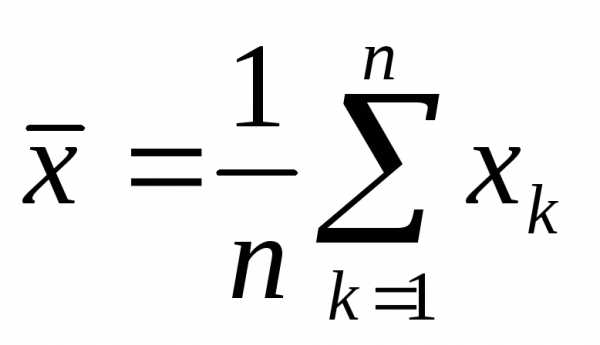 .
.
Оценка несмещенная,т.к..
Оценка состоятельная, т.к. по закону больших чисел.
Оценки дисперсии ГС:
Выборочная дисперсия

Это – смещенная, состоятельная оценка.
2. Несмещенная, состоятельная оценка дисперсии
Можно показать, что .
Пример. Вычислим оценки для приведенного выше ряда распределения
xk
0
1
3
5
nk
5
2
1
2

1/2
1/5
1/10
1/5
,
.
Интервальные оценки.
Доверительный
интервал– это интервал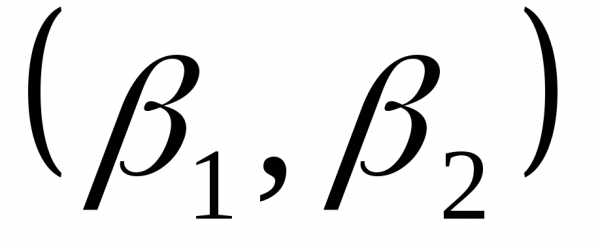 ,
такой, что,
,
такой, что,
где  —доверительная вероятность.
—доверительная вероятность.
Общее правило
построения доверительного интервала
для любого параметра основано на
центральной предельной теореме, по
которой при больших n (n>50)
оценка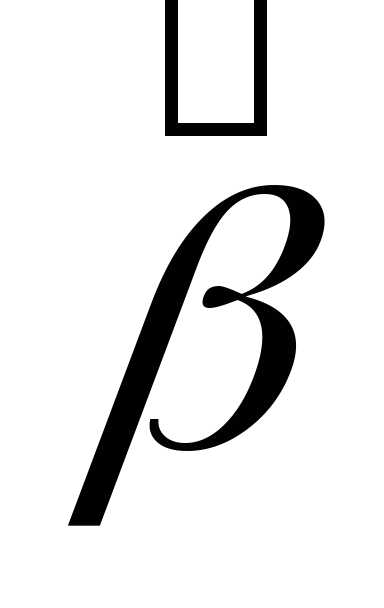 имеет
нормальное распределение с,
если
имеет
нормальное распределение с,
если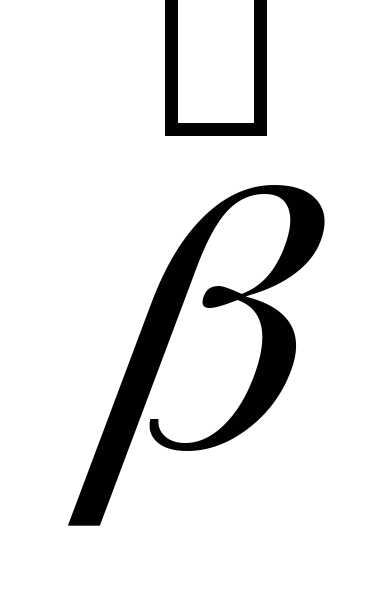 — несмещенная оценка, а функция
распределения случайной величины
— несмещенная оценка, а функция
распределения случайной величины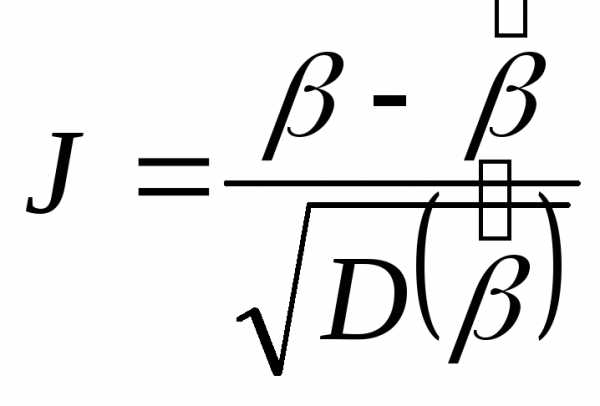 сходится по вероятности прик функции стандартного нормального
распределения.
сходится по вероятности прик функции стандартного нормального
распределения.
Квантиль (уровня
(уровня 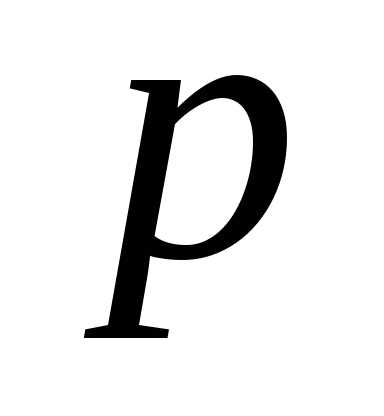 ) случайной величиныXс функцией распределенияF(x)
– это такое значение
) случайной величиныXс функцией распределенияF(x)
– это такое значение 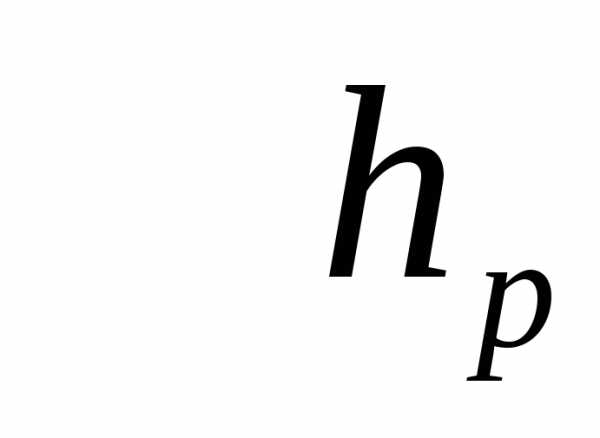 случайной величиныX, что
случайной величиныX, что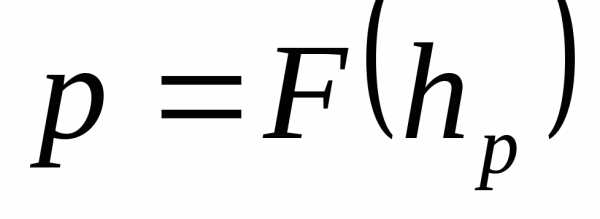 .
.
стандартного
нормального распределения. По симметрии
плотности нормального распределения 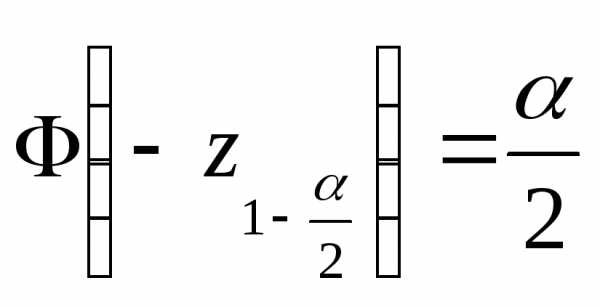 .
Так как.
.
Так как.
Так как
распределение случайной величины  стремится к стандартному нормальному
распределению, то.
Отсюда получаемдоверительный интервал
стремится к стандартному нормальному
распределению, то.
Отсюда получаемдоверительный интервал
.
Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
Если ГС имеет нормальное распределение, то и любая выборка распределена нормально. Известно, что сумма нормальных случайных величин тоже распределена нормально. Поэтому оценка математического ожидания – выборочное среднее – нормально распределенная случайная величина с — известно.
Поэтому, если
 известно, то
известно, то ,
идоверительный интервал дляматематического ожиданиястроится
так:
,
идоверительный интервал дляматематического ожиданиястроится
так:
с доверительной вероятностью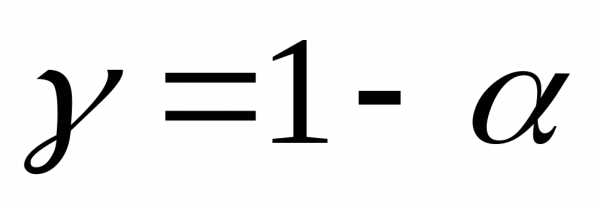 .
Квантили проще всего искать по таблицам
квантилей нормального распределения.
.
Квантили проще всего искать по таблицам
квантилей нормального распределения.
Если
 неизвестно,то нормированная случайная величина
неизвестно,то нормированная случайная величина (вместо
(вместо подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности
подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности определяют
определяют ,
по таблице квантилей определяют квантиль
,
по таблице квантилей определяют квантиль уровня
уровня .
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
.
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
Если n> 20, то квантиль можно искать по таблицам квантилей нормального распределения.
studfiles.net
Точечные оценки параметров случайной величины
Точечными оценкамипараметров называют такие оценки, которые выражаются каким-то одним числом (точкой).
Таким
числом могут быть, например, параметры  и
и нормального распределения или параметр
нормального распределения или параметр закона Пуассона. Не все переменные могут
быть оценками.
закона Пуассона. Не все переменные могут
быть оценками.
Качество оценки определяют, проверяя, обладает ли она свойствами несмещенности, самостоятельности и эффективности.
1. Несмещенность. Оценка не должна содержать систематической ошибки. Это означает, что математическое ожидание оценки некоторого параметра, взятое по всем возможным выборкам, должно быть равно действительному значению параметра.
Если
действительное значение оцениваемого
параметра обозначить 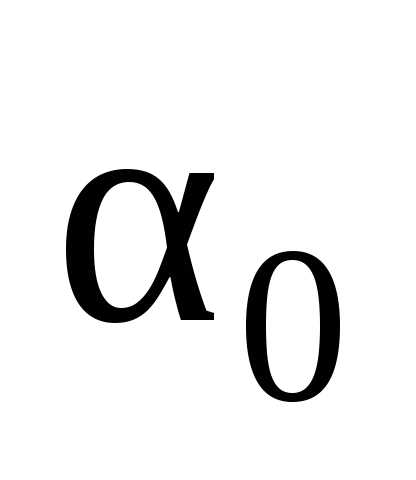 ,
а его оценку
,
а его оценку ,
то требование несмещенности запишется
в виде
,
то требование несмещенности запишется
в виде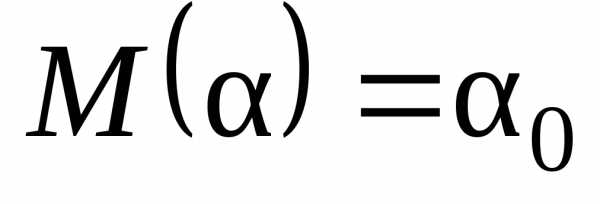 .
.
2. Состоятельность. Оценка  должна приближаться
к
должна приближаться
к 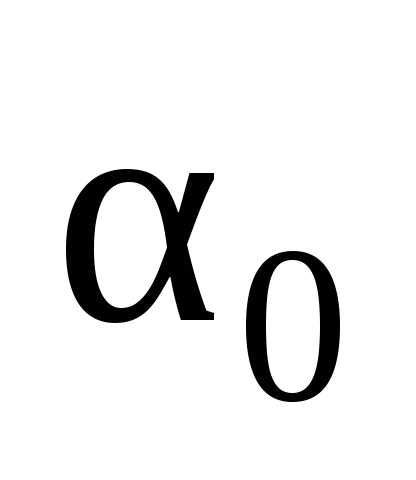 по мере увеличения объема выборки. Но
ввиду того, что оценка
по мере увеличения объема выборки. Но
ввиду того, что оценка является случайной величиной, об этом
приближении можно говорить только
в вероятностном смысле.
является случайной величиной, об этом
приближении можно говорить только
в вероятностном смысле.
Для
состоятельности оценки  ,
получаемой при выборке объема
,
получаемой при выборке объема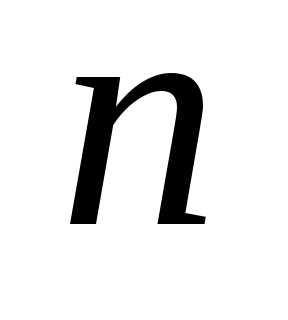 , должно выполняться
условие сходимости по вероятности
, должно выполняться
условие сходимости по вероятности  к
к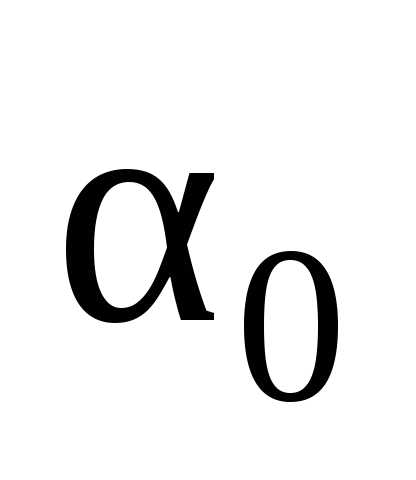 ,
т.е..
,
т.е..
Свойство состоятельности обязательно для любого правила оценивания (несостоятельные оценки не используются!).
3. Эффективность. Несмещенная оценка  параметра
параметра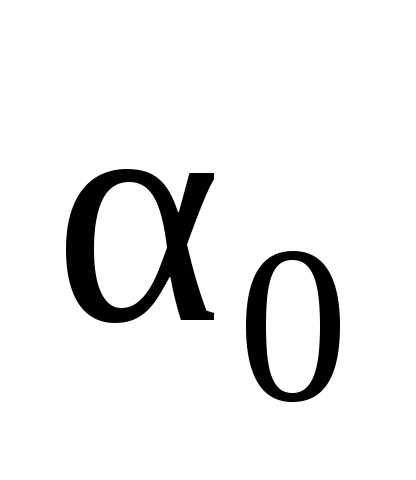 называется эффективной, если она имеет
наименьшую дисперсию среди всех возможных
несмещенных оценок
называется эффективной, если она имеет
наименьшую дисперсию среди всех возможных
несмещенных оценок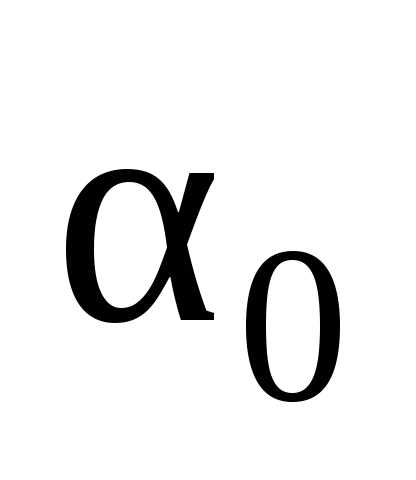 ,
то есть оценкаэффективна,
если ее дисперсия минимальна.
,
то есть оценкаэффективна,
если ее дисперсия минимальна.
Отметим, что на практике не всегда удается удовлетворить всем перечисленным выше требованиям, и поэтому приходится довольствоваться оценками, не обладающими сразу всеми тремя свойствами.
Рассмотрим
несмещенные точечные оценки параметров
распределения. Запишем в виде таблицы
полученные в результате изучения
выборки значения признака 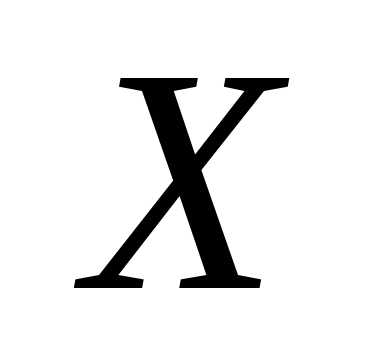 в неубывающем
порядке . Такая последовательность
называется вариационным
рядом, а сами значения
вариантами. Если
среди вариантов есть одинаковые, то
вариационный ряд записывают в виде
таблицы.
в неубывающем
порядке . Такая последовательность
называется вариационным
рядом, а сами значения
вариантами. Если
среди вариантов есть одинаковые, то
вариационный ряд записывают в виде
таблицы.
Варианты, | | | … | |
Частоты, | | | … | |
При этом сумма частот равна объёму выборки, т.е.
. (1.1)
Величины 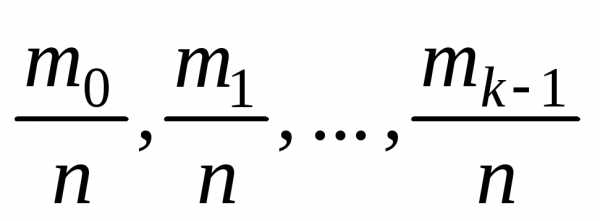 называются относительными частотами
или частостями. Из (1.1) следует
называются относительными частотами
или частостями. Из (1.1) следует
.
Часто вариационный ряд, записанный в виде такой таблицы, называют статистическим рядом распределения.
Если во второй строке статистического ряда распределения вместо частот записать частости, то полученная таблица будет иметь большое сходство с рядом распределения дискретной случайной величины.
Тогда
для указанной выборки можно построить
полигон распределения и выборочную
(эмпирическую) функцию распределения
аналогично тому, как это делалось для
дискретной случайной величины 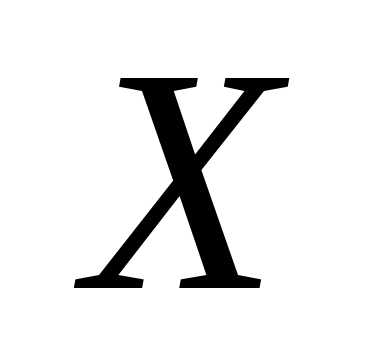 .
.
Если значения признака изменяются непрерывно в некотором промежутке, то строят интервальный ряд, имеющий вид:
Интервалы | | | … | |
Частоты | | | … | |
Графическим представлением интервального ряда является гистограмма, пример которой изображен на рис. 1.1.
Поскольку
точные значения параметров распределения
признака 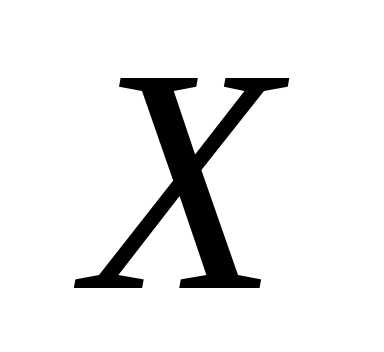 в генеральной
совокупности
в генеральной
совокупности 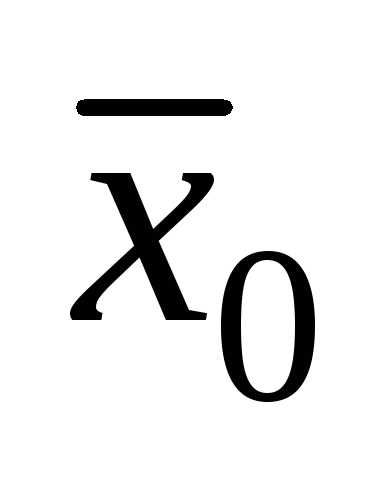 и
и 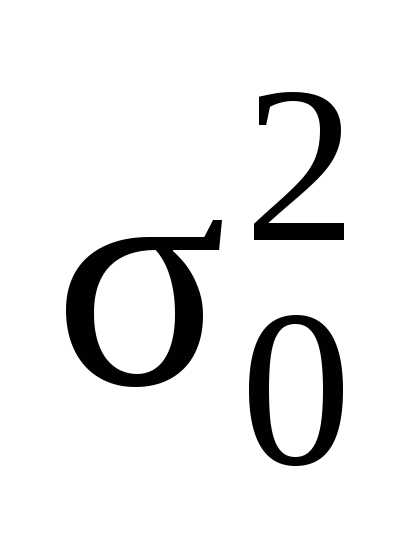 в большинстве случаев определить не
представляется возможным, то эти
параметры следует оценить, используя
соответствующие параметры выборки.
в большинстве случаев определить не
представляется возможным, то эти
параметры следует оценить, используя
соответствующие параметры выборки.
Выборочная
средняя  представляет собой
среднее значение признака
представляет собой
среднее значение признака 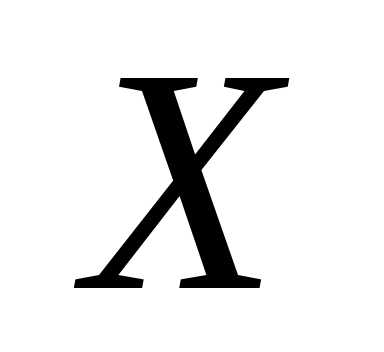 в выборке и определяется по формуле
в выборке и определяется по формуле
.

Рис. 1.1. Пример гистограммы интервального ряда для 6 интервалов
Если используется интервальный ряд, то за варианты принимаются, как правило, середины интервалов.
Выборочная
дисперсия 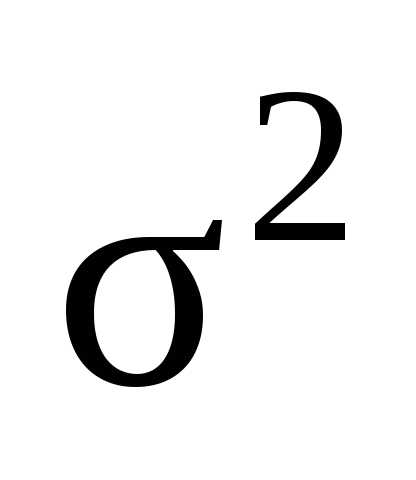 определяется по формуле
определяется по формуле
,
или по упрощенной формуле
 ,
,
где 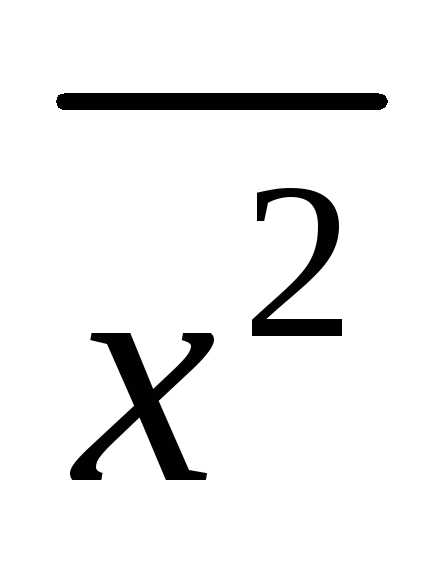 определяется по формуле
определяется по формуле
.
Выборочное
среднее квадратическое отклонение  определяется как квадратный корень
из
определяется как квадратный корень
из 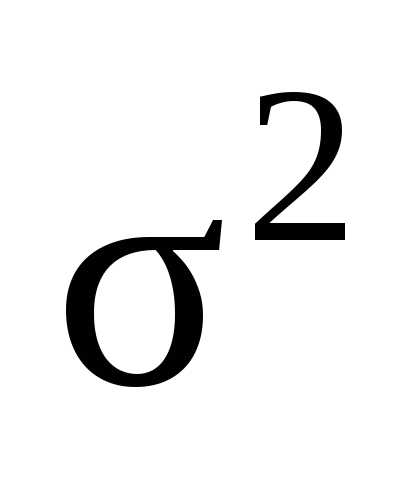 .
В качестве точечной оценки параметров
генеральной совокупности может
приниматься соответствующий параметр
выборки. Можно доказать следующее.
.
В качестве точечной оценки параметров
генеральной совокупности может
приниматься соответствующий параметр
выборки. Можно доказать следующее.
1.  является несмещенной
точечной оценкой
является несмещенной
точечной оценкой 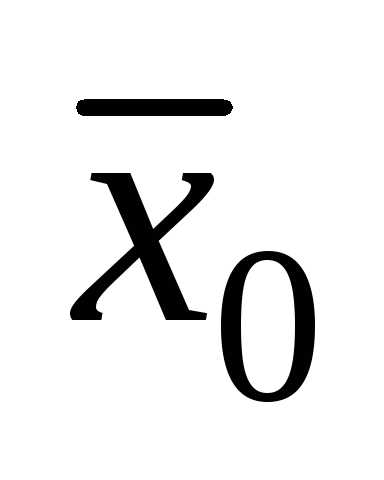 ,
т.е.
,
т.е.
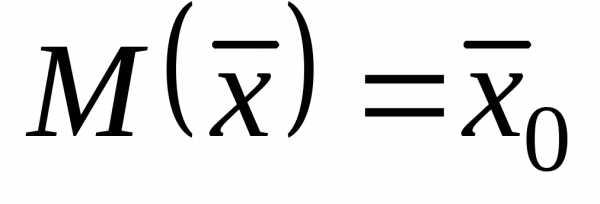 .
.
2.
Оценка 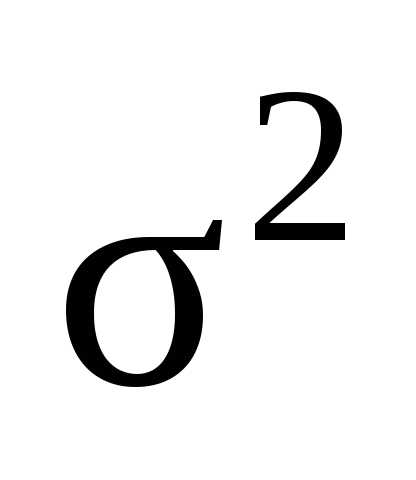 для генеральной дисперсии
для генеральной дисперсии 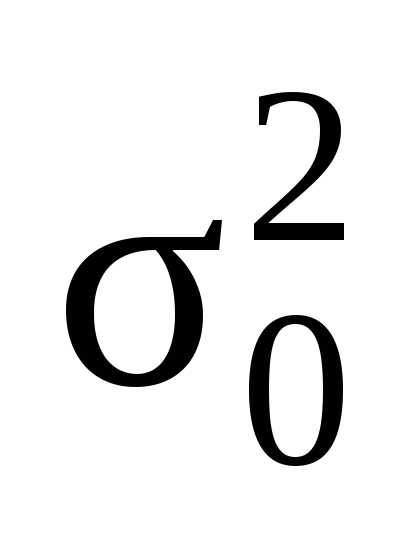 является состоятельной, нонесмещенной.
Поэтому вводят величину
является состоятельной, нонесмещенной.
Поэтому вводят величину
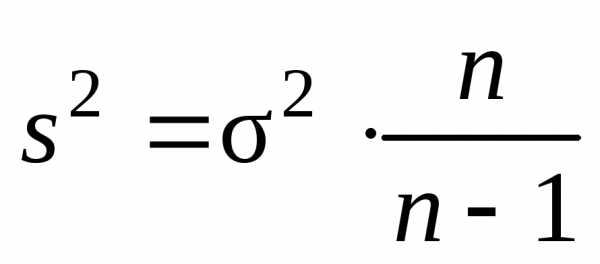 ,
,
которая
называется исправленной статистической
выборочной дисперсией. Эта величина
является несмещенной оценкой генеральной
дисперсии 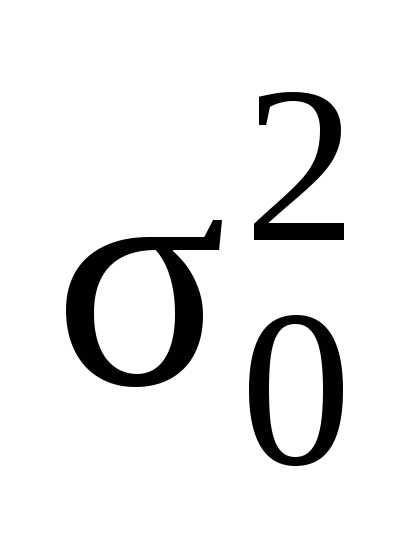 ,
т.е.
,
т.е.
 .
.
Величина 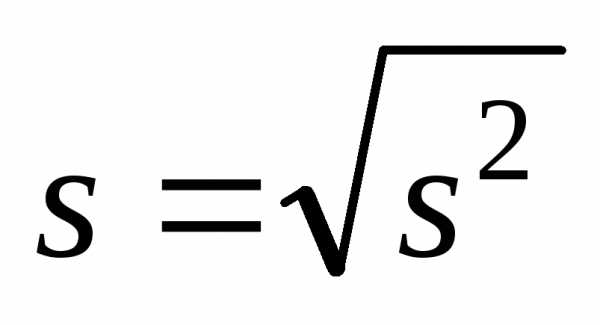 называется
исправленным выборочным средним
квадратическим отклонением и является
несмещенной точечной оценкой генерального
среднего квадратического отклонения
называется
исправленным выборочным средним
квадратическим отклонением и является
несмещенной точечной оценкой генерального
среднего квадратического отклонения 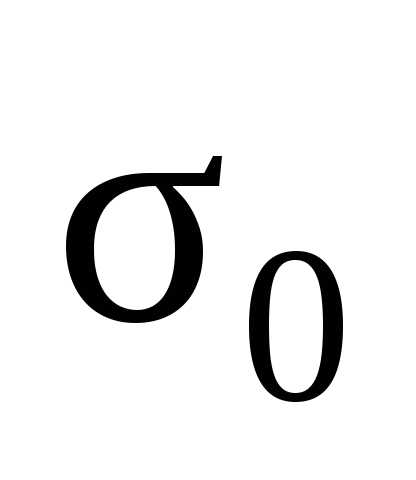 ,
т.е.
,
т.е.
 .
.
Для решения статистических задач используются специальные распределения случайных величин, сконструированных на основе нормального распределения. Рассмотрим частные случаи этого вида распределения.
Распределение
«хи квадрат» 
Важным
частным случаем нормального распределения
является так называемое распределение 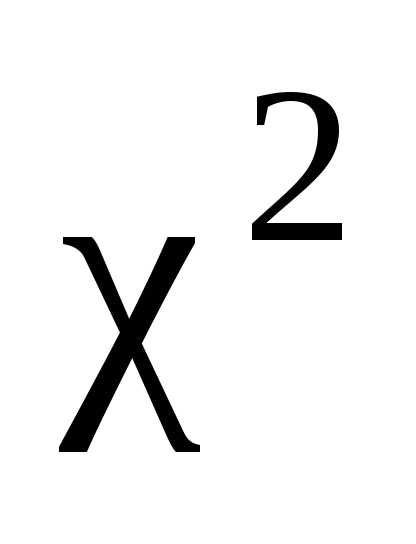 .
Это распределение является
двухпараметрическим и описывает
случайные величины, распределенные на
полуинтервале
.
Это распределение является
двухпараметрическим и описывает
случайные величины, распределенные на
полуинтервале 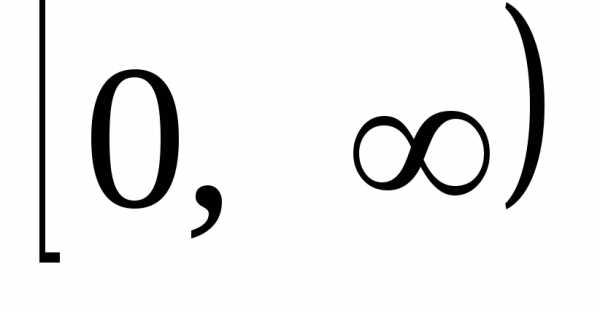 .
.
Пусть
имеется 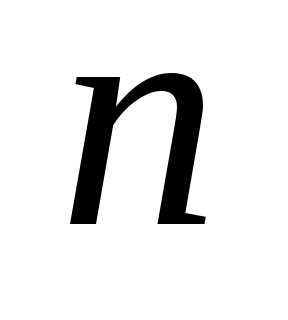 независимых случайных величин
,
распределенных по нормальному закону
с математическим ожиданием, равным
нулю, и дисперсией, равной единице. Тогда
случайная величина
независимых случайных величин
,
распределенных по нормальному закону
с математическим ожиданием, равным
нулю, и дисперсией, равной единице. Тогда
случайная величина
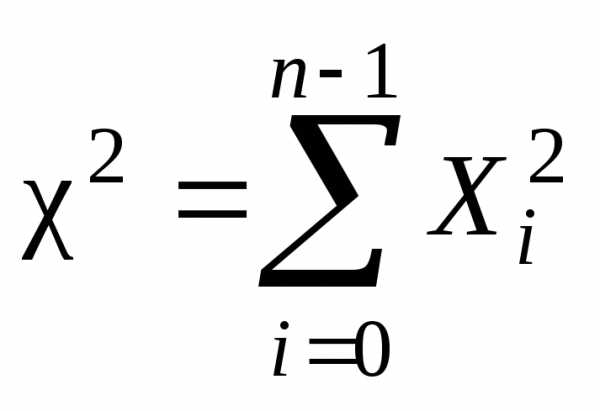
распределена
по закону Пирсона или  – «хи квадрат», с характеристиками
– «хи квадрат», с характеристиками 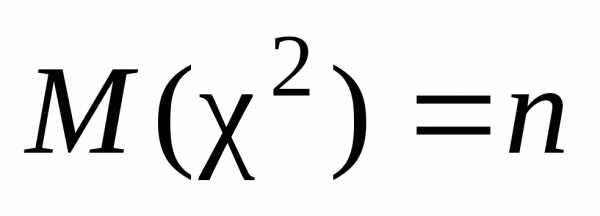 ,
, 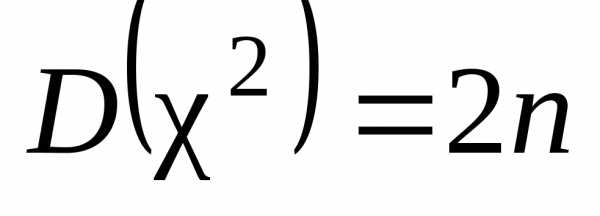 .
.
Распределением 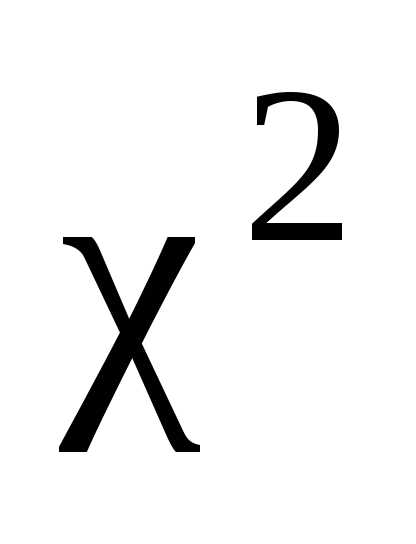 с
с 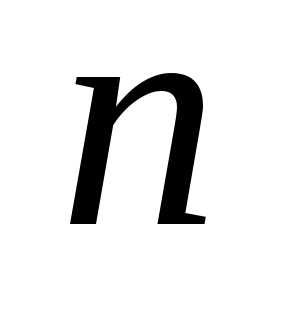 степенями свободы
называется распределение суммы квадратов
степенями свободы
называется распределение суммы квадратов 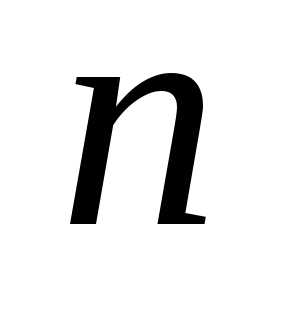 независимых случайных
величин, каждая из которых подчинена
нормальному закону с математическим
ожиданием, равным нулю, и дисперсией,
равной единице.
независимых случайных
величин, каждая из которых подчинена
нормальному закону с математическим
ожиданием, равным нулю, и дисперсией,
равной единице.
Очевидно,
что 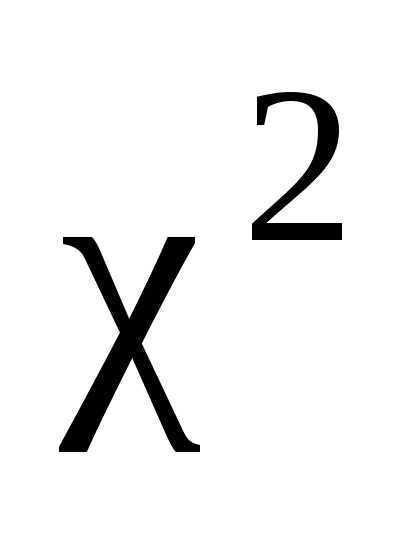 может принимать лишь неотрицательные
значения. График плотности распределения
случайной величины представляет собой
кривую, изображенную на рис. 1.2.
может принимать лишь неотрицательные
значения. График плотности распределения
случайной величины представляет собой
кривую, изображенную на рис. 1.2.

Рис.
1.2. Кривая плотности распределения 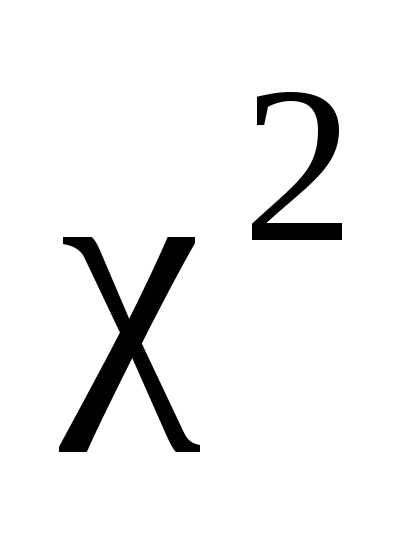
Для
того чтобы определить вероятность
попадания случайной величины 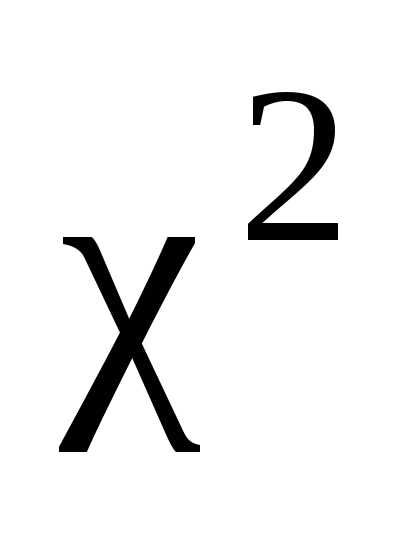 в какой-либо промежуток из множества
положительных чисел, пользуются таблицей
распределения
в какой-либо промежуток из множества
положительных чисел, пользуются таблицей
распределения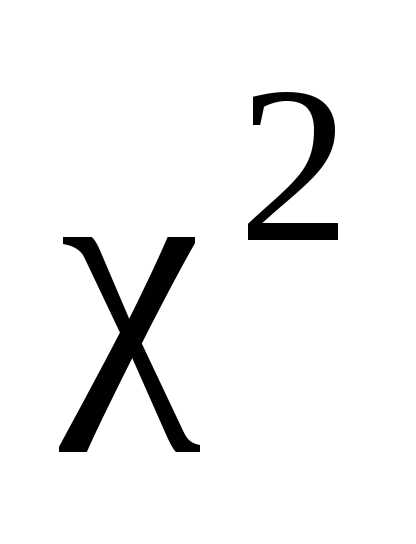 (прил. 2).
(прил. 2).
Обычно
такая таблица позволяет по заданной
вероятности  и по числу степеней
свободы
и по числу степеней
свободы 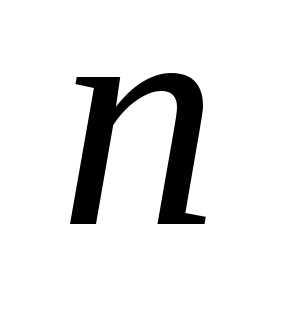 определить так
называемый квантиль
определить так
называемый квантиль 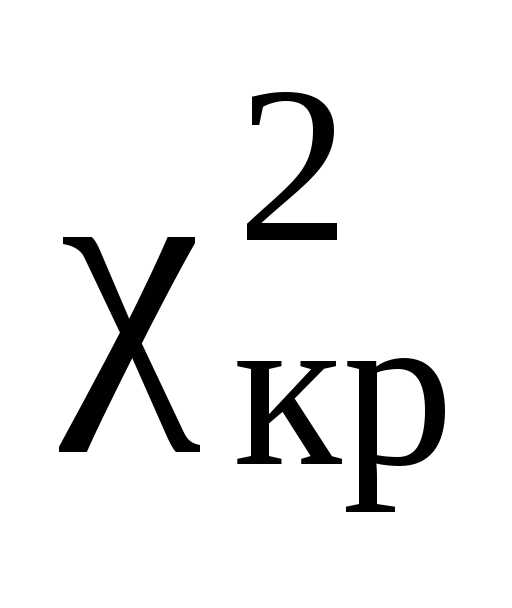 – критическое
значение
– критическое
значение 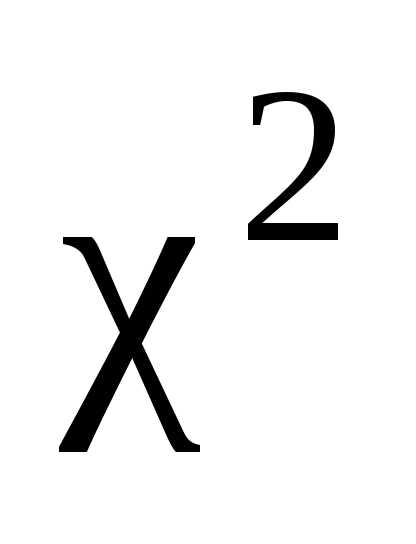 ,
если
,
если и
и  связаны соотношением:
связаны соотношением:
.
Эта
формула означает: вероятность того, что
случайная величина 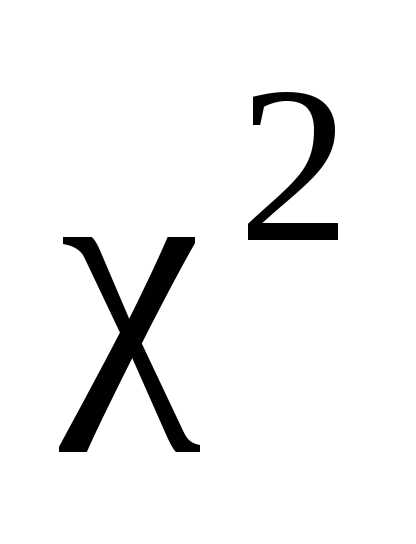 примет значение большее, чем табличное
значение
примет значение большее, чем табличное
значение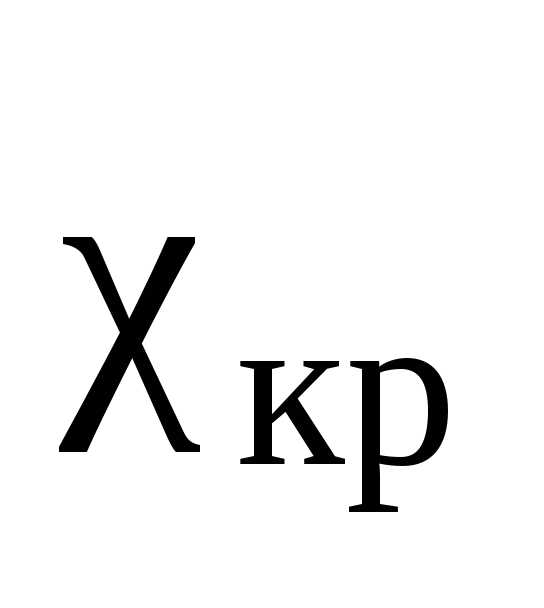 ,
равна
,
равна .
Из таблицы (прил. 2) очевидно, что случайная
величина
.
Из таблицы (прил. 2) очевидно, что случайная
величина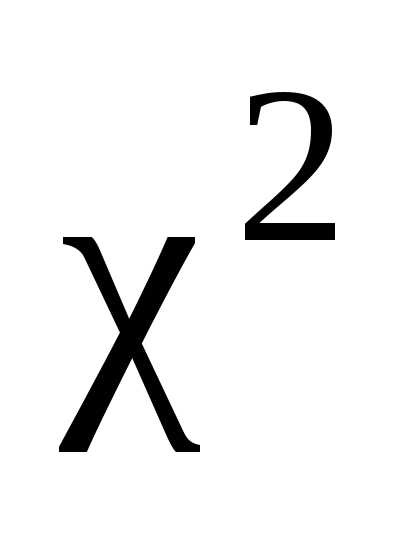 с 10 степенями свободы с вероятностьюпри-нимает значение, равное 3,94.
с 10 степенями свободы с вероятностьюпри-нимает значение, равное 3,94.
Распределение Стьюдента (или t-распределение)
Другим важным случаем нормального распределения является однопараметрическое распределение Стьюдента (рис. 1.3). Ему подчиняется случайная величина, распределенная на всей числовой оси. Пусть – независимые стандартные нормальные случайные величины . Тогда случайная величина
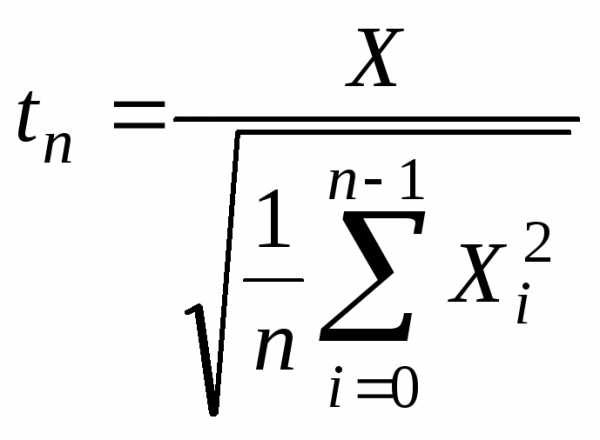
имеет
распределение Стьюдента с 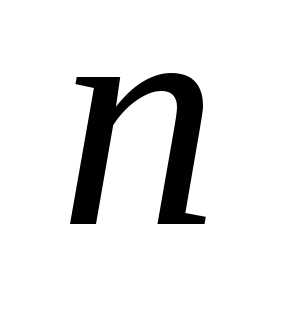 степенями свободы.
степенями свободы.
Если
число степеней свободы 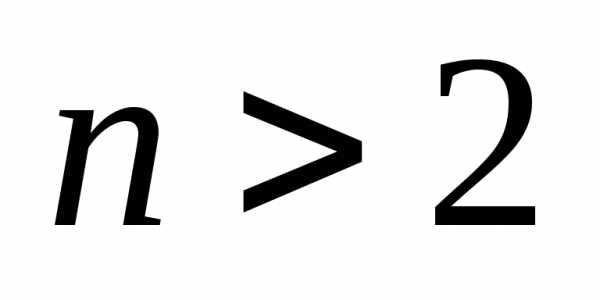 ,
то
,
то
 ,
,  .
.

Рис. 1.3. Стандартное нормальное распределение (1) и распределение Стьюдента (2)
При распределение Стьюдента стремится к
нормальному с математическим ожиданием
0 и дисперсией 1.
Уже при 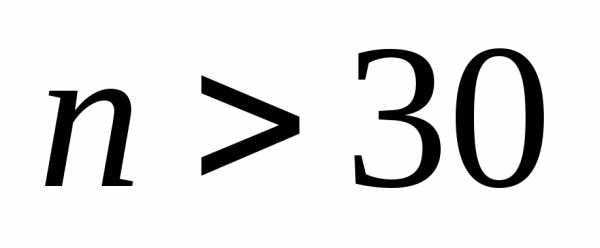 распределение Стьюдента можно приближенно
заменить на стандартное нормальное.
распределение Стьюдента можно приближенно
заменить на стандартное нормальное.
Распределение Фишера
Пусть
независимые
случайные величины, где 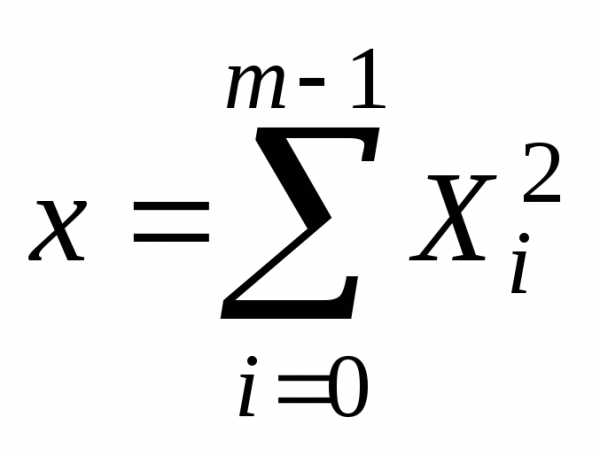 и
и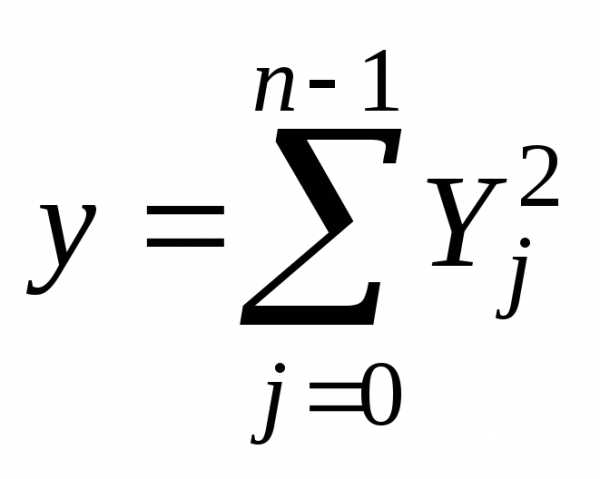 .
Тогда случайная величина
.
Тогда случайная величина
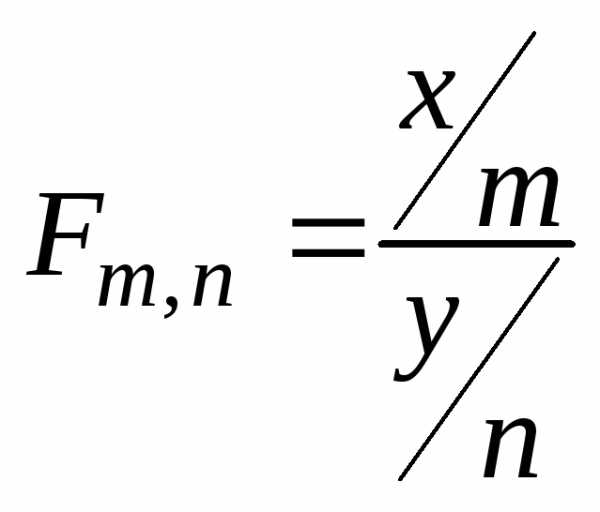
распределена
по закону Фишера со степенями свободы 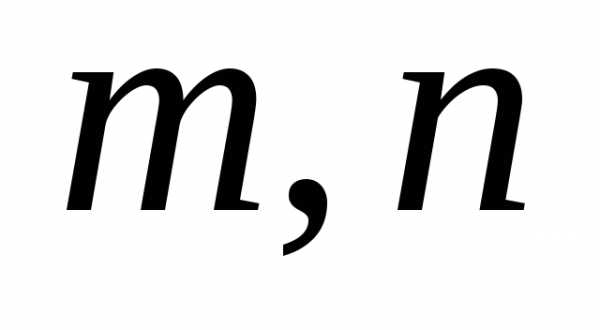 с математическим ожиданием (если
с математическим ожиданием (если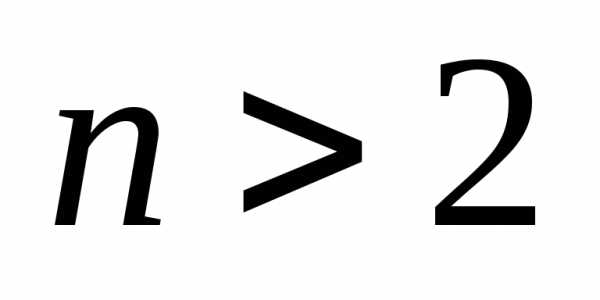 )
)
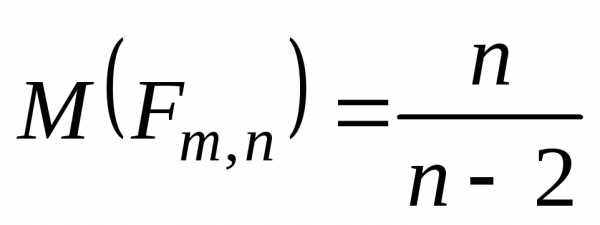 и
,
если
и
,
если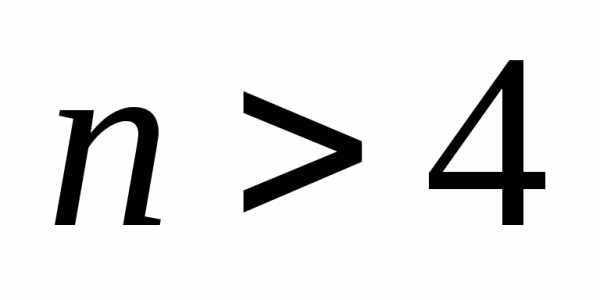 .
.
При
заданных числах 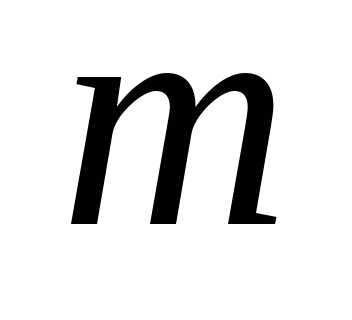 и
и ,
вероятности
,
вероятности по прил. 6 определяется значение
по прил. 6 определяется значение такое,
что
такое,
что
.
Обычно
таблицы составляются для значений  ,
равных 0,05 или 0,01, а иногда для обоих этих
значений. В таблицах значений закона
Фишера иногда вместо обозначений
,
равных 0,05 или 0,01, а иногда для обоих этих
значений. В таблицах значений закона
Фишера иногда вместо обозначений и
и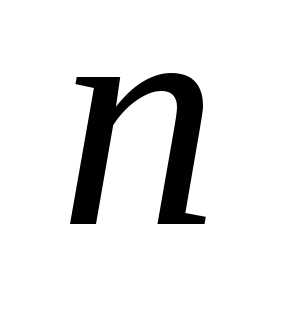 используются
используются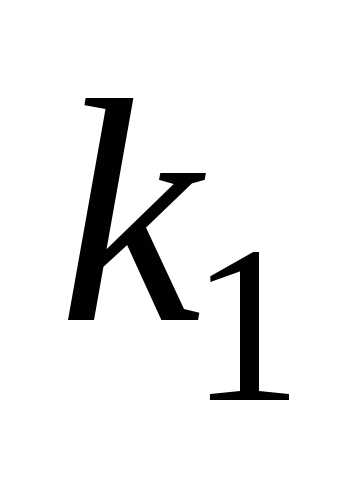 и
и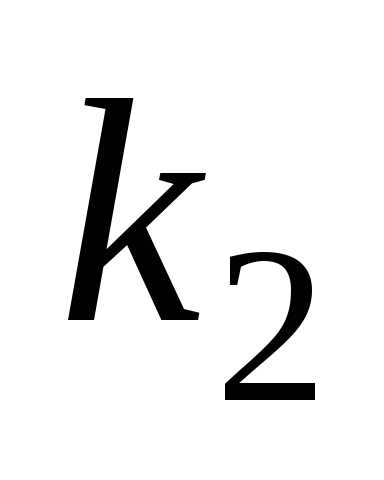 соответственно. Пример плотности
распределения случайной величины
соответственно. Пример плотности
распределения случайной величины 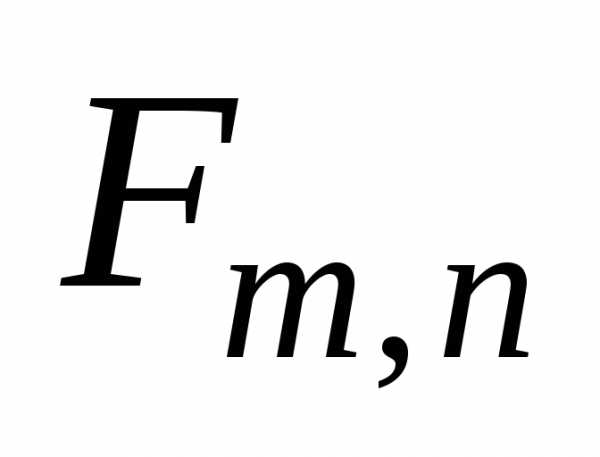 приведён на рис.
1.4.
приведён на рис.
1.4.

Рис.
1.4. Плотность распределения случайной
величины 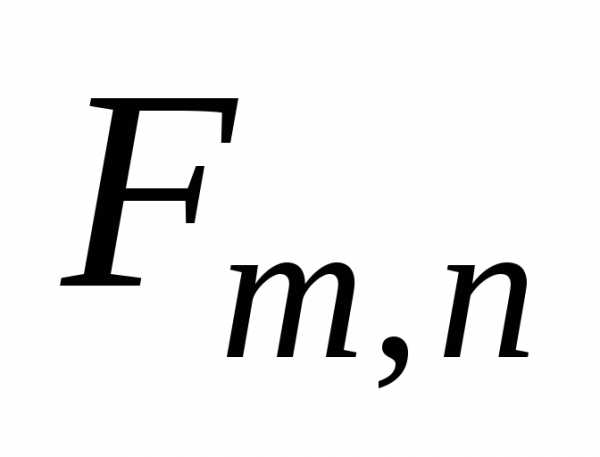 при
при и
и
studfiles.net
Точечные оценки математического ожидания и дисперсии
Пусть случайная выборка порождена наблюдаемой случайной величиной ξ, математическое ожиданиеи дисперсиякоторой неизвестны. В качестве оценок для этих характеристик было предложено использовать выборочное среднее

и выборочную дисперсию
. (3.14)
Рассмотрим некоторые свойства оценок математического ожидания и дисперсии.
1. Вычислим математическое ожидание выборочного среднего:
. (3.15)
Следовательно,
выборочное среднее является несмещенной
оценкой для 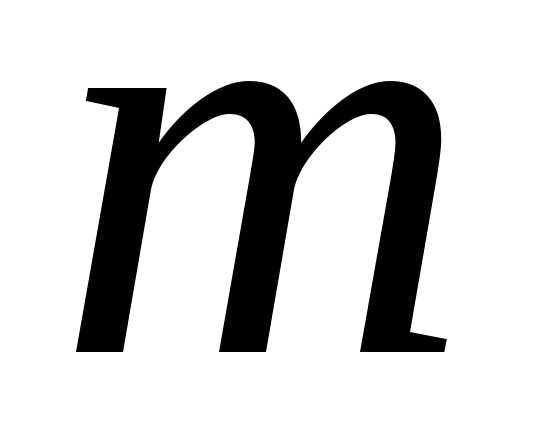 .
.
2. Напомним, что
результаты
наблюдений – независимые случайные
величины, каждая из которых имеет такой
же закон распределения, как и величина ,
а значит,,,
,
а значит,,,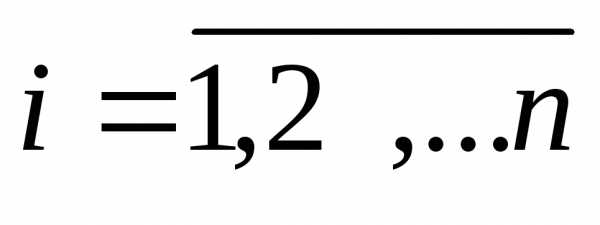 .
Будем предполагать, что дисперсия
.
Будем предполагать, что дисперсия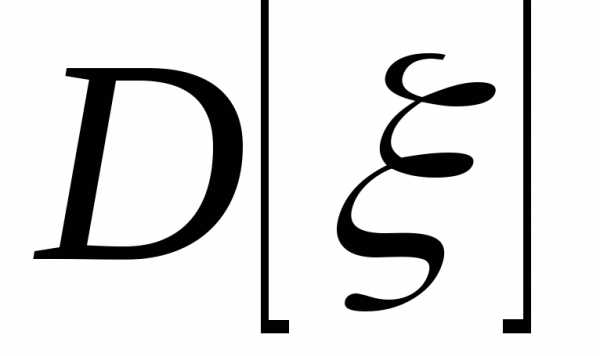 конечна. Тогда, согласно теореме Чебышева
о законе больших чисел, для любогоε> 0 имеет место равенство
конечна. Тогда, согласно теореме Чебышева
о законе больших чисел, для любогоε> 0 имеет место равенство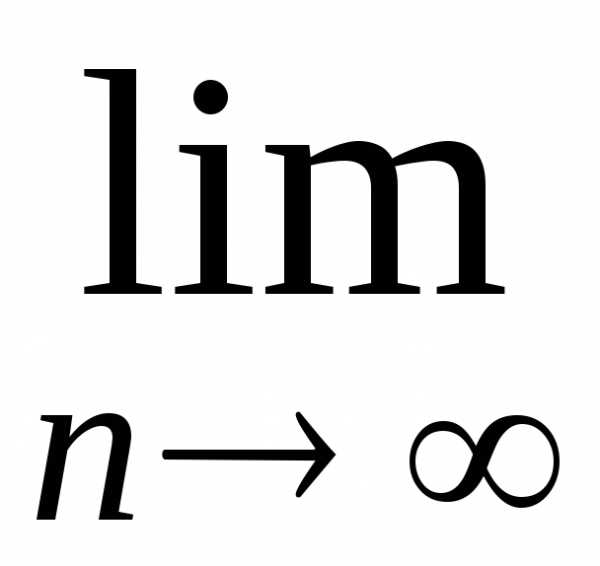 ,
,
которое можно записать так: . (3.16)
Сравнивая (3.16) с
определением свойства состоятельности
(3.11), видим, что оценка 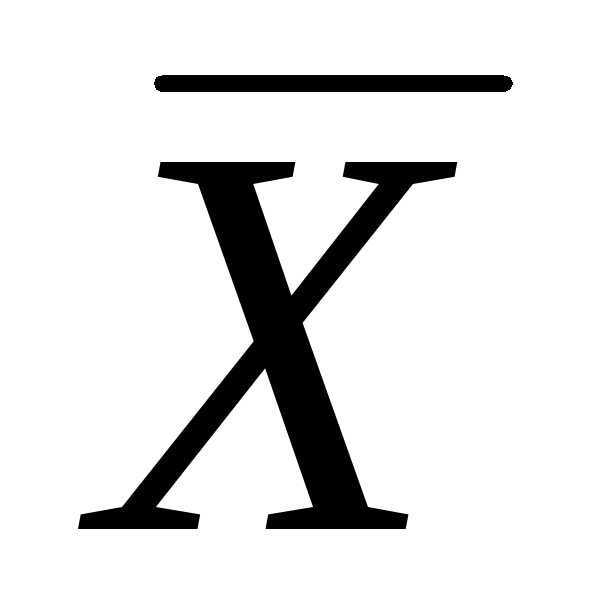 является состоятельной оценкой
математического ожидания
является состоятельной оценкой
математического ожидания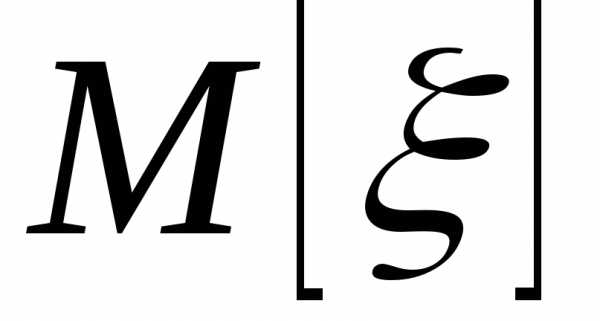 .
.
3. Найдем дисперсию выборочного среднего:
. (3.17)
Таким образом, дисперсия оценки математического ожидания уменьшается обратно пропорционально объему выборки.
Можно доказать,
что если случайная величина ξраспределена нормально, то выборочное
среднее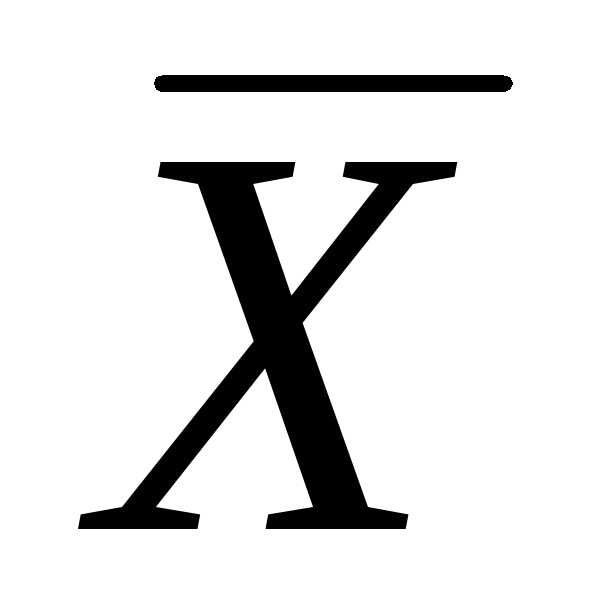 является эффективной оценкой
математического ожидания
является эффективной оценкой
математического ожидания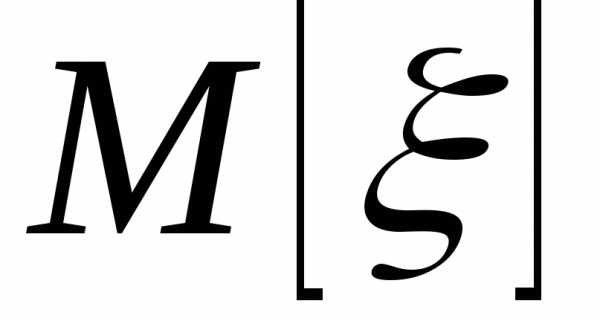 ,
то есть дисперсия
,
то есть дисперсия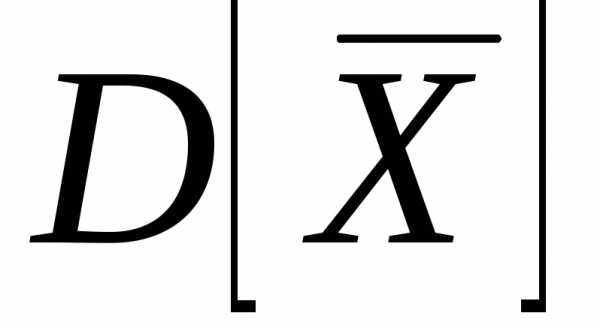 принимает наименьшее значение по
сравнению с любой
другой оценкой математического ожидания.
Для других законов распределенияξэто может быть и не так.
принимает наименьшее значение по
сравнению с любой
другой оценкой математического ожидания.
Для других законов распределенияξэто может быть и не так.
Выборочная дисперсия 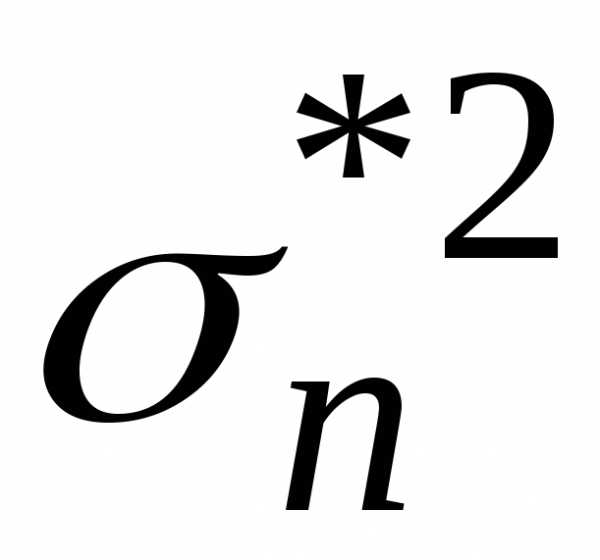 является смещенной оценкой дисперсии
является смещенной оценкой дисперсии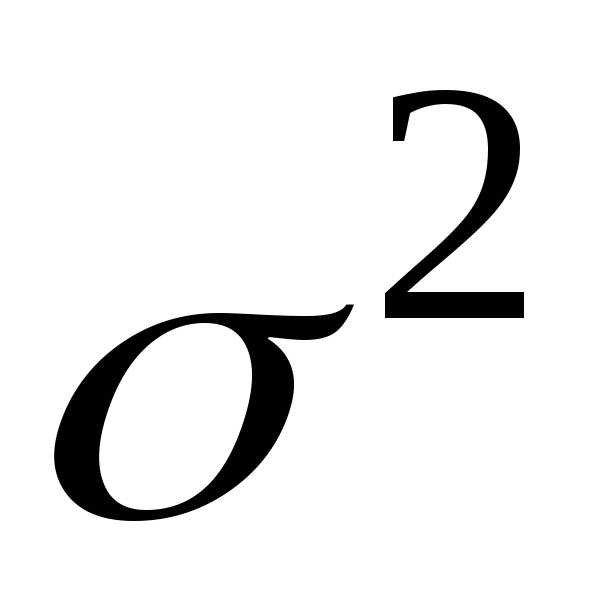 ,
так как.
(3.18)
,
так как.
(3.18)
Действительно, используя свойства математического ожидания и формулу (3.17), найдем
.
Чтобы получить
несмещенную оценку дисперсии, оценку
(3.14) нужно исправить, то есть домножить
на 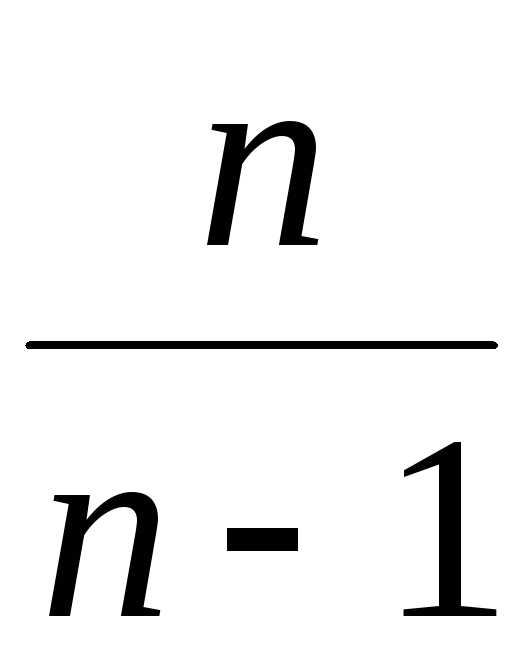 .
Тогда получим несмещенную выборочную
дисперсию
.
Тогда получим несмещенную выборочную
дисперсию
. (3.19)
Отметим, что формулы
(3.14) и (3.19) отличаются лишь знаменателем,
и при больших значениях 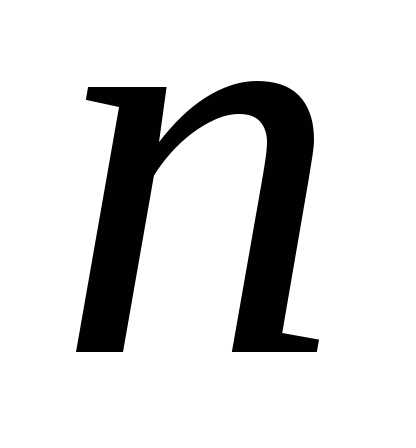 выборочная и несмещенная дисперсии
отличаются мало. Однако при малом объеме
выборки
выборочная и несмещенная дисперсии
отличаются мало. Однако при малом объеме
выборки следует пользоваться соотношением
(3.19).
следует пользоваться соотношением
(3.19).
Для оценки среднего
квадратического отклонения случайной
величины используют так называемое
“исправленное” среднее квадратическое
отклонение, которое равно квадратному
корню из несмещенной дисперсии: 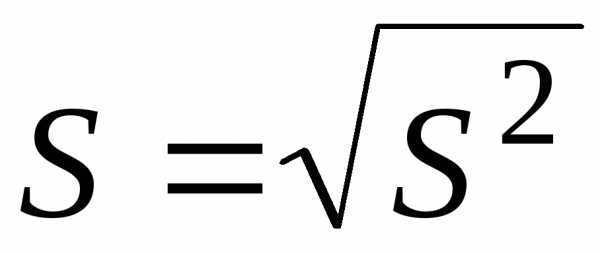 .
.
3.4. Интервальные оценки
В статистике имеются два подхода к оцениванию неизвестных параметров распределений: точечный и интервальный. В соответствии с точечным оцениванием, которое рассмотрено в предыдущем разделе, указывается лишь точка, около которой находится оцениваемый параметр. Желательно, однако, знать, как далеко может отстоять в действительности этот параметр от возможных реализаций оценок в разных сериях наблюдений.
Ответ на этот вопрос – тоже приближенный – дает другой способ оценивания параметров – интервальный. В соответствии с этим способом оценивания находят интервал, который с вероятностью, близкой к единице, накрывает неизвестное числовое значение параметра.
studfiles.net
Точечные оценки числовых характеристик
Статистической
оценкой  параметраQ распределения называется приближенное
значение параметра, вычисленное по
результатам эксперимента (по выборке).
Статистические оценки делятся на
точечные и интервальные.
параметраQ распределения называется приближенное
значение параметра, вычисленное по
результатам эксперимента (по выборке).
Статистические оценки делятся на
точечные и интервальные.
Точечной называется оценка, определяемая одним
числом. Точечная оценка  параметраQ случайной
величины X в общем случае равна
,
гдеxi – значения выборки. Очевидно, что оценка
параметраQ случайной
величины X в общем случае равна
,
гдеxi – значения выборки. Очевидно, что оценка  – это случайная величина и значения
– это случайная величина и значения будут изменяться от выборки к выборке
случайным образом. К оценкам предъявляется
ряд требований.
будут изменяться от выборки к выборке
случайным образом. К оценкам предъявляется
ряд требований.
1.
Оценка  называетсясостоятельной,
если при увеличении объема выборки n она сходится по вероятности к значению
параметра Q:
называетсясостоятельной,
если при увеличении объема выборки n она сходится по вероятности к значению
параметра Q:
.
Состоятельность – это минимальное требование к оценкам.
2.
Состоятельная оценка  называетсянесмещенной, если ее математическое ожидание точно
равно параметру Q для любого объема выборки:
называетсянесмещенной, если ее математическое ожидание точно
равно параметру Q для любого объема выборки:
.
3.
Состоятельная несмещенная оценка  являетсяэффективной,
если ее дисперсия минимальна по отношению
к дисперсии любой другой оценки этого
параметра:
являетсяэффективной,
если ее дисперсия минимальна по отношению
к дисперсии любой другой оценки этого
параметра:
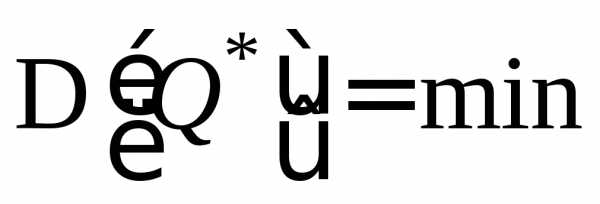 .
.
Состоятельная,
несмещенная и эффективная точечная
оценка математического
ожидания вычисляется как среднее арифметическое
значений выборки 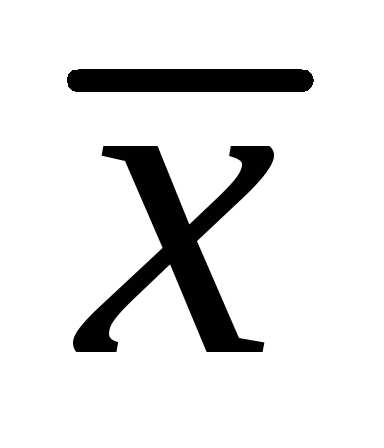 ,
называемое выборочным средним:
,
называемое выборочным средним:
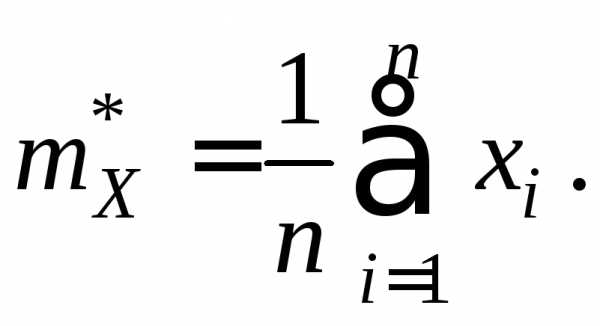 (10.5)
(10.5)
Состоятельная несмещенная точечная оценка дисперсии равна
(10.6)
Состоятельная несмещенная точечная оценка среднеквадратического отклонения равна
(10.7)
Интервальные оценки числовых характеристик
Доверительным называется интервал
,
в
который с заданной вероятностью
(надежностью) g попадает истинное значения параметра Q,
где  —
несмещенная точечная оценка параметраQ. Вероятность g выбирается близкой к 1: 0,9; 0,95; 0,975; 0,99.
—
несмещенная точечная оценка параметраQ. Вероятность g выбирается близкой к 1: 0,9; 0,95; 0,975; 0,99.
Согласно
центральной предельной теореме, при
достаточно большом объеме выборки n ()
закон распределения несмещенных точечных
оценок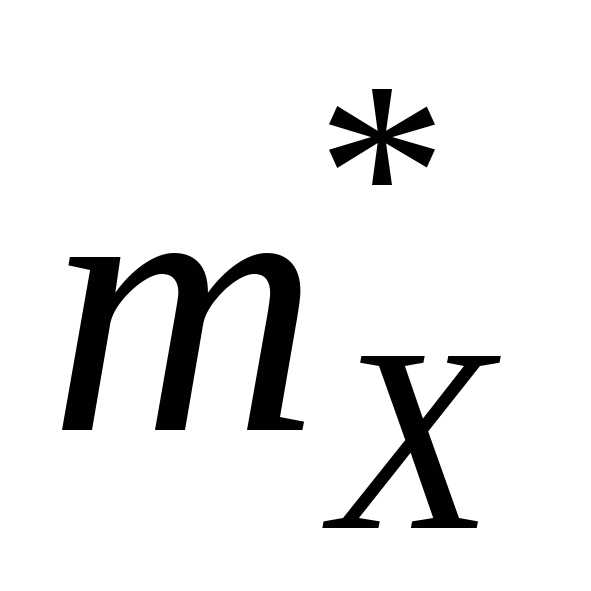 и
и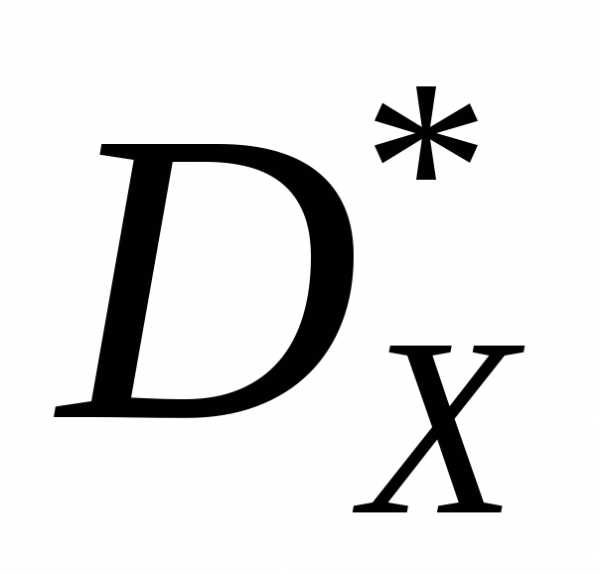 можно считать нормальным прилюбом законе распределения случайной величины
и доверительные
интервалы для математического ожидания
и дисперсии могут быть определены по
следующим формулам.
можно считать нормальным прилюбом законе распределения случайной величины
и доверительные
интервалы для математического ожидания
и дисперсии могут быть определены по
следующим формулам.
Доверительный интервал для математического ожидания имеет вид
(10.8)
где 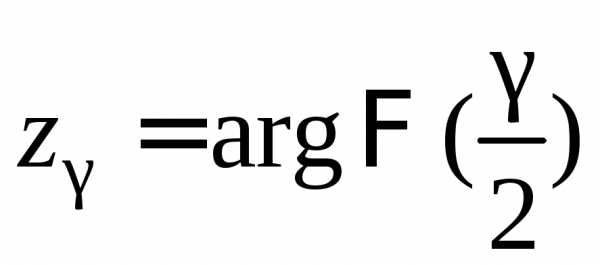 — значение аргумента функции Лапласа,
т.е. Ф(z)
=
— значение аргумента функции Лапласа,
т.е. Ф(z)
= 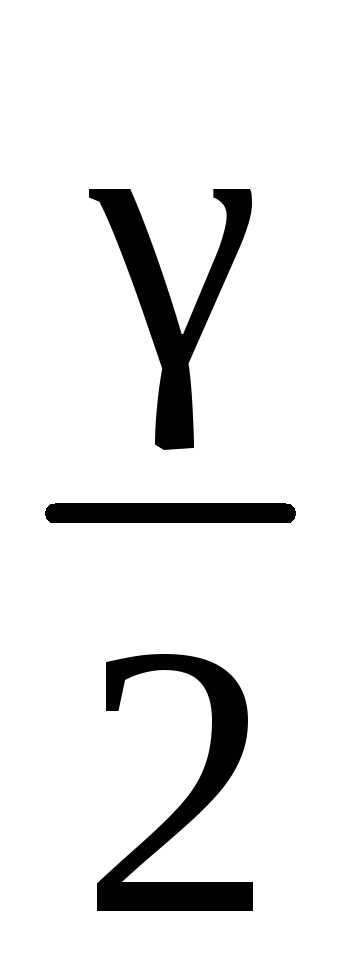 .
.
Доверительный интервал для дисперсии имеет вид
. (10.9)
Проверка статистических гипотез
Статистической
гипотезой называется всякое непротиворечивое
множество утверждений
относительно
свойств распределения случайной
величины. Простейшей гипотезой является
двухальтернативная: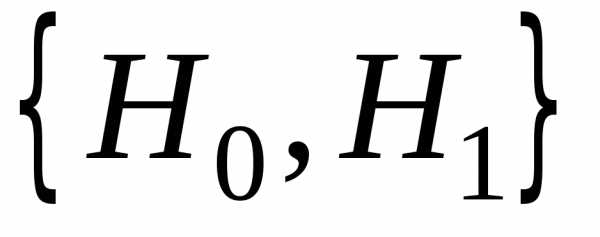 .
В этом случае альтернативуH0 называют нулевой гипотезой, а H1—
конкурирующей гипотезой.
.
В этом случае альтернативуH0 называют нулевой гипотезой, а H1—
конкурирующей гипотезой.
Критерием называется случайная величина
,
гдеxi – значения выборки, которая позволяет
принять или отклонить нулевую гипотезу 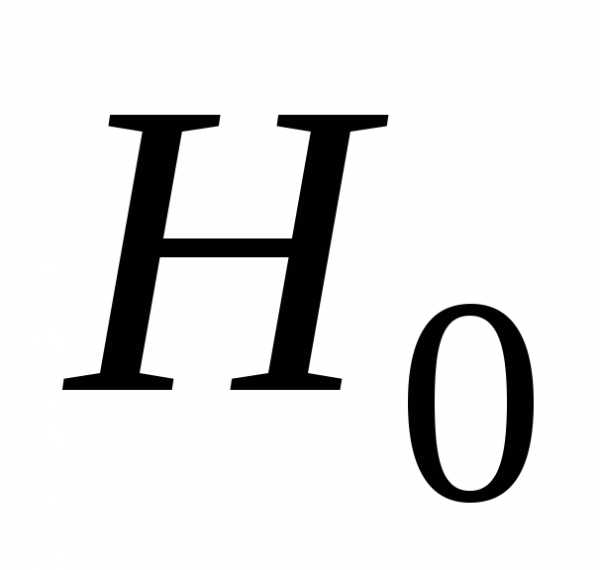 . Ошибка
первого рода состоит в том, что будет отклонена
гипотеза
. Ошибка
первого рода состоит в том, что будет отклонена
гипотеза 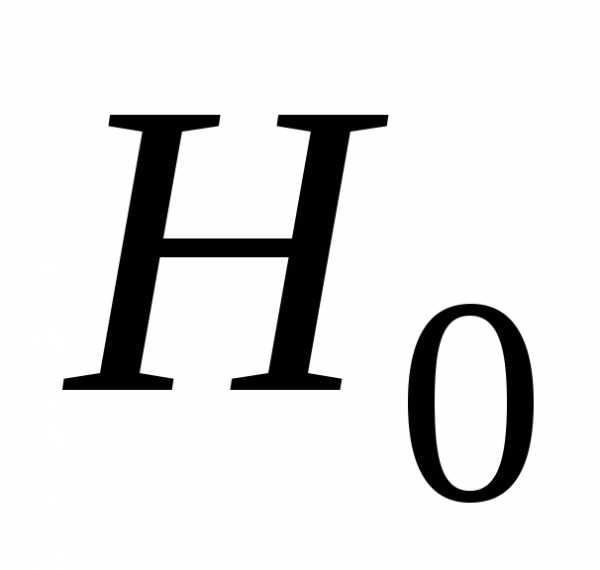 , если она верна («пропуск цели»). Вероятность
совершить ошибку первого рода обозначается
и называется уровнем
значимости.
Наиболее часто на практике принимают,
что
= 0,05 или
= 0,01.
, если она верна («пропуск цели»). Вероятность
совершить ошибку первого рода обозначается
и называется уровнем
значимости.
Наиболее часто на практике принимают,
что
= 0,05 или
= 0,01.
Критериями согласия называются критерии, используемые для проверки гипотез о предполагаемом законе распределения.
Гипотеза о законе распределения выдвигается следующим образом.
1. Построить по вариационному ряду график
эмпирической
функции распределения  и гистограммы по
интервальным статистическим рядам
(равноинтервальному и равновероятностному).
и гистограммы по
интервальным статистическим рядам
(равноинтервальному и равновероятностному).
2. По виду графиков выдвинуть двухальтернативную гипотезу о предполагаемом (гипотетическом) законе распределения:
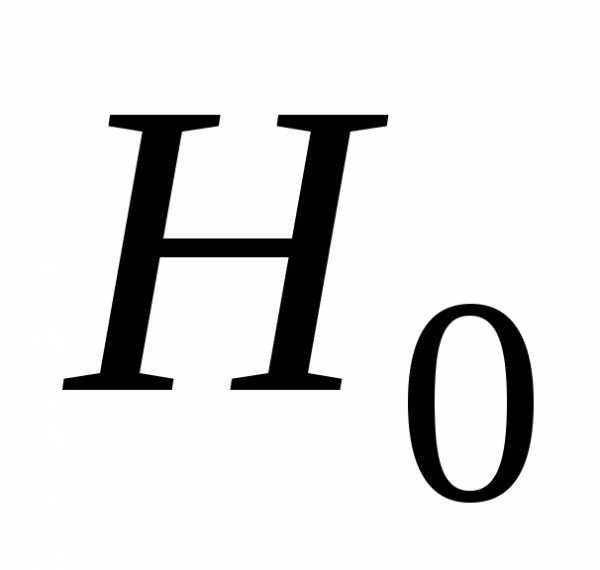 –величина X распределена по такому-то закону:
–величина X распределена по такому-то закону:
 –величина X не распределена по такому-то закону:
–величина X не распределена по такому-то закону:
где – плотность и функция распределения гипотетического закона распределения.
График
эмпирической
функции распределения 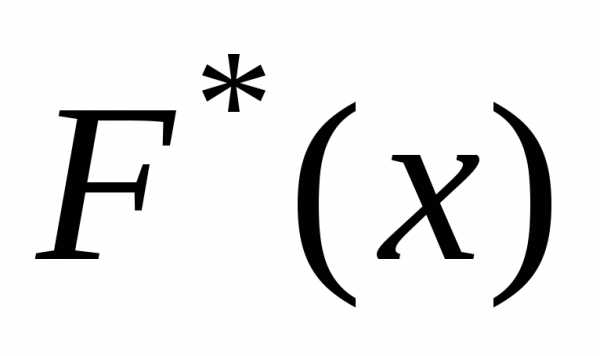 должен быть похож на график функции
распределения
должен быть похож на график функции
распределения  гипотетического закона, а гистограммы
на график плотности гипотетического
распределения
гипотетического закона, а гистограммы
на график плотности гипотетического
распределения 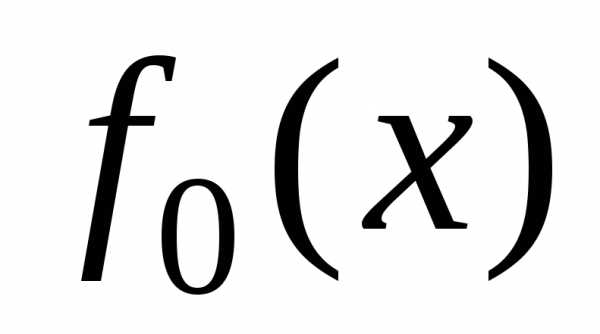 .
Ниже приведены графики и аналитические
выражения плотности и функции распределения
для часто встречающихся на практике
законов.
.
Ниже приведены графики и аналитические
выражения плотности и функции распределения
для часто встречающихся на практике
законов.
Равномерное
распределение имеет непрерывная случайная величина Х,
если ее плотность вероятности в некотором
интервале а;
b] постоянна:
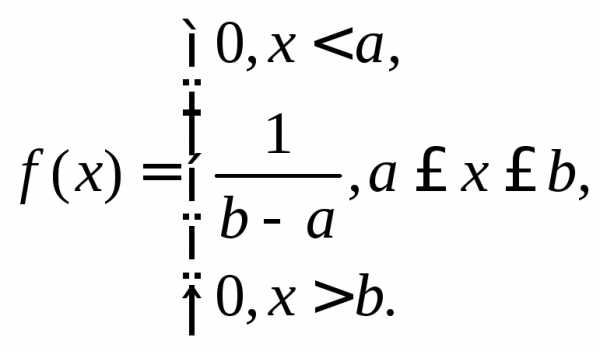
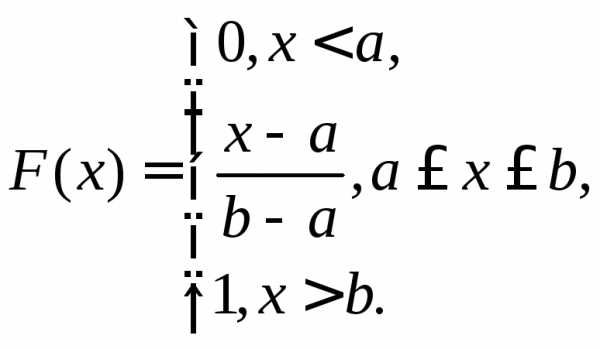 (10.10)
(10.10)
где а, b – параметры распределения (b > a).
Графики плотности и функции равномерного распределения при a = 1 и b = 3 показаны на рис. 10.1:
Рис. 10.1
Экспоненциальное распределение имеет непрерывная случайная величина T, принимающая только положительные значения, если ее плотность вероятности и функция распределения равны:
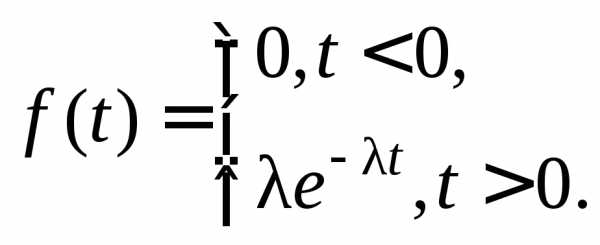
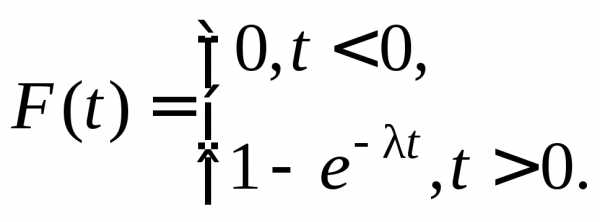 (10.11)
(10.11)
где – параметр распределения ( >0).
Графики плотности и функции экспоненциального распределения при =1 показаны на рис. 10.2:
Рис. 10.2
Нормальное распределение (распределение Гаусса) имеет непрерывная случайная величина Х, если ее плотность вероятности и функция распределения равны:
,, (10.12)
где m, σ – параметры распределения ( σ >0),
 —функция
Лапласа.
—функция
Лапласа.
Графики плотности и функции нормального распределения при m =0, σ =1 показаны на рис. 10.3:
Рис. 10.3
3. Вычислить точечные оценки математического
ожидания 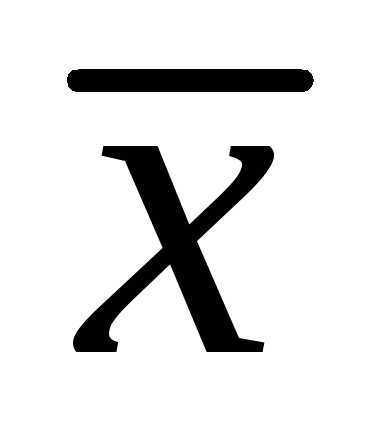 и
дисперсии
и
дисперсии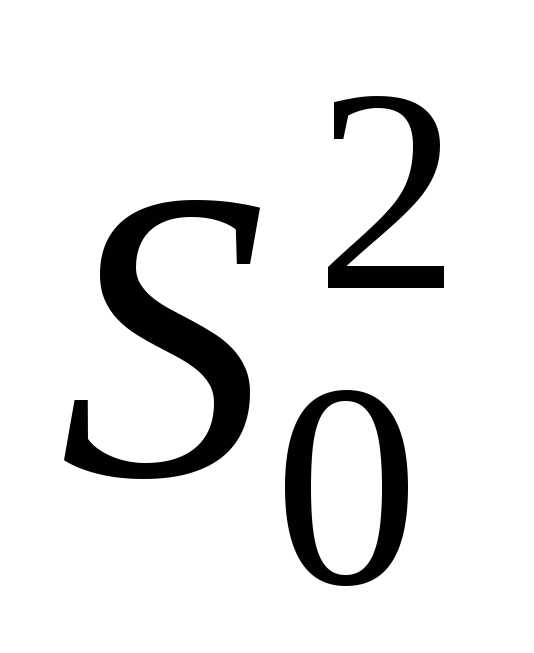 и, используя метод моментов, определить
оценки неизвестных параметров
и, используя метод моментов, определить
оценки неизвестных параметров  гипотетического закона распределения,
где
гипотетического закона распределения,
где – число неизвестных параметров
гипотетического закона распределения.
– число неизвестных параметров
гипотетического закона распределения.
Оценки неизвестных параметров а, b равномерного распределения можно определить по формулам
(10.13)
или
(10.14)
где 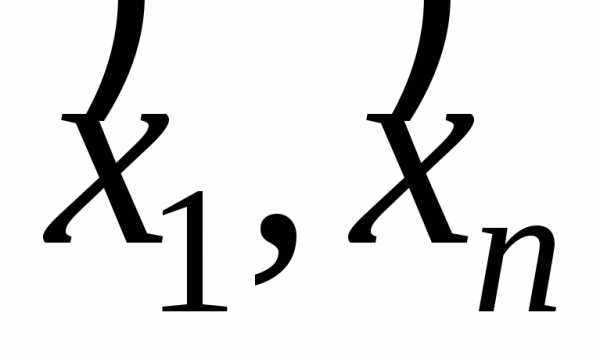 – первое и последнее значение вариационного
ряда соответственно.
– первое и последнее значение вариационного
ряда соответственно.
Оценку неизвестного параметра экспоненциального распределения можно определить по формуле
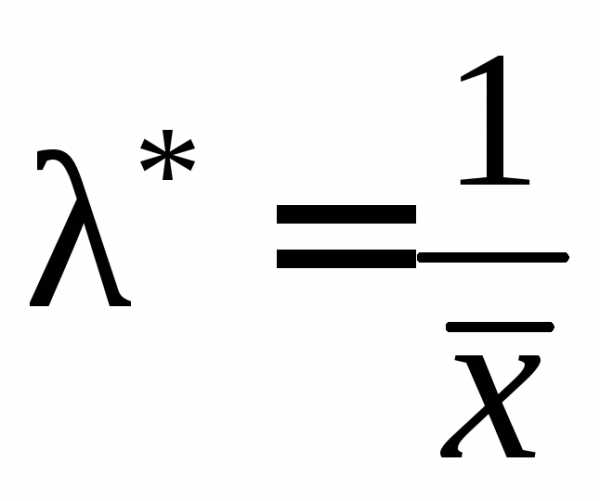 (10.15)
(10.15)
Оценки
неизвестных параметров 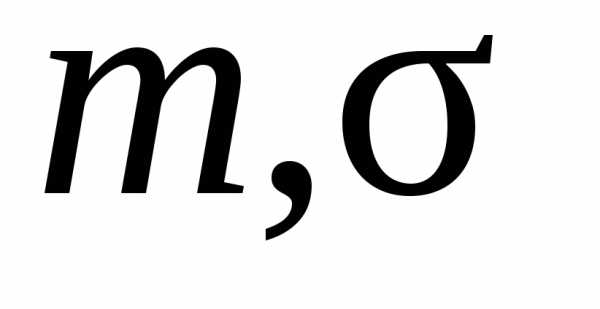 нормального распределения можно определить по
формулам:
нормального распределения можно определить по
формулам:
(10.16)
4. Проверить гипотезу о предполагаемом законе распределения при помощи критерия согласия.
Критерий
согласия Пирсона (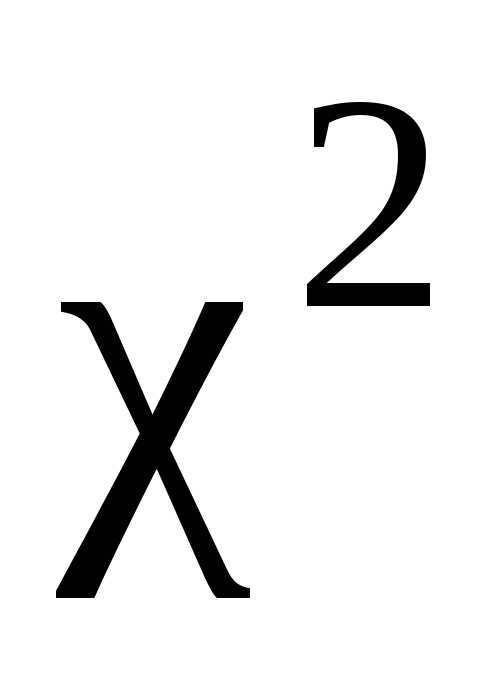 ) – один из наиболее часто применяемых
критериев. Алгоритм проверки гипотезы
о предполагаемом законе распределения
следующий.
) – один из наиболее часто применяемых
критериев. Алгоритм проверки гипотезы
о предполагаемом законе распределения
следующий.
1.
По интервальному
статистическому ряду (равноинтервальному
или равновероятностному) вычислить
значение критерия 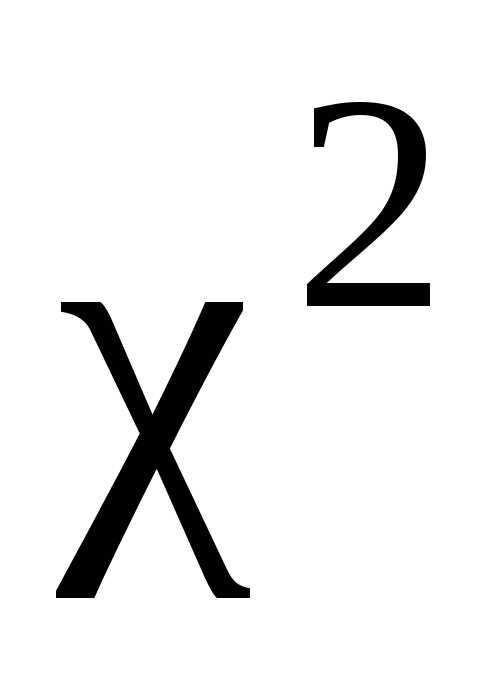 по
формуле:
по
формуле:
, (10.17)
где 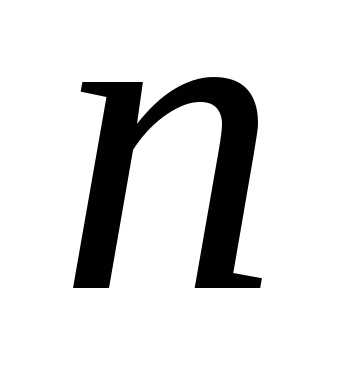 – объем выборки;
– объем выборки;
M – число интервалов интервального статистического ряда;
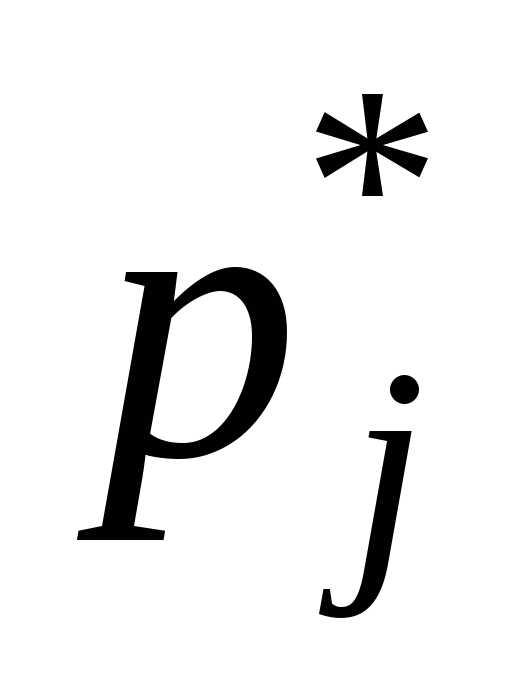 –частота
попадания в j-й
интервал;
–частота
попадания в j-й
интервал;
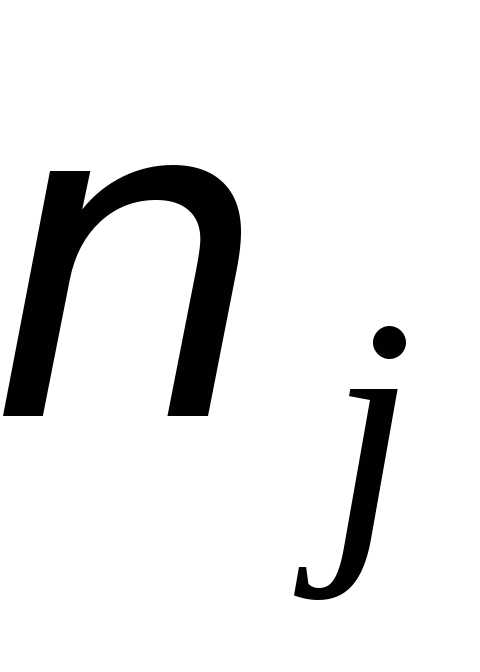 –количество
чисел в выборке, попадающих в j-й
интервал;
–количество
чисел в выборке, попадающих в j-й
интервал;
pj – теоретическая вероятность попадания
случайной величины в j—
й интервал при условии, что гипотеза  верна:
верна:
. (10.18)
где 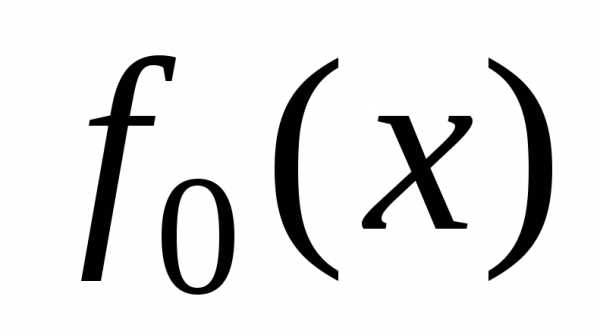 ,
,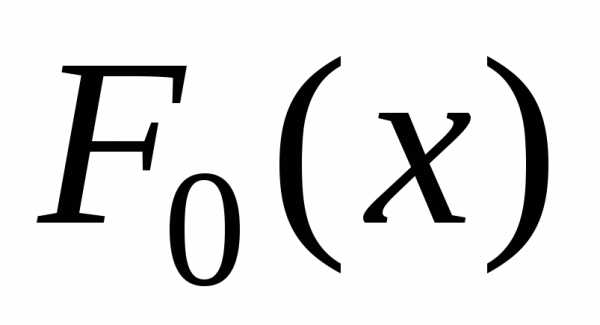 – плотность и функция распределения
гипотетического закона распределения.
– плотность и функция распределения
гипотетического закона распределения.
При расчете p1 и pM в качестве крайних границ первого и последнего интервалов A1,BM следует использовать теоретические границы гипотетического закона распределения.
Если
проверяется гипотеза о равномерном законе
распределения, то 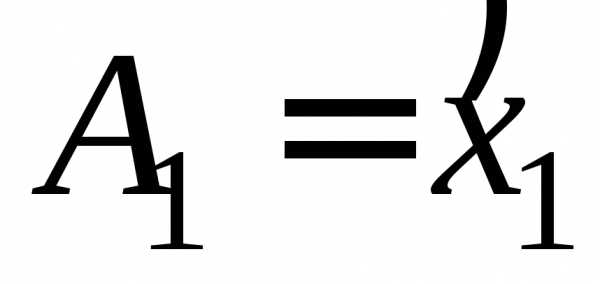 ,
,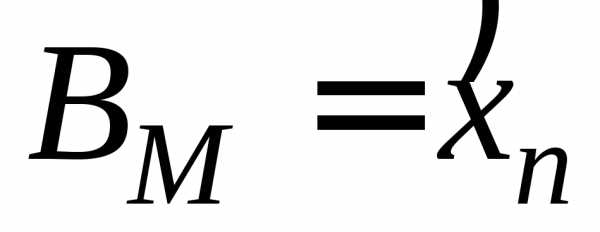 ,
а гипотетическая функция распределения
будет иметь следующий вид (см. (10.10) и
(10.14)):
,
а гипотетическая функция распределения
будет иметь следующий вид (см. (10.10) и
(10.14)):
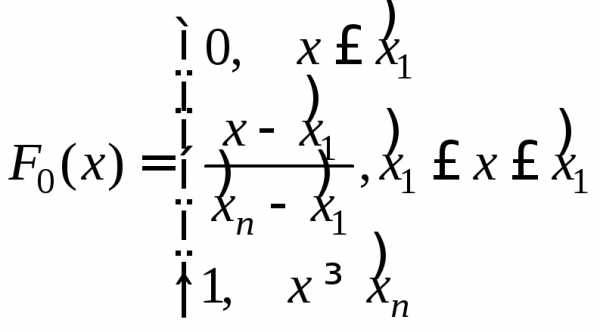 (10.19)
(10.19)
и теоретические вероятности попадания в интервалы будет вычисляться по формуле
(10.20)
Если
проверяется гипотеза об экспоненциальном законе распределения, то 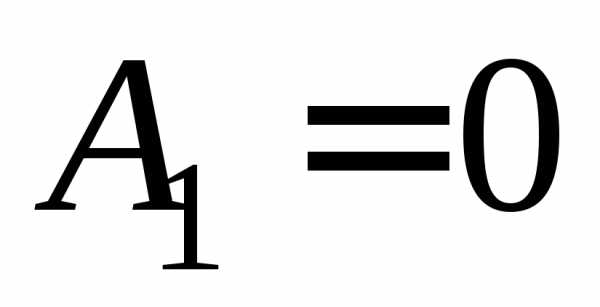 ,
,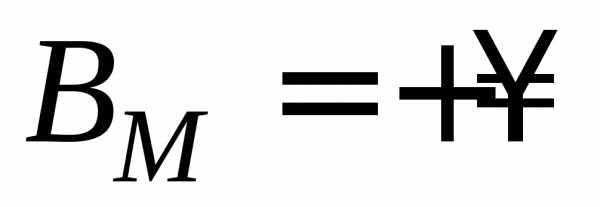 ,
и гипотетическая функция распределения
будет иметь вид (см. (10.11) и (10.15)):
,
и гипотетическая функция распределения
будет иметь вид (см. (10.11) и (10.15)):
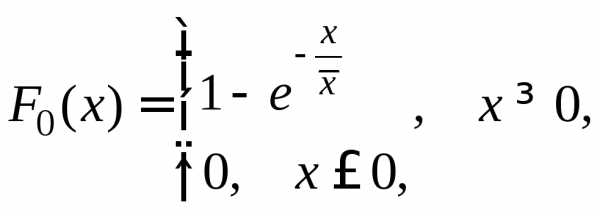 (10.21)
(10.21)
а теоретические вероятности попадания в интервалы будет вычисляться по формуле:
(10.22)
Если
проверяется гипотеза о нормальном законе распределения, то 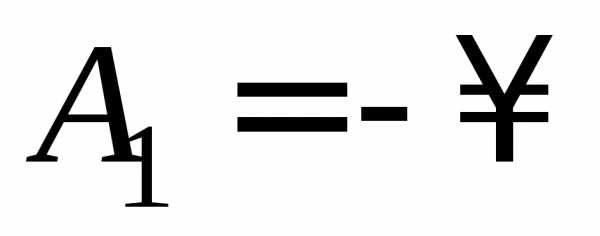 ,
, ,
и гипотетическая функция распределения
будет иметь вид (см. (10.12) и (10.16)):
,
и гипотетическая функция распределения
будет иметь вид (см. (10.12) и (10.16)):
(10.23)
а теоретические вероятности попадания в интервалы будет вычисляться по формулам:
(10.24)
При
правильном вычислении вероятностей  должно выполняется контрольное
соотношение
должно выполняется контрольное
соотношение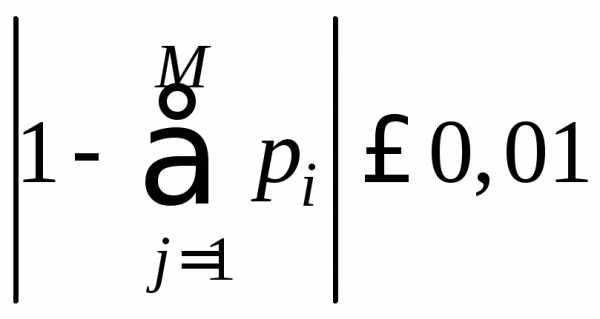 .
.
Величина 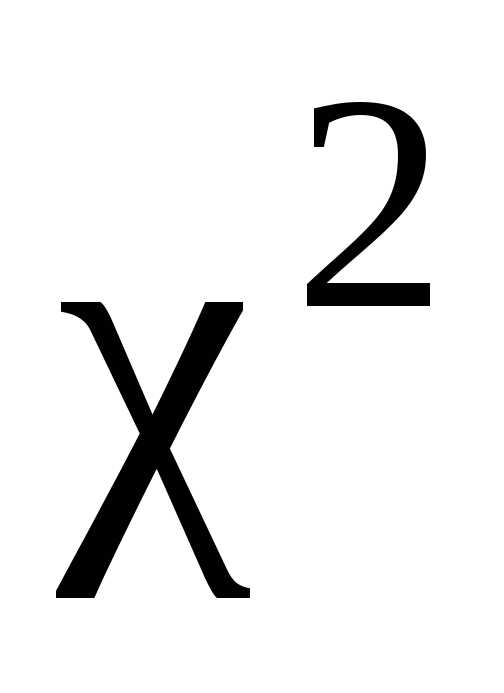 распределена по закону, который называется
распределением
распределена по закону, который называется
распределением .
Данное распределение не зависит от
закона распределения величиныX,
а зависит от параметра k,
который называется числом степеней
свободы.
.
Данное распределение не зависит от
закона распределения величиныX,
а зависит от параметра k,
который называется числом степеней
свободы.
2.
Из таблицы распределения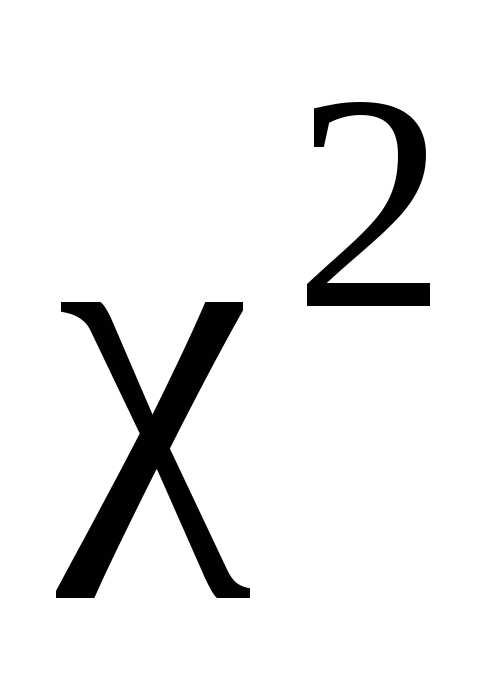 выбирается критическое значение
выбирается критическое значение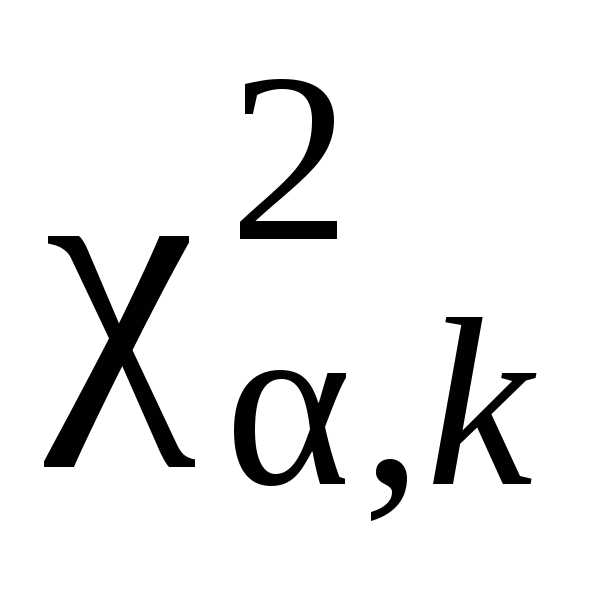 ,
гдеa
— заданный уровень значимости (a
= 0,05 или a =
0,01), а k — число степеней свободы, которое
определяется по формуле:
,
гдеa
— заданный уровень значимости (a
= 0,05 или a =
0,01), а k — число степеней свободы, которое
определяется по формуле:
(10.25)
где M – число слагаемых в формуле (10.17), т.е. число интервалов интервального статистического ряда,
s — число неизвестных параметров
гипотетического закона распределения,
значения (для равномерного закона 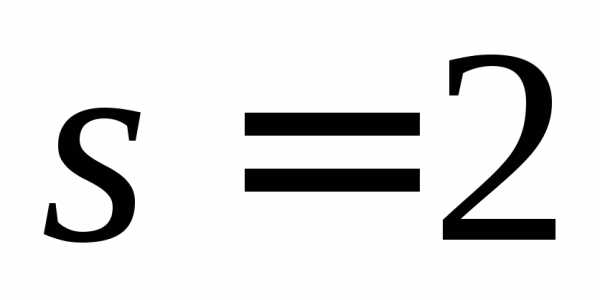 , экспоненциального
, экспоненциального 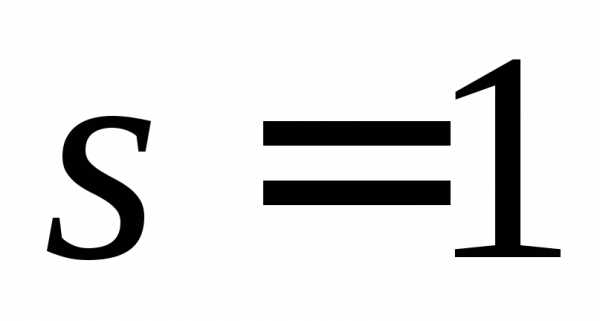 , нормального
, нормального  ).
).
3.
Если значение 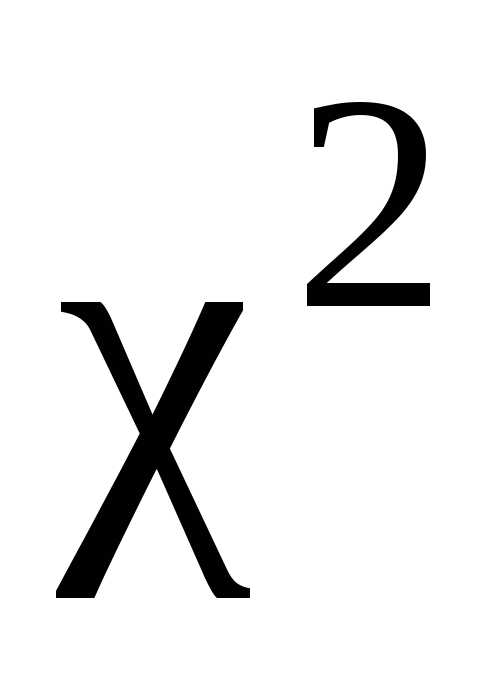 ,
вычисленное по выборочным данным на
шаге 1, больше, чем критическое значение,
т.е.
,
вычисленное по выборочным данным на
шаге 1, больше, чем критическое значение,
т.е. 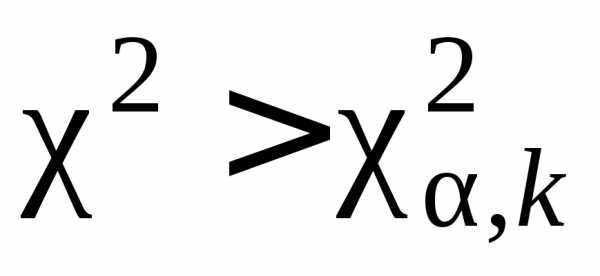 ,
то гипотеза
,
то гипотеза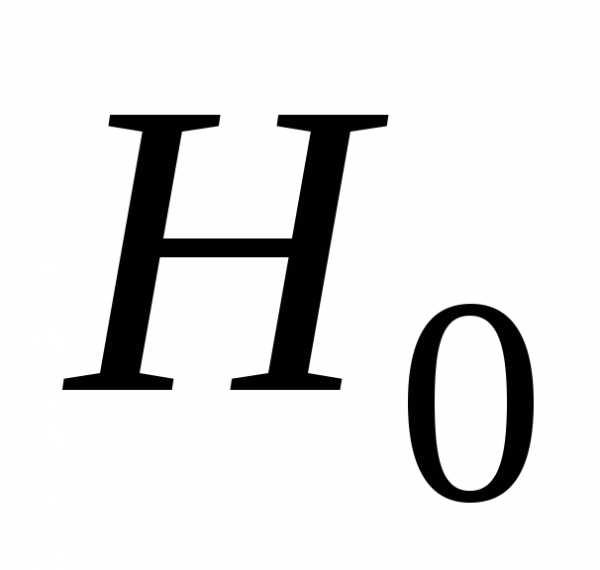 отклоняется, в противном случае нет
оснований ее отклонить.
отклоняется, в противном случае нет
оснований ее отклонить.
Критерий согласия Колмогорова. Алгоритм проверки гипотезы о предполагаемом законе распределения следующий.
1.
На основании эмпирической
функции распределения 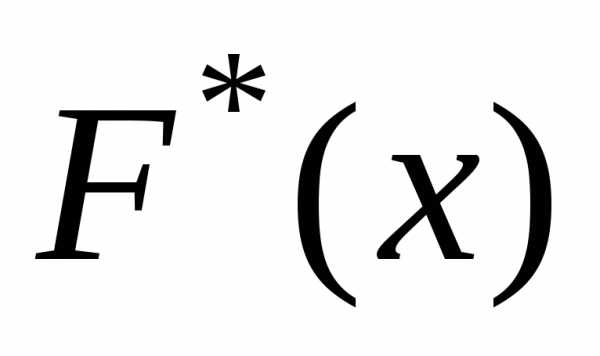 вычислить значение критерия Колмогорова
вычислить значение критерия Колмогорова
(10.26)
где 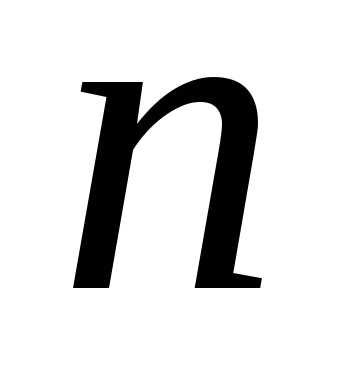 – объем выборки;
– объем выборки;
–максимальный
модуль отклонения
эмпирической
функции распределения 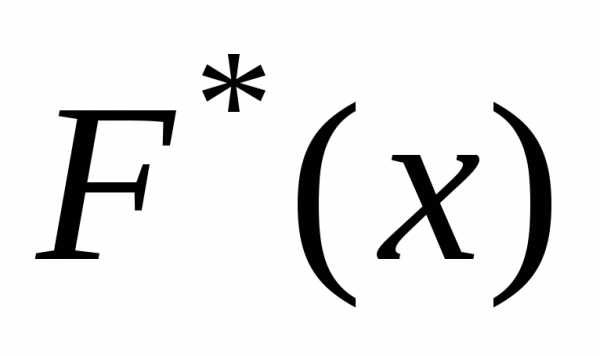 от гипотетической
функции распределения
от гипотетической
функции распределения 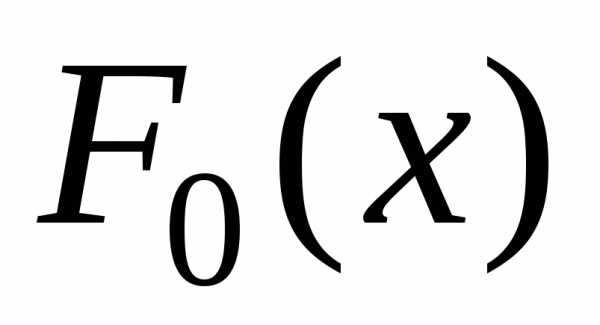 ,
определенный по всем n значения xi исходной выборки.
,
определенный по всем n значения xi исходной выборки.
Значение Z с
достаточной точностью может быть
определено по графикам
функций 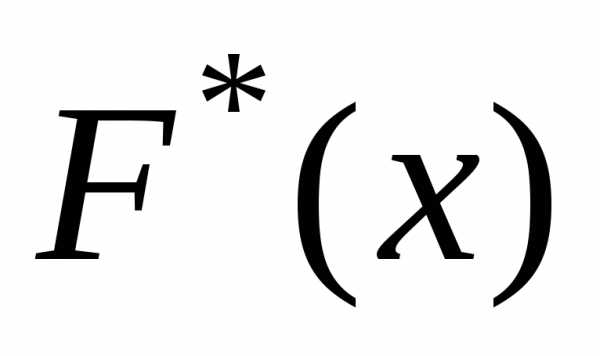 и
и 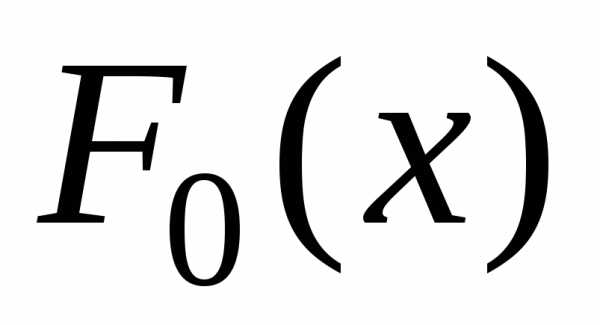 ,
которые
стоят в одной системе координат на
масштабно-координатной бумаге
(«миллиметровке»). Для построения графика
,
которые
стоят в одной системе координат на
масштабно-координатной бумаге
(«миллиметровке»). Для построения графика 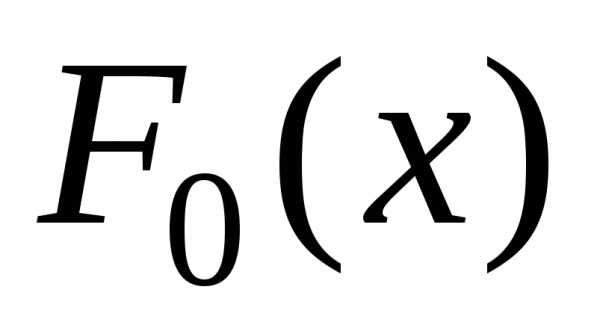 достаточно
рассчитать значения функции
достаточно
рассчитать значения функции 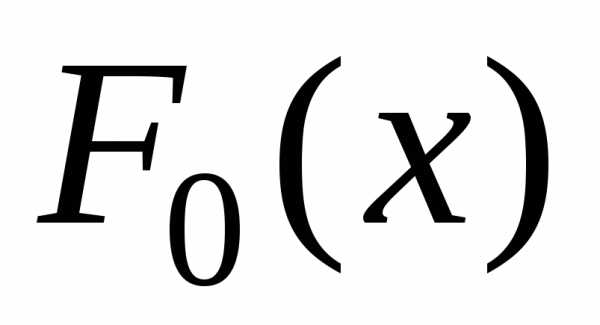 в 10…20 равноотстоящих точках, которые
затем соединить плавной кривой.
в 10…20 равноотстоящих точках, которые
затем соединить плавной кривой.
Величина λ распределена по закону Колмогорова, который не зависит от закона распределения величины X.
2.
Из
таблицы
распределения Колмогорова
выбрать критическое значение 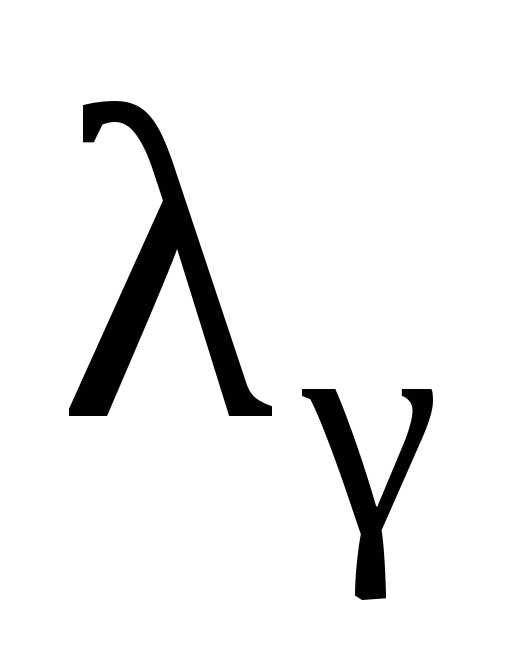 ,
,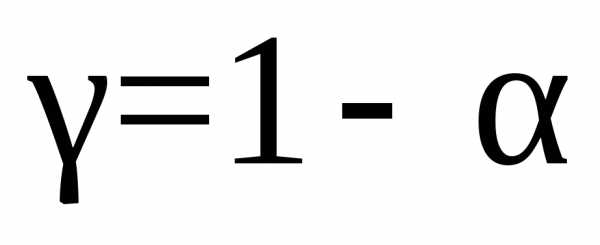 ,
гдеa
— заданный уровень значимости (a
= 0,05 или a =
0,01).
,
гдеa
— заданный уровень значимости (a
= 0,05 или a =
0,01).
3.
Если значение l,
вычисленное на шаге 1, больше, чем
критическое значение, т.е. l> lg , то гипотеза 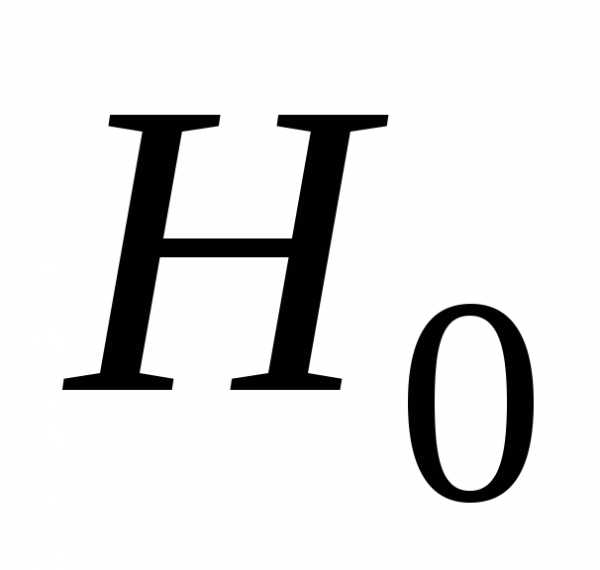 отклоняется, в противном случае нет
оснований ее отклонить.
отклоняется, в противном случае нет
оснований ее отклонить.
studfiles.net
Точечные оценки параметров распределения.
Пусть неизвестен
параметр распределения ,
любая функцияна выборке
,
любая функцияна выборке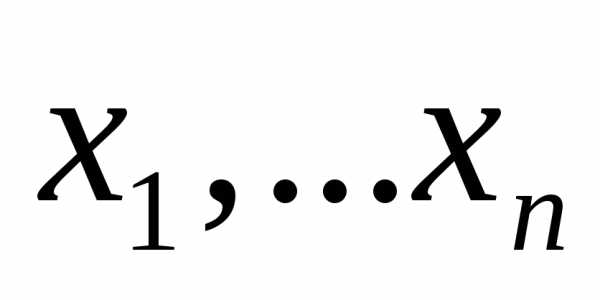 называетсяточечной оценкой
называетсяточечной оценкой  .
Оценки тоже являются случайными
величинами.
.
Оценки тоже являются случайными
величинами.
Требования к оценкам.
Несмещенность

Состоятельность
Эффективность (по сравнению с другими оценками) – если дисперсия оценки меньше дисперсий других оценок.
Можно показать, что несмещенная оценка состоятельна, если ее выборочная дисперсия стремится к нулю при .
Оценки ищут различными методами: методом моментов, методом максимального правдоподобия, методом наименьших квадратов и др.
Оценка среднего
значения ГС (математического ожидания)
– выборочное среднее. 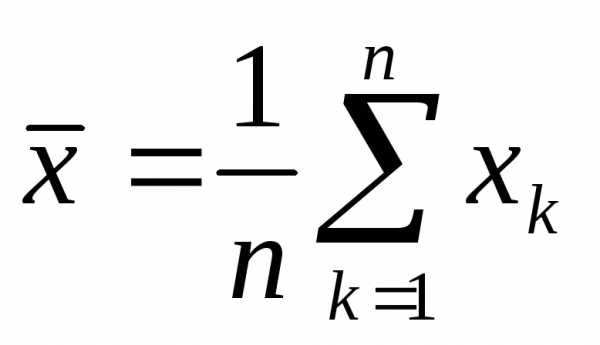 .
.
Оценка несмещенная,т.к..
Оценка состоятельная, т.к. по закону больших чисел.
Оценки дисперсии ГС:
Выборочная дисперсия

Это – смещенная, состоятельная оценка.
2. Несмещенная, состоятельная оценка дисперсии
Можно показать, что .
Пример. Вычислим оценки для приведенного выше ряда распределения
xk
0
1
3
5
nk
5
2
1
2

1/2
1/5
1/10
1/5
,
.
Интервальные оценки.
Доверительный
интервал– это интервал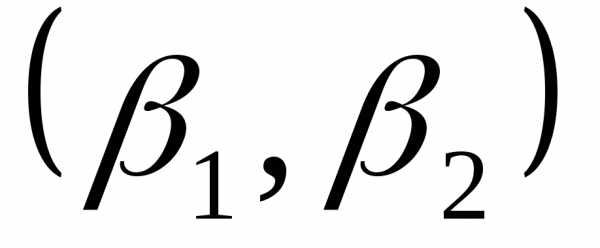 ,
такой, что,
,
такой, что,
где  —доверительная вероятность.
—доверительная вероятность.
Общее правило
построения доверительного интервала
для любого параметра основано на
центральной предельной теореме, по
которой при больших n (n>50)
оценка имеет
нормальное распределение с,
если
имеет
нормальное распределение с,
если — несмещенная оценка, а функция
распределения случайной величины
— несмещенная оценка, а функция
распределения случайной величины сходится по вероятности прик функции стандартного нормального
распределения.
сходится по вероятности прик функции стандартного нормального
распределения.
Квантиль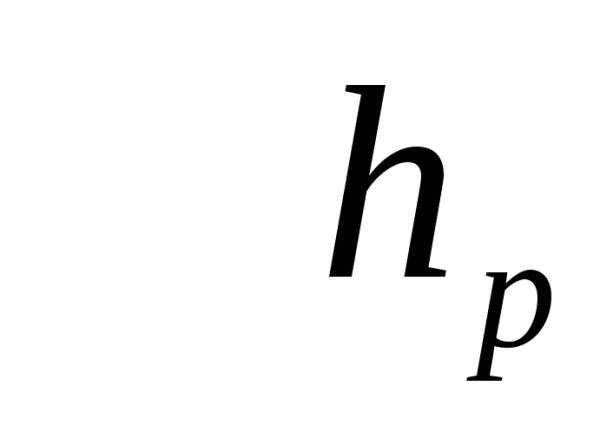 (уровня
(уровня  ) случайной величиныXс функцией распределенияF(x)
– это такое значение
) случайной величиныXс функцией распределенияF(x)
– это такое значение 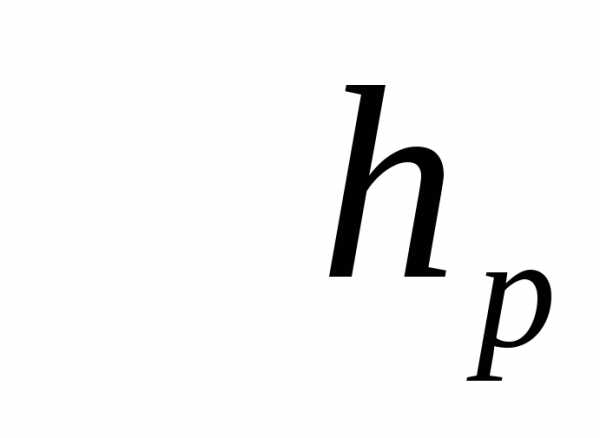 случайной величиныX, что
случайной величиныX, что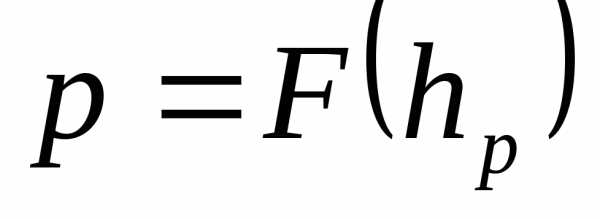 .
.
стандартного
нормального распределения. По симметрии
плотности нормального распределения 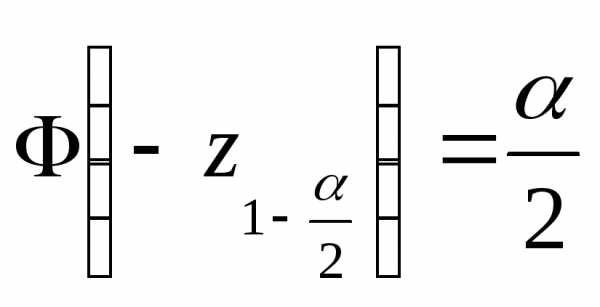 .
Так как.
.
Так как.
Так как
распределение случайной величины 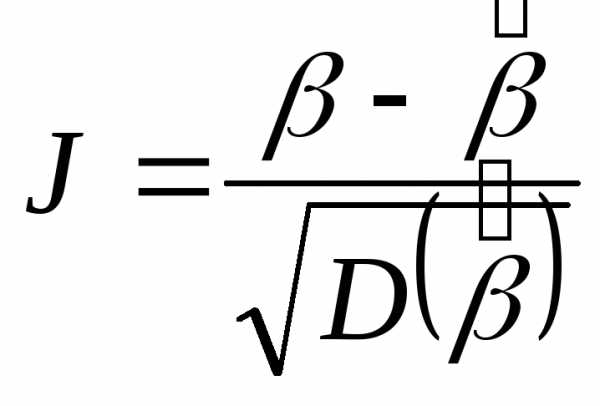 стремится к стандартному нормальному
распределению, то.
Отсюда получаемдоверительный интервал
стремится к стандартному нормальному
распределению, то.
Отсюда получаемдоверительный интервал
.
Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
Если ГС имеет нормальное распределение, то и любая выборка распределена нормально. Известно, что сумма нормальных случайных величин тоже распределена нормально. Поэтому оценка математического ожидания – выборочное среднее – нормально распределенная случайная величина с — известно.
Поэтому, если
 известно, то
известно, то ,
идоверительный интервал дляматематического ожиданиястроится
так:
,
идоверительный интервал дляматематического ожиданиястроится
так:
с доверительной вероятностью .
Квантили проще всего искать по таблицам
квантилей нормального распределения.
.
Квантили проще всего искать по таблицам
квантилей нормального распределения.
Если
 неизвестно,то нормированная случайная величина
неизвестно,то нормированная случайная величина (вместо
(вместо подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности
подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности определяют
определяют ,
по таблице квантилей определяют квантиль
,
по таблице квантилей определяют квантиль уровня
уровня .
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
.
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
Если n> 20, то квантиль можно искать по таблицам квантилей нормального распределения.
studfiles.net

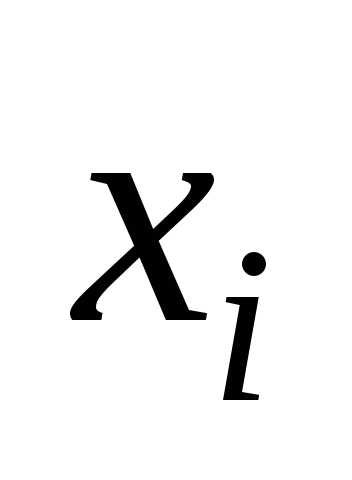
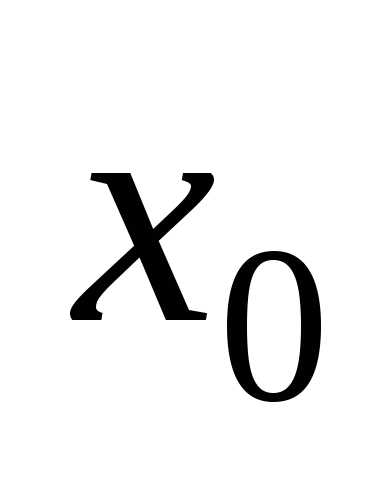
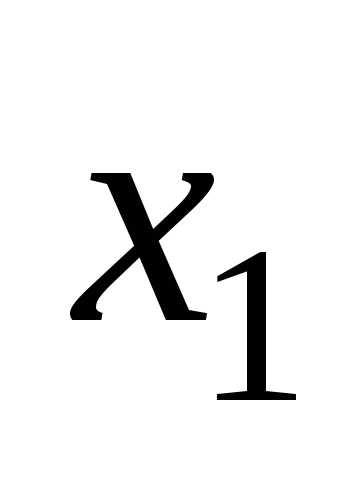
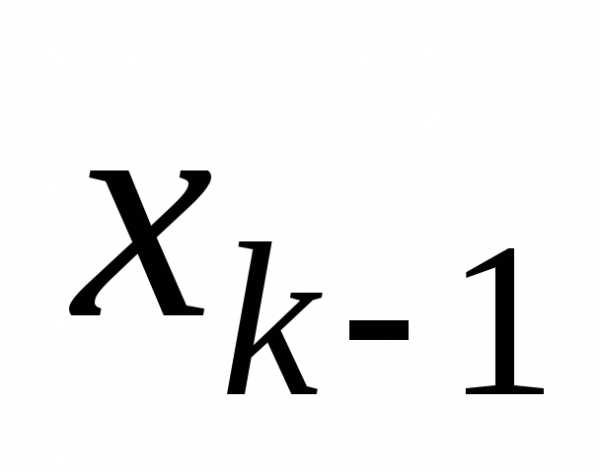
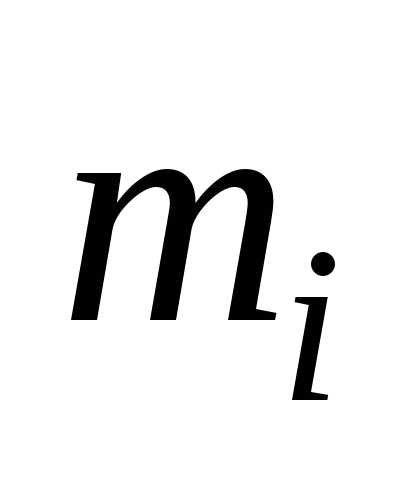
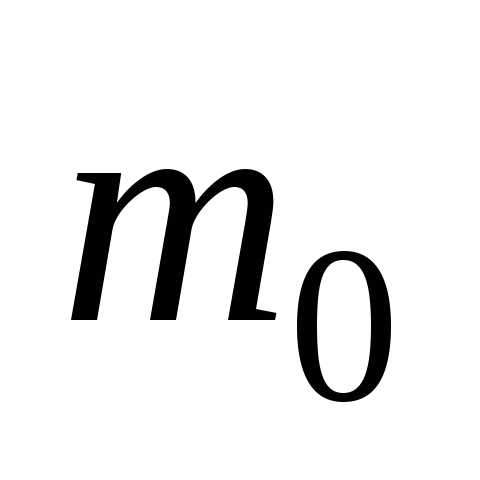
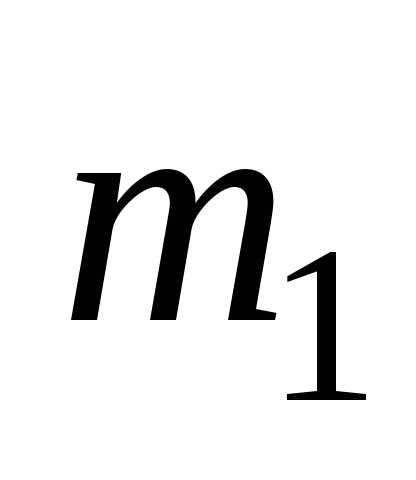
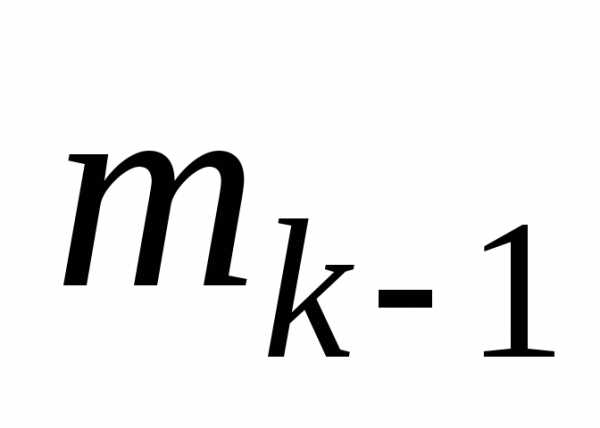
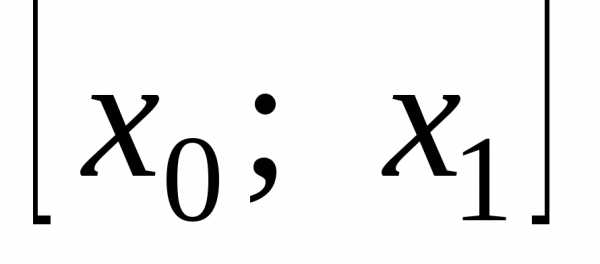
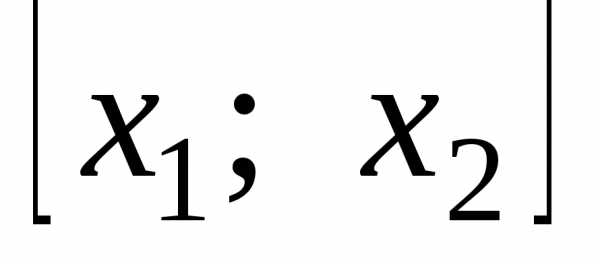

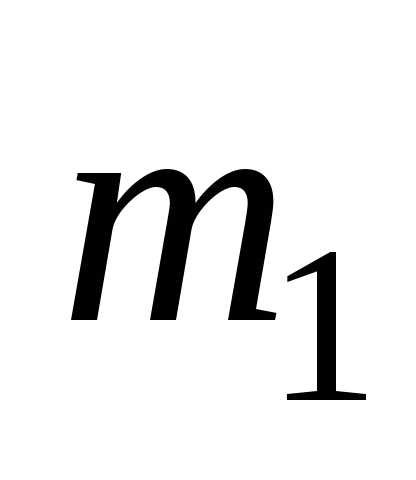
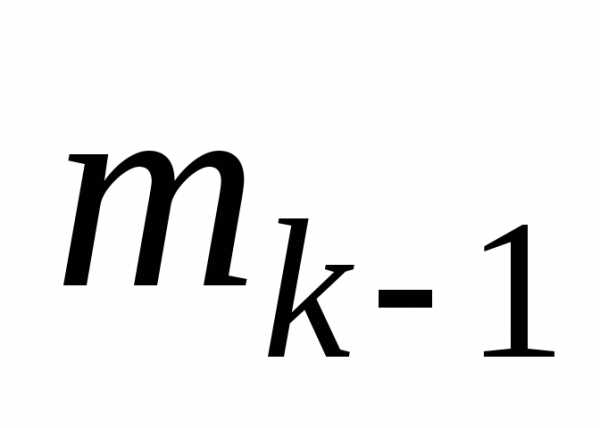
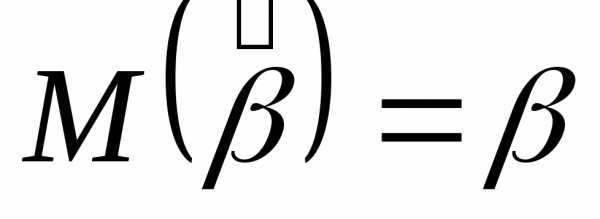
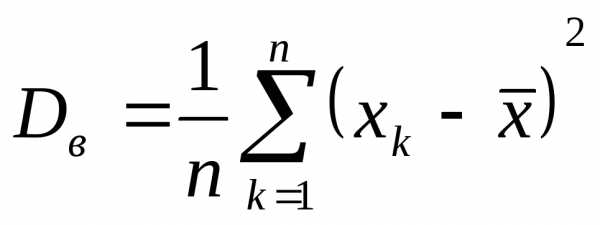

 известно, то
известно, то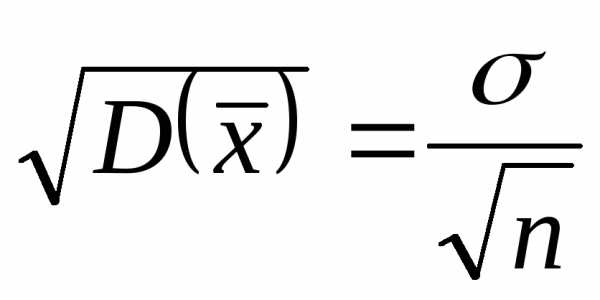 ,
идоверительный интервал дляматематического ожиданиястроится
так:
,
идоверительный интервал дляматематического ожиданиястроится
так: неизвестно,то нормированная случайная величина
неизвестно,то нормированная случайная величина (вместо
(вместо подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности
подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности определяют
определяют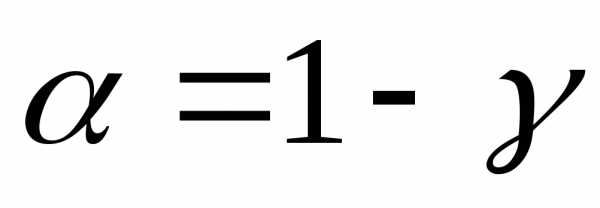 ,
по таблице квантилей определяют квантиль
,
по таблице квантилей определяют квантиль уровня
уровня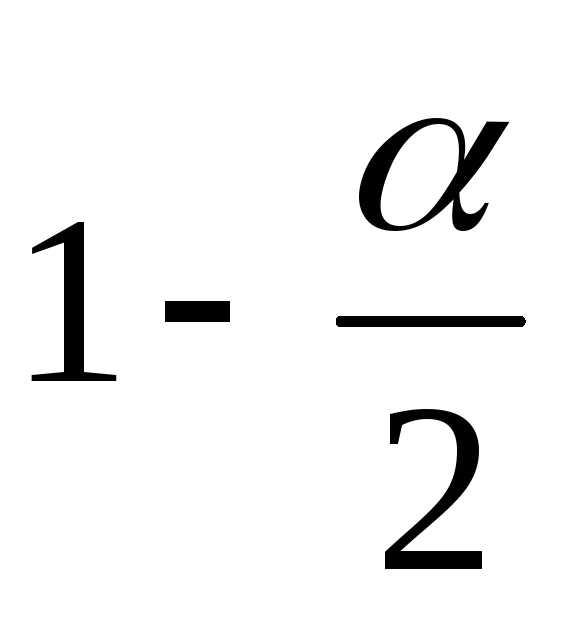 .
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
.
Затем по той же схеме строятдоверительный
интервал для математического ожидания .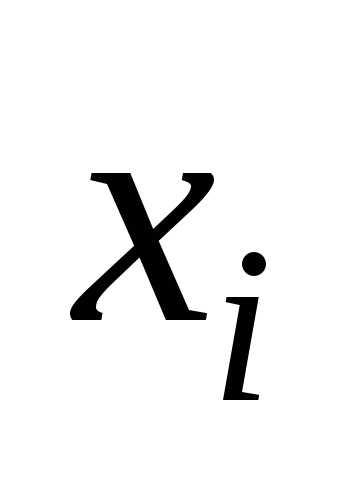

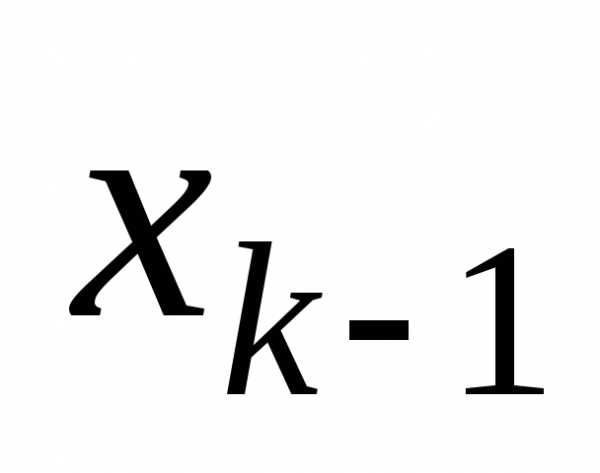
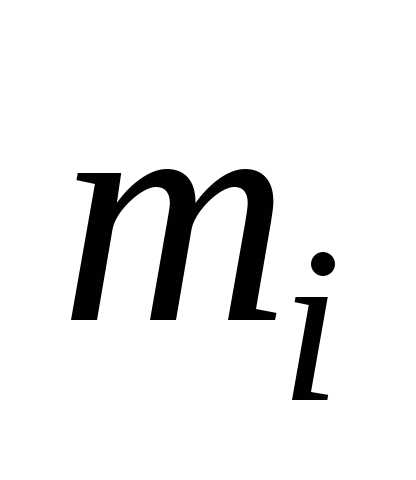

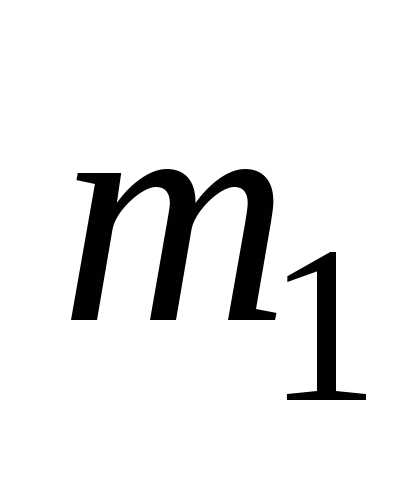
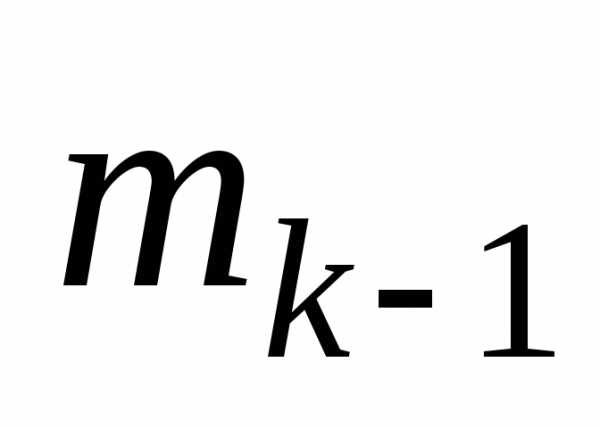
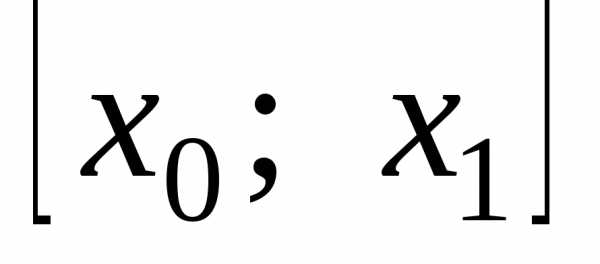
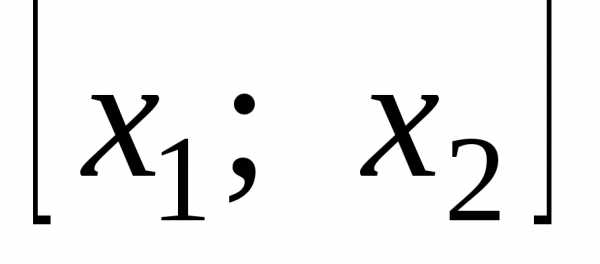
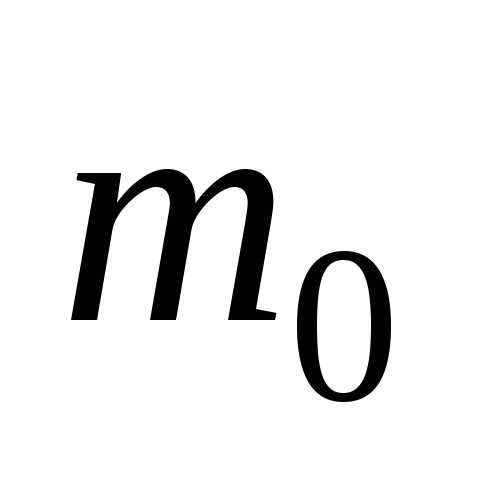

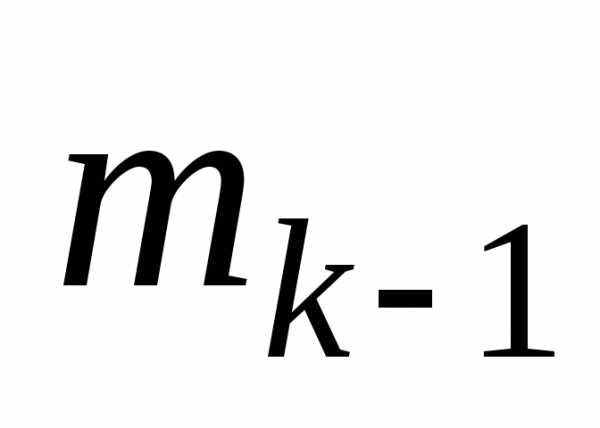
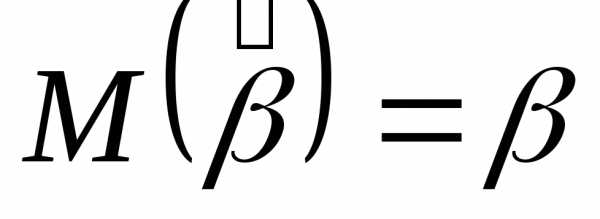
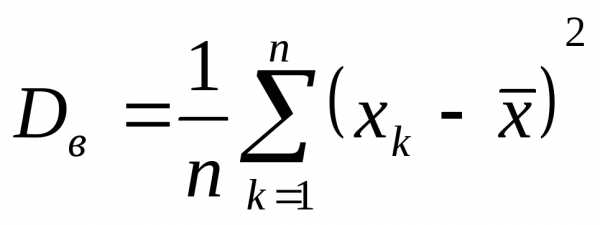
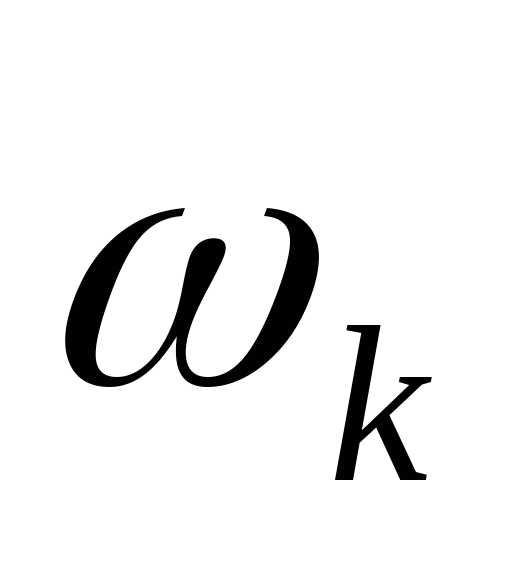
 известно, то
известно, то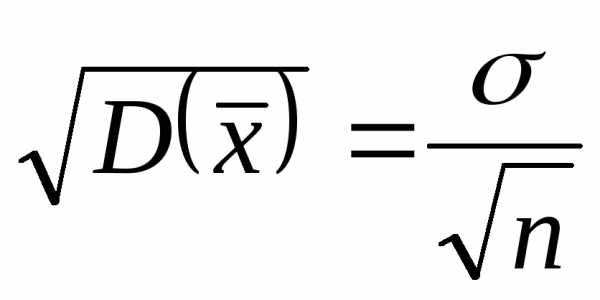 ,
идоверительный интервал дляматематического ожиданиястроится
так:
,
идоверительный интервал дляматематического ожиданиястроится
так: неизвестно,то нормированная случайная величина
неизвестно,то нормированная случайная величина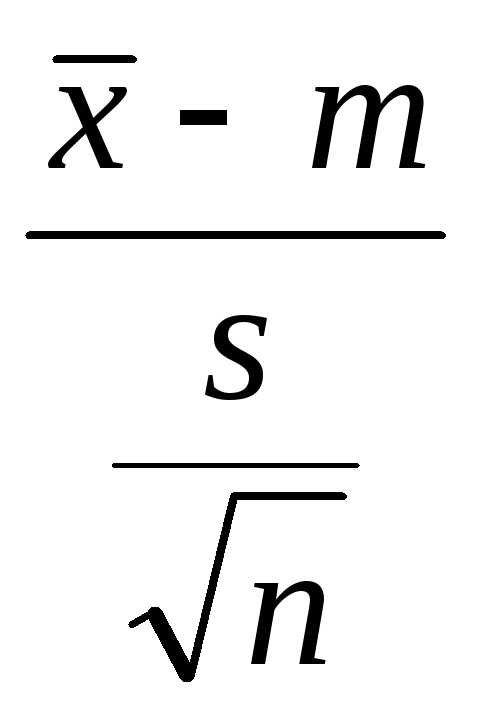 (вместо
(вместо подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности
подставлена его оценкаs)
уже не распределена нормально.Она
имеет распределение Стъюдента с n-1 степенями свободы. Есть таблицы
квантилей распределения Стъюдента. По
доверительной вероятности определяют
определяют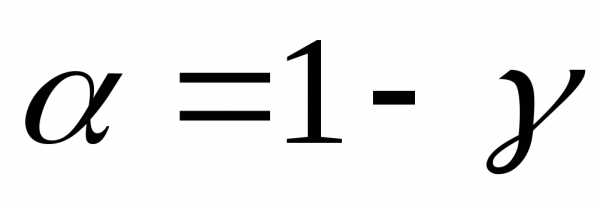 ,
по таблице квантилей определяют квантиль
,
по таблице квантилей определяют квантиль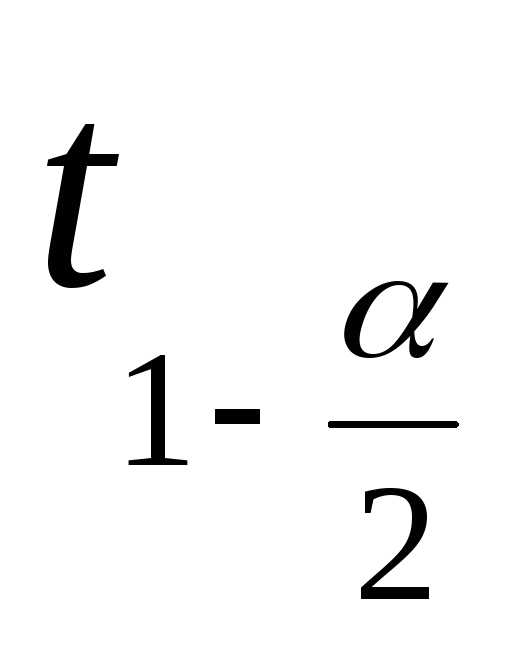 уровня
уровня .
Затем по той же схеме строятдоверительный
интервал для математического ожидания .
.
Затем по той же схеме строятдоверительный
интервал для математического ожидания .