Свойства квадратичной функции
Здесь рассматриваются свойства квадратичной функции вида ,график квадратичной функции и решаются задачи на чтение графиков и задачи с параметром.
Напоминание
Определение. Квадратичной функцией называется функция вида
, где .
График – парабола (см. Рис. 1) с вершиной в точке , где.
Рис. 1. График функции , где
. Функция непрерывна на всей .
Свойства функции
в случае .
Пусть .
Свойства:
1. ;
2. ;
3. убывает при;возрастает при;
4. — не существует;
5. Непрерывна;
6. Выпукла вниз.
Свойства функции
в случае .
Пусть .
Свойства (см. Рис. 2):
1. ;
2. ;
3. возрастает при;убывает при;
4. — не существует;
5. Непрерывна;
6. Выпукла вверх.
Задача 1 на нахождение пределов изменения конкретной квадратичной функции
Найдите пределы изменения функции, прочитайте график.
а.
Ответ: ;убывает при;возрастает при.
| |
| б. |
Ответ: ;убывает при;возрастает при.
Задача 2 на нахождение пределов изменения конкретной квадратичной функции
Найдите пределы изменения функции, прочитайте график.
| |
|
| а. |
Ответ: ;возрастает при;убывает при.
б.
Ответ: ;возрастает при;убывает при.
Задача 1 с параметром
Найдите число корней уравнения с параметром, где,.
Ответ (см. Рис. 3):
Рис. 3. График функции , рассеченный прямыми, гдеи.
1. Корней нет при ;
2. Уравнение имеет
— один корень при ;
— два корня при .
Задача 2 с параметром
Найдите все значения параметра , при каждом из которых уравнение, где,, имеет хотя бы один корень (см. Рис. 4).
Ответ: .
Задача на построение и чтение графика функции
Постройте и прочитайте график функции
,
Ответ: (см. Рис. 5)
Рис. 5. График функции
1. Возрастает при ;
2. Убывает при .
Задача 3 с параметром
Найдите число корней уравнения , где.
Ответ: уравнение имеет (см. Рис. 6)
Рис. 6. График функции ,
рассеченный прямыми , гдеи.
1. Один корень при ;
2. Два корня при ;
3. Три корня при .
Задачи на степенные функции
Здесь вспомним свойства степенных функций с целым отрицательным показателем и используем их при решении задач на степенную функцию.
Напоминание: график и свойства функции
Функция
Основные свойства:
1.
2.
3. Функция четная.
4. Две характерные фиксированные точки для всех кривых:
5. Асимптоты: прямые
6. Если тоy возрастает,
Если тоy убывает,
Напоминание: график и свойства функции
Функция
Основные свойства:
1.
2.
3. Функция нечетная.
4. Две фиксированные характерные точки для всех кривых:
5. Асимптоты: прямые
6. Если тоy убывает,
Если тоy убывает,
Решение задач
Рассмотрим типовые задачи:
1. Какая из точек – А или В – принадлежит графику функции если
Решение:
т. А:
т. А принадлежит графику.
т. В:
т. В не принадлежит графику.
Ответ: т. А.
2. Какая из точек А, В, С принадлежит графику функции если
Решение:
т. А:
т. В:
т. С:
Ответ: т. В принадлежит графику.
3. Постройте график функции и прочтите его.
Решение:
Построим график функции (Рис. 5). Его асимптоты – прямыеи.
Чтобы получить график функции необходимо графиксдвинуть на 1 вверх по осиyи на 1 единицу влево по оси x
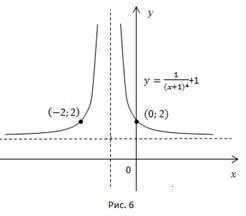
Асимптоты полученного графика – прямые и, характерные точки
Если тоy возрастает,
Если тоy убывает,
4. Найдите все значения параметра m, при каждом из которых уравнение
имеет хотя бы одно решение.
Решение:
Нам необходимо построить график функции , пересечь его семейством прямых, найти точки пересечения и записать ответ (Рис. 7).
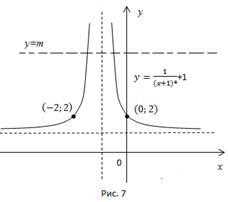
Ответ:
5. Найти все значения параметра m, при каждом из которых уравнение
1. Не имеет решений.
2. Имеет только отрицательные решения.
3. Имеет два корня разных знаков.
Решение:
Ответ:
1.
2.
3.
6. Постройте график функции и прочитайте его.
Решение:
Построим график функции (Рис. 8).
Теперь чтобы получить график функции сдвинем кривуюна 2 вправо вдоль осиx, и на 3 вверх по осиy (Рис. 9).
Прямые иявляются асимптотами.
Характерные точки –
Если тоy убывает,
Если тоy убывает,
7. Найти все значения параметра m, при каждом из которых уравнение
имеет решения
1. На луче
2. На луче
Решение:
Изобразим график функции и пересечем его семейством прямых(Рис. 10).
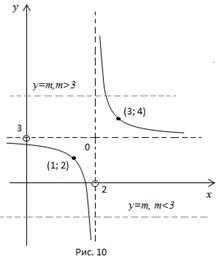
Ответ:
1.
2.
8. Решите графически неравенство
Решение:
Построим в одной системе координат график функции и график функции(Рис. 11).
Графики пересекаются в точке
Чтобы выполнялось неравенство криваядолжна располагаться выше прямой
Ответ:
9. Даны две функции, и, где
Докажите, что
Доказательство:
Тождество доказано.
studfiles.net
Определение и основные свойства квадратичной функции
Функция вида называется квадратичной функцией.Квадратичную функцию можно представить в виде
Областью определения этой функции является множество всех действительных чисел.
Область значений лежит в промежутке , если a > 0, и в промежутке , если a < 0.
Графиком квадратичной функции является парабола. Вершина параболы находится в точке
Парабола симметрична относительно прямой . Ветви параболы направлены вверх, если a > 0.
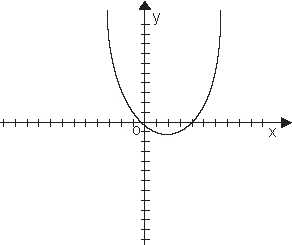
Ветви параболы направлены вниз, если a < 0.

Парабола пересекает ось ОХ в точках x1 и x2 , где x1 и x2 — корни квадратного уравнения .
Если квадратное уравнение не имеет корней (дискриминант отрицательный), то парабола лежит выше или ниже оси ОХ, (если a < 0, то ниже; если a > 0, то выше).

Пример: Построить график функции .
Графиком функции является парабола. Ветви параболы направлены вверх. Вершина параболы находится в точке . Осью симметрии параболы будет прямая . Парабола пересекает ось ОХ в точках .
Для точности построения, построим таблицу:
Строим график:
Квадратичная функция (парабола) [wiki.eduVdom.com]
Квадратичная функция — это функция, заданная формулой вида $у = ах^2 + bх + с$, где х — аргумент, $a, b, c \in \mathbb{R} , a \neq 0$.
Рассмотрим функцию, заданную формулой $у = ах^2 (a\neq 0)$.
Свойства функции $y = ах^2$:
Если x=0, то y=0, то есть график функции проходит через начало координат.
Если x\neq 0, то у>0 при а>0 и у<0 при а<0.
График функции симметричен относительно оси y.
При а>0 функция убывает на промежутке $(-\infty;\; 0]$ и возрастает на промежутке $[0;\; +\infty)$; при a<0 функция возрастает на промежутке $(-\infty;\;0]$ и убывает на промежутке $[0;\; +\infty)$.
При $а>0\,y_{мин} = 0\text{ , при }а<0\,y_{макс} = 0$.
График функции $у = ах^2 + n$ получается из графика функции $у = ах^2$ параллельным переносом вдоль оси y на n единиц вверх при n>0 или на (-n) единиц вниз, если n<0.
График функции $y = a(x-m)^2$ получается из графика функции $у = ах^2$ параллельным переносом вдоль оси x на m единиц вправо при m>0 или на (-m) единиц влево, если m<0.
Вершина параболы — это точка пересечения параболы с её осью симметрии.
Вершина параболы $y = ax^2 + bx + c$ имеет координаты $(-\frac{b}{2a}\;;\;\frac{b^2-4ac}{4a})$.
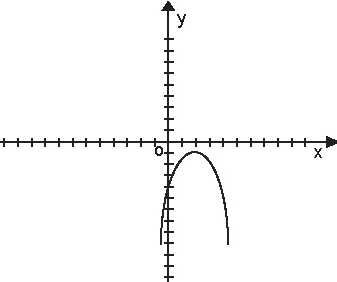
Пример 1. На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера.
Функция убывает на промежутке [1; +∞) .
Наименьшее значение функции равно −4 .
f(−2) < f(3) .
Видео-решение.
subjects/mathematics/квадратичная_функция.txt · Последние изменения: 2013/04/26 16:56 — ¶
www.wiki.eduvdom.com
Квадратичная функция: ее график и свойства
Функция вида y =a*x^2+b*x+c, где a,b,c – некоторые вещественные числа, причем а отлично от нуля, а x,y – переменные, называется квадратичной функцией. Графиком квадратичной функции y =a*x^2+b*x+c является линия, называемая в математике параболой. Общий вид параболы представлен на рисунке ниже.
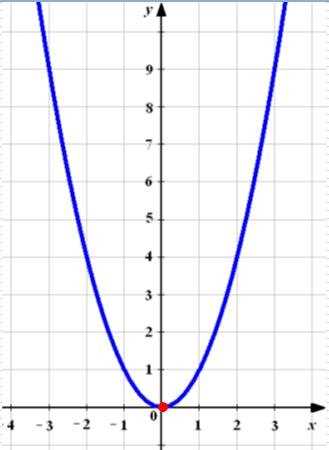
Стоит отметить, что если у функции коэффициент а>0, то парабола направлена ветвями вверх, а если аГрафик квадратичной функции симметричен относительно оси симметрии. Осью симметрии параболы служит прямая проведенная через точку x=(-b)/(2*a), параллельно оси Оу.
Координатами вершины параболы определяются по следующим формулам:
x0=(-b)/(2*a) y0=y(x0)=(4*a*c-b^2)/4*a.
На рисунке ниже представлен график произвольной квадратичной функции. Построение графика квадратичной функции. Также на рисунке отмечены вершина параболы и ось симметрии.
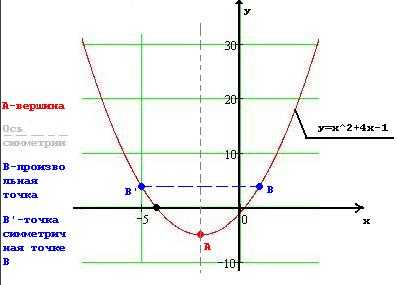
В зависимости от значения коэффициента а, вершина параболы будет являться минимальным или максимальным значением квадратичной функции. При a>0, вершина является минимальным значение квадратичной функции, при этом максимального значения не существует. При аОсь симметрии проходит через вершину параболы. Областью определения квадратичной функции является все множество вещественных чисел R.
Квадратичную функцию y =a*x^2+b*x+c всегда можно преобразовать к виду y=a*(x+k)^2+p, где k=b/(2*a), p=(4*a*c-b^2)/(4*a). Для этого необходимо выделить полный квадрат.
Обратите внимание, что точка с координатами (-k;p) будет являться вершиной параболы. График квадратичной функции y=a*(x+k)^2+p можно получить из графика функции y=a*x^2 с помощью параллельного переноса.
Нужна помощь в учебе?
Предыдущая тема: Разложение квадратного трехчлена на множители: теорема и формулы
Следующая тема:   Графики функции: от чего зависит вид графика функции
Все неприличные комментарии будут удаляться.
www.nado5.ru
