Таблица функции производные – Полная таблица производных для студентов

Производные математических функций. Определение, таблица основных производных, правила их вычисления

Справочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.

Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть

Таблица производных основных математических функций:

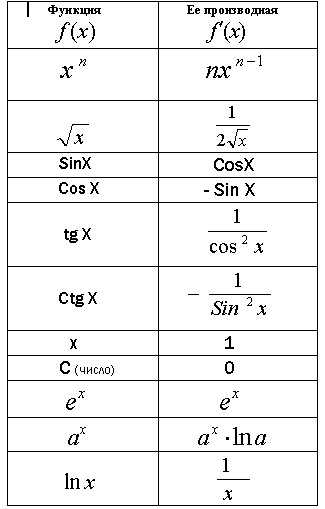
Правила вычисления производных

Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)

Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).

Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).

Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!

Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.

Производная от произведения числа на функцию. Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.

Производная сложной функции:

Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.

Ваши комментарии и отзывы к странице с производными:

Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.

Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.

Виртуальный математический справочник.
Колпаков Александр Николаевич, репетитор по математике.

Метки: Алгебра, Справочник репетитора, Ученикам

ankolpakov.ru

Формулы производных функции

Рассмотрим функцию которая определена и непрерывна на некотором интервале произвольную точку и соответствующее значение функции в этой точке Зададим аргументу функции приращение в точке В результате получим величину и соответствующее значение функции

ОПРЕДЕЛЕНИЕ Производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента в этой точке, при условии, что последний стремится к нулю:

   

Если данный предел конечен, то рассматриваемая функция называется дифференцируемой в точке .

Дифференцирование – это процесс нахождения производной функции. Его проводят с использованием таблицы производных и правил дифференцирования. На этой странице разобраны все формулы производных функции.

Таблица производных, список формул

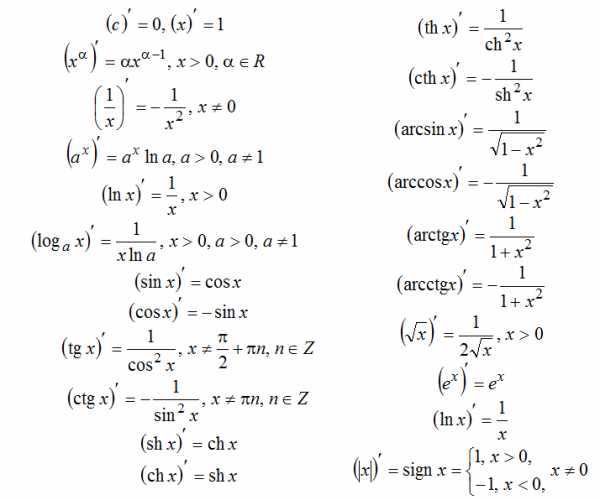
Правила дифференцирования

   

   

   

   

ПРИМЕР 1

Задание	Найти производную функции
Решение	Искомая производная равна:
Ответ

ПРИМЕР 2

Задание	Продифференцировать функцию
Решение	Искомая производная     Производная разности равна разности производных:     Производную первого слагаемого найдем по таблице производных, второго – как производную частного:
Ответ

ru.solverbook.com

Таблица производных. Таблица производных функций. Табличные производные. Формулы производных.

Если x — независимая переменная, то:
Производная степенной функции	Производная степенной функции
—
Производная экспоненциальной функции	Производная экспоненты
Производная сложной экспоненциальной функции	Производная экспоненциальной функции
—
Производная логарифмической функции	Производная натурального логарифма
	Производная натурального логарифма функции
—
Производная синуса	Производная косинуса
Производная косеканса	Производная секанса
Производная арксинуса	Производная арккосинуса
Производная арксинуса	Производная арккосинуса
Производная тангенса	Производная котангенса
Производная арктангенса	Производная арккотангенса
Производная арктангенса	Производная арккотангенса
Производная арксеканса

dpva.ru

12 Таблица основных формул дифференцирования

Функция	Производная	Функция	Производная

Производные высших порядков

Если функция имеет производную в каждой точке своей области определения, то ее производная есть функция от . Функция , в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом . Таким образом

адание. Найти вторую производную функции 

Решение. Для начала найдем первую производную:

Для нахождения второй производной продифференцируем выражение для первой производной еще раз:

Ответ. 

15.Признак возрастания ,убывания функции.

Одна из основных задач исследования функции — это нахождение промежутков ее возрастания и убывания. Такое исследование легко провести с помощью производной. Сформулируем соответствующие утверждения. Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I. Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I. Доказательство этих признаков проводится на основании формулы Лагранжа (см. п. 19). Возьмем два любых числа х

1 и x₂ из интервала. Пусть x₁<x₂. По формуле Лагранжасуществует число с∈(х₁, x₂), такое, что

(1)

Число с принадлежит интервалу I, так как точки х₁ и x₂ принадлежат I. Если f'(x)>0 для х∈I то f’(с)>0, и поэтому F(x₁)<F(x₂) — это следует из формулы (1), так как x₂ — x₁>0. Этим доказано возрастание функции f на I. Если же f’ (x)<0 для х∈I то f'(с)<0, и потому f(x₁)>f (х₂) — следует из формулы (1), так как x₂—x₁>0. Доказано убывание функции f на I.  Наглядный смысл признаков ясен из физических рассуждений (рассмотрим для определенности признак возрастания).  Пусть движущаяся по оси ординат точка в момент времени t имеет ординату y = f(t). Тогда скорость этой точки в момент времени t равна f'(t) (см. Мгновенная скорость). Если f’ (t)>0 в каждый момент времени из промежутка t, то точка движется в положительном направлении оси ординат, т. е. если t

1 <t₂, то f (t₁)<f (t₂). Это означает, что функция f возрастает на промежутке I. Замечание 1. Если функция f непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку. Замечание 2. Для решения неравенств f’ (х)>0 и f’ (х)<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу) : точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f’ сохраняет постоянный знак. (Этот факт доказывается в курсах математического анализа.) Знак можно определить, вычислив значение f’ в какой-нибудь точке промежутка.

16.Экстремум функции. Необходимое и достаточное условие экстремума

Необходимое условие экстремума

      Функция g(x) в точкеимеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точкии для всех точек x  некоторой области:, выполнено соответственно неравенство

(в случае максимума) или (в случае минимума).

Экстремум функции находиться из условия:, если производная существует, т.е. приравниваем первую производную функции к нулю.

Достаточное условие экстремума

1) Первое достаточное условие: 

Если:

а) f(x) непрерывная функция и определена в некоторой окрестности точкитакой, что первая  производная в данной точке равна нулю или не существует.

б) f(x) имеет конечную производную в окрестности задания и непрерывности функции

в) производная сохраняет определенный знак справа от точкии слева от этой же точки, тогда точкуможно охарактеризовать следующим образом

     Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.

2) Второе достаточное условие

     Если функция g(x) обладает второй производнойпричем в некоторой точкепервая производная равна нулю, а вторая производная отлично от нуля. Тогда точкаэкстремум функции g(x), причем если, то точка является максимумом; если, то точка является минимумом.

3) Третье достаточное условие

     Пусть функция g(x) имеет в некоторой окрестности точки N производных, причем значение первых (N — 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:

а) Если N — четно, то точка экстремум функции:у функции точка максимума,у функции точка минимума.

б) Если N — нечетно, то в точкеу функции g(x) экстремума нет.

Абсолютный экстремум

     Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента.

studfiles.net

Таблица производных функций

Вот полная таблица производных основных функций:

1. sin´x = cosx

2. cos´x = -sinx

3. tg ´x =

4. ctg ´x =

5. (a^x)´ =ln a · a^x , где a>0, когда a = e тогда (e^x)´ = e^x

6. (xⁿ)´ = n · x^n-1 , где n постоянное вещественное число

7. (lnx)´ =

8. (arcsinx)´ =

8. (arccosx)´ =

9. (log_ax)´ =

10. (arctgx)´ =

11. (arcctgx)´ =

Упражнения.

Применяя таблицу производных и свойства производной вычислите следующие производные:

a) y=x²+x+1, y′ -?                                                       b) y=x cosx, y′ -?

c) y=x sinx, y′ -?                                                           d) y=sin(2x), y′ -?

 

Докажем теперь к примеру первую формулу.

Доказательство:

1. sin´x = cosx

sin´x =

воспользуемся формулой sin α – sin β = 2 sin() cos():

sin (x+ Δ x) – sin x = 2 sin() cos()

sin (x+ Δ x) – sin x = 2 sin() cos()

Подставляем это выражение в верхнее равенство:

sin´x =

 

sin´x =

по первому замечательному пределу

поэтому:

sin´x = cosx

Этим же путем докажите формулу cos´x = -sinx

Упражнение.

Применяя формулу ()´=  докажите формулы 3 и 4.

Задача.

При помощи второго замечательного предела докажите формулу (e^x)´ = e^x.

Таблица производных функций незаменима при вычислении производных поэтому советую Вам записать их.

tendey.kz