Уравнения и неравенства с модулем
Данная статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение |x2 − 5x + 4| = 4.
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
x2 − 5x + 4 = 4 или x2 − 5x + 4 = −4.
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Ответ: 0; 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
1. |2 − x| = 5 − 4x
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: x = 1. У второй системы решений нет.
Ответ: 1.
2. x2 + 4|x − 3| − 7x + 11 = 0.
Первый случай: x ≥ 3. Снимаем модуль:
Число x2, будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число x 1. Для этого составим разность и определим её знак:
Значит, x1 больше трёх и потому является корнем исходного уравнения
Второй случай: x < 3. Снимаем модуль:
Число x3 больше, чем , и потому не удовлетворяет условию x < 3. Проверим x4:
Значит, x4 является корнем исходного уравнения.
Ответ:
3. |2x2 − 3x − 4| = 6x − 1.
Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не точный квадрат. Давайте лучше воспользуемся следующим соображением: уравнение вида |A| = B равносильно совокупности двух систем:
То же самое, но немного по-другому:
Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию B ≥ 0.
Приступаем. Сначала решаем первое уравнение:
Затем решаем второе уравнение:
Теперь в каждом случае проверяем знак правой части:
Стало быть, годятся лишь x1 и x3.
Ответ:
Квадратные уравнения с заменой |x| = t
Решим уравнение: x2 + 2|x| − 3 = 0.
Поскольку x2 = |x|2, удобно сделать замену |x| = t. Получаем:
Ответ: ±1.
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: |3x2 + 5x − 9| = |6x + 15|. Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Решим уравнение: |x − 1| − 2|x − 2| + 3|x − 3| = 4.
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Ответ: [1; 2] ∪ {5}.
Модуль в модуле
Решим уравнение: ||3 − x| − 2x + 1| = 4x − 10.
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
2) x ≥ 3. Имеем:
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Ответ: 4.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Неравенства с модулем
Никаких принципиально новых идей здесь не возникает. Всеми необходимыми знаниями вы уже владеете. Поэтому мы разберём лишь две задачи. Остальное — на занятиях и в домашних заданиях.
1. 2|x − 4| + |3x + 5| ≥ 16.
1) x ≥ 4. Имеем:
Полученное неравенство выполняется при всех рассматриваемых x ≥ 4. Иными словами, все числа из промежутка [4; +∞) являются решениями нашего неравенства.
2) Имеем в данном случае:
Учитывая, в каком промежутке мы сейчас находимся, получаем в качестве решений исходного неравенства множество [3; 4].
3) . Имеем:
Так как − , то все значения x из полученного промежутка служат решениями исходного неравенства.
Остаётся объединить множества решений, полученные в трёх рассмотренных случаях.
Ответ:
2. |x2 − 2x − 3| < 3x − 3.
Это задача №6 теоретической части урока 8 книги В. В. Ткачука «Математика — абитуриенту». Автор решает её методом интервалов. Обязательно разберите авторское решение!
Заметим, что метод интервалов здесь проходит весьма безболезненно по той причине, что корни квадратного трёхчлена под модулем — целые числа. А если дискриминант не будет точным квадратом? Замените, например, под модулем −3 на −5. Объём вычислительной работы тогда существенно возрастёт.
Мы покажем вам другой способ решения этой задачи, не зависящий от капризов дискриминанта.
Наше неравенство имеет вид |A| < B. Очевидны следующие утверждения.
• Если B ≤ 0, то неравенство не имеет решений.
• Если B > 0, то неравенство равносильно двойному неравенству −B < A < B или, что то же самое, системе
Иными словами, мы берём пересечение множества решений данной системы с множеством решений неравенства B > 0, то есть решаем систему
В нашей задаче получаем:
Изобразим множества решений этих неравенств на рисунке. Чёрным цветом показаны решения первого (двойного) неравенства; зелёный цвет — решения совокупности; синий цвет — решения последнего неравенства системы.
Решением системы служит пересечение этих множеств, т. е. множество, над которым присутствуют линии всех трёх цветов. Оно заштриховано.
Ответ: (2; 5).
Звоните нам: 8 (800) 775-06-82
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Неравенства с модулем, примеры решений
Схема решения простейших неравенств:
1) неравенство вида при равносильно системе ; при неравенство решений не имеет.
2) неравенство , при равносильно совокупности неравенств
при решением неравенства является множество ; – вся числовая ось, то есть .
При решении неравенства вида или , обе части неравенства возводят в квадрат. Если неравенство содержит несколько выражений под знаком модуля, то применяется метод интервалов.
Примеры
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Уравнения и неравенства с модулями
Сегодня порешаем немного заданий с модулями, вспомним, как они раскрываются, будут и уравнения, и неравенства. Поехали…
Задание 1. Решить уравнение:
Совсем простое уравнение. Раскрываем модуль со знаком «плюс» слева от точки 2 и со знаком «минус» – справа, так как в этой точке подмодульное выражение меняет знак с плюса на минус: , .
Получаем систему:
Решение найдено на промежутке , и, соответственно, этому промежутку не принадлежит, поэтому этот корень уравнения посторонний. Ответ:
Задание 2. Решить уравнение:
Приравняем к нулю оба подмодульных выражения, чтобы определить точки перемены их знаков:
Расставляем полученные точки на координатной оси, они нам ее разобьют на три промежутка. Расставляем знаки подмодульных выражений на каждом получившемся промежутке. Это просто сделать, подставив любое число из данного промежутка в модуль и определив, получается положительное число или отрицательное.
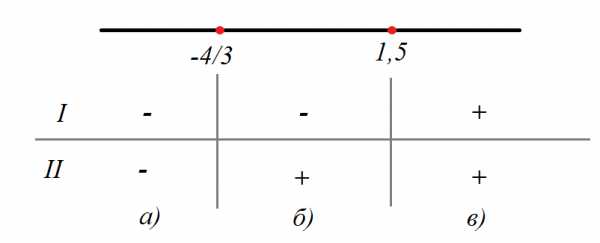
Раскрываем модуль
Теперь видно, с каким знаком надо раскрыть модуль на каждом интервале. Придется решить три уравнения, раскрыв модули с нужными знаками на каждом из них.
Интервал а) – оба модуля раскрываем со знаком «минус»:
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»:
Интервал в) – оба модуля раскрываем со знаком «плюс»: – эта точка не принадлежит своему интервалу, поэтому этот корень – посторонний. Ответ: ,
Задание 3. Решить уравнение:
Решать можно либо графическим способом, либо постепенно раскрывая модули снаружи, как будто снимая листья с кочана капусты. Мы сделаем и тем способом, и другим. Сначала – аналитически (то есть раздевая капусту), снимаем первый модуль:
Раскрываем второй модуль:
Раскрываем третий модуль:
Теперь решим графически. Построим сначала прямую :
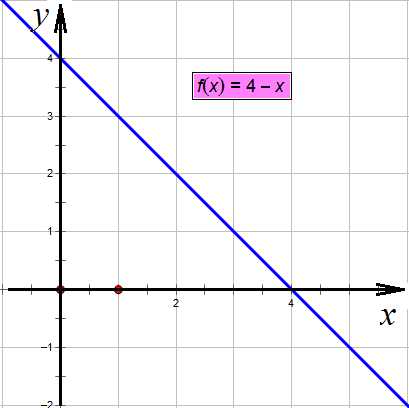
Построение прямой
Теперь «наденем» на нее модуль, то есть отразим всю ее часть, что оказалась ниже оси х, вверх:
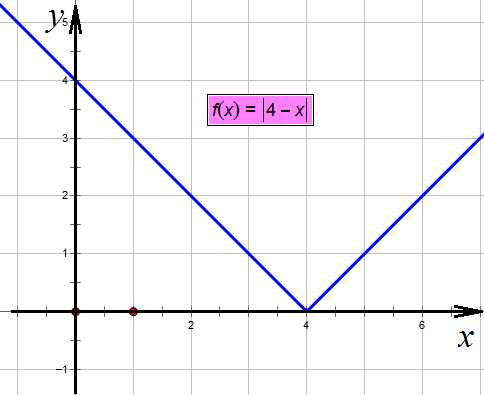
Отражаем вверх все, что ниже оси х
Теперь построим – минус перевернет наш график вверх тормашками:
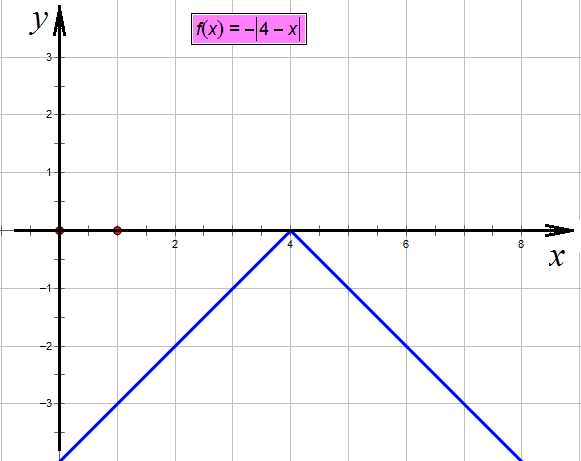
Снова отражаем
Поднимаем все вверх на три единицы:
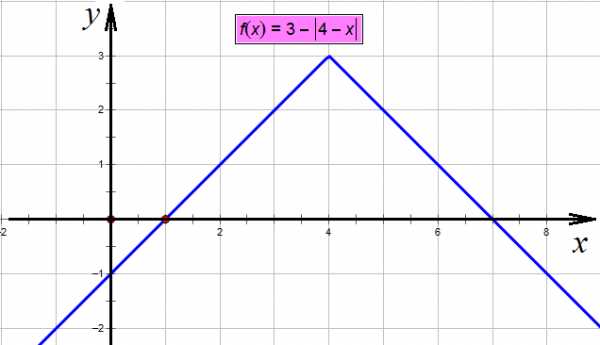
Поднимаем вверх
«Надеваем» второй модуль, то есть снова отражаем всю отрицательную часть вверх:
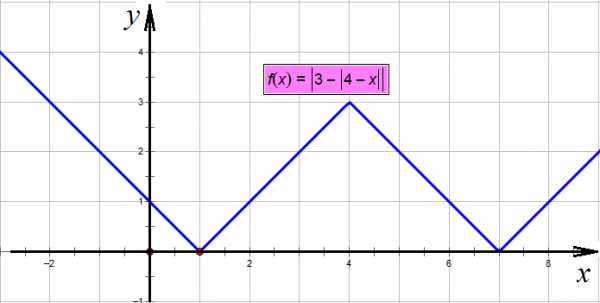
Второй модуль
Снова ставим «минус»:
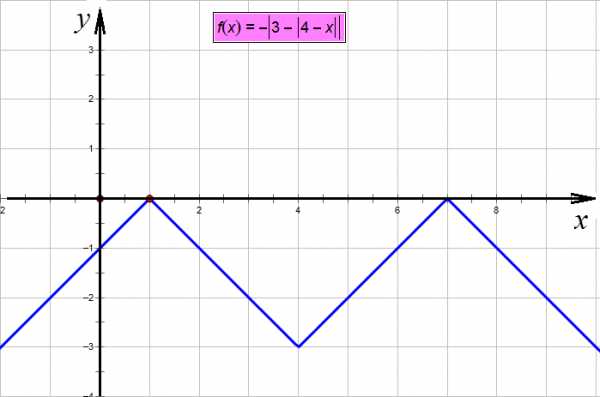
Снова отражаем
Снова поднимаем вверх на три единицы:
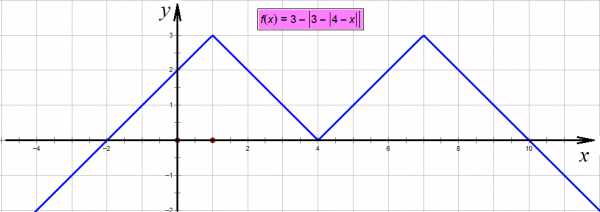
Поднимаем
Наконец, последний модуль:
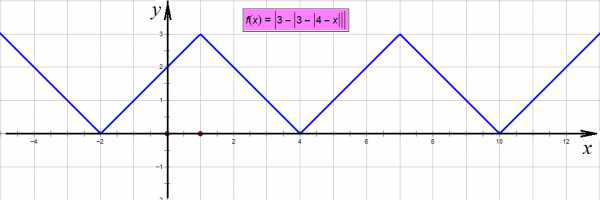
Последний модуль
И проводим прямую , пересечения с которой и есть искомые корни:
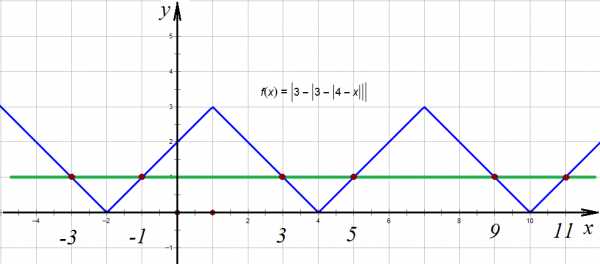
Прямая пересекает график
Ответ:
Задание 4. Решить неравенство:
Это неравенство также можно решить графически. Справа имеем прямую , слева под знаком модуля – парабола. Модуль переворачивает ту часть параболы, которая находится под осью х, вверх. Требуется найти те интервалы (отрезки), где прямая располагается выше параболы.
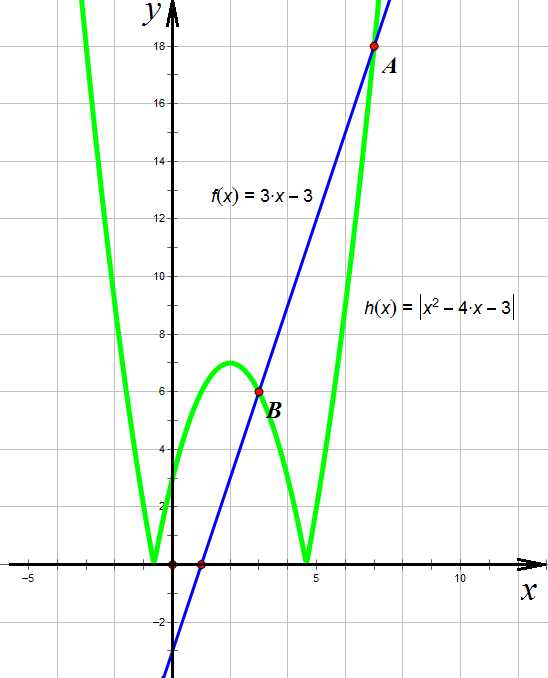
Графическое решение
Нас интересует, очевидно, интервал ВА, точки В и А не войдут в решение, так как неравенство строгое:
Можно также решить аналитически: раскрываем модуль с положительным и отрицательным знаками.
На рисунке показаны решения первого неравенства и второго, и область пересечения этих решений закрашена.
Пересечение решений
Ответ:
Задание 5. Решить уравнение:
Определяем точку перемены знака модуля:
Справа от этой точки модуль раскроем со знаком «минус», слева – со знаком «плюс»
Первое решение сделано на промежутке , точка этому промежутку не принадлежит, поэтому этот корень – посторонний. Ответ:
Задание 6. Решить уравнение:
Приравниваем показатели степеней:
Определяем точки перемены знаков подмодульных выражений:
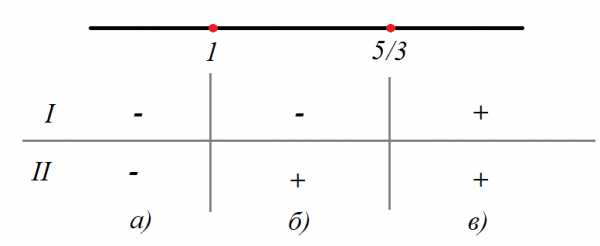
Раскрываем модуль
Раскрываем модули с соответствующими знаками на каждом из промежутков:
Интервал а) – оба модуля раскрываем со знаком «минус»:
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»:
Интервал в) – оба модуля раскрываем со знаком «плюс»: -нет решений. Получается, что уравнению будет удовлетворять любое число из промежутка (]
Задание 7. Решить уравнение:
Воспользуемся формулой разности логарифмов и заменим ее частным:
По определению логарифма:
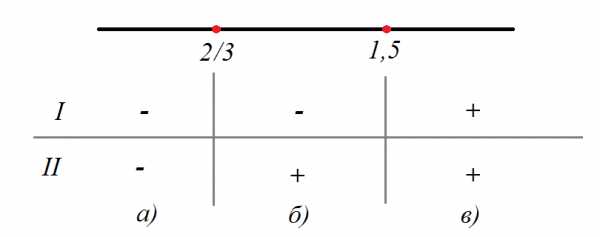
Раскрываем модуль
Интервал а) – оба модуля раскрываем со знаком «минус»: ,
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»: , ,
Интервал в) – оба модуля раскрываем со знаком «плюс»: , – этот корень своему промежутку не принадлежит, он посторонний. Ответ:
Задание 8. Решить неравенство:
В основании логарифма – модуль, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется.
Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а)
То есть область, где решение будет существовать, такая:
На этой области при решении основного неравенства мы поменяем знак:
б) Вторая область:
Знак неравенства не меняем, так как основание логарифма больше 1:
Осталось внимательно и аккуратно наложить области решения неравенства на те промежутки, где они существуют:
Наложение решений на промежутки
Ответ: ( ] [)
Задание 9. Решить неравенство:
В основании логарифма – модуль х, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется. Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а)
Этот промежуток изображен на рисунке: Тогда знак неравенства меняем, так как основание логарифма меньше 1:
б) Знак неравенства не меняем, так как основание логарифма больше 1:
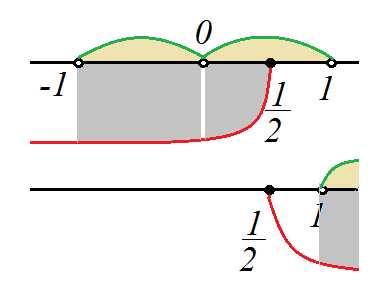
Наложим решения на области их существовавния
Наложим решения на области, к которым эти решения относятся:
Ответ: (]
easy-physic.ru
25. Неравенства с модулем | Решение задач по математике и другим предме
I тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:
где (3.27)
Решение зависит от знака числа А.
1. Если то неравенство (3.27) не имеет решений.
2. Если то неравенство (3.27) равносильно системе неравенств
где (3.28)
1. Если то неравенство (3.28) не имеет решений.
2. Если то неравенство (3.28) равносильно уравнению
3. Если , то неравенство (3.28) равносильно системе неравенств
где (3.29)
1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что
3. Если то неравенство (3.29) равносильно совокупности
где (3.30)
1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
2. Если то неравенство (3.30) равносильно совокупности
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
(3.31)
Где – некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения
1. Если
(3.32)
То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).
2. Если
То решением является множество всех значений Х, которые удовлетворяют системе
3. Если решение определяется системой
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
где (3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
Решение неравенства (3.33) сводится к решению неравенства
Аналогично решают неравенства IV типа (3.33), если они заданы со знаками
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) 2)
3) 4)
5) 6)
Решение. 1) Решаем как неравенство I типа:
Получаем ответ:
2) Решаем как неравенство I типа:
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
Его решение: это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:
Получаем ответ:
4) Заданное неравенство может быть записано в виде
Заменим переменную Решаем неравенство
Его решение
Возвращаемся к переменной Х и решаем совокупность
Получаем
Т. е. приходим к ответу
5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ:
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
(3.34)
Решаем неравенство
Получаем
Система (3.34) сводится к системе
На данном промежутке решений нет.
Б)
Если , то С учетом рассматриваемого промежутка имеем:
Получаем
В)
Решением является промежуток:
Объединим полученные решения и приходим к ответу:
6)
ОДЗ:
Введем новую переменную:
тогда и приходим к неравенству вида
Решаем его
Используем метод интервалов (рис. 3.11).
Рис. 3.11
Запишем полученное решение в виде совокупности:
Вернемся к переменной Х:
(3.35)
– выполняется при любых
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
Получаем ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
5.4. Неравенства с модулем
Рассмотрим некоторые виды неравенств, содержащих знак модуля, и методы их решения.
1. 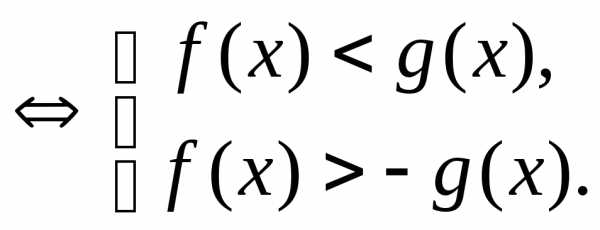
В частности, 
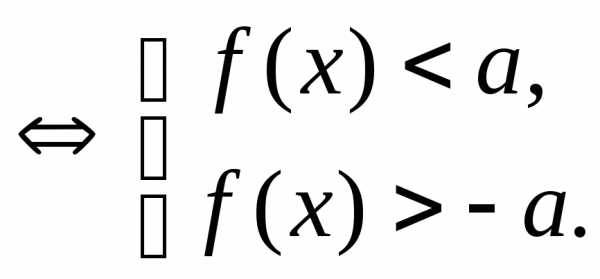 ,
где
,
где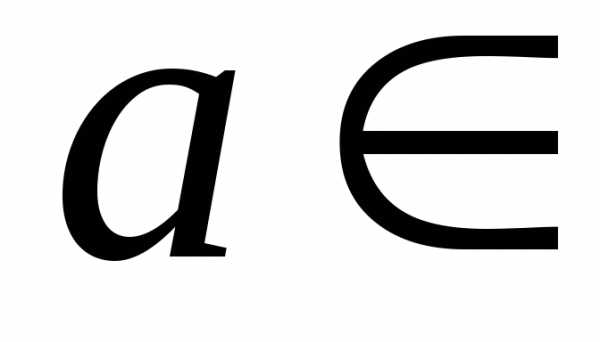
 ,
,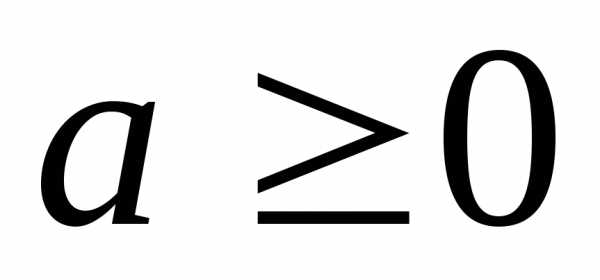 .
При
.
При неравенство решений не имеет.
неравенство решений не имеет.
2. 
В частности, 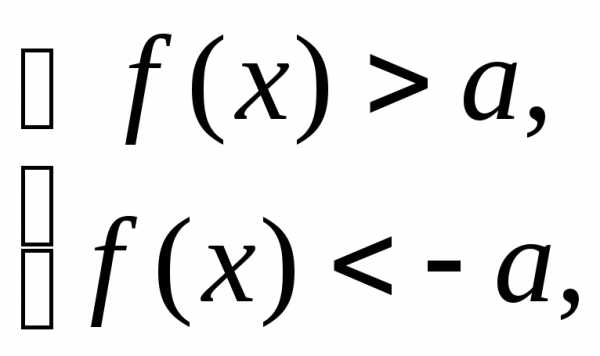
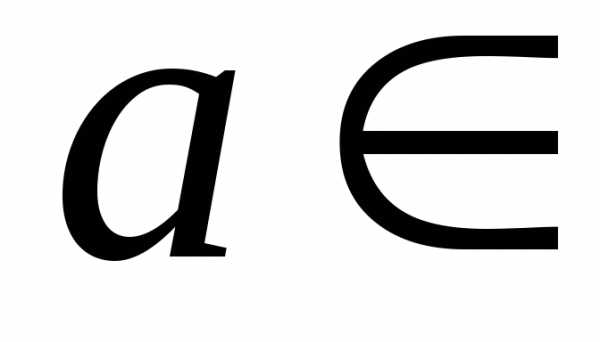
 ,
,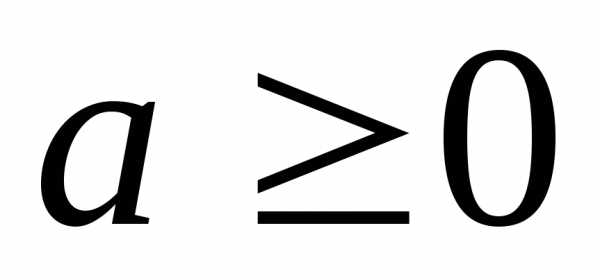 .
При
.
При неравенство выполняется для всех
неравенство выполняется для всех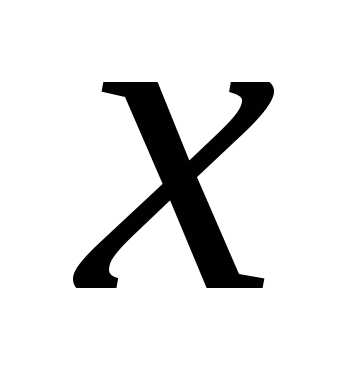 при которых функция
при которых функция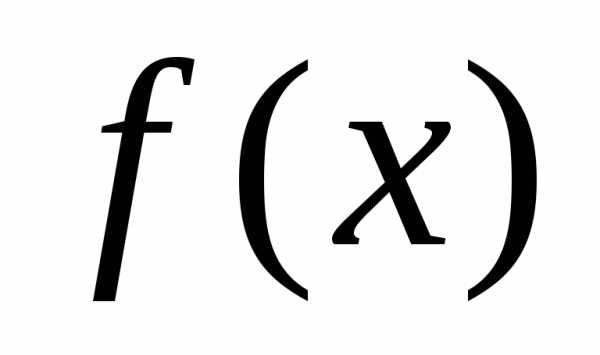 определена.
определена.
3.
.
Последнее неравенство решается методом интервалов.
4. Неравенство вида 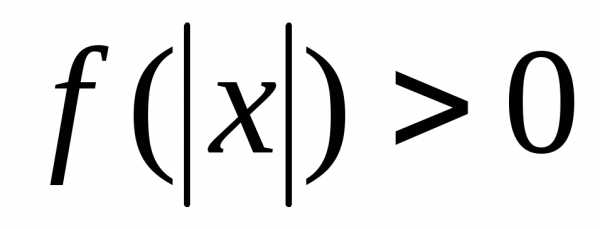 решают с помощью замены.
решают с помощью замены.
Пример 5.6. Решить
неравенство 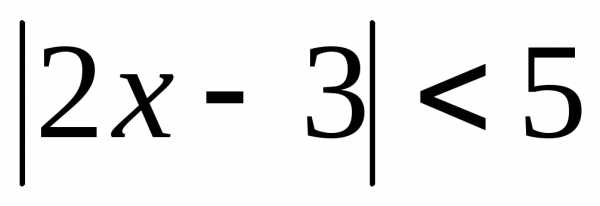 .
.
Решение. .
Ответ: 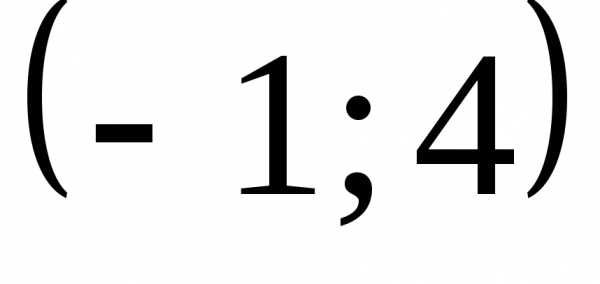 .
.
Пример 5.7. Решить
неравенство 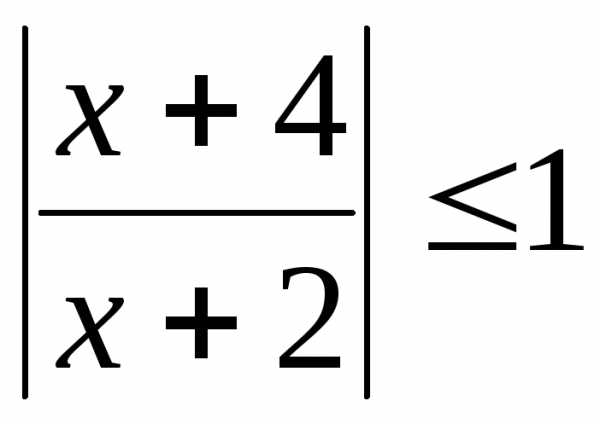 .
.
Решение. 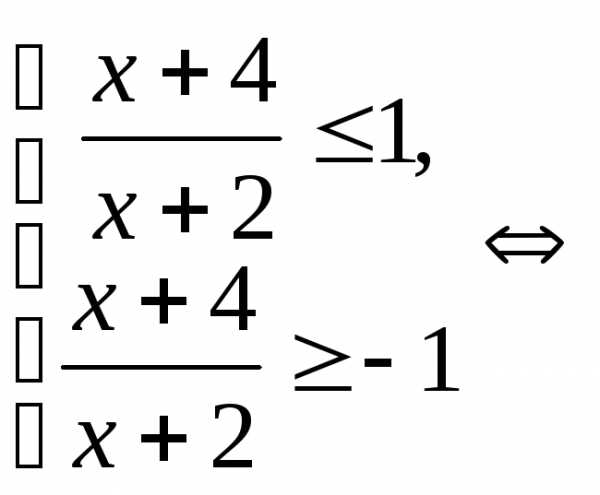
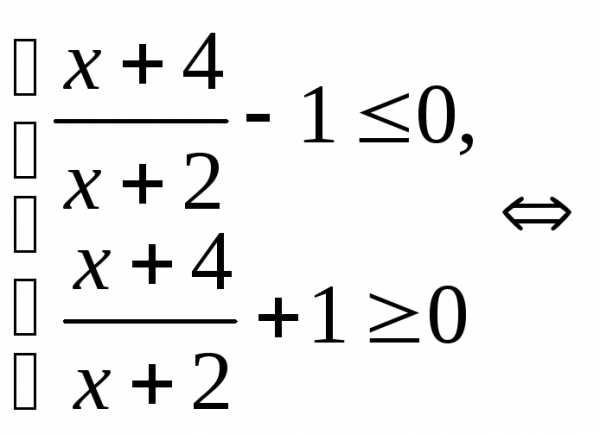
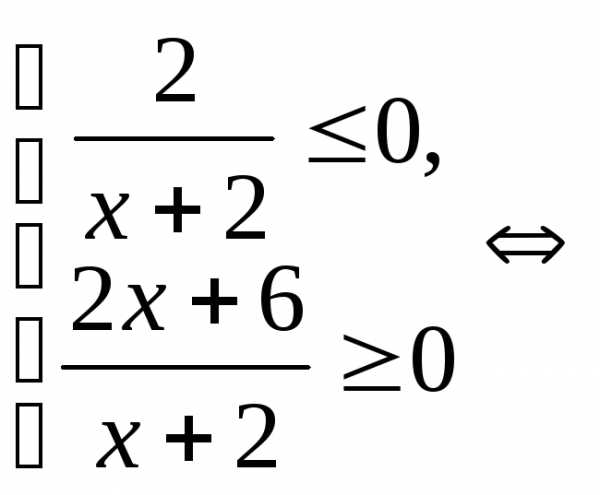
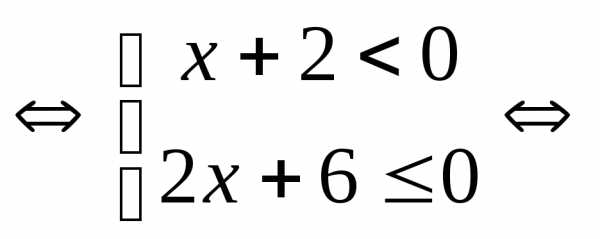
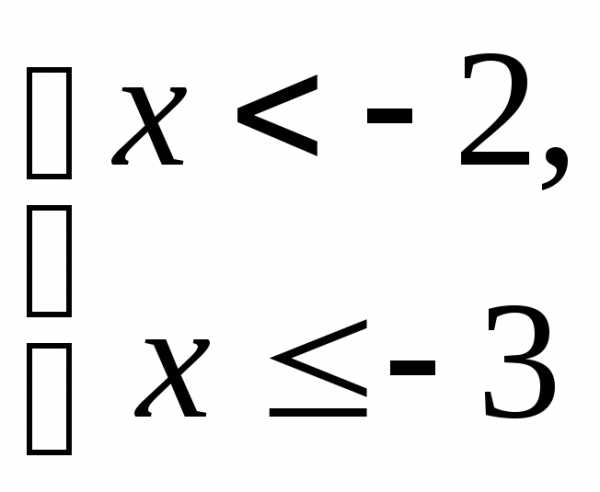 .
.
Ответ: 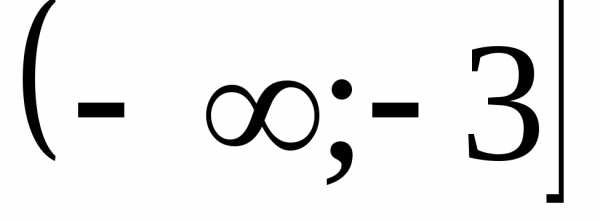 .
.
Пример 5.8. Решить неравенство .
Решение.
.
Ответ: .
Пример 5.9. Решить неравенство .
Решение.
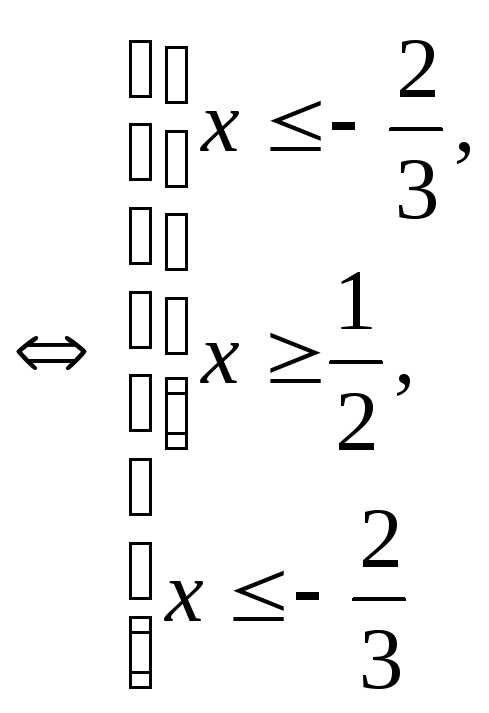 .
.
Ответ: .
Пример 5.10. Решить неравенство .
Решение. Из свойств модуля следует, что . Поэтому
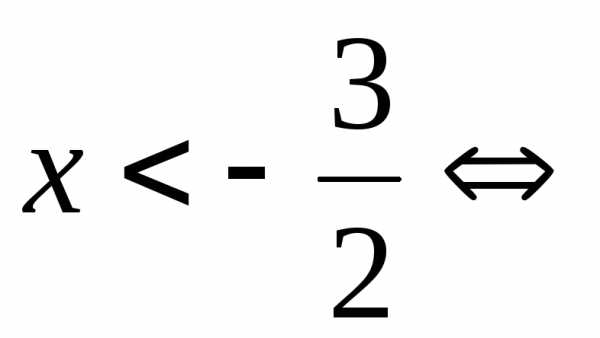
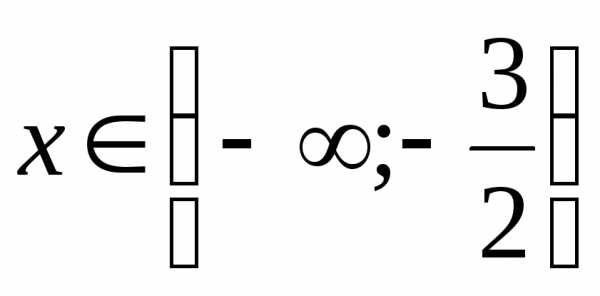 .
.
Ответ: 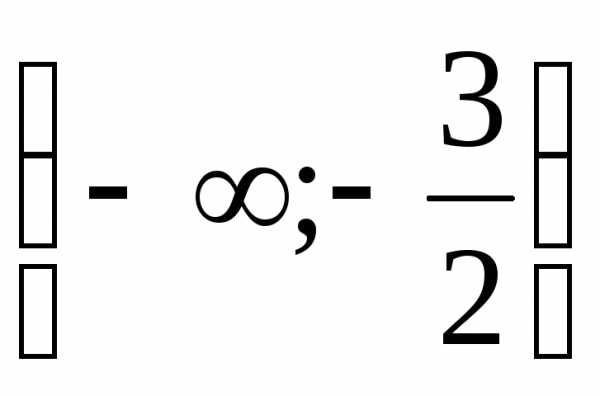 .
.
Пример 5.11. Решить неравенство .
Решение.
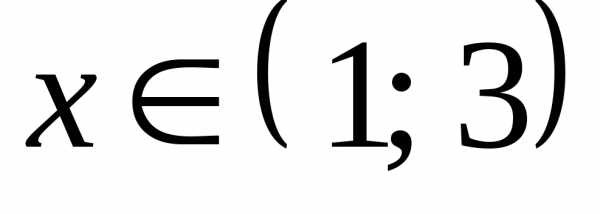
Ответ: 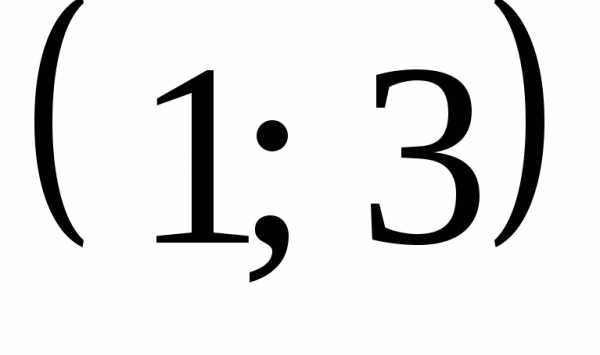 .
.
Пример 5.12. Решить неравенство .
Решение. Введем замену , тогда исходное неравенство имеет вид:
.
Переходя обратно
к переменной 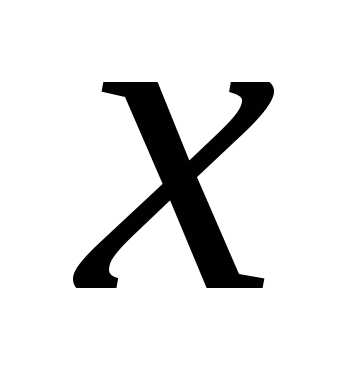 ,
получим:
,
получим:
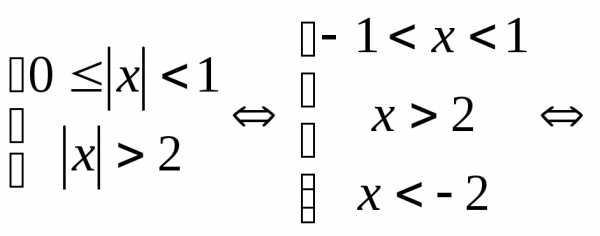 .
.
Ответ: .
Пример 5.13. Решить неравенство .
Решение.
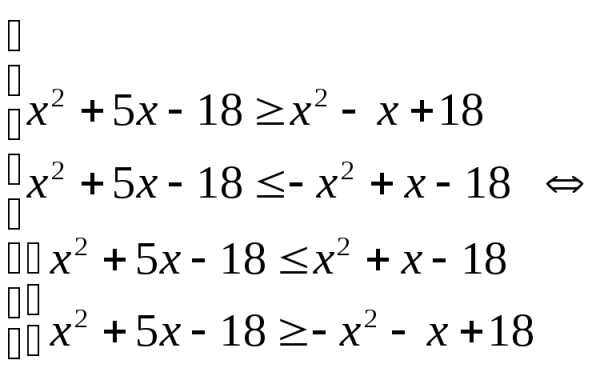
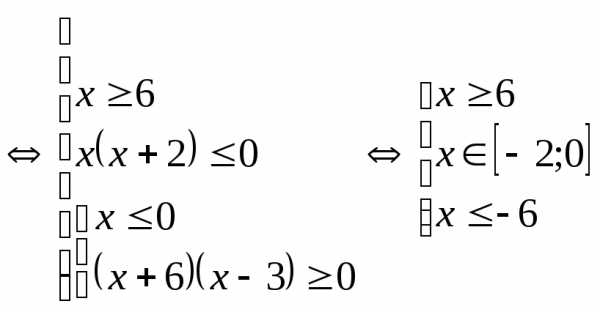 .
.
Ответ: .
Пример 5.14. Решить неравенство .
Решение.
.
Ответ: .
5.5. Иррациональные неравенства
К основным методам решения иррациональных неравенств относятся:
1. сведение исходного неравенства к равносильной системе рациональных неравенств или к совокупности неравенств:
a) 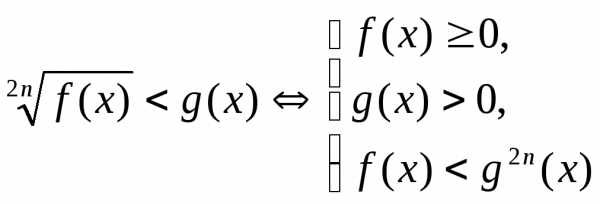 ,
,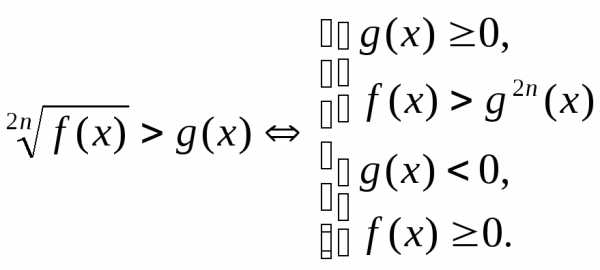
в частности, для 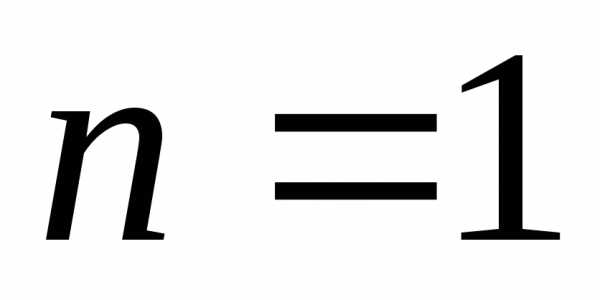
 ,
, 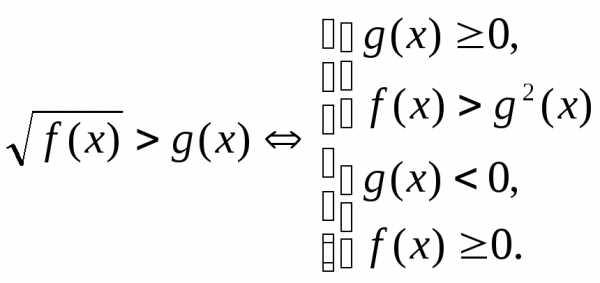
б) ,,
в частности, для 
,
б) ,
в частности, для 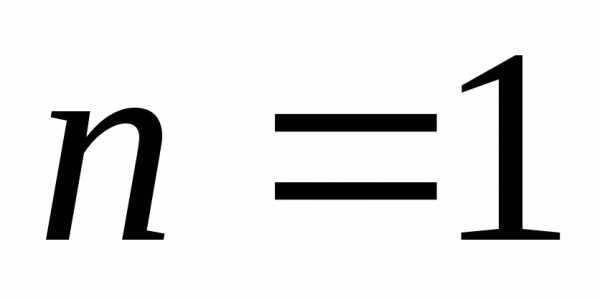
, ;
2. введение новой переменной;
3. ,
4.
Пример 5.15. Решить неравенство .
Решение.
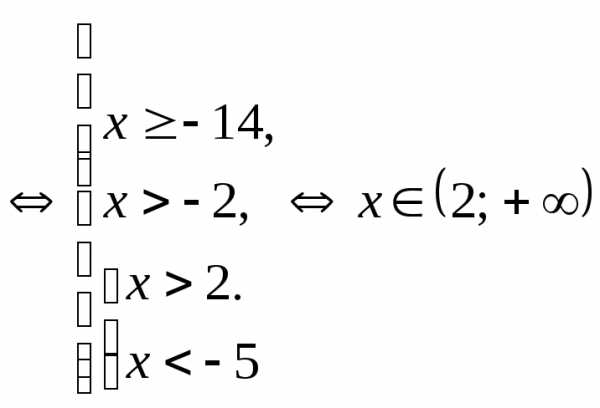 .
.
Ответ: 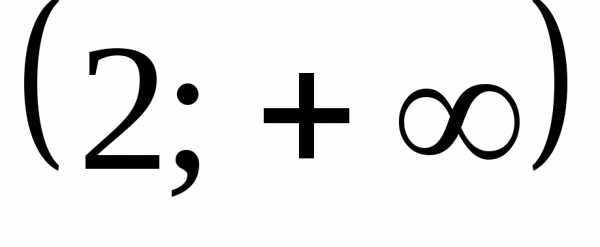 .
.
Пример 5.16. Решить неравенство .
Решение. 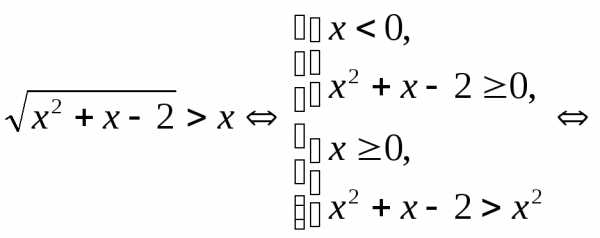
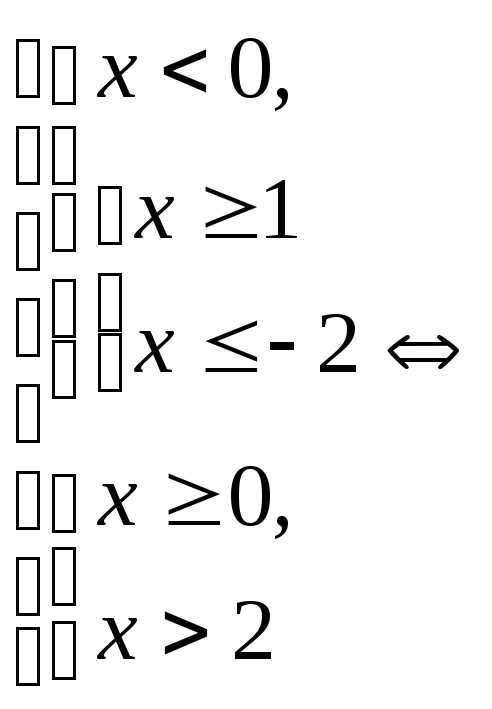
.
Ответ: .
Пример 5.17. Решить неравенство
.
Решение.
,
последняя система, а, следовательно, и исходное неравенство, решений не имеет.
Ответ: решений нет.
Пример 5.18. Решить неравенство .
Решение.
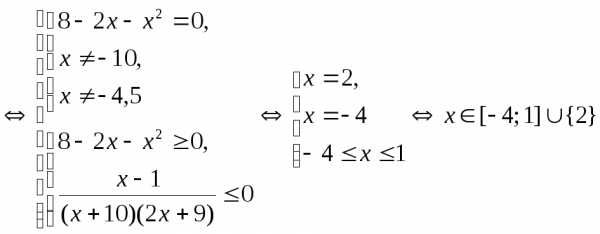 .
.
Ответ: .
Задачи для самостоятельного решения Группа а
1. Укажите длину промежутка, который является решением неравенства:
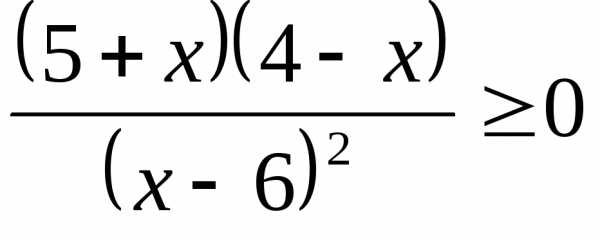 (Ответ:
(Ответ:  .)
.)
2. Найти произведение всех целых решений неравенства:
.
(Ответ:  .)
.)
Решить неравенство (3-15)
3. .
(Ответ: 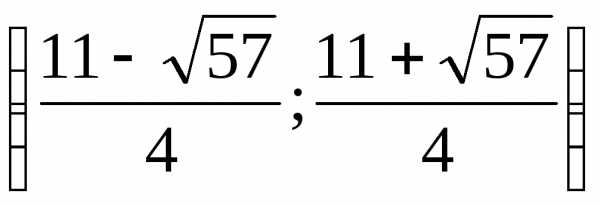 .)
.)
4. (Ответ: .)
5. (Ответ: 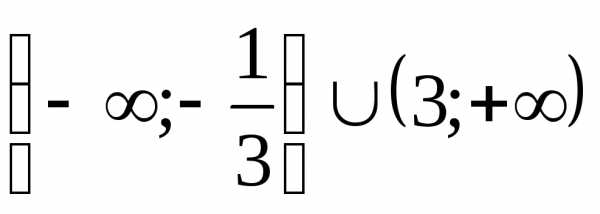 .)
.)
6. 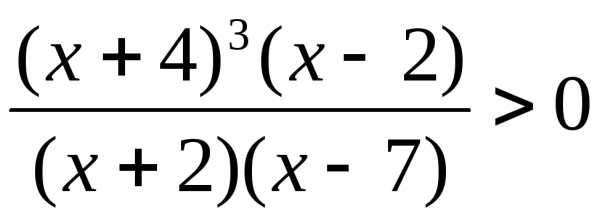 .
(Ответ: .)
.
(Ответ: .)
7. 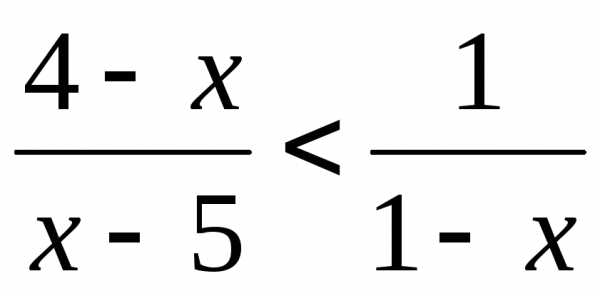 .
(Ответ: .)
.
(Ответ: .)
8.
.
(Ответ: 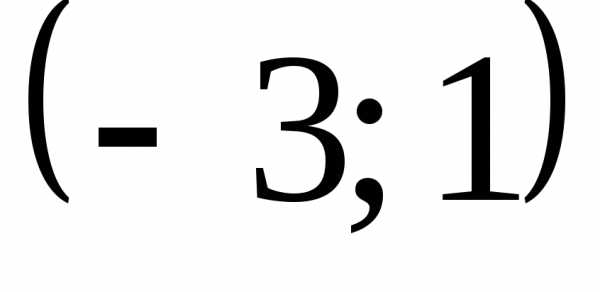 .)
.)
9. 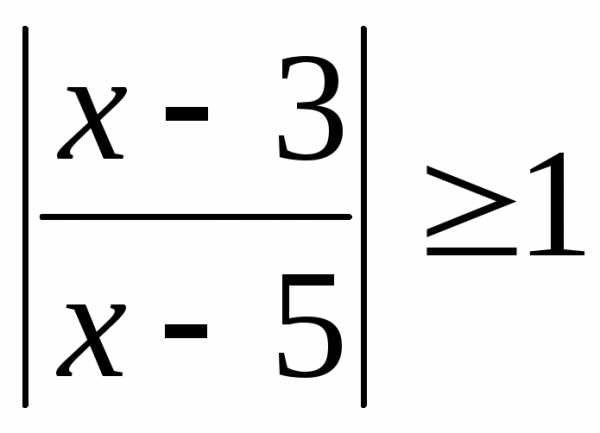 .
(Ответ: .)
.
(Ответ: .)
10.
.
(Ответ: 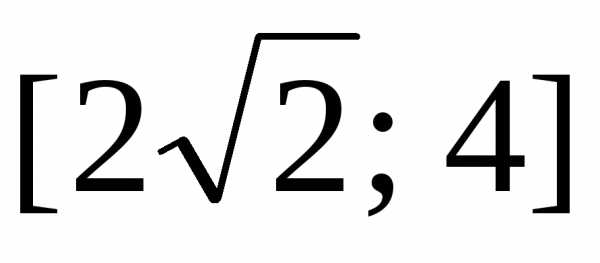 .)
.)
11.
.
(Ответ:  .)
.)
12. . (Ответ: .)
13.
.
(Ответ: 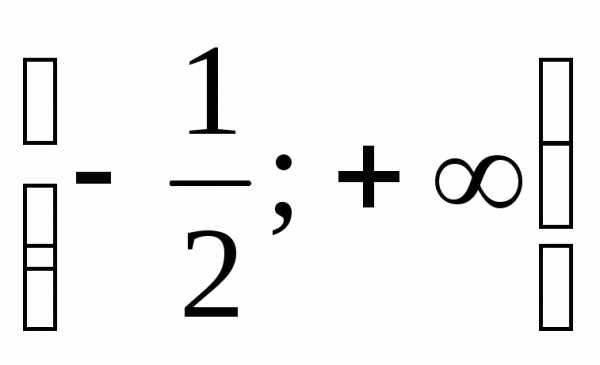 .)
.)
12.
.
(Ответ: 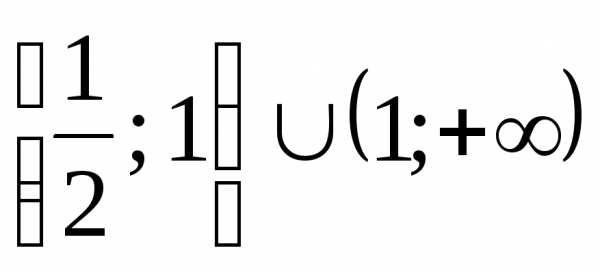 .)
.)
13. . (Ответ: .)
14. . (Ответ: .)
15.
.
(Ответ:  .)
.)
studfiles.net
Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.
Как решать неравенства с модулем?
Методы решения систем линейных неравенств отличаются от методов решения линейных уравнений тем, что знаки неравенства не позволяют выполнять подстановку, как мы это делаем с уравнениями. Тем не менее, мы решаем по определенной системе. Система линейных неравенств включает в себя несколько выражений, которые при решении могут дать ряд решений.
\(|x|\)— расстояние на числовой прямой от \(0\) до точки \(a\).
- \(|u|=u\) \(—>\) \(u\geq0\)
- \(|u|=-u\) \(—>\) \(u\le \: 0\)
- \(|u|=|v|\) \(—>\) \(v^2=u^2\)
- \(|x|<a \) \(—>\) \(-a<x<a\) Система
- \(|x|\le \:a \) \(—>\) \(-a\le \:x\le \:a\)
- \(|x|> a \) \(—>\) \(\left[ \begin{gathered} x < -a \\ x >a \\ \end{gathered} \right.\) Совокупность
- \(|x|\geq a \) \(—>\) \(\left[ \begin{gathered} x \le \: -a \\ x \geq a \\ \end{gathered} \right.\)
Пример 1. Решить неравенство \(|3+x| \geq|x|\).
Решение. \(|3+x| \geq|x|\)\(—>\) \((3+x)^2\geq x^2\) \(—>\) \(x^2+6x+9\geq x^2\) \(—>\) \(6x\geq -9\) \(—>\) \(x\geq -1,5\)
Ответ: \([-1,5; +∞)\)
Пример 2. Решить неравенство \(\left|3+2x\right|\le \:7\). Система
Решение. \(\left|3+2x\right|\le \:7\) \(—>\) \(3+2x\le \:7\) и \(3+2x\ge \:-7\) или \(-7\le \:3+2x\le \:7\)
\(x\le \:2\) и \(x\ge \:-5\) \(-5\le \:x\le \:2\)
Ответ: [-5;2];
Пример 3. Решить неравенство \(\left|3x-5\right|<\:4\)
Решение: \(-4<3x-5<4\) \(—>\) \(\frac{1}{3}<x<3\)
Ответ: \((\frac{1}{3};3)\);
Пример 4. Решить неравенство \(\left|x-8\right|\ge \:\:3\)
Решение: Совокупность \(\) \(\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.\) \(—>\) \(\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.\)
Ответ: \((+∞;5)⋃ (11;+∞)\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) по теме: Тема 7. НЕРАВЕНСТВА С МОДУЛЕМ. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА. Теория. Ключевые методы решения задач. Упражнения.
Тема 7. Неравенства с модулем. Иррациональные алгебраические неравенства.
IV. Неравенства с модулем.
При решении неравенств с неизвестным под знаком модуля пользуемся определением
Решение неравенств, содержащих модули, в большинстве случаев строится аналогично решению соответствующих уравнений. Основное отличие состоит в том, что после освобождения от модулей требуется решить, естественно, не уравнение, а неравенство. Есть еще одно отличие. Если при решении уравнений можно широко пользоваться проверкой полученных решений, то для случая неравенств отбросить посторонние решения проверкой может быть затруднительно. Это означает, что при решении неравенств стараются использовать в основном, равносильные переходы.
Пример. Решить неравенство +
Решение. Нули подмодульных выражений разделяют числовую ось на три промежутка
x x 4.
-1 4 x
На левом промежутке оба модуля раскрываются со знаком «-«; на среднем — первый модуль раскрывается со знаком «-«, а второй — со знаком «+»; на правом — оба раскрываются со знаком «+». В результате получаем, что исходное неравенство равносильно совокупности трех систем неравенств
Решите эти системы самостоятельно и объедините полученные ответы:
x(-2; -1) [-1; 4) [4; 5) x(-2; 5).
Ответ: x(-2; 5).
Неравенство вида можно решать, исходя из определения модуля, но во многих случаях удобнее перейти к системе неравенств
Пример. Решить неравенство .
Решение. В соответствии с приведенной схемой запишем систему неравенств, равносильную исходному неравенству:
Решением первого неравенства является отрезок x, а решением второго — объединение двух лучей
Пересечение полученных множеств решений неравенств является решением системы и служит ответом в данной задаче.
Ответ: x.
Неравенство вида удобнее решать, переходя к совокупности неравенств
Пример. Решить неравенство 2.
Решение. Запишем совокупность неравенств, равносильную исходному неравенству
Решением первого неравенства является объединение интервалов , а решением второго интервал . Объединяя полученные множества решений неравенств, находим решение совокупности.
Ответ: .
Решить неравенства.
- . Ответ:
- . Ответ:
- . Ответ:
- . Ответ:
- . Ответ:
V. Иррациональные неравенства.
При решении иррациональных неравенств необходимо помнить, что корни нечетной степени рассматриваются при всех действительных значениях подкоренных выражений, а корни четной степени — только арифметические.
Избавляясь от иррациональности, помните, что неравенство нельзя возводить в четную степень, если хотя бы одна из его частей отрицательна, поскольку при этом знак неравенства может измениться!
Иррациональные неравенства, предлагаемые на вступительных экзаменах, часто сводятся к простейшим следующих видов.
Схемы решения иррациональных неравенств.
- .
Пример.
1) Решить неравенство
Решение.
Ответ:
- Решить неравенство
Решение.
Ответ: .
- Решить неравенство
Решение.
Неравенство решим по правилу решения дробно-рациональных неравенств (см. III).
Найдем нули числителя и знаменателя дроби. Это х=2, х=. Нанесем эти точки на числовую ось и определим знак дроби
— + —
2 х
в каждом промежутке.
Ответ: .
- Решить неравенство
Решение.
Ответ:
Решить неравенства
- Ответ:
- . Ответ:
- Ответ:
- Ответ:
- Ответ:
nsportal.ru
