Таблица нормированная функция лапласа – Таблица лапласа, полная таблица значений функции Лапласа на сайте webmath.ru

Нормированная функция Лапласа

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6

00000 03983 07926 11791 15542 19146 22575 25804 28814 31594 34134 36433 38493 40320 41924 43319 44520 45543 46407 47128 47725 48214 48610 48928 49180 49379 49534

00399 04380 08317 12172 15910 19497 22907 26115 29103 31859 34375 36650 38686 40490 42073 43448 44630 45637 46485 47193 47778 48257 48645 48956 49202 49396 49547

00789 04776 08706 12552 16276 19847 23237 26424 29389 32121 34614 36864 38877 40658 42220 43574 44738 45728 46562 47257 47831 48300 48679 48983 49224 49413 49560

01197 05172 09095 12930 16640 20194 23565 26730 29673 32381 34850 37076 39065 40824 42364 43699 44845 45818 46638 47320 47882 48341 48713 49010 49245 49430 49573

01595 05567 09483 13307 17003 20540 23891 27035 29955 32639 35083 37286 39251 40988 42507 43822 44950 45907 46712 47381 47932 48382 48745 49036 49266 49446 49585

01994 05962 09871 13683 17364 20884 24215 27337 30234 32894 35314 37493 39435 41149 42647 43943 45053 45994 46784 47441 47982 48422 48778 49061 49286 49461 49598

02392 06356 10257 14058 17724 21226 24537 27637 30511 33147 35543 37698 39617 41308 42786 44062 45154 46080 46856 47500 48030 48461 48806 49086 49305 49477 49609

02790 06749 10642 14431 18082 21566 24857 27935 30785 33398 35769 38000 39796 41466 42922 44179 45254 46164 46926 47558 48077 48500 48840 49111 49324 49492 49621

03188 07142 11026 14803 18439 21904 25175 28230 31057 33646 35993 38100 39973 41621 43056 44295 45352 46246 46995 47615 48124 48537 48870 49134 49343 49506 49632

03586 07535 11409 15173 18793 22240 25490 28524 31327 33891 36214 38298 40147 41774 43189 44408 45449 46327 47062 47670 48169 48574 48899 49158 49361 49520 49643

studfiles.net

Таблица значений функции Лапласа —

Таблица значений функции Лапласа

X	Ф(х))		Ф(х)	X	Ф(х)	X	Ф(х)
0	0.0000	0.64	0.2389	1.28	0.3997	1.92	0.4726
0.02	0.0080	0.66	0.2454	1.30	0.4032	1.94	0.4738
0.04	0.0160	0.68	0.2517	1.32	0.4066	1.96	0.4750
0.06	0.0239	0.70	0.2580	1.34	0.4099	1.98	0.4761
0.08	0.0319	0.72	0.2642	1.36	0.4131	2.00	0.4772
0.10	0.0398	0.74	0.2703	1.38	0.4162	2.05	0.4798
0.12	0.0478	0.76	0.2764	1.40	0.4192	2.10	0.4821
0.14	0.0557	0.78	0.2823	1.42	0.4222	2.15	0.4842
0.16	0.0636	0.80	0.2881	1.44	0.4251	2.20	0.4861
0.18	0.0714	0.82	0.2939	1.46	0.4279	2.25	0.4878
0.20	0.0793	0.84	0.2995	1.48	0.4306	2.30	0.4893
0.22	0.0871	0.86	0.3051	1.50	0.4332	2.35	0.4907
0.24	0.0948	0.88	0.3106	1.52	0.4357	2.40	0.4918
0.26	0.1026	0.90	0.3159	1.54	0.4382	2.45	0.4929
0.28	0.1103	0.92	0.3212	1.56	0.4406	2.50	0.4938
0.30	0.1179	0.94	0.3264	1.58	0.4429	2.55	0.4947
0.32	0.1255	0.96	0.3315	1.60	0.4452	2.60	0.4953
0.34	0.1331	0.98	0.3365	1.62	0.4474	2.65	0.4960
0.36	0.1406	1.00	0.3413	1.64	0.4495	2.70	0.4965
0.38	0.1480	1.02	0.3461	1.66	0.4515	2.75	0.4970
0.40	0.1554	1.04	0.3508	1.68	0.4535	2.80	0.4974
0.42	0.1628	1.06	0.3554	1.70	0.4554	2.85	0.4978
0.44	0.1700	1.08	0.3599	1.72	0.4573	2.90	0.4981
0.46	0.1772	1.10	0.3643	1.74	0.4591	2.95	0.4985
0.48	0.1844	1.12	0.3686	1.76	0.4608	3.00	0.49865
0.50	0.1915	1.14	0.3729	1.78	0.4625	3.20	0.49931
0.52	0.1985	1.16	0.3770	1.80	0.4641	3.40	0.49966
0.54	0.2054	1.18	0.3810	1.82	0.4656	3.60	0.49984
0.56	0.2123	1.20	0.3849	1.84	0.4671	3.80	0.499928
0.58	0.2190	1.22	0.3883	1.86	0.4686	4.00	0.499968
0.6	0.2257	1.24	0.3925	1.88	0.4699	4.50	0.499997
0.62	0.2324	1.26	0.3962	1.90	0.4713	5.00	0.499997

einsteins.ru

Таблица значений функции Лапласа

Таблица значений функции Лапласа

Таблица значений функции Лапласа

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00	0,00000	0,50	0,19146	1,00	0,34134	1,50	0,43319	2,00	0,47725	3,00	0,49865
0,01	0,00399	0,51	0,19497	1,01	0,34375	1,51	0,43448	2,02	0,47831	3,05	0,49886
0,02	0,00798	0,52	0,19847	1,02	0,34614	1,52	0,43574	2,04	0,47932	3,10	0,49903
0,03	0,01197	0,53	0,20194	1,03	0,34849	1,53	0,43699	2,06	0,48030	3,15	0,49918
0,04	0,01595	0,54	0,20540	1,04	0,35083	1,54	0,43822	2,08	0,48124	3,20	0,49931
0,05	0,01994	0,55	0,20884	1,05	0,35314	1,55	0,43943	2,10	0,48214	3,25	0,49942
0,06	0,02392	0,56	0,21226	1,06	0,35543	1,56	0,44062	2,12	0,48300	3,30	0,49952
0,07	0,02790	0,57	0,21566	1,07	0,35769	1,57	0,44179	2,14	0,48382	3,35	0,49960
0,08	0,03188	0,58	0,21904	1,08	0,35993	1,58	0,44295	2,16	0,48461	3,40	0,49966
0,09	0,03586	0,59	0,22240	1,09	0,36214	1,59	0,44408	2,18	0,48537	3,45	0,49972
0,10	0,03983	0,60	0,22575	1,10	0,36433	1,60	0,44520	2,20	0,48610	3,50	0,49977
0,11	0,04380	0,61	0,22907	1,11	0,36650	1,61	0,44630	2,22	0,48679	3,55	0,49981
0,12	0,04776	0,62	0,23237	1,12	0,36864	1,62	0,44738	2,24	0,48745	3,60	0,49984
0,13	0,05172	0,63	0,23565	1,13	0,37076	1,63	0,44845	2,26	0,48809	3,65	0,49987
0,14	0,05567	0,64	0,23891	1,14	0,37286	1,64	0,44950	2,28	0,48870	3,70	0,49989
0,15	0,05962	0,65	0,24215	1,15	0,37493	1,65	0,45053	2,30	0,48928	3,75	0,49991
0,16	0,06356	0,66	0,24537	1,16	0,37698	1,66	0,45154	2,32	0,48983	3,80	0,49993
0,17	0,06749	0,67	0,24857	1,17	0,37900	1,67	0,45254	2,34	0,49036	3,85	0,49994
0,18	0,07142	0,68	0,25175	1,18	0,38100	1,68	0,45352	2,36	0,49086	3,90	0,49995
0,19	0,07535	0,69	0,25490	1,19	0,38298	1,69	0,45449	2,38	0,49134	3,95	0,49996
0,20	0,07926	0,70	0,25804	1,20	0,38493	1,70	0,45543	2,40	0,49180	4,00	0,49997
0,21	0,08317	0,71	0,26115	1,21	0,38686	1,71	0,45637	2,42	0,49224	4,05	0,49997
0,22	0,08706	0,72	0,26424	1,22	0,38877	1,72	0,45728	2,44	0,49266	4,10	0,49998
0,23	0,09095	0,73	0,26730	1,23	0,39065	1,73	0,45818	2,46	0,49305	4,15	0,49998
0,24	0,09483	0,74	0,27035	1,24	0,39251	1,74	0,45907	2,48	0,49343	4,20	0,49999
0,25	0,09871	0,75	0,27337	1,25	0,39435	1,75	0,45994	2,50	0,49379	4,25	0,49999
0,26	0,10257	0,76	0,27637	1,26	0,39617	1,76	0,46080	2,52	0,49413	4,30	0,49999
0,27	0,10642	0,77	0,27935	1,27	0,39796	1,77	0,46164	2,54	0,49446	4,35	0,49999
0,28	0,11026	0,78	0,28230	1,28	0,39973	1,78	0,46246	2,56	0,49477	4,40	0,49999
0,29	0,11409	0,79	0,28524	1,29	0,40147	1,79	0,46327	2,58	0,49506	4,45	0,50000
0,30	0,11791	0,80	0,28814	1,30	0,40320	1,80	0,46407	2,60	0,49534	4,50	0,50000
0,31	0,12172	0,81	0,29103	1,31	0,40490	1,81	0,46485	2,62	0,49560	4,55	0,50000
0,32	0,12552	0,82	0,29389	1,32	0,40658	1,82	0,46562	2,64	0,49585	4,60	0,50000
0,33	0,12930	0,83	0,29673	1,33	0,40824	1,83	0,46638	2,66	0,49609	4,65	0,50000
0,34	0,13307	0,84	0,29955	1,34	0,40988	1,84	0,46712	2,68	0,49632	4,70	0,50000
0,35	0,13683	0,85	0,30234	1,35	0,41149	1,85	0,46784	2,70	0,49653	4,75	0,50000
0,36	0,14058	0,86	0,30511	1,36	0,41309	1,86	0,46856	2,72	0,49674	4,80	0,50000
0,37	0,14431	0,87	0,30785	1,37	0,41466	1,87	0,46926	2,74	0,49693	4,85	0,50000
0,38	0,14803	0,88	0,31057	1,38	0,41621	1,88	0,46995	2,76	0,49711	4,90	0,50000
0,39	0,15173	0,89	0,31327	1,39	0,41774	1,89	0,47062	2,78	0,49728	4,95	0,50000
0,40	0,15542	0,90	0,31594	1,40	0,41924	1,90	0,47128	2,80	0,49744	5,00	0,50000
0,41	0,15910	0,91	0,31859	1,41	0,42073	1,91	0,47193	2,82	0,49760
0,42	0,16276	0,92	0,32121	1,42	0,42220	1,92	0,47257	2,84	0,49774
0,43	0,16640	0,93	0,32381	1,43	0,42364	1,93	0,47320	2,86	0,49788
0,44	0,17003	0,94	0,32639	1,44	0,42507	1,94	0,47381	2,88	0,49801
0,45	0,17364	0,95	0,32894	1,45	0,42647	1,95	0,47441	2,90	0,49813
0,46	0,17724	0,96	0,33147	1,46	0,42785	1,96	0,47500	2,92	0,49825
0,47	0,18082	0,97	0,33398	1,47	0,42922	1,97	0,47558	2,94	0,49836
0,48	0,18439	0,98	0,33646	1,48	0,43056	1,98	0,47615	2,96	0,49846
0,49	0,18793	0,99	0,33891	1,49	0,43189	1,99	0,47670	2,98	0,49856

 



www.matem96.ru

Функция Лапласа — Энциклопедия по машиностроению XXL

Для определения величины соответствующих площадей (ограниченных верхним и нижним пределом допуска), расположенных по обе стороны центра рассеяния, используем приведенную функцию Лапласа при аргументе г = —  [c.70]

Коэффициент риска К выбирают в зависимости от принятого риска Р. При нормальном законе распределения элементарных погрешностей и равновероятном их выходе за обе границы поля допуска значение Р связано со значением функции Лапласа Ф К) формулой  [c.71]

Функция (2.17) называется нормированной функцией Лапласа. Для облегчения расчетов эта функция представлена таблицами, приведенными, например, в [1]. Так доверительному интервалу А, равному значению среднеквадратичной погрешности о, соответствует доверительная вероятность 0,68 доверительному интервалу, равному 2о, — доверительная вероятность 0,95 доверительному интервалу, равному За, — доверительная вероятность 0,997.  [c.42]

Нормированная функция Лапласа 42  [c.356]

Из соответствующих математических таблиц по значениям аргументов — 5,2 и 2а = о находим функции Лапласа — Гаусса (интегралы вероятности) Фх г = 1 и Ф-Аи) = 0.  [c.634]

При заданном ресурсе Т = подсчитывается вероятность безотказной работы Р (Т), которая и служит характеристикой надежности изделия. В этом случае все параметры, определяющие аргумент функции Лапласа, известны, и, используя таблицы этой функции [183, 221 ], подсчитывается Р (Г).  [c.137]

Для изделий с высокими требованиями к надежности обычно задается Р (Т) и необходимо подсчитать ресурс Тр, обеспечивающий данный уровень безотказности. В этом случае в формуле (31) искомым является значение Т, которое входит в аргумент функции Лапласа. Аргумент функции Лапласа будет являться квантилем Хр нормального распределения, т. е. тем его значением, которое соответствует данной вероятности Р (Т). Для квантилей нормального распределения имеются таблицы, например [221].  [c.137]

При использовании таблиц квантилей следует обращать внимание, для какой функции Лапласа (нормированной или нет) они приведены. Так, таблицы квантилей [221 ] приведены для значений вероятностей Р > 0,5, т. е. при Хр = О Я=0,5. Поэтому член 0,5 в формуле (31) уже учтен равенством (34).  [c.138]

Фц — закон нормального распределения Ф —функция Лапласа Л1 — нормирующий множитель.  [c.297]

В качестве количественного выражения нормального распределения воспользуемся функцией Лапласа Ф (2) (интеграл вероятностей)  [c.217]

При этом с помощью таблицы функции Лапласа легко найти для данного случая величину д, а именно  [c.66]

Фо (2) Фо (2) — функция Лапласа фпроизводная функции Ф (2) — коэффициент при показателе  [c.77]

Второе слагаемое выражается через функцию Лапласа  [c.182]

Используя выражение для функции Лапласа, уравнение (4.81) можно переписать в виде  [c.182]

С использованием самой функции Лапласа можно получить другую представляющую интерес величину — вероятность того, что за время зарегистрируется число импульсов N, не превосходящее заданного значения N  [c.136]

Необходимый при испытании результат — вероятность безотказной работы изделия фт(/) можно получить как на основании параметров кривой фт(0, так и на основании параметров кривой (pd i) и ее смещения во времени по данному закону Xn t) = Xij + bt. При некоторых условиях вероятность безотказной работы в интервале (О, /) будет определяться вероятностью непревышения квантилем распределения выходного параметра допустимых границ в момент t. Если оба сопряженных распределения подчиняются нормальному закону, то, пользуясь функцией Лапласа, получим две эквивалентные формулы для вероятности безотказной работы  [c.78]

По таблицам интеграла вероятностей находим значение аргумента и функции Лапласа [Ф(гг) = 0,465] и = 1,82,  [c.72]

Значения pi теоретических вероятностей попадания отклонений в интервалы (xi xi+i) найдены по формуле 2.2.4 [3] с использованием функции Лапласа  [c.194]

Таблица XIV. ФУНКЦИЯ ЛАПЛАСА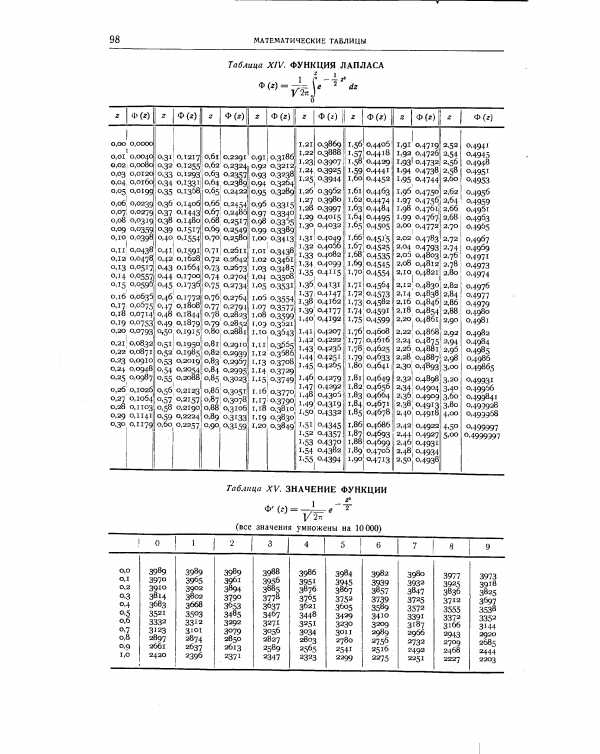

Функции (6, f) суть сферические функции Лапласа, Р ( os т ) — полином Лежандра.  [c.249]

В некоторых руководствах функции Лапласа Ф(г) даются  [c.294]

Если ввести переменную — — то данный интеграл сводится к функции Лапласа и, учитывая, что вероятность безотказной работы Р (Т) I — F (Т), получдм  [c.132]

---

mash-xxl.info