53)Вывести таблицу интегралов из определения неопределенного интеграла .
Таблица интегралов.
1) ∫xαdx = +C (α≠-1)
= =xα
2) α=-1 => ∫x-1dx = ∫=ln|x|+C
ln|x|=ln(x) при x>0 и ln(-x) при x<0
(ln|x|)’= 1/x при x>0 и 1/x при x<0
∫= arctgx + C или –arctgx + C
∫=
∫= arcsinx + C или –arcsinx + C
∫= ln|x+|+C = (+)Arshx + Cили (-) Archx + C
∫axdx = + C
∫exdx = ex + C
∫sinxdx = -cosx + C
∫cosxdx = sinx + C
∫= tgx + C
∫= ctgx + С
∫shxdx = chx + C
∫chxdx = shx + C
∫= thx + C
∫= -cthx + C
Дополнение к таблице интегралов.
1) ∫=
∫= ∫==
2) ∫=
∫= ===
∫=
∫= ==
4) = arcsin+ C
= == arcsin+ C
5) = ln|x +| + C
= ==+ C =+C= ln|x +| — lna + C = ln|x +| + C1
6) = ±+ C
= ==+ C = =±+ C
7)
= |x=asint, dx=acostdt,=acost| == ====+ C = =+ C =+ C =,при cos2t=, sint=x/a, cost=, t=arcsin(x/a).
8) dx =
________________________________________________________________________
54) Замена переменной в неопределенном интеграле.
Теорема: пусть ф-я x=ϕ(t) определена и дифференцируема на (α;β), а мн-во ее значений есть (a,b).
Пусть для ф-и f(x) на (a,b) существует первообразная F(x), т.е. ∫f(x)dx= F(x)+C.Тогда всюду на (α;β) существует первообразная для ф-и f(ϕ(t))*ϕ’(t) и имеет место ф-ла
∫f(x)dx = ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t)) + C
Док-во: F(x) – первообразная для f(x). найдем дифференциал d(F(ϕ(t))+C)=(F(ϕ(t))+C) t’dt = =F’(ϕ(t))*ϕ’(t)dt = f(ϕ(t))*ϕ’(t)dt => ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t))+C (1)
d(F(ϕ(t))+C)=f(ϕ(t))*ϕ’(t)dt=f(x)dx при x=ϕ(t), ϕ’(t)dt=xt’dt=dx
∫f(x)dx=f(ϕ(t))+C (2)
Объединяя (1) и (2)б, получаем:
∫f(x)dx=∫f(ϕ(t))*ϕ’(t)dt=F(ϕ(t))+C. полученная ф-ла назыв. ф-лой замены переменной в неопределенном интеграле.
В некоторых примерах, когда под знаком корня стоят выр-я, содержащие x2б аналогичные замены ен приводят к верному решению. Для интегралов такого вида сещуствуют спец. Замены:
∫R(x,)dx =>замена x=asint, dx=arccost+dt(a>0)
= === a|cost| = acost
x=asint => sint = => t=arcsin, tϵ[], cost>0
∫R(x,)dx = ∫R(asint, acost)*acostdt
∫R(x,)dx =>замена x=asht, dx=acht+dt(a>0)
= === a|cht| = acht
ch2t – sh2t = 1
∫R(x,)dx = ∫R(asht, acht)*achtdt
Либо: x=atgt, dx=
= ===
1 + tg2t = 1 + =
x=atgt => tgt = => t = arctg, tϵ[]
∫R(x,)dx = ∫R(atgt,)
∫R(x,)dx =>замена x=acht, dx=ashtdtб либо x=
= === a|sht| = asht
∫R(x,)dx = ∫R(acht, asht)*ashtdt
Либо: x=,dx=
= === a|ctgt|= actgt.
=== ctg2t
∫R(,actgt)actgtdt.
________________________________________________________________________
55)Интегрирование по частям в неопределенном интеграле.
Теор.: пусть каждая из ф-й u(x) и v(x) определены и диффер. на (a,b) и пусть на этом мн-ве сущ. первообразная для ф-и u(x)*v’(x). Тогда на (a,b) сущ. первообразная для ф-и v(x)*u‘(x) и имеет место ф-ла ∫u(x)*v’(x)dx = uv — ∫v(x)*u’(x)dx или ∫udv = uv — ∫vdu.
Док-во: рассмотрим дифференциал d(uv) = vdu + udv
udv = d(uv) – vdu |∫ => ∫udv = ∫d(uv) — ∫vdu
∫udv = uv — ∫vdu – формула интегрирования по частям
Для применения этой формулы подынтегральные выр-я нужно представить в виде одной ф-и на дифференциал другой ф-и.
Применяется к ∫ след вида:
∫f(x)dx, где f(x) – обратная ф-я
f(x) = {lnx, ,arcsinx, arccosx, arctgx, arcctgx}, f(x)=u, dx=dv
∫f(x)P(x)dx, где f(x)= {lnx, ,arcsinx, arccosx, arctgx, arcctgx}, f(x)=u, P(x)dx=dv, P(x) – рациональная или иррациональная ф-я.
∫P(x)f(x)dx, где P(x)-многочлен, f(x) = {ex, ax, sinx, cosx, tgx, ctgx}, P(x)=г
∫eaxcosbxdx и ∫eaxsinbxdx – круговые интегралы.
Эти интегралы вычисляются 2 раза по частям. В результате двукратного применения ф-лы интегрирования по частям, в правой части получаем такой же интеграл, что и в левой. Вычисляем этот интеграл, решая алгебраическое уравнение. В круговых интегралах не важно, какую из ф-й обозначить за u.
eiϕ=cosϕ+isinϕ, cosϕ=Re eiϕ, sinϕ=Im eiϕ. Re-действительная часть, Im-мнимая часть.
________________________________________________________________________
studfiles.net
Таблица интегралов
В школе у многих не получается решить интегралы или возникают какие-либо трудности с ними. Данная статья поможет вам в этом разобраться, так как в ней вы найдете все таблицы интегралов.
Интеграл является одним из главных вычислений и понятием в математическом анализе. Его появление получилось от двух целей:
Первая цель — восстановить функцию с помощью ее производной.
Вторая цель — вычисление площади, находящейся на расстоянии от графика к функции f(x) на прямой где, а больше или равна х больше или равен b и ось абсцисс.
Данные цели подводят нас к определенным и неопределенным интегралам. Связь между данными интегралами лежит в поиске свойств и вычислении. Но все течет и все меняется со временем, находились новые пути решения, выявлялись дополнения тем самым приводя определенные и неопределенные интегралы к иным формам интегрирования.
Что такое неопределенный интеграл спросите Вы. Это первообразная функция F(x) одной переменной x в интервале а больше х больше b. называется любой функцией F(x), в данном интервале для любого обозначения х, производная равняется F(x). Понятно что F(x) первообразная для f(x) в промежутке а больше х больше b. Значит F1(x) = F(x) + C. С -является любым постоянным и первообразным для f(x) в данном интервале. Данное утверждение обратимо, для функции f(x) — 2 первообразные отличаются только постоянной. Опираясь на теорему интегрального исчисления получается, что каждая непрерывная в интервале a
Для наглядности изучения данной темы, предлагаю посмотреть видео. В нем подробно рассказывается и показывается как находить интегралы.
Каждая таблица интегралов сама по себе очень полезна, так как помогает в решении конкретного вида интегралов.
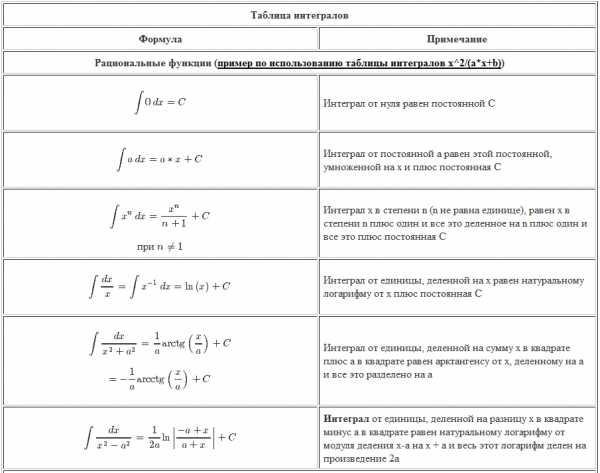

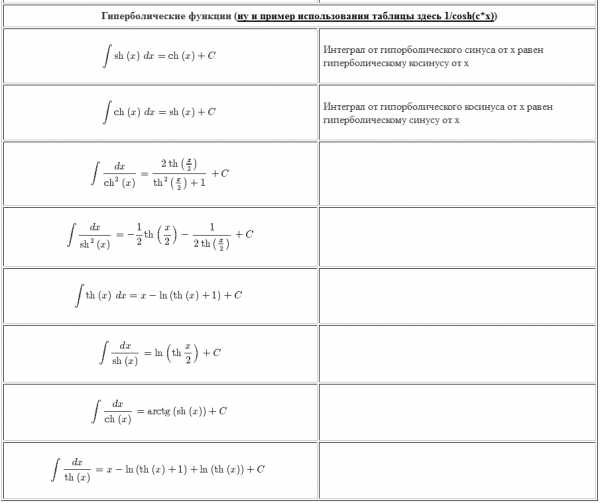



Все возможные виды канцтоваров и не только. Вы можете приобрести через интернет-магазин v-kant.ru. Либо просто перейдите по ссылке Канцтовары Самара (http://v-kant.ru) качество и цены Вас приятно удивят.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Таблица определенных интегралов — Энциклопедия по машиностроению XXL
При вычислении интегралов Мора пользуемся таблицей определенных интегралов в Приложении (табл. 2). [c.374]ТАБЛИЦА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ [c.178]
Т а f) л и ц а 2-7 Таблица определенных интегралов
С помощью таблиц определенных интегралов и выполнения обратного синус-преобразования Фурье получим [c.325]
В любой таблице определенных интегралов мы найдем [c.278]
Опуская интеграл с импульсной функцией, получим Используя таблицу определенных интегралов, найдем [c.226]
Пользуясь таблицами определенных интегралов, можно установить, что интеграл, находящийся во втором слагаемом правой [c.307]
Определенные интегралы этого типа собраны в таблицы ) а если написать [c.43]
Формула (4.11) является основным инструментом точного вычисления определенных интегралов, в связи с чем существенное значение приобретает нахождение первообразных функций. Техника нахождения первообразных функций основана на применении свойств интеграла, различных подстановок и, в конечном счете, стандартных таблиц (см. табл. 4.2 [41— 43]. [c.100]
После несложных преобразований, включающих нахождение определенных интегралов, чьи значения легко находятся по таблицам, получим [c.334]
В приложении приведены свойства функции V т]) показано ее применение к вычислению сложных определенных интегралов составлена таблица соответствий изображение — оригинал в преобразовании Лапласа указана ее связь с другими специальными функциями приведена таблица четырех функций, описывающих процессы, протекающие в обменных системах. [c.57]
Интегралы Ферми—Дирака обсуждались в нескольких работах имеется ряд таблиц их значений [23]. Здесь мы рассмотрим некоторые проблемы, относящиеся к их использованию для анализа данных по жидким полупроводникам. Появление техники ЭВМ сделало возможным использование более сложных определенных интегралов, зависящих от более чем одного параметра мы рассмотрим связанные с этим вопросы.
Численным дифференцированием и интегрированием называются операции по нахождению производных и определенных интегралов от функции при условии использования только таблицы ее значений, которая или задается (если мы имеем дело с табличной функцией) или может быть вычислена. [c.655]
В тех случаях, когда данные по теплоемкости как функции температуры представлены в форме таблиц или графика и неизвестны эмпирические постоянные уравнений для теплоемкости, как в уравнении (1-58), интегралы уравнений (10-8) и (10-10) можно вычислить графически и полученные значения АНт и AS°T подставить непосредственно в уравнение (10-6) для AFt Этот метод проще и короче, чем определение постоянных уравнений для теплоемкостей и использование затем аналитических выражений. [c.296]
Неподвижный непрерывно действующий источник теплоты переменной мощности. Определение приращений температуры точек тела при действии источника теплоты переменной мощности принципиально ничем не отличается от ранее рассмотренных случаев с источниками теплоты постоянной мощности. Если мощность источника теплоты изменяется во времени, т. е. q = q t), то необходимо взамен постоянной величины q в уравнения (6.9), (6.12) и (6.14) подставить функцию q t), а затем провести интегрирование. Разумеется, при этом может оказаться, что интегралы взять невозможно. В таких случаях их определение следует производить численно, составляя таблицы или программу для ЭВМ. [c.165]
Значения интегралов, часто встречающихся при определении деформаций кривой бруса, даны в таблице 11.7, а в таблице 11.8 приведены значения перемещений и значения наибольших изгибающих моментов для некоторых брусьев малой кривизны. [c.327]
При численном определении дисперсий (когда таблицей интегралов (6.6.66) воспользоваться нельзя) бесконечные пределы интегрирования заменяют конечными числовое значение о 0 зависит от требуемой точности результата. [c.402]
Приращения удельной тяги AR соответственно в идеальном и в вязком приближениях определяются по отношению к удельной тяге R сопел sO с плавным сужением и с изломом в точке а. Для идеального газа из сопел с плавным сужением они реализуют максимум R. Согласно табл. 1 и 2, такое же преимущество сопел с изломом сохраняется и для вязкого газа. Отрицательный вклад (AR ) в тягу осевой компоненты интеграла сил трения по стенкам дают в процентах (отнесенные к R ) — предпоследние столбцы таблиц. Наряду с этим вязкость оказывает влияние на интегральные характеристики сопел через вытесняющий и сглаживающий (см. ниже) эффекты. Принятый способ определения тяги и расхода через соответствующие интегралы в сечении выхода из сопла учитывает суммарное воздействие всех этих эффектов. Информацию о всех потерях удельной тяги R дает приведенное в последнем столбце таблиц ее отношение к соответствующей идеальной величине R[ . Здесь R[ — удельная тяга сопла Лаваля, реализующего на выходе при тех же F /Fa равномерный поток идеального газа. [c.344]
Следует иметь в виду, что h совпадает с AL — величиной интервала в формулах для определения частот и частостей распределений. При расчетах без ЭВМ составляются таблицы, позволяющие вычислить сразу все интегралы. [c.66]
Рассмотренная выше задача очень хорошо иллюстрирует сходство между методами преобразований Фурье и Лапласа в одномерных задачах подобного типа. Во-первых, если в нашем распоряжении имеются соответствующие таблицы преобразованных функций, то работа, которую необходимо проделать при расчетах по одному и другому методу, одинакова. Во-вторых, если таблиц преобразованных функций нет, то в любом случае необходимо провести определенное количество расчетов с интегралами, полученными из формулы обращения. Существенное преимущество преобразования Лапласа для задач этого типа проявляется в связи с граничными условиями, поскольку в нем рассматриваются одинаковым образом все граничные условия. Однако ранее было необходимо использовать преобразование по синусам, так как при X = О была задана температура тела v если бы был задан тепловой поток на граничной поверхности, следовало бы использовать преобразование по косинусам в случае граничного условия третьего ряда ни одно из этих преобразований не подходит и следует разработать преобразование нового типа в случае граничного условия типа Е, приведенного в 9 гл. I, потребуется уже другое преобразование и т. д. [c.449]
Нормированное нормальное распределение позволяет составить таблицу для определения интегральной функции. Сделаем в интеграле (42) замену переменной [c.61]
Приведен расчет потенциальной энергии взаимодействия между двумя атомами водорода и кислорода в их основных электронных состояниях. Рассмотрены значения второго вириального коэффициента для системы О—Н. Даны некоторые теплофизические характеристики систем О—Н, Н—ОН, О—ОН, ОН—ОН. Рассчитаны интегралы столкновений, которые могут быть использованы при определении коэффициентов переноса. Таблиц 5. Библиографий 10. Иллюстраций 1. [c.404]
Связь с определенными 1 — 173 — Таблицы 1 — 154, 165 —несобственные 1 — 174, 177 — Сходимость и расходимость — Признаки Коши 1 — 176 Интегралы определенные 1 — 172 [c.426]
Ньютону, как и Барроу, была известна геометрическая интерпретация интеграла функции как площади соответствующей криволинейной трапеции, а также то, что производная этой площади по абсциссе является ординатой этой кривой. Понятия определенного интеграла у Ньютона нет, однако есть, хоть и не полная, но достаточно обширная таблица неопределенных интегралов. Большинство положений своего математического анализа он продемонстрировал в процессе решения конкретных задач, оставив своим последователям возможность построения стройной математической теории. [c.67]
В которых относительные температуры для материала 9ч и для газа 0г определяются безразмерными числами высоты слоя У и времени 2 У,=кЛ1сггат(, Z=kvт ы l — —/),а/о(х) является функцией Бесселя первого рода от мнимого аргумента. Расчет по приведенным формулам облегчен наличием таблиц показательных функций и функций Бесселя, Определение интегралов в ( Х,19) и (1Х.20) может быть произведено любым из известных способов. [c.306]
Из рассмотре( кых примеров видно, что при определении перемещений для бруса, изогнутого ио дуге окружности, приходится брать интегралы от простейших трш-онометрических (функций в различных комбинациях. Так как эти ко.мбииации довольно типичны, представляется целесообразным даль сводку наиболее часто нстре-чающихед при решении подобных задач интегралов (см. таблицу 5). [c.181]
Отправляясь от определенных начальных условий, можно строить интегралы так, чтобы положение и скорость были согласованы при переходе от одной частичной дуги (вдоль которой р рассматривается как постоянная) к следующей. Результаты численного подсчета собираются затем в таблицы, в которых табулируются четыре функции от псевдоскорости и ). [c.101]
Из Приведенных соотношений видно, что теория динамического поведения произвольной однопролетной балки, для которой с определенной точностью можно достаточно хорошо выделять резонансные частоты колебаний, может быть сведена к единственному соотношению, если для каждой системы полученных условий определены параметры эффективных масс и жесткостей. Для ряда случаев интегралы и ряды в выражении (5.18) можно вычислить с помощью таблиц нормальных форм колебаний, составленных Бишопом и Джонсоном [5.19]. Некоторые из этих интегралов и рядов приведены в табл. 5.1 для ряда концевых условий. [c.218]
Этот расчёт проведён в т, н. приближении энергетических центров тяжести [4]. Из сравнения (6) и (2) видно, что параметр А квазиклассич. теории определяется обменной энергией А, т, е, A = zsA. Для определения величины и знака А нужна более точная теория, к-рую лают, напр , микроскопич. расчёты обменных взаимодействий в металлах методом функционала спиновой плотности, исходя лишь из кристаллич. структурьг и порядкового номера в таблице Менделеева [II]. Используются также нек-рые усложнения гейзенберговского гамильтониана, иапр. с помощью учёта неск. типов обменных интегралов между разл. соседями в узлах решётки (подробнее см. Спиновый гамильтониан). При низких Т, используя метод вторичного квантования, удалось провести более точный расчёт энергетич. спектра ферромагнетика. Ограничиваясь состояниями, близкими к основному (при О К), в к-ром спины всех магнитно-активных электронов взаимно параллельны, можно найти собств. значения оператора [c.297]
Некоторые усовершенствования теории сохраняют возможность аналитического определения характеристик. Например, если коэффициент сопротивления сечения задать в виде Са = = So + Si t + то расчет профильной мощности будет уточнен и в то же время соответствующие интегралы можно найти аналитически. Но получаемые формулы оказываются все-таки весьма сложными, и потому результаты часто представляют в виде графиков характеристик, построенных для какого-либо типичного винта. Вследствие сложности аэродинамики несущего винта большинство методов расчета характеристик, кроме тех, которые основаны на простейших формулах, сопряжено с большим объемом вычислений. Поэтому результаты таких расчетов удобно и экономично представлять в виде графиков или таблиц характеристик. Если использовать быстродействующие ЦВМ, то численный анализ характеристик практически приемлем и для конкретных винтов. Такой анализ необходим, когда в нем учитываются многие конкретные особенности данного винта, такие, как форма лопасти в плане и набор ее профилей. [c.288]
Определение диффузного углового коэффициента между двумя элементарными площадками в соответствии с (3.5) не представляет труда. Однако вычисление локальных и средних угловых кдэффициентов требует одно- и двукратного интегрирования по поверхности. Такие интегралы, за исключением случаев самых простых форм поверхностей, довольно сложны. Гамиль-тон и Морган [1] вычислили диффузные угловые коэффициенты для простых конфигураций, включая прямоугольники, треугольники и цилиндры, и представили результаты в виде графиков и таблиц. В работах [2—4] собраны угловые коэффициенты для различных тел простой формы. Источники, содержащие определения угловых коэффициентов, сведены в таблицу в книге Хауэлла и Зигеля [5]. Сводка других данных по угловым коэффициентам приведена в работах [6—8]. Различные аналитические и экспериментальные методы определения диффузных угловых коэффициентов описаны в книге Якоба [9]. В работе [10] представлена программа расчета угловых коэффициентов для цилиндрических ребер, составленная на языке ФОРТРАН. Ниже рассматриваются некоторые аналитические методы, применяемые для расчета диффузных угловых коэффициентов. [c.141]
Представлены функции потенциальной энергии взаимодействия атомов лития, натрия, калия, рубидия, цезия для состояний в области энергий порядка 0,1 эв, аппроксимированные уравнениями экспоненциального типа. Потенциалы 2 + определены методом RKRV и с помощью функции Хульбурт-Гиршфельдера, Для определения потенциалов предложена эмпирическая методика, правильность которой проверена и подтверждена. Вычислены интегралы столкновений атомов щелочных мета.члов с возможной погрешностью 6%. Таблиц 6, Библиографий 23, [c.406]
Для облегчения пользования выведенными в настоящем параграфе формулами при определении перемещений в практических задачах нами составлена таЬл. 42 для интегралов B B dz, при этом числовые значения коэффициентов г, в, 1 к р, входящих в формулы этой таблицы, даны в приложении 11. [c.305]
mash-xxl.info
