Найти корень из комплексного числа онлайн, подробное решение
Онлайн калькулятор предназначен для вычисления корня n-ой степени из комплексного числа, с описанием подробного хода решения на русском языке. Для нахождения корня n-ой степени, сначала необходимо выбрать (алгебраическую, тригонометрческую или показательную) форму представления комплексного числа. Далее приведены минимальные теоретические сведения, необходимые для понимания решения, выдаваемого калькулятором.
Согласно теории, корень n-ой степени из любого числа (n∈Z) имеет ровно n значений. Например:
Пример, по интереснее:
где i — мнимая единица. Можете попробовать возвести все значения в куб, и действительно получите 8. Возникает вопрос: как найти все n значений корня n-ой степени из числа? Для этого необходимо использовать формулу Муавра, причем комплексное число должно быть записано в тригонометрической форме. Наш калькулятор автоматически осуществит перевод введенного числа в тригонометрическую форму, если потребуется.
www.mathforyou.net
Поиск значений в списке данных
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
Предположим, вам нужно найти расширение телефона сотрудника с помощью его номера, а также правильно оценить коэффициент Комиссии для суммы продажи. Вы ищете данные, чтобы быстро и эффективно находить определенные данные в списке и автоматически проверять, правильно ли используются данные. После того как вы просмотрит данные, вы можете выполнить вычисления и отобразить результаты, указав возвращаемые значения. Есть несколько способов поиска значений в списке данных и отображения результатов.В этой статье
-
Поиск значений в списке по вертикали по точному совпадению
-
Поиск значений в списке по вертикали по приблизительному совпадению
Поиск значений по вертикали в списке неизвестного размера с точным соответствием
-
Поиск значений в списке по горизонтали по точному совпадению
-
Поиск значений в списке по горизонтали с использованием приблизительного совпадения
-
Создание формулы подстановки с помощью мастера подстановок (только в Excel 2007)
Поиск значений в списке по вертикали по точному совпадению
Для выполнения этой задачи можно использовать функцию ВПР или сочетание функций индекс и ПОИСКПОЗ.
Примеры использования функции ВПР

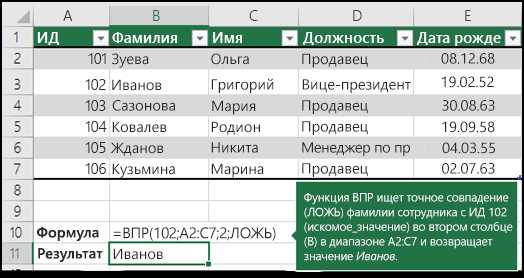
Дополнительные сведения можно найти в разделе функция ВПР.
Примеры ИНДЕКСов и СОВПАДЕНИй
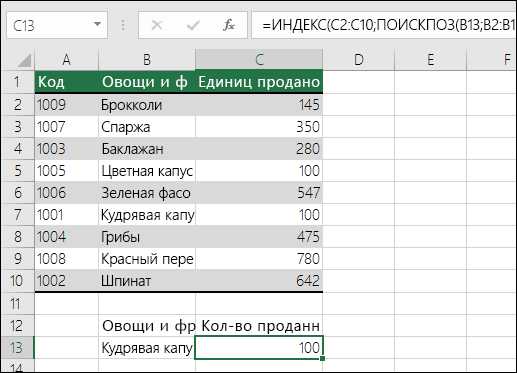
Что означает:
=ИНДЕКС(нужно вернуть значение из C2:C10, которое будет соответствовать ПОИСКПОЗ(первое значение «Капуста» в массиве B2:B10))
Дополнительные сведения можно найти в разделе Функция индекс и функция ПОИСКПОЗ.
К началу страницы
Поиск значений в списке по вертикали по приблизительному совпадению
Для этого используйте функцию ВПР.
Важно: Убедитесь, что значения в первой строке отсортированы в возрастающем порядке.
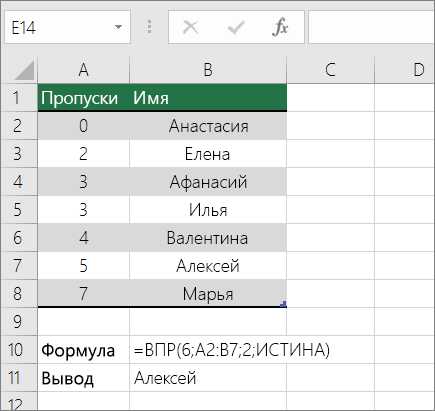
В приведенном выше примере функция ВПР ищет имя учащегося, у которого есть 6 тардиес в диапазоне A2: B7. В таблице нет записи для 6 тардиес, поэтому функция ВПР ищет следующее самое высокое соответствие ниже 6 и находит значение 5, связанное с первым именем Дэйв, и, следовательно, возвращает Дэйв.
Дополнительные сведения можно найти в разделе функция ВПР.
К началу страницы
Поиск значений по вертикали в списке неизвестного размера с точным соответствием
Для выполнения этой задачи используйте функции СМЕЩ и ПОИСКПОЗ.
Примечание: Этот подход используется, если данные находятся в диапазоне внешних данных, который вы обновляете каждый день. Вы знаете, что в столбце B есть Цена, но вы не знаете, сколько строк данных возвращает сервер, а первый столбец не отсортирован по алфавиту.
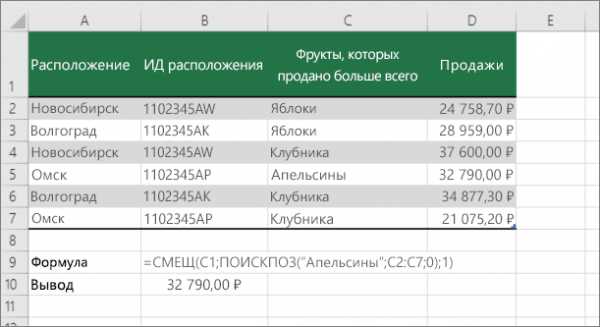
C1 — это верхняя левая ячейка диапазона (также называемая начальной ячейкой).
Match («апельсины»; C2: C7; 0) ищет оранжевый цвет в диапазоне C2: C7. Не следует включать начальную ячейку в диапазон.
1 — количество столбцов справа от начальной ячейки, для которых должно быть возвращено возвращаемое значение. В нашем примере возвращаемое значение находится в столбце D, Sales.К началу страницы
Поиск значений в списке по горизонтали по точному совпадению
Для выполнения этой задачи используется функция ГПР. Ниже приведен пример.
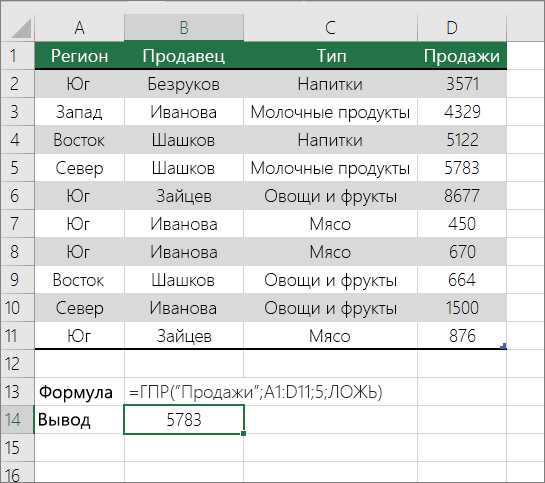
Функция ГПР выполняет поиск по столбцу Sales и возвращает значение из строки 5 в указанном диапазоне.
К началу страницы
Поиск значений в списке по горизонтали с использованием приблизительного совпадения
Для выполнения этой задачи используется функция ГПР.
Важно: Убедитесь, что значения в первой строке отсортированы в возрастающем порядке.
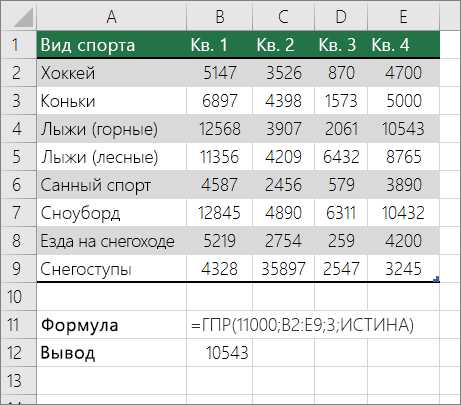
В приведенном выше примере функция ГПР ищет значение 11000 в строке 3 в указанном диапазоне. Он не находит 11000 и, следовательно, ищет следующее наибольшее значение, которое меньше 1100 и возвращает число 10543.
Дополнительные сведения можно найти в разделе функции ГПР.К началу страницы
Создание формулы подстановки с помощью мастера подстановок (толькоExcel 2007 )
В Excel 2007 мастер подстановок создает формулу подстановки на основе данных листа, имеющих заголовки строк и столбцов. Мастер подстановок помогает находить другие значения в строке, когда вы знаете значение в одном столбце, и наоборот. Мастер подстановок использует индекс и СОВПАДЕНИе в создаваемых формулах.
-
Щелкните ячейку в диапазоне.
-
На вкладке формулы в группе решения нажмите кнопку Подстановка .
Если команда подстановка недоступна, необходимо загрузить мастер подстановок надстройка программу.
Загрузка программы-надстройки «Мастер подстановок»
-
Нажмите кнопку Microsoft Office , щелкните Параметры Excelи выберите категорию надстройки.
-
В поле Управление выберите элемент Надстройки Excel и нажмите кнопку Перейти.
-
В диалоговом окне надстройки установите флажок Мастер подстановоки нажмите кнопку ОК.
-
Следуйте инструкциям мастера.
К началу страницы
support.office.com
Найти все значения , при которых сходится ряд :
1.53. | 1.54. . | |
1.55. . | ||
1.56. . | ||
Исследовать на сходимость ряд с помощью признака Даламбера:
Исследовать на сходимость ряд с помощью признака Коши:
1.67. | 1.68. |
1.69. | 1.70. |
1.71. | 1.72. |
1.73. | 1.74. . |
Исследовать на
сходимость ряд 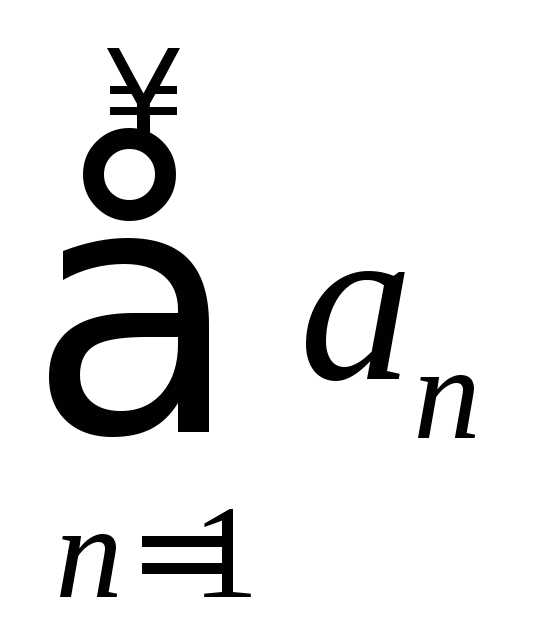 с помощью признака Раабе или признака
Гаусса:
с помощью признака Раабе или признака
Гаусса:
1.75. | 1.76. | |
1.77. | 1.78. . | |
1.79. . | ||
1.80. . | ||
Исследовать на
сходимость ряд 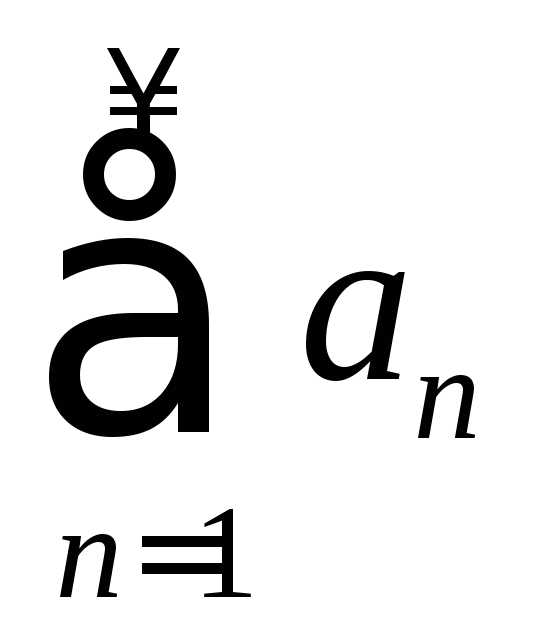 :
:
1.81. | 1.82. . |
1.83. | 1.84. . |
1.85. | 1.86. |
1.87. | 1.88. |
1.89. | 1.90. . |
Ответы: 1.33. Сходится. 1.34. Расходится. 1.35. Сходится. 1.36. Сходится. 1.37. Сходится. 1.38. Расходится. 1.39. Сходится. 1.40. Расходится. 1.41. Расходится. 1.42. Сходится. 1.43. Сходится. 1.44. Сходится. 1.45. Сходится. 1.46. Сходится. 1.47. Сходится. 1.48. Расходится. 1.49. Расходится. 1.50. Сходится. 1.51. Сходится. 1.52. Сходится. 1.53. 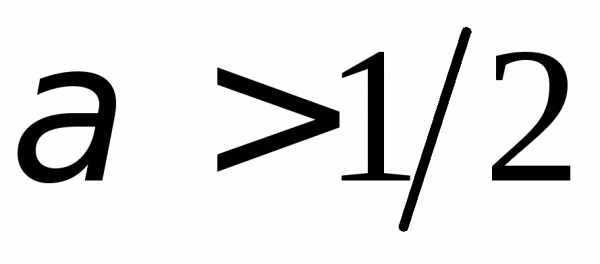 .1.54.
.1.54. 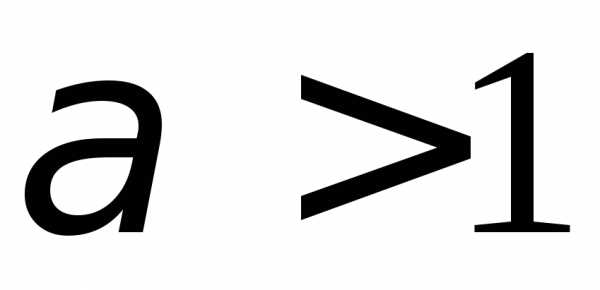 .1.55.
.1.55. 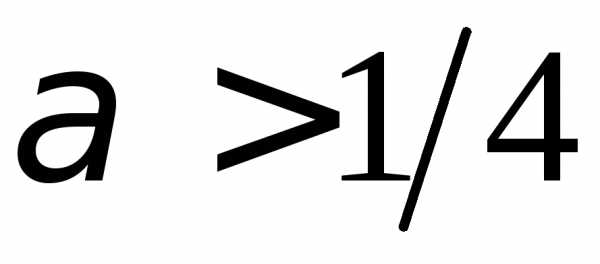 .1.56.
.1.56. 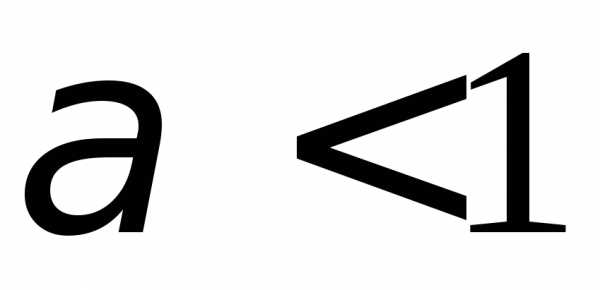 .1.57. Сходится. 1.58.
Сходится при
.1.57. Сходится. 1.58.
Сходится при  ,
расходится при
,
расходится при .1.59. Признак Даламбера не решает вопроса о
сходимости данного ряда. 1.60. Расходится. 1.61. Сходится. 1.62. Сходится. 1.63. Сходится. 1.64. Сходится. 1.65. Сходится. 1.66. Сходится. 1.67. Сходится. 1.68. Сходится. 1.69. Расходится. 1.70. Сходится. 1.71. Сходится. 1.72. Сходится. 1.73. Сходится. 1.74. Сходится. 1.75. Сходится при
.1.59. Признак Даламбера не решает вопроса о
сходимости данного ряда. 1.60. Расходится. 1.61. Сходится. 1.62. Сходится. 1.63. Сходится. 1.64. Сходится. 1.65. Сходится. 1.66. Сходится. 1.67. Сходится. 1.68. Сходится. 1.69. Расходится. 1.70. Сходится. 1.71. Сходится. 1.72. Сходится. 1.73. Сходится. 1.74. Сходится. 1.75. Сходится при 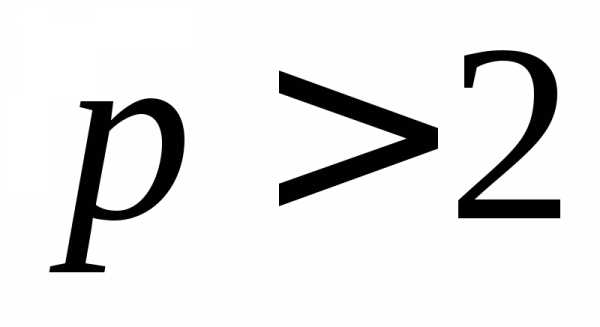 .1.76. Сходится, если
.1.76. Сходится, если 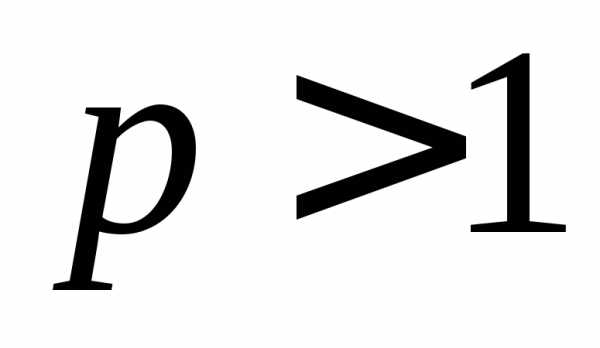 ,
и расходится, если
,
и расходится, если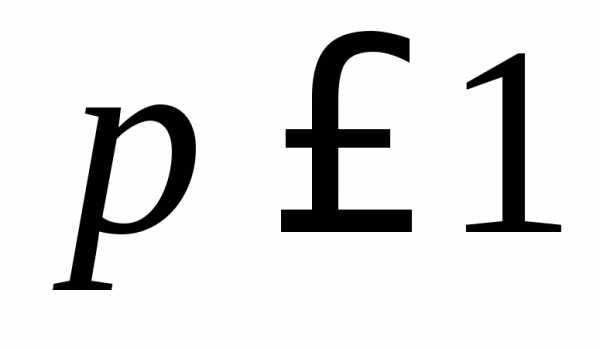 .1.77. Сходится, если
,
и расходится, если.1.78. Сходится при
.1.77. Сходится, если
,
и расходится, если.1.78. Сходится при 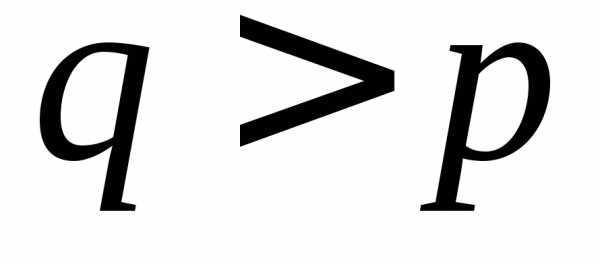 .1.79. Сходится. 1.80. Сходится при
.1.79. Сходится. 1.80. Сходится при 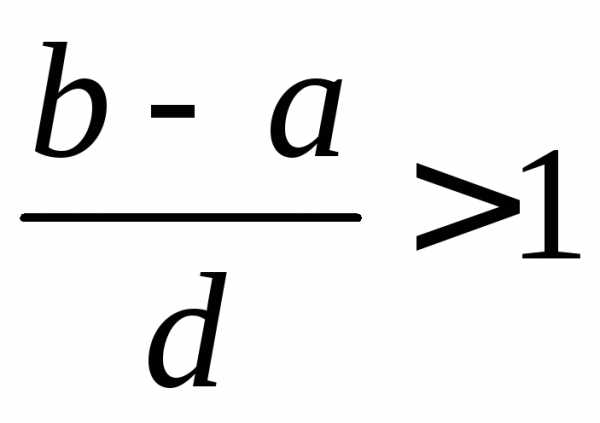 .1.81. Сходится. 1.82. Сходится. 1.83. Сходится. 1.84. Сходится при
.1.81. Сходится. 1.82. Сходится. 1.83. Сходится. 1.84. Сходится при 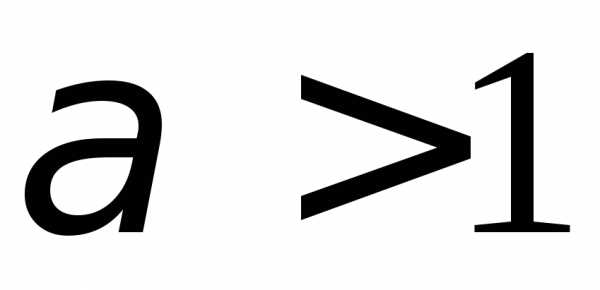 и при
и при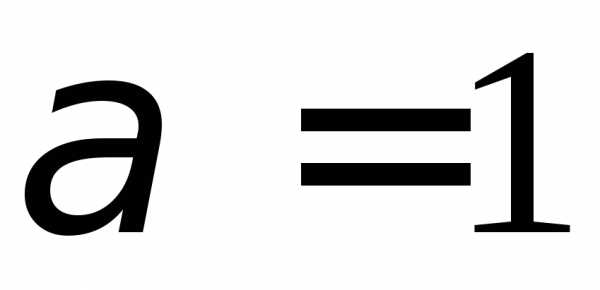 ,
если
,
если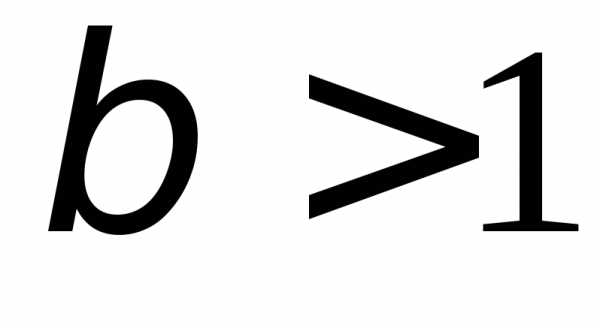 .1.85. Сходится. 1.86. Сходится. 1.87. Сходится. 1.88. Расходится. 1.89. Сходится. 1.90. Сходится.
.1.85. Сходится. 1.86. Сходится. 1.87. Сходится. 1.88. Расходится. 1.89. Сходится. 1.90. Сходится.
1.3. Знакопеременные ряды. Абсолютная и условная сходимость
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Ряд 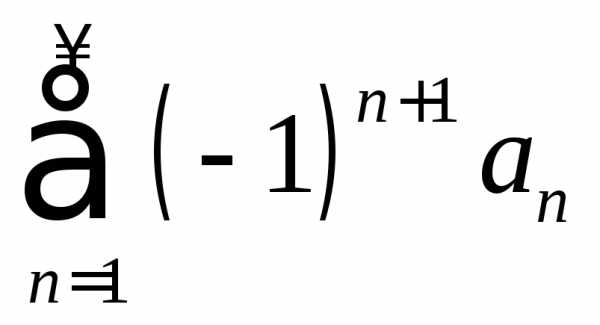 ,
где
,
где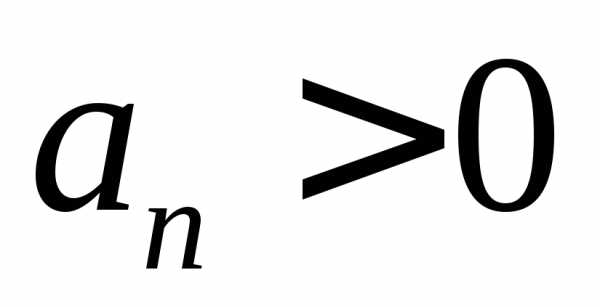 ,
называетсязнакочередующимся, или альтернирующим.
,
называетсязнакочередующимся, или альтернирующим.
Абсолютно сходящимся рядом называется сходящийся ряд 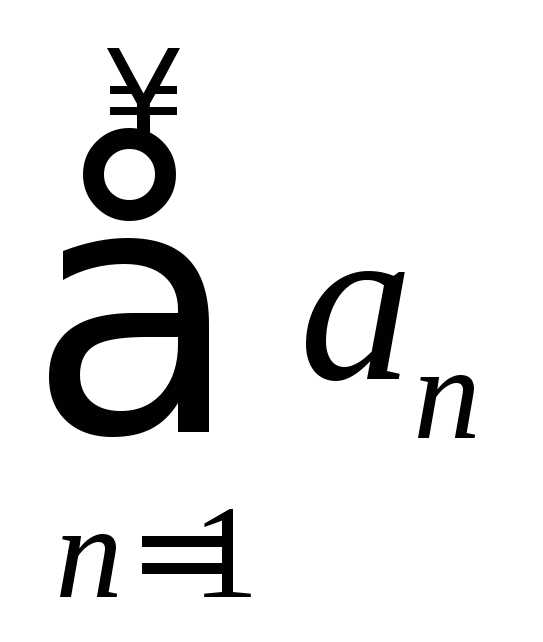 ,
для которого сходится и ряд
,
для которого сходится и ряд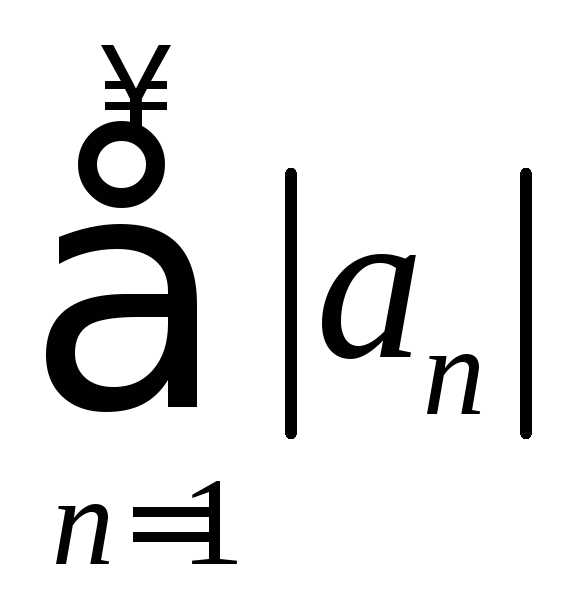 .
.
Свойства абсолютно сходящихся рядов таковы.
1. Абсолютно
сходящийся ряд сходится, т. е. из сходимости
ряда 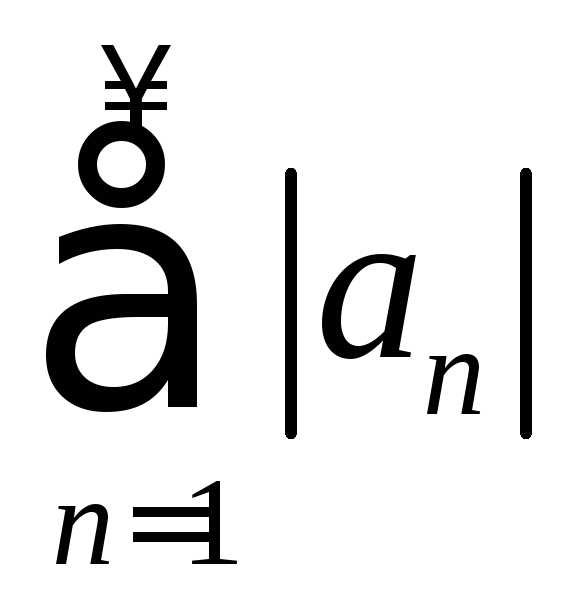 следует сходимость ряда
следует сходимость ряда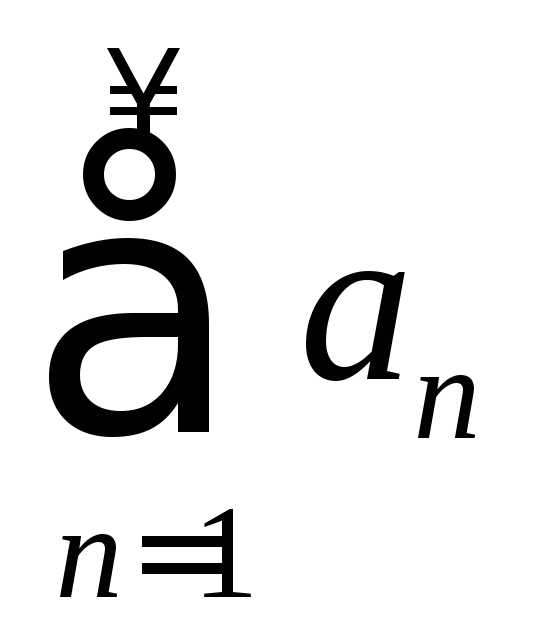 .
.
Если ряды
 и
и абсолютно сходятся, то при любых
абсолютно сходятся, то при любых и
и ряд
ряд также абсолютно сходится.
также абсолютно сходится.Если ряд абсолютно сходится, то ряд, составленный из тех же членов, но взятых в другом порядке, также абсолютно сходится, и его сумма равна сумме исходного ряда.
4. Правило
Коши. Если
ряды 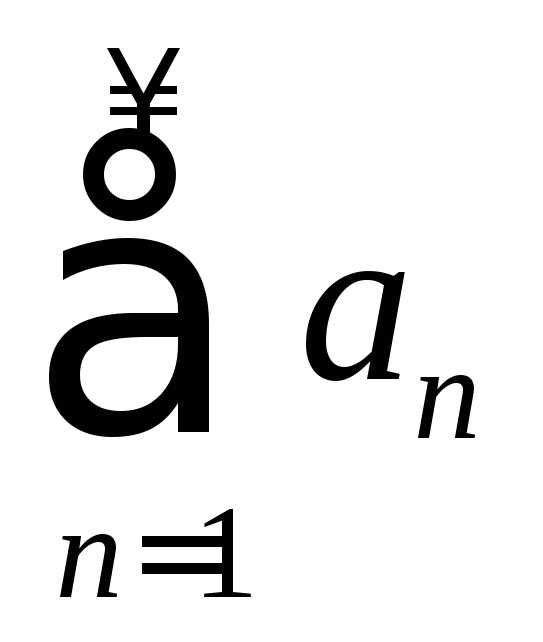 и
и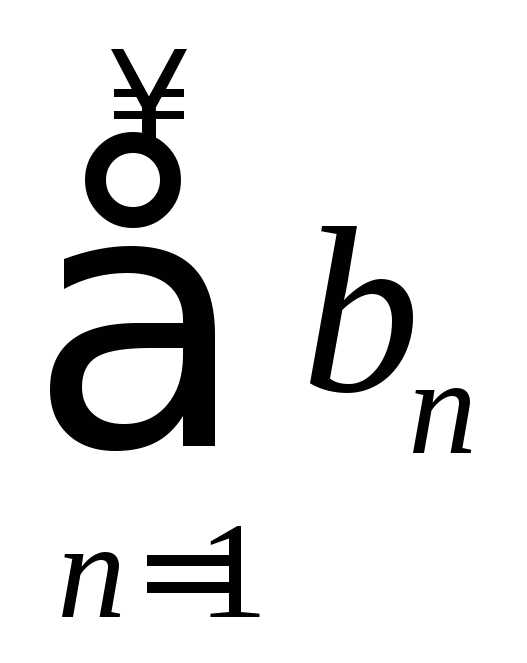 абсолютно сходятся, то
абсолютно сходятся, то
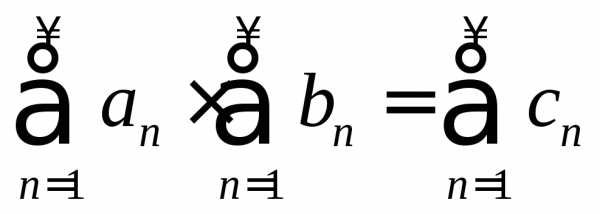 ,
,
где .
Ряд 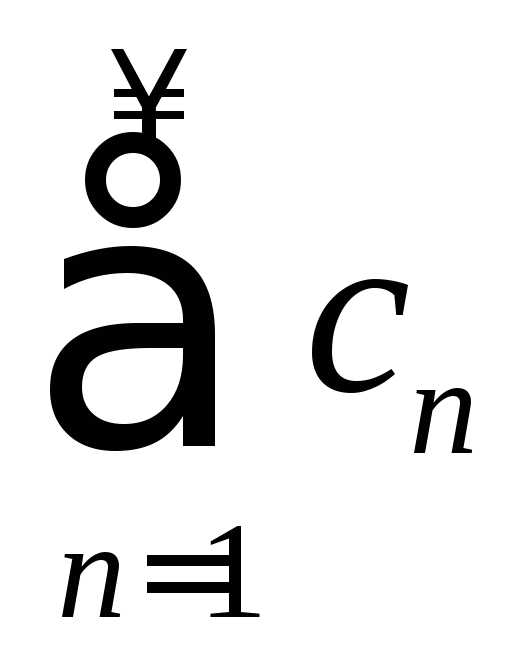 также абсолютно сходится, а его сумма
равна
также абсолютно сходится, а его сумма
равна ,
где
,
где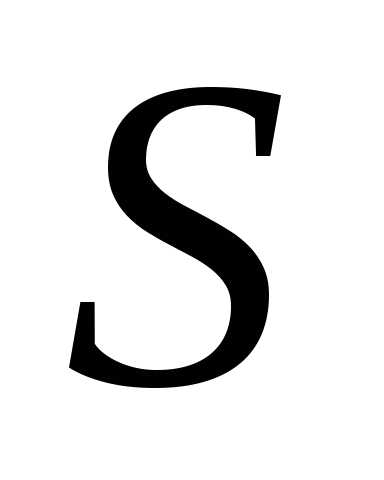 и
и – суммы рядов
– суммы рядов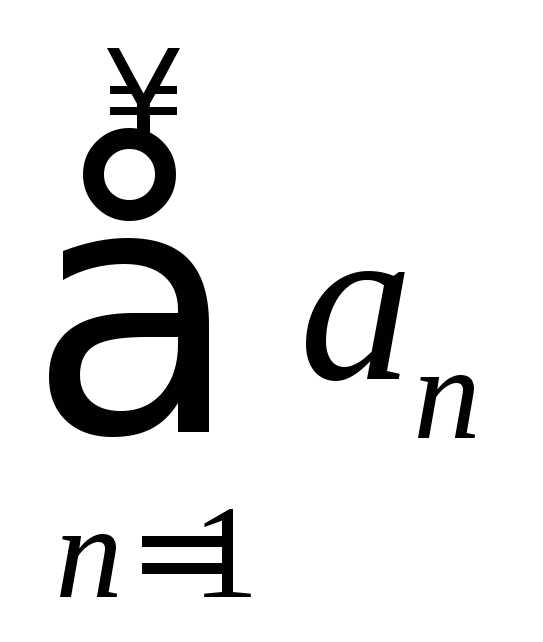 и
и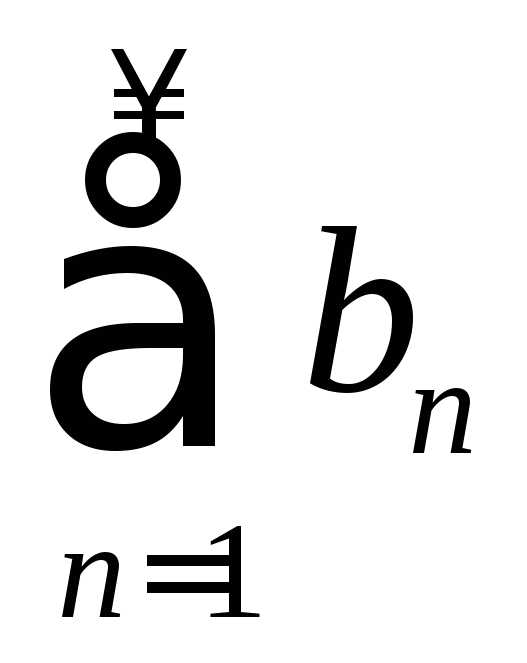 .
.
Если ряд 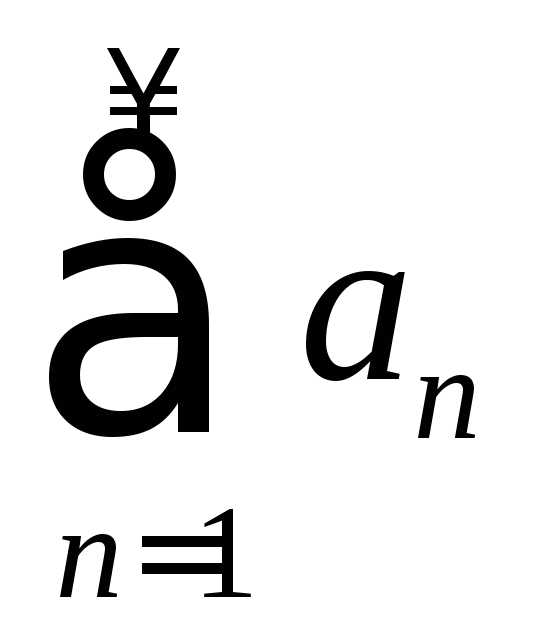 сходится, а ряд
сходится, а ряд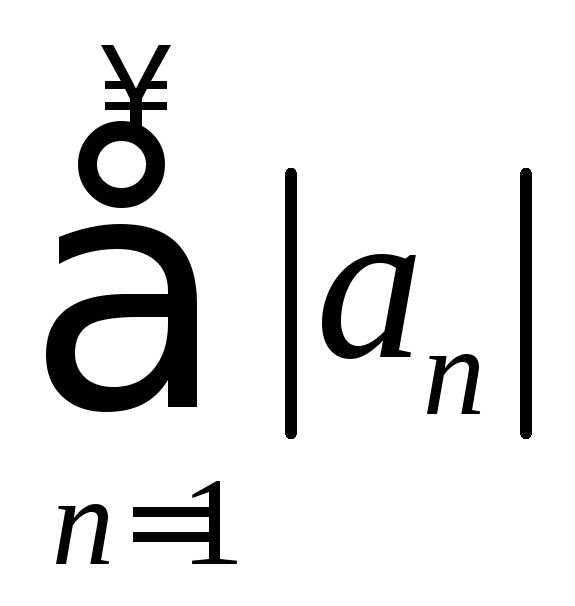 расходится, то такой ряд называетсяусловно сходящимся.
расходится, то такой ряд называетсяусловно сходящимся.
Если один из рядов 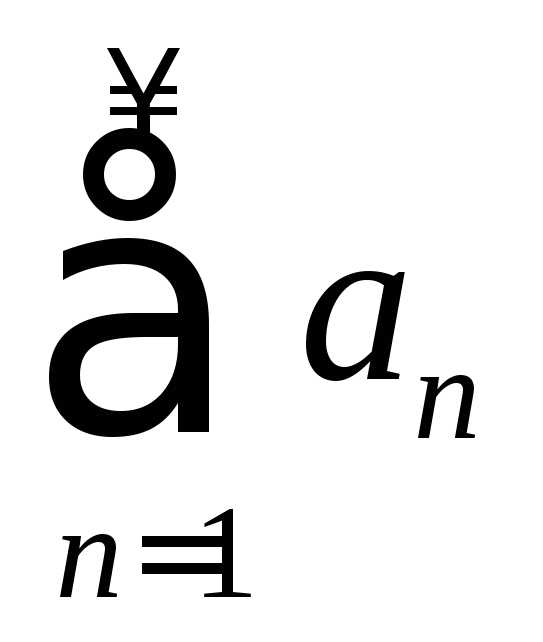 или
или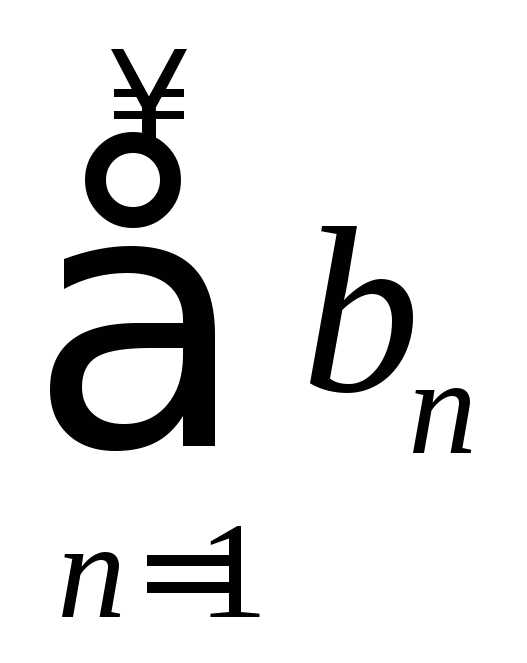 сходится условно, а второй – абсолютно,
то для их произведения справедливо
правило Коши.
сходится условно, а второй – абсолютно,
то для их произведения справедливо
правило Коши.
Теорема Римана. Если ряд 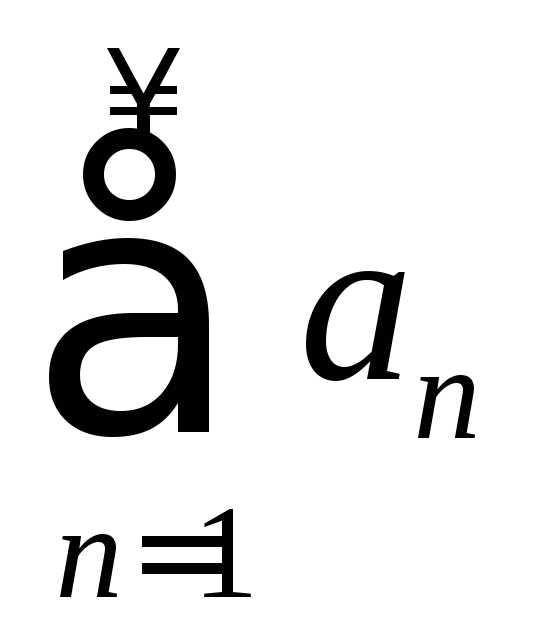 сходится условно, то каким бы ни было
число
сходится условно, то каким бы ни было
число ,
можно так переставить члены ряда, что
сумма полученного ряда будет равна
,
можно так переставить члены ряда, что
сумма полученного ряда будет равна .
.
Признак
сходимости Лейбница. Пусть
для ряда 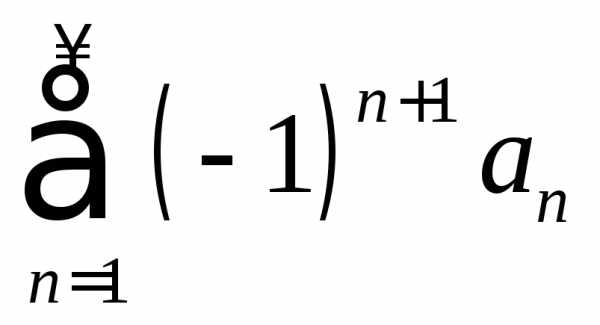 выполнены
условия:
выполнены
условия:
1.
; 2.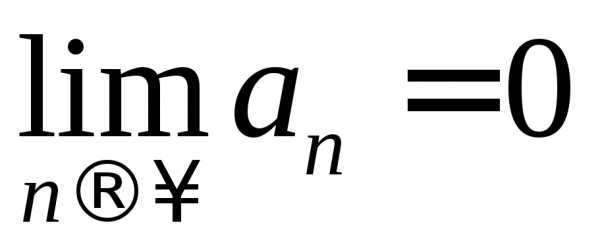 .
.
Тогда этот ряд
сходится и его сумма удовлетворяет
неравенству 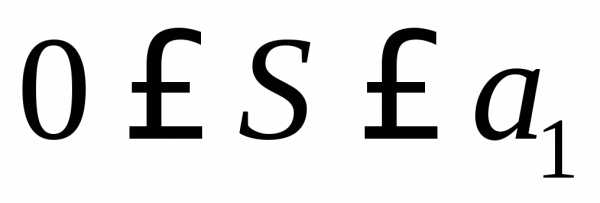 .
.
Для остатка альтернирующего ряда справедливо неравенство. Таким образом,модуль остатка не превосходит модуля первого из отбрасываемых членов.
Признак Абеля. Если ряд 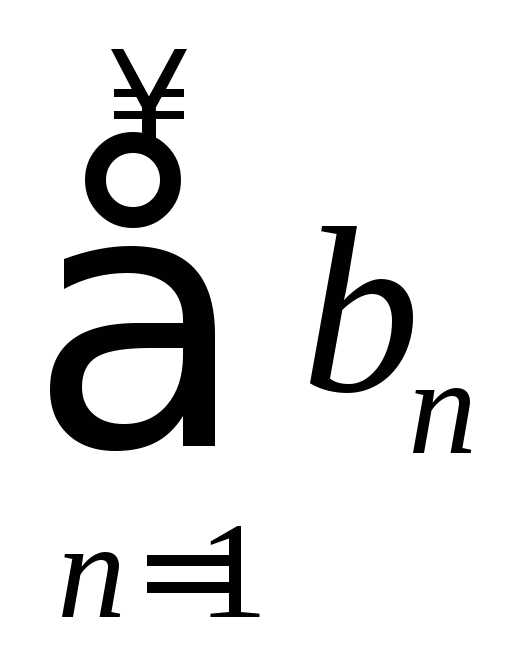 сходится, а числа
сходится, а числа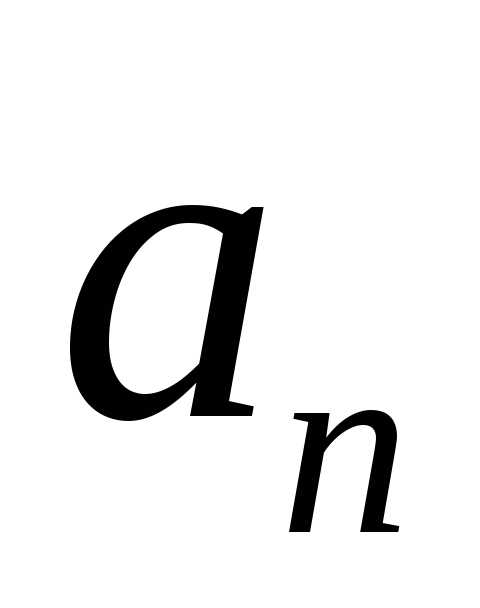 образуют монотонную и ограниченную
последовательность, то ряд
образуют монотонную и ограниченную
последовательность, то ряд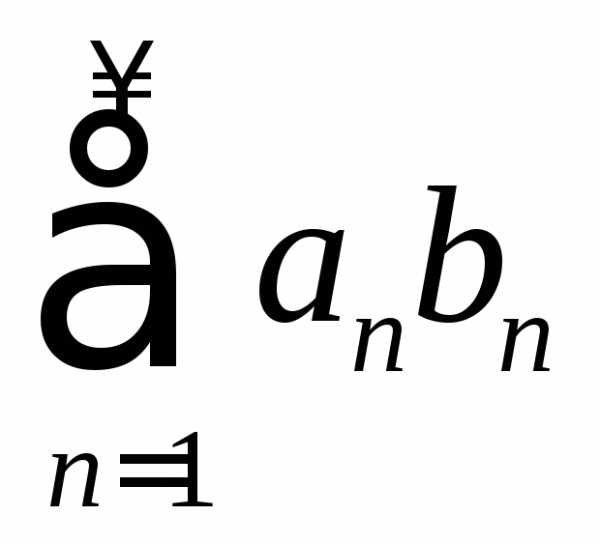 сходится.
сходится.
Признак Дирихле. Если частичные суммы ряда 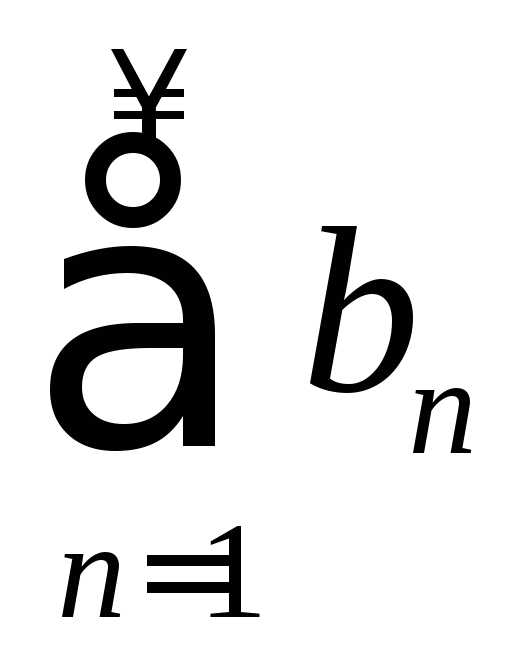 ограничены в совокупности (т. е.
ограничены в совокупности (т. е.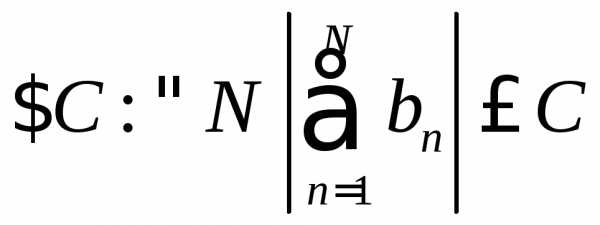 ),
а последовательность
),
а последовательность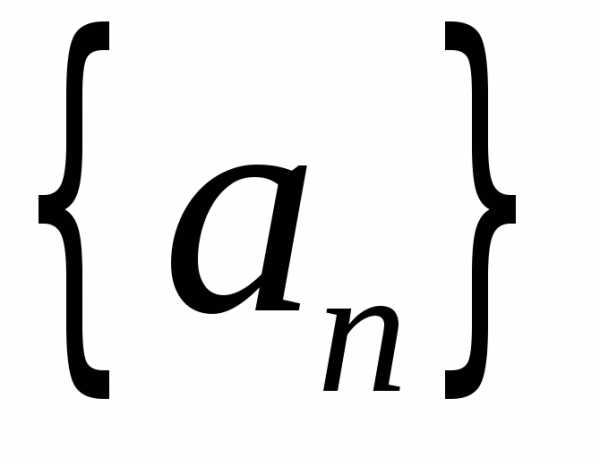 монотонно стремится к нулю, то ряд
монотонно стремится к нулю, то ряд сходится.
сходится.
Следствие
признака Дирихле. Если последовательность 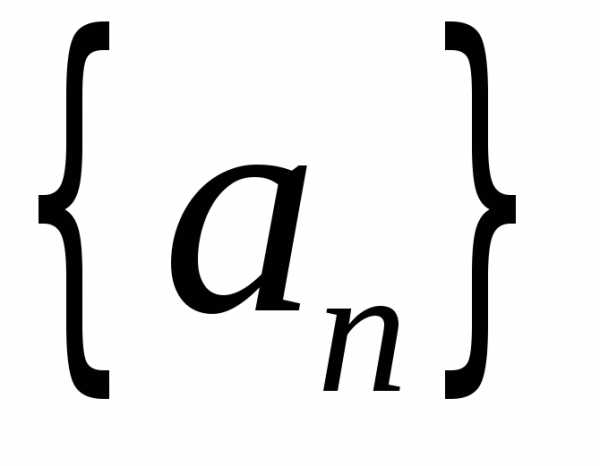 моно-
моно-
тонно стремится
к нулю, то ряд 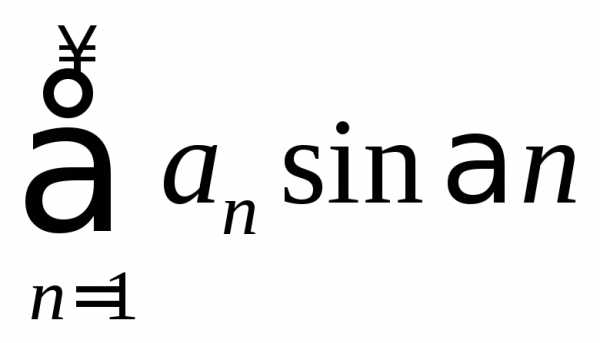 сходится при любом
сходится при любом ,
а ряд
,
а ряд
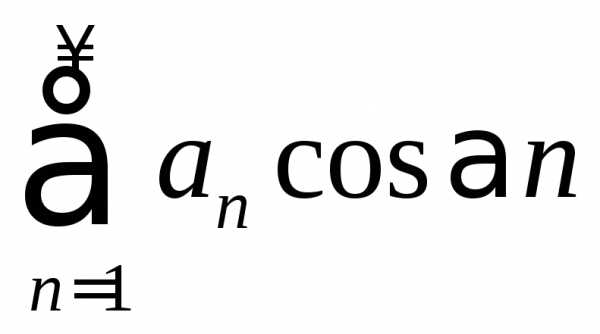 сходится при
.
сходится при
.
Пример 1.6. Исследовать
на сходимость ряд 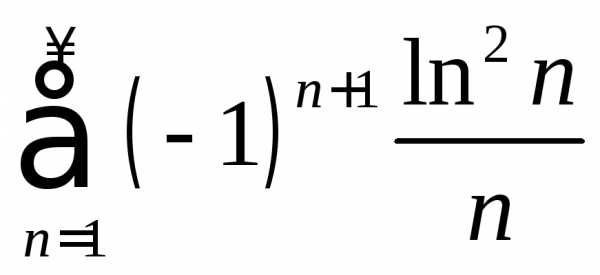 .
.
Решение. Это знакочередующийся ряд. Проверим выполнение условий признака Лейбница.
Рассмотрим функцию
 .
Тогда,
.
Тогда,
 ,
если
,
если .
Значит, при
.
Значит, при функция
функция монотонно убывает.
монотонно убывает..
Ряд сходится.
Пример 1.7. Исследовать на сходимость и абсолютную сходимость ряды:
а) 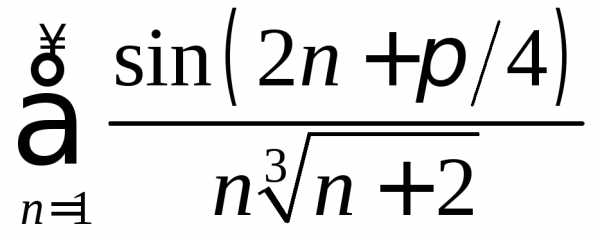 ; б)
; б)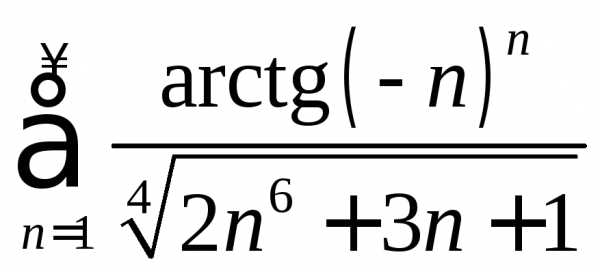 ; в)
; в)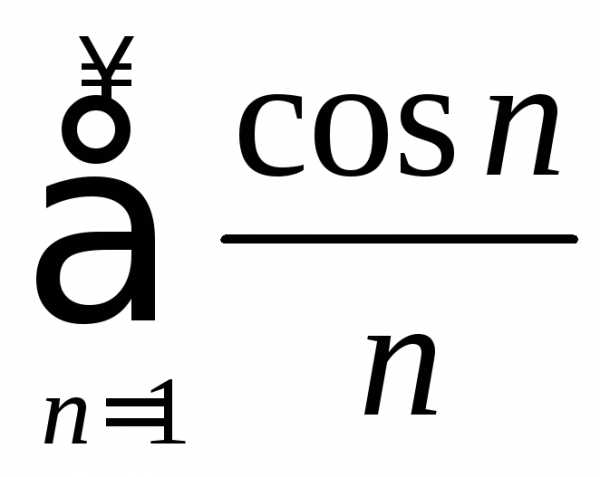 .
.
Решение. а)
Используя неравенства
,,
получаем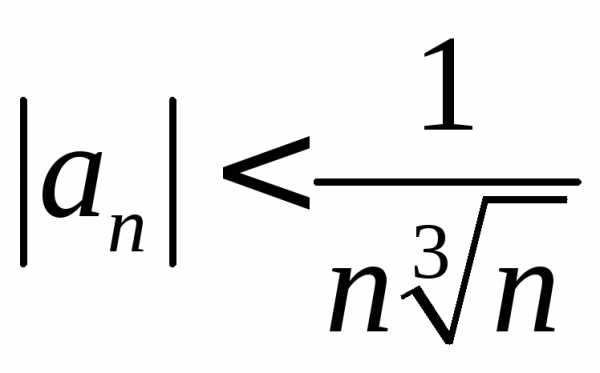 .
Из сходимости ряда
.
Из сходимости ряда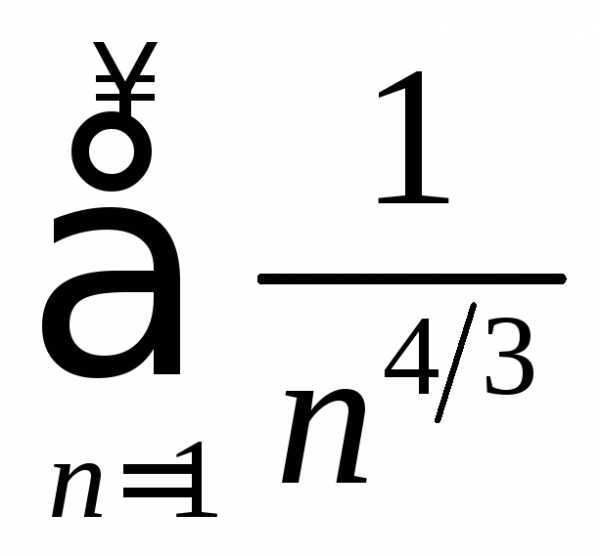 по признаку сравнения следует сходимость
ряда
по признаку сравнения следует сходимость
ряда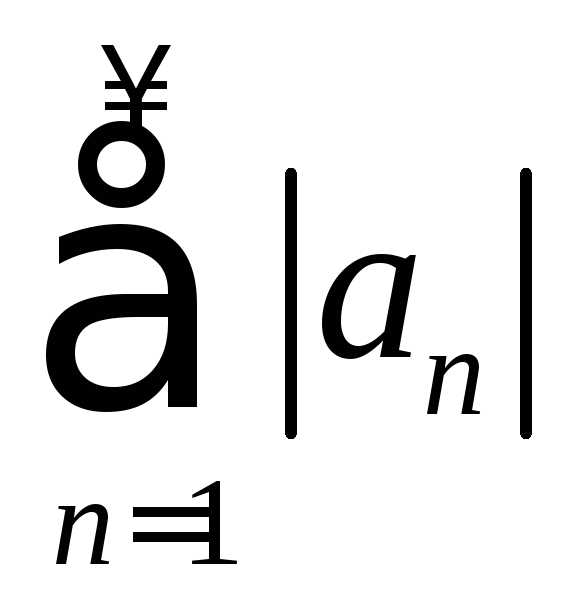 ,
т. е. абсолютная сходимость ряда
,
т. е. абсолютная сходимость ряда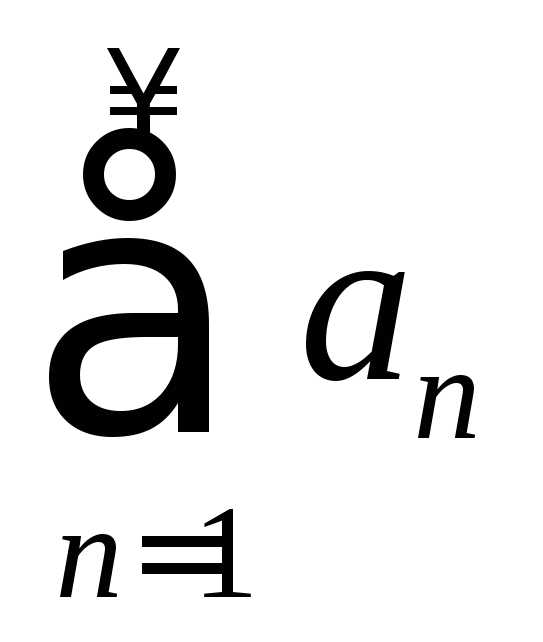 .
.
б) Используя
неравенства
,,
получаем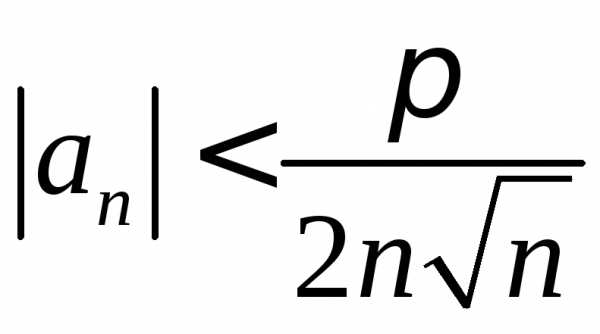 .
Из сходимости ряда
.
Из сходимости ряда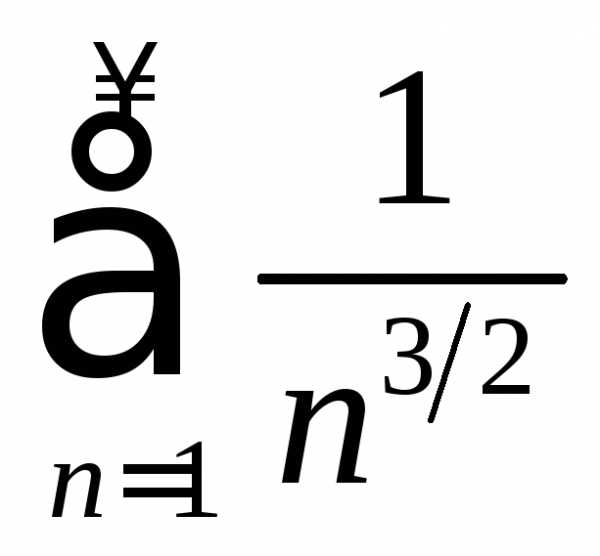 по признаку сравнения следует сходимость
ряда
по признаку сравнения следует сходимость
ряда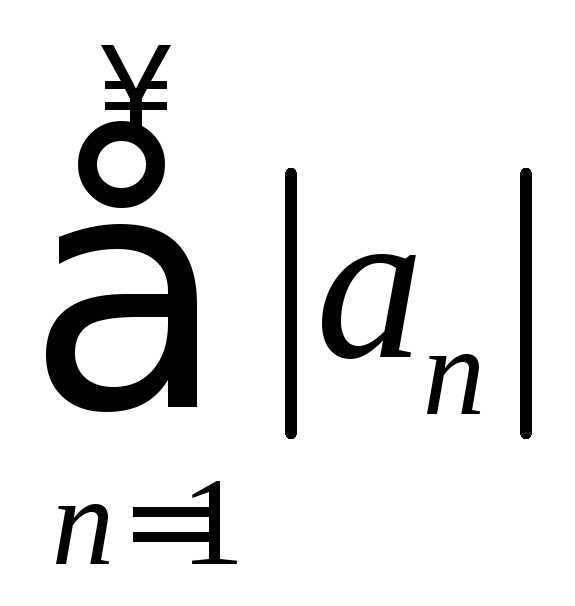 ,
т. е. абсолютная сходимость ряда
,
т. е. абсолютная сходимость ряда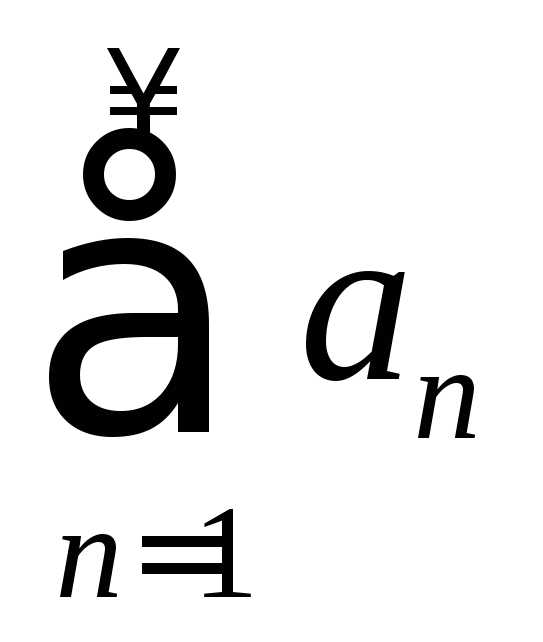 .
.
в) Используя
неравенство
,
получаем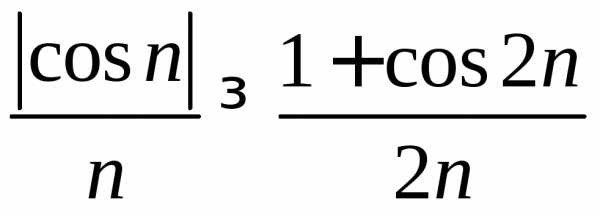 .
Ряд
.
Ряд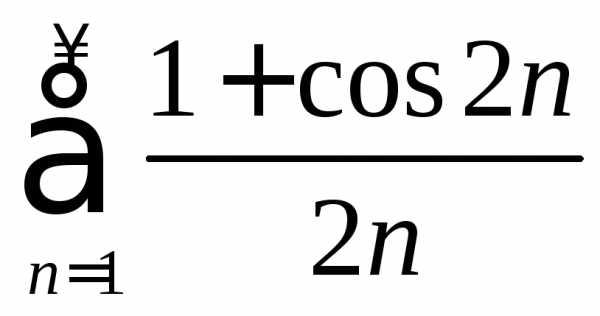 расходится, т. к.
расходится, т. к. 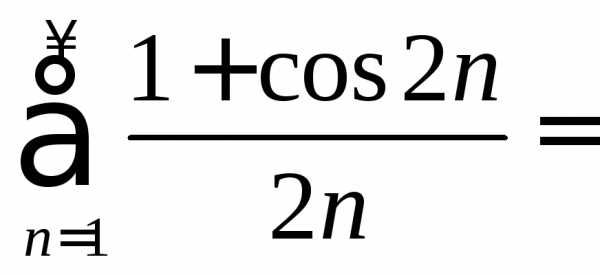
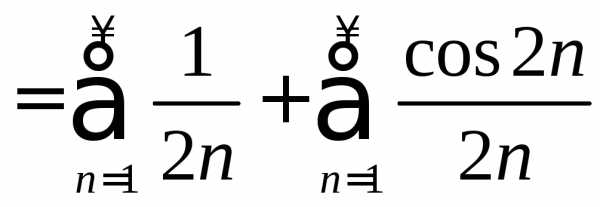 и
ряд
и
ряд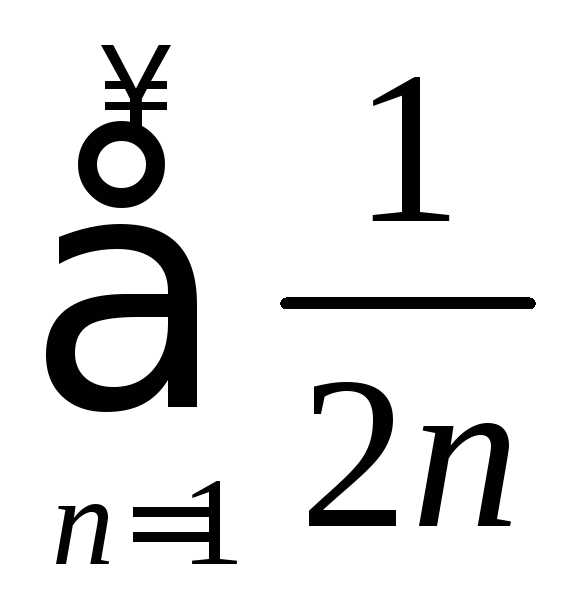 расходится, а ряд
расходится, а ряд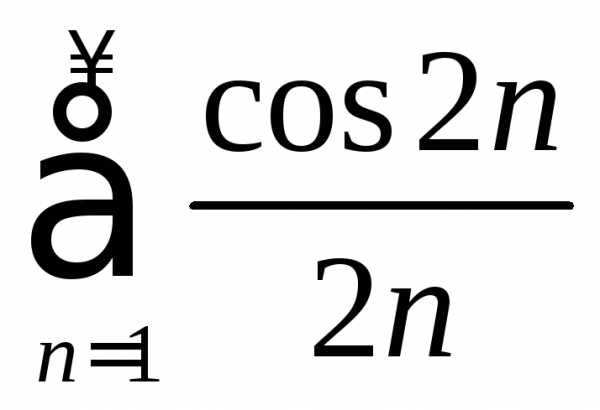 сходится. Проверим условную сходимость.
Последовательность
сходится. Проверим условную сходимость.
Последовательность монотонно стремится к нулю; следовательно,
ряд
монотонно стремится к нулю; следовательно,
ряд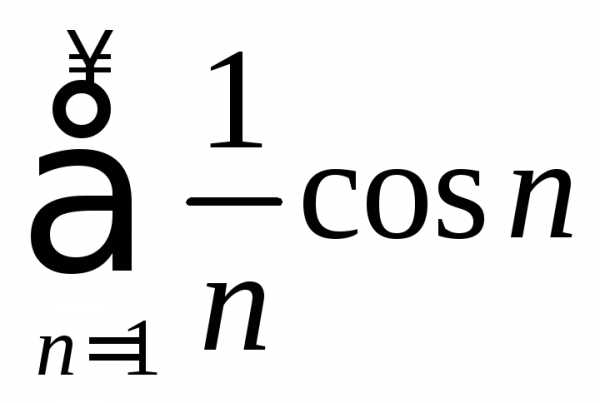 сходится. Рядсходится условно.
сходится. Рядсходится условно.
Доказать, что ряды абсолютно сходятся:
1.91. | 1.92. |
1.93. | 1.94. |
Исследовать на сходимость ряды:
1.95. | 1.96. |
1.97. | 1.98. |
Исследовать на сходимость и абсолютную сходимость ряды:
1.99. | 1.100. |
1.101. |
Исследовать на сходимость ряды:
1.102. | 1.103. |
1.104. . |
Найти все значения  ,
при которых ряд: а) абсолютно сходится;
б) условно
сходится:
,
при которых ряд: а) абсолютно сходится;
б) условно
сходится:
1.105. | 1.106. | |
1.107. | 1.108. | |
1.109. | 1.110. . | |
1.111. | 1.112. | |
1.113. . | ||
1.114. . | ||
Найти все значения  и
и ,
при которых ряд: а) абсолютно сходится;
б) условно сходится:
,
при которых ряд: а) абсолютно сходится;
б) условно сходится:
1.115. . | |
1.116. . | |
1.117. . |
1.118. Пользуясь одним из равенств
,
,
где 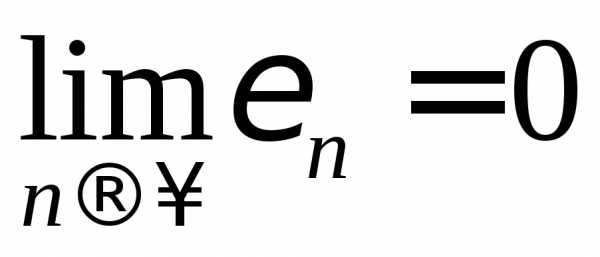 ,
доказать, что
,
доказать, что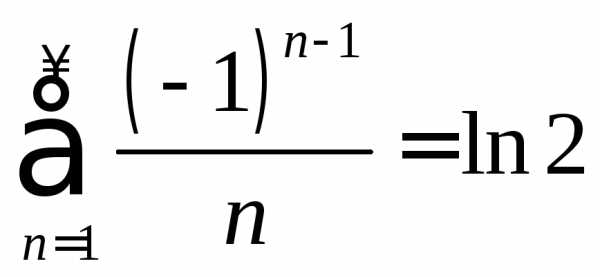 .
.
Пользуясь тем, что 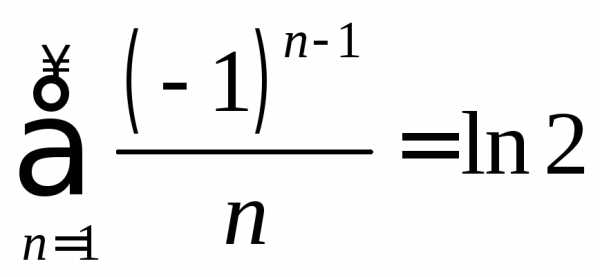 ,
найти суммы следующих рядов, полученных
из данного перестановкой его членов:
,
найти суммы следующих рядов, полученных
из данного перестановкой его членов:
1.119. . | |
1.120. . | |
1.121. . |
1.122. Пусть
ряд 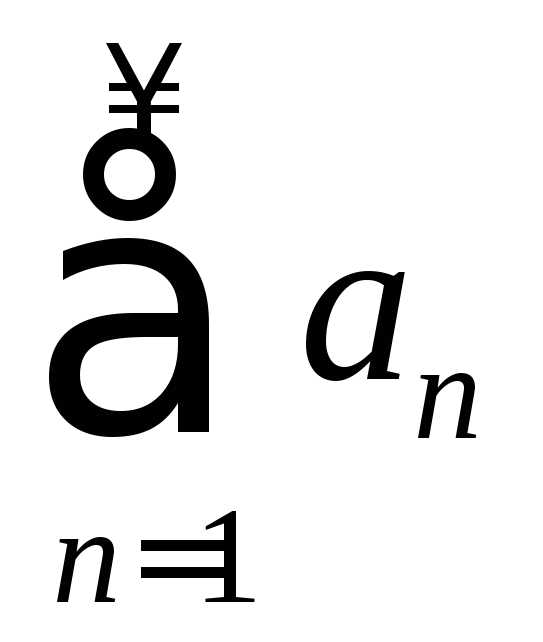 сходится и
сходится и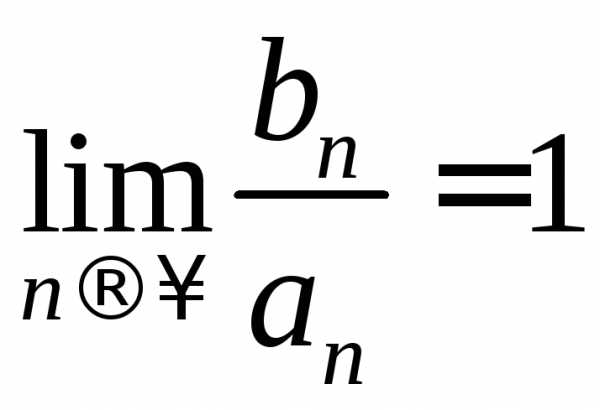 .
Следует ли отсюда, что ряд
.
Следует ли отсюда, что ряд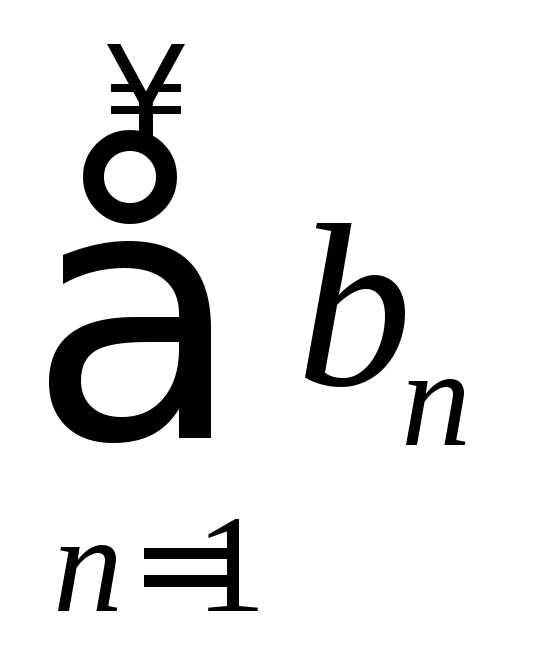 также сходится?
также сходится?
Ответы: 1.95. Сходится. 1.96. Сходится. 1.97. Сходится. 1.98. Сходится. 1.99. Сходится
условно. 1.100. Сходится абсолютно. 1.101. Сходится условно. 1.102. Сходится. 1.103. Расходится. 1.104. Расходится. 1.105. а) 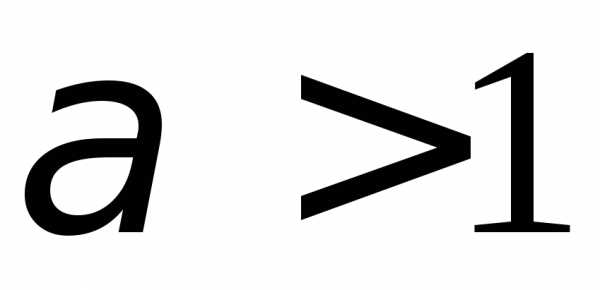 ;
б).1.106. а)
;
б).1.106. а) 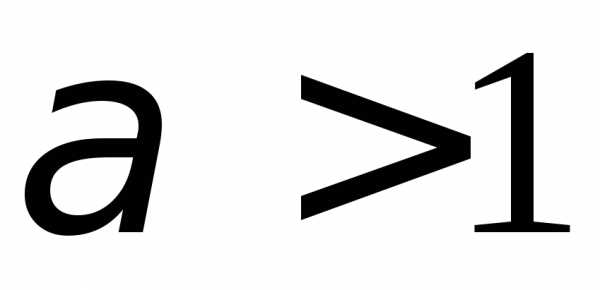 ;
б).1.107. а)
;
б).1.107. а) 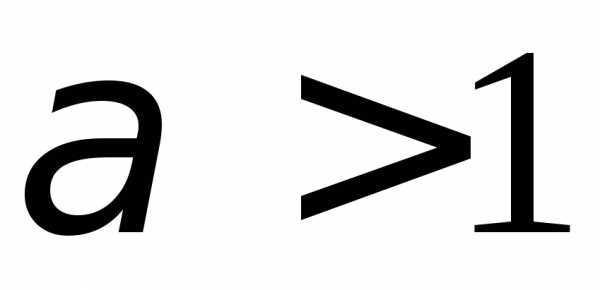 ;
б).1.108. а)
;
б).1.108. а) 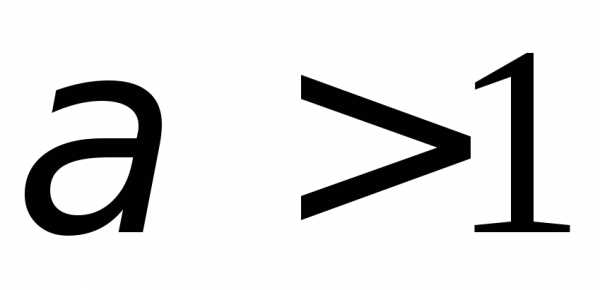 ;
б).1.109. а)
;
б).1.109. а) 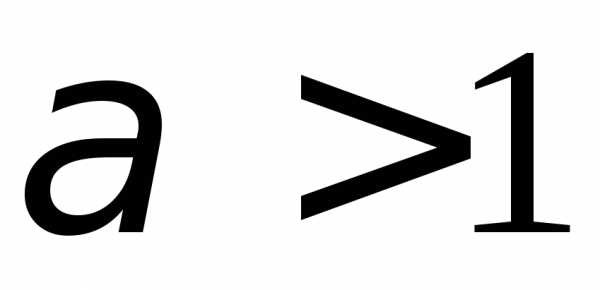 ;
б).1.110. а)
;
б).1.110. а) 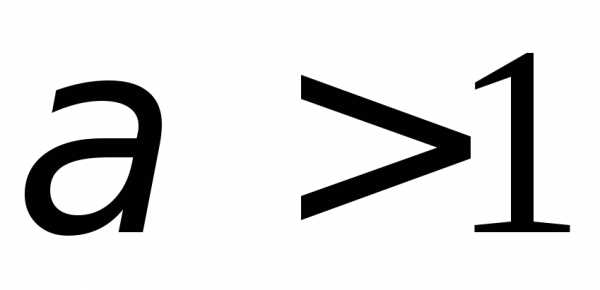 ;
б)
;
б)  любое. 1.111. а)
,
любое. 1.111. а)
,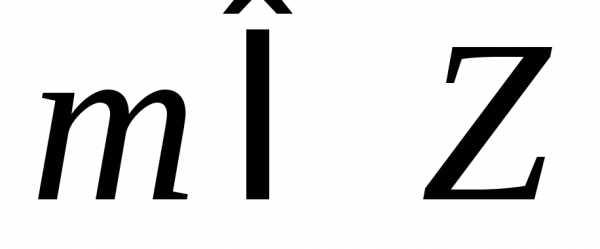 ;
б),
;
б),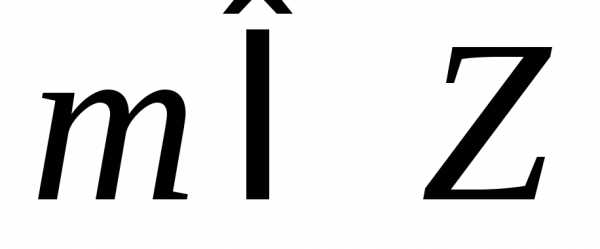 .1.112. а) ,
.1.112. а) ,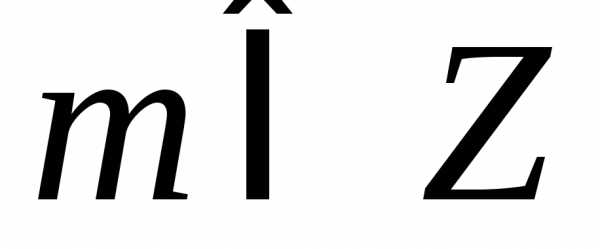 ;
б),
;
б),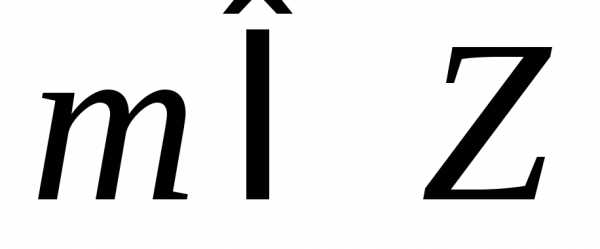 .1.113. а)
.1.113. а) 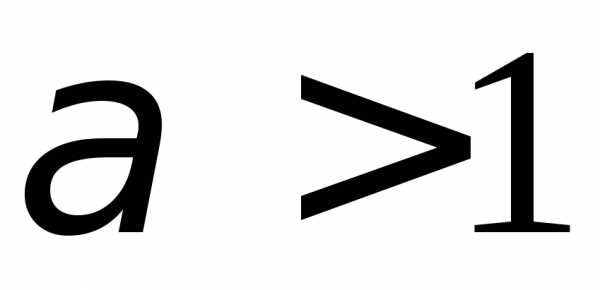 ;
б)
;
б)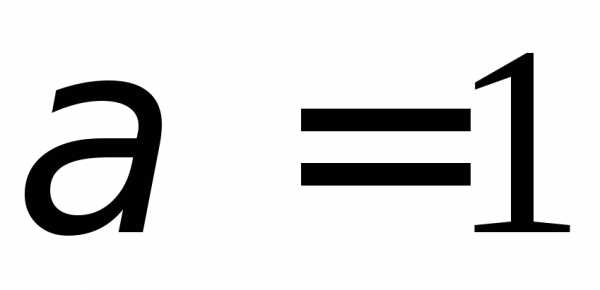 .1.114. а)
.1.114. а) 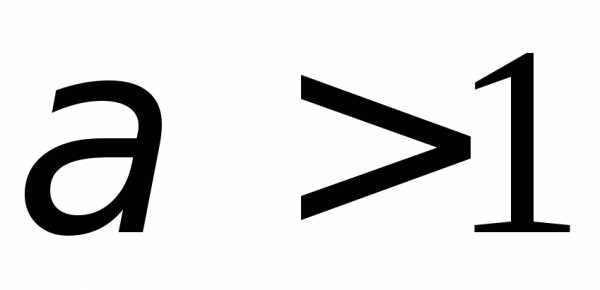 ;
б).1.115. а)
;
б) .1.116. а)
;
б).1.115. а)
;
б) .1.116. а) 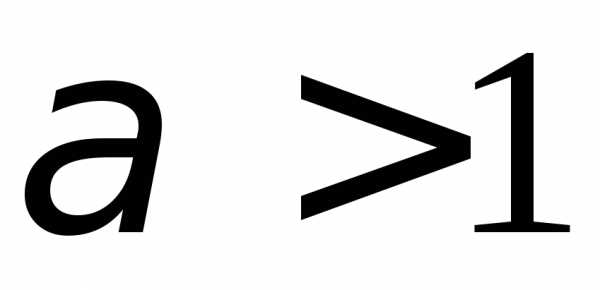 ,
,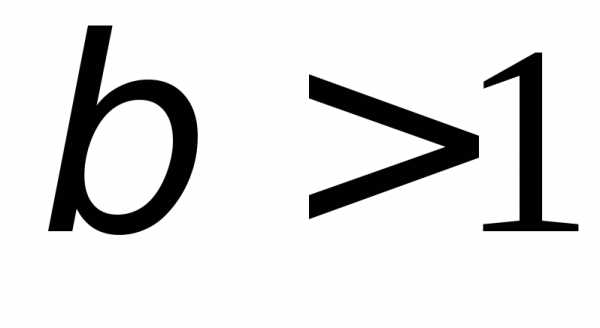 ;
б).1.117. а)
;
б).1.117. а) 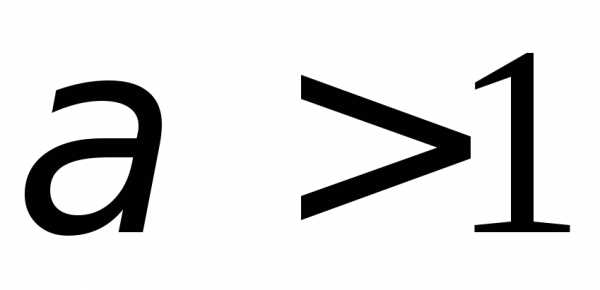 ,
,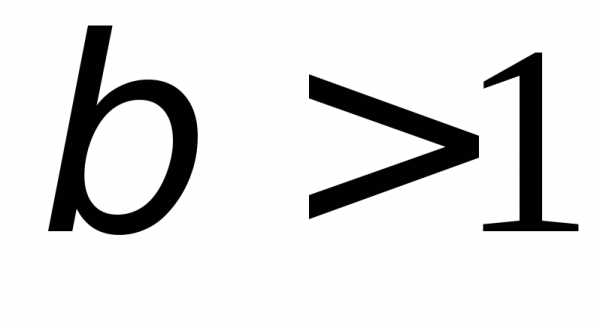 ;
б) .1.119.
;
б) .1.119. 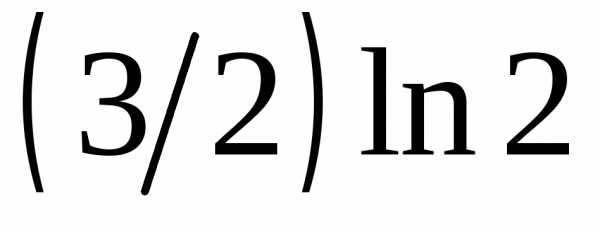 .1.120.
.1.120. 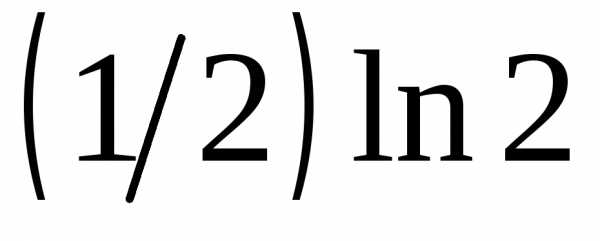 .1.121. 0. 1.122. Нет. Пример:
,.
.1.121. 0. 1.122. Нет. Пример:
,.
studfiles.net
Поиск значений с помощью функций ВПР, ИНДЕКС и ПОИСКПОЗ
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
Предположим, что у вас есть список номеров расположений Office, и вам нужно знать, какие сотрудники входят в каждый из них. Электронная таблица огромна, поэтому вы можете предположить, что она является сложной задачей. Это довольно просто сделать с помощью функции Просмотр.
Функции ВПР и ГПР вместе с функцией индекс и ПОИСКПОЗявляются наиболее полезными функциями в Excel.
Примечание: Функция «Мастер подСтановок» больше не доступна в Excel.
Вот пример того, как использовать функцию ВПР.
=ВПР(B2;C2:E7,3,ИСТИНА)
В этом примере ячейка B2 является первым аргументом— элементом данных, для работы которого необходима функция. Для функции ВПР первым аргументом является значение, которое нужно найти. Этим аргументом может быть ссылка на ячейку или фиксированное значение, например «Иванов» или «21 000». Второй аргумент — это диапазон ячеек с ячейкой C2: E7, в которой нужно найти искомое значение. Третьим аргументом является столбец в этом диапазоне ячеек, который содержит искомое значение.
Четвертый аргумент является необязательным. Введите значение истина или ложь. Если ввести значение TRUE или оставить аргумент пустым, функция возвращает приблизительное совпадение значения, указанного в первом аргументе. Если введено значение ложь, функция будет соответствовать значению, предоставленному первым аргументом. Другими словами, если оставить четвертый аргумент пустым — или ввести значение TRUE, вы получите большую гибкость.
В этом примере показано, как работает функция. При вводе значения в ячейке B2 (первый аргумент) функция ВПР ищет ячейки в диапазоне C2: E7 (второй аргумент) и возвращает ближайшее приблизительное совпадение из третьего столбца в диапазоне, столбец E (Третий аргумент).
Четвертый аргумент пустой, поэтому функция возвращает приблизительное совпадение. Если это не так, необходимо было бы ввести одно из значений в столбцах C или D, чтобы получить результат.
Когда вы хорошо знакомы с функцией ВПР, функция ГПР очень проста в использовании. При вводе одних и тех же аргументов выполняется поиск в строках, а не в столбцах.
Использование функции индекс и СОВПАДЕНИе вместо функции ВПР
Существуют определенные ограничения с использованием функции ВПР — функция ВПР может искать значение слева направо. Это означает, что столбец, содержащий искомое значение, всегда должен располагаться слева от столбца, содержащего возвращаемое значение. Теперь, если электронная таблица не построена таким образом, не используйте функцию ВПР. Вместо этого используйте сочетание функций индекс и ПОИСКПОЗ.
В данном примере представлен небольшой список, в котором искомое значение (Воронеж) не находится в крайнем левом столбце. Поэтому мы не можем использовать функцию ВПР. Для поиска значения «Воронеж» в диапазоне B1:B11 будет использоваться функция ПОИСКПОЗ. Оно найдено в строке 4. Затем функция ИНДЕКС использует это значение в качестве аргумента поиска и находит численность населения Воронежа в четвертом столбце (столбец D). Использованная формула показана в ячейке A14.
Дополнительные примеры использования функции индекс и MATCH вместо ВПР см. в статье https://www.MrExcel.com/Excel-Tips/Excel-VLOOKUP-index-Match/ Билл Джилена, Microsoft MVP.
Попробуйте попрактиковаться
Если вы хотите поэкспериментировать с функциями подстановок до их последующей работы с данными, воспользуйтесь приведенными ниже примерами данных.
Пример функции ВПР на работе
Скопируйте следующие данные в пустую электронную таблицу.
Совет: Прежде чем вставлять данные в Excel, задайте ширину столбцов для столбцов от A до 250 пикселей и нажмите кнопку Перенос текста (вкладка «Главная «, Группа » Выравнивание «).
Плотность | Вязкость | Температура |
|---|---|---|
|
0,457 |
3,55 |
500 |
|
0,525 |
3,25 |
400 |
|
0,606 |
2,93 |
300 |
|
0,675 |
2,75 |
250 |
|
0,746 |
2,57 |
200 |
|
0,835 |
2,38 |
150 |
|
0,946 |
2,17 |
100 |
|
1,09 |
1,95 |
50 |
|
1,29 |
1,71 |
нулев |
|
Формула |
Описание |
Результат |
|
=ВПР(1,A2:C10,2) |
Используя приблизительное соответствие, функция ищет в столбце A значение 1, находит наибольшее значение, которое меньше или равняется 1 и составляет 0,946, а затем возвращает значение из столбца B в той же строке. |
2,17 |
|
=ВПР(1,A2:C10,3,ИСТИНА) |
Используя приблизительное соответствие, функция ищет в столбце A значение 1, находит наибольшее значение, которое меньше или равняется 1 и составляет 0,946, а затем возвращает значение из столбца C в той же строке. |
100 |
|
=ВПР(0,7,A2:C10,3,ЛОЖЬ) |
Используя точное соответствие, функция ищет в столбце A значение 0,7. Поскольку точного соответствия нет, возвращается сообщение об ошибке. |
#Н/Д |
|
=ВПР(0,1,A2:C10,2,ИСТИНА) |
Используя приблизительное соответствие, функция ищет в столбце A значение 0,1. Поскольку 0,1 меньше наименьшего значения в столбце A, возвращается сообщение об ошибке. |
#Н/Д |
|
=ВПР(2,A2:C10,2,ИСТИНА) |
Используя приблизительное соответствие, функция ищет в столбце A значение 2, находит наибольшее значение, которое меньше или равняется 2 и составляет 1,29, а затем возвращает значение из столбца B в той же строке. |
1,71 |
Пример функции ГПР
Скопируйте всю таблицу и вставьте ее в ячейку A1 пустого листа Excel.
Совет: Прежде чем вставлять данные в Excel, задайте ширину столбцов для столбцов от A до 250 пикселей и нажмите кнопку Перенос текста (вкладка «Главная «, Группа » Выравнивание «).
Оси | Подшипники | Болты |
|---|---|---|
|
2-4 |
2-4 |
рис |
|
17:00 |
7 |
10 |
|
рис |
8:00 |
279 |
|
Формула |
Описание |
Результат |
|
=ГПР(«Оси»;A1:C4;2;ИСТИНА) |
Поиск слова «Оси» в строке 1 и возврат значения из строки 2, находящейся в том же столбце (столбец A). |
2-4 |
|
=ГПР(«Подшипники»;A1:C4;3;ЛОЖЬ) |
Поиск слова «Подшипники» в строке 1 и возврат значения из строки 3, находящейся в том же столбце (столбец B). |
7 |
|
=ГПР(«П»;A1:C4;3;ИСТИНА) |
Поиск буквы «П» в строке 1 и возврат значения из строки 3, находящейся в том же столбце. Так как «П» найти не удалось, возвращается ближайшее из меньших значений: «Оси» (в столбце A). |
17:00 |
|
=ГПР(«Болты»;A1:C4;4) |
Поиск слова «Болты» в строке 1 и возврат значения из строки 4, находящейся в том же столбце (столбец C). |
279 |
|
=ГПР(3;{1;2;3:»a»;»b»;»c»;»d»;»e»;»f»};2;ИСТИНА) |
Поиск числа 3 в трех строках константы массива и возврат значения из строки 2 того же (в данном случае — третьего) столбца. Константа массива содержит три строки значений, разделенных точкой с запятой (;). Так как «c» было найдено в строке 2 того же столбца, что и 3, возвращается «c». |
c |
Примеры ИНДЕКСов и СОВПАДЕНИй
В последнем примере функции индекс и ПОИСКПОЗ используются вместе, чтобы возвращать самый ранний номер счета и соответствующую дату для каждого из пяти городов. Так как дата возвращается как число, мы используем функцию текст, чтобы отформатировать ее как дату. Функция индекс фактически использует результат функции ПОИСКПОЗ в качестве аргумента. Сочетание функций индекс и ПОИСКПОЗ используются дважды в каждой формуле — сначала, чтобы возвратить номер счета, а затем вернуть дату.
Скопируйте всю таблицу и вставьте ее в ячейку A1 пустого листа Excel.
Совет: Прежде чем вставлять данные в Excel, задайте ширину столбцов В столбцах от A до 250 пикселей и нажмите кнопку Перенос текста (вкладка «Главная «, Группа » Выравнивание «).
Счет | Город | Дата выставления счета | Счет с самой ранней датой по городу, с датой |
|---|---|---|---|
|
3115 |
Коломна |
07.04.12 |
=»Казань = «&ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Казань»,$B$2:$B$33,0),1)& «, Дата выставления счета: » & ТЕКСТ(ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Казань»,$B$2:$B$33,0),3),»m/d/yy») |
|
3137 |
Коломна |
09.04.12 |
=»Орел = «&ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Орел»,$B$2:$B$33,0),1)& «, Дата выставления счета: » & ТЕКСТ(ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Орел»,$B$2:$B$33,0),3),»m/d/yy») |
|
3154 |
Коломна |
11.04.12 |
=»Челябинск = «&ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Челябинск»,$B$2:$B$33,0),1)& «, Дата выставления счета: » & ТЕКСТ(ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Челябинск»,$B$2:$B$33,0),3),»m/d/yy») |
|
3191 |
Казань |
21.04.12 |
=»Нижний Новгород = «&ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Нижний Новгород»,$B$2:$B$33,0),1)& «, Дата выставления счета: » & ТЕКСТ(ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Нижний Новгород»,$B$2:$B$33,0),3),»m/d/yy») |
|
3293 |
Коломна |
25.04.12 |
=»Москва = «&ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Москва»,$B$2:$B$33,0),1)& «, Дата выставления счета: » & ТЕКСТ(ИНДЕКС($A$2:$C$33,ПОИСКПОЗ(«Москва»,$B$2:$B$33,0),3),»m/d/yy») |
|
3331 |
Коломна |
27.04.12 |
|
|
3350 |
Коломна |
28.04.12 |
|
|
3390 |
Коломна |
01.05.12 |
|
|
3441 |
Коломна |
02.05.12 |
|
|
3517 |
Казань |
08.05.12 |
|
|
3124 |
Орел |
09.04.12 |
|
|
3155 |
Остин |
11.04.12 |
|
|
3177 |
Остин |
19.04.12 |
|
|
3357 |
Остин |
28.04.12 |
|
|
3492 |
Орел |
06.05.12 |
|
|
3316 |
Челябинск |
25.04.12 |
|
|
3346 |
Dallas (Даллас) |
28.04.12 |
|
|
3372 |
Dallas (Даллас) |
01.05.12 |
|
|
3414 |
Dallas (Даллас) |
01.05.12 |
|
|
3451 |
Dallas (Даллас) |
02.05.12 |
|
|
3467 |
Dallas (Даллас) |
02.05.12 |
|
|
3474 |
Dallas (Даллас) |
04.05.12 |
|
|
3490 |
Dallas (Даллас) |
05.05.12 |
|
|
3503 |
Челябинск |
08.05.12 |
|
|
3151 |
Нижний Новгород |
09.04.12 |
|
|
3438 |
Новый Орлеан |
02.05.12 |
|
|
3471 |
Нижний Новгород |
04.05.12 |
|
|
3160 |
Москва |
18.04.12 |
|
|
3328 |
Москва |
26.04.12 |
|
|
3368 |
Москва |
29.04.12 |
|
|
3420 |
Москва |
01.05.12 |
|
|
3501 |
Москва |
06.05.12 |
См. также
Краткий справочник: автообновление ВПР
Функции поиска и справки (Справка)
Использование аргумента инфо_таблица в функции ВПР
support.office.com
Найти все значения корня (комплексные числа)
Если извлекается корень 4 степени, то у данного комплексного числа будет 4 корня. Представим комплексное число (-4) в тригонометрической форме: -4 = 4*(-1 + 0 * i) = 4*(cos (Pi) + i * sin (Pi)) Теперь вынесем скобку с синусом и косинусом из-под знака корня: (4 * (cos(Pi) + i*sin(Pi)))^(1/4) = 4^(1/4) * (cos ((Pi+2*Pi*k)/4) + i*sin((Pi+2*Pi*k)/4)) = 2^(1/2) * (cos ((Pi+2*Pi*k)/4) + i*sin((Pi+2*Pi*k)/4)) Подставим значения k=0,1,2,3: k=0: z0 = 2^(1/2) * ( cos (Pi/4) + i*sin(Pi/4) ) k=1: z1 = 2^(1/2) * (cos ((Pi+2*Pi)/4) + i*sin((Pi+2*Pi)/4)) = 2^(1/2) * (cos (3Pi/4) + i*sin(3Pi/4) ) k=2: z2 = 2^(1/2) * (cos ((Pi+2*Pi*2)/4) + i*sin((Pi+2*Pi*2)/4)) = 2^(1/2) * (cos (5Pi/4) + i*sin(5Pi/4) ) = 2^(1/2) * ( cos (Pi/4) + i*sin(Pi/4) ) k=3: z3 = 2^(1/2) * (cos ((Pi+2*Pi*3)/4) + i*sin((Pi+2*Pi*3)/4)) = 2^(1/2) * (cos (7Pi/4) + i*sin(7Pi/4) ) = 2^(1/2) * ( cos (3Pi/4) + i*sin(3Pi/4) ) Всего получилось 4 корня (z0, z1, z2, z3), но они кратные (z0 = z2, z1 = z3), поэтому ответ можно записать вот так: z0, z2 = 2^(1/2) * ( cos (Pi/4) + i*sin(Pi/4) ) z1, z3 = 2^(1/2) * ( cos (3Pi/4) + i*sin(3Pi/4) )
<a rel=»nofollow» href=»http://umal.me/0t1″ target=»_blank»>JediSith666 Посмотри, тут есть на странице 191</a>
Загрузите лучше свое задание на сайт: reshebnik. biz
Могу подробно помочь Вам с решением, напишите сюда: dmitrykoval11(далее собачка) mail.ru
Посмотрите подобные задания на <a rel=»nofollow» href=»https://author24.ru/spravochniki/matematika/kompleksnye_chisla_i_mnogochleny/kompleksnye_chisla_osnovnye_ponyatiya/» target=»_blank» >комплексные числа</a> и попробуйте по примерам решить.
touch.otvet.mail.ru
Исправление ошибки #ЗНАЧ! в функциях НАЙТИ, НАЙТИБ, ПОИСК и ПОИСКБ
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
В этом разделе приводятся сведения о наиболее распространенных случаях возникновения ошибки #ЗНАЧ! в функциях НАЙТИ, НАЙТИБ, ПОИСК и ПОИСКБ.
Некоторые важные сведения о функциях НАЙТИ и ПОИСК
-
Функции поиска и поиска очень похожи. Они работают точно так же, как Поиск символа или текстовой строки в другой текстовой строке. Различие между этими двумя функциями заключается в том, что поиск выполняется с учетом регистра, а поиск выполняется не с учетом регистра. Поэтому, если вы не хотите учитывать регистр в текстовой строке, используйте поиск.
-
Если вам нужно вернуть строку, содержащую указанное количество символов, используйте функцию ПСТР вместе с функцией НАЙТИ. Сведения об использовании функций ПСТР и НАЙТИ в сочетании друг с другом и примеры приведены в разделе справки по функции НАЙТИ.
-
Синтаксис этих функций одинаков: искомый_текст; просматриваемый_текст; [нач_позиция]). Обычным языком это можно выразить так: что нужно найти; где это нужно найти; с какой позиции следует начать.
Проблема: значение аргумента искомый_текст не удалось найти в строке просматриваемый_текст
Если функции не удается найти искомый текст в указанной строке, она выводит ошибку #ЗНАЧ!.
Например, рассмотрим следующую функцию:
Она выведет ошибку #ЗНАЧ!, так как в строке нет слова «перчатки», но есть слово «Перчатки». Помните, что функция НАЙТИ учитывает регистр, поэтому значение аргумента искомый_текст должно иметь точное совпадение в строке, указанной в аргументе просматриваемый_текст.
Однако функция ПОИСК вернет в этом случае значение 1, так как она не учитывает регистр:
Решение: Исправьте синтаксис необходимым образом.
Проблема: значение аргумента нач_позиция равно нулю (0)
Аргумент нач_позиция является необязательным. Если его опустить, используется значение по умолчанию, равное 1. Однако если этот аргумент указан и его значение равно 0, возникнет ошибка #ЗНАЧ!.
Решение: Удалите аргумент нач_позиция, если он не нужен, или присвойте ему правильное значение.
Проблема: длина значения нач_позиция превышает длину значения просматриваемый_текст
Например, рассмотрим следующую функцию:
Она ищет букву «и» в строке «Функции и формулы» (просматриваемая_строка) начиная с 25-го символа (нач_позиция), но возвращает ошибку #ЗНАЧ!, так как в строке всего 22 знака.
Совет: Чтобы определить общее количество символов в текстовой строке, используйте функцию ДЛСТР.
Решение: При необходимости исПравьте начальный номер.
У вас есть вопрос об определенной функции?
Задать вопрос на форуме сообщества, посвященном Excel
Помогите нам улучшить Excel
У вас есть предложения по улучшению следующей версии Excel? Если да, ознакомьтесь с темами на портале пользовательских предложений для Excel.
См. также
Исправление ошибки #ЗНАЧ!
Функции найти и НАЙТИБ
ФУНКЦИИ ПОИСКА И ПОИСКБ
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Все функции Excel (по алфавиту)
Функции Excel (по категориям)
support.office.com
Найти все значения х — Край друзей
Найдите все значения х, для которых точки графика функции лежат выше соответствующих точек графика функцииТребование этой необычной, как будто бы графической задачи записывается в виде самого обычного неравенства, исследование которого, к тому же, упрощается тем, что знаменатели обеих его частей одинаковы.
Правда, в связи с данной постановкой задачи возникает весьма тонкий вопрос: куда девать те значения х, для которых одна функция определена, а другая — нет или, того хуже, обе не определены? Брать такие значения в ответ или нет? Например, можно ли сказать, что несуществующая точка лежит выше какой-то другой, данной точки?
• С одной стороны, кажется, что нет, выше не лежит, т.к. ее просто нет.
• Но, с другой стороны, и ниже-то она ведь тоже не лежит. Не лежит и прямо в данной точке. Значит, выходит, все-таки выше?
Чтобы отмести получившийся логический казус, толковать требование задачи, по-видимому, нужно так: ищутся такие значения х для каждого из которых значение первой функции определено и при этом больше значения второй функции (которое, кстати, тогда тоже определено, что видно из сравнения двух данных формул друг с другом).
Решение 1.

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.
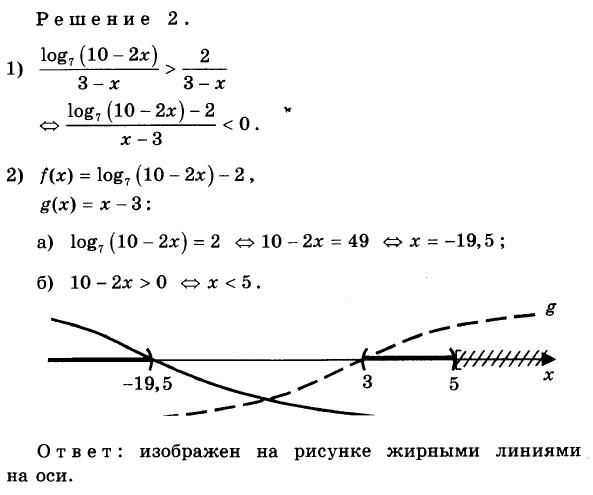
Изображение уменьшено. Щелкните, чтобы увидеть оригинал.
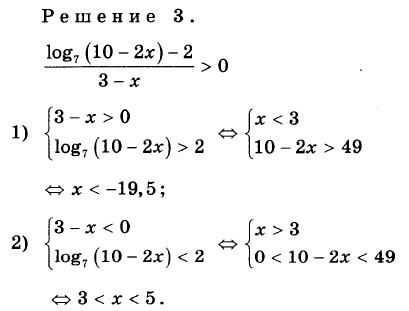
Изображение уменьшено. Щелкните, чтобы увидеть оригинал.
Решение оказалось совсем несложным, но будь задача потруднее — преимущества других методов были бы убедительнее (а мы, конечно, должны рассчитывать и на более серьезные задачи).
kraidruzei.ru

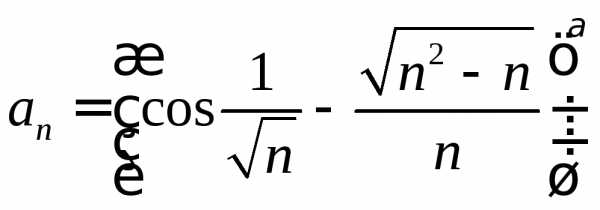 .
.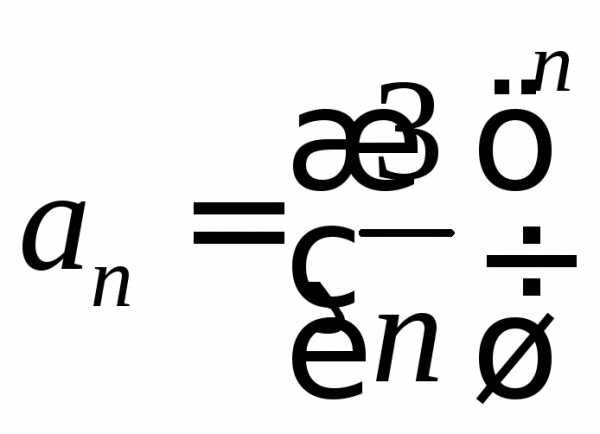 .
.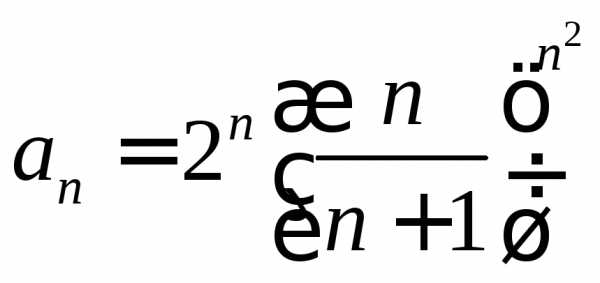 .
.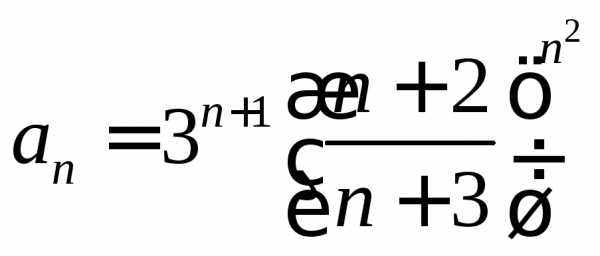 .
.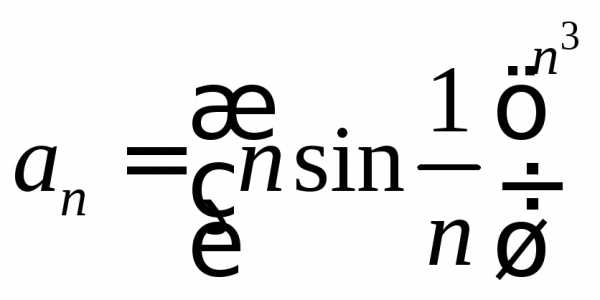 .
.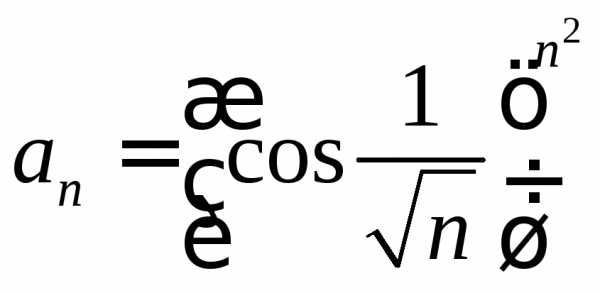 .
.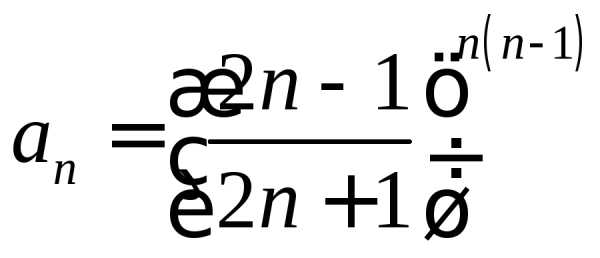 .
.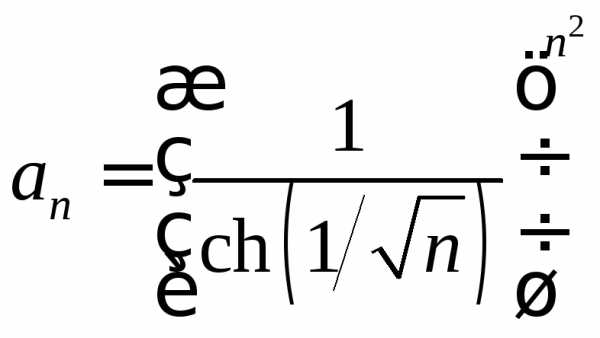 .
.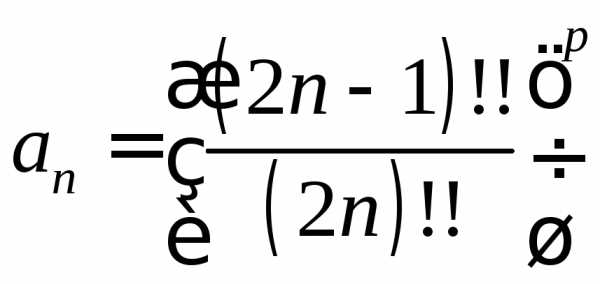 .
.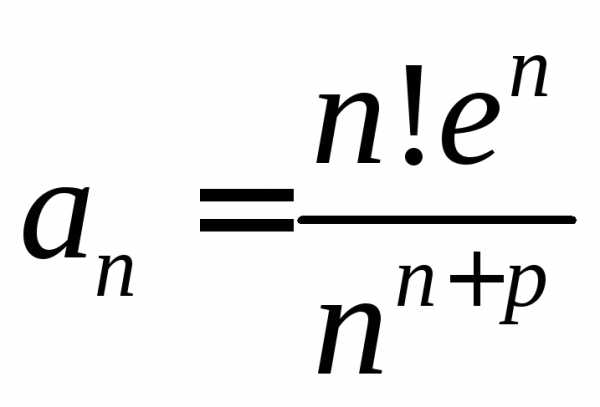 .
. .
.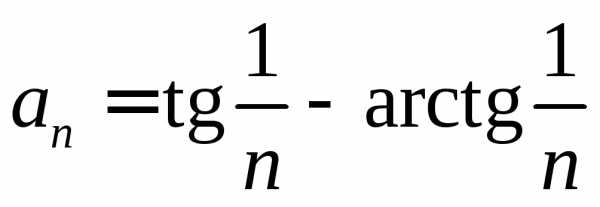 .
.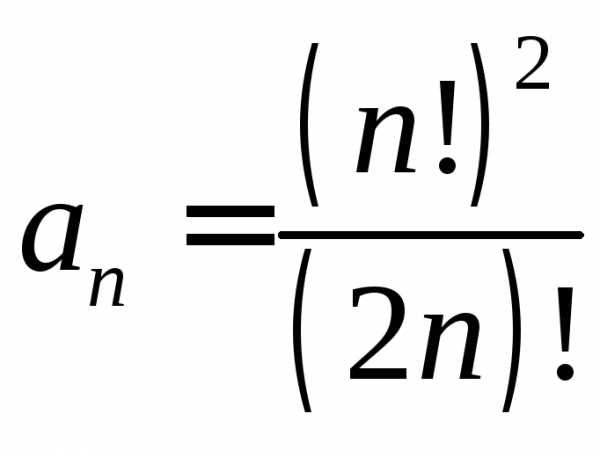 .
.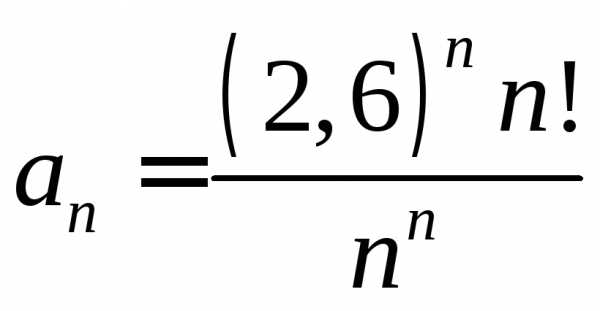 .
.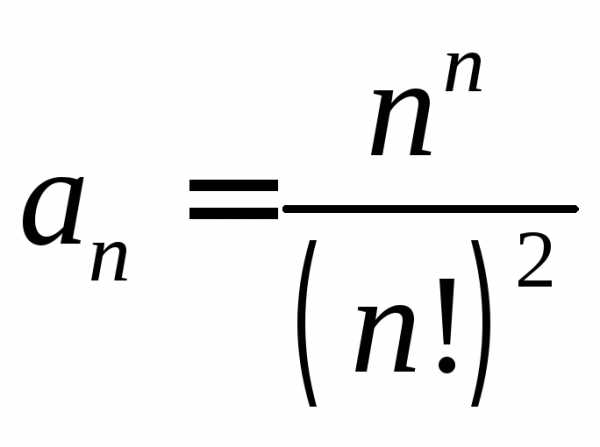 .
.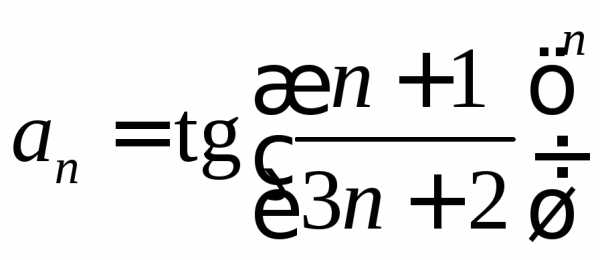 .
.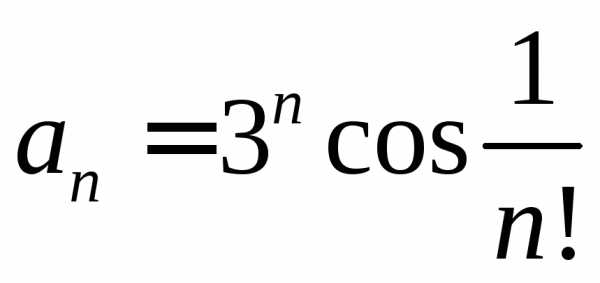 .
.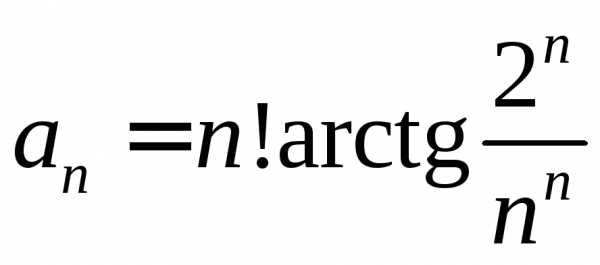 .
.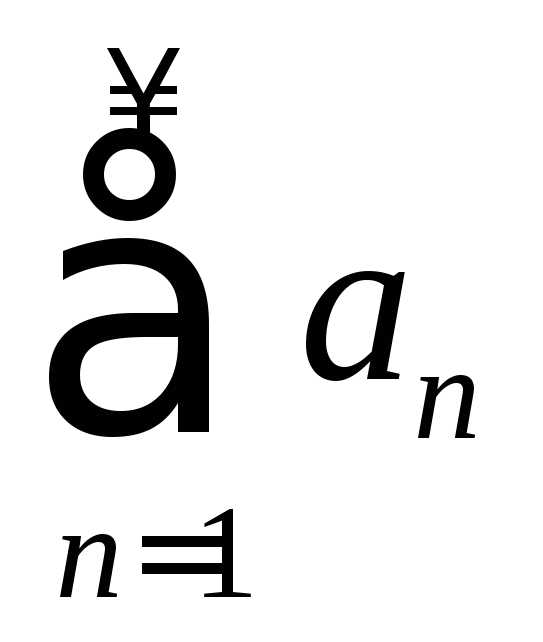 и
и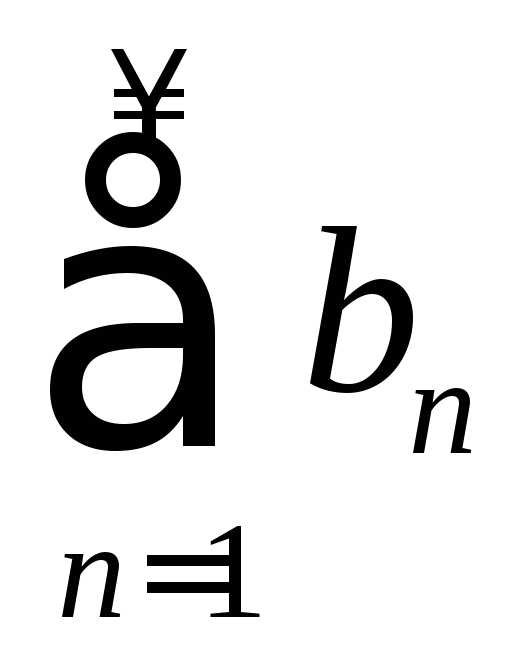 абсолютно сходятся, то при любых
абсолютно сходятся, то при любых и
и ряд
ряд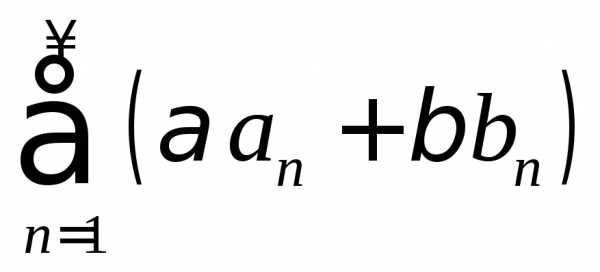 также абсолютно сходится.
также абсолютно сходится.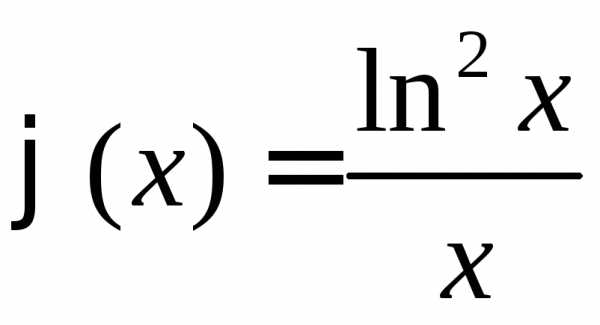 .
Тогда,
.
Тогда,
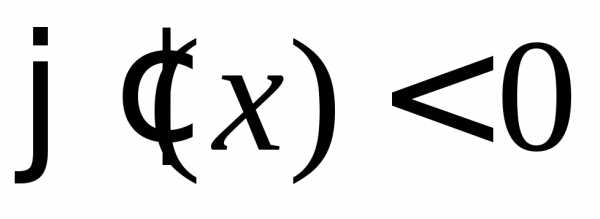 ,
если
,
если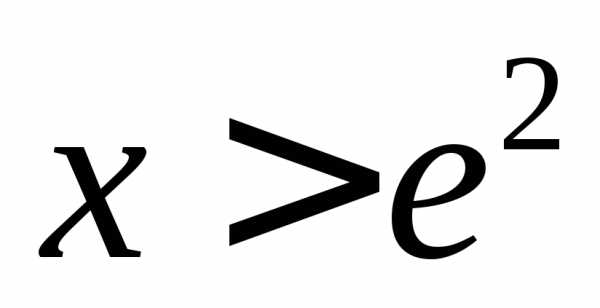 .
Значит, при
.
Значит, при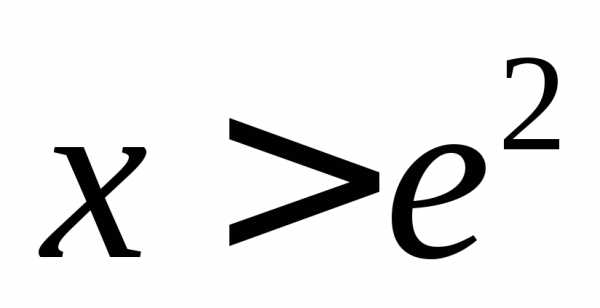 функция
функция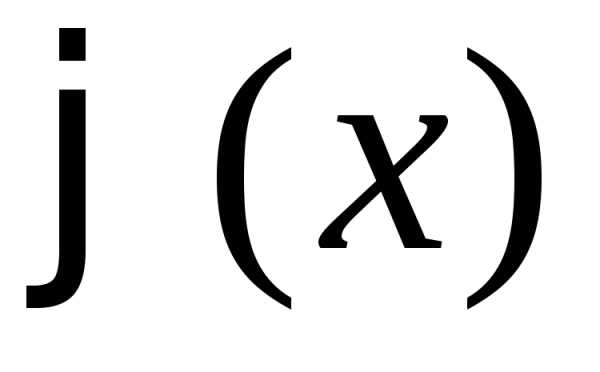 монотонно убывает.
монотонно убывает. .
. .
. .
.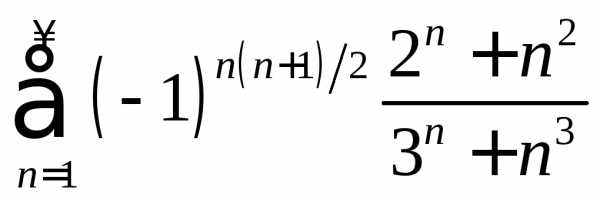 .
.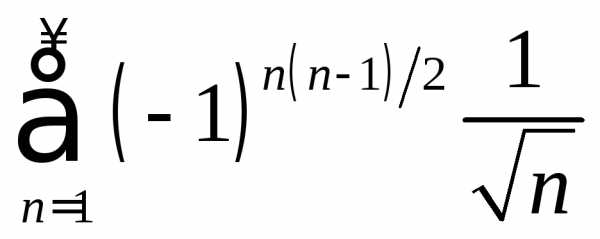 .
.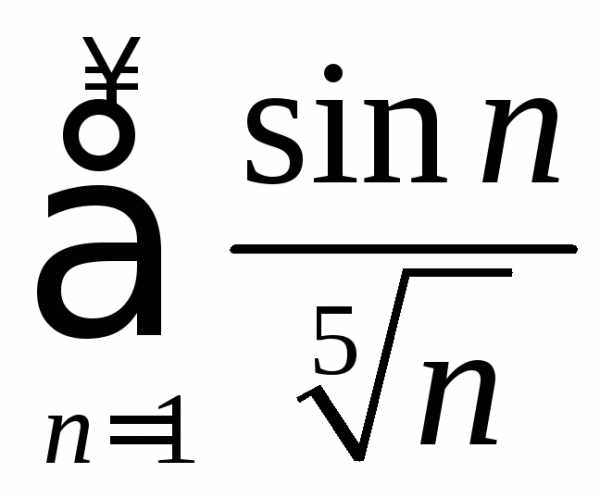 .
.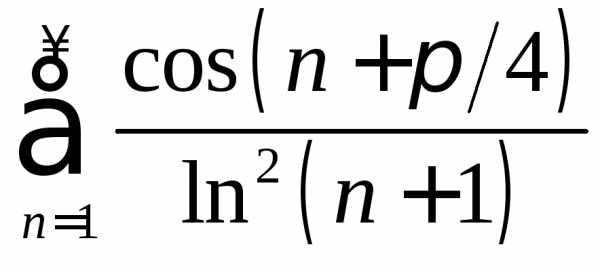 .
. .
. .
. .
. .
. .
. .
. .
.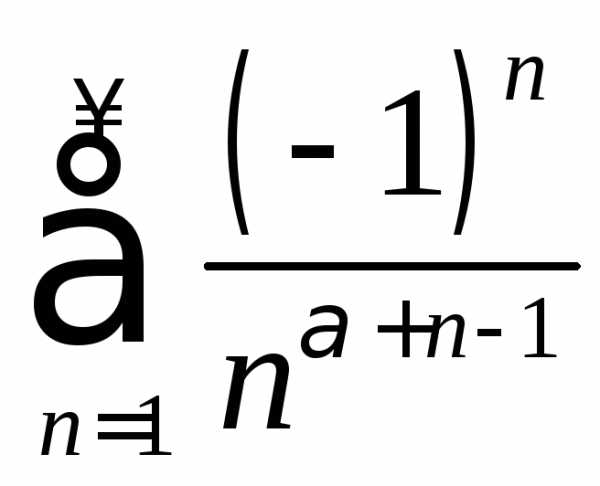 .
.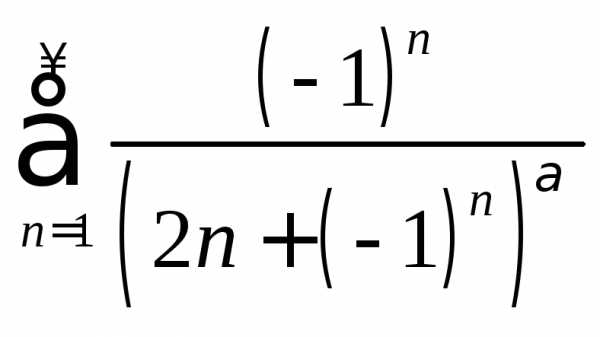 .
.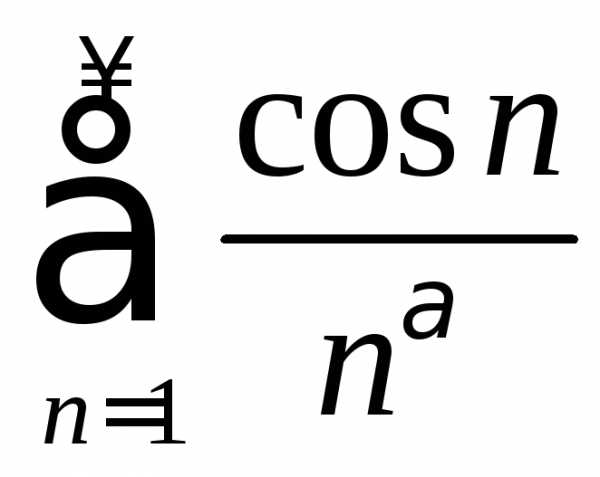 .
.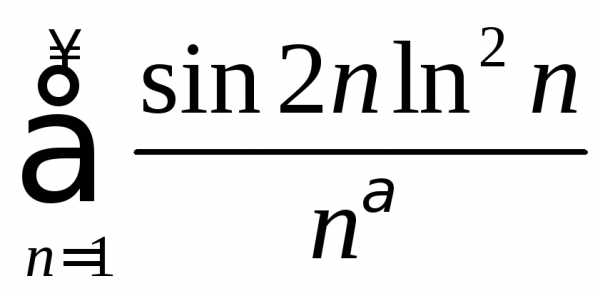 .
. .
. .
.