Квадратный корень из комплексного числа » Аналитическая геометрия f(x)dx.Ru
п.6. Извлечение квадратного корня из комплексного числа. Формула квадратных корней из комплексного числа.
В дальнейшем нам понадобится одна числовая функция:
обозначим .
Эту функцию называют знаком числа х и читается она так: «сигнум икс».
Теорема. Пусть . Тогда
(7) , где квадратные корни в скобках являются арифметическими квадратными корнями из положительных чисел.
Доказательство. Как мы уже выяснили существует ровно два квадратных корня из комплексного числа, причем они являются противоположными числами. Пусть , где . Тогда или . Возведем в квадрат левую часть этого равенства и воспользуемся условиями равенства двух комплексных чисел. Получаем:
(8) .
Возведем в квадрат каждое уравнение этой системы: . Прибавим второе уравнение к первому:
.
Здесь – обычный арифметический квадратный корень из положительного действительного числа. Далее, если полученная система имеет решение, то по обратной теореме Виета и являются корнями квадратного уравнения . Находим дискриминант . Отсюда . Оба корня квадратного уравнения оказываются положительными, т.к., очевидно, . При выборе корней учитываем равенства (8), а именно . Отсюда следует, что и
. Осталось правильно выбрать знаки перед знаками радикалов. Из равенств (8) следует, что . Положим , тогда , откуда и следует доказываемая формула. Теорема доказана.
Пример. Вычислить .
Решение. Используем только что доказанную формулу корней. Здесь . Подставляем в формулу и получаем:
.
Ответ: .
Замечание. Можно не запоминать формулу (7) ввиду ее громоздкости, а при решении использовать алгоритм доказательства теоремы. Решим таком образом предыдущий пример.
Пусть . Тогда . Это возможно лишь тогда равны вещественные и мнимые части обоих комплексных чисел: . Возводим оба уравнения системы в квадрат: . Прибавляем второе уравнение к первому: . Применяем обратную теорему Виета:
. Решаем квадратное уравнение: . Так как , то . Принимаем . Так как , то . Получили один из двух корней: . Второй корень противоположен первому.
Ответ: .
Конечно, этот способ, в отличие от первого, занимает у нас некоторое время, но зато алгоритмы запоминаются лучше, нежели формулы.
Нам будет интересен частный случай формулы (7), когда мнимая часть числа z равна нулю.
Следствие. Пусть – произвольное действительное число. Тогда имеет место следующая формула:
(9) .
Доказательство очевидно, достаточно подставить в формулу (7) и вспомнить, что арифметический квадратный корень из квадрата действительного числа равен его модулю: .
Теперь, если , то формула (9) дает оба корня из положительного действительного числа а: .
Не будем забывать, что квадратный корень в левой части формулы (9) обозначает все множество корней из комплексного числа , а квадратные корни в правой части формулы (9) обозначают арифметические квадратные корни из неотрицательных действительных чисел. Обозначение одно и то же, с помощью знака радикала, а смысл различный.
Пусть теперь . Тогда и формула (9) дает равенство: . Здесь – арифметический квадратный корень из положительного числа .
Случай очевиден: .
Интерес представляет случай корня квадратного из отрицательного числа. Сформулируем этот случай отдельно в виде следствия.
Следствие. Пусть и . Тогда оба квадратных корня из числа z могут быть найдены по формуле:
(10) .
Примеры: , , .
Замечание. Обратите внимание на последнее равенство:
.
Это верное равенство, т.е. по определению есть множество всех корней из числа –1, в то время как равенство неверное, с этой точки зрения! Именно поэтому нельзя переносить свойства корней из действительных чисел на корни из комплексных чисел, как показывает следующий простой пример.
Пример. Найдите ошибку в следующих преобразованиях:
.
С другой стороны, легко доказать следующую теорему.
Теорема. (О вынесении действительного множителя из под знака корня.) Пусть, n – произвольное натуральное число. Тогда
(11) ,
где есть обычный арифметический корень из положительного числа.
Доказательство. Равенство (11) здесь нужно понимать как равенство двух множеств: – множество всех корней n-й степени из комплексного числа , – множество всех корней n-й степени из комплексного числа z,
.
Отсюда вытекает и способ доказательства. Мы докажем, что оба множества состоят из одних и тех же элементов.
Пусть . Тогда . Отсюда следует, что . Обратно, Пусть . Тогда . Следовательно, , ч.т.д. Теорема доказана.
Замечание. Предыдущее следствие можно вывести и из только что доказанной теоремы.
Следствие. Пусть и Тогда .
Доказательство. Рассматриваем отрицательное число а как комплексное число . Тогда доказываемое равенство сразу же следует из только что доказанной теоремы: .
Пример. Вычислить .
Решение. Применим только что доказанную теорему: .
Ответ: .
Возможно найдутся ответы здесь:
fxdx.ru
1.12. Извлечение квадратного корня из комплексного числа
Извлечение корня из комплексного числа можно осуществить, не обращаясь к тригонометрической форме. Выведем алгебраическую формулу для выполнения этого действия.
Пусть
.
Интересен случай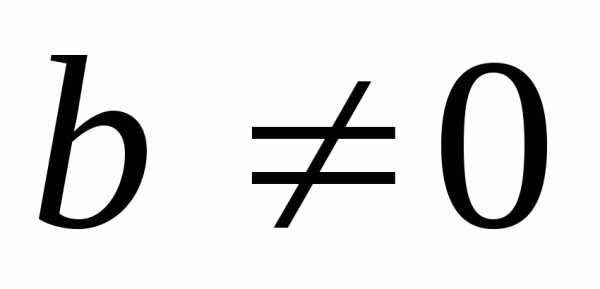 ,
поэтому рассмотрим только его. Тогда.
Это равносильно системе уравнений:
,
поэтому рассмотрим только его. Тогда.
Это равносильно системе уравнений:
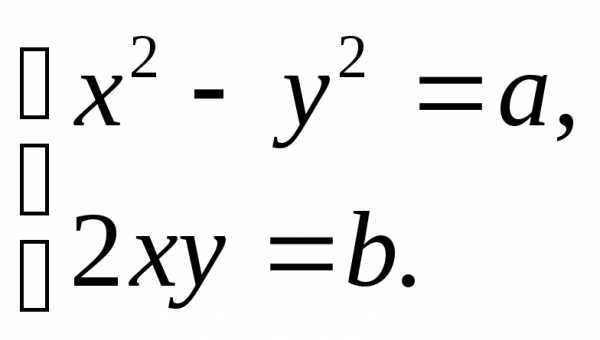 (1.12)
(1.12)
Эта задача имеет
вещественные решения, так как всегда
существует квадратный корень из
комплексного числа. Из второго уравнения
системы 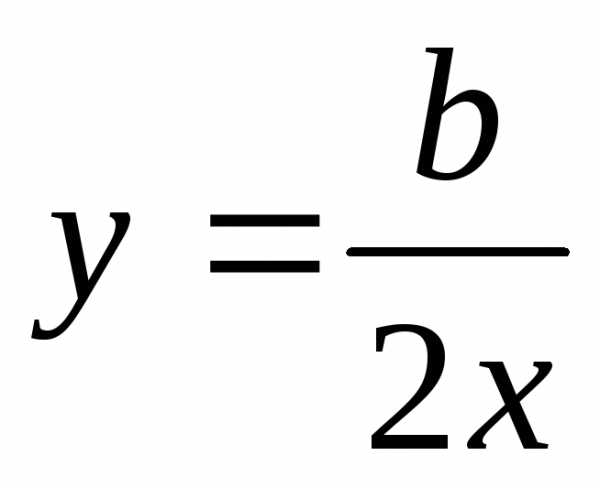
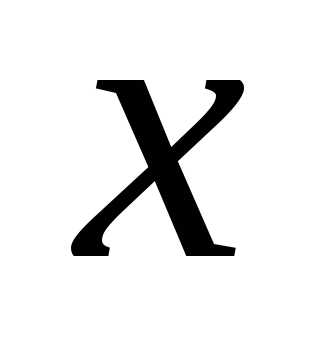 .
Его решениями являются
.
Его решениями являются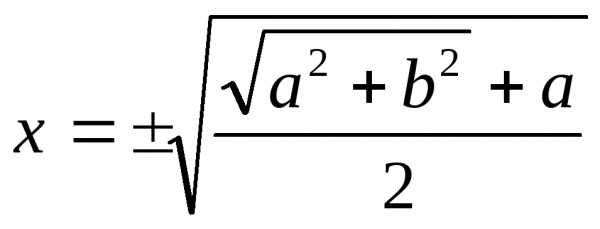 ,
поэтому
,
поэтому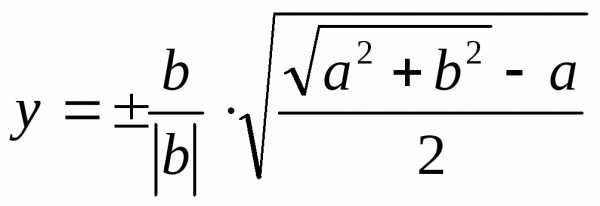 .
Для любого вещественного числаtсуществует функция
.
Для любого вещественного числаtсуществует функция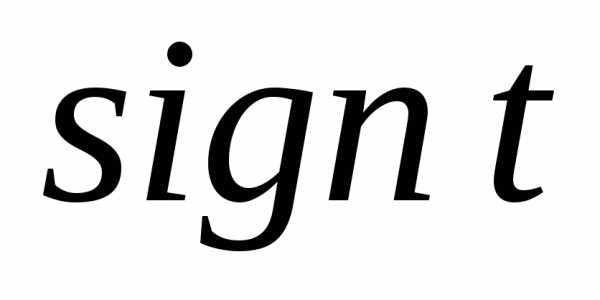 ,
которая задается следующим образом:
,
которая задается следующим образом: 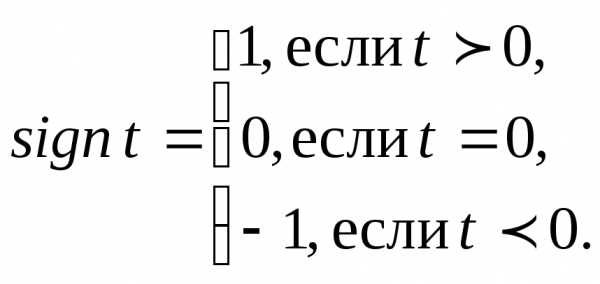 (1.13)
(1.13)
С учетом введенной функции получаем формулу для нахождения квадратного корня из комплексного числа:
. (1.14)
П р и м е р. Найти корни уравнения.
Решение.Корни
уравненияравны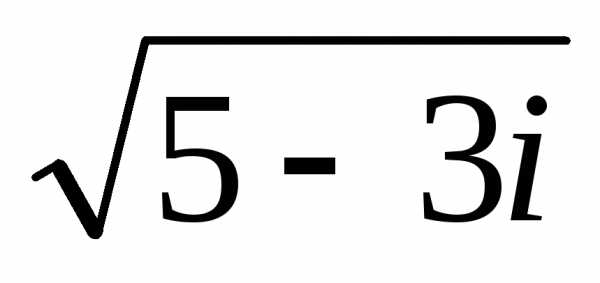 .
Пусть
.
Пусть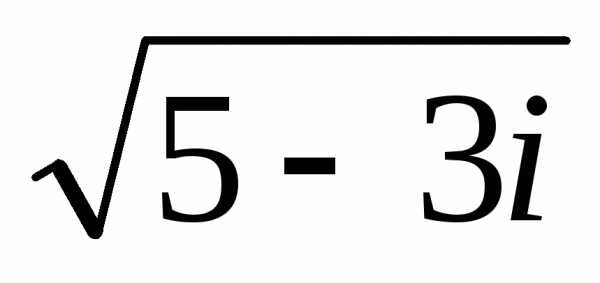 =
=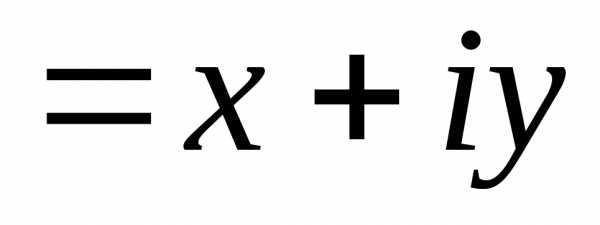 .
Относительно неизвестных
.
Относительно неизвестных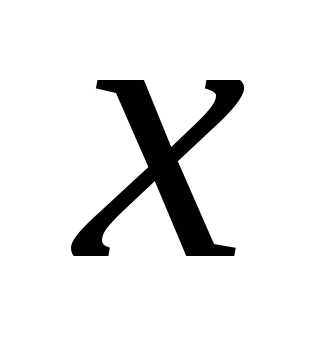 и
и имеем систему уравнений
имеем систему уравнений
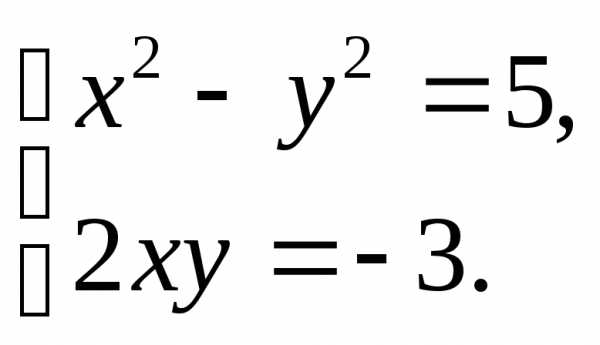
Из второго уравнения
этой системы 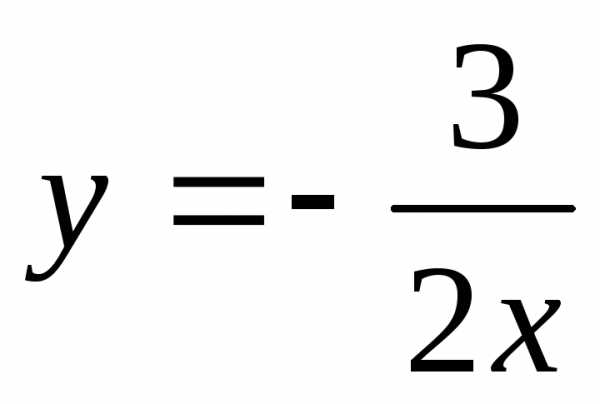 ,
поэтому относительно неизвестного
,
поэтому относительно неизвестного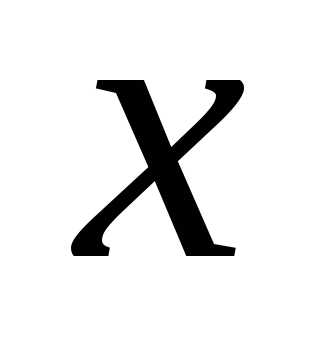
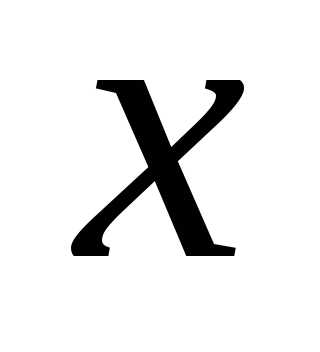 вещественное число,
находим,
т. е.
вещественное число,
находим,
т. е.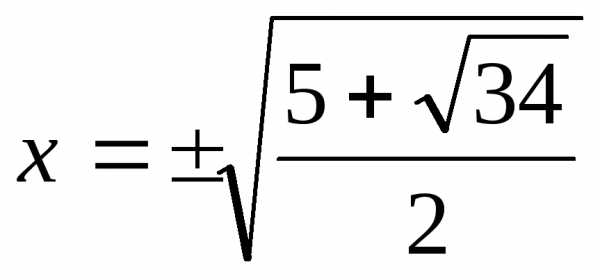 .
Следовательно,
.
Следовательно,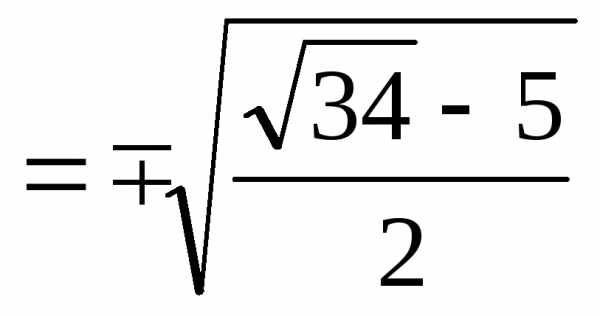 .
Таким образом,.
.
Таким образом,.1.13. Показательная форма комплексного числа
В различных разделах современной математики, а также ее приложениях применяется показательная форма комплексного числа. В основе показательной формы лежит формула Эйлера, устанавливающая связь между тригонометрическими функциями действительного аргумента и показательной функцией мнимого аргумента.
Первая формула Эйлера (без вывода):
, (1.15) где е – иррациональное число, принятое за основание натуральных логарифмов (е 2,718).
Если в формуле
произвести замену по формуле (1.15), то
получим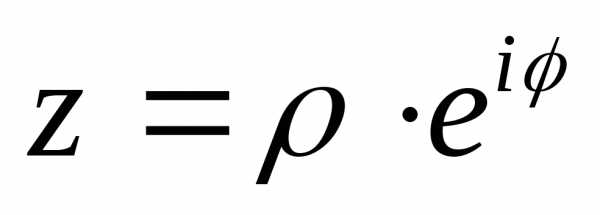
 .
В этой записи
.
В этой записи − модуль комплексного числа,
− модуль комплексного числа, − его аргумент. Заменим в формуле (1.15)
− его аргумент. Заменим в формуле (1.15) на —
на — ,
получим вторую формулу Эйлера:
,
получим вторую формулу Эйлера:. (1.16)
Из формул (1.15) и (1.16) следует, что
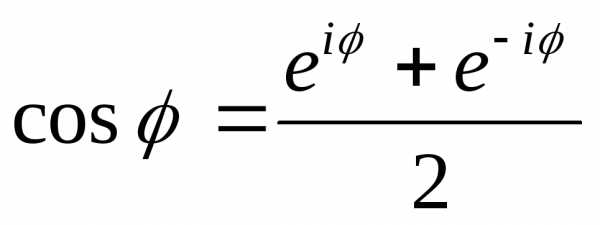
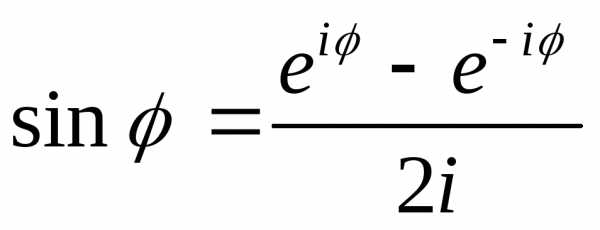 .
(1.17)
.
(1.17) Равенства (1.17)
также называются формулами Эйлера и
выражают тригонометрические функции
действительного переменного  через показательные функции мнимого
аргумента. Формулы (1.17) справедливы и
тогда, когда
через показательные функции мнимого
аргумента. Формулы (1.17) справедливы и
тогда, когда заменяется любым комплексным числом
заменяется любым комплексным числом ,
т. е.
,
т. е.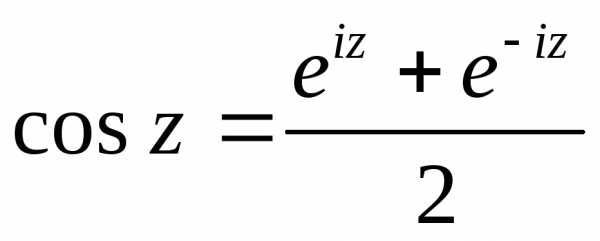 ,
,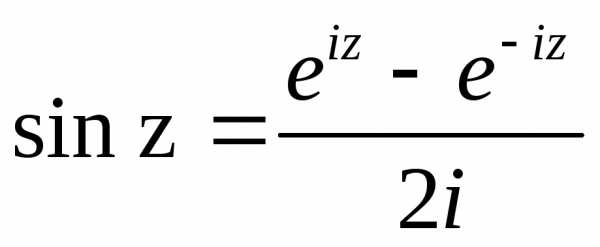 .
Эти равенства принимают за определение
косинуса и синуса комплексного аргумента.
.
Эти равенства принимают за определение
косинуса и синуса комплексного аргумента.
Тригонометрические
функции комплексного переменного также
периодичны, причем период 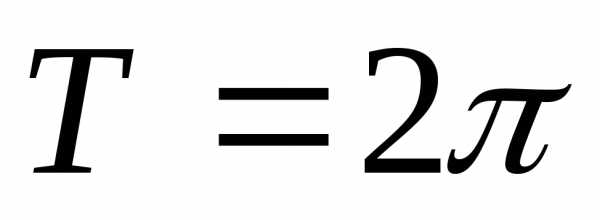
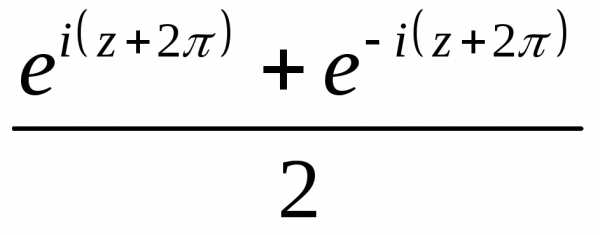 =
=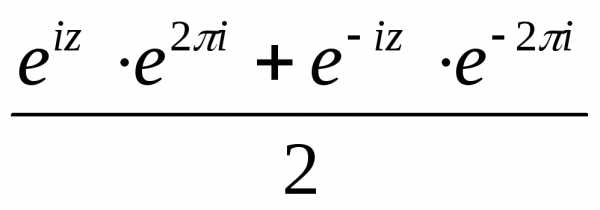 =
=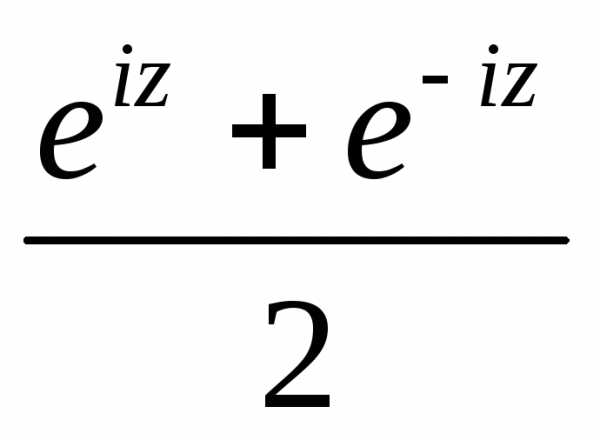 =
= ,
так как по формулам Эйлера,.
Примечательно, что все формулы обычной
тригонометрии сохраняют свою силу в
комплексной плоскости, например,.
Однако в отличие от действительных
чисел могут иметь место неравенства
,
так как по формулам Эйлера,.
Примечательно, что все формулы обычной
тригонометрии сохраняют свою силу в
комплексной плоскости, например,.
Однако в отличие от действительных
чисел могут иметь место неравенства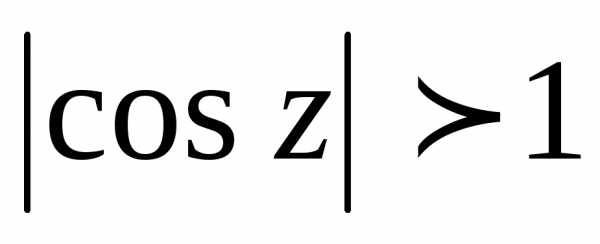 и
и .
Например,
.
Например,.
Многочлены
Многочлен от одной переменной. Действия
Над многочленами. Корни многочленов. Теорема Безу
Определение.Одночленом от переменной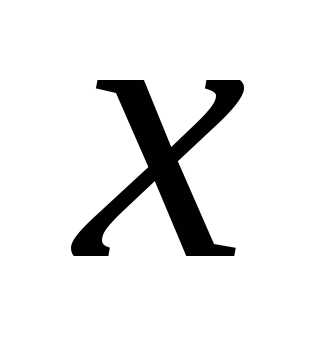 с коэффициентом из множестваАназывается выражение вида
с коэффициентом из множестваАназывается выражение вида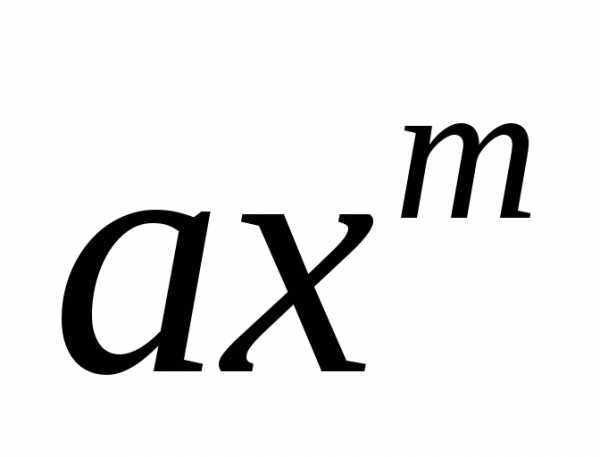 ,
где
,
где ,
,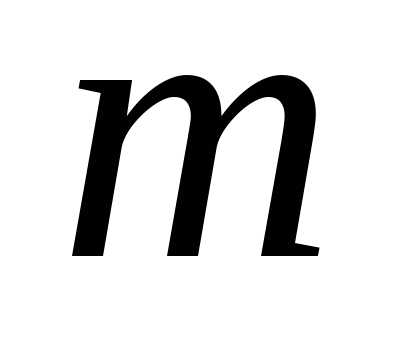 − целое неотрицательное число.
− целое неотрицательное число.
Считается, что 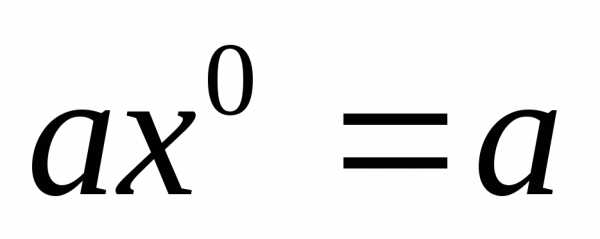 ,
поэтому все элементы множестваАявляются одночленами частного вида.
,
поэтому все элементы множестваАявляются одночленами частного вида.
Определение.Одночлены называются подобными, если
показатели степени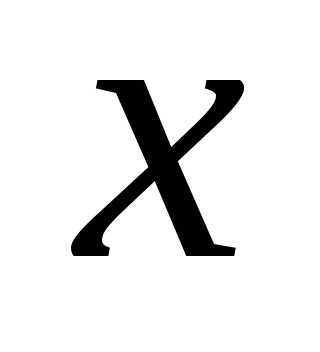 одинаковы.
одинаковы.
Подобные одночлены складываются по правилу , которое называетсяправилом приведения подобных членов. Для одночленов определяется и действие умножения.
Определение.Многочленомn-й степени от неизвестногохназывается сумма целых неотрицательных степеней, не превышающихп, неизвестногох, взятых с некоторыми числовыми коэффициентами, т. е. выражение вида
, (2.1)
причем 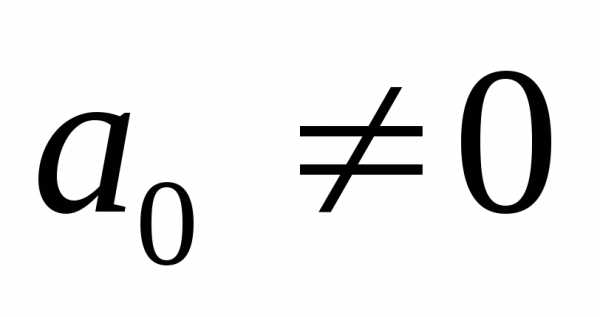 .
.
В многочлене
порядок слагаемых безразличен, и подобные
одночлены можно соединять по правилу
приведения подобных членов. Запись
(2.1) называется канонической формоймногочлена. Иногда удобно записывать
многочлены в порядке возрастания
показателей. Многочлены обозначаются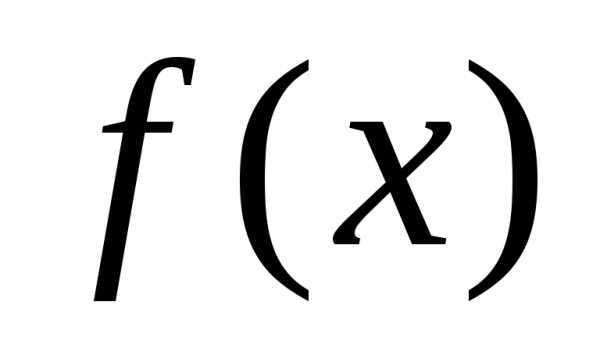 ,
,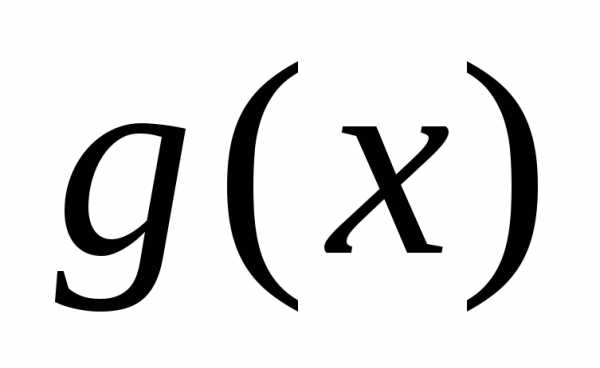 ,
,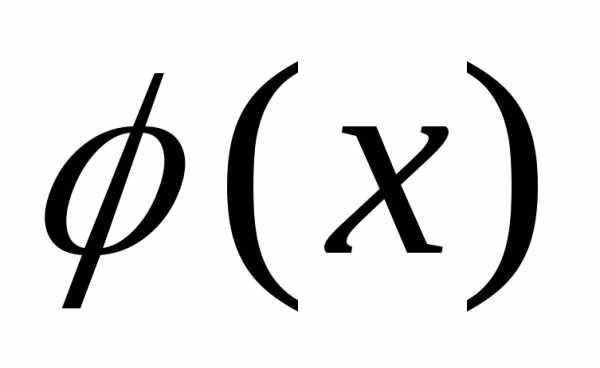 и т. д.
и т. д.
Пусть
,
причем .
Одночлен
.
Одночлен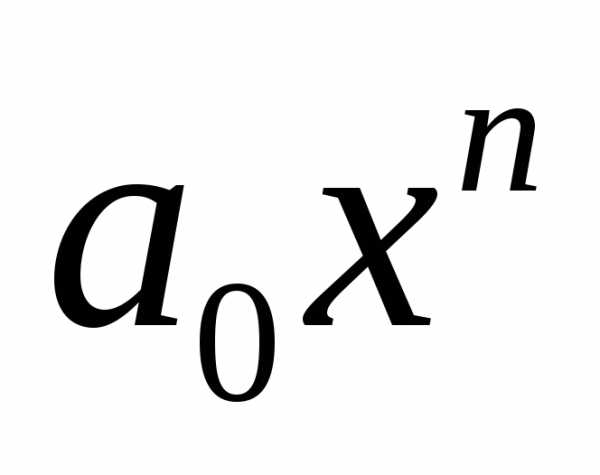 называетсявысшим (старшим) членоммногочлена
называетсявысшим (старшим) членоммногочлена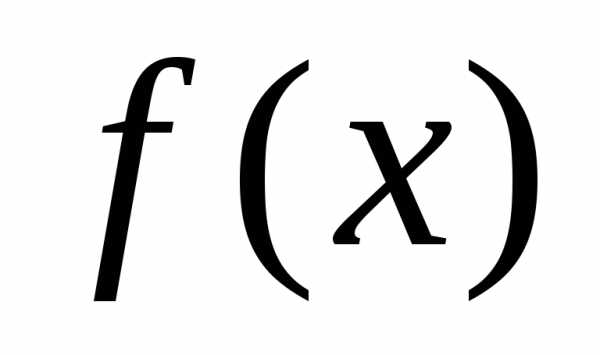 ,
а показатель
,
а показатель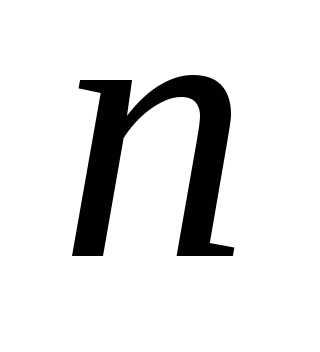 −степеньюмногочлена
−степеньюмногочлена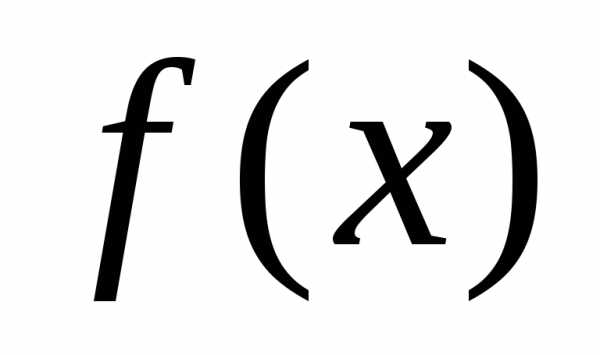 и обозначается
и обозначается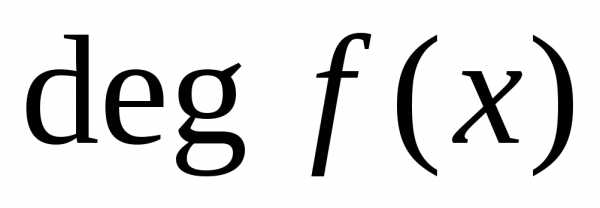 .
Нулевой многочлен не имеет высшего
члена в смысле данного определения и
считается, что он равен 0. Степень нулевого
многочлена считается равной символу
.
Нулевой многочлен не имеет высшего
члена в смысле данного определения и
считается, что он равен 0. Степень нулевого
многочлена считается равной символу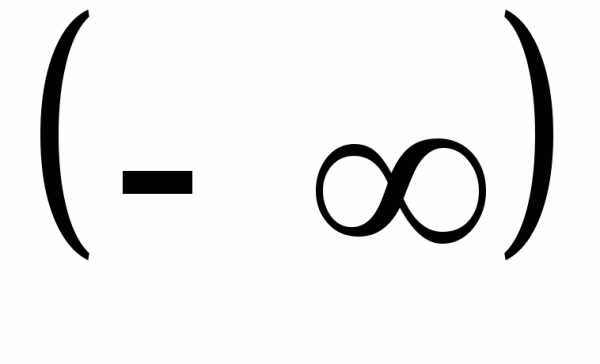 .
.
Определение.Два многочлена называются равными (или
тождественно равными), если они составлены
в канонической записи из одинаковых
одночленов, т.е.в том и только в том случае, если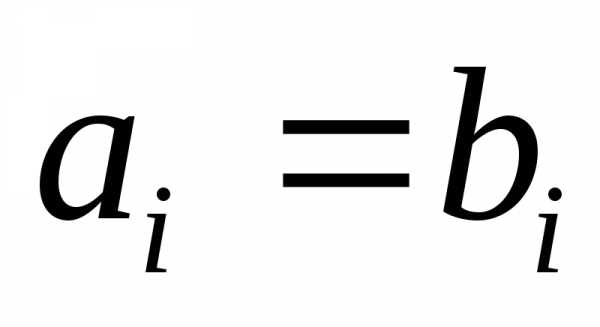 ,.
,.
Иными словами, в равных многочленах равны коэффициенты при одинаковых степенях неизвестного х.
Определение.Суммойдвух многочленов называется
многочлен, получающийся при объединении
одночленов, составляющих слагаемые.
После объединения необходимо привести
подобные члены. Таким образом,=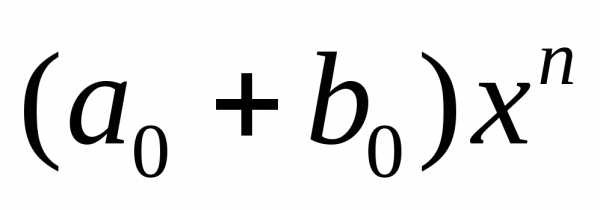 ++ … + +
++ … + +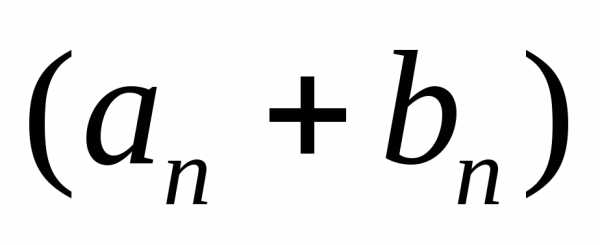 .
.
Определение.Произведениемдвух многочленов называется многочлен, составленный из произведений всех членов первого сомножителя на все члены второго. После приведения подобных членов получим, что=.
Коэффициент при 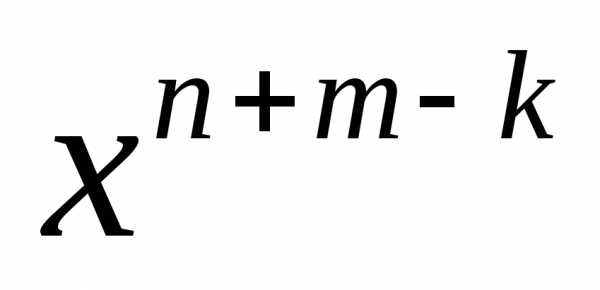 равен,
если считать, что
равен,
если считать, что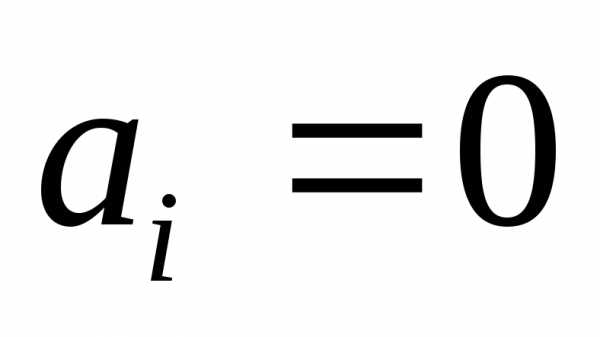 при
при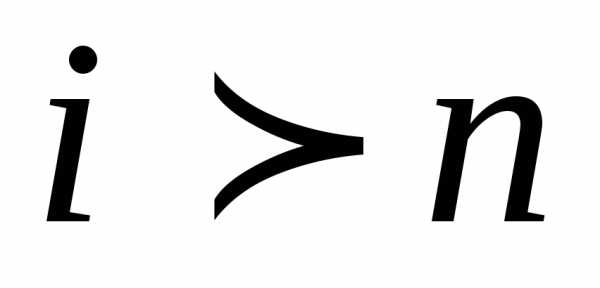 и
и при
при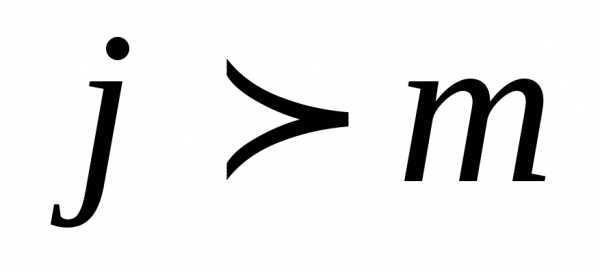 .
.
Пусть даны два
многочлена
и,
причем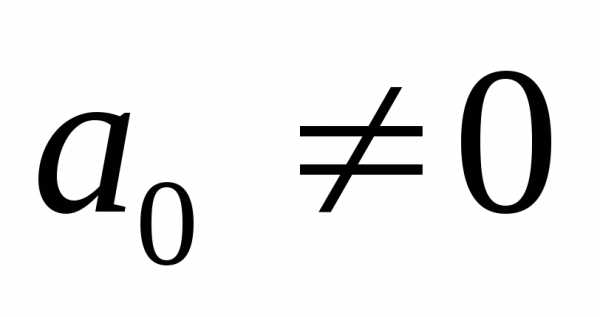 и
и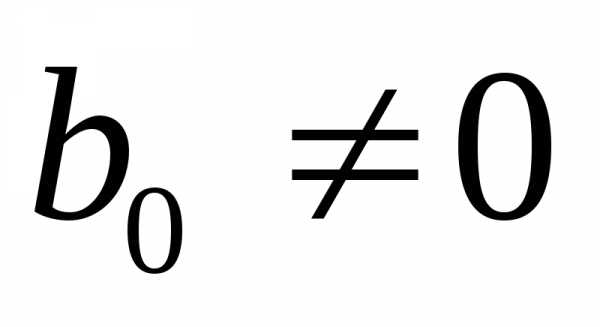 .
Тогда произведениесодержит ненулевой одночлен, который
будет высшим для произведения данных
многочленов, так как остальные произведения
членов
.
Тогда произведениесодержит ненулевой одночлен, который
будет высшим для произведения данных
многочленов, так как остальные произведения
членов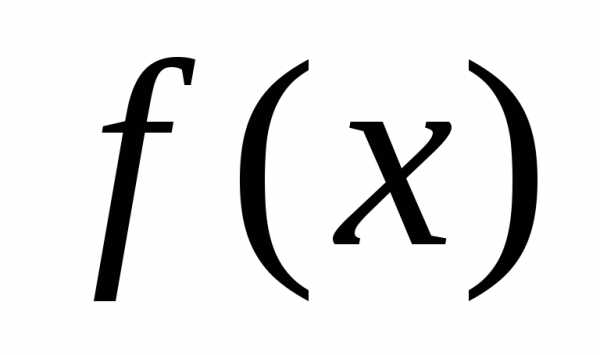 на члены
на члены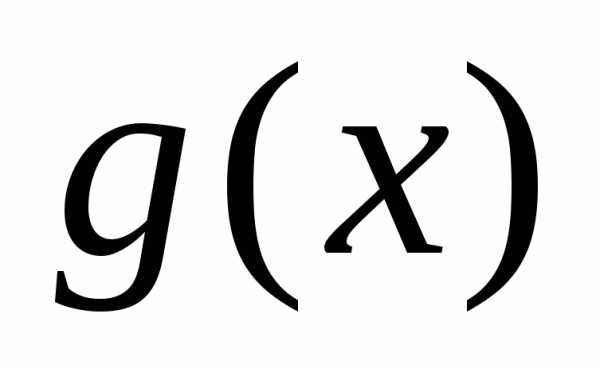 имеют меньшую, чем
имеют меньшую, чем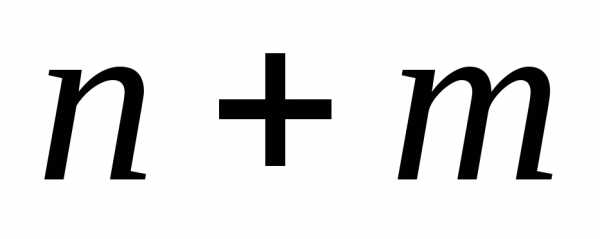 степень.
степень.
Для любых двух
многочленов 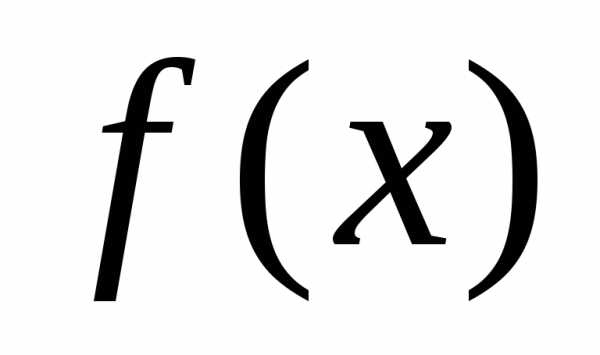 и
и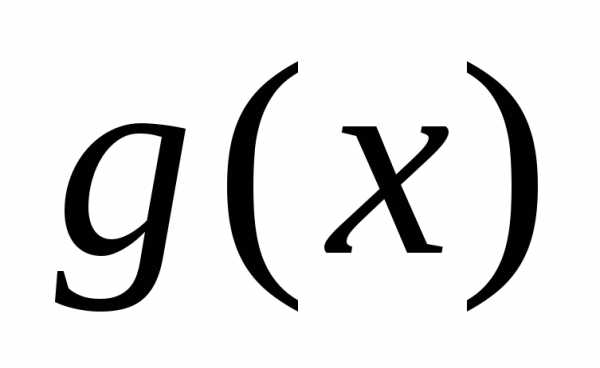 можно найти такие многочлены
можно найти такие многочлены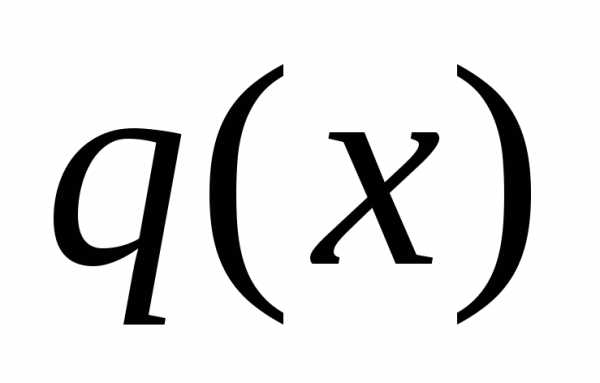 и
и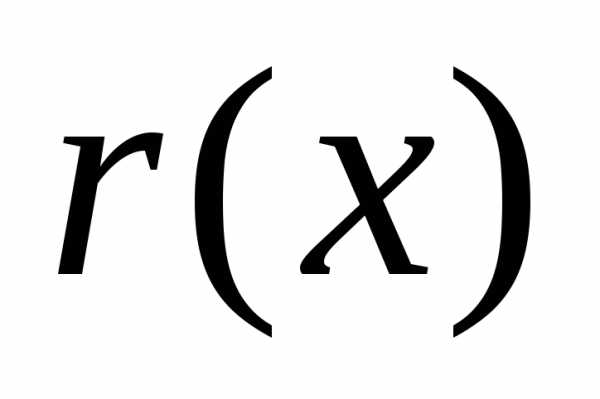 ,
что
,
что
, (2.2)
причем степень  меньше степени
меньше степени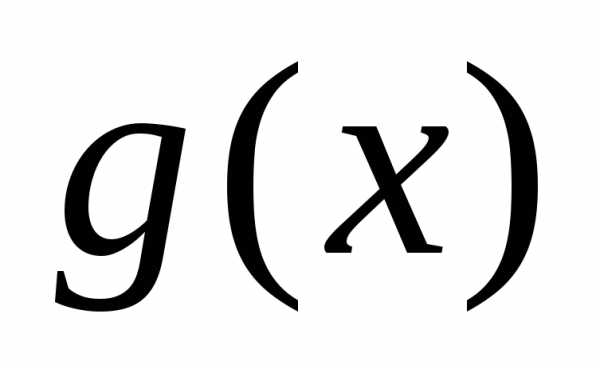 или же
или же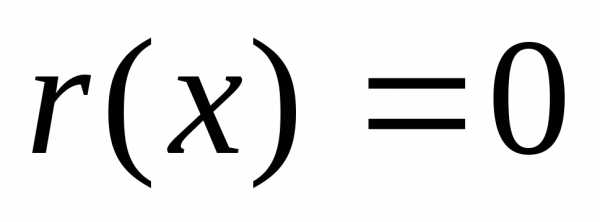 .
Многочлены
.
Многочлены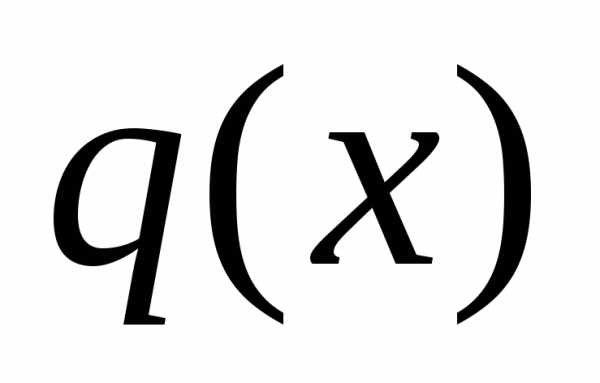 и
и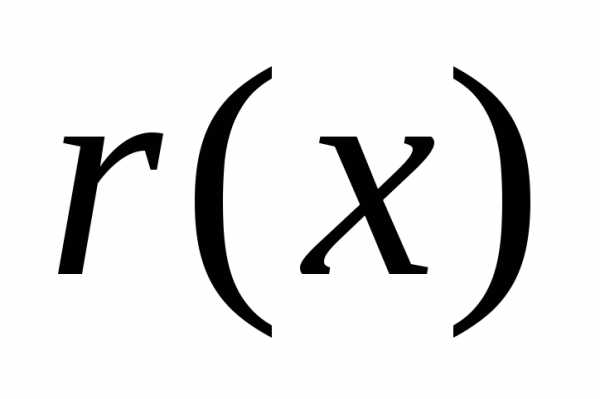 ,
удовлетворяющие условию (2.2), определяются
однозначно. Многочлен
,
удовлетворяющие условию (2.2), определяются
однозначно. Многочлен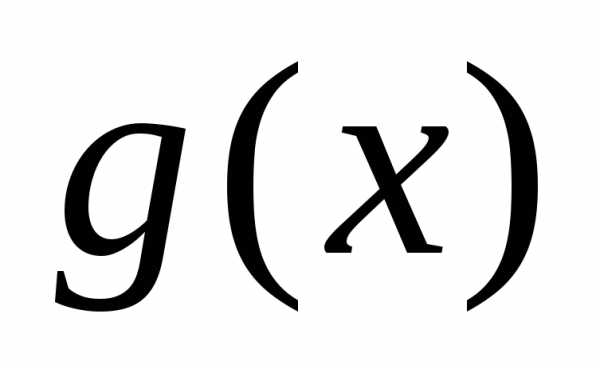 называетсячастным, а
называетсячастным, а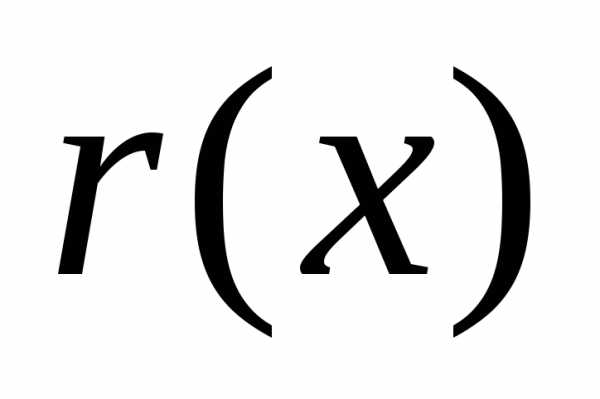 −остатком.
−остатком.
Определение. Пусть даны два ненулевых многочлена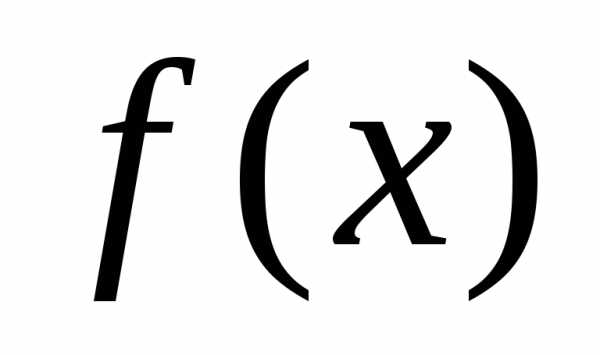 и
и .
Если остаток от деления
.
Если остаток от деления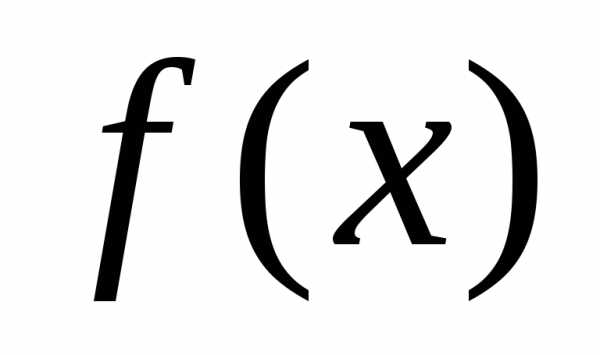 на
на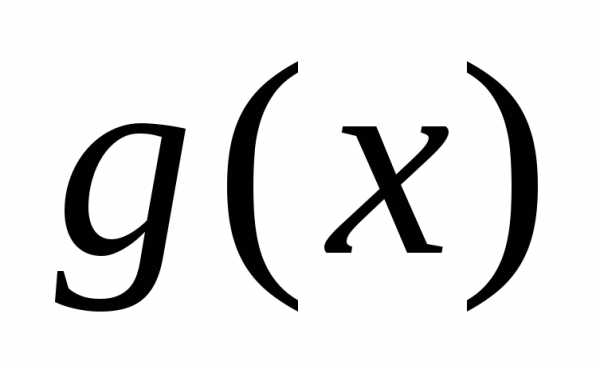 равен нулю, то многочлен
равен нулю, то многочлен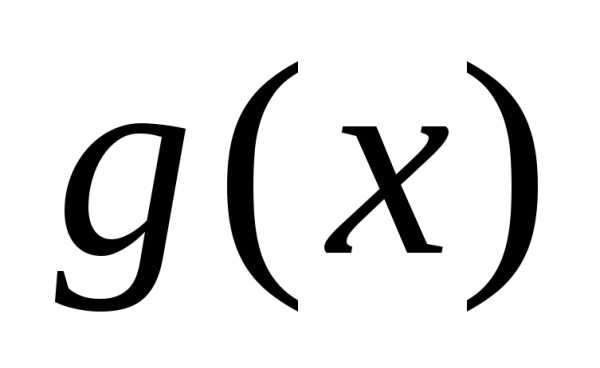 называетсяделителеммногочлена
называетсяделителеммногочлена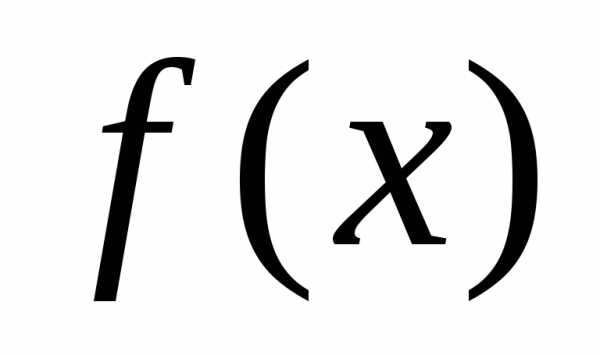 .
.
Определение.Если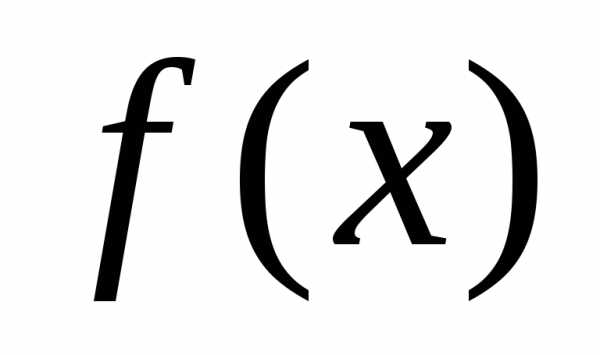 − многочлен,,
то
− многочлен,,
то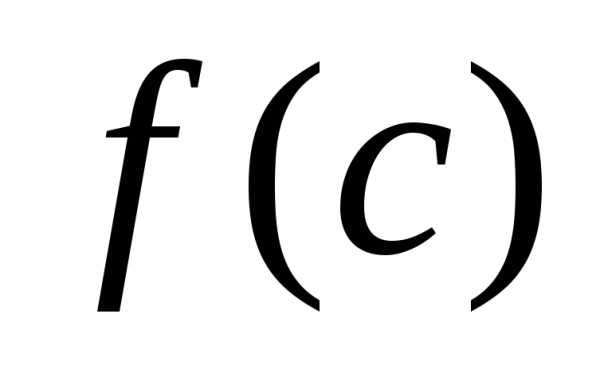 называется значением многочлена
называется значением многочлена при
при .
.
Теорема.Остаток от деления многочлена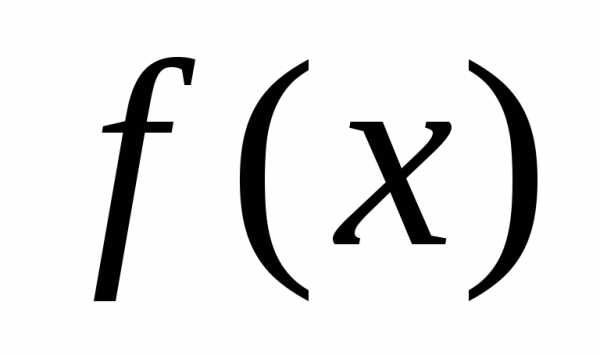 на линейный многочлен
на линейный многочлен равен значению
равен значению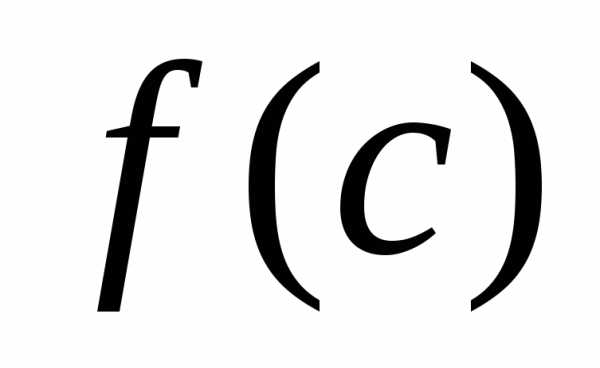 многочлена
многочлена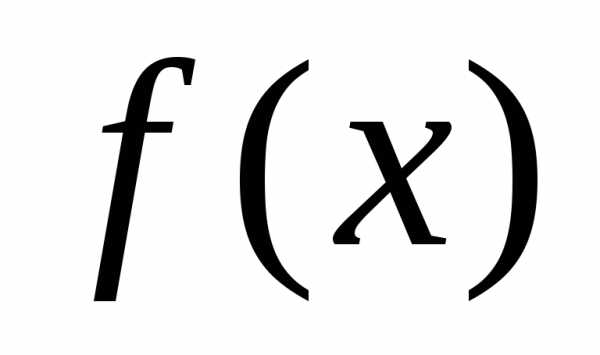 при
при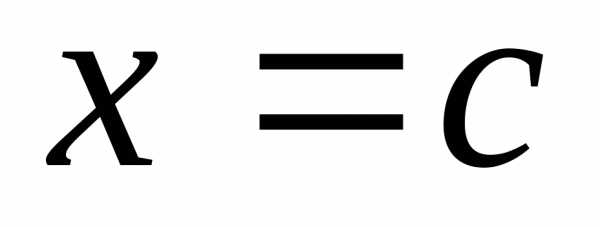 .
.
Доказательство.Согласно (2),
где − многочлен нулевой степени, т. е.
константа. Переходя в этом равенстве к
значениям при
− многочлен нулевой степени, т. е.
константа. Переходя в этом равенстве к
значениям при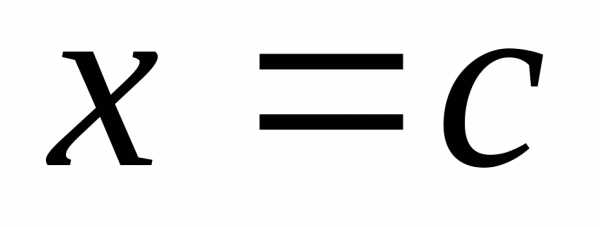 ,
получим,
откуда
,
получим,
откуда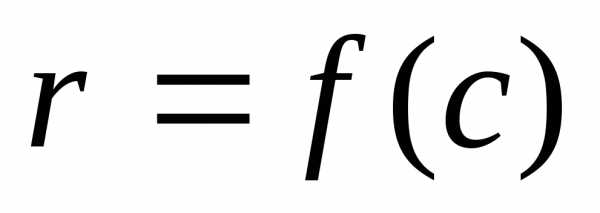 .
Теорема доказана.
.
Теорема доказана.
П р и м е р. Найти остаток от деления многочленана многочлен.
Решение. По доказанной ранее теореме.
Если для полиномов 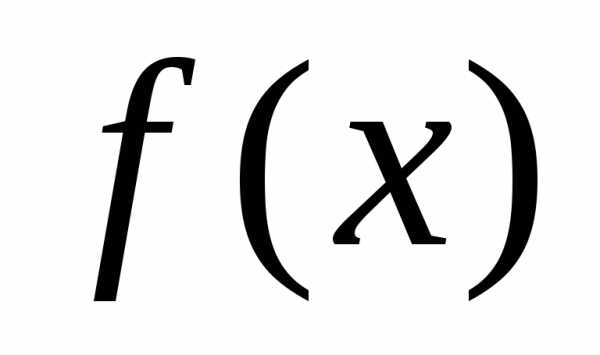 и
и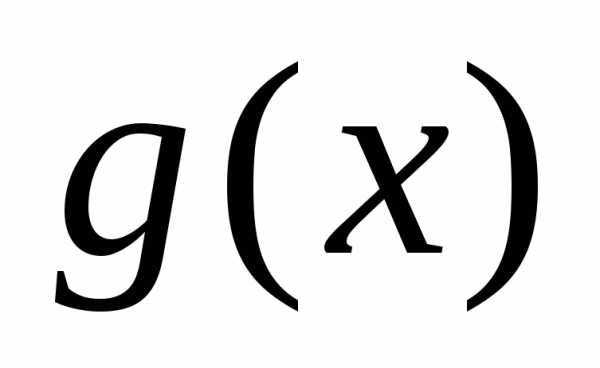 существует такой полином
существует такой полином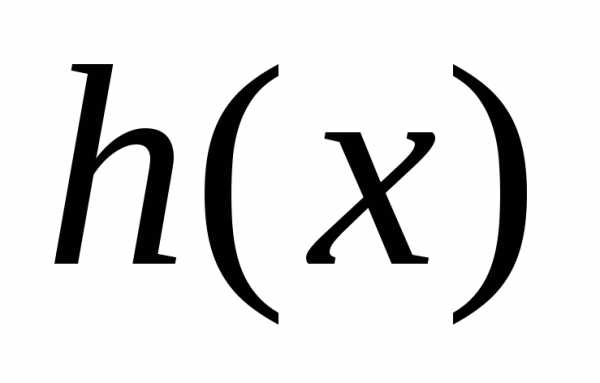 ,
что,
то говорят, что полином
,
что,
то говорят, что полином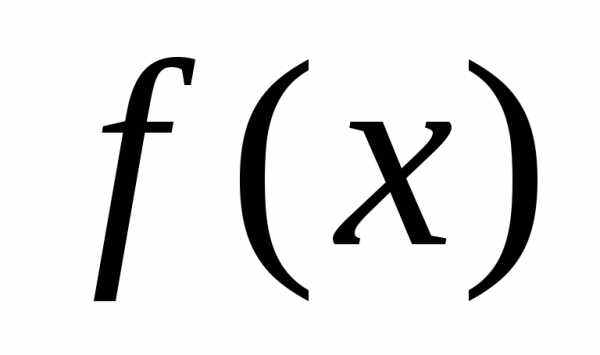 делится на полином
делится на полином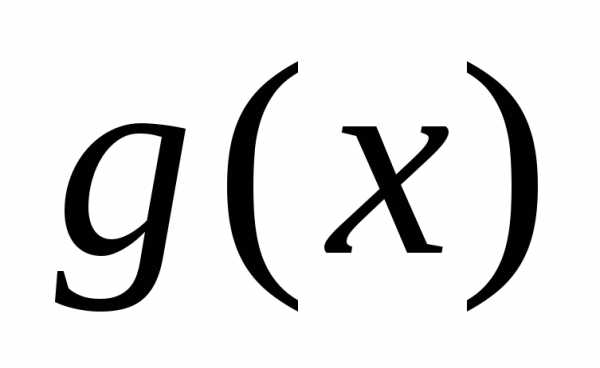 .
Рассмотрим вопрос о делимости
.
Рассмотрим вопрос о делимости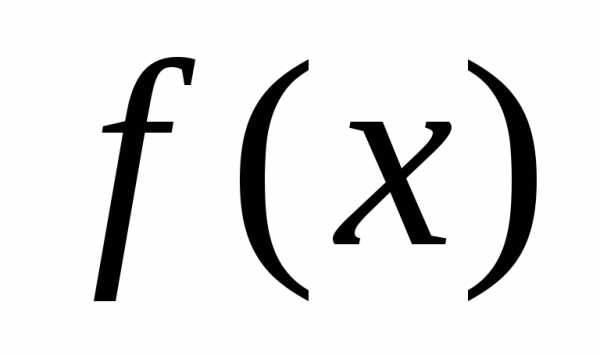 на линейный двучлен
на линейный двучлен ,
где.
,
где.
Теорема (Безу).Для того чтобы полином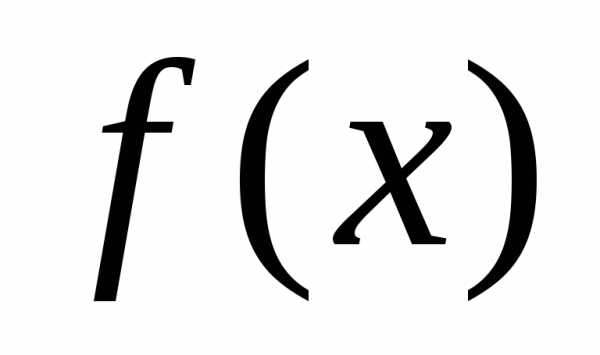 делился на
делился на ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы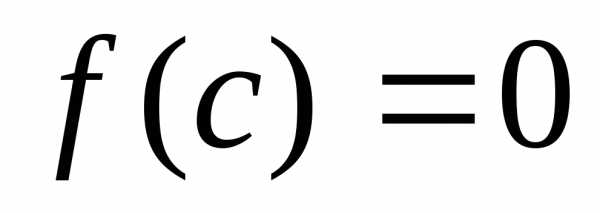 .
.
Доказательство.А.Необходимость.Пусть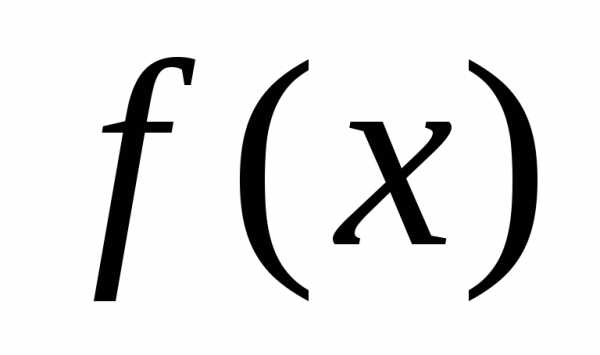 делится на
делится на ,
т. е..
Тогда
,
т. е..
Тогда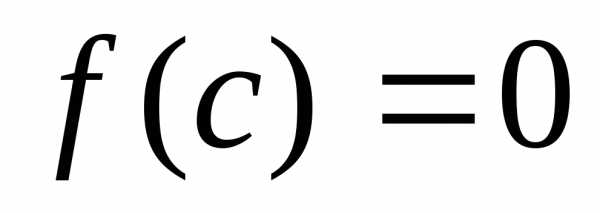 .
Б.Достаточность. Пусть
.
Б.Достаточность. Пусть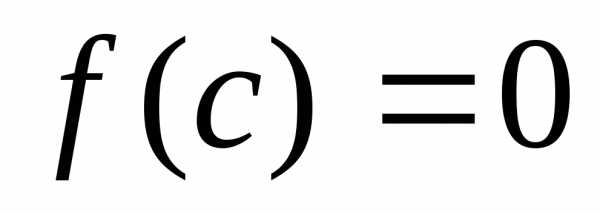 .
Тогда в равенствебудет,
т. е..
Теорема доказана.
.
Тогда в равенствебудет,
т. е..
Теорема доказана.
Определение.Числосназываетсякорнем полинома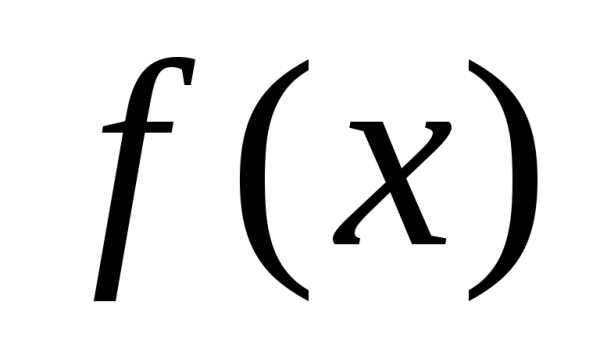 ,
если
,
если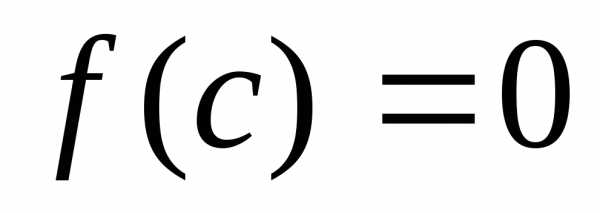 .
.
С использованием
этого определения теорема Безу может
быть сформулирована следующим образом:
для того чтобы полином 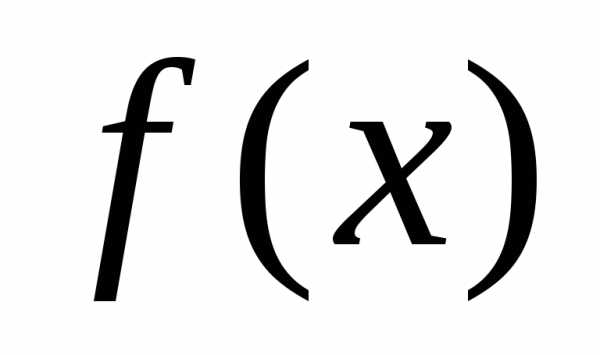 делился на двучлен
делился на двучлен ,
необходимо и достаточно, чтобыс было
корнем
,
необходимо и достаточно, чтобыс было
корнем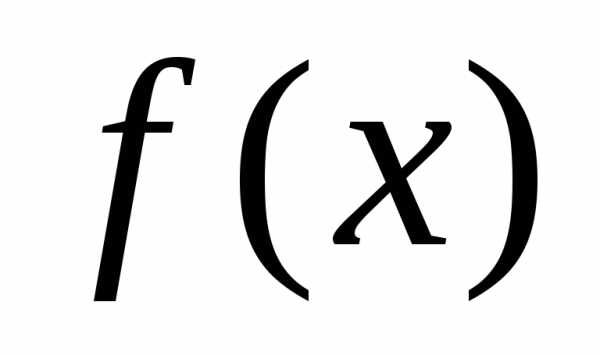 .
Таким образом, отыскание корней многочлена
равносильно отысканию его линейных
делителей.
.
Таким образом, отыскание корней многочлена
равносильно отысканию его линейных
делителей.
П р и м е р.Является ли линейный многочлен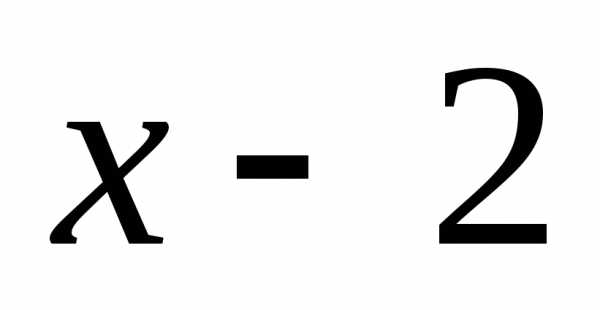 делителем многочлена?
делителем многочлена?
Решение.Найдем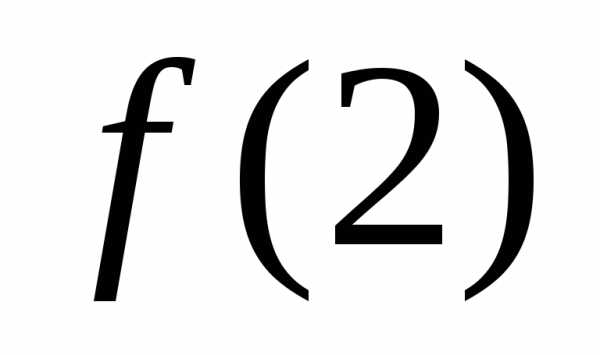 :,
следовательно,
:,
следовательно,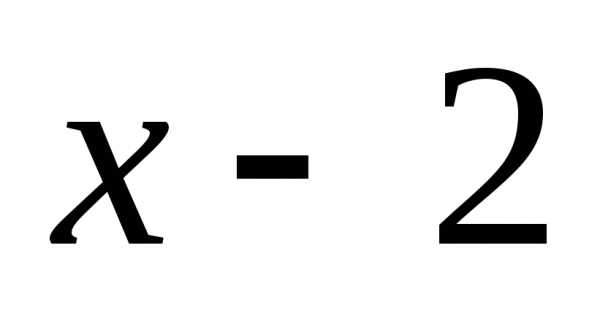 не является делителем многочлена.
не является делителем многочлена.
studfiles.net
кубический корень из комплексного числа : Школьная алгебра
Кубический корень — многозначная функция, т.е., если формально, то — не число, а множество, вообще говоря (а именно, при ), из 3 элементов. Например,.
Поэтому правильнее говорить не о кубическом корне из числа , а об одном из значений кубического корня из .
Это если мы работаем с комплексными числами. Если же ограничиться только действительными числами, то:
1) Есть понятие арифметического кубического корня. Он определен только при и определяется как решение уравнения .
2) Поскольку — нечетное число, то можно определить корень кубический из произвольного действительного числа как решение уравнения .
Но пользоваться этими понятиями кубического корня можно, только если мы работаем исключительно в поле действительных чисел. Если в промежуточных выкладках мы используем комплексные числа, то использование этих понятий незаконно и может привести к противоречиям.
dxdy.ru
кубический корень из комплексного числа : Школьная алгебра
Кубический корень — многозначная функция, т.е., если формально, то — не число, а множество, вообще говоря (а именно, при ), из 3 элементов. Например,.
Поэтому правильнее говорить не о кубическом корне из числа , а об одном из значений кубического корня из .
Это если мы работаем с комплексными числами. Если же ограничиться только действительными числами, то:
1) Есть понятие арифметического кубического корня. Он определен только при и определяется как решение уравнения .
2) Поскольку — нечетное число, то можно определить корень кубический из произвольного действительного числа как решение уравнения .
Но пользоваться этими понятиями кубического корня можно, только если мы работаем исключительно в поле действительных чисел. Если в промежуточных выкладках мы используем комплексные числа, то использование этих понятий незаконно и может привести к противоречиям.
dxdy.ru
Извлечение корня из комплексного числа.
Пусть комплексное число записано в тригонометрической форме .
Запишем его корень также в тригонометрической форме записи
По определению корня имеем .
Возводя в степень по формуле Муавра, получаем
. Отсюда находим модуль корня
и аргумент
; .
Итак, корень степени n из комплексного числа извлекается по формуле
где
Для любого комплексного числа различных корней степени n ровно n штук. Все они расположены на окружности с центром в начале координат
с радиусом и делят эту окружность на n равных частей.
Пример 2.Вычислить .
Запишем число i в тригонометрической форме .
Применим формулу извлечения корня из комплексного числа
при .
Подставляя получаем различные значения корня
Извлечение корня квадратного из комплексного числа
в алгебраической форме записи.
Запишем квадратный корень из числа в алгебраической форме
. Возведем это равенство в квадрат:
Приравнивая действительные и мнимые части, а также, учитывая, что модуль числа равен квадрату модуля его корня, получаем систему
Решая эту систему, находим , откуда
.
Пример 3.Вычислить .
Действительная и комплексная части равны a=3 и b=4. Вычислим по найденной формуле действительную и комплексную части его корня
Итак, .
Многочлены. Разложение на множители.
Рассмотрим многочлен степени n с комплексными коэффициентами от комплексной переменной
, где комплексная переменная;
комплексные числа.
Любой многочлен можно поделить на многочлен с остатком,
то есть представить в виде
где
– делитель, – остаток, – частное.
Определение.Число z0называется корнем многочлена , если =0.
Теорема Безу.Число является корнем многочлена тогда и только тогда, если делится нацело на .
Доказательство.
Необходимость.
Пусть – корень многочлена . Поделим на многочлен
с остатком: , где R – число.
Положим в этом равенстве . Так как – корень, то , следовательно и делится нацело на .
Достаточность.
Пусть делится на без остатка, тогда . Подставляя в это равенство , получаем , следовательно, по определению, является корнем многочлена .
Определение.Число – корень многочлена кратности k , если многочлен можно представить в виде , где не является корнем многочлена , то есть .
Утверждение.Число является корнем кратности k многочлена тогда и только тогда, если является корнем этого многочлена и всех его производных до порядка включительно, то есть а .
Доказательство.
Необходимость. Пусть известно, что , где .
Очевидно, что , то есть является корнем многочлена. Покажем, что является корнем производных многочлена до порядка включительно. Вычислим производную порядка по формуле
Ньютона-Лейбница
При все слагаемые в правой части в точке будут равны нулю, и тогда . Если же , то в точке все слагаемые, кроме последнего, равны нулю. Последнее же слагаемое отлично от нуля в силу условия . Отсюда
Достаточность. Разложим многочлен в точке по формуле Тейлора
Так как первые k слагаемых в правой части обращаются в ноль, то многочлен можно представить в виде
.
При этом многочлен
в точке в ноль не обращается, так как по условию.
Тогда будет корнем кратности k по определению.
Основная теорема алгебры (без доказательства).
Пусть многочлен от комплексной переменной степени n, с комплексными коэффициентами. Тогда он имеет ровно n корней и его можно представить в виде
, где
– корень кратности
Лемма 1.Если z0 – корень кратности k многочлена , то сопряжённое число является корнем кратности k для сопряженного многочлена .
Доказательство. Если z0– корень кратности k многочлена , то многочлен можно представить в виде , где .
Возьмём сопряжённое к левой и правой частям последнего равенства
. По свойствам сопряжённых чисел имеем
. В левой части этого равенства стоит значение сопряженного многочлена в точке и оно представимо в виде где Положив в этой формуле , получим . Обозначим ,
тогда , где
Это и означает, что – корень кратности k многочлена .
Лемма 2. Пусть – многочлен с действительными коэффициентами, но от комплексной переменной.
Если корень кратности k многочлена , то также является корнем кратности k многочлена .
Доказательство. По лемме 1 число является корнем кратности k сопряженного многочлена . Поскольку коэффициентымногочлена действительны, то сопряженный многочлен совпадает с самим многочленом и число является корнем кратности k многочлена .
Теорема.Многочлен от действительной переменной с действительными коэффициентами представляется в виде произведения линейных множителей и квадратных с отрицательным дискриминантом:
, где
– действительный корень кратности ; ; .
Доказательство. Рассмотрим многочлен как многочлен от комплексной переменной .
Тогда, по основной теореме алгебры, его можно представить в виде
, где – корень кратности .
Если — действительное число, то скобку не преобразовываем.
Если то , где . По лемме 2, если – корень
кратности для , то также корень кратности для . Сопряженное число запишется как , тогда произведение
можно представить в виде степени, в основании которой лежит квадратный трехчлен с отрицательным дискриминантом
так как .
Таким образом, разложили многочлен в произведение линейных множителей и квадратных с отрицательным дискриминантом. Положив , получим искомое разложение для .
infopedia.su
Кубический корень — Википедия
Материал из Википедии — свободной энциклопедии
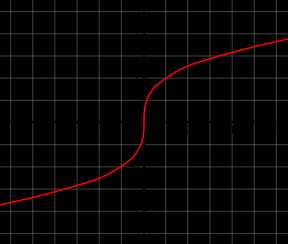 График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}
График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}Куби́ческий ко́рень из a, обозначающийся как a3{\displaystyle {\sqrt[{3}]{a}}} или как a1/3 — это число x,{\displaystyle x,} куб которого равен a.{\displaystyle a.} Другими словами, это решение уравнения x3=a{\displaystyle x^{3}=a} (обычно подразумеваются вещественные решения).
Вещественный корень
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):
- −x3=−x3{\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}
Видео по теме
Комплексный корень
Кубический корень из комплексного числа (из любого числа) c{\displaystyle c} имеет ровно три значения (частный случай свойства корня n-ой степени):
- c3=|c|3(cosϕ+2kπ3+isinϕ+2kπ3),k=0,1,2,ϕ=argc.{\displaystyle {\sqrt[{3}]{c}}={\sqrt[{3}]{\left|c\right|}}\left(\cos {\frac {\phi +2k\pi }{3}}+i\sin {\frac {\phi +2k\pi }{3}}\right),\quad k=0,1,2,\quad \phi =\arg {c}.}
Здесь под |c|3{\displaystyle {\sqrt[{3}]{\left|c\right|}}} понимается арифметический корень из положительного числа |c|.{\displaystyle \left|c\right|.}
В частности
- 13={1cos2π3+isin2π3=−12+i32cos2π3−isin2π3=−12−i32{\displaystyle {\sqrt[{3}]{1}}={\begin{cases}1\\\cos {\frac {2\pi }{3}}+i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {2\pi }{3}}-i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
- −13={−1cosπ3+isinπ3=12+i32cosπ3−isinπ3=12−i32{\displaystyle {\sqrt[{3}]{-1}}={\begin{cases}-1\\\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}={\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {\pi }{3}}-i\sin {\frac {\pi }{3}}={\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
Два комплексных значения кубического корня получаются из вещественных по формуле:
- x32,3=x3(−12±i32).{\displaystyle {\sqrt[{3}]{x}}_{2,3}={\sqrt[{3}]{x}}\left(-{\frac {1}{2}}\pm i{\frac {\sqrt {3}}{2}}\right).}
Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.
Показательная форма
Корень из комплексных чисел можно определить так:
- x1/3=exp(13lnx){\displaystyle x^{1/3}=\exp({\tfrac {1}{3}}\ln {x})}
Где ln — главная ветвь натурального логарифма.
Если представить x{\displaystyle x} как
- x=rexp(iθ){\displaystyle x=r\exp(i\theta )}
то формула кубического числа такова:
- x3=r3exp(13iθ).{\displaystyle {\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp({\tfrac {1}{3}}i\theta ).}
Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если x{\displaystyle x} комплексное, то −83{\displaystyle {\sqrt[{3}]{-8}}} будет обозначать не −2{\displaystyle -2}, а будет 1+i3.{\displaystyle 1+i{\sqrt {3}}.}
Интересные факты
Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.
При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.
Способы вычисления
Столбиком
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
Алгоритм таков:
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a{\displaystyle a}. Вычислите по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} такое число x{\displaystyle x}, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x{\displaystyle x} справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} и произведите вычитание. Перейдите к пункту 3.
См. также
Литература
- Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.
wiki2.red
Кубический корень Википедия
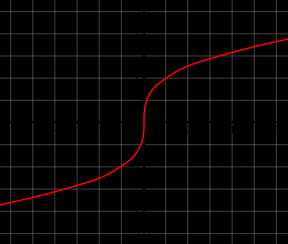 График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}
График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}Куби́ческий ко́рень из a, обозначающийся как a3{\displaystyle {\sqrt[{3}]{a}}} или как a1/3 — это число x,{\displaystyle x,} куб которого равен a.{\displaystyle a.} Другими словами, это решение уравнения x3=a{\displaystyle x^{3}=a} (обычно подразумеваются вещественные решения).
Вещественный корень[ | ]
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):
- −x3=−x3{\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}
Комплексный корень[ | ]
Кубический корень из комплексного числа (из любого числа) c{\displaystyle c} имеет ровно три значения (частный случай свойства корня n-ой степени):
- c3=|c|3(cosϕ+2kπ3+isinϕ+2kπ3),k=0,1,2,ϕ=argc.{\displaystyle {\sqrt[{3}]{c}}={\sqrt[{3}]{\left|c\right|}}\left(\cos {\frac {\phi +2k\pi }{3}}+i\sin {\frac {\phi +2k\pi }{3}}\right),\quad k=0,1,2,\quad \phi =\arg {c}.}
Здесь под
ru-wiki.ru
