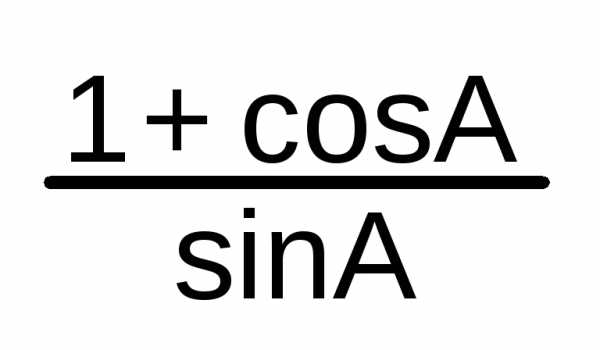Таблица тригонометрических углов – синуса, косинуса, тангенса, котангенса. Как пользоваться

Таблица тригонометрических функций

Опять возвращаемся к пройденному: зная тригонометрическую функцию мы знаем соответствующий угол и наоборот.

Мы уже вскользь касались таблиц Брадиса. Между тем, эти таблицы бывают разные. Есть даже такие, где есть возможность узнать, например, sin49⁰8^,, достаточно выбрать необходимый угол и получить искомый результат. На сегодняшний день с помощью хорошего калькулятора можно вычислить любую тригонометрическую функцию за несколько секунд, но все-таки среди огромного количества таблиц и значений существует таблица с особыми углами. Об этих углах мы изучаем в школьной программе практически все, на них построена вся геометрия и тригонометрия, это их «основа основ». Если Вас спросят, например, чему равен sin40⁰, и вы не сможете ответить – не страшно, но если вы не будете знать значение синуса угла из числа особых, например, sin30⁰ — готовьтесь к плохой оценке.

Значения тригонометрических функций для таких особых углов свели в таблицу, широко известную как

таблица тригонометрических функций. Таких особых углов насчитывается семнадцать, но их можно разделить на 3 группы. Рассмотрим их поближе.

Первая группа углов.

Сюда входят пять углов: 0⁰, 90⁰, 180⁰, 270⁰, 360⁰.

Вот так выглядит таблица с тригонометрических функций для этих углов:

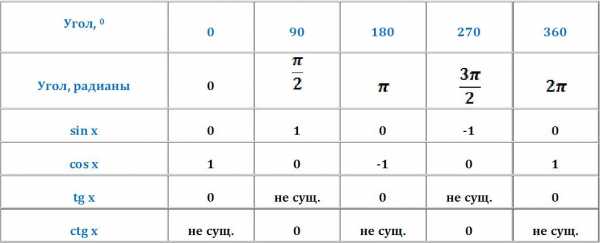
Эту таблицу желательно знать наизусть, но гораздо проще и, главное, полезнее для ума уметь выводить их самостоятельно. Как? – спросите Вы. Воспользовавшись тригонометрическим кругом, который представляет собой обычный круг с центром, находящимся в нуле системы координат XY, с отмеченными табличными углами 0⁰, 90⁰, 180⁰, 270⁰, 360⁰:

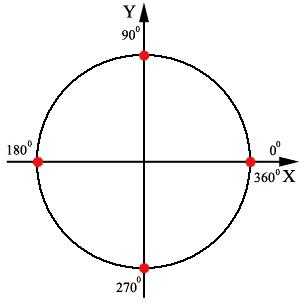
Как видно из рисунка, особенность этих углов заключается в том, что они в точности попадают на оси координат. Так как круг занимает все 360

0, углы 0⁰ и 360⁰ сходятся в одной точке, надеюсь, это понятно. Из этого вытекает одно очень полезное обстоятельство, что собственно и видно в таблице – тригонометрические функции у этих углов абсолютно одинаковы.

Допустим идет экзамен, и вот в ответственный момент Вас посетили смутные сомнения – синус 0⁰ равен 0 или 1? Вот тут-то Вас и спасет один чудный прием, с помощью которого Вы получите абсолютно правильный ответ, без каких бы то ни было сомнений.

Возьмем тот же злополучный sin0⁰, заодно и cos0⁰ посчитаем (именно с этими значениями обычно и случается путаница). Воспользуемся нашим кругом и нарисуем любой понравившийся угол х, но такой, который бы лежал в первой четверти. Далее отмечаем на осях sin и cos этого угла:

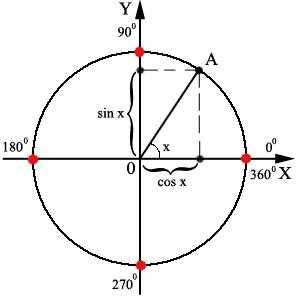
А теперь возьмем и уменьшим наш угол, вот так:

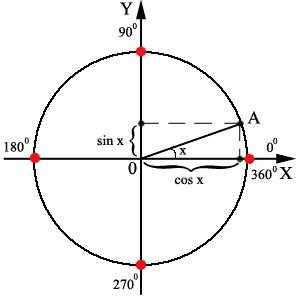
Что нам подсказывает логика? При уменьшении угла х синус также уменьшается. А косинус? Правильно – увеличивается. Что же произойдет с синусом, когда угол превратится в 0 и точка А окажется на оси Х? Он также исчезнет, т.е. станет равен 0. При этом косинус вырастет до длины подвижной части угла (радиуса тригонометрического круга), т.е. 1!

Вот мы и вычислили искомые синус и косинус нуля, причем быстро, а главное – надежно. Правда – очень удобно?

Аналогично можно вычислить синус 180⁰ или косинус 270⁰.

Как видите, эта группа углов не нуждается в заучивании, достаточно воспользоваться волшебным кругом, это ведь проще, чем искать таблицу или вспоминать – правильно или неправильно.

Это же касается тангенса и котангенса. Нарисуем на круге линию тангенса или котангенса и нам всё становится видно — где он равен нулю, а где — не существует.

Идем дальше.

Вторая группа углов.

Сюда относятся следующие углы: 30⁰, 45⁰ и 60⁰. Для них также существуют табличные значения тригонометрических функций:

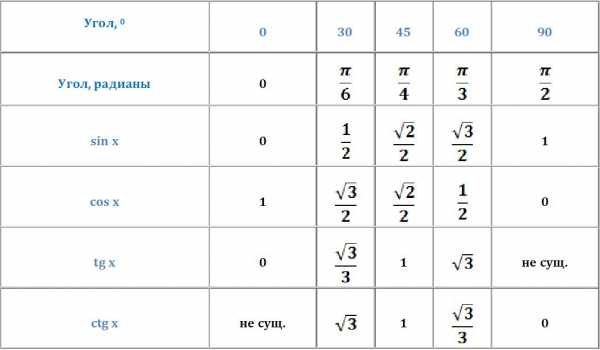
Я вставил сюда значения для 0⁰ и 90⁰ для завершённости первой четверти круга, мы используем это в дальнейшем.

Эти значения также необходимо знать наизусть. Но и здесь есть одна полезная особенность. Значения синусов и косинусов совпадают с точностью до наоборот, т.е. при возрастании угла от 0⁰ до 90⁰ его синус увеличивается от 0 до 1, а косинус наоборот – уменьшается от 1 до 0. Это же правило касается тангенсов и катангенсов, только значения другие. Получается, что достаточно записать это правило в память и учить станет намного меньше. Для остальных углов не из этой компании это правило уже не работает, скажем для 20⁰

или 40⁰.

Переходим к следующей группе.

Третья группа углов.

Сюда входят углы:120⁰, 135⁰, 150⁰, 210⁰, 225⁰, 240⁰, 300⁰, 315⁰, 330⁰. Для них просто надо твердо знать таблицу sin и cos.

Присмотревшись к этой группе углов, мы заметим, что она состоит из углов первых двух групп. Давайте проверим:

120⁰ = 90⁰ + 30⁰

135⁰ = 90⁰ + 45⁰

150⁰ = 90⁰ + 60⁰ и т.д.

Можно для разнообразия использовать не сумму, а разность:

120⁰ = 180⁰ — 60⁰

150⁰ = 180⁰ — 30⁰ и т.д.

Однако не будем спешить. Если Вы подумали, что это же правило действует и для синусов и косинусов, то Вы ошибаетесь. Синус суммы углов совсем не равен сумме синусов каждого угла. Но разложив угол третьей группы на сумму или разность углов из первой и второй групп мы упростим себе задачу нахождения соответствующей ему тригонометрической функции, причем не используя таблицу sin и cos.

Посмотрим, как это работает на практике. Допустим, надо найти cos150⁰.

Смотрим внимательно – из каких особых углов состоит наш угол. Советую выбирать в качестве угла из первой группы 180⁰ или 360⁰, потом станет понятно почему. Ближе всех расположен угол 180⁰:

150⁰ = 180⁰ — 30⁰

Далее нарисуем знакомый тригонометрический круг, отмечаем угол 150⁰ и получаем точку А на круге и смежный угол 30⁰. Другими словами, мы взяли подвижную сторону угла, на которой уместилась точка А, когда она находилась на оси Х, и отмотали по часовой стрелке на 30⁰. При этом получили вот такую картину:

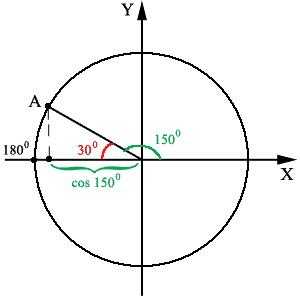
Зелёным цветом мы обозначили угол 150

0 и его cos, а красным — вспомогательный угол в 30⁰, правда отметили его мы не по правилам, что легко поправимо:

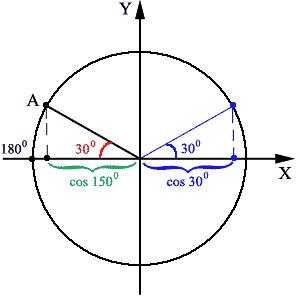
Правильные 30⁰ отсчитаны от положительной полуоси Х. Этот угол, как и его косинус, отметим синим цветом.

Сразу становится видно, что cos150⁰ равен cos30⁰, но с противоположным знаком, ведь треугольники справа и слева одинаковы. А уж cos30⁰ мы знаем, как табличный, и тогда:

cos150⁰ = — cos30⁰ = — /2

Аналогично можно найти sin150⁰. Снова воспользуемся тригонометрическим кругом, только теперь отмечаем синус угла синус на оси У:

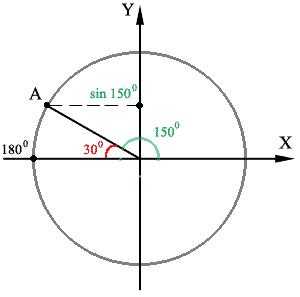
И снова отмечаем правильный угол в 30⁰ и его синус. Опять мы видим, что sin 150⁰ и 30⁰ равны. Пускай углы в 30

0 находятся вне треугольников, ведь всё равно, треугольники — одинаковые.

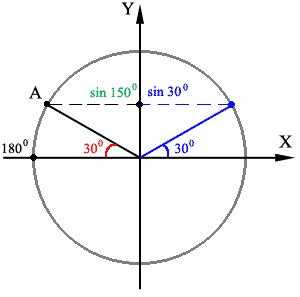
Получаем:

sin150⁰ = sin30⁰ = 1/2

Итак, к чему же мы пришли? Любой угол из третьей группы легко разлаживается на сумму или разность углов 180⁰ (или 360⁰) и 30, 45, 60 (смотря что подойдёт). Значит, мы всегда получим на тригонометрическом круге вспомогательный угол 30⁰, 45⁰ или 60⁰. И нет абсолютно никакой разницы, в какой из 4-х четвертей получится вспомогательный угол. Достаточно лишь изобразить правильный угол, расположенный в первой четверти, и найти одинаковые треугольники и сравнить их синусы (косинусы). Вот и все. И не надо зубрить таблицу тригонометрических функций для этих углов.

Еще небольшой примерчик.

Необходимо найти cos240⁰. Обойдемся без таблицы тригонометрических функций. Разложим угол на два:

240⁰ = 180⁰ + 60⁰

Рисуем тригонометрический круг:

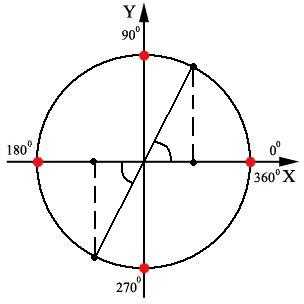
Мы видим, что вспомогательный угол 60⁰ находится в третьей четверти, треугольники одинаковые, поэтому ясно, что cos240⁰ = cos60⁰, но со знаком «минус», т.к. попадает на отрицательную полуось Х. Получаем:

cos240⁰ = — cos60⁰ = -1/2

заметка: для изучающих иностранные языки курсы английского языка (http://www.anglo-club.ru/napravleniya-obucheniya.html) придутся кстати.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

reshit.ru

Тригонометрия в таблицах

Разделы: Математика

---

Таблицы по тригонометрии

Основные тригонометрические тождества:

 

Тригонометрические функции суммы и разности двух аргументов:

Представление суммы одноименных тригонометрических функций в виде произведения:

Преобразование произведения тригонометрических функций в сумму:

Формулы двойных аргументов:

Выражение тригонометрических функций через тангенс половинного аргумента:

Формулы приведения («формулы лошади»): a - острый угол!!!

Вопросы лошадке:

1) функция меняется?

2) какой был знак и какой поставить в ответ?

Решение тригонометрических уравнений:

cos x=1 <=>

cos x=0 <=>

cos x= — 1 <=>

Формулы тройных аргументов:

 

Кроме того, необходимо знать:

Соотношения между тригонометрическими функциями одного и того же аргумента:

18.07.2012

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Таблицы тригонометрических функций

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, … градусов

Из тригонометрических определений функций $\sin$, $\cos$, $\tan$ и $\cot$ можно узнать их значения для углов $0$ и $90$ градусов:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ не определяется;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ не определяется.

В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.

Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $\frac{\pi}{6}$, $\frac{\pi}{4}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т.п.

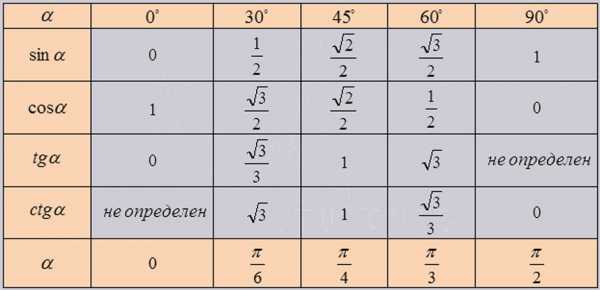
При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2\pi$ радиан:

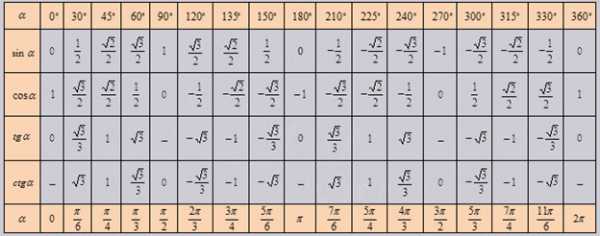
Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 \cdot 360°$, и для угла $0°+3 \cdot 360°$ и т.д.

С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.

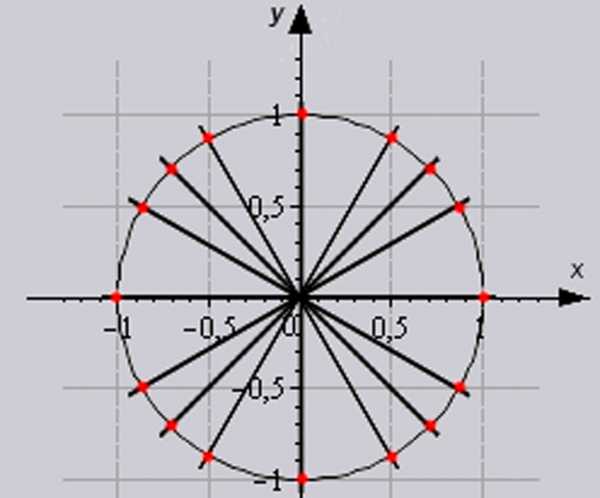
В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.

Использование таблицы

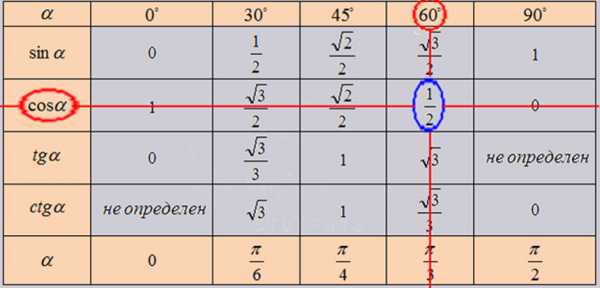
В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

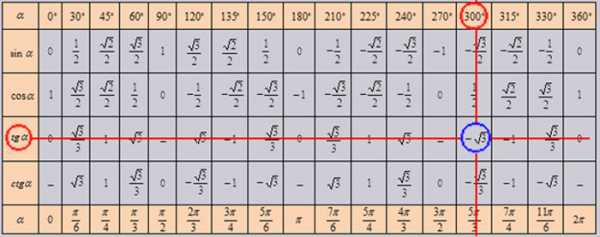
Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300°$:

Таблицы Брадиса основных тригонометрических функций

Возможность расчета тригонометрической функции абсолютно любого значения угла для целого значения градусов и целого значения минут дает использование таблиц Брадиса. Например, найти значение $\cos⁡34°7’$. Таблицы разделены на 2 части: таблицу значений $\sin$ и $\cos$ и таблицу значений $\tan$ и $\cot$.

Таблицы Брадиса дают возможность получить приближенное значение тригонометрических функций с точностью до 4-х знаков после десятичной запятой.

Использование таблиц Брадиса

Используя таблицы Брадиса для синусов, найдем $\sin⁡17°42’$. Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42’$. На их пересечении получаем искомое значение:

$\sin17°42’=0,304$.

Для нахождения значения $\sin17°44’$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42’$, которое есть в таблице, нужно добавить поправку для $2’$, которая равна $0,0006$. Получим:

$\sin17°44’=0,304+0,0006=0,3046$.

Для нахождения значения $\sin17°47’$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $\sin17°48’$ и отнимаем поправку для $1’$:

$\sin17°47’=0,3057-0,0003=0,3054$.

При расчете косинусов выполняем аналогичные действия, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, $\cos20°=0,9397$.

Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $\tan 78°37’$, который по таблице равен $4,967$.

Найдем $\cot 2°13’=25,83$.

spravochnick.ru

Тригонометрические формулы. Таблица углов. Формулы приведения

Факт 1.
\(\bullet\) Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:

 

Факт 2.
\(\bullet\) Знаки синуса, косинуса:

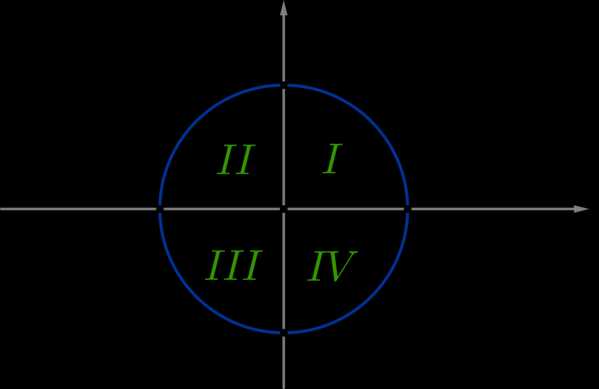
Так как \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}\) и \(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}\), то тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны во \(II\) и \(IV\) четвертях.  

Факт 3.
Формулы приведения.
\(\bullet\) Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi\pm \alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi\pm \alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол \(\alpha\) находится в \(I\) четверти.   \(\bullet\) Случай 2. Если угол можно представить в виде \(n\cdot \pi+\dfrac{\pi}2\pm\alpha\), где \(n\in\mathbb{N}\), то \[\sin\left(n\cdot \pi+\dfrac{\pi}2\pm \alpha\right)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi+\dfrac{\pi}2\pm \alpha\). \[\cos\left(n\cdot \pi+\dfrac{\pi}2\pm \alpha\right)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi+\dfrac{\pi}2\pm \alpha\).
Знак определяется таким же образом, как и в случае \(1\).

 

Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Алгоритм применения формул приведения для тангенса и котангенса полностью аналогичен.  

Пример 1. Найти \(\cos \dfrac{13\pi}{3}\).  

Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\), следовательно, \(\cos \dfrac{13\pi}{3}=\cos \left(4\pi+\dfrac{\pi}3\right)=\cos\dfrac{\pi}3=\dfrac12\)

 

Пример 2. Найти \(\sin \dfrac{17\pi}{6}\).  

Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\), следовательно, \(\sin \dfrac{17\pi}{6}=\sin \left(3\pi-\dfrac{\pi}6\right)=\sin\dfrac{\pi}6=\dfrac12\)

 

Пример 3. Найти \(\mathrm{tg}\,\dfrac{15\pi}4\).  

Преобразуем угол: \(\dfrac{15\pi}4=\dfrac{16\pi-\pi}4=4\pi-\dfrac{\pi}4\), следовательно, \(\mathrm{tg}\,\dfrac{15\pi}4=\mathrm{tg}\left(4\pi-\dfrac{\pi}4\right)= -\mathrm{tg}\,\dfrac{\pi}4=-1\)

 

Пример 4. Найти \(\mathrm{ctg}\,\dfrac{19\pi}3\).  

Преобразуем угол: \(\dfrac{19\pi}3=\dfrac{18\pi+\pi}3=6\pi+\dfrac{\pi}3\), следовательно, \(\mathrm{ctg}\,\dfrac{19\pi}3=\mathrm{ctg}\left(6\pi+\dfrac{\pi}3\right)= \mathrm{ctg}\,\dfrac{\pi}3=\dfrac{\sqrt3}3\)

shkolkovo.net

Справочные таблицы по Тригонометрии

Рис. 1

Определения тригонометрических функций(рис. 1)

Формулы выражения тригонометрических функций

Синус – sin x =  / r

sin α

cos α

tg α

ctg α

Косинус – cos x =  / r

sin α

sin α







Тангенс – tg x =  / 

Котангенс – ctg x =  / 

Секанс – sec x = r / 

cos α



cos α





Косеканс – соsec x = r / 

cos x = sin ( /2 – x)

tg x = ctg ( /2 – x)

sin x = cos ( /2 – x)

ctg x = tg ( /2 – x)

tg α





tg α

Соотношения в прямоугольном тр-ке

Знаки функций по четвертям

sin A = BC/AB

sin x

cos x

tg x

ctg x

cos A = AC/AB

I

+

+

+

+

ctg α





ctg α

tg A = BC/AC

II

+

—

—

—

ctg A = AC/BC

III

—

—

+

+

sec A = AB/AC

cosec A = AB/BC

IV

—

+

—

—

Знак выбирается в зависимости от четверти нахождения угла α

Значение тригонометрических функций для некоторых углов

Сумма и разность аргуметов

Аргумент

sin

cos

tg

ctg

sec

cosec

sin(A+B) = sinAcosB + cosAsinB

sin(A-B) = sinAcosB — cosAsinB

0

0

0

1

0

—

1

—

cos(A+B) = cosAcosB — sinAsinB

cos(A-B) = cosAcosB + sinAsinB

/6

30

1/2

√3/2

√3/3

√3

2√3/3

2

tg(A+B) =

 ≠ π/2 + nπ; n  Z  ≠ π/2 + nπ; n  Z  +  ≠ π/2 + nπ; n  Z

/4

45

√2/2

√2/2

1

1

√2

√2

/3

60

√3/2

1/2

√3

√3/3

2

2√3/3

tg(A-B) =

/2

90

1

0

—

0

—

1

2/3

120

√3/2

-1/2

-√3

-√3/3

-2

2√3/3

ctg(A+B) =

 ≠ nπ; n  Z  ≠ nπ; n  Z  +  ≠ nπ; n  Z

3/4

135

√2/2

-√2/2

-1

-1

-√2

√2

5/6

150

1/2

-√3/2

-√3/3

-√3

-2√3/3

2

ctg(A-B) =



180

0

-1

0

—

-1

—

7/6

210

-1/2

-√3/2

√3/3

√3

-2√3/2

-2

Sin(A+B+C) = sinAcosBcosC + cosAsinBcosC + cosAcosBsinC — sinAsinBsinC

5/4

225

-√2/2

-√2/2

1

1

-√2

-√2

Cos(A+B+C) = cosAcosBcosC + sinAsinBcosC + sinAcosBsinC — cosAsinBsinC

4/3

240

-√3/2

-1/2

√3

√3/3

-2

-2√3/3

3/2

270

-1

0

—

0

—

-1

sin 2A = 2sinAcosA =

cos 2A = cos2A – sin2A =

5/3

300

-√3/2

1/2

-√3

-√3/3

2

-2√3/3

7/4

315

-√2/2

√2/2

-1

-1

√2

-√2

11/6

330

-1/2

√3/2

-√3/3

-√3

2√3/3

-2

sin 3A = 3sinA – 4sin3A

cos 3A = 4cos3A – 3cosA

2

360

0

1

0

—

1

—

sin4A = 8cos3AsinA — 4cosAsinA

sin4A = 8cos4A — 8cos2A + 1

Основные тригонометрические тождества

tg2A = =

ctg2A = =

sin2 A + cos2 A = 1

ctg A = cos A/sinA

tg2 A + 1 = 1/cos2 A

tg A = sin A/cosA

ctg2 A + 1 = 1/sin2 A

tg A ctg A = 1

tg3A =

ctg3A =

cosec2 A – ctg2 A = 1

sin A ∙ cosec A = 1

cos A ∙ sec A = 1

Формулы приведения

tg4A =

ctg4A =

π + α

π — α

2π + α

2π — α

½π + α

½π — α

1,5π + α

1,5π — α

sin

-sinα

sin α

sin α

-sin α

cos α

cos α

-cosα

-cosα

Половинные аргументы

cos

-cosα

-cosα

cos α

cos α

-sin α

sin α

sin α

-sin α

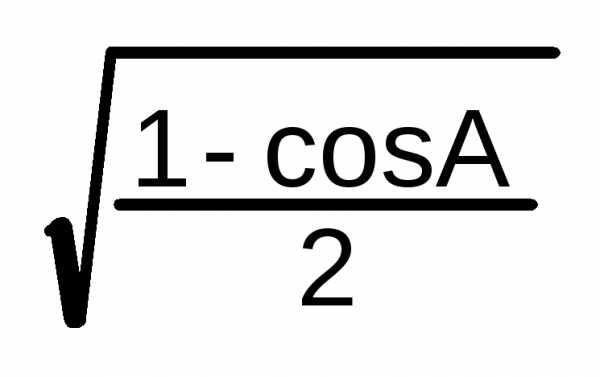
sin A/2 = 

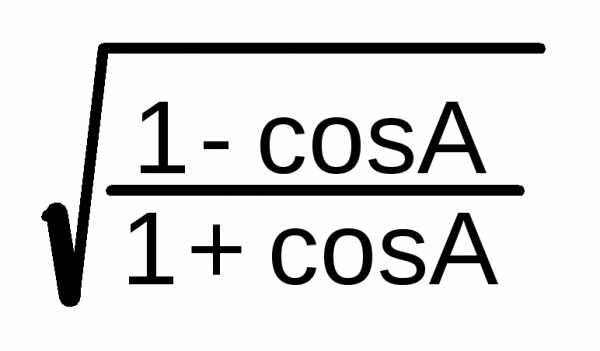
tg A/2 = ==

tg

tg α

-tg α

tg α

-tg α

-ctg α

ctg α

-ctg α

ctg α

ctg

ctg α

-ctg α

ctg α

-ctg α

-tg α

tg α

-tg α

tg α

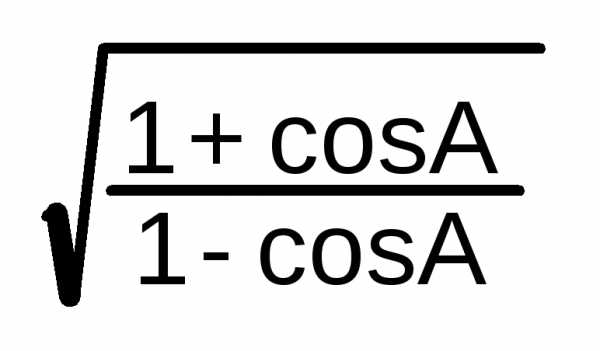
cos A/2 = 

ctg A/2 = ==

1

2

studfiles.net

Таблицы по тригонометрии, величины углов.

ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА

SIN² α+COS² α =1 SIN² α=1- COS² α COS² α = 1- SIN² α

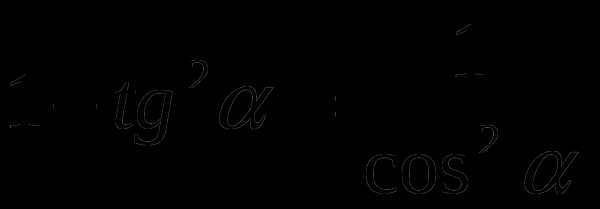
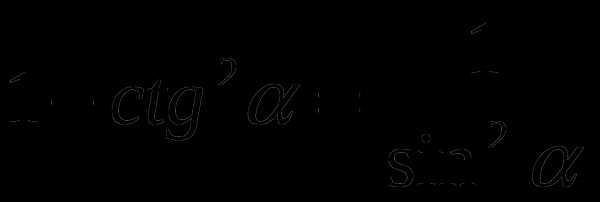
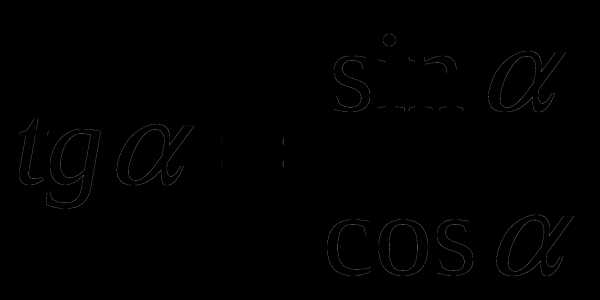
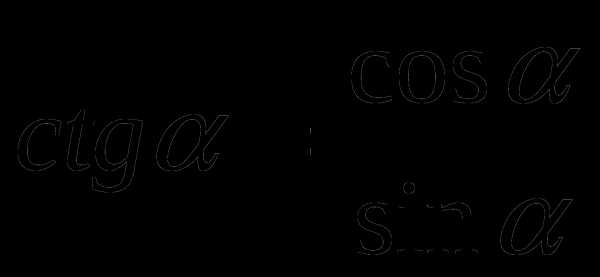tg α ctg α=1

ФОРМУЛЫ СЛОЖЕНИЯ

SIN (α+ β)= SIN α C OS β + C OS α SIN β

SIN (α- β)= SIN α C OS β — C OS α SIN β

C OS(α+ β)= C OS α C OS β — SIN α SIN β

C OS(α — β)= C OS α C OS β + SIN α SIN β

————————————————————————————————————

ФОРМУЛЫ ДВОЙНОГО УГЛА

SIN 2α= 2 SIN α C OS α C OS 2α = COS² α — SIN² α =1-2 SIN² α

C OS 2α=2COS² α-1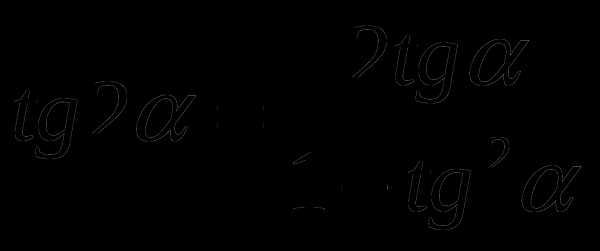

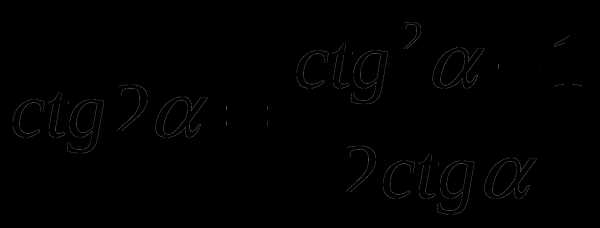
ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ СУММЫ В ПРОИЗВЕДЕНИЕ

ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ПРОИЗВЕДЕНИЯ В СУММУ

ФОРМУЛЫ ПОНИЖЕНИЯ СТЕПЕНИ

2COS² α= 1+ COS 2α 2SIN² α= 1 — COS 2α

ФОРМУЛЫ ПОЛОВИННОГО АРГУМЕНТА

ФОРМУЛЫ ПРИВЕДЕНИЯ

X

+

—

2—

+

—

+

—

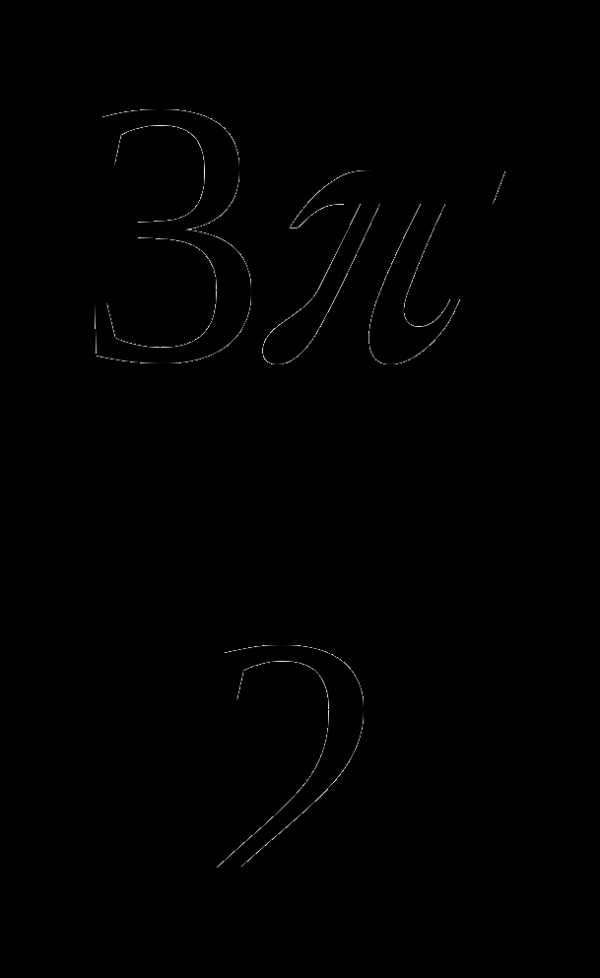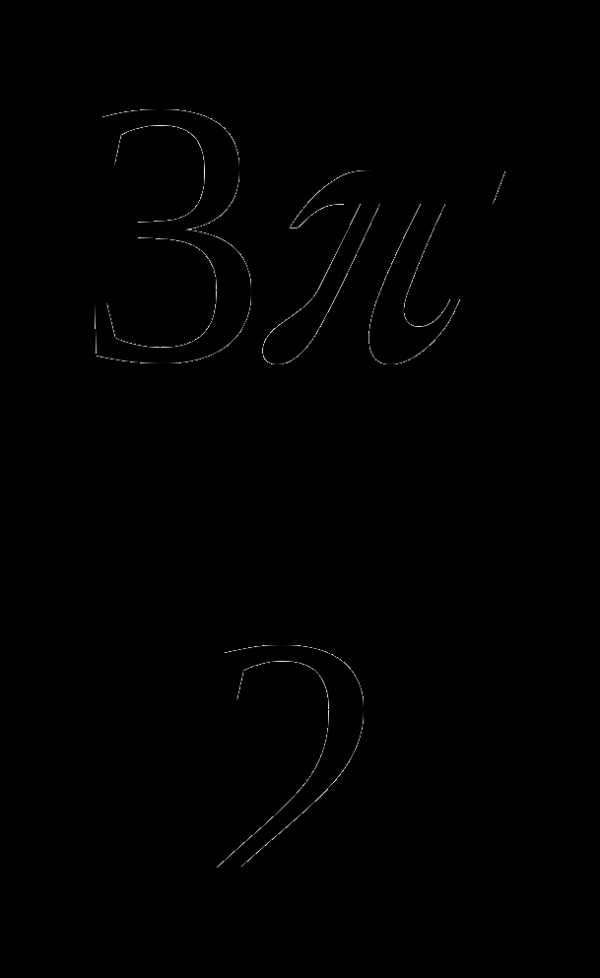180^о +α

180^{о —}α

360^{о —}α

90^о +α

90^о -α

270^о +α

270^о -α

SIN x

-SIN

SIN

-sin

COS

COS

-COS

-COS

COS x

-COS

-COS

COS

-SIN

SIN

SIN

-SIN

tg x

tg

-tg

-tg

-ctg

ctg

-ctg

ctg

Ctg x

ctg

-ctg

-ctg

-tg

tg

-tg

tg

Значения тригонометрических функций некоторых углов

—

—

—

—

0

-90^о

-60^о

-45^о

-30^о

0^о

30^о

45^о

60^о

90^о

180^о

sin

-1

—

—

—

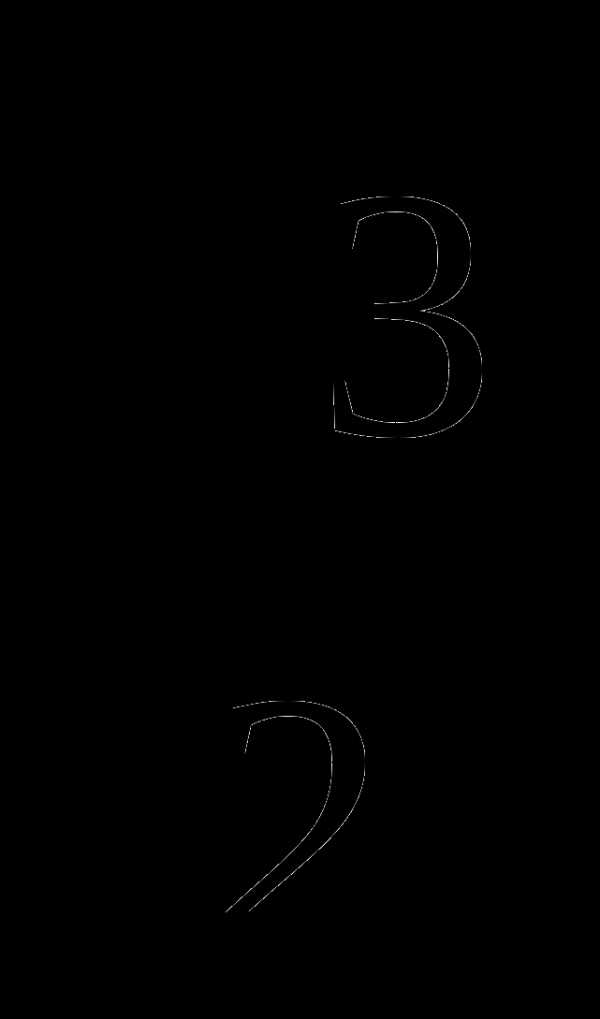
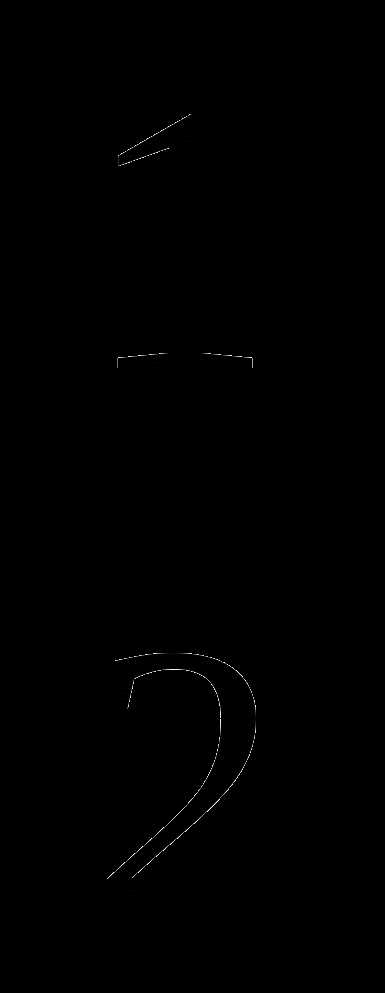
0

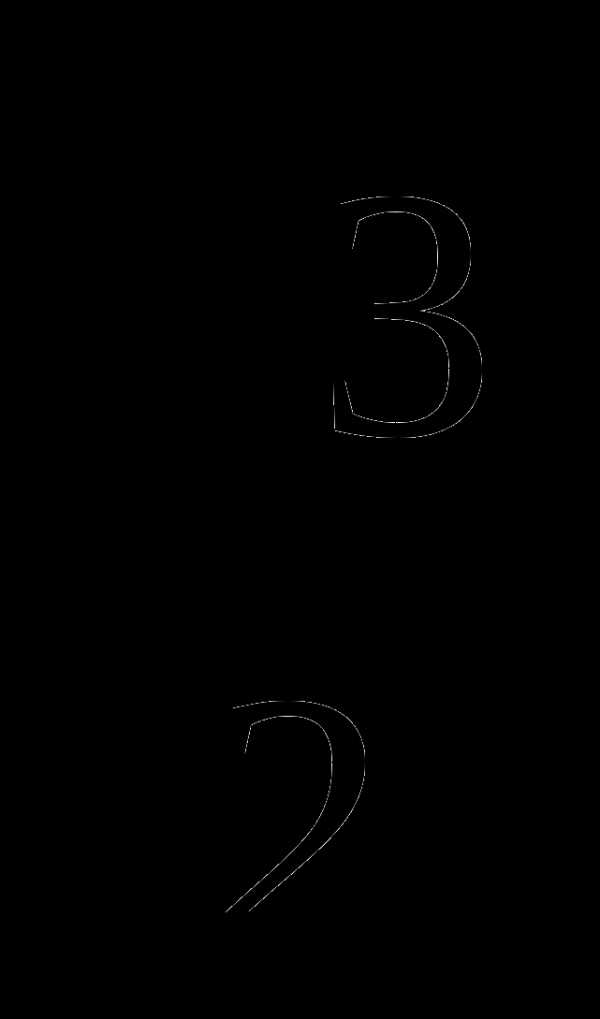
1

0

Tg

—-

—

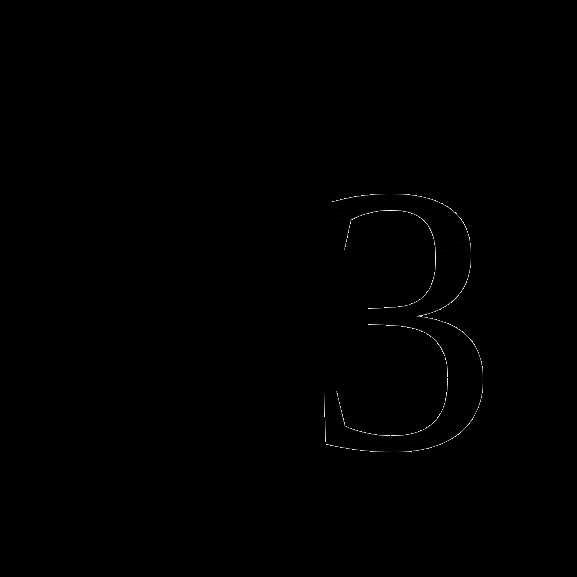
-1

—

0

1

—-

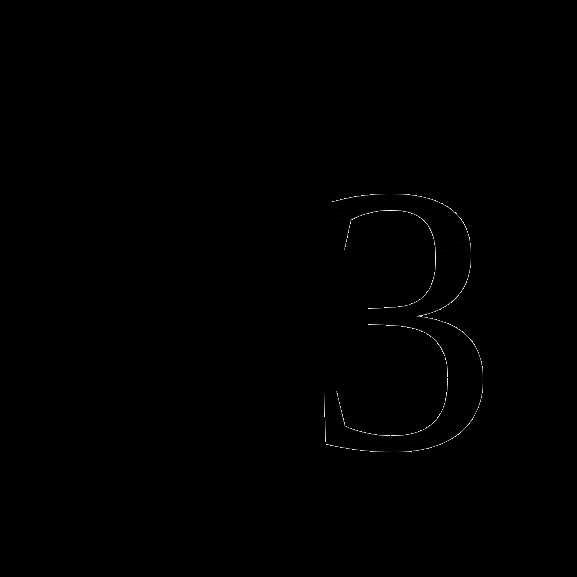
0

0

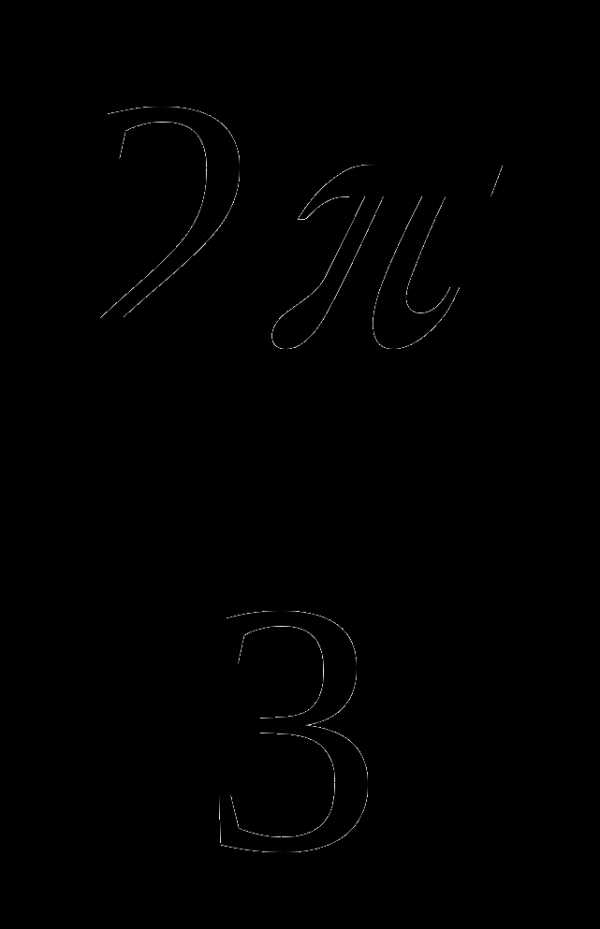
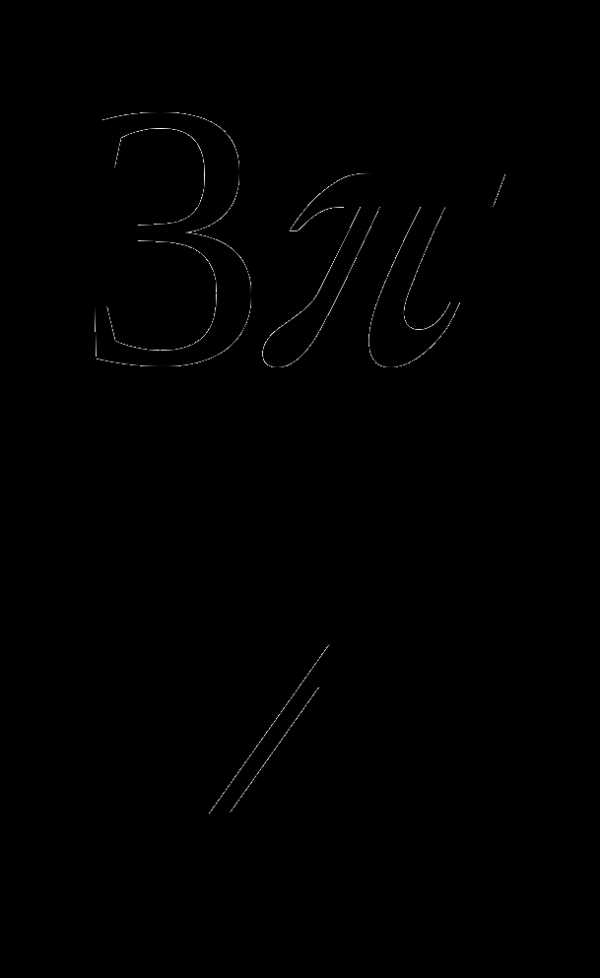
0^о

30^о

45^о

60^о

90^о

120^о

135^о

150^о

180^о

270^о

cos

1

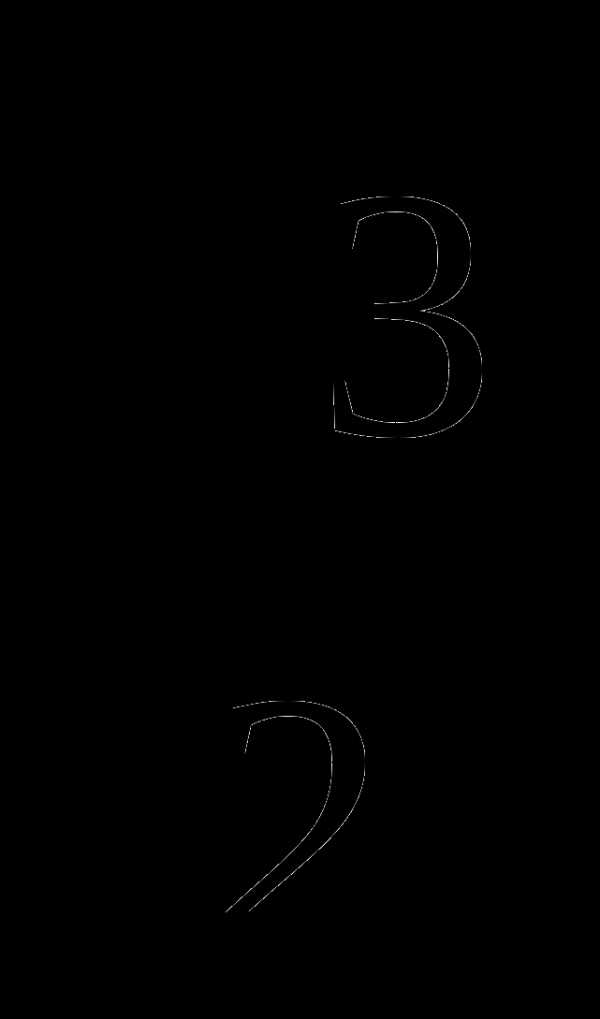
0

—

—

—

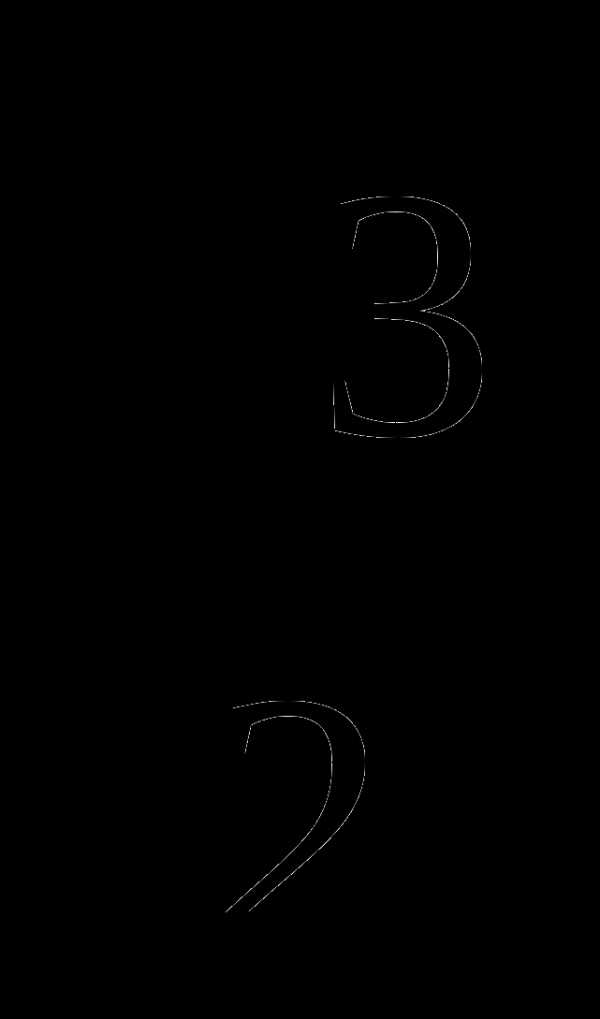
-1

0

ctg

—-

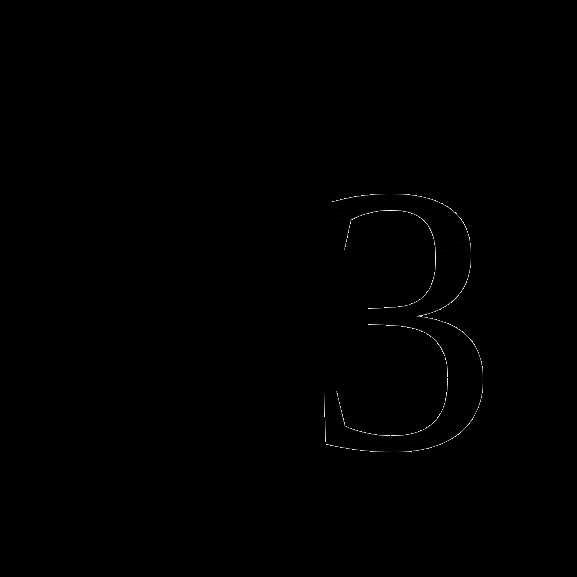
1

0

—

-1

—

—-

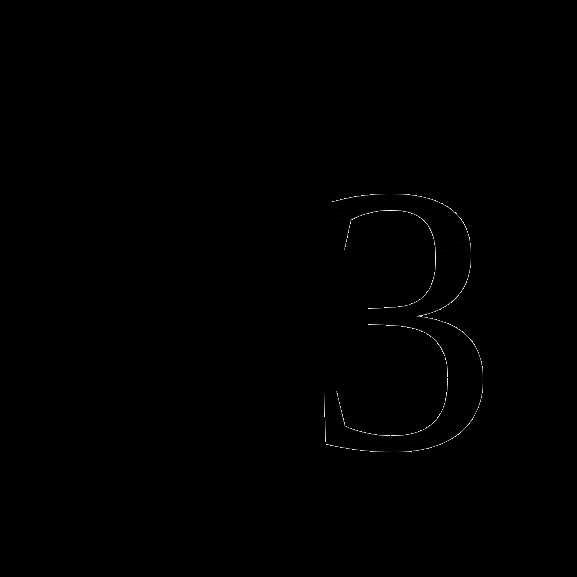
0

Решения тригонометрических уравнений

SIN x=а cos x= a

Х=(-1)^к arcsin a +πk , k Є Z Х=±arccos a+ 2πn , n Є Z

SIN x=0 Х=πk , k Є Z cos x= 0 x= π/2+ πn, n Є Z

SIN x=1 Х=π/2+ 2πk , k Є Z cos x=1 x= 2πn, n Є Z

SIN x=-1 Х= -π/2+ 2πk , k Є Z cos x=-1 Х=π+ 2πn, n Є Z

Tgx=a ctgx=a

X=arctg a +πn, n Є Z X=arcctg a +πn, n Є Z

infourok.ru
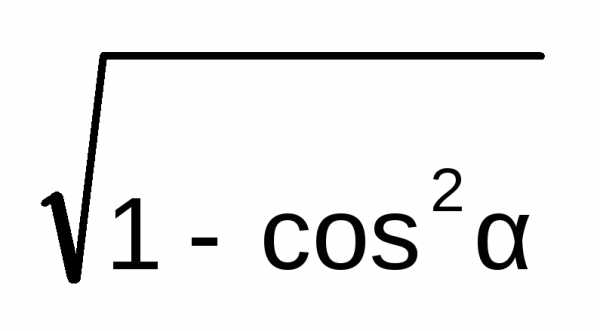
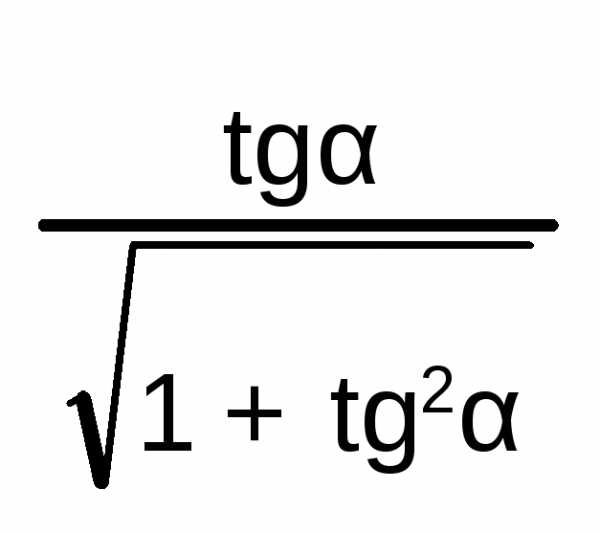
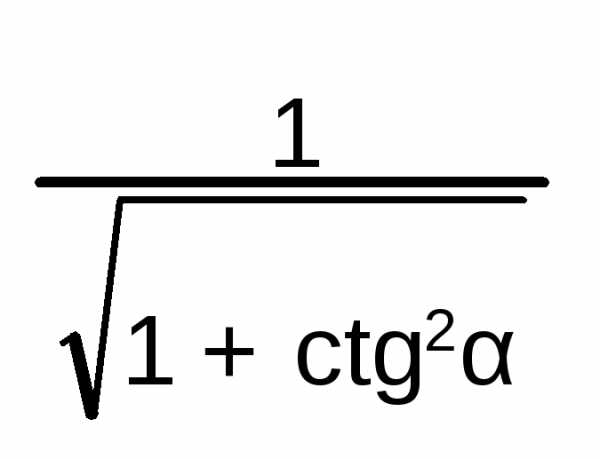
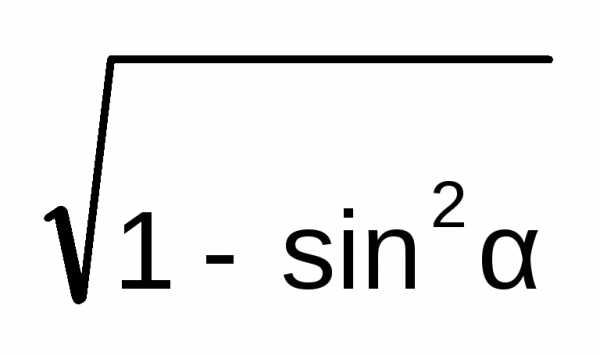
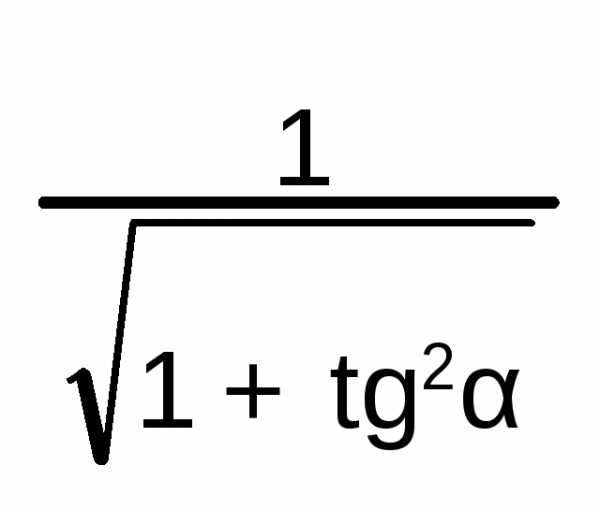
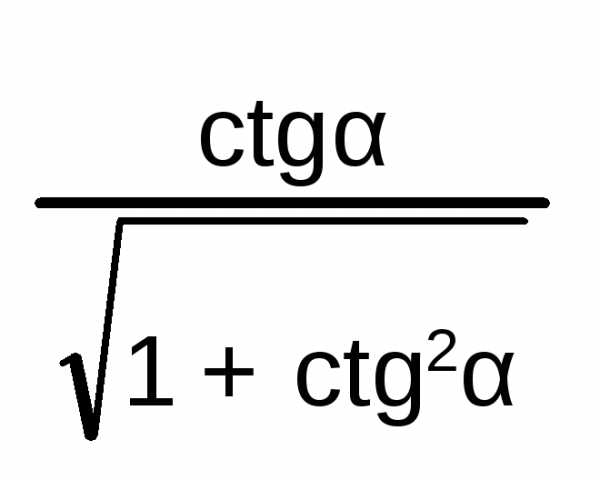
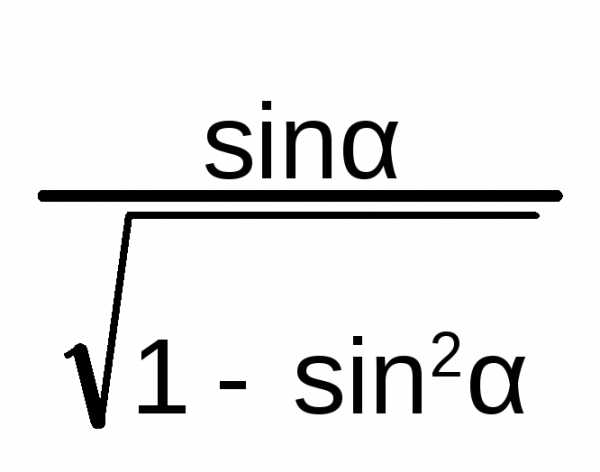
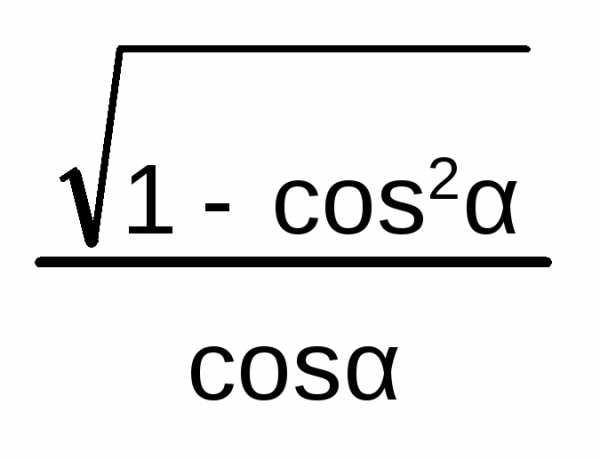
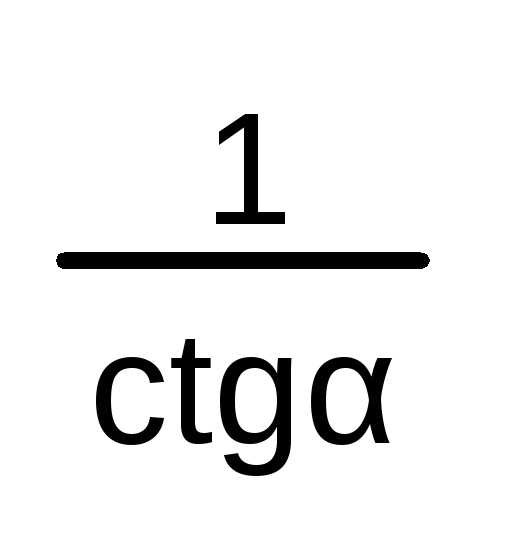
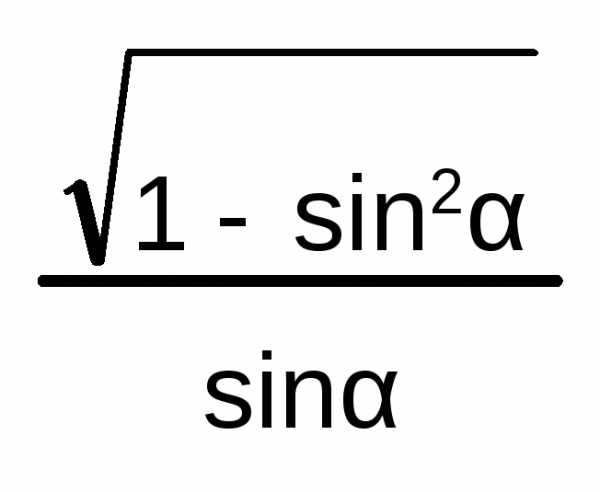
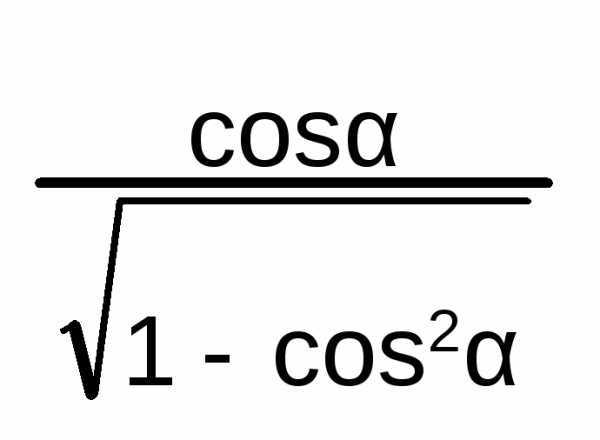
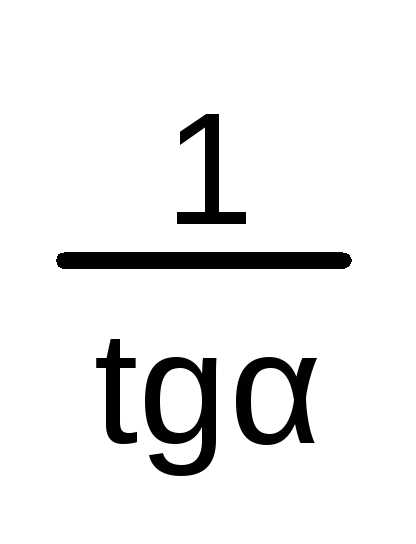
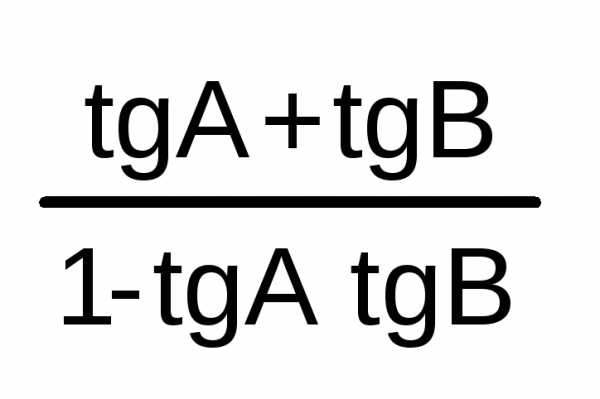
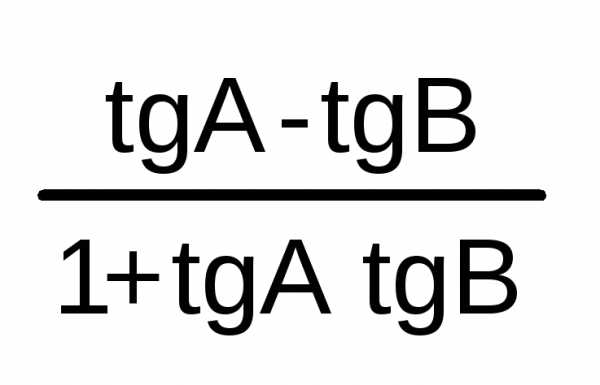
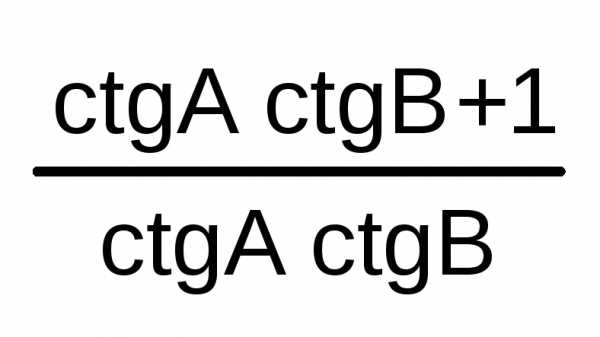
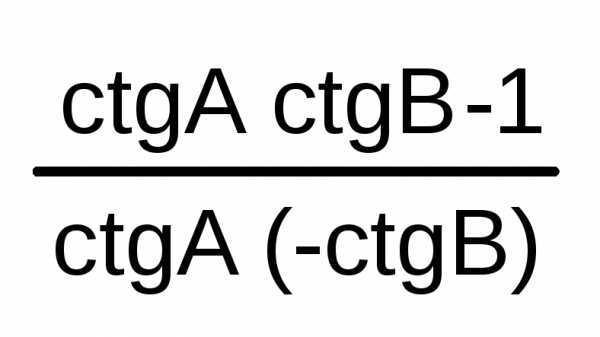
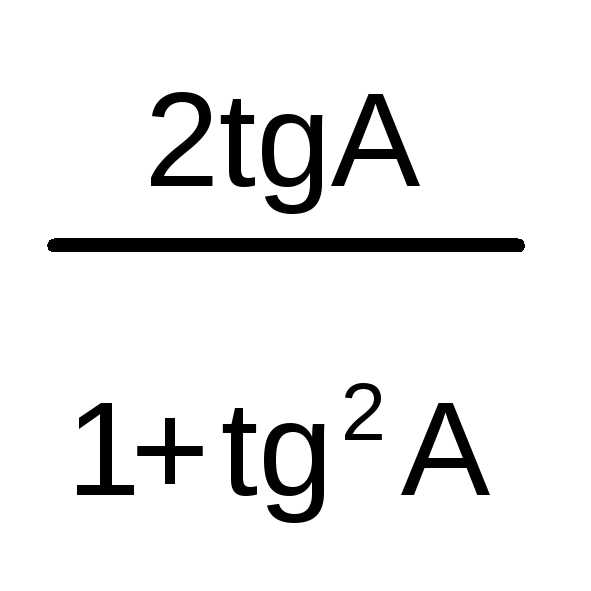
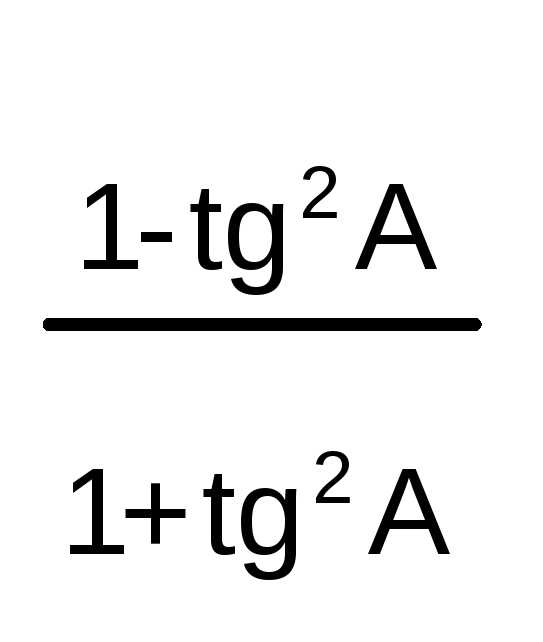
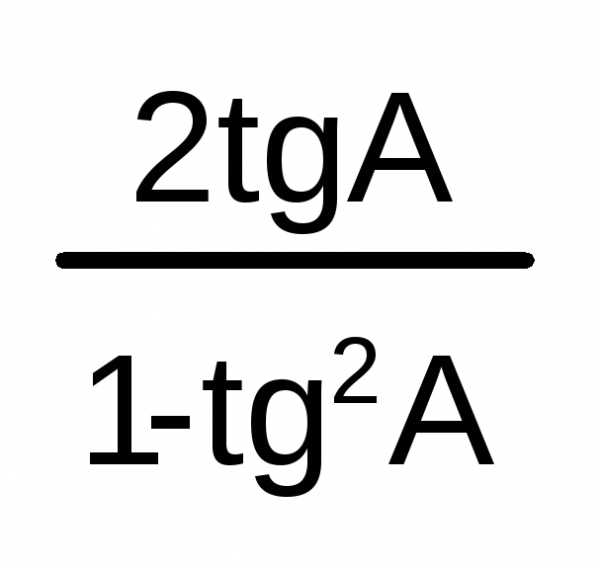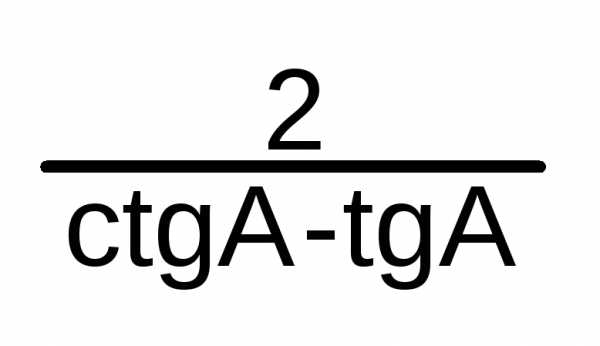
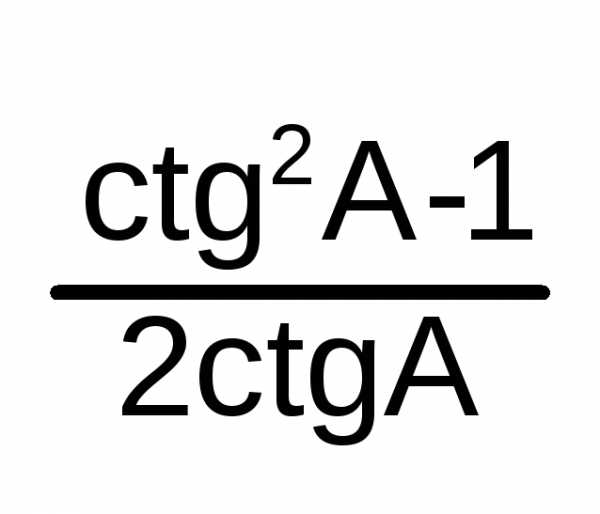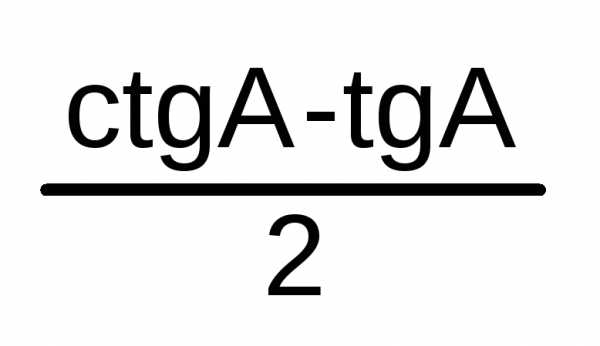
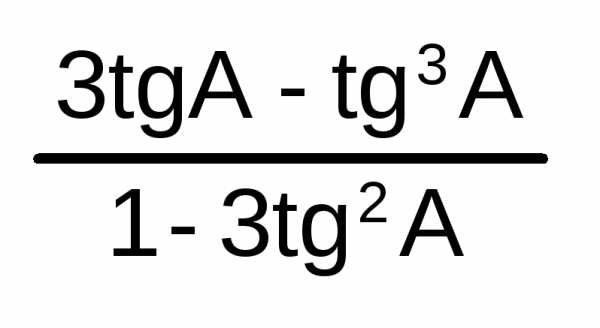
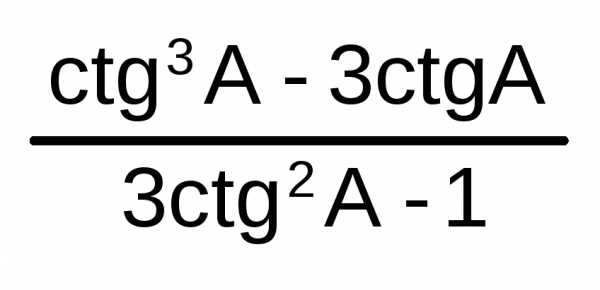
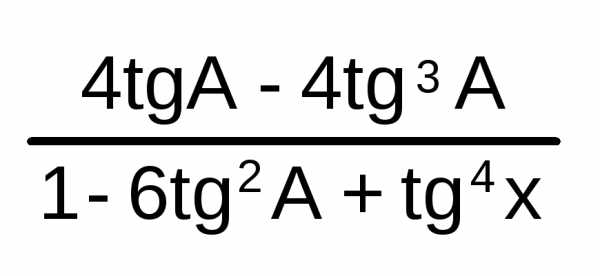
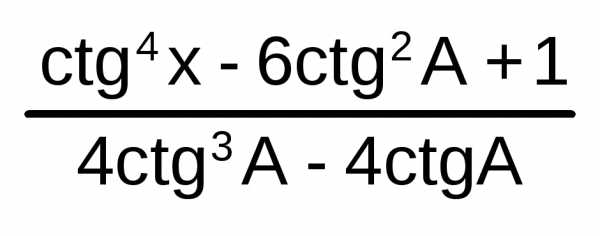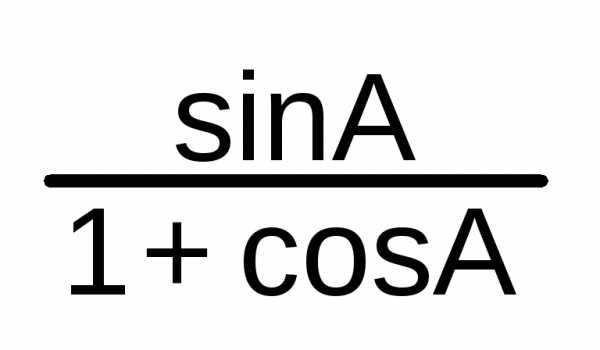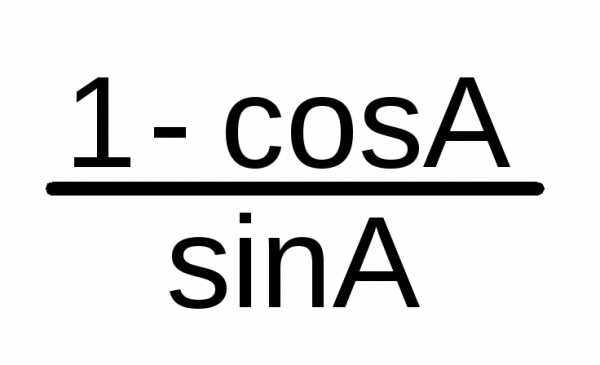
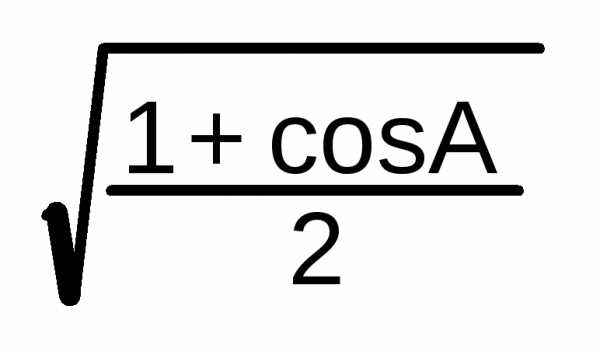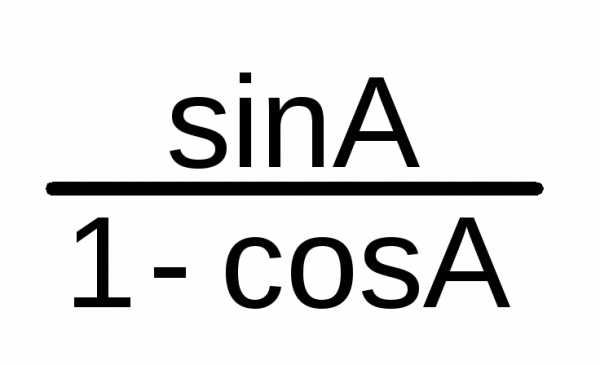