Тангенс гиперболический производная – Гиперболический тангенс th(x), формулы и примеры

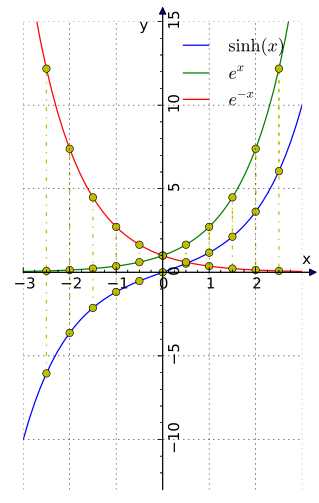
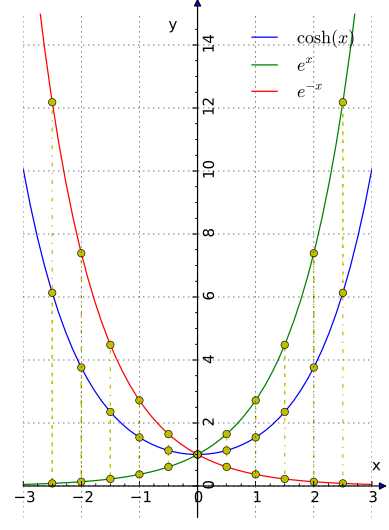
Гиперболический тангенс th(x), формулы и примеры

или через экспоненту

   

причем .

Свойства гиперболического тангенса

Тангенс гиперболический является возрастающей нечетной функцией, т.е.

   

График функции изображен на рисунке 1.

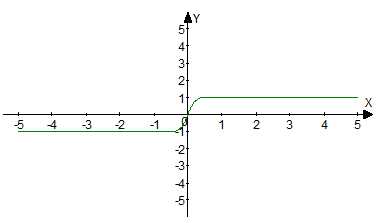
Рис. 1

Связь между гиперболическим и круговым тангенсами

   

   

где – мнимая единица.

Формула сложения

   

Формула двойного угла

   

Произведение тангенсов гиперболических

   

Формула суммы (разности) тангенсов гиперболических

   

Производная тангенса гиперболического

   

Интеграл

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Гиперболический котангенс cth(x), формулы и примеры

Свойства гиперболического котангенса

Котангенс гиперболический неопределен в точке , т.е. область определения , а область значений

Котангенс гиперболический является нечетной функцией, которая убывает на промежутках и .

График функции изображен на рисунке 1.

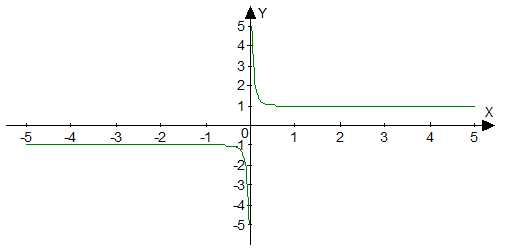
Рис. 1

Формула сложения

   

Формула двойного угла

   

Произведение котангенсов гиперболических

   

Формула суммы (разности) котангенсов гиперболических

   

Производная котангенса гиперболического

   

Интеграл

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Обратные гиперболические функции их графики и формулы

Определения обратных гиперболических функций, их области определений и значений

arsh x — обратный гиперболический синус

Обратный гиперболический синус (ареасинус),   – это функция, обратная к гиперболическому синусу ( x = sh y ), имеющая область определения   –∞ < x < +∞   и множество значений   –∞ < y < +∞.

Ареасинус строго возрастает на всей числовой оси.

arch x — обратный гиперболический косинус

Обратный гиперболический косинус (ареакосинус),   – это функция, обратная к гиперболическому косинусу ( x = сh y ), имеющая область определения   1 ≤  x < +∞   и множество значений   0 ≤  y < +∞.

Ареакосинус строго возрастает на своей области определения.

Вторая ветвь ареакосинуса также определена при x ≥ 1 и расположена симметрично относительно оси абсцисс,   – ∞ < y ≤ 0 :
. Она строго убывает на области определения.

arth x — обратный гиперболический тангенс

Обратный гиперболический тангенс (ареатангенс),   – это функция, обратная к гиперболическому тангенсу ( x = th y ), имеющая область определения   – 1 < x < 1   и множество значений   –∞ < y < +∞.

Ареатангенс строго возрастает на своей области определения.

arcth x — обратный гиперболический котангенс

Обратный гиперболический котангенс (ареакотангенс),   – это функция, обратная к гиперболическому котангенсу ( x = cth y ), имеющая область определения   |x| > 1   и множество значений   y ≠ 0.

Ареакотангенс строго убывает на своей области определения.

Графики обратных гиперболических функций

График обратного гиперболического синуса (ареасинуса)   y = arsh x

График обратного гиперболического косинуса (ареакосинуса)   y = arch x ,   x ≥ 1
Пунктиром показана вторая ветвь ареккосинуса.

График обратного гиперболического тангенса (ареатангенса)   y = arth x ,   |x| < 1

График обратного гиперболического котангенса (ареакотангенса)   y = arcth x ,   |x| > 1

Формулы с обратными гиперболическими функциями

Связь с тригонометрическими функциями

Arsh iz = i Arcsin z;     Arch z = i Arccos z;
Arcsin iz = i Arsh z;     Arccos z = – i Arch z;
Arth iz = i Arctg z;     Arcth iz = – i Arcctg z;
Arctg iz = i Arth z;     Arcctg iz = – i Arcth z;
Здесь   i – мнимая единица,   i² = –1.

Четность

arsh(–x) = – arsh x;   arch(–x) ≠ &pm; arch x;
arth(–x) = – arth x;   arcth(–x) = – arcth x.

Функции   arsh(x),   arth(x),   arcth(x) – нечетные. Функция   arch(x)   – не является четной или нечетной.

Формулы связи обратных гиперболических синусов через тангенсы и косинусов через котангенсы

;
;
;
.

Формулы суммы и разности

;
;
;
.

Производные обратных гиперболических функций

;
.

Интегралы от arsh x, arch x, arth x, arcth x

arsh x

Для вычисления интеграла от гиперболического арксинуса, делаем подстановку   x = sh t   и интегрируем по частям:
.

arch x

Аналогично, для гиперболического арккосинуса. Делаем подстановку   x = ch t   и интегрируем по частям учитывая, что t ≥ 0:
.

arth x

Делаем подстановку   x = th t   и интегрируем по частям:
;
;
;
.

arcth x

Аналогично получаем:
.

Разложения в ряды

arsh x

При   |x| < 1   имеет место следующее разложение:

arth x

При   |x| < 1   имеет место следующее разложение:

arcth x

При   |x| > 1   имеет место следующее разложение:

Обратные функции

Гиперболический синус

При   – ∞ < y < ∞   и   – ∞ < x < ∞   имеют место формулы:
,
.

Гиперболический косинус

При   1 ≤ y < ∞   и   0 ≤ x < ∞   имеют место формулы:
,
.

Гиперболический тангенс

При   – 1 < y < 1   и   – ∞ < x < ∞   имеют место формулы:
,
.

Гиперболический котангенс

При   – ∞ < y < – 1   или   1 < y < ∞   и   x ≠ 0   имеют место формулы:
,
.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 29-07-2014

1cov-edu.ru

Производные гиперболических функций

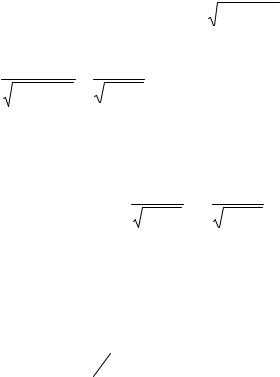
Поскольку

y [−

π

;

π

],

что

соответствует

первой

и

четвертой

четвертям

2

2

тригонометрического

круга,

то

cos y ≥ 0 . Следовательно,cos y =

1 −sin2 y ,

где

sin y = x . Тогда для производной для функцииy = arcsin x справедливо равенство:

(arcsinx)′ =

1

=

1

.

1 −sin2 y

1 − x2

Для вычисления

производной

от

функции y = arccos x

используем

соотношение

arcsin x + arccosx =

π

и

выразим

из

него

arccos x =

π

− arcsinx .

Долее можно

2

2

использовать правило дифференцирования разности двух функций.

(arccosx)′ = (

π

−arcsinx)′

= (

π

)′ −(arcsinx)′ = 0−

1

= −

1

.

2

2

1 − x2

1 − x2

Функция

y = arctg x задана на промежуткеx (−∞; ∞) и ее значения принадлежат

промежутку

y (−

π

,

π

). На промежутке

y (−

π

,

π

) определена обратная функция

2

2

2

x = tg y.

2

Для

вычисления

ее

производной

можно

использовать

правило

дифференцирования обратной функции.

′

1

1

1

2

y′x

= (arctgx)x

=

=

=

= cos

y .

(tgy)′y

1cos2 y

x′y

Из основного

тригонометрического

тождества

1 + tg2 y =

1

следует,

что

2

y

cos

cos2 y =

1

. Следовательно,

(arctgx)x′ = cos

2 y =

1

=

1

.

+ tg2

+ tg2

1

y

1

y 1 + x2

Для вычисления производной от функции

y = arcctgx

используем

соотношение

arctg x + arcctgx =

π

и выразим из него arcctg x =

π

− arctg x . Долее можно использовать

2

2

правило дифференцирования разности двух функций.

(arcctgx)′ = (

π

−arctgx)′

= (

π

)′

−(arctgx)′ = 0−

1

= −

1

.

1

+ x2

+ x2

2

2

1

Гиперболическими называются следующие функции:

sh x =

ex

−e−x

– гиперболический синус;

ch x =

ex+e−x

– гиперболический косинус;

2

2

th x =

sh x

– гиперболический тангенс; cth x =

ch x

– гиперболический котангенс.

ch x

sh x

Для гиперболических функций справедливы соотношения:

ch 2 x −sh3 x =1; ch3 x +sh3 x = ch 2x; 2 shx chx = sh 2x ;

th x cthx =1;

1 + th3 x =

1

;

1 + cth3 x =

1

.

ch 2 x

sh 2

x

Для производных гиперболических функций справедливы соотношения:

′	′	′	1			′	1
(shx) = chx;	(chx) = shx;	(thx)	=		;	(cthx)	= −			.
				ch 2 x				sh 2 x
		17

studfiles.net

Производные гиперболических функций

Для производных гиперболических функций справедливы соотношения:

′

′

′

1

′

1

(shx)

= chx;

(chx) = shx;

(thx)

=

;

(cthx)

= −

.

ch 2 x

sh 2 x

Доказательство

′

ex

−e−x

′

ex+e−x

′

ex+ e−x

′

ex−e−x

(shx)

=

= chx ; (chx)

=

= shx .

2

=

2

=

2

2

′

sh x ′

sh′x chx −ch′x shx

ch3 x −sh3

x

1

(thx)

=

=

=

=

, так как

ch x

ch3 x

ch3 x

ch3

x

1 ′

ch 2 x −sh3 x =1.

′

1

1

ch 2 x

1

1

(cthx)

=

= −

= −

= −

.

th 2

ch 2

sh 2 x

ch

2 x

sh 2

x

th x

x

x

Полученные результаты запишем в таблицу 3.1.1.

Таблица 3.1.1. Производные основных элементарных функций.

(xα)′ = α xα−1

(arcsinx)′ =

1

1

− x2

(ex )′ = ex

(arccosx)′ = −

1

1 − x2

(ax )′ = ax ln a

(arctgx)′ =

1

+ x2

1

′

1

′

1

(lnx)

=

studfiles.net

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ И ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

И

ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Гиперболические функции

Определение

Гиперболические функции задаются следующими формулами:

(в англоязычной литературе обозначается )

(в англоязычной литературе обозначается )

(в англоязычной литературе обозначается )

Свойства

Связь с тригонометрическими функциями:

Гиперболические функции выражаются через тригонометрические функцииотмнимогоаргумента.

.

.

Важные соотношения:

2. Чётность:

3. Формулы сложения:

4. Формулы двойного угла:

5. Формулы кратных углов:

6. Произведения

7. Суммы

8. Формулы понижения степени

9. Производные:

10. Интегралы:

Неравенства:

Для всех выполняется:

Разложение в степенные ряды:

(Ряд Лорана)

Здесь —числа Бернулли.

Графики:

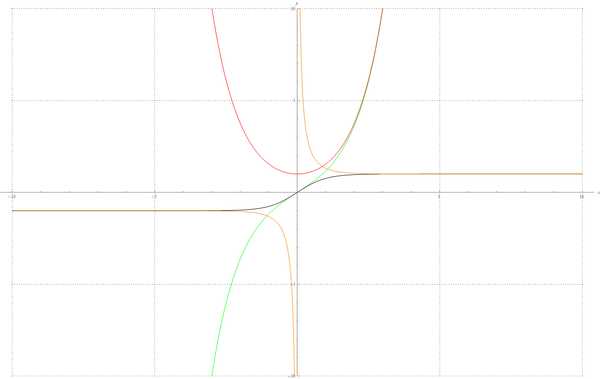
sh(x), ch(x), th(x), cth(x)

sh, ch и th

csch, sech и cth

Обратные гиперболические функции

—обратный гиперболический синус, гиперболический арксинус, ареасинус:

—обратный гиперболический косинус, гиперболический арккосинус, ареакосинус.

—обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс.

—обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс.

—обратный гиперболический секанс, гиперболический арксеканс, ареасеканс.

—обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс.

Графики:

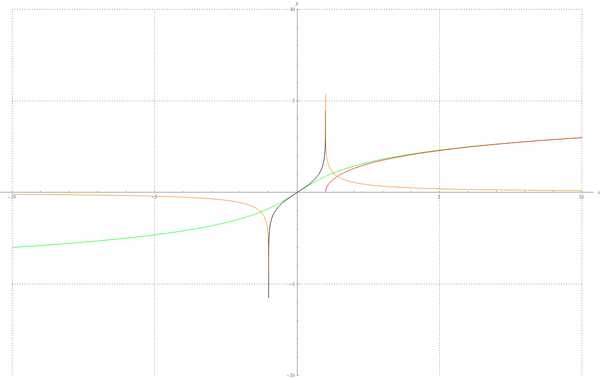
arsh(x), arch(x), arth(x), arcth(x)

Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями:

где i — мнимая единица.

Эти функции имеют следующее разложение в ряд:

ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Обратные гиперболические функции

Название функции	Обозначение в русской литературе	Обозначение в английской литературе
ареасинус	arsh	arsinh, sinh−1
ареакосинус	arch	arcosh, cosh−1
ареатангенс	arth	artanh, tanh−1
ареакотангенс	arcth	arcotanh, cotanh−1
ареасеканс	arsech	arsech, sech−1
ареакосеканс	arcsch	arcsch, csch−1

Определения функций

Гиперболический ареасинус для действительного аргумента

Гиперболический ареакосинус для действительного аргумента

Гиперболический ареатангенс для действительного аргумента

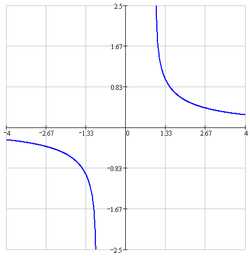
Гиперболический ареакотангенс для действительного аргумента

Гиперболический ареасеканс для действительного аргумента

Гиперболический ареакосеканс для действительного аргумента

В комплексной плоскостифункции можно определить формулами:

Разложение в ряд

Обратные гиперболические функции можно разложить в ряды:

Асимптотическое разложение arsh x даётся формулой:

Производные

Для действительных x:

Пример дифференцирования: если θ = arsh x, то:

Комбинация гиперболических и обратных гиперболических функций

Дополнительные формулы

studfiles.net

Производные гиперболических функций

Для производных гиперболических функций справедливы соотношения:

′

′

′

1

′

1

(shx)

= chx;

(chx) = shx;

(thx)

=

;

(cthx)

= −

.

ch 2 x

sh 2 x

Доказательство

′

ex

−e−x

′

ex+e−x

′

ex+ e−x

′

ex−e−x

(shx)

=

= chx ; (chx)

=

= shx .

2

=

2

=

2

2

′

sh x ′

sh′x chx −ch′x shx

ch3 x −sh3

x

1

(thx)

=

=

=

=

, так как

ch x

ch3 x

ch3 x

ch3

x

1 ′

ch 2 x −sh3 x =1.

′

1

1

ch 2 x

1

1

(cthx)

=

= −

= −

= −

.

th 2

ch 2

sh 2 x

ch

2 x

sh 2

x

th x

x

x

Полученные результаты запишем в таблицу 3.1.1.

Таблица 3.1.1. Производные основных элементарных функций.

(xα)′ = α xα−1

(arcsinx)′ =

1

1

− x2

(ex )′ = ex

(arccosx)′ = −

1

1 − x2

(ax )′ = ax ln a

(arctgx)′ =

1

+ x2

1

′

1

′

1

(lnx)

=

studfiles.net