Теорема средней линии – Теорема Фалеса. Средняя линия треугольника [wiki.eduVdom.com]

∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии треугольника ABC, откуда $$ KD = \frac{1}{2}AC = 4 см. \\ MD = \frac{1}{2}AB = 5 см. $$ Периметр прямоугольника К DMА равен 18 см.

Работа над теоремой «Средняя линия треугольника»

Работа над теоремой «Средняя линия треугольника»

1.Мотивация изучения теоремы.

Людям свойственно ошибаться, не ошибается лишь тот, кто ничего не делает. А эпиграфом нашей работы будут слова Карла Поппера, австрийского философа: «Я могу ошибаться, и ты можешь ошибаться, но совместными усилиями мы можем постепенно приближаться к истине». Поэтому давайте вместе не будем бояться, будем смело высказывать свои мысли, гипотезы.

1.Работа с чертежами, которые изображены на рисунке.

-Какие геометрические фигуры изображены на рисунке? (Треугольники)

Интересные факты о треугольниках.

Ребята, треугольник-геом.фигура, самая популярная в школьном курсе геометрии, сегодня мы пополним багаж ваших знаний о свойствах этой фигуры..Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности. Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.

А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.

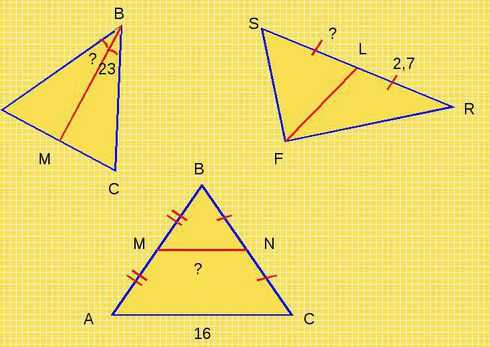
Давайте устно решим эти задачи?

-Чему равен угол АВМ на 1 чертеже?(23 градуса).

Почему?(Так как по условию дано что ВМ- биссектриса, значит она делит угол В пополам).

-Чему равна сторонаSL на 2 чертеже?(так как на чертеже указано что стороны SL и RL равны следовательно сторона SL =2,7см).

-Следовательно, FL чем является в треугольнике? (медианой).

-На третьем чертеже МN чему равна?(дети затрудняются ответить).

-Мы не можем с вами сразу ответить на вопрос. Что для этого нужно знать? (надо узнать ,что это за прямая и как ее можно найти).

2.Работа над структурой теоремы

Сегодня мы с вами познакомимся с определением и свойствами этой прямой, узнаем чему она равна в треугольнике, и в конце урока ответим на вопрос нашей задачи, которую мы сейчас не смогли решить.

1.Для изучения новой темы нам необходимо повторить понятие подобия треугольников и признаки подобия треугольников

Верно ли

1.Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.

2.Два равносторонних треугольника иногда подобны. Нет

3.Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Да

4.Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 70°, то такие треугольники подобны. Да

2.Введение определения средней линии треугольника.

Работа с чертежом задачи

-Давайте посмотрим на чертеж нашей задачи.

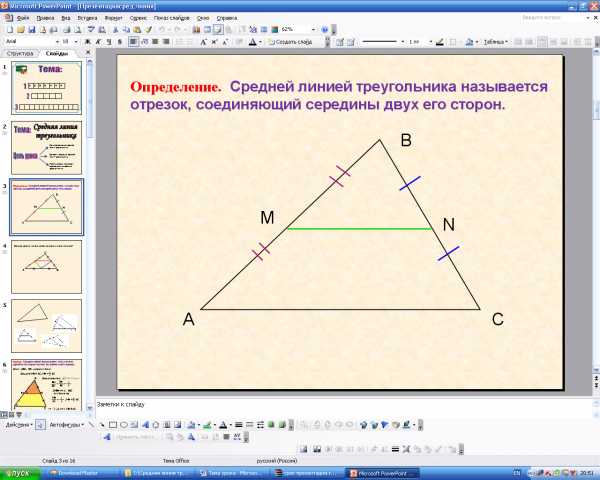
Где находится отрезок, который нам надо найти? (в середине треугольника)

Что нам дано по чертежу? ( отрезок АМ=МВ, СN=NB).

-Следовательно, что делает отрезок MN со сторонами треугольника? (делит стороны пополам).

Где лежат точки отрезка MN?(на серединах сторон треугольника). Какой вывод можем сделать?(МN- отрезок, соединяющий середины двух сторон треугольника).

-Отсюда идет названия отрезка –MN-называется средней линией треугольника.

3.Запись в тетрадях определения средней линии и чертеж задачи.

Определение: Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.

В тетрадях рисунок и запись: Если АМ = МВ и СN = NВ, то МN— средняя линия треугольника

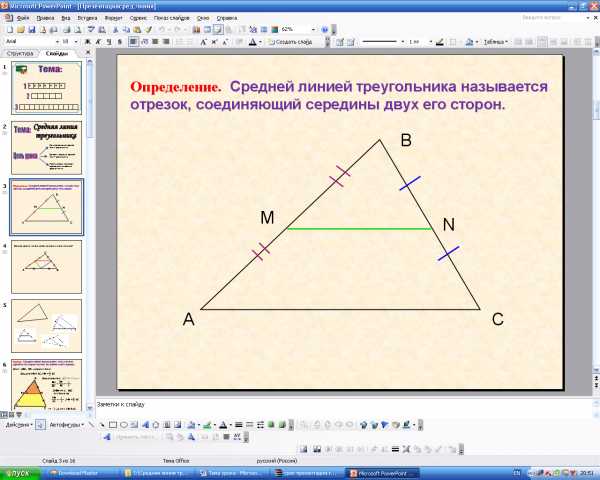
4.Работа по готовым чертежам (отработать умение распознавать на чертежах ср. л. треугольника)

-Сколько средних линий можно построить в треугольнике? Почему?(3 средние линии, потому что в треугольнике 3 стороны)

-Назовите по чертежу ср. л. в треугольнике?(KM; CA; CL)

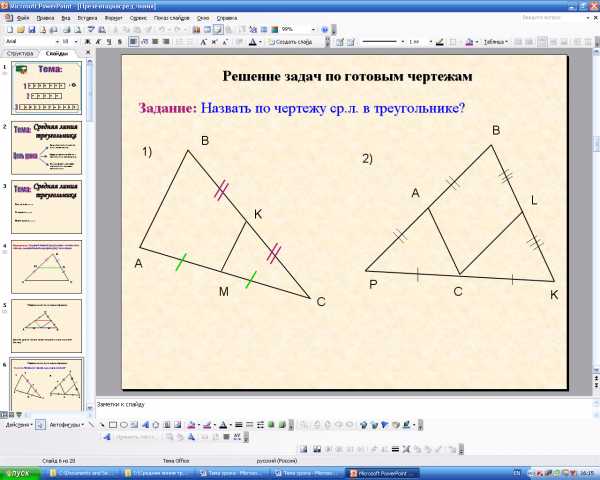
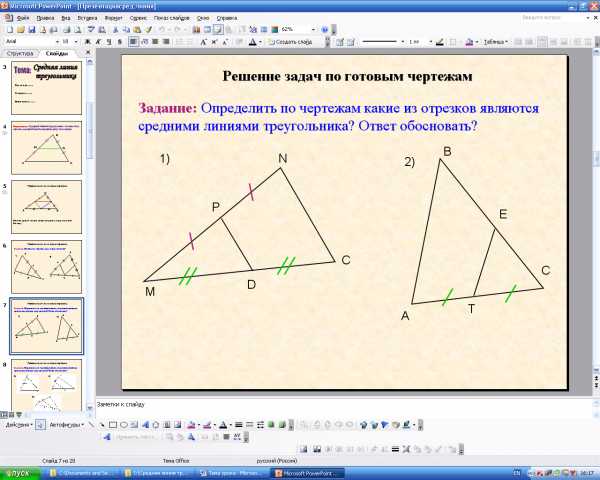
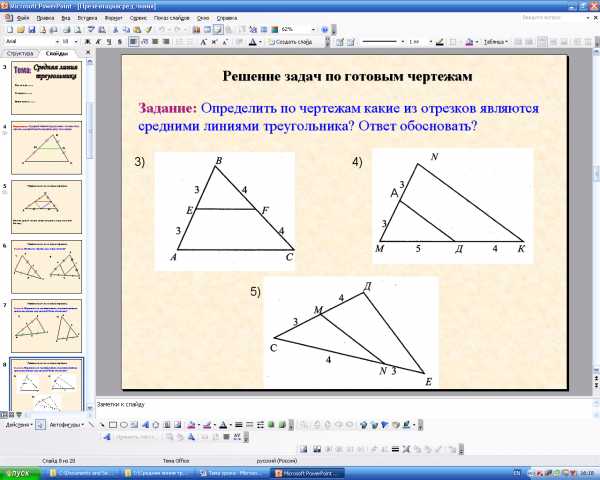
-Определите по чертежам, какие из отрезков являются средними линиями треугольника? Ответ обосновать.(PD,так как концы отрезка соединяют середины сторон треугольника; EF,так как делит делит стороны треугольника пополам(на равные отрезки)).

3.Построение чертежа и краткая запись содержания теоремы.

Свойство ср. л. треугольника. Продолжим изучение нового материала. Работаем ребята с тем же чертежом. Проведем эксперимент, с помощью линейки, угольников по рядам:

-Что значит выяснить взаимное расположение прямых?(прямые пересекаются, не пересекаются).

-Что мы можем сказать о прямых МN и АС?(они не пересеаются, значит МN II АС)

-Сравните длины отрезков МN и АС.Что можно сказать о их длинах?(MN в 2 раза меньше АС)

Вот мы ребята и вывели основное свойство о ср. л. треугольника.

Может быть кто-то попробует сформулировать свойство о ср. л. треугольника.

Теорема. 

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине

Построение чертежа в тетрадях и краткая запись содержания теоремы учащимися.

Дано: АВС

МN-средняя линия

Доказать: MN АC

MN=AC

4.Поиск доказательства, доказательство и его запись.

Рассмотрим треугольник АВС. МN-средняя линия этого трегольника.Докажем ,что MN АC,и MN=AC.

-Ск треугольников мы видем на чертеже?Назовите их.(АВС и MBN).

-Что мы можем о них сказать?Что мы видем?(угол В-общий;средняя линия разделила стороны пополам, следовательно сторона МВ в 2 раза меньше стороны АВ,а BN в 2 раза меньше стороны ВС, следовательно ; ,следовательно треугольники подобны по 2 признаку),

Тогда как относиться сторона MN к АC?(также по свойству пропорции )Значит МN== AC .Мы доказали с вами что средняя линия равна половине основания треуголника.

Докажем что они параллельны.

Раз треугольники подобны значит углы все у них тоже равны,тоесть угол А=углуМ.

А какие это углы ?(соответсвенные) Следовательно…?(прямые MN и АC параллельные по признаку параллельности прямых.)Что и требовалось доказать.

Запись в тетрадях доказательство теоремы.

Доказательство

МN-средняя линия трегольника АВС.Докажем ,что MN АC,и MN=AC.

1.Рассмотрим АВС и MBN: ;(по определению средней линии), <В-общий ; MBN подобен АВС(по 2 признаку)

; MN= AC(по свойству пропорции).

2. <BMNи<BAC-соответсвенные; <BMN=<BAC(по определению подобных треугольников) MN АC что и требовалось доказать.

5.Закрепление теоремы.

Давайте разберем задачу,которую мы не смогли решить .

Что такое MN?(средняя линия тр.)

Почему вы так решили?(Потому что соединяет середины сторон треуг.)

Что вы можете сказать о средней линии треуг.?(она параллельна основанию и равна ее половине).

Почеуму так?Как вы поняли это из доказательства?(так как треугольники подобны,значит углы соответсвенные равны,и следовательно по признаку параллельности прямых средняя линия и основание треугольника параллельны,а также маленький треугольник в 2 раза меньше большого,значит коэфицент подобия равен ½,следовательно средняя линия треуголника ,котороя является основанием маленького треугольника в 2 раза меньше основания большого трегольника,тоесть средняя линия треуг.равна половине основания данного треугольника).

Чему равна MN?(8см по свойству средней линии)

Работа по готовым чертежам. Научиться применять основное свойство ср. л. треугольника.

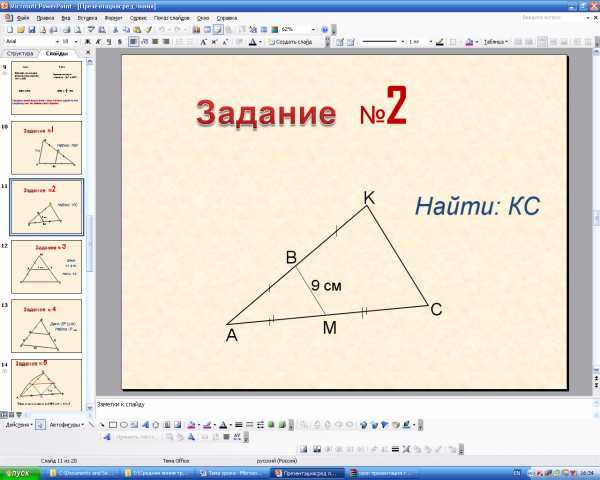
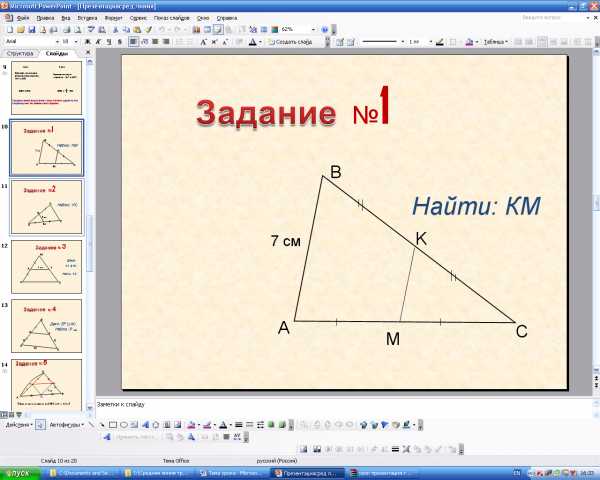
Задание: Найти неизвестный элемент, используя свойство ср. л. треугольника.

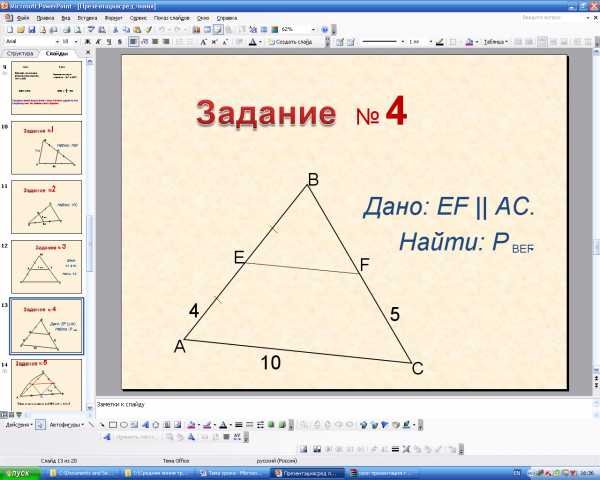
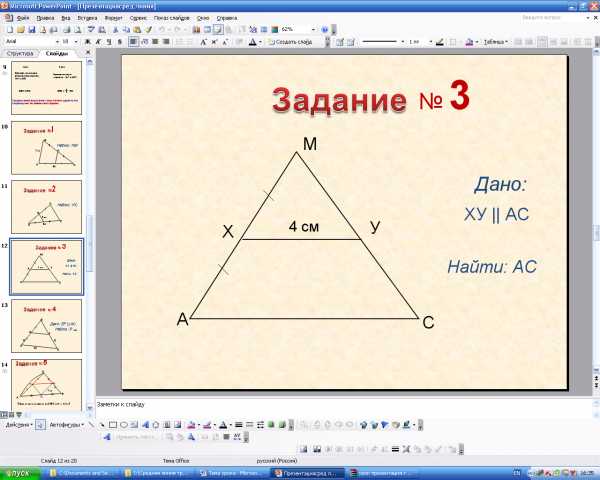
6.Применение теоремы

Работа в тетрадях

Задача 1

Точки P и Q-середины сторон АВ и АС треугольника АВС. Найдите периметр треугольника АВС ,если периметр треугольника APQ равен 21 см

Дано: АВС; PиQ-середины сторон АВ и АС

Р(APQ)=21см

Найти: Р(AВС)=? см

Решение

Так как Pи Q середины сторон АВ и АС АВ=2АР,АС=2А, ВС=2РQ.

(т.к PQ-средняя линия треугольника АВС(по определению ср.л))

Р(АВС)= АВ+ВС+АС=2(АР+РQ+AQ)=2*21=42см

Ответ: Р(АВС)= 42см

Задача 2

Дан треугольник со сторонами 8,7 и 5 см.Найдите периметр треугольника,вершнами которого я вляются середины сторон данного треугольника.

Дано:АВ=8см,ВС=7см,АС=5см

M,N,K-середины сторон АВ,ВС,АС

Найти Р(MNK)-?см

Решение

Р( MNK)= MN+NK+КМ

Так как M,N,K-середины сторон АВ,ВС,АС(по условию) MN,NK,КМ-средние линии треуг. АВС(по определению ср.л) КМ=АВ=4см,

МN=ВС=3,5см, N К=АС=2,5см Р( MNK)=4см+3,5см+2,5см=10см

Ответ: Р( MNK) =10см

infourok.ru

2.3. Пример работы над теоремой о средней линии трапеции.

Логико-математический анализ теоремы: «средняя линия трапеции параллельна основаниям и равна их полусумме».

Теорема сформулирована в категорической форме.

Сформулируем ее в условной форме, выделив явно разъяснительную часть: в любой трапеции, если есть ее средняя линия, то она параллельна основаниям и равна их полусумме.

Итак, структура теоремы такова:

Разъяснительная часть – в любой трапеции;

Условие – отрезок есть средняя линия трапеции;

Заключение – 1) отрезок параллелен основаниям; 2) отрезок равен полусумме оснований.

Теорема содержит два заключения, значит она сложная по структуре (но не обязательно сложным является ее доказательство).

Этапы обучения доказательству теоремы (в основе проблемное обучение, метод эксперимента).

1-й этап. Мотивация необходимости изучения данной теоремы: решение небольшой практической задачи, проблемная ситуация.

2-й этап. Актуализация опорных знаний (расчленить теорему на ряд элементарных шагов и выявить опорные знания, необходимые для понимания доказательства). Формы организации: кратковременная самостоятельная работа, решение обобщающей задачи.

Проанализировав доказательство теоремы, следует выделить опорные знания и повторить их на этапе актуализации. В данном случае уместно повторить свойство средней линии треугольника и решить следующую задачу.

Дано: ABO и DCO, АВ||CD, BO=CO.

Доказать: ABO=DCO.

3-й этап. Введение теоремы

Возможно дедуктивное введение теоремы и синтетический способ ее доказательства.

Однако активизации познавательной деятельности учащихся будет способствовать метод эксперимента. Свойства средней линии трапеции можно «открыть» параллельно с процессом построения средней линии в произвольных трапециях. Учащимся предлагается:

Сравнить визуально взаимное расположение средней линии и оснований трапеции;

Построить отрезок, длина которого равна сумме длин оснований трапеции. Сколько раз средняя линия укладывается на этом отрезке?

На основе выполнения задания выдвигается гипотеза о том, что средняя линия параллельна основаниям трапеции и равна ее половине.

Далее формулируется теорема, делается чертеж, записывается, что дано и требуется доказать.

Дано:ABCD – трапеция, AD и ВС – основания, QP – средняя линия.

Доказать:

1. QP||AD, QP||BC,

2. QP=1/2(AD+BC).

4-й этап. Анализ. Поиск путей доказательства:

Дайте определение трапеции. Какие прямые в нашем случае параллельны, как они называются? Требуется доказать, что средняя линия параллельна двум основаниям, то есть двум параллельным прямым. Как упростить путь доказательства этого факта? Достаточно доказать параллельность одному из оснований.

Чем можно воспользоваться? Для какой фигуры, кроме трапеции определено понятие средней линии? Нельзя ли использовать теорему о средней линии треугольника для доказательства? Можно ли отыскать или провести дополнительные построения, чтобы получить треугольник, средняя линия которого совпадает со средней линией трапеции?

5-й этап. Синтез. Составление плана доказательства.

6-й этап. Осуществление доказательства. Запись.

Доказательство:

1. Дополнительное построение: проведем луч ВР до пересечения с лучом AD. Е – точка пересечения.

2. Рассмотрим BCP и EDP:

СР=DP (P – середина CD),

BPC=EPD (как вертикальные углы),

BCP=EDP (как накрест лежащие углы при параллельных BC и AD и секущей CD),

BCP=EDP (по второму признаку).

Значит BC=DE, BP=PE (из равенства треугольников).

3. ABE:

Q – середина AB, P – середина CD,

QP – средняя линия ABE:

QP||AE, QP=1/2AE=1/2(AD+DE)=1/2(AD+BC) (по свойству средней линии и по построению).

4. BC||AD, QP||AD, значит QP||BC (по теореме о параллельности двух прямых третьей).

7-й этап. Усвоение содержания теоремы и ее доказательства:

Повторить формулировку теоремы и основные этапы ее доказательства или предложить учащимся прочитать соответствующий материал в учебнике.

Можно также применить и другой порядок работы:

Наметить план доказательства;

Провести доказательство устно;

Провести повторное доказательство с краткой записью.

8-й этап. Первичное закрепление теоремы. Уместны устные задачи по готовым чертежам. Например, такие:

studfiles.net

Докажите с помощью векторов теорему о средней линии треугольника. — Учеба и наука

Значит, вектора ac и 2df параллельны и их длины равны

Значит, длина ас = 2 * df  .

www.liveexpert.ru