Тригонометрические формулы. Основные тригонометрические тождества. Тригонометрические тождества
Основные тригонометрические тождества
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
- ctg (α — β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Переход от суммы к произведению
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
Основные формулы тригонометрии
Основное тригонометрическое тождество, синус суммы и разности, косинус суммы и разности. Основные формулы тригонометрии.
Тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Их всего четыре:
- Синус \( \displaystyle sin\left( x \right) \)
- Косинус \( \displaystyle cos\left( x \right) \)
- Тангенс \( \displaystyle tg\left( x \right) \)
- Котангенс \( \displaystyle ctg\left( x \right) \)
Существует два способа решения тригонометрических уравнений:
Первый способ — с использованием формул.
| \( \displaystyle A \) | \( \displaystyle a \) | \( \displaystyle -1 \) | \( \displaystyle 0 \) | \( \displaystyle 1 \) |
| \( \displaystyle \sin x=A \) | \( \displaystyle {{\left( -1 \right)}^{n}}\arcsin \alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{2}+2\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{2}+2\pi n \) |
| \( \displaystyle \cos x=A \) | \( \displaystyle \pm \arccos \alpha +2\pi n \) | \( \displaystyle \pi +2\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle 2\pi n \) |
| \( \displaystyle tgx=A \) | \( \displaystyle arctg\alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{4}+\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
| \( \displaystyle ctgx=A \) | \( \displaystyle arcctg\alpha +\pi n \) | \( \displaystyle \dfrac{3\pi }{4}+\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
Второй способ — через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.
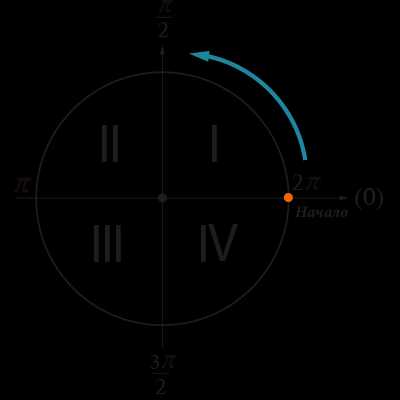
Основные формулы Тригонометрии:
Основное тригонометрическое тождество (нужно его помнить, даже если тебя разбудили среди ночи и спросили!)
\[ \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1 \]
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)
\[ \displaystyle tg\ \alpha =\dfrac{sin\ \alpha }{cos\ \alpha } \]
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)
\[ \displaystyle ctg\ \alpha =\dfrac{cos\ \alpha }{sin\ \alpha }=\dfrac{1}{tg\ \alpha } \]
Синус суммы и разности:
\[ \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \]
Косинус суммы и разности:
\[ \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \]
Тангенс суммы и разности:
\[ \displaystyle tg\left( \alpha \pm \beta \right)=\dfrac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta } \]
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
\[ \displaystyle si{{n}^{2}}\alpha =\dfrac{1-cos2\alpha }{2} \]
\[ \displaystyle co{{s}^{2}}\alpha =\dfrac{1+cos2\alpha }{2} \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
\[ \displaystyle t{{g}^{2}}\alpha =\dfrac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \dfrac{\pi }{2}+\pi n,n\in Z \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
Из данных формул можно в частности вывести формулы тройного угла:
\[ \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \]
\[ \displaystyle cos3a=4co{{s}^{3}}a-3cosa \]
\[ \displaystyle tg3\alpha =\dfrac{3tg\alpha -t{{g}^{3}}\alpha }{1-3t{{g}^{2}}\alpha } \]
\[ \displaystyle ctg3\alpha =\dfrac{3ctg\alpha -ct{{g}^{3}}\alpha }{1-3ct{{g}^{2}}\alpha } \]
Формулы преобразования суммы функций
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
\[ \displaystyle sin\alpha \pm sin\beta =2sin\dfrac{\alpha \pm \beta }{2}cos\dfrac{\alpha \mp \beta }{2} \]
\[ \displaystyle cos\alpha +cos\beta =2cos\dfrac{\alpha +\beta }{2}cos\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle cos\alpha -cos\beta =-2sin\dfrac{\alpha +\beta }{2}sin\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle tg\alpha \pm tg\beta =\dfrac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta } \]
\[ \displaystyle ctg\alpha \pm ctg\beta =\dfrac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta } \]
Формулы преобразования произведений функций
\[ \displaystyle sin\alpha sin\beta =\dfrac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2} \]
\[ \displaystyle sin\alpha cos\beta =\dfrac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2} \]
\[ \displaystyle cos\alpha cos\beta =\dfrac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2} \]
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Тригонометрические формулы | LAMPA — онлайн-учебник, который каждый может улучшить
Тригонометрические функции некоторых углов
| 000 | 30∘30^{\circ}30∘ | 45∘45^{\circ}45∘ | 60∘60^{\circ}60∘ | 90∘90^{\circ}90∘ | 180∘180^{\circ}180∘ | 270∘270^{\circ}270∘ | |
|---|---|---|---|---|---|---|---|
| α\alphaα | 000 | π6\frac{\pi }{6}6π | π4\frac{\pi }{4}4π | π3\frac{\pi }{3}3π | π2\frac{\pi }{2}2π | π\piπ | 3π2\frac{3\pi }{2}23π |
| sinα\sin\alphasinα | 000 | 12\frac{1}{2}21 | 22\frac{\sqrt{2}}{2}22 | 32\frac{\sqrt{3}}{2}23 | 111 | 000 | −1-1−1 |
| cosα\cos\alphacosα | 111 | 32\frac{\sqrt{3}}{2}23 | 22\frac{\sqrt{2}}{2}22 | 12\frac{1}{2}21 | 000 | −1-1−1 | 000 |
| tgα\text{tg}\alphatgα | 000 | 33\frac{\sqrt{3}}{3}33 | 111 | 3\sqrt{3}3 | ∞\infty∞ | 000 | ∞\infty∞ |
| ctgα\text{ctg}\alphactgα | ∞\infty∞ | 3\sqrt{3}3 | 111 | 33\frac{\sqrt{3}}{3}33 | 000 | ∞\infty∞ | 000 |
Эти же точки, отмеченные на тригонометрическом круге. cosα\cos \alphacosα — координата xxx, sinα\sin\alphasinα — координата yyy.
Формулы приведения
Для определения значения f(x+πk2)f(x+\frac{\pi k}{2})f(x+2πk), где fff — одна из функций sin\sinsin, cos\coscos, tg\text{tg}tg или ctg\text{ctg}ctg, используются формулы приведения.
| β=\beta=β= | π2+α\frac{\pi }{2}+\alpha2π+α | π+α\pi +\alphaπ+α | 3π2+α\frac{3\pi }{2}+\alpha23π+α | π2−α\frac{\pi }{2}-\alpha2π−α | π−α\pi -\alphaπ−α | 3π2−α\frac{3\pi }{2}-\alpha23π−α |
| sinβ\sin\betasinβ | cosα\cos\alphacosα | −sinα-\sin\alpha−sinα | −cosα-\cos\alpha−cosα | cosα\cos\alphacosα | sinα\sin\alphasinα | cosα\cos\alphacosα |
| cosβ\cos\betacosβ | −sinα-\sin\alpha−sinα | −cosα-\cos\alpha−cosα | sinα\sin\alphasinα | sinα\sin\alphasinα | −cosα-\cos\alpha−cosα | −sinα-\sin\alpha−sinα |
| tgβ\text{tg}\betatgβ | −ctgα-\text{ctg}\alpha−ctgα | tgα\text{tg}\alphatgα | −ctgα-\text{ctg}\alpha−ctgα | ctgα\text{ctg}\alphactgα | −tgα-\text{tg}\alpha−tgα | ctgα\text{ctg}\alphactgα |
| ctgβ\text{ctg}\betactgβ | −tgα-\text{tg}\alpha−tgα | ctgα\text{ctg}\alphactgα | −tgα-\text{tg}\alpha−tgα | tgα\text{tg}\alphatgα | −ctgα-\text{ctg}\alpha−ctgα | tgα\text{tg}\alphatgα |
Вместо запоминания формул можно использовать . Координата xxx точки круга соответствует косинусу, а координата yyy — синусу.
Например, если отложить углы α\alphaα и π2+α\frac{\pi }{2}+\alpha2π+α, можно увидеть, что cos(π2+α)=−sinα\cos(\frac{\pi }{2}+\alpha )=-\sin\alphacos(2π+α)=−sinα.
Тригонометрические функции имеют 2π\,\,2\pi2π. Это означает, что если к величине угла прибавить 2π2\pi2π (или 4π4\pi4π, 6π6\pi6π, …), то значение функции не изменится. Например, sin(x+49π)=sin(x+π)=−sinx\sin (x+49 \pi )=\sin(x+\pi )=-\sin xsin(x+49π)=sin(x+π)=−sinx.
Выражение одних тригонометрических функций через другие
Если xxx — острый угол, то есть 0<x<π20\lt x\lt \frac{\pi }{2}0<x<2π, то одни выражаются через другие по формулам:
Через косинус угла
sinx=1−cos2x,tgx=1−cos2xcosx,ctgx=cosx1−cos2x\sin x=\sqrt{1-\cos^2 x},\,\, \text{tg} x=\frac{\sqrt{1-\cos^2 x}}{\cos x}, \,\, \text{ctg} x=\frac{\cos x}{\sqrt{1-\cos^2 x} }sinx=1−cos2x,tgx=cosx1−cos2x,ctgx=1−cos2xcosx;
Через синус угла
cosx=1−sin2x,tgx=sinx1−sin2x,ctgx=1−sin2xsinx\cos x=\sqrt{1-\sin^2 x},\,\, \text{tg} x=\frac{\sin x}{\sqrt{1-\sin^2 x} }, \,\, \text{ctg} x=\frac{\sqrt{1-\sin^2 x}}{\sin x}cosx=1−sin2x,tgx=1−sin2xsinx,ctgx=sinx1−sin2x;
Через тангенс угла
sinx=tgx1+tg2x,cosx=11+tg2x,ctgx=1tgx\sin x=\frac{\text{tg} x}{\sqrt{1+\text{tg}^2 x} }, \,\,\,\, \cos x=\frac{1}{\sqrt{1+\text{tg}^2 x} }, \,\,\,\, \text{ctg} x=\frac{1}{\text{tg} x}sinx=1+tg2xtgx,cosx=1+tg2x1,ctgx=tgx1.
Формулы двойного аргумента
sin2x=2sinxcosx\sin 2x=2\sin x\cos xsin2x=2sinxcosx — синус двойного угла;
cos2x=cos2x−sin2x\cos 2x=\cos^2 x-\sin^2 xcos2x=cos2x−sin2x — косинус двойного угла;
tg2x=2tgx1−tg2x\text{tg} 2x=\frac{2\text{tg} x}{1-\text{tg}^2 x}tg2x=1−tg2x2tgx — тангенс двойного угла.
Формулы понижения степени
Переход к двойному аргументу позволяет понизить степень тригонометрических функций:
cos2x=1+cos2x2\cos^2x= \frac{1+\cos 2x}{2}cos2x=21+cos2x;
sin2x=1−cos2x2\sin^2x= \frac{1-\cos 2x}{2}sin2x=21−cos2x.
Эти формулы дают обратное преобразование по сравнению с .
Формулы половинного аргумента
2sin2x2=1−cosx2\sin^2 \frac{x}{2}=1-\cos x2sin22x=1−cosx — синус половинного угла;
2cos2x2=1+cosx2\cos^2 \frac{x}{2}=1+\cos x2cos22x=1+cosx — косинус половинного угла;
tg2x2=1−cosx1+cosx\text{tg}^2 \frac{x}{2}=\frac{1-\cos x}{1+\cos x}tg22x=1+cosx1−cosx — тангенс половинного угла;
tgx2=sinx1+cosx=1−cosxsinx\text{tg} {\frac{x}{2}}=\frac{\sin x}{1+\cos x}=\frac{1-\cos x}{\sin x}tg2x=1+cosxsinx=sinx1−cosx — тангенс половинного угла.
Формулы сложения
sin(α+β)=sinαcosβ+cosαsinβ \sin (\alpha + \beta )=\sin \alpha\, \cos \beta + \cos \alpha\, \sin \betasin(α+β)=sinαcosβ+cosαsinβ
sin(α−β)=sinαcosβ−cosαsinβ \sin (\alpha — \beta )=\sin \alpha\, \cos \beta — \cos \alpha\, \sin \betasin(α−β)=sinαcosβ−cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ \cos (\alpha + \beta )=\cos \alpha \,\cos \beta — \sin \alpha\,\sin \betacos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβ \cos (\alpha — \beta )=\cos \alpha\, \cos \beta + \sin \alpha\, \sin \betacos(α−β)=cosαcosβ+sinαsinβ
tg(α+β)=tgα+tgβ1−tgαtgβ \text{tg} (\alpha + \beta )=\frac{\text{tg} \alpha + \text{tg} \beta }{1-\text{tg} \alpha\, \text{tg} \beta }tg(α+β)=1−tgαtgβtgα+tgβ
tg(α−β)=tgα−tgβ1+tgαtgβ \text{tg} (\alpha — \beta )=\frac{\text{tg} \alpha — \text{tg} \beta }{1+\text{tg} \alpha\, \text{tg} \beta }tg(α−β)=1+tgαtgβtgα−tgβ
(в последних двух формулах α≠π2+πn,β≠π2+πn\alpha \neq \frac{\pi }{2}+\pi n, \beta \neq \frac{\pi }{2}+\pi nα≠2π+πn,β≠2π+πn и соответственно α+β≠π2+πn,α−β≠π2+πn\alpha + \beta \neq \frac{\pi }{2} + \pi n, \alpha -\beta \neq \frac{\pi }{2}+\pi nα+β≠2π+πn,α−β≠2π+πn, nnn — целое)
ctg(α+β)=ctgαctgβ−1ctgα+ctgβ \text{ctg} (\alpha + \beta )=\frac{\text{ctg} \alpha\, \text{ctg} \beta — 1}{\text{ctg} \alpha + \text{ctg} \beta }ctg(α+β)=ctgα+ctgβctgαctgβ−1
ctg(α−β)=ctgαctgβ+1ctgα−ctgβ \text{ctg} (\alpha — \beta )=\frac{\text{ctg} \alpha\, \text{ctg} \beta + 1}{\text{ctg} \alpha — \text{ctg} \beta }ctg(α−β)=ctgα−ctgβctgαctgβ+1
(в последних двух формулах α≠πn,β≠πn\alpha \neq \pi n, \beta \neq \pi nα≠πn,β≠πn и соответственно α+β≠πn,α−β≠πn\alpha + \beta \neq \pi n, \alpha -\beta \neq \pi nα+β≠πn,α−β≠πn, nnn — целое)
lampa.io
Тангенс угла
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 900. Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым. В развернутом угле 180 градусов.
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла — называется катетом.
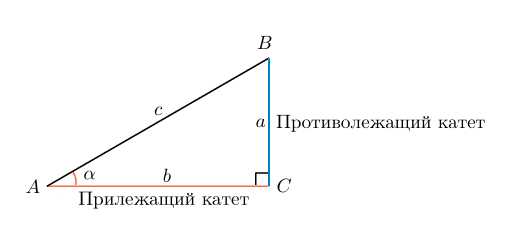
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
cosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса — это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:
тангенс 30 — 0,577
тангенс 45 — 1,000
тангенс 60 — 1,732
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
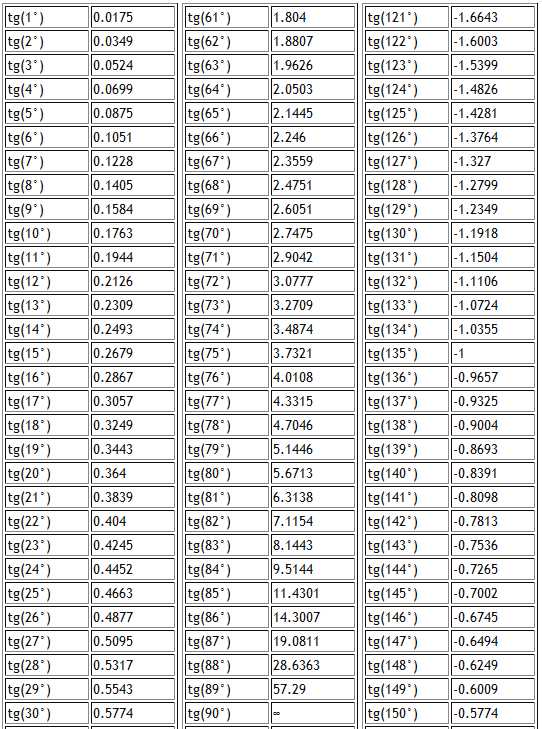
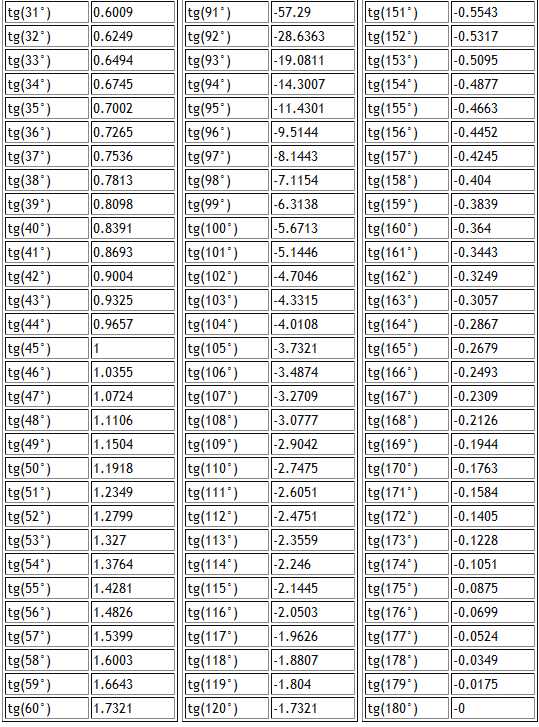
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
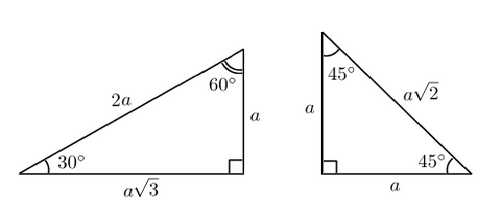
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Тангенс и котангенс. Формулы и определение
Тангенс tg(x) — это отношение синуса sin(x) к косинусу cos(x). Котангенс ctg(x) — это отношение косинуса cos(x) к синусу sin(x).
Помимо синуса и косинуса в тригонометрии имеется еще огромное количество функций, в частности, тангенс и котангенс, о котором мы поговорим на данном уроке.
Определение тангенса:
Тангенс tg(x) — это отношение синуса sin(x) к косинусу cos(x)
Формула тангенса:
\[ \LARGE tg\ x = \dfrac{\sin\ x}{\cos\ x} \]
Определение котангенса:
Котангенс ctg(x) — это отношение косинуса cos(x) к синусу sin(x).
Формула котангенса:
\[ \LARGE ctg\ x = \dfrac{\cos\ x}{\sin\ x} \]
Определения для прямоугольного треугольника:
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Определения для числа:
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t, то есть, tg(t)=y/x.
Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t, то есть, ctg(t)=x/y.
Так как делить на ноль нельзя, то значения в знаменателе не может быть равным нулю, т.е.
\( tg\ x = \dfrac{sin\ x}{cos\ x} \), где \( x \neq \dfrac{\pi}{2}+\pi k \)
\( ctg\ x = \dfrac{cos\ x}{sin\ x} \), где \( x \neq \pi k \)
Таблица знаков тангенса и котангенса по четвертям (составить ее можно, опираясь на таблицу синусов и косинусов, применяя правило деление чисел с отрицательными знаками):
| I | II | III | IV | |
| tg x | + | – | + | – |
| ctg x | + | – | + | – |
Как видите, значения тангенса и котангенса очень просто найти, зная значения синуса и косинуса, тем не менее также существует таблица и для данных функций, которая существенно упрощает жизнь. Здесь я представлю самые распространенные значения. А для всех остальных значений существуют специальные таблицы Брадиса.
| \( \frac{\pi}{6} \) | \( \frac{\pi}{4} \) | \( \frac{\pi}{3} \) | \( \frac{\pi}{2} \) | 0 | |
| tg x | \( \frac{\sqrt{3}}{3} \) | 1 | \( \sqrt{3} \) | – | 0 |
| ctg x | \( \sqrt{3} \) | 1 | \( \frac{\sqrt{3}}{3} \) | 0 | – |
Завершая разговор про данные тригонометрические функции нельзя не сказать про еще две важные формулы:
Для любого допустимого значения х справедливы равенства:
\[ tg\ (-x) = -tg\ x \]
\[ ctg\ (-x) = -ctg\ x \]
Для любого допустимого значения х также справедливы следующие равенства:
\[ tg\ (x+\pi)= tg\ \pi \]
\[ ctg\ (x+\pi)= ctg\ \pi \]
Ну вот теперь вроде все, более подробно и углубленно изучать мы будем все функции в процессе дальнейшего обучения.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей.
Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.
Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.
Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для
www.math10.com
tg (a + b)
Данное выражение tg (a + b) носит название тангенса суммы. Рассмотрим варианты, как можно его расписать и как можно применить на конкретных примерах.
В формуле тангенса суммы в качестве аргументов могут стоять любые два угла, за исключением углов Пи/2, 3Пи/2 и т.д., через промежутки, равные числу Пи. Таким же условиям должна соответствовать и сумма этих углов.
Формулу для всех остальных углов записывают так:
Формулу легко можно получить, если вспомнить свойство тангенса, согласно которому он является отношением синуса к косинусу. То есть тангенс сумы можно получить, если разделить синус суммы а и b на косинус суммы этих же аргументов:
В тригонометрии формулы суммы аргументов применяют с разными целями. Например, используя тангенс суммы можем проверить следующую формулу приведения:
Используем выше рассмотренную формулу и получим:
Таким образом, формула приведения доказана.
Также с помощью тригонометрических формул сложения аргументов можно вычислять точные значения функций углов, которые отличаются от основных.
Рассмотрим пример.
Пример.
Вычислим значение тангенса 75 градусов.
Решение.
Аргументом тангенса выступает угол 75 градусов. Представим его как сумму 45 градусов и 30 градусов. С помощью выше рассмотренной формулы вычислим тангенс:
Ответ. 3,7326.
ru.solverbook.com
