Тригонометрия задачи и решения – Задачи с тригонометрическими функциями — задачи с решениями

Задачи с решением — Тригонометрические уравнения

1.       Решить уравнение cos2x = 1/2.

Используем метод решения простейших тригонометрических уравнений и получаем:

2x = ±arccos(1/2) + 2πn = ±π/3 + 2πn (здесь и далее, n ∈ Z).

Откуда x = ±π/6 + πn.

Ответ: x = ±π/6 + πn.

2.       Решить уравнение sin(3 — 2x) = -1/2.

Используем формулу из методов решений, имеем:

3 — 2x = (-1)n(arcsin(-1/2)) + πn = (-1)n(-π/6) + πn (здесь и далее n ∈ Z).

Делаем преобразование и получаем x = 3/2 + π/12(-1)n — πn/2.

Ответ: x = 3/2 + π/12(-1)n — πn/2.

3.       Решить уравнение cos2x — 3sinx = 2.

 

Воспользуемся формулой удвоенного угла косинуса (cos2a = 1 — 2sin2a) и получим:

1 — 2sin2x — 3sinx = 2.

Воспользуемся методом замены, обозначим sinx = y. Уравнение примет вид:

2y2 + 3y + 1 = 0.

Находим его корни: y1 = -1, y2 = -1/2.

Возвращаемся к исходной переменной и получаем совокупность sinx = -1 и sinx = -1/2.

Из первого получаем решение — x = -π/2 + 2πn, из второго — x = (-1)m(-π/6) + πm (m, n ∈ Z).

Ответ: x = -π/2 + 2πn или x = (-1)m(-π/6) + πm.

4.       Решить уравнение 2tgx — 3ctgx = 1.

Так как ctgx = 1/tgx при x ≠ πn/2 (n ∈ Z) получаем уравнение

2tgx — 3/tgx = 1 или 2tg2x — tgx — 3 = 0.

Вводим новую переменную tgx = y и решаем квадратное уравнение 2y2 — y — 3 = 0 относительно y.

Оно имеет два решения y1 = 3/2, y2 = -1.

Возвращаемся к исходной переменной и решаем два уравнения:

tgx = 3/2, откуда x = arctg(3/2) + πn, n ∈ Z.

tgx = -1, откуда x = arctg(-1) + πm = -π/4 + πm, m ∈ Z.

Ответ: x = arctg(3/2) + πn или x = -π/4 + πm.

5.       Решить уравнение 3cosx — sin2x = 1 — sin3x.

Сделаем следующее преобразование 3(cosx + sinx) = 1 + sin2x.

Замена cosx + sinx = t приведет к уравнению 3t = t2. Оно имеет корни t1 = 0, t2 = 3.

Берем первый корень, возвращаем замену и получаем cosx + sinx = 0, делим на cosx ≠ 0, откуда tgx = -1, x = -π/4 + πn (n ∈ Z).

Второй корень t2 дает уравнение cosx + sinx = 3. Это уравнение не имеет решений, т.к. и cosx, и cosx меньше равны 1, в сумме меньше равны 2.

Ответ: x = -π/4 + πn.

6.       Решить уравнение cos2x + cos4x + cos6x = 0.

Проделаем следующие преобразования

(cos2x + cos6x) + cos4x = 0;

2cos4xcos2x + cos4x = 0;

cos4x(2cos2x + 1) = 0.

Имеем два случая:

cos4x = 0, откуда 4x = π/2 + πn, x = π/8 + πn/4 (n ∈ Z).

2cos2x + 1 = 0 или cos2x = -1/2, откуд

www.sites.google.com

Задачи по тригонометрии — уровень B. Подготовка к ЕГЭ по математике

Для учеников, имеющих средний или слабый уровень знаний по тригонометрии репетитор по математике разбивает подготовку к задачам С1 с ЕГЭ на несколько этапов. Один из них — решение уравнений на замену переменной. Прорешайте размещенный ниже комплект заданий, а затем уже переходите к рассмотрению уравнений с ограничениями. Я собирал номера из разных задачников. Некоторые составлял сам. Главная цель, которая преследовалась — предоставить репетитору по математике достаточное количество номеров на отработку навыков выполнения замены в разных ситуациях. Все уравнения снабжены ответами. Учебный дидактический комплект для качественной подготовки к ЕГЭ по математике с репетитором.

Уравнение на моментальную замену переменной

————————————————————————————
1)

Ответ:

————————————————————————————
2)

Ответ:

————————————————————————————
3)

Ответ:

————————————————————————————

4)

Ответ:

————————————————————————————
5)

Ответ:

————————————————————————————
6)

Ответ:

————————————————————————————
Уравнения на замену переменной после некоторого преобразования

————————————————————————————
7)

Ответ:

————————————————————————————
8)

Ответ:

————————————————————————————
9)

Ответ:

10)

Ответ:

————————————————————————————

11)

Ответ:

————————————————————————————
12)

Ответ:

————————————————————————————
13)

Ответ:

————————————————————————————
14)

Ответ:

————————————————————————————
Уравнения на формулы двойного угла и замену переменной (отобрано репетитором по математике)

————————————————————————————
15)

Ответ:

————————————————————————————
16)

Ответ:

————————————————————————————

17)

Ответ:

————————————————————————————
18)

Ответ:

————————————————————————————
19)

Ответ:

————————————————————————————
20)

Ответ:

————————————————————————————
21)

Ответ:

————————————————————————————
22)

Ответ:

————————————————————————————
23)

Ответ:

————————————————————————————
Уравнения на замену с применением формул приведения

————————————————————————————
24)

Ответ:

————————————————————————————
25)

Ответ:

————————————————————————————
26)

Ответ:

————————————————————————————
Скоро будут доступны другие уравнения, также сортированные по типам.

Указание репетитора по математике: предлагать ученику подобные уравнения можно только после отработки с ним темы «обратные тригонометрические функции» и «простейшие тригонометрические уравнения». Кроме этого нужно повторить с формулы двойного угла и основное тригонометрическое тождество. Каждое решение должно сопровождаться рисунком, даже если школьник справляется c уравнениями и без них. Слабому ученику репетитору желательно подготовить теоретический листочек с необходимыми формулами и примерами рисунков к простейшим типовым уравнениям вида Cosx=a; Sinx=a; tgx=a и ctgx=a.

Колпаков А.Н. Репетитор по математике — составитель комплекта. Москва. Строгино.

Метки: ЕГЭ по математике, Тригонометрия

ankolpakov.ru

Тригонометрические уравнения. Задания ЕГЭ по математике (профильный уровень)

а) 1. Согласно формуле приведения, ctg\left( \frac{3\pi }2-x\right) =tgx. Областью определения уравнения будут такие значения x, что \cos x \neq 0 и tg x \neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 \cos ^2 \frac x2=1+\cos x. Получим уравнение: 5(1+\cos x) =\frac{11+5tgx}{1+tgx}.

Заметим, что \frac{11+5tgx}{1+tgx}= \frac{5(1+tgx)+6}{1+tgx}= 5+\frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 \cos x=5 +\frac{6}{1+tgx}. Отсюда \cos x =\frac{\dfrac65}{1+tgx}, \cos x+\sin x =\frac65.

2. Преобразуем \sin x+\cos x по формуле приведения и формуле суммы косинусов: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left( x-\frac\pi 4\right) = \frac65.

Отсюда \cos \left(x-\frac\pi 4\right) =\frac{3\sqrt 2}5. Значит, x-\frac\pi 4= arc\cos \frac{3\sqrt 2}5+2\pi k, k \in \mathbb Z,

или x-\frac\pi 4= -arc\cos \frac{3\sqrt 2}5+2\pi t, t \in \mathbb Z.

Поэтому x=\frac\pi 4+arc\cos \frac{3\sqrt 2}5+2\pi k,k \in \mathbb Z,

или x =\frac\pi 4-arc\cos \frac{3\sqrt 2}5+2\pi t,t \in \mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=\frac\pi 4+arccos \frac{3\sqrt 2}5 и b=\frac\pi 4-arccos \frac{3\sqrt 2}5.

1. Докажем вспомогательное неравенство:

\frac{\sqrt 2}{2}<\frac{3\sqrt 2}2<1.

Действительно, \frac{\sqrt 2}{2}=\frac{5\sqrt 2}{10}<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.

Заметим также, что \left( \frac{3\sqrt 2}5\right) ^2=\frac{18}{25}<1^2=1, значит \frac{3\sqrt 2}5<1.

2. Из неравенств (1) по свойству арккосинуса получаем:

arccos 1<arc\cos \frac{3\sqrt 2}5<arc\cos \frac{\sqrt 2}2,

0<arccos\frac{3\sqrt2}{5}<\frac{\pi}{4}.

Отсюда \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,

0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,

0<a<\frac\pi 2.

Аналогично, -\frac\pi 4<arccos\frac{3\sqrt2}{5}<0,

0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,

0<b<\frac\pi 2.

При k=-1 и t=-1 получаем корни уравнения a-2\pi и b-2\pi.

\Bigg( a-2\pi =-\frac74\pi +arccos \frac{3\sqrt 2}5,\, b-2\pi =-\frac74\pi -arccos \frac{3\sqrt 2}5\Bigg). При этом -2\pi <a-2\pi <-\frac{3\pi }2,

-2\pi <b-2\pi <-\frac{3\pi }2. Значит, эти корни принадлежат заданному промежутку \left( -2\pi , -\frac{3\pi }2\right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если k\geqslant 1 и t\geqslant 1, то корни больше 2\pi. Если k\leqslant -2 и t\leqslant -2, то корни меньше -\frac{7\pi }2.

academyege.ru

Практические задачи с использованием тригонометрии.

Практические задачи с использованием тригонометрии.

Существует ряд практических ситуаций, в которых необходимо использовать тригонометрию для определения неизвестных сторон и углов треугольников.

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. ниже. Определить площадь поля.

 

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

 

Решение:

Угол конька крыши В=180^o

— 35^o— 41^o=104^o

По теореме синусов

,

Откуда

.

Также по теореме синусов:

Откуда

.

(используется таблица синусов)

Следовательно, длины скатов крыши равны 6 м и 7 м с точностью до см.

Примечание: сторона а — сторона против угла А, сторона с — сторона против угла С.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁.

 

Решение:

<CAB=180^o — 45^o=135^o.

Согласно теореме косинусов:

СА² = V₁²+V₂² — 2V₁V₂ cosCBA=

=50² + 90² — 2*50*90cos135^o=16963.(по таблице косинусов)

Результирующий вектор CA=(16963)^1/2 =130,2B.

Cогласно теореме синусов,

,

Откуда

,

Следовательно угол АСВ приблизительно равен 29^о. (по таблице синусов)

Итак, результирующий вектор напряжения равен 130,2В и составляет угол в 29^о с V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Решение:

По теореме синусов,

, откуда

Значит, В=arcsin0,2431≈ 14 ^o (по таблице синусов )

Следовательно, шатун AB составляет угол 14 ^o с горизонталью.

<ОАВ=180^o-45^o-14^o=121^o

По теореме синусов:

, откуда

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. Определить площадь поля.

Проведенная из В в D диагональ делит четырехугольник на два треугольника.

 

 Решение:

 Площадь четырехугольника ABCD= площадь треугольника ABD+площадь треугольника BCD, т.е.

 S_ABCD =1/2*(40)*(21)*sin115^o + 1/2*(45)*(23)*sin55^o=804,582 м²

 

tehtab.ru

Практические задачи с применением тригонометрии

Занятие по математике на тему «Практические задачи с применением тригонометрии»

группа МС-16-1

Преподаватель: Пересыпкина Е. А.

Практические задачи с применением тригонометрии

ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ

Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия,

   в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике,

в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии,

в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках,

в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве,

в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Восход и заход солнца

Изменение фаз Луны

Чередование времен года

Затмение и движение планет

Вращение колеса

Морские приливы и отливы

Эпидемии гриппа

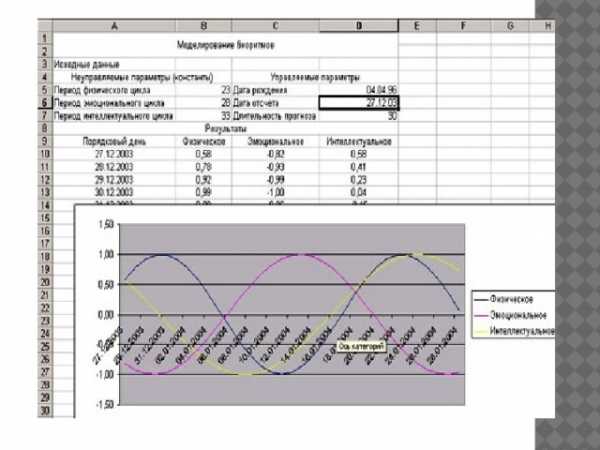
Модель биоритмов

• Модель биоритмов можно построить с помощью тригонометрических функций
• Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).

Тригонометрия в медицине

Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

Тригонометрия в физике

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений, например:

Механические колебания

Гармонические колебания

Механические колебания

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.

Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.

Теория радуги

• Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
•   sin α / sin β = n 1 / n 2

n 1 показатель преломления первой среды

n 2  показатель преломления второй среды

α -угол падения, β -угол преломления

Северное сияние

• Оно возникает при проникновении в верхние слои атмосферы планет заряженных частиц солнечного ветра, и определяется взаимодействием магнитного поля планеты с солнечным ветром.
• Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца.

  Fл = q·V·B·sin a

q- величина заряда движущегося во внешнем магнитном поле

  V- модуль скорости движущегося заряда  B- модуль вектора индукции внешнего магнитного поля   a- угол между вектором скорости заряда и вектором магнитной индукции.

Тригонометрия в архитектуре

• Детская школа Гауди в Барселоне

• Страховая корпорация Swiss Re в Лондоне

Взмах крыльев птицы при полете напоминает синусоиду

Какой четверти принадлежит угол(у доски):

1. 185°

6 . 590°

2. 102°

7. 746°

3. -102°

8. -15°

4. 250°

9. 312°

5. -250°

10. -192°

0 6. сos315°2. cos212° 0 7. tg15° 0 3. tg365° 0 8. sin470°4. ctg290° 0 9. ctg143°5. sin94° 10. соs56° «

Найдитe ошибки(устно):

1. sin128° 0

6. сos315°

2. cos212° 0

7. tg15° 0

3. tg365° 0

8. sin470°

4. ctg290° 0

9. ctg143°

5. sin94°

10. соs56°

Определите знак выражения(у доски):

1. sin213°tg46°cos389°

2. cos819°sin119°tg512°

3 . tg212°cos200°sin89°

4. cos72°sin179°cos600°

Найдите значение выражения(у доски):

• 2cos0° — 4sin90° + 5tg180°
• 2ctg90° — 3cos270° + 5sin180°
• 6tg30° + 4sin60° — ctg30°
• 4sin90° — 3cos180°
• 8cos90° + 7sin360° + 12tg180°

Основные тригонометрические формулы(самостоятельно)

.

Вариант 1

Вариант 2

Найдите :

Найдите:

sinα, tgα, ctgα,

sinα, cosα, сtgα,

если

если

tgα= 2

cosα= — 5/13

π

π/2

Упростите выражение(самостоятельно):

вариант 1 вариант 2

1. 1 – sin²α 1. 1 — cos²α

2. sin²α + cos²α + tg²α 2. sin²α + cos²α +сtg²α

3. tgαctgα + ctg²α 3. tgαctgα + tg²α

4. 1 – cos²α — sin²α 4. -1 + cos²α + sin²α

5. sin²α – tgαctgα 5. cos ²α – tgαctgα

6. sinαctgα 6. cosαtgα

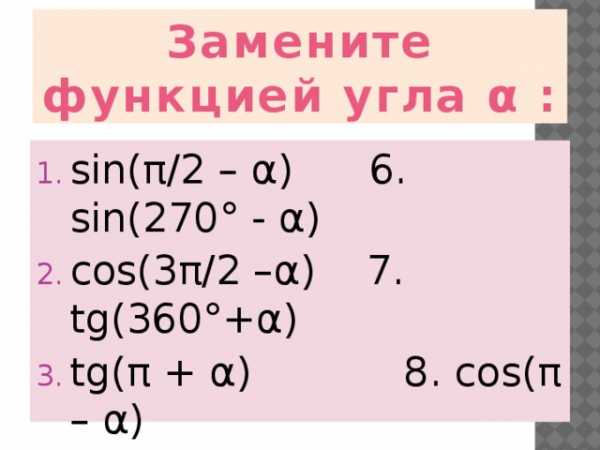
Замените функцией угла α :

• sin(π/2 – α) 6. sin(270° — α)
• cos(3π/2 –α) 7. tg(360°+α)
• tg(π + α) 8. cos(π – α)
• cos(2π –α) 9. ctg(90°- α)
• ctg(π/2 + α) 10. sin(180°+α)

Задачи на косвенное измерение величин.

Знание тригонометрических функций позволяет нам решать такие задачи с большей точностью.

1.Определить высоту предмета, к основанию которого подойти нельзя.

Например, нужно определить высоту телевизионной антенны, которая отделена от нас рекой.

Астролябия

Астролябия – инструмент используется для измерения

небесной высоты. Небесная высота относительная «высота»

звезды, планеты или другого небесного объекта над горизонтом.

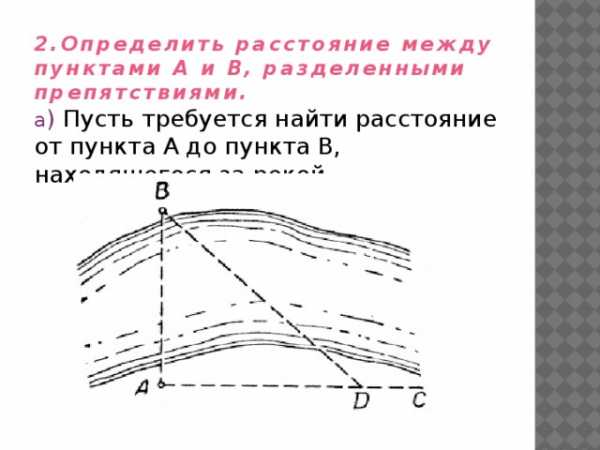
2.Определить расстояние между пунктами А и В, разделенными

препятствиями.

а ) Пусть требуется найти расстояние от пункта А до пункта В, находящегося за рекой.

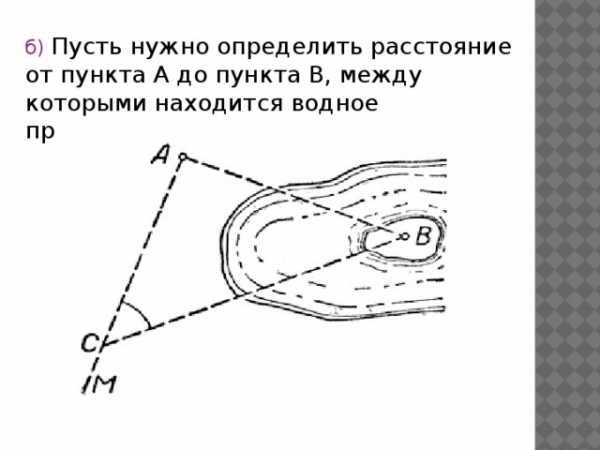
б) Пусть нужно определить расстояние от пункта А до пункта В, между которыми находится водное пространство .

3.Определить значение величин в задачах, в которых непосредственное измерение произвести невозможно

в )На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью показанном на рис .

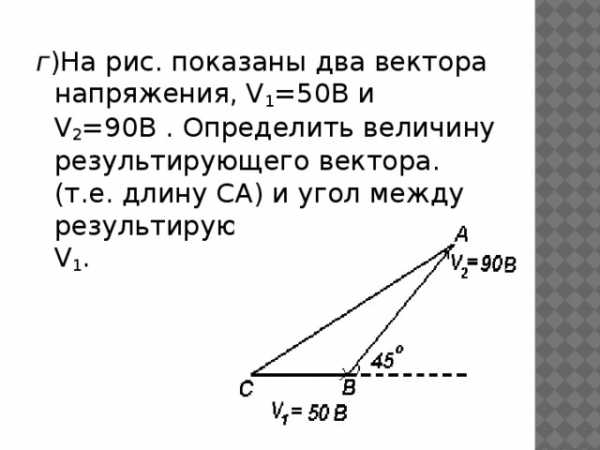
г )На рис. показаны два вектора напряжения, V 1 =50В и V 2 =90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V 1 .

 

Тригонометрия в нашей специальности

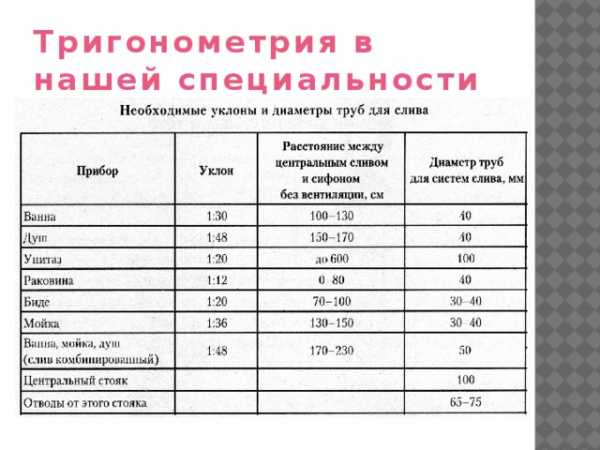
Примеры минимальных уклонов канализации

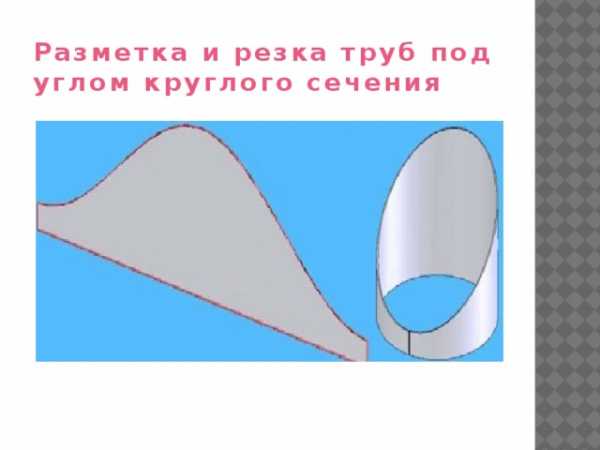
Разметка и резка труб под углом круглого сечения

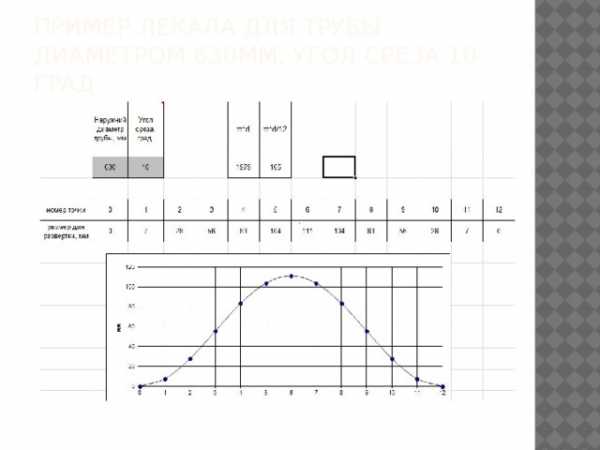
Пример лекала для трубы диаметром 630мм, угол среза 10 град.

Резка трубы под углом

производится по бумажным лекалам, обернутым вокруг заготовки.

Какой бы способ резки труб не был выбран, необходимо следить за точностью нанесения разметки. От этого зависит точность реза.

Поэтому изготовим лекала с помощью миллиметровой бумаги.

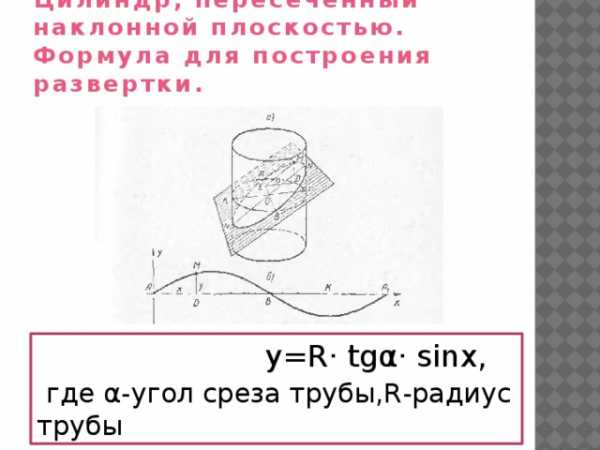
Цилиндр, пересеченный наклонной плоскостью. Формула для построения развертки.

y=R· tgα· sinx,

где α-угол среза трубы,R-радиус трубы

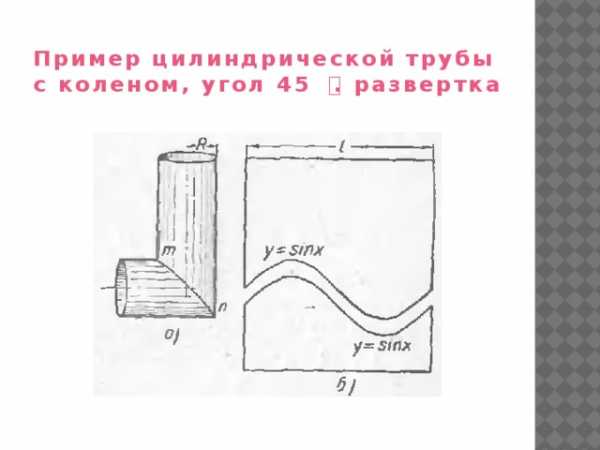
Пример цилиндрической трубы с коленом, угол 45 ͦ. развертка

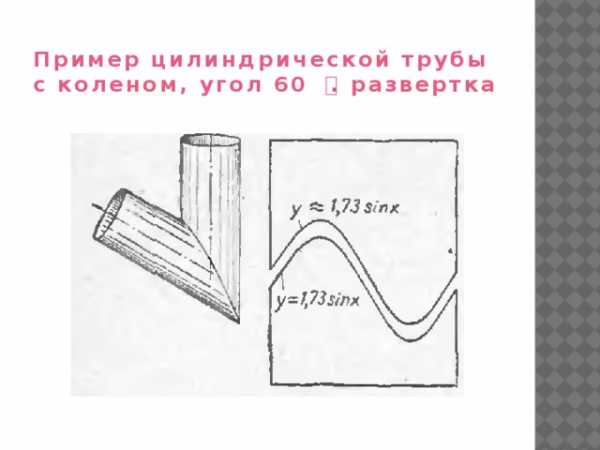
Пример цилиндрической трубы с коленом, угол 60 ͦ. развертка

Задание по вариантам(выполняется на миллиметровой бумаге)

• 1й вариант — построить лекало трубы диаметром 40мм, угол среза 30 ͦ.

• 2й вариант — построить лекало трубы диаметром 50мм, угол среза 60 .

• 3й вариант — — построить лекало трубы диаметром 30мм, угол среза 45 ͦ

Рефлексия

1. На уроке я работал                 активно / пассивно

2. Своей работой на уроке я   доволен / не доволен

3. Урок для меня показался     коротким / длинным 

4. За урок я                                     не устал / устал

5. Мое настроение              стало лучше / стало хуже

6. Материал урока мне был     понятен / не понятен, полезен / бесполезен

multiurok.ru

Использование геометрии при решении тригонометрических задач

Разделы: Математика

---

Геометрия является самым могущественным средством
для изощрения наших умственных способностей и
дает нам возможность правильно мыслить и рассуждать.

Г.Галлилей

Алгебра – не что иное, как записанная в символах геометрия,
а геометрия — это просто алгебра, воплощенная в фигурах

София Жермен

Многие тригонометрические задачи не решаются привычными для них методами или решаются очень сложно, а использование какого-нибудь геометрического приема дает короткое решение. Тригонометрические функции — это испытанный аппарат геометрии и их тоже нужно излагать, отправляясь от простых наглядных задач, как они практически и возникли — из решения треугольников

В школе мы начинаем изучать тригонометрию с вывода тригонометрических зависимостей из прямоугольного треугольника. Еще в 8-м классе, я начинаю работу по обучению детей тригонометрии, так как значительное число упражнений с аргументами из промежутка (0; ) выполняются геометрически. При таком подходе очевидны следующие плюсы.

Во-первых, раннее ознакомление учеников с тригонометрическими заданиями способствует раскрытию творческого потенциала учеников. Во-вторых, расширению математического кругозора. В-третьих, увеличению объема предметных умений. В-четвертых, использование свойств равнобедренного и прямоугольного треугольников, формул для нахождения площадей фигур, теорем синусов и косинусов приобретают устойчивость.

В 10-м классе геометрический метод дает порой более легкий способ решения тригонометрических заданий. Геометрически можно показать интересные решения тригонометрических задач и проявить при этом смекалку и эрудицию.

Несколько примеров с использованием равнобедренного треугольника.

При решении используются следующие утверждения:

1⁰ Высота равнобедренного треугольника, проведенная к основанию. Является медианой и биссектрисой.

2⁰ Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на косинус угла при основании.

3⁰ Биссектриса угла делит противоположную сторону треугольника на части пропорциональные прилежащим сторонам.

Задача 1. Вычислите cos15°.

В 10-м классе используется формула cos (45° – 30°)

В 8-м классе можно решить, используя равнобедренный треугольник

Для нахождения sin.cos. tg угла 22°30’ используем равнобедренный треугольник с углом против основания 45° далее аналогичное решение.

Задача 2. Найти sin 18°

В 10-м классе можно решить следующим образом.

sin 36°= cos 54°= cos (18° + 36°)

2 sin18° cos18° = cos18° cos36° – sin18° sin36°;

2 sin18° cos18°= cos18°(1 – 2sin²18°) – 2sin²18°cos18°

2 sin18° = 1 – 4sin²18°, решаем квадратное уравнение и учтем, что sin18° > 0, получим

sin18° = .

Эту задачу можно решить геометрически

Строим равнобедренный треугольник АВС с АВ=ВС и АВС=36°, тогда ВАС — ВСА = 72° (см рис. 2)

Проведем AD биссектрису ВАС. Получим равнобедренные AВD и AСD. Обозначим AD=ВD=АС= а и АВ=b, тогда СD= а– b. Далее используем подобие треугольников или свойство биссектрисы угла и решим квадратное уравнение получим

Так как sin18° = cos72°. Рассмотрим AСD СD = 2АС·cos72° (свойство2⁰) <–> cos = =

sin18° = cos

Рис. 2

При решении многих тригонометрических задач удобно применять прямоугольный треугольник

Задачи, связанные с обратными тригонометрическими функциями, решаются геометрически быстрее и проще

Задача 3. Вычислите Переформулируем задачу “Вычислить косинус суммы углов ”

Рис. 3

Построим углы . Из рисунка видно, что ANB = DSC (по двум катетам), следовательно т.е.

Задача 4. Вычислите

В 10-м классе можно решить задачу с помощью формул, затратив на это немало усилий. Геометрически эта задача решается намного проще

Рис. 4

Обозначим . tg. Вычислим Построим прямоугольный АВС, где ВС=5n, АС=12n, тогда АВ=13n и ВАС = . Для угла строим ВСК, так, чтобы катет ВС был прилежащим к углу . В результате построения АВD равнобедренный, АВ=АD=13n . АВD= АDВ = , 2

0, т.е. = 0.

Задача 5. Решить уравнение: arcsin x + arcsin 2x =

Пусть arcsin x = , arcsin 2x = , где + = , тогда sin = x, sin = 2x.

Отметим, что x > 0 (иначе arcsin x < 0, arcsin 2x < 0, их сумма < 0).Построим прямоугольные треугольники, так чтобы + образовали прямой угол.

(рис. 5)

АВСD – прямоугольник.

Пусть АС = 1, тогда ВС = 1 · sin = sin = x, и CD = 1 · sin = sin = 2x.

По теореме Пифагора из треугольника АВС:

AB² + BC² = AC²,

(2x)² + x² = 1,

5x² = 1,

x² = ,

x = , x = – – не подходит по условию задачи.

Ответ: .

Задача 6. Решить уравнение: arcsin x + arcsin 2x = .

Пусть arcsin x = , arcsin 2x = , тогда + = .

x = sin , 2x = sin . Заметим, что x > 0.

РИС. 6

Построим АОМ = , АОВ = , МОВ = + = . АМОМ.

Пусть ОА = 1, тогда, из треугольника АОМ, АМ = 1 · sin = sin = 2x.

Проведём АКОВ. Из треугольника АОК АК = 1 · sin = sin = x.

Проведём КС ОМ. СКА = КОМ = – как углы с взаимно перпендикулярными сторонами.

Проведём АD КС. Из АDК KD = AK · cos 60° = x · = .

DC = AM = 2x. Значит, КС = KD + DC = + 2x = .

Из АОК по теореме Пифагора:

ОК = = .

Из ОКС: ОК · sin 60° = KC

Ответ: .

Примеры решения тригонометрических уравнений.

Задача 7. Решить уравнение cos x – sin x = 1.

cos x – sin x = 1

Разделим левую и правую часть уравнения на корень квадратный из суммы квадратов коэффициентов при cos x и sin x, т. е. на = :

 Геометрическое решение:

Рис. 7

cos x – sin x = 1

ВС = 1 · sin x = sin x,

АС = 1 · cos x = cos x.

Следовательно, АС – ВС = 1. Но в АВС каждая сторона больше разности двух других сторон, т. е.

АВ > АС – ВС <=> АС – ВС < 1, т. к. АВ = 1. Но по условию задачи требуется, чтобы АС – ВС = 1. Это возможно только, если ABС превратится в отрезок, т.е.

если АС = 1, а ВС = 0, т.е. x₁ = 0 + 2k, x₁ = 2k, kZ

если АС = 0, а ВС = 1, т.е. x₂ = –x₂ = – + 2l, lZ

Ответ: 2k; – + 2l, kZ.

Задача 8 Решить уравнение , если х – острый угол

Геометрическое решение. Проведем BDAC.

Сумма двух отрезков равна 4 .Отрезки найдены по теореме косинусов

 

Многие математические задачи допускают несколько вариантов решения. Часто первый избранный бывает далеко не самым удачным. Нахождение “наиболее простых”, оригинальных путей решения нередко является результатом длительной и кропотливой работы. Умение решать задачу различными способами является одним из признаков хорошей математической подготовки

Решение тригонометрических задач методом, основанным на наглядно-геометрической интерпретации развивает логическое мышление и пространственное воображение

Литература

1. А Г Мордкович. Алгебра и начала математического анализа. Учебник для 10 класса. Москва, “Мнемозина”, 2010.
2. А.Ф. Бермант, Л.А. Люстерник. Тригонометрия. Москва, 1957.
3. Савин А. Тригонометрия Квант, 1996. – №4.

Презентация

7.08.2012

xn--i1abbnckbmcl9fb.xn--p1ai

Задание 6 — геометрия с элементами тригонометрии

14 апреля 2011

Сегодня рассмотрим задачи B8 c тригонометрией в ее классическом понимании, где изучаются обычные прямоугольные треугольники. Поэтому никаких тригонометрических окружностей и отрицательных углов сегодня не будет — только обычные синусы и косинусы.

Такие задачи составляют примерно 30% от общего числа. Помните: если в задаче B8 хоть раз упоминается угол π, она решается совсем другими способами. Мы обязательно рассмотрим их в ближайшее время. А сейчас — главное определение урока:

Треугольник — фигура на плоскости, состоящая из трех точек и отрезков, которые их соединяют. Фактически, это замкнутая ломаная из трех звеньев. Точки называются вершинами треугольника, а отрезки — сторонами. Важно заметить, что вершины не должны лежать на одной прямой, иначе треугольник вырождается в отрезок.

Довольно часто треугольником называют не только саму ломаную, но и часть плоскости, которая этой ломаной ограничена. Таким образом, можно определить площадь треугольника.

Два треугольника называются равными, если один можно получить из другого путем одного или нескольких движений плоскости: сдвига, поворота или симметрии. Кроме того, существует понятие подобных треугольников: их углы равны, а соответствующие стороны пропорциональны…

Все, что написано выше, можно было не читать. Потому что это не нужно. Вы что, не знаете, что такое треугольник? Вы действительно не знаете, как он выглядит? Хорошо, я сейчас покажу.

Это треугольник ABC. Более того, это прямоугольный треугольник: в нем ∠C = 90°. Именно такие чаще всего и встречаются в задаче B8.

Все, что надо знать для решения задачи B8 — это несколько простых фактов из геометрии и тригонометрии, а также общая схема решения, в которой эти факты используются. Затем останется просто «набить руку».

Начнем с фактов. Они разбиты на три группы:

1. Определения и следствия из них;
2. Основные тождества;
3. Симметрии в треугольнике.

Нельзя сказать, что какая-то из этих групп важнее, сложнее или проще. Но информация, которая в них содержится, позволяет решить любую задачу B8. Поэтому знать надо все. Итак, поехали!

Группа 1: определения и следствия из них

Рассмотрим треугольник ABC, где ∠C — прямой. Для начала — определения:

Синус угла — это отношение противолежащего катета к гипотенузе.

Косинус угла — это отношение прилежащего катета к гипотенузе.

Тангенс угла — это отношение противолежащего катета к прилежащему.

Один угол или отрезок может входить в разные прямоугольные треугольники. Более того, очень часто один и тот же отрезок является катетом в одном треугольнике и гипотенузой — в другом. Но об этом — дальше, а пока будем работать с обычным углом А. Тогда:

1. sin A = BC : AB;
2. cos A = AC : AB;
3. tg A = BC : AC.

Основные следствия из определения:

1. sin A = cos B; cos A = sin B — самые часто используемые следствия
2. tg A = sin A : cos A — связывает тангенс, синус и косинус одного угла
3. Если ∠A + ∠B = 180°, т.е. углы смежные, то: sin A = sin B; cos A = −cos B.

Хотите — верьте, хотите — нет, но этих фактов достаточно, чтобы решить примерно треть всех тригонометрических задач B8.

Группа 2: основные тождества

Первое и самое главное тождество — теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику ABC, рассмотренному выше, эту теорему можно записать так:

AC ² + BC ² = AB ²

И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии.

Второе тождество — из тригонометрии. Выглядит следующим образом:

sin ²A + cos ²A = 1

Оно так и называется: основное тригонометрическое тождество. С его помощью можно через синус выразить косинус и наоборот.

Группа 3: Симметрии в треугольнике

То, что написано ниже, относится только к равнобедренным треугольникам. Если в задаче таковой не фигурирует, то для решения достаточно фактов из первых двух групп.

Итак, рассмотрим равнобедренный треугольник ABC, где AC = BC. Проведем к основанию высоту CH. Получим следующие факты:

1. ∠A = ∠B. Как следствие, sin A = sin B; cos A = cos B; tg A = tg B.
2. CH — не только высота, но и биссектриса, т.е. ∠ACH = ∠BCH. Аналогично, равны и тригонометрические функции этих углов.
3. Также CH — это медиана, поэтому AH = BH = 0,5 · AB.

Теперь, когда все факты рассмотрены, перейдем непосредственно к методам решения.

Общая схема решения задачи B8

Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно.

Для начала, следует обозначить неизвестную сторону (если таковая имеется) за X. Затем применяем схему решения, которая состоит из трех пунктов:

1. Если в задаче есть равнобедренный треугольник, применить к нему все возможные факты из третьей группы. Найдите равные углы и выразите их тригонометрические функции. Кроме того, равнобедренный треугольник редко бывает прямоугольным. Поэтому ищите в задаче прямоугольные треугольники — они там обязательно есть.
2. Применить к прямоугольному треугольнику факты из первой группы. Конечная цель — получить уравнение относительно переменной X. Найдем X — решим задачу.
3. Если фактов из первой группы оказалось недостаточно, применяем факты из второй группы. И снова ищем X.

Примеры решения задач

А теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует 🙂

Задача. В треугольнике ABC угол C равен 90°, AB = 5, BC = 3. Найдите cos A.

По определению (группа 1), cos A = AC : AB. Гипотенуза AB нам известна, а вот катет AC придется искать. Обозначим его AC = x.

Переходим к группе 2. Треугольник ABC — прямоугольный. По теореме Пифагора:

AC ² + BC ² = AB ²;
x² + 3² = 5²;
x² = 25 − 9 = 16;
x = 4.

Теперь можно найти косинус:

cos A = AC : AB = 4 : 5 = 0,8.

Задача. В треугольнике ABC угол B равен 90°, cos A = 4/5, BC = 3. BH — высота. Найдите AH.

Обозначим искомую сторону AH = x и рассмотрим треугольник ABH. Он прямоугольный, причем ∠AHB = 90° по условию. Поэтому cos A = AH : AB = x : AB = 4/5. Это пропорция, ее можно переписать так: 5 · x = 4 · AB. Очевидно, мы найдем x, если будем знать AB.

Рассмотрим треугольник ABC. Он также прямоугольный, причем cos A = AB : AC. Ни AB, ни AC нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество:

sin ²A + cos ²A = 1;
sin ²A = 1 − cos ²A = 1 − (4/5)² = 1 − 16/25 = 9/25.

Поскольку тригонометрические функции острого угла положительны, получаем sin A = 3/5. С другой стороны, sin A = BC : AC = 3 : AC. Получаем пропорцию:

3 : AC = 3 : 5;
3 · AC = 3 · 5;
AC = 5.

Итак, AC = 5. Тогда AB = AC · cos A = 5 · 4/5 = 4. Наконец, находим AH = x:

5 · x = 4 · 4;
x = 16/5 = 3,2.

Задача. В треугольнике ABC AB = BC, AC = 5, cos C = 0,8. Найдите высоту CH.

Обозначим искомую высоту CH = x. Перед нами равнобедренный треугольник ABC, в котором AB = BC. Следовательно, из третьей группы фактов имеем:

∠A = ∠C ⇒ cos A = cos C = 0,8

Рассмотрим треугольник ACH. Он прямоугольный (∠H = 90°), причем AC = 5 и cos A = 0,8. По определению, cos A = AH : AC = AH : 5. Получаем пропорцию:

AH : 5 = 8 : 10;
10 · AH = 5 · 8;
AH = 40 : 10 = 4.

Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника ACH:

AH ² + CH ² = AC ²;
4² + x² = 5²;
x² = 25 − 16 = 9;
x = 3.

Задача. В прямоугольном треугольнике ABC ∠B = 90°, AB = 32, AC = 40. Найдите синус угла CAD.

Поскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A: cos A = AB : AC = 32 : 40 = 0,8. Это был факт из первой группы.

Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы):

sin ²A + cos ²A = 1;
sin ²A = 1 − cos ²A = 1 − 0,8² = 0,36;
sin A = 0,6.

При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Из первой группы фактов имеем:

∠BAC + ∠CAD = 180°;
sin CAD = sin BAC = sin A = 0,6.

Задача. В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A.

Треугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 · AB = 0,5 · 8 = 4. Это факт из третьей группы.

Теперь рассмотрим треугольник ACH: в нем ∠AHC = 90°. Можно выразить тангенс: tg A = CH : AH. Но AH = 4, поэтому остается найти сторону CH, которую обозначим CH = x. По теореме Пифагора (факт из группы 2) имеем:

AH ² + CH ² = AC ²;
4² + x² = 5²;
x² = 25 − 16 = 9;
x = 3.

Теперь все готово, чтобы найти тангенс: tg A = CH : AH = 3 : 4 = 0,75.

Задача. В треугольнике ABC AC = BC, AB = 6, cos A = 3/5. Найдите высоту AH.

Обозначим искомую высоту AH = x. Снова треугольник ABC — равнобедренный, поэтому заметим, что ∠A = ∠B, следовательно, cos B = cos A = 3/5. Это факт из третьей группы.

Рассмотрим треугольник ABH. По условию, он прямоугольный (∠AHB = 90°), причем известна гипотенуза AB = 6 и cos B = 3/5. Но cos B = BH : AB = BH : 6 = 3/5. Получили пропорцию:

BH : 6 = 3 : 5;
5 · BH = 6 · 3;
BH = 18/5 = 3,6.

Теперь найдем AH = x по теореме Пифагора для треугольника ABH:

AH ² + BH ² = AB ²;
x² + 3,6² = 6²;
x² = 36 − 12,96 = 23,04;
x = 4,8.

Дополнительные соображения

Бывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах.

Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач.

Задача. В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что ∠A = 23°. Найдите ∠MCH.

Заметим, что медиана CM проведена к гипотенузе AB, поэтому M — центр описанной окружности, т.е. AM = BM = CM = R, где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и ∠ACM = ∠CAM = 23°.

Теперь рассмотрим треугольники ABC и CBH. По условию, оба треугольника прямоугольные. Кроме того, ∠B — общий. Следовательно, треугольники ABC и CBH подобны по двум углам.

В подобных треугольника соответствующие элементы пропорциональны. В частности:

BCH = BAC = 23°

Наконец, рассмотрим ∠C. Он прямой, и, кроме того, ∠C = ∠ACM + ∠MCH + ∠BCH. В этом равенстве ∠MCH — искомый, а ∠ACM и ∠BCH известны и равны 23°. Имеем:

90° = 23° + MCH + 23°;
MCH = 90° − 23° − 23° = 44°.

Задача. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Обозначим стороны прямоугольника: AB = x, BC = y. Выразим периметр:

P_ABCD = 2 · (AB + BC) = 2 · (x + y) = 34;
x + y = 17.

Аналогично выразим площадь: S_ABCD = AB · BC = x · y = 60.

Теперь рассмотрим треугольник ABC. Он прямоугольный, поэтому запишем теорему Пифагора:

AB ² + BC ² = AC²;
AC ² = x² + y².

Заметим, что из формулы квадрата разности следует равенство:

x² + y² = (x + y)² − 2 · x · y = 17² − 2 · 60 = 289 − 120 = 169

Итак, AC ² = 169, откуда AC = 13.

Смотрите также:

1. Задача B8: отрезки и углы в треугольниках
2. Центральные и вписанные углы в задании 6
3. Дополнительные соображения
4. Тест к уроку «Площади многоугольников на координатной сетке» (средний)
5. Сложные логарифмические неравенства
6. Задача B5: площадь фигуры без клеток

www.berdov.com

No related posts.