Как найти точки пересечения графиков функций – Как найти точки пересечения графиков функций

Как найти координаты точек пересечения графика функции: примеры решения

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Пример 1

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

$5x = x- 2$;

$4x = -2$;

$x=-\frac{1}{2}$

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-\frac{1}{2} – 2 = — 2\frac12$.

Точка пересечения будет $(-\frac{1}{2};- 2\frac12)$.

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Пример 2

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Составим систему:

$\begin{cases} y=2x^2-2x-1 \\ y= x + 1 \\ \end{cases}$

Второе уравнение проще первого, поэтому подставим его вместо $y$:

$x+1 = 2x^2 – 2x-1$;

$2x^2 – 3x – 2 = 0$.

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

$x_1=2; x_2 = -\frac{1}{2}$

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — \frac{1}{2} = \frac{1}{2}$.

Точки пересечения будут $(2;3)$ и $(-\frac{1}{2}; \frac{1}{2})$.

Третий способ

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Пример 3

Найдите точку пересечения графиков на общем рисунке.

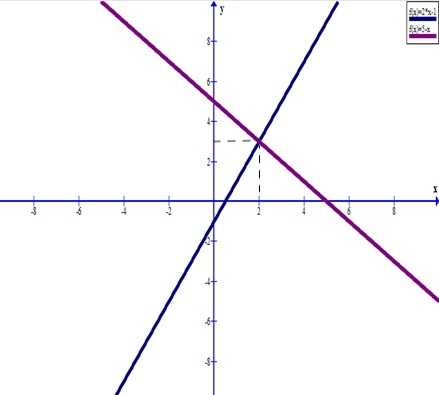
Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

spravochnick.ru

Точки пересечения графиков в Excel

Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.

Строим графики с точками пересечений

Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.



Находим точку пересечения графиков в Excel

В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ. Найти общие значения в рядах данных для указанных функций.

В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).

Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

Получается такой рисунок:

Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

exceltable.com

Точки пересечения графика осями | Алгебра

Как найти точки пересечения графика функции с осями координат?

С осью абсцисс график функции может иметь любое количество общих точек (или ни одной). С осью ординат — не более одной (так как по определению функции каждому значению аргумента ставится в соответствие единственное значение функции).

Чтобы найти точки пересечения графика функции y=f(x) с осью абсцисс, надо решить уравнение f(x)=0 (то есть найти нули функции).

Чтобы найти точку пересечения графика функции с осью ординат, надо в формулу функции вместо каждого x подставить нуль, то есть найти значение функции при x=0: y=f(0).

Примеры.

1) Найти точки пересечения графика линейной функции y=kx+b с осями координат.

Решение:

В точке пересечения графика функции с осью Ox y=0:

kx+b=0, => x= -b/k. Таким образом, линейная функция пересекает ось абсцисс в точке (-b/k; 0).

В точке пересечения с осью Oy x=0:

y=k∙0+b=b. Отсюда, точка пересечения графика линейной функции с осью ординат — (0; b).

Например, найдём точки пересечения с осями координат графика линейной функции y=2x-10.

2x-10=0; x=5. С Ox график пересекается в точке (5; 0).

y=2∙0-10=-10. С Oy график пересекается в точке (0; -10).

2) Найти точки пересечения графика квадратичной функции y=ax²+bx+c с осями координат.

Решение:

В точке пересечения графика с осью абсцисс y=0. Значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью Ox, надо решить квадратное уравнение ax²+bx+c=0.

В зависимости от дискриминанта, парабола  пресекает ось абсцисс в одной точке или в двух точках либо не пересекает Ox.

В точке пересечения графика с осью Oy x=0.

y=a∙0²+b∙0+c=с. Следовательно, (0; с) — точка, в которой парабола пересекает ось ординат.

Например, найдём точки пересечения с осями координат графика функции y=x²-9x+20.

x²-9x+20=0

x1=4; x2=5. График пересекает ось абсцисс в точках (4; 0) и (5; 0).

y=0²-9∙0+20=20. Отсюда, (0; 20) — точка пересечения параболы y=x²-9x+20 с осью ординат.

www.algebraclass.ru

Найти точку пересечения графиков линейных функций — Науколандия

Если даны две линейные функции вида y = kx + m, то их графики (прямые) могут вообще не пересекаться, если параллельны друг другу. Во всех остальных случаях они будут пересекаться в одной точке.

Графики двух линейных функций параллельны друг другу, если имеют одинаковый угловой коэффициент (k) и различное значение m (если и m будет одно и то же, то это будет одна и та же функция). Действительно, ведь k определяет угол между осью x и прямой, а значит у графиков линейных функций, отличающихся лишь значением m, угол с осью абсцисс один и тот же, и, следовательно, графики будут параллельны. Пример: графики функций y = 2x – 3 и y = 2x + 1 параллельны и, следовательно, не пересекаются.

Если две линейные функции имеют различные k, но одинаковые m, то они пересекаются в точке (0; m). Действительно, если x = 0, то независимо от того, чему равен k, y становится равен m. Пример: y = –1.3x + 8 и y = 2.1x + 8.

Если две линейные функции имеют различные и k и m, то они пересекаются в какой-то точке, которую можно найти графическим способом. Сначала на координатной плоскости чертится одна прямая, затем вторая, далее находится их точка пересечения. Для того, чтобы начертить прямую линейной функции, надо найти две точки, которые принадлежат прямой. Для этого берут два различных x и вычисляют y. Это нужно сделать для каждой из двух функция. При этом не обязательно брать одинаковые x. Следует брать те, вычислять с которыми удобнее, или их будет проще нанести на координатную плоскость.

Также можно решить уравнение. Ведь точка пересечения — это та точка, где у обоих функций одинаковы x и y. Если y одинаковы, то правая часть одного уравнения равна правой части другой. То есть их можно приравнять и найти значение x, при котором это равенство верно. А далее, имея x, можно вычислить y, через любую из функций. Пример:
Даны y = 4x – 5 и y = –2x + 1
4x – 5 = –2x + 1
4x + 2x = 1 + 5
6x = 6
x = 1
y = 4 * 1 – 5 = –1 или y = –2 * 1 + 1 = –1

Таким образом точка пересечения (1; –1).

scienceland.info

Как вычислить координаты точек пересечения графиков функций

Построить кривую, заданную уравнением в полярной системе координат. Есть следующее уравнение r = 2sin4? r- это у меня «ро» f- это «фи» К сожалению,не нашла в своих лекциях подробного описания как это сделать. Полазив по интернету поняла только,что это будет многолистник или.

Как найти координаты точки пересечения графиков функций?

Случай двух линейных функций

Рассмотрим две линейные функции и. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения и и найти и. Затем повторить тоже самое и с функцией. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда. Иначе, в случае функции параллельны друг другу, так как — это коэффициент угла наклона. Если, но, тогда точкой пересечения будет. Это правило желательно запомнить для ускоренного решения задач.

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций и. Замечаем, что, поэтому существует одна точка пересечения. Найдём её с помощью уравнения :

Переносим слагаемые с в левую часть, а остальные в правую:

Получили абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим в любое из уравнений хоть в, либо в :

Итак, — является точкой пересечения графиков двух линейных функций.

Случай двух нелинейных функций

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни:

Разносим по разным сторонам уравнения члены с и без него:

Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты. Подставляем в любое из двух уравнений условия задачи. Например:

— точка пересечения графиков функций

В статье: «Как найти координаты точки пересечения графиков функций?» было рассказано о случае двух линеных функций, и разобран случай с нелинейными. Были приведены способы, методы решения, а так же практические примеры.

Как вычислить координаты точек пересечения графиков функций

Науколандия

Статьи по естественным наукам и математике

Найти точку пересечения графиков линейных функций

Если даны две линейные функции вида y = kx + m, то их графики (прямые) могут вообще не пересекаться, если параллельны друг другу. Во всех остальных случаях они будут пересекаться в одной точке.

Графики двух линейных функций параллельны друг другу, если имеют одинаковый угловой коэффициент ( k ) и различное значение m (если и m будет одно и то же, то это будет одна и та же функция). Действительно, ведь k определяет угол между осью x и прямой, а значит у графиков линейных функций, отличающихся лишь значением m, угол с осью абсцисс один и тот же, и, следовательно, графики будут параллельны. Пример: графики функций y = 2x – 3 и y = 2x + 1 параллельны и, следовательно, не пересекаются.

Если две линейные функции имеют различные k, но одинаковые m, то они пересекаются в точке (0; m ). Действительно, если x = 0, то независимо от того, чему равен k, y становится равен m. Пример: y = –1.3 x + 8 и y = 2.1 x + 8.

Если две линейные функции имеют различные и k и m, то они пересекаются в какой-то точке, которую можно найти графическим способом. Сначала на координатной плоскости чертится одна прямая, затем вторая, далее находится их точка пересечения. Для того, чтобы начертить прямую линейной функции, надо найти две точки, которые принадлежат прямой. Для этого берут два различных x и вычисляют y. Это нужно сделать для каждой из двух функция. При этом не обязательно брать одинаковые x. Следует брать те, вычислять с которыми удобнее, или их будет проще нанести на координатную плоскость.

Также можно решить уравнение. Ведь точка пересечения — это та точка, где у обоих функций одинаковы x и y. Если y одинаковы, то правая часть одного уравнения равна правой части другой. То есть их можно приравнять и найти значение x, при котором это равенство верно. А далее, имея x, можно вычислить y, через любую из функций. Пример:

Как вычислить координаты точек пересечения графиков функций

Науколандия

Статьи по естественным наукам и математике

Найти точку пересечения графиков линейных функций

Если даны две линейные функции вида y = kx + m, то их графики (прямые) могут вообще не пересекаться, если параллельны друг другу. Во всех остальных случаях они будут пересекаться в одной точке.

Графики двух линейных функций параллельны друг другу, если имеют одинаковый угловой коэффициент ( k ) и различное значение m (если и m будет одно и то же, то это будет одна и та же функция). Действительно, ведь k определяет угол между осью x и прямой, а значит у графиков линейных функций, отличающихся лишь значением m, угол с осью абсцисс один и тот же, и, следовательно, графики будут параллельны. Пример: графики функций y = 2x – 3 и y = 2x + 1 параллельны и, следовательно, не пересекаются.

Если две линейные функции имеют различные k, но одинаковые m, то они пересекаются в точке (0; m ). Действительно, если x = 0, то независимо от того, чему равен k, y становится равен m. Пример: y = –1.3 x + 8 и y = 2.1 x + 8.

Если две линейные функции имеют различные и k и m, то они пересекаются в какой-то точке, которую можно найти графическим способом. Сначала на координатной плоскости чертится одна прямая, затем вторая, далее находится их точка пересечения. Для того, чтобы начертить прямую линейной функции, надо найти две точки, которые принадлежат прямой. Для этого берут два различных x и вычисляют y. Это нужно сделать для каждой из двух функция. При этом не обязательно брать одинаковые x. Следует брать те, вычислять с которыми удобнее, или их будет проще нанести на координатную плоскость.

Также можно решить уравнение. Ведь точка пересечения — это та точка, где у обоих функций одинаковы x и y. Если y одинаковы, то правая часть одного уравнения равна правой части другой. То есть их можно приравнять и найти значение x, при котором это равенство верно. А далее, имея x, можно вычислить y, через любую из функций. Пример:

poiskvstavropole.ru

Как не выполняя построения, найти координаты точки пересечения графиков линейных функций?

<a rel=»nofollow» href=»http://v.ht/Nwsm?0=167238″ target=»_blank»>Георгий посмотри здесь, страница 834</a>

Реши систему уравнений из этих 2-х функций. х — будет коррдината по оси ох, а у по оси оу

Линейные функции это система линейных уравнений, корни системы — точки пересечения графиков. Жаль, что ты об этом раньше не догадывался.

Поясню на примере. Дупоустим даны 2 линейные функции: y=2х+1 и y=х+4 Что бы без построения найти точки их пересечения, надо приравнять эти графики: 2х+1=х+4 x=3 В этой точке значение у=7. Значит, точка с координатами (3,7) будет являтся общей точкой для графиков у=2х+1 и у=х+4 (или иначе говоря точкой пересечения этих двух графиков).

Смотрите: у них есть точка пересечения, значит они пересекаются. Вам даны 2 функции. Они одинаковы (точнее их результаты). Убираете из функций «y» (игрек), пишите одну функцию (любую, из двух), затем = (равно), и другую функцию, тоже без игрека. Получилось уравнение, в левую часть неизвестные с числами, в другую числа (надеюсь такие уравнения вы можете решать)). Вышел ответ (чему равен икс). Теперь находим игрек. Пишем любую функцию из двух (с игреком), но вместо икса подставляем число, которое вышло в уравнение. И выходит новое уравнение, только надо найти игрек. Решаем уравнение. Первый ответ (где икс находили) записываем (это одна координата), а второй ответ другая координата. Пример: y=3х+2 и y=4+х Выйдет уравнение: 3х+2=4+х 3х-х=4-2 2х=2 х=1 Это одна координата, берем любую функцию из двух, и подставляем х. y=4+1 y=5 Выходит: (1;5) (х; y) Это их точки пересечения)

touch.otvet.mail.ru

Как найти точку пересечения графиков функций в excel

РЕШЕНИЕ: ||| Вариант решения 1. ||| 1) Высота, проведенная из вершины прямого угла, делит треугольник на два подобных треугольника между собой и подобных данному. Из подобия треугольников АВС и НСВ следует: В=НСА. 2) Медиана, проведенная из вершины прямого угла, равна половине.

Как найти точку пересечения графиков функций в excel

Этот файлик может пригодиться для оформления задач поиска точки пересечения линейных графиков, построенных по экспериментальным данным.

Графики выстраиваются по точкам эксперимента. Рассчитываются коэффициенты А и В функций, рассчитывается точка пересечения и отображается на графике. Теперь при изменении значений точка корректно отображается на графике.

Нашел у Павлова пример с поиском многоточечных пересечений. Совсем немножко добавил от себя.

Может тоже пригодиться для оформления лабораторных.

Как найти точку пересечения графиков функций в excel

Точка пересечения графиков в Excel

Изучим способы поиска Точек пересечения двух графиков и графика с осью координат, а также варианты их отображения в Excel.

Если графики заданы какими-либо алгебраическими функциями, то точное решение оптимальнее искать математически, приравняв функции друг к другу.

В данной статье мы разберем как Найти точки пересечения для линейного графика, в котором линии имеют одинаковые координаты по оси абсцисс (горизонтальная) и различные координаты по оси ординат (вертикальная).

Как мы помним из школьного курса математики, через две любые несовпадающие точки можно провести прямую и только одну.

Поэтому зная их координаты мы можем составить уравнение прямой. Таким образом решая систему уравнений, состоящую из уравнений двух прямых, мы можем найти место пересечения:

Пересечение двух графиков

Предположим, что у нас имеется таблица с координатами двух линий:

Построим на основе этих данных точечную диаграмму. Выделяем диапазон данных A1:K3 и на панели вкладок выбираем Вставка -> Диаграмма -> Точечная -> Точечная с прямыми отрезками.

В итоге получаем точечную диаграмму с двумя линиями:

Как видим на диаграмме линии пересеклись в 5 местах. В общем случае подобных точек может быть сколь угодно много, поэтому вручную находить каждую из них представляется достаточно трудоемким процессом.

Чтобы упростить работу и автоматизировать расчет воспользуемся средствами Visual Basic.

Переходим в редактор VBA (в панели вкладок выбираем Разработчик -> Visual Basic или воспользуемся сочетанием клавиш Alt + F11), создаем модуль и записываем в него макрос (напротив каждой строчки даются пояснения к коду):

Переходим обратно в Excel, нажимаем на диаграмму (для активации) и запускаем макрос:

Осталось только добавить на свое усмотрение некоторые детали для улучшения визуализации и получаем итоговый вариант:

Для удобства и экономии времени, определение вида и цвета отображаемой точки, формата подписи данных и прочих настроек, можно также добавить в код макроса.

Пересечение графика с осями координат

Аналогичное решение можно применить и в случае поиска мест пересечения графика с осью абсцисс.

Для этого в качестве координат одной из линий установим нулевые значения:

Применяем к графику макрос и получаем:

Удачи вам и до скорых встреч на страницах блога Tutorexcel. ru!

Поделиться с друзьями:

Поиск по сайту:

Похожие статьи:

Комментарии (6)

Очень здорово, вопрос один. А если график 3 или более функций и можно ли как то значения автоматом в таблицу занести

В случае если на графике 3 линии, то в макросе нужно будет дополнительно прописать проверки на пересечение каждой пары линий (т. е. первой и второй, первой и третьей, второй и третьей).

Координаты точек пересечений хранятся в массивах ArrayT1 (ось X) и ArrayT2 (ось Y), соответственно чтобы занести эти координаты в таблицу, мы должны приравнять значения ячеек таблицы к элементам массивов.

Спасибо за ответ, только если честно я конструктор, и незнаком с программированием, скажите возможно ли связаться с Вами для решения моей проблемы?

Здравствуйте, помогите пожалуйста, мне нужно найти пересечение двух графиков, точки взяты произвольно, формул никаких нет. Я пробовала вставить вашу программу, но выдает ошибку

Анастасия, в данной статье разбирается случай, когда графики имеют одинаковые координаты по горизонтальной оси, и разные координаты по вертикальной.

В приведенном примере, в случае с красной линией, это условие не выполняется, вероятно по этой причине возникает ошибка.

Добавить комментарий Отменить ответ

Даты и время (6) Дашборды (2) Диаграммы (13) Диапазоны (5) Книги и листы (12) Макросы/VBA (9) Математика (13) Основы (4) Приемы (10) Сводные таблицы (1) Текст (13) Функции (17)

Свежие записи

Содержание

Читайте ранее:

Обратная матрица в Excel

Подробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР.

Как найти точку пересечения графиков функций в excel

Точки пересечения графиков — MS Excel

Надо найти точки пересечения их. я сделал, но они почему то не пересекаются, может кто подсказать что я делал не так? сейчас скину формулу из ячеек

Как в графике отобразить точки пересечения? А также также рядом указать сумму точки x+y как в примере. То есть пример точки 31=30+1 или.

Доброго времени суток! Являюсь полным нубом относительно Excel. Задача такая: Построить графики двух уравнений и найти их точки.

Здравствуйте! Помогите, пожалуйста, правильно построить графики в Excel. Вот на этом рисунке данные и графики, которые у меня получаются.

Доброго времени суток. Нужна ваша помощь. Есть некие графики сделанные мною в другой программе, но потребовалась все это построить в.

Помогите построить 5 графиков в одной сетке(поле) зависимость объема от обратного давления. Первый столбец — объем, он постоянен для всех.

Здравствуйте, у меня есть задания которые необходимо выполнить в excele. У меня не получается выполнить задание под буквой В в первом.

Да, дейстаительно они не пересекаются. Т.е. система уравнений не имеет корней.

А откуда третье уравнение?

Решение из маткад, у системы комплексные корни

Bantline везет же вам с задачами.

Krasme, я знаю, что не окружность. то я вчера где-то накосячил. Сам сегодня удивился

Здравствуйте, уважаемые Специалисты! Помогите пожалуйста с совмещением двух графиков различного типа(если это конечно возмож

poiskvstavropole.ru