1.7. Сложение и умножение понятий
В предыдущих параграфах мы говорили о логических операциях ограничения, обобщения, определения и деления понятий. Теперь рассмотрим еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой:
Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий
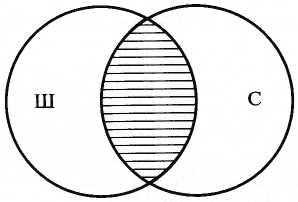
Выше были приведены примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями (о которых речь шла в § 1.3) результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже таблице штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.
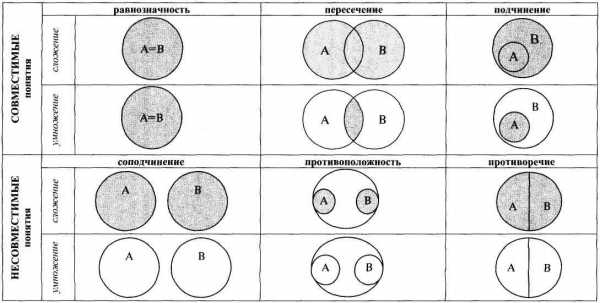
Как видим, результаты сложения и умножения понятий полностью совпадают только в случае равнозначности между ними, частично совпадают в пересечении и подчинении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.
Как правило, в естественном языке (то есть том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит В.И. Свинцов в уже упоминавшемся нами учебнике по логике (Свинцов В.И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным».
Однако следует отметить, что и в данном случае могут возникнуть недоразумения. Дело в том, что разделительный союз или может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз
studfiles.net
1.13. Как складываются и умножаются понятия?. Логика. Учебное пособие
1.13. Как складываются и умножаются понятия?
Помимо ограничения, обобщения, определения и деления понятий существуют еще две логические операции – сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий
Умножение понятий – это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением
, на схеме Эйлера изображается штриховкой (так же, как и результат сложения):Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Читатель без труда сможет определить их для всех случаев отношений между понятиями с помощью круговых схем. Так, если два понятия находятся в отношении подчинения, например, карась и рыба, то результатом их сложения является родовое понятие рыба (т. е. логической суммой понятий карась и рыба будет множество всех рыб):
Результатом умножения понятий карась и рыба, находящихся в отношении родовидового подчинения, будет видовое понятие карась (т. е. логическим произведением понятий карась и рыба является множество всех карасей):
Так же, если два понятия находятся в отношении соподчинения, например, береза и сосна, то результат их сложения – это два объема данных понятий (т. е. логической суммой понятий береза и сосна будет как множество всех берез, так и множество всех сосен):
Результатом умножения соподчиненных понятий береза и сосна является нулевое понятие (т. е. логическое произведение понятий береза и сосна представляет собой пустое множество – не существует ни одной березы, которая могла бы быть сосной и наоборот):
Точно так же устанавливаются результаты сложения и умножения объемов двух понятий, которые находятся в отношениях равнозначности, противоположности и противоречия (см. 1.5.). Так, например, нетрудно догадаться, что если два понятия находятся в отношении равнозначности, то результат их сложения будет полностью совпадать с результатом их умножения (логическая сумма равнозначных понятий равна их логическому произведению). Так же понятно, что результатом умножения противоположных и противоречащих понятий является нулевое понятие и т. п.
Как правило, в естественном языке (т. е. том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.
Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит в своем учебнике по логике известный отечественный автор В. И. Свинцов (Логика. Элементарный курс для гуманитарных специальностей. М.: Скорина, 1998. С. 60–61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом:
Здесь следует отметить неоднозначность разделительного союза или, который может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, т. к. можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, т. к. если он родился в 1987 году, то – никак не в 1989 году и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить далее). Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В. И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являющийся показателем логического сложения, надо воспринимать в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.
В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны разночтения, которые нередко приводят к различным и существенным недоразумениям.
Поделитесь на страничкеСледующая глава >
fil.wikireading.ru
4.3. Сложение, умножение и вычитание понятий (точнее
Кроме ограничения, обобщения и деления, существуют и другие операции с объемами понятий, в результате которых образуются новые понятия. Речь идет об операциях, которые по аналогии с математическими называют сложением, умножением и вычитанием. Эти операции, как правило, называют операциями с множествами.
Сложение понятий — операция с объемами понятий, которая заключается в объединении двух или нескольких множеств, составляющих объемы соответствующих понятий, в одно множество.
Полученный результат является множеством, что составляет объем нового понятия, имя которого содержит имена исходных понятий, связанных союзом «или».
Результат сложения зависит от того, каковы исходные понятия — они совместимы или несовместимы, а если совместимы, то к какому виду совместимых понятий относятся — тождественных, перекрестных или до тех, что находятся в отношении подчинения.
Результат сложения несовместимых понятий равна сумме слагаемых. Скажем, взяв выходными понятие «злаковая растение» (обозначим объем этого понятия буквой а) и «бобовое растение» (объем которого — Ь) и добавив объемы этих понятий, получим новое понятие «злаковое или бобовое растение», объем которого будет равен а + Ь
Добавление совместимых понятий связано с определенными трудностями, которые легче преодолеть, приняв во внимание то, что слагаемые могут быть и недодатними числами. Так, добавив объемы понятий «студент» (а) и «спортсмен» (Ь), получим понятие «студент или спортсмен», объем которого будет меньше а + Ь, но больше или по крайней мере равным объему одного слагаемого, поскольку названные понятия являются перекрестными (схема 9).
Схема 9
Результатом сложения понятий, находящихся в отношении подчинения, понятие, объем которого равен объему соответствующего родового понятия. Так, понятие «житель села Городище или человек, который
совершила преступление X» равен объему понятия «житель села Городище», если известно, что преступник является жителем указанного села: а + Ь = а (схема 10).
Схема 10
Результатом добавления тождественных понятий является понятие с объемом, который равен объему одного из этих понятий (любого из них, поскольку они имеют одинаковый объем). Так, объем понятия «квадрат или прямоугольный ромб» равен объему понятия «квадрат» (или объема понятия «прямоугольный ромб»): а + Ь = а(а + Ь = Ь) (схема 11).
Схема 11
Умножение понятий — операция с понятиями, которая заключается в образовании нового понятия, объемом которого есть элементы, общие для всех исходных понятий.
Результатом умножения несовместимых понятий является понятие с мнимым объемом, т.е. нулевое. Так, умножив понятие «существительное» и «глагол», получим новое понятие, имя которого будет «существительное и глагол», а объем — пустое множество, поскольку нет таких слов, которые одновременно были бы и глаголами, и существительными.
Перемножив совместимые понятия, получим новое понятие, в объеме которого мыслятся реально существующие (или существовавшие) предметы.
В результате умножения двух перекрестных понятий получают новое понятие, объем которого будет уже от объема одного из исходных понятий. Так, перемножив понятия «водитель» и «футболист», получим новое понятие «водитель и футболист» или «водитель-футболист».
Объем нового понятия, получают при умножении понятий, находящихся в отношении подчинения, совпадает с объемом подчиненного понятия. Так, перемножив понятия «юрист» и «прокурор», получим понятие «юрист и прокурор», объем которого равен объему «прокурор», поскольку только прокуроры является одновременно и прокурорами и юристами.
Новое понятие, которое образуется при умножении тождественных понятий, совпадает по объему с любым исходным понятием. Так, перемножив понятия «представление» и «воссоздания в памяти облика предметов», получим понятие «представление и воссоздания в памяти облика предметов», объем которого равен как первому, так и второму исходным понятием (в одиночку). Ведь каждое представление и только представление, является воспроизведением в памяти внешности предметов.
Вычитание (возражения) понятий — операция с понятиями, с помощью которой путем отрицания понятия «а» образуют новое понятие «не-а», объем которого в сумме с объемом понятия «а» составляет множество той предметной сферы, которая мыслится нами.
Так, имея понятие «число натурального ряда», объемом которого охвачено всю соответствующую предметную сферу, и, мысленно выделив из него часть объема с помощью понятия «простое число», мы получим остаток (разницу) — «простое число». Именно поэтому операцию и называют вычитанием.
Иногда вычитанием называют и такую логическую операцию, в процессе которой «не-а» конкретизируется. Так, с исходным понятием «пора года» операцию вычитания можно осуществить двумя способами. Первый: «весна» — «невесна». Второй: «весна» — «лето», «осень», «зима».
Книга: ЛОГИКА ДЛЯ ЮРИСТОВ: ЛЕКЦИИ. / Правовой колледж ЛНУ им. Франко
СОДЕРЖАНИЕ
На предыдущую
lybs.ru
|
ТОП 10: |
В предыдущих параграфах мы говорили о логических операциях ограничения, обобщения, определения и деления понятий. Теперь рассмотрим еще две логические операции – сложение и умножение понятий. Сложение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник и спортсмен образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой,на схеме Эйлера изображается штриховкой:
Умножение понятий– это логическая операция объединения двух и большего количества понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник и спортсмен образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением,на схеме Эйлера изображается штриховкой (так же, как и результат сложения):
Выше были приведены примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения (школьник и спортсмен). В других случаях отношений между понятиями (о которых речь шла в § 1.3) результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже таблице штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.
Как видим, результаты сложения и умножения понятий полностью совпадают только в случае равнозначности между ними, частично совпадают в пересечении и подчинении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое. Как правило, в естественном языке (то есть том, на котором мы общаемся) результат сложения понятий выражается союзом или, а умножения – союзом и. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно. Относительно употребления союзов или и и в естественном языке в качестве выражения результатов логических операций сложения и умножения понятий удачный пример приводит В.И. Свинцов в уже упоминавшемся нами учебнике по логике (Свинцов В.И. Логика. Элементарный курс для гуманитарных специальностей. – М.: Скорина, 1998. – С. 60 – 61), отрывок из которого приводится ниже. «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным». Однако следует отметить, что и в данном случае могут возникнуть недоразумения. Дело в том, что разделительный союз или может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании: Можно изучать английский язык или немецкий союз или употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другое не исключает. В данном случае разделительный союз или очень близок к соединительному союзу и. С другой стороны, в высказывании: Он родился в 1987 году или в 1989 году союз или употребляется в строгом значении, так как если он родился в 1987 году, то – никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза или мы еще будем говорить в § 2.6, посвященном видам сложных суждений.) Если в рассмотренное выше правило пользования городским транспортом поставить союз или вместо союза и, как предлагает В.И. Свинцов, то получится следующее: «Безбилетный проезд или бесплатный провоз багажа наказываются штрафом». В данном случае союз или, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза или всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется.
Глава 2. СУЖДЕНИЕ
|
infopedia.su
С этим файлом связано 36 файл(ов). Среди них: Evolwhite.pdf, 28Md_POLOZhENIE.pdf, Demchenko_A_P__Ed__Advanced_Fluorescence_Reporters_in_Chemistry_, John_E_McMurry_Robert_C_Fay_-_Chemistry_6th_ed__-_2012.pdf, Demchenko_A_P__Ed__Advanced_Fluorescence_Reporters_in_Chemistry_, Bachmann_M_Thermodynamics_and_Statistical_Mechanics_of_Macromole, Programm_BPPC-2017.pdf, Chelpanov_G_I_-_Uchebnik_logiki.pdf, Gusev_D_A_Udivitelnaya_logika.pdf и ещё 26 файл(а). Показать все связанные файлы Либо школьник, либо спортсмен (Сложение и умножение понятий) Помимо рассмотренных нами логических операций ограничения, обобщения, определения и деления понятия, существуют еще две важные операции. Это сложение и умножение понятий. Сложение понятий – этологическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник Ш) и спортсмен (С) образуется новое понятие, в объем которого входят как все школьники, таки все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. Умножение понятий – этологическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, приумножении понятий школьник Ш) и спортсмен С) образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (рис. Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения школьники спортсмен. При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение, разумеется, будут иными. Результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично совпадают в пересечении и совершенно не совпадают в соподчинении, противоположности и ДА. Гусев. Удивительная логика» 31 противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие. В отношении подчинения результатом сложения является родовое понятие, а результатом умножения – видовое. Как правило, в естественном языке (томна котором мы общаемся) результат сложения понятий выражается союзом ИЛИ, а умножения – союзом ИВ результате сложения понятий школьники спортсмен образуется новое понятие, в объем которого входит любой человек, если он является ИЛИ школьником, ИЛИ спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является И школьником, И спортсменом одновременно. О возможных разночтениях при употреблении союзов ИЛИ и ИВ. И. Свинцов 4 пишет Что касается союзов ИЛИ и И, то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом Безбилетный проезди бесплатный провоз багажа наказываются штрафом Представим себе два подмножества, которые могут быть выделены во множестве пассажиров- нарушителей. Водно из них войдут пассажиры, не взявшие билеты, в другое не оплатившие провоз багажа. Если союз И рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (ноне какой-то один из них. Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза ИЛИ здесь следует признать предпочтительным». Однако следует отметить, что ив данном случае из-за неоднозначности разделительного союза ИЛИ могут возникнуть недоразумения. Дело в том, что этот союз может употребляться в нестрогом (неисключающем) значении ив строгом (исключающем. Например, в высказывании Можно изучать английский язык или немецкий союз ИЛИ употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другого не исключает. В данном случае разделительный союз ИЛИ очень близок к соединительному союзу И. С другой стороны, в высказывании Он родился в 1987 году или в 1989 году союз ИЛИ употребляется в строгом значении, так как если он родился в 1987 году, то никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза ИЛИ мы еще будем говорить далее.) Если в рассмотренное выше правило пользования городским транспортом поставить союз ИЛИ вместо союза И, как предлагает В. И. Свинцов, то получится следующее Безбилетный проездили бесплатный провоз багажа наказываются штрафом. В данном случае союз ИЛИ, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать ив строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проездили же только на тех, которые бесплатно провозят багаж Свинцов В. И. Логика. Элементарный курс для гуманитарных специальностей. – М Скорина, 1998. С. 60–61. ДА. Гусев. Удивительная логика» 32 Правда, в этом случае не совсем понятно, кто же наказывается штрафом те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера ив зависимости от ситуации. В силу всего сказанного надо отметить, что употребление союза ИЛИ всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны различного рода недоразумения. Поэтому нередко употребляется своеобразный союз-гибрид ИЛИ/И, указывающий на то, что союз ИЛИ используется в некоем тексте в его нестрогом значении. Таким образом, наиболее целесообразно сформулировать правило оплаты проезда в городском пассажирском транспорте следующим образом Безбилетный проезд или/и бесплатный провоз багажа наказываются штрафом. В данной, может быть, не совсем удобной, сточки зрения языка, формулировке всевозможные разночтения и недоразумения исключаются ДА. Гусев. Удивительная логика» 34 Параллельные прямые не пересекаются (Что такое суждение) Суждение (высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например Все сосны являются деревьями, Некоторые люди – это спортсмены, Ни один кит – не рыба, Некоторые животные не являются хищниками. Рассмотрим несколько важных свойств суждения, которые в тоже время отличают его от понятия. Любое суждение состоит из понятий, связанных между собой. Например, если связать понятия карасьи рыба, то могут получиться суждения Все караси являются рыбами, Некоторые рыбы являются карасями. Любое суждение выражается в форме предложения как мы помним, понятие выражается словом или словосочетанием. Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда что-либо утверждает или отрицает, в силу чего суждение выражается в форме повествовательного предложения. Тем не менее есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание И какой же русский не любит быстрой езды представляет собой риторическое вопросительное предложение (риторический вопрос, так как в нем в форме вопроса утверждается, что всякий русский любит быструю езду. В подобном вопросе заключено суждение. Тоже самое можно сказать о риторических восклицаниях. Например, в высказывании Попробуй найти черную кошку в темной комнате, если ее там нет в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос (например: Как тебя зовут) не выражает суждение, точно также, как не выражает его настоящее, а не риторическое восклицание (например Прощай, свободная стихия!). Чтобы лучше уяснить, что такое суждение, рассмотрим несколько примеров. • Неужели тыне знал, что Земля вращается вокруг Солнца? (Риторический вопрос – является суждением). • Прощай, немытая Россия Восклицание – суждением не является). • Кто написал философский трактат Критика чистого разума»? (Вопрос – суждением не является). • Логика появилась примерно в V в. дон. э. в Древней Греции. (Повествование – является суждением). • Первый президент Америки. Понятие – суждением не является). • Разворачивайтесь в марше Восклицание – суждением не является). • Мы все учились понемногу… (Повествование – является суждением). • Попробуй-ка двигаться со скоростью света Риторическое восклицание – является суждением). • Средняя школа № 469 г. Москвы. Понятие – суждением не является). • Как тебе только не стыдно Риторический вопрос – является суждением ДА. Гусев. Удивительная логика» 35 • Каким образом решается знаменитая задача о квадратуре круга? (Вопрос – суждением не является). • Общая теория относительности А. Эйнштейна. Понятие суждением не является). • Почему нельзя делить на ноль Вопрос – суждением не является). • Бескрайние просторы Вселенной. Понятие – суждением не является). • Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Повествование – является суждением. Любое суждение является истинным или ложным. Если суждение соответствует действительности, оно истинное, а если не соответствует ложное. Например, суждение Все розы – это цветы является истинным, а суждение Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета ложное и т. п. Но разве понятия Змей Горыныч, Кощей Бессмертный, вечный двигатель не ложные Нет, эти понятия являются нулевыми (пустыми, ноне истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает какой-либо объект, и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, а не к понятиям. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом. Как видим, суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части субъект, предикат, связка и квантор. Субъект (обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники. Предикат (обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении Все учебники являются книгами о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т. п. Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т. п. Рассмотрим суждение Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если в каком-то суждении отсутствует связка или квантор, то они все равно подразумеваются. Например, в суждении Тигры это хищники квантор отсутствует, но он подразумевается – это слово все. С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму. Например, если у суждения Все прямоугольники – это геометрические фигуры отбросить содержание и оставить форму то получится Все S есть Р. Логическая форма суждения Некоторые животные не являются млекопитающими есть Некоторые S не есть Р. Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие логические отношения равнозначности, пересечения, подчинения и несовместимости ДА. Гусев. Удивительная логика» 37 Отношение несовместимости означает что субъект и предикат суждения являются несовместимыми (соподчиненными) понятиями. В суждении Все планеты не являются звездами субъект планеты и предикат звезды находятся в отношении несовместимости, так как ни одна планета не может быть звездой, и ни одна звезда не может быть планетой (рис. В приведенных ниже суждениях субъект и предикат находятся в отношении несовме- стимости: Параллельные прямые не пересекаются (несовместимость). Учебники не могут быть развлекательными книгами (несовместимость). Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить, какое понятие данного суждения является субъектом, а какое предикатом. Для примера определим отношение между субъектом и предикатом в суждении Некоторые военнослужащие являются россиянами. Сначала находим субъект суждения, – это понятие военнослужащие, затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения ДА. Гусев. Удивительная логика» 38 (военнослужащий может быть россиянином и может им не быть; и россиянин может как быть, таки не быть военнослужащим). Следовательно, в указанном суждении субъект и предикат пересекаются. Точно также в суждении Все планеты – это небесные тела субъект и предикат находятся в отношении подчинения, а в суждении Ни один кит не является рыбой субъект и предикат несовместимы. Как правило, все суждения подразделяют натри вида: Атрибутивные суждения (от лат. attributum – неотъемлемый признак) – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение Все воробьи – это птицы – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта, ведь быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей). Надо отметить, что в атрибутивном суждении необязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении Некоторые птицы – это воробьи как видим, по сравнению свыше- приведенным примером, субъект и предикат поменялись местами) субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта. Экзистенциальные суждения (от лат. existentia – существование) – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение Вечных двигателей не бывает является экзистенциальным, так как его предикат не бывает свидетельствует о несуществовании субъекта (вернее – предмета, который обозначен субъектом). Релятивные суждения (от лат. relativus – относительный) – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение Москва основана раньше Санкт-Петербурга является релятивным, потому что его предикат основана раньше Санкт-Петербурга указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения. В мышлении и языке большую часть составляют атрибутивные суждения. Они встречаются чаще, чем экзистенциальные и релятивные. Кроме того, последние, в принципе, можно представить как атрибутивные. Вернемся к экзистенциальному суждению Вечных двигателей не бывает. Его предикат (не быть или не существовать) вполне можно рассматривать как атрибут субъекта (вечные двигатели, ведь не существовать – это действительно неотъемлемый признак вечных двигателей, следовательно, данное суждение возможно расценивать как атрибутивное. Теперь обратимся к релятивному суждению Москва основана раньше Санкт-Петербурга, предикат которого (быть основанным раньше Санкт- Петербурга) вполне можно рассматривать как атрибут субъекта (Москва), ведь быть старше Санкт-Петербурга (ранее основанным городом) это действительно неотъемлемый признак Москвы. Таким образом, это суждение также возможно охарактеризовать как атрибутивное ДА. Гусев. Удивительная логика» перейти в каталог файлов |
biologo.ru
Либо школьник, либо спортсмен (Сложение и умножение понятий) — КиберПедия
Помимо рассмотренных нами логических операций ограничения, обобщения, определения и деления понятия, существуют еще две важные операции. Это сложение и умножение понятий.
Сложение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой все элементы объемов исходных понятий. Например, при сложении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. 15).
Умножение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объемом, охватывающим собой только совпадающие элементы объемов исходных понятий. Например, при умножении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (рис. 16).
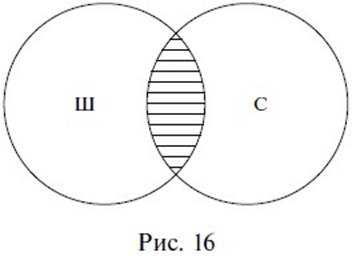
Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: школьник и спортсмен. При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. Результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично совпадают в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трех случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а результатом умножения – видовое.
Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом ИЛИ, а умножения – союзом И. В результате сложения понятий школьник и спортсмен образуется новое понятие, в объем которого входит любой человек, если он является ИЛИ школьником, ИЛИ спортсменом, а в результате умножения этих понятий в объем нового понятия входит любой человек, если он является И школьником, И спортсменом одновременно.
О возможных разночтениях при употреблении союзов ИЛИ и ИВ. И. Свинцов[4] пишет: «Что касается союзов ИЛИ и И, то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: Безбилетный проезд и бесплатный провоз багажа наказываются штрафом! Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билеты, в другое – не оплатившие провоз багажа.
Если союз И рассматривать как показатель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза ИЛИ здесь следует признать предпочтительным».
Однако следует отметить, что и в данном случае из-за неоднозначности разделительного союза ИЛИ могут возникнуть недоразумения. Дело в том, что этот союз может употребляться в нестрогом (неисключающем) значении и в строгом (исключающем). Например, в высказывании Можно изучать английский язык или немецкий союз ИЛИ употребляется в нестрогом значении, так как можно изучать и тот, и другой язык одновременно, одно другого не исключает. В данном случае разделительный союз ИЛИ очень близок к соединительному союзу И. С другой стороны, в высказывании Он родился в 1987 году или в 1989 году союз ИЛИ употребляется в строгом значении, так как если он родился в 1987 году, то никак не в 1989 году, и наоборот, два варианта здесь друг друга исключают. (О различных значениях союза ИЛИ мы еще будем говорить далее.)
Если в рассмотренное выше правило пользования городским транспортом поставить союз ИЛИ вместо союза И, как предлагает В. И. Свинцов, то получится следующее: Безбилетный проезд или бесплатный провоз багажа наказываются штрафом. В данном случае союз ИЛИ, являясь показателем логического сложения, должен восприниматься в его нестрогом, неисключающем значении. Но ведь в указанной фразе этот союз можно истолковать и в строгом, исключающем значении. Тогда получится, что штраф накладывается или только на тех пассажиров, которые не оплатили проезд, или же только на тех, которые бесплатно провозят багаж. Правда, в этом случае не совсем понятно, кто же наказывается штрафом – те или другие. Поразмыслив, можно прийти к выводу, что штрафу подвергаются то те, то другие – на усмотрение контролера и в зависимости от ситуации.
В силу всего сказанного надо отметить, что употребление союза ИЛИ всякий раз нуждается в комментарии относительно того, в строгом или нестрогом значении он используется. Понятно, что без этого комментария вполне возможны различного рода недоразумения. Поэтому нередко употребляется своеобразный союзгибрид ИЛИ/И, указывающий на то, что союз ИЛИ используется в некоем тексте в его нестрогом значении. Таким образом, наиболее целесообразно сформулировать правило оплаты проезда в городском пассажирском транспорте следующим образом: Безбилетный проезд или/и бесплатный провоз багажа наказываются штрафом. В данной, может быть, не совсем удобной, с точки зрения языка, формулировке все возможные разночтения и недоразумения исключаются.
Суждение
cyberpedia.su
Умножение / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
В математике существует знак для умножения — это точка посередине строки между числами, которые нужно перемножить.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
6 — первый множитель
4 — второй множитель
24 — произведение
Числа при умножении
Первый множитель
Второй множитель
Результат умножения, или Произведение
Чтение числовых выражений
6 • 4 = 24
Этот пример можно прочитать по-разному.
- 6 умножить на 4 равняется 24.
- 6 увеличить в 4 раза – получится 24.
- Первый множитель – 6, второй множитель – 4, произведение – 24.
- Произведение 6 и 4 равно 24.
Свойство умножения
3 • 4 = 12
4 • 3 = 12
Значит, 3 • 4 = 4 • 3
От перестановки мест сомножителей произведение не изменится.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.

Умножение на 0

8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10

8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения

8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
2 + 2 + 2 + 2 = 4 (к.)
Заменяем сложение умножением и получаем:
2 • 4 = 8 (к.)
Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Умножение на двузначное и трёхзначное число
Правило встречается в следующих упражнениях:
2 класс
Страница 65. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы
Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 95, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 44, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 50, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 51, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 64, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 37, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 71, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 21, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
5 класс
Упражнение 36, Мерзляк, Полонский, Якир, Учебник
© 2019 — budu5.com, Буду отличником!
budu5.com
