2.2 Законы логики
Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:
–закон тождества.
–закон исключенного третьего
–закон противоречия
–дизъюнкция с нулем
–конъюнкция с нулем
–дизъюнкция с единицей
–конъюнкция с единицей
 –закон
двойного отрицания
–закон
двойного отрицания–коммутативность конъюнкции
–коммутативность дизъюнкции
–ассоциативность конъюнкции
–ассоциативность дизъюнкции
–дистрибутивность конъюнкции
–дистрибутивность дизъюнкции
–законы идемпотентности
; – законы поглощения
; – законы де Моргана
–закон, выражающий импликацию через дизъюнкцию
–закон контрапозиции
–законы, выражающие эквиваленцию через другие логические операции
Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.
2.3 Равносильные преобразования. Упрощение формул
Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей.
Пример
1: Если
в законе де Моргана
вместоХ подставить  ,
а вместоY подставить
,
а вместоY подставить 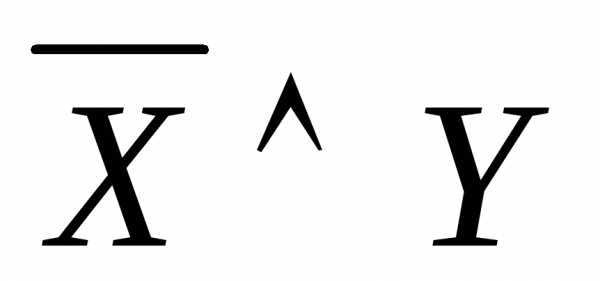 ,
то получим новую равносильность.
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
,
то получим новую равносильность.
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
Если
какую-нибудь формулу  ,
являющуюся частью формулыF,
заменить формулой
,
являющуюся частью формулыF,
заменить формулой  ,
равносильной формуле
,
равносильной формуле ,
то полученная формула окажется
равносильной формуле
,
то полученная формула окажется
равносильной формуле
Тогда для формулы из примера 2 можно провести следующие замены:
–закон двойного отрицания;
–закон де Моргана;
–закон двойного отрицания;
–закон ассоциативности;
–закон идемпотентности.
По свойству транзитивности отношения равносильности можем утверждать, что .
Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы.
Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная.
Пример 2.2: Упростим формулу .
.
На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания.
Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией.
Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями.
Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности.
 .
.Принцип двойственности утверждает следующее:
Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны.
studfiles.net
2.2 Законы логики
Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:
–закон тождества.
-
–закон исключенного третьего
–закон противоречия
 –закон
двойного отрицания
–закон
двойного отрицания–коммутативность конъюнкции
–коммутативность дизъюнкции
–ассоциативность конъюнкции
–ассоциативность дизъюнкции
–дистрибутивность конъюнкции
–дистрибутивность дизъюнкции
–законы идемпотентности
; – законы поглощения
; – законы де Моргана
–закон, выражающий импликацию через дизъюнкцию
–закон контрапозиции
–законы, выражающие эквиваленцию через другие логические операции
Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.
2.3. Упрощение формул.
Пример 1. Упростить формулу (АvВ) ^ (АvС) Решение.а) Раскроем скобки ( A vB ) ^ ( A v C ) ^ v ^C v B^A v B^C б) По закону идемпотентности A^A , следовательно, ^ v ^C v B^A v B^C v ^C v B^A v B^C в) В высказываниях А и А· C вынесем за скобки А и используя свойство Аv1 1, получим АvА^Сv ^ v ^C ( ^ v С v ^ v ^С v ^ v ^С
Аналогично пункту в) вынесем за скобки высказывание А. v^ v ^С ^ v ^С v ^С Таким образом, мы доказали закон дистрибутивности.
Пример 2. Упростить выражение v ^
Решение. v ^ v — поглощение
Пример 3. Упростить выражение ^ v ^ Решение. ^ v ^ v — склеивание
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям. Пример 4. Преобразовать формулу так, чтобы не было отрицаний сложных высказываний. Примечание!!!! знак «+» — дизъюнкция; знак «∙»-конъюнкция.
Решение.1. Воспользуемся формулой де Моргана, получим: 2. Для выражения применим еще раз формулу де Моргана, получим:
Любую формулу можно тождественно преобразовать так, что в ней не будут использованы: — знаки логического сложения; — знаки логического умножения. — знаки отрицания и логического умножения; — знаки отрицания и логического сложения.
Пример 5. Преобразовать формулу так, чтобы в ней не использовались знаки логического сложения. Решение. Воспользуемся законом двойного отрицания, а затем формулой де Моргана.
Пример 6. Преобразовать формулу так, чтобы в ней не использовались знаки логического умножения. Решение. Используя формулы де Моргана и закон двойного отрицания получим:
Эквиваленция выражается через конъюнкцию и импликацию:
Из (3) и (1) получаем: Y X (4) Эта равносильность выражает эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2) получаем равносильность: = (5), выражающую эквиваленцию через конъюнкцию и отрицание.
2.4. Равносильные преобразования. Упрощение формул
Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей.
Пример
1: Если
в законе де Моргана
вместоХ подставить  ,
а вместоY подставить
,
а вместоY подставить 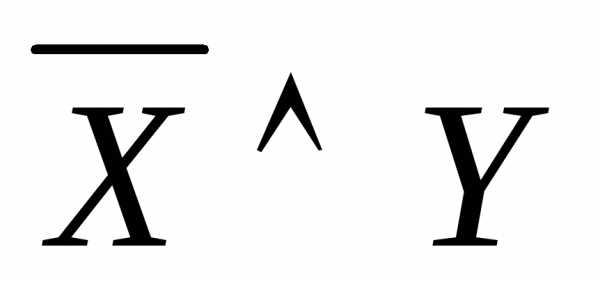 ,
то получим новую равносильность.
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
,
то получим новую равносильность.
Справедливость полученной равносильности
легко проверить с помощью таблицы
истинности.
Если
какую-нибудь формулу  ,
являющуюся частью формулыF,
заменить формулой
,
являющуюся частью формулыF,
заменить формулой  ,
равносильной формуле
,
равносильной формуле ,
то полученная формула окажется
равносильной формулеF.
,
то полученная формула окажется
равносильной формулеF.
Тогда для формулы из примера 2 можно провести следующие замены:
–закон двойного отрицания;
–закон де Моргана;
–закон двойного отрицания;
–закон ассоциативности;
–закон идемпотентности.
По свойству транзитивности отношения равносильности можем утверждать, что .
Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы.
Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная.
Пример 2: Упростим формулу .
.
На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания.
Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией.
Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями.
Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности.
Две формулы, не содержащие знаков импликации и эквиваленции, называются двойственными, если каждую из них можно получить из другой заменой знаков соответственно на.
Принцип двойственности утверждает следующее:
Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны.
Вопросы для контроля:
Равносильные предложения. Равносильные формулы.
Свойства отношения равносильности.
Равносильные преобразования.
Упрощение формул.
Применение равносильных преобразований.
Принцип двойственности.
studfiles.net
Упрощение логических выражений
Замечание 1
Логическую функцию можно записать с помощью логического выражения, а затем можно перейти к логической схеме. Упрощать логические выражения надо для того, чтобы получить как можно более простую (а значит, и более дешёвую) логическую схему. По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
Для упрощения логических выражений используют законы алгебры логики.
Какие-то преобразования похожи на преобразования формул в классической алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), а другие преобразования основаны на свойствах, которыми операции классической алгебры не обладают (использование распределительного закона для конъюнкции, законов поглощения, склеивания, правил де Моргана и др.).
Законы алгебры логики формулируются для базовых логических операций — “НЕ” – инверсия (отрицание), “И” – конъюнкция (логическое умножение) и “ИЛИ” – дизъюнкция (логическое сложение).
Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее дважды, то в итоге логическое значение не изменится.
Закон исключенного третьего гласит, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если $A=1$, то $\bar{A}=0$ (и наоборот), а, значит, конъюнкция этих величин всегда равно нулю, а дизъюнкция равна единице.
Операции с константами и закон повторения легко проверяются по таблицам истинности операций “И” и “ИЛИ”.
Переместительный и сочетательный законы выглядят так же, как и в математике. Почти всегда “работает” аналогия с классической алгеброй, нужно только помнить, что в логике $1 + 1 = 1$, а не $2$.
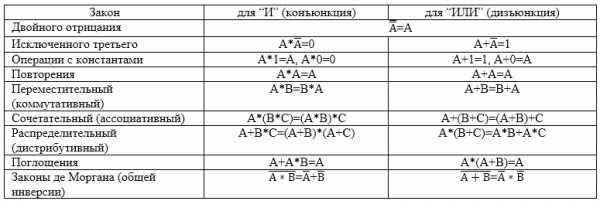
Рисунок 1.
Распределительный закон для дизъюнкции — это просто раскрытие скобок. А вот для конъюнкции выражение незнакомое, и в математике это равенство неверно. Доказательство начинаем с правой части. Раскроем скобки:
$(A+B) \cdot (A+C) = A \cdot A+A \cdot C+B \cdot A+B \cdot C$
Используем закон повторения
$A \cdot A = A$,
Далее $A \cdot A+C \cdot A = A+C \cdot A = A \cdot (1+C)=A \cdot 1 = A$
Аналогично
$A+A \cdot B = A \cdot (1+B) = A \cdot 1=A$, таким образом,
$(A+B) \cdot (A+C) = A+B \cdot C$
Равенство доказано.
Попутно был доказан закон поглощения для операции “И”.
Из распределительного закона следует полезная формула
$A+ \bar{A} \cdot B = (A+ \bar{A}) \cdot (A+B) = A+B$
Замечание 2
Правила, которые позволяют раскрывать инверсию сложных выражений, получили своё название в честь де Моргана, шотландского математика и логика. Важно следующее: “общее” отрицание не просто переходит на отдельные выражения, но и конъюнкция заменяется на дизъюнкцию (и наоборот). Доказать эти правила можно с помощью таблиц истинности.
Большинство законов и аксиом алгебры логики записаны парами. При внимательном изучении пар можно вывести принцип двойственности– если в тождестве произвести взаимные замены операций дизъюнкции и конъюнкции, а также элементы $0$ и $1$, в случае если они имеются, то получим тоже тождество. Такое свойство принято называть принципом двойственности.
Примеры упрощения логических выражений
$(A \cdot B) + (A \cdot \bar{B}) = A \cdot (B + B)= A \cdot 1 = A$
Рисунок 2.
здесь был использовано правило де Моргана для дизъюнкции и закон двойного отрицания, далее вынесли за скобку сомножитель $\bar{X}$, получили в скобках закон исключённого третьего и использовали операцию с константами.
Пример 1
Кто из учеников $A$, $B$, $C$ и $D$ играет, а кто не играет в шахматы, если известно следующее:
а) если $A$ или $B$ играет, то $C$ не играет;
б) если $B$ не играет, то играют $C$ и $D$;
в) $C$ играет
Решение. Определим следующие простые высказывания:
$A$ — «ученик $A$ играет в шахматы»;
$B$ — «ученик $B$ играет в шахматы»;
$C$ — «ученик $C$ играет в шахматы»;
$D$ — «ученик $D$ играет в шахматы».
С помощью простых высказываний запишем высказывания из условия:
а) ($A + B) → C$;
б) $B → C \cdot D$;
в) $C$.
Составим конъюнкцию записанных сложных высказываний:
$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$
Упростим эту формулу:
Рисунок 3.
Отсюда следует, что $A = 0$, $B = 1$, $C = 1$, $D = 1$.
Ответ: в шахматы играют ученики $B$, $C$ и $D$, а ученик $A$ не играет.
При упрощении логических выражений можно выполнять такую последовательность действий:
- Заменить все “небазовые” операции (эквивалентность, импликацию, исключающее ИЛИ и др.) на их выражения через базовые операции инверсию, конъюнкцию и дизъюнкцию.
- Раскрыть инверсии сложных выражений по правилам де Моргана таким образом, чтобы операции отрицания остались только у отдельных переменных.
- Затем упростить выражение, используя раскрытие скобок, вынесение общих множителей за скобки и другие законы алгебры логики.
Пример 2
Здесь последовательно использованы правило де Моргана, распределительный закон, закон исключенного третьего, переместительный закон, закон повторения, вновь переместительный закон и закон поглощения.
Рисунок 4.
Также можно использовать упрощение логических выражений для нахождения решений логического уравнения.
Пример 3
Требуется найти все решения уравнения
Рисунок 5.
Упрощаем выражение, заменяя импликацию по формуле $А → В = \bar{А} + В$, и получаем
Рисунок 6.
Используем правило де Моргана
$B + C + \bar{A} + \bar{A} \cdot \bar{C} + D = 0$
и закон поглощения
$B + C + \bar{A} + D = 0$
Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому
$A = 1$, $B = 0$, $C = 0$, $D = 0.$
Пример 4
Выполнить преобразование логической функции
Рисунок 7.
Применим последовательно следующие законы алгебры логики: правило де Моргана для конъюнкции, правило де Моргана для дизъюнкции, закон двойного отрицания, закон исключённого третьего, вынос общего множителя за скобки и операцию с константой
Рисунок 8.
spravochnick.ru
Упрощение логических выражений
Разделы: Информатика
Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим: X – логическое высказывание, – инверсия, & – конъюнкция, – дизъюнкция, – импликация, – эквиваленция.
Применение основных законов логики для упрощения логических выражений.
Представленные примеры демонстрируют основные приемы упрощения логических выражений.
Упростить логическое выражение:
1)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
2)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Применим закон склеивания
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
Таким образом,
4)
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию .
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Применим закон идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
Таким образом,
5)
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.
Воспользуемся законом идемпотенции.
Таким образом,
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания
Воспользуемся операцией переменной с ее инверсией.
Таким образом,
3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель , что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания
Таким образом,
6)
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Таким образом,
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
| X | Y | Z | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X | Y | Z | ||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | Y | Z | |||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
xn--i1abbnckbmcl9fb.xn--p1ai
6.2. Равносильные преобразования. Упрощение формул алгебры логики
Равносильные преобразования — это замена одной формулы другой, равносильной формулой. Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными.
Под упрощением формулы будем понимать равносильные преобразования, приводящие к формуле, содержащей меньшее числа переменных, чем исходная. Такие преобразования формул логики (логических функций) необходимы при синтезе, анализе, контроле дискретных устройств, а в последнее время — в системах искусственного интеллекта (логического вывода).
Мощным аппаратом для таких равносильных преобразований помимо рассмотренных законов алгебры логики являются так называемые основные формулы равносильных преобразований, полученные с использованием этих законов.
Пусть — некоторая переменная, причем символ~означает, что неважно, инверсная они или нет, т.е.Î{а,}; тогдаÎ{,а}.
Пустьf[(,),,…]- некоторая функция, зависящая как от переменной х и ее инверсии, так и от других переменных ,…. Под одноименностью будем понимать и соответствие знаков инверсии (т.е. одновременное наличие или отсутствие). Тогда, если переменнаянаходится в конъюнкции с некоторой функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименныепеременные заменяются на константу 1, а все переменные, инверсные одноименной, — на константу 0. Сама же переменная перед функцией остается без изменения. Таким образом,
×f[(,),,…]=×f[(1,0),,…].
Такая запись означает, что
х×f[(х,),,…]=х×f[(1,0),,…];
×f[(х,),,…]=×f[(0,1),,…].
Условно замену переменных на константу в функции fобозначаем стрелками.
Примеры:
f1(авс)=а(вÚа)(Úс)=а(вÚ1)(0Úа)=ас;
f2(авс)=(вÚа)(Úс)=(вÚ0)(1Úс)=×в.
Для облегчения запоминания рекомендуется мнемоническое правило. Представим формулу равносильного преобразования относительно конъюнкции из вида переключательной схемы, в которой конъюнкции и функцииfсоответствует их последовательное соединение. Такое соединение напоминает символ 1 (рис.6.1). Для простоты на рис.6.1 не указаны переменные функцииf. Это значит, что одноименные переменныевfзаменяются на константу 1. Соответственно переменныевfзаменяются на константу 0.
Рис.6.1. Иллюстрация мнемонического правила
для формулы равносильных преобразований
относительно конъюнкции
Рассмотрим формулу равносильных преобразований относительно дизъюнкции. Если переменнаялогически складывается с функцией, зависящей от данной переменной и от других переменных, то в этой функции все одноименныепеременные заменяются на константу 0, а все переменные, инверсные одноименной, заменяются на константу 1. Сама же переменная, логически складываемая с функцией, остается без изменения:
Úf[(,),,…]=Úf[(0,1),,…].
Это означает, что
хÚf[(х,),,…]=хÚf[(0,1),,…];
Úf[(х,),,…]=Úf[(1,0),,…].
Здесь также замена переменных на константы в функции fусловно показана стрелками.
Примеры:
f(авс)=аÚ(вÚа)(Úс)=аÚ=аÚв;
f(авс)=авÚ(Ú)(Ú).
В этой функции в явном виде нет отдельной переменной (), однако нетрудно заметить, что ав=(Ú). Поэтому обозначим ав, например, х:
f(асх)=хÚ(Ú)=хÚÚ.
Отсюда
f(авс)=авÚÚс=1×вÚÚс=ÚвÚс.
Имеется соответствующее мнемоническое правило. Представим формулу равносильного преобразования относительно дизъюнкции в виде релейной структуры, в которой дизъюнкции и функцииfсоответствует их параллельное соединение. Такое соединение напоминает символ 0 (рис.6.2). Это значит, что одноименные переменныевfзаменяются на константу 0. Соответственно переменныевfзаменяются на константу 1.
Рис.6.2. Иллюстрация мнемонического правила
для формулы равносильных преобразований
относительно дизъюнкции
Основные формулы равносильных преобразований можно доказать методом подстановки в них вместо переменной х ее возможных значений 0, 1 и сравнения правой и левой частей уравнения.
Докажем, например, формулу
хÚf[(х,),…]=хÚf[(0,1),…].
Пусть х=0; тогда левая часть формулы
0Úf[(0,1),…],
а правая
0Úf[(0,1),…],
т.е. равенство справедливо.
Пусть х=1; тогда левая часть формулы
1Úf[(1,0),…]-1,
а правая часть формулы
1Úf[(0,1),…]=1.
Равенство также справедливо, несмотря на отличия в функции f.
Аналогично доказывается формула для конъюнкции, например
х×f[(х,),…]=х×f[(1,0),…].
При х=0
0×f[(0,1),…]=0×f[(1,0),…]=0,
равенство справедливо, несмотря на отличия в функции f.
При х=1
1×f[(1,0),…]=1×f[(1,0),…],
равенство также справедливо.
Основные формулы равносильных преобразований имеют следствия, которые позволяют разложить логическую функцию по любой переменной.
Следствие 1:
f[(x,),,…]=x×f[(1,0),,…]Úf[(0,1),,…].
Следствие может быть доказано путем конъюнкции функции с тождественно истинной формулой хÚи последующего применения формул равносильного преобразования:
f(хÚ)=fхÚf=xf[(1,0),,…]Úf[(0,1),,…].
(Это известное разложение Шеннона).
Пример 1. Разложить логическую функцию по переменной в:
f(авсd)=аÚ(Úв)с[аÚd(Úв)]=
=в{а×0Ú(Ú1)×с[а×0Úd(Ú1)]}Ú{а×1Ú(Ú0)×с[а×1Úd(Ú0)]}=
=в{0Ú1×с[0Úd×1]}Ú{аÚ×с[аÚd]}=всdÚ(аÚсd).
Следствие 2:
f[(x,),,…]={xÚf[(0,1),,…]}
{Úf[(1,0),,…]}.
Доказательство:
f=fÚ0=fÚх×=(fÚх)(fÚ)=
={xÚf[(0,1),,…]}{Úf[(1,0),,…]}.
Пример 2: Разложим ту же функцию f(авсd) (пример 1) по переменной а с помощью следствия 2:
f(авсd)={аÚ0×Ú(1Úв)×с[0×Úd(1Úв)]}×
×{Ú1×Ú(0Úв)×с[1×Úd(0Úв)]}=
={аÚсd}{ÚÚвс[Údв]}=(аÚсd)(ÚÚсd).
Указанные следствия могут быть применены для преобразования структур релейно-контактных автоматов, когда необходимо привести их к какому-либо одному переключающему контакту или когда исходная структура не может быть сразу записана в аналитической форме.
studfiles.net
Равносильные преобразования
§ 3 Равносильные преобразования
Определение 1. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в них высказываний
(АВ).
Важнейшие равносильности можно разбить на три группы:
I. Основные равносильности:
1. законы
2. идемпотентности.
3.
4.
5.
6.
7. — закон противоречия.
8. — закон исключенного третьего.
9. — закон снятия двойного отрицания.
10. законы
11. поглощения.
II. Равносильности, выражающие одни логические операции через другие:
1.
2.
3. законы
4. де Моргана.
5.
6.
III. Равносильности, выражающие основные законы алгебры логики:
1. — коммутативность конъюнкции.
2. — коммутативность дизъюнкции.
3. — ассоциативность конъюнкции.
4. — ассоциативность дизъюнкции.
5. — дистрибутивность конъюнкции относительно дизъюнкции.
6. — дистрибутивность дизъюнкции относительно конъюнкции.
Используя равносильности группы I, II и III, можно часть формул алгебры логики или всю формулу заменить равносильной ей формулой. Такие преобразования называются равносильными. Равносильные преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Пример 1. Доказать равносильность .
Решение. Для доказательства равносильности подвергнем ее левую часть равносильным преобразованиям: .
Определение 2. Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.
Определение 3. Формула А называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных.
Пример 2. Доказать тождественную истинность формулы:
.
Решение. Подвергнем формулу А равносильным преобразованиям
.
Для проверки усвоения теоретического материала можно перейти к выполнению Проверочной работы №2.
logica2006.narod.ru
 Равносильные преобразования формул
 Используя равносильности I, II, III групп можно часть формулы или формулу заменить равносильной ей формулой. такие преобразования формул называются равносильными.
 Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
 Формула \(A\) считается проще равносильной ей формулы \(В\), если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентности и импликации заменяются операциями дизъюнкции и конъюнкции, а отрицание относятся к элементарным высказываниям. Рассмотрим ряд примеров.
 Пример 1. Доказать равносильность \(x \leftrightarrow y \equiv \bar{x} \wedge \bar{y} \vee x \wedge y\).
 Решение. Используя равносильности I, II, III групп запишем цепочку равносильных формул: $$x \leftrightarrow y \equiv ( x \rightarrow y) \wedge (y \rightarrow x) \equiv (\bar{x} \vee y) \wedge ( \bar{y} \vee x) \equiv$$
$$\equiv \bar{x} \wedge \bar{y} \vee \bar{x} \wedge x \vee y \wedge \bar{y} \vee y \wedge x \equiv$$
$$\equiv \bar{x} \wedge \bar{y} \vee 0 \vee 0 \vee y \wedge x \equiv \bar{x} \wedge \bar{y} \vee y \wedge x \equiv \bar{x} \wedge \bar{y} \vee x \wedge y.$$
 Пример 2. Упростить формулу \(( \overline{( x \vee y ) }\rightarrow x \vee y) \wedge y\).
 Решение. Запишем цепочку равносильных формул:
$$(\overline{\overline{( x \vee y )}} \vee x \vee y) \wedge y \equiv ( x \vee y \vee x \vee y) \wedge y \equiv ( x \vee y ) \wedge y \equiv y.$$
 Пример 3. Доказать тождественную истинность формулы:
$$( x \rightarrow y) \rightarrow ((y \rightarrow z) \rightarrow ( x \vee y \rightarrow z)).$$
 Решение. Запишем цепочку равносильных формул, используя равносильности:
$$( x \rightarrow y) \rightarrow ((y \rightarrow z) \rightarrow ( x \vee y \rightarrow z)) \equiv$$ $$\equiv \overline{( \bar{x} \vee y)} \vee (\overline{ \bar{y} \vee z } \vee \overline{ x \vee y} \vee z) \equiv \bar{\bar{x}} \wedge \bar{y} \vee \bar{\bar{y}} \wedge \bar{z} \vee \bar{x} \wedge \bar{y} \vee z \equiv$$ $$\equiv x \wedge \bar{y} \vee y \wedge \bar{z} \vee \bar{x} \wedge \bar{y} \vee z \equiv ( x \wedge \bar{y} \vee \bar{x} \wedge \bar{y} ) \vee ( y \wedge \bar{z} \vee z) \equiv$$ $$\equiv \bar{y} \wedge ( x \vee \bar{x} ) \vee ( y \vee z) \wedge ( \bar{z} \vee z ) \equiv \bar{y} \wedge 1 \vee ( y \vee z) \wedge 1 \equiv$$ $$\equiv \bar{y} \vee y \vee z \equiv ( \bar{y} \vee y ) \vee z \equiv 1 \vee z\equiv 1.$$
2012-11-03 • Просмотров [ 7604 ]
primat.org

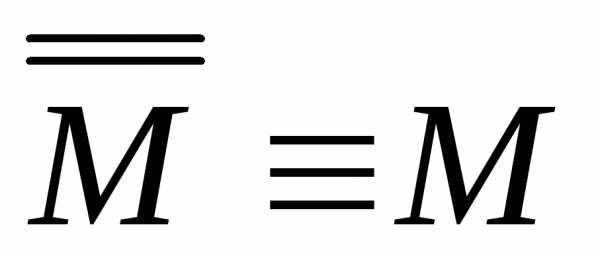 –закон
двойного отрицания
–закон
двойного отрицания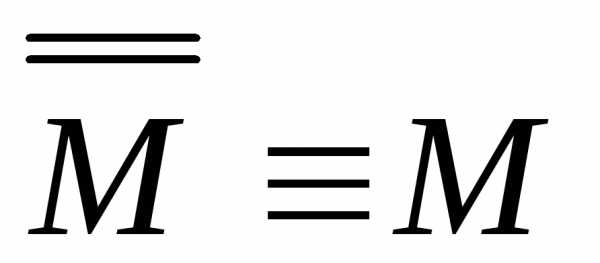 –закон
двойного отрицания
–закон
двойного отрицания