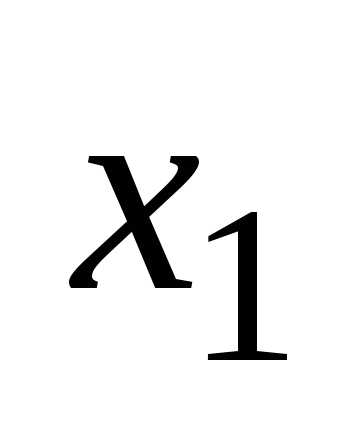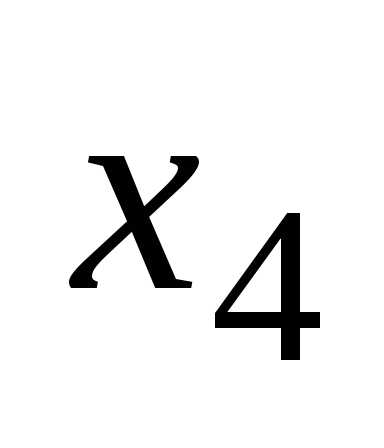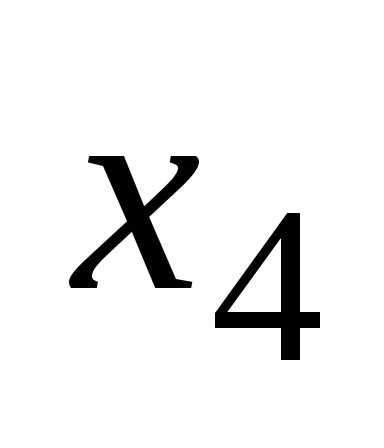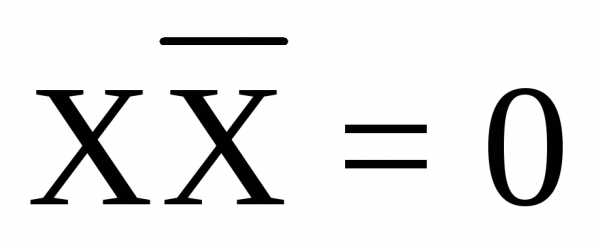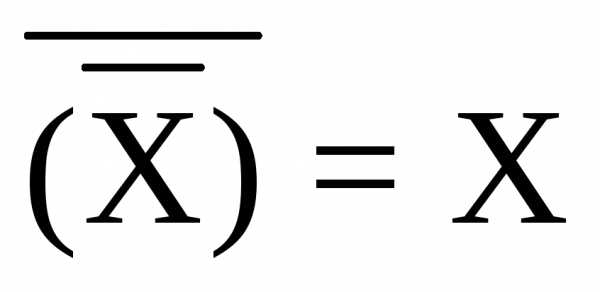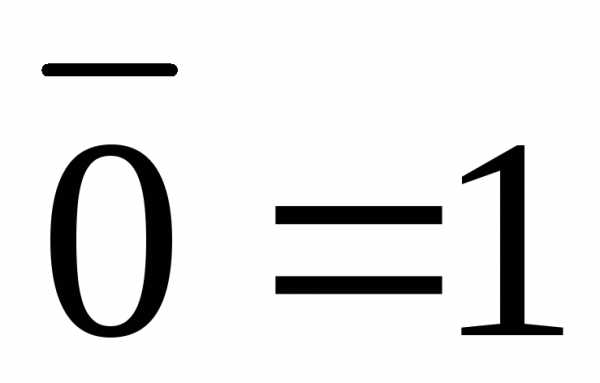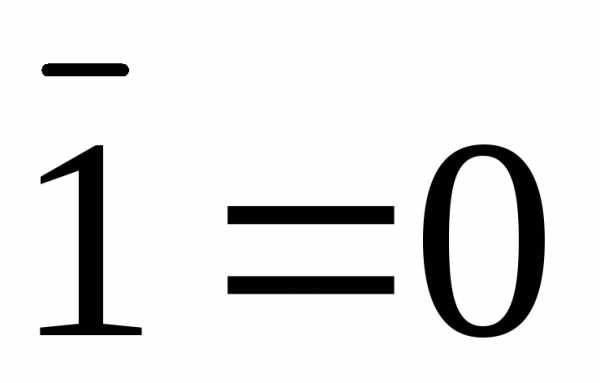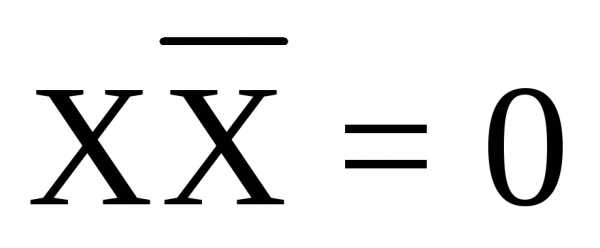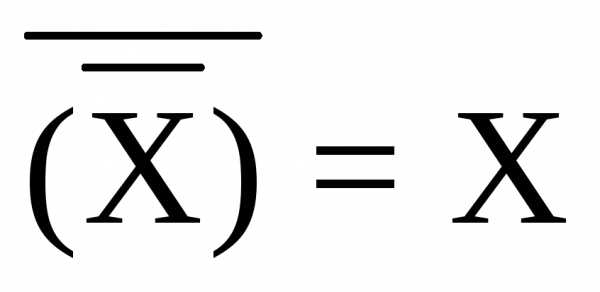Упрощение логических функций – Упрощение логических выражений — Sciterm

Глава 1. Упрощение и минимизация логических функций

1.1. Задача минимизации булевых функций

Как уже отмечалось, сложность логического выражения определяется числом букв, входящих в это выражение, т.е. числом переменных и их инверсий. В частности, выражение в форме логической суммы минтермов с минимальным числом литерал называют минимальной суммой, т.е. минимальной НДФ (МНДФ). Минимальным числом литерал должны отличаться и минимальные НКФ (МНКФ), т.е. минимальные произведения макстермов (конституэнтов нуля).

Очевидно, что сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок. К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно (диаграммы Вейча), метод Квайна — Мак-Класки и др. Эти методы наиболее пригодны для обычной технической практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В достаточно редких случаях, когда число переменных больше шести, обычно используют метод Квайна — Мак-Класки.

1.2. Метод минимизирующих карт.

В процессе минимизации той или иной логической функции, обычно, следует учитывать в каком базисе эффективнее всего можно будет реализовать ее минимальную форму при помощи электронных схем.

Как было отмечено выше, одним из способов представления ФАЛ от небольшого числа переменных (обычно не больше 5) являются диаграммы Карно или Вейча, которые строятся на развёртках многомерных кубов на плоскость. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется путём пометки кодов вершин, соответствующих наборам, на которых ФАЛ равна единице.

Прежде, чем продолжить дальнейшее рассмотрение, приведем некоторые определения, которые понадобятся при дальнейшем изложении [1].

Определение. Булева функция , называетсяимпликантой булевой функцией , если на каком-либо наборе переменных,где функцияравна единице, функциятакже равна единице.

Простой импликантой логической функции называется элементарная конъюнкция, которая сами является импликантой функции, но никакая ее часть не будет импликантой функции

.

Простые импликанты представляют собой самые короткие элементарные конъюнкции, входящие в данную логическую функцию.

Для того чтобы найти простые импликанты логической функции надо выписать все элементарные конъюнкции, входящие в данную функцию, и выбрать из их числа те, собственные части которых в эту функцию не входят.

Любая логическая функция равняется дизъюнкции всех своих простых импликант. Дизъюнкция всех простых импликант называется сокращенной дизъюнктивной нормальной формой логической функции, дизъюнкцию простых импликант, ни одну из которых исключить нельзя, называется тупиковой НДФ заданной функции. Некоторые булевы функции имеют несколько тупиковых форм, тогда та тупиковая форма, которая содержит наименьшее количество букв, будет минимальной.

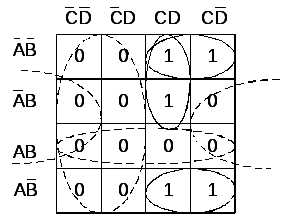
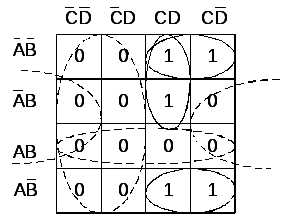
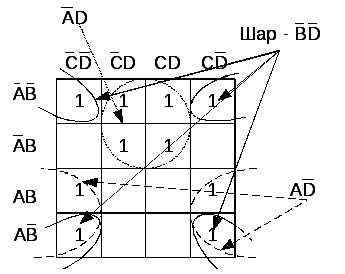
В методе минимизирующих карт в заданной функции, представленной в СНДФ, отыскиваются все соседние слагаемые и производится их склеивание. Два слагаемых функции, представленной в СНДФ, или вообще два любых терма, отличающихся только одной переменной (в одном она имеет отрицание, а в другом — нет), называются соседними.

Пример 1.1. Рассмотрим использование карт Карно для минимизации следующих функций:

а)

б)

Этим функциям соответствуют графическое представление (см. рис. 1.1 а, б):

Рис.1.1. Графическое представление функци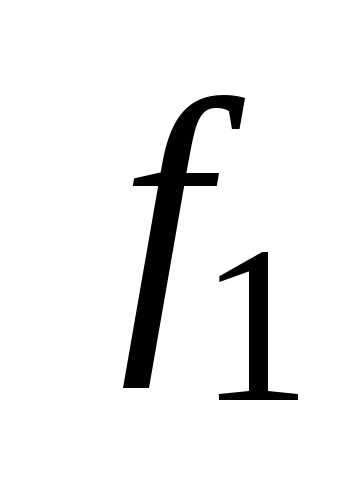й и в виде карт Карно и склеивание соседних клеток карты

Используя результаты склеивания переменных, которые представлены на рис.1, запишем минимальную дизъюнктивную нормальную форму функций

и

Карты Карно обычно используются для ручной минимизации булевых функций небольшого числа переменных, поскольку этот метод плохо алгоритмизируется. Правила минимизации булевых функций можно сформулировать так:

— две соседние клетки карты (два 0-куба) образуют один 1-куб.

При этом клетки карты, находящиеся на границах, также являются соседними, а, следовательно, их можно склеивать, образовывая 1-куб (см. рис. 1.1 в). Независимая переменная обозначена символом X;

— четыре соседние клетки карты могут объединяться, образуя 2-куб (рис. 1 в, импликанта X10X), содержащий две переменные;

— восемь клеток куба после склеивания, образуют один 3-куб и т.д.

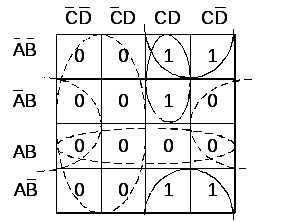
Пример 1.2. Булева функция задана таблицей истинности (табл. 1.1). Построить карту Карно и определить МДНФ.

Таблица 1.1.

Таблица истинности

0	0	0	0	0	1	0	0	0	0
0	0	0	1	1	1	0	0	1	1
0	0	1	0	0	1	0	1	0	1
0	0	1	1	1	1	0	1	1	1
0	1	0	0	0	1	1	0	0	0
0	1	0	1	1	1	1	0	1	1
0	1	1	0	0	1	1	1	0	0
0	1	1	1	1	1	1	1	1	0

Из таблицы истинности собираем СДНФ и создаем карты Карно для четырех переменных (рис.1.2). Поиск МДНФ сводится к определению минимального количества элементарных конъюнкций, которые покрывают все единицы начальной СДНФ.

Используя полученные импликанты (рис. 1.2), запишем МДНФ так

Карты Карно, приведенные на рис. 1.1 и рис 1.2, несколько отличаются, но результат минимизации не зависит от способа построения карт.

studfiles.net

1.6.2. Правила упрощения логических функций

 Дана некоторая логическая функция либо в аналитическом виде, либо в виде таблицы, в которой перечислены значения функции при всех возможных наборах аргументов.

Требуется определить вид простейшей формулы, выражающей заданную функцию, которая содержит минимальное количество элементарных логических функций И, ИЛИ, НЕ.

Эта простейшая формула может иметь

1. либо нормальную дизъюнктивную форму

2. либо нормальную конъюнктивную форму

3. либо какой-нибудь еще тип.

Нахождение такой простейшей формулы, выражающей заданную функцию, удобно выполнять в несколько этапов.

На первомэтапе логическая функция представляется вСДНФили вСКНФ.

Если количество наборов аргументов, при которых функция равна 1, меньше количества наборов, при которых она равна0, то наиболее простой окажетсяСДНФ, в противном случае —СКНФ.

Если исходная функция задана аналитически, то преобразование ее в СДНФ или СКНФ выполняется в такой последовательности:

1)Путем последовательного применения законов инверсии, логическая функция приводится к нормальной форме, в которой инверсия применяется только к аргументам, но не к функциям от них.

2)Путем раскрытия скобок (по известным формулам) логическая функция приводится к дизъюнктивной нормальной или конъюнктивной нормальной форме (гдеДНФ— дизъюнкция ряда членов, которые есть конъюнкция аргументов, взятых с инверсией или без нее; аКНФ — конъюнкция ряда членов, которые есть дизъюнкция аргументов, взятых с инверсией или без нее.)

3)Если этоДНФ, и каждый член представляет собой конъюнкцию менееnчленов, (n- количество аргументов функции), то каждый такой член умножается на выражение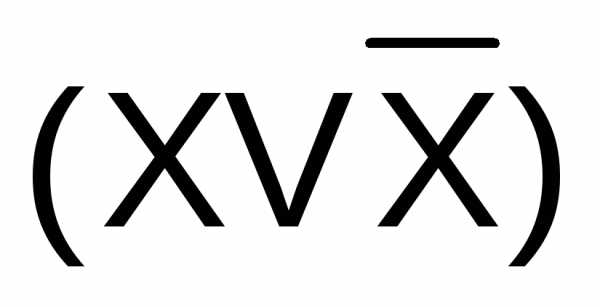, тождественно равное1(Х — один из аргументов, которые в данной дизъюнкции отсутствуют). В результате чего конъюнкция превращается в дизъюнкцию двух конъюнкций (расширениеДНФ):

 

Если же это КНФ, то к каждому члену, представляющему собой дизъюнкцию менееnчленов (n- количество аргументов), добавляется член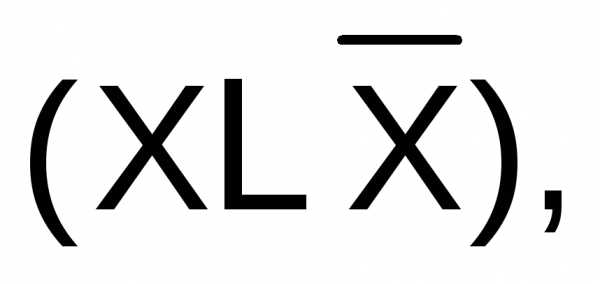тождественно равный0(Х — аргумент, отсутствующий в данной дизъюнкции). В результате чего каждый из этих членов превращается в конъюнкцию 2-х дизъюнкций (расширениеКНФ):

 ^

4) Приводятся подобные члены.

Далее п.п. 3., 4. повторяются до тех пор, пока функция не будет представлена в СДНФилиСКНФ, т.е. количество членов в каждой конъюнкции (дизъюнкции) не станет равнымnи не станет совпадающих дизъюнкций (конъюнкций).

На второмэтапе происходит преобразование (минимизация) полученной логической функции по известным правилам, приведенным выше.

1.6.3. Контрольные вопросы по теме «Законы и правила упрощения логических функций»

1. Назовите основные соотношения алгебры логики.

2. Как формулируется закон отрицания конъюнкции?

3. Как формулируется закон отрицания дизъюнкции?

4. Сформулируйте переместительный закон алгебры логики.

5. Сформулируйте сочетательный закон алгебры логики.

6. Какие формы дистрибутивный (распределительный) закон имеет в алгебре логики?

7. Сформулируйте правило склеивания для ДНФ.

8. Сформулируйте правило склеивания для КНФ.

9. Сформулируйте правило поглощения для ДНФ.

10. Сформулируйте правило поглощения для КНФ.

11. Сформулируйте правило свертки для ДНФ.

12. Сформулируйте правило свертки для КНФ.

13. Назовите этапы упрощения логической функции, заданной аналитически.

14. Назовите этапы упрощения логической функции, заданной таблично.

15. Сформулируйте правило расширения для ДНФ.

16. Сформулируйте правило расширения для КНФ.

studfiles.net

Упрощение логических схем

Л а б о р а т о р н а я р а б о т а №3

Цель работы: Изучение способов упрощения логических функций, в том числе частично определенных (недоопределенных) функций. Приобретение практических навыков по разработке и расчету схем на базе логических элементов, в том числе на основе базовых логических элементов.

Лабораторная работа состоит из двух этапов:

1. Подготовка к выполнению лабораторной работы. Заключается в выполнении студентом индивидуального задания в соответствии с вариантом, указанным преподавателем. Задание предъявляется для проверки преподавателю до начала лабораторной работы. Студент допускается к выполнению лабораторной работы, если задание выполнено правильно.

2. Практическая часть. Заключается в моделировании, макетировании и проверке работоспособности схем индивидуального задания.

1. Теоретическая часть

1.1. Упрощение логических функций

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы пропорциональны числу операций и числу вхождений перемещений или их отрицаний. Логическая функция может быть упрощена с помощью аксиом и теорем алгебры логики, однако такие преобразования требуют громоздких выкладок и навыков. Для упрощения применяются правила, приведенные в таблице 1.1.

Таблица 1.1 – Правила вычисления

Наименование	Для умножения	Для сложения
Коммутативный закон	Х1Х2= Х2Х1	Х1+Х2= Х2+Х1
Ассоциативный закон	Х1(Х2Х3) = (Х1Х2)Х3	Х1+(Х2+Х3) = (Х1+Х2)+Х3
Дистрибутивный закон	Х1(Х2+Х3) = Х1Х2+Х1Х3
Правило повторения	ХХ = Х	Х+Х=Х
Правило отрицания
Правило двойного отрицания
Теоремы де Моргана:
Операции с 0 и 1:	Х1 = 1 Х0 = 0	Х+1 = 1 Х+0 = Х

Рассмотрим булево выражение:

.

Для реализации данного выражения необходимо 2 инвертора, 3 конъюнктора (И) и 1 дизъюнктор (ИЛИ).

Упростим данное логическое выражение:

.

Таким образом, все логическое выражение сведено к логической операции ИЛИ.

На практике для упрощения логических выражений, описывающих работу устройства, применяют карты Карно. Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте в виде клетки. Карта образуется путем такого расположения клеток, при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.

Карта Карно для 2-х переменных имеет вид, представленный на рисунке 1.1.а.

а)	б)	в)
Рис. 1.1 – Упрощение логического выражения с помощью карты Карно

Минимизируем исходное логическое выражение посредством применения карты Карно. Поставим 1 в карте Карно в тех клетках, которые соответствуют наборам функции, присутствующим в логическом выражении, рисунок 1.1.б.

Отыскание минимальной формы сводится к максимальному склеиванию по некоторому аргументу: по В – вертикаль и по А – горизонталь. Единицы, находящиеся в соседних клетках, объединим контурами (рисунок 1.1.в). Возможно объединение 2, 4, 8 и т.д. единиц, стоящих в соседних клетках. Кроме этого, карта Карно может быть свернута в горизонтальный или вертикальный цилиндры, или шар, что также позволяет объединить единицы, стоящие в соседних крайних клетках свернутых карт.

Т.к. у нас два контура, то новое выражение будет состоять из двух членов, связанных функцией ИЛИ. Например, для нижнего контура аргумент А встречается с и В, но в соответствии с правилом булевой алгебры аргументыи В дополняют друг друга, и их можно опустить, т.е. остается только аргумент А.

В результате значение функции будет также сведено к логической операции ИЛИ.

Рассмотрим пример построения карты Карно для трех переменных. Пусть дано логическое выражение:

.

Карта Карно и результат минимизации представлены на рисунке 1.2.

Рис. 1.2 – Пример карты Карно для 3-х переменных

Рассмотрим пример построения карты Карно для четырех переменных, рисунок 1.3.

Рис. 1.3 – Карта Карно для 4-х переменных

В рассмотренных примерах осуществлялась минимизация по 1, однако в некоторых случаях более удобной может оказаться минимизация по 0. Пример такого случая представлен на рисунке 1.4. Минимизация по нулям показана штрихпунктирной линией, а по единицам – сплошной.

	Минимизация по 0
	Минимизация по 1
Рис. 1.4 – Минимизация по 0

При минимизации по нулям получается отрицательная функция. Поставив с двух сторон отрицание и используя теорему Де-Моргана, можно перейти к положительной функции и реализовать полученное значение на требуемых логических элементах:

,,

studfiles.net

1.8. Упрощение и минимизация логических функций

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы, пропорциональны числу операций и числу вхождений перемещений или их отрицаний.

Логическая функция может быть упрощена с помощью аксиом и теорем алгебры логики, однако такие преобразования требуют громоздких выкладок и навыков.

На практике для упрощения логических выражений описывающих работу устройства применяют Карты Карно

Рассмотрим булево выражение:

Для реализации данного выражения необходимо 2 инвертора, 3 конъюнктора (И) и 1 дизъюнктор (ИЛИ).

Упростим данное логическое выражение

Таким образом, все логическое выражение сведено к логической операции ИЛИ (конъюнктор).

Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте виде клетки.

Карта образуется путем такого расположения клеток при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.

Карты Карно для 2 переменных имеет вид, представленный на Рис.1.10.а.

Минимизируем исходное логическое выражение посредством применения карт Карно.

Проставим 1 в карту Карно в те клетки, которые соответствуют наборам функции присутствующим в логическом выражении.

Отыскание минимальной формы сводится к максимальному склеиванию по некоторому аргументу – по В – вертикаль и по А – горизонталь.

Соседние 1 объединим контуром (Рис.1.10.в. ). Возможно объединение 2, 4, 8 и т.д. единиц, стоящих в соседних клетках, кроме этого карта карно может быть свернута в горизонтальный или вертикальный цилиндры, или шар, что также позволяет объединить 1 стоящие в соседних крайних клетках свернутых карт.

Т.к. у нас два контура, то новое выражение будет состоять из двух членов связанных функцией ИЛИ.

а)	б)	с)
Рис.1.10. Упрощение логического выражения с помощью карты Карно

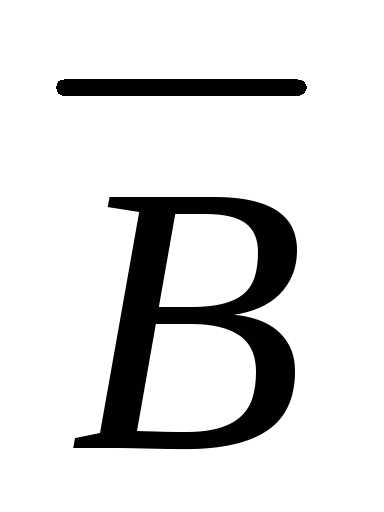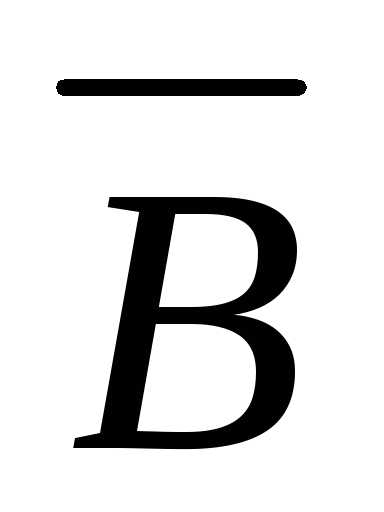Для нижнего контура аргумент А встречается си В, но в соответствии с правилом булевой алгебры аргументыи В дополняют друг друга и их можно опустить, т.е.остается только аргумент А.

В результате значение функции будет также сведено к логической операции ИЛИ.

Рассмотрим пример построения карты Карно на три переменные. Пусть дано логическое выражение

Карта Карно и результат минимизации представлены на Рис.1.11.

Рис.1.10. Пример карты Карно для 3-х переменных

Рассмотрим пример построения карты Карно на четыре переменные (Рис.1.11)/

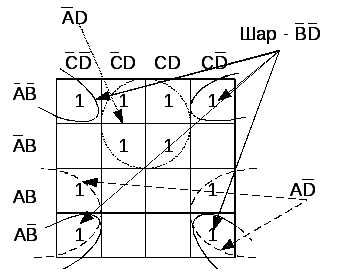
В рассмотренных примерах осуществлялась минимизация по 1, однако в некоторых случаях более удобной может оказаться минимизация по 0. Пример такого случая представлен на Рис.1.12.

Минимизация по нулям показана штрихпунктирной линией, а по единицам – сплошной.

При минимизации по нулям получается отрицательная функция. Поставив отрицание с двух сторон.

Рис.1.11. Карта карно на 4 переменных.

	Минимизация по 0
	Минимизация по 1
Рис.1.12. Минимизация по 0

Используя теорему Де-Моргана можно перейти к положительной функции и реализовать полученное значение на требуемых логических элементах.

studfiles.net

1.2. Частично определенная функция и ее упрощение

Частично определенной (недоопределенной) функцией называется функция, значение которой на некоторых наборах запрещено или некоторые наборы входных значений не используются в работе схемы. Значение функции на таких наборах можно задать по своему усмотрению (1 или 0), т.е. доопределить функцию. Доопределение функции не отразится на работе устройства, но облегчит его реализацию.

При минимизации недоопределенных булевых функций в картах Карно, которые соответствуют запрещенным наборам, ставят прочерки, которые могут доопределяться 1 или 0 для удобства конкретной минимизации.

Пример минимизации недоопределенной функции показан на рисунке 1.5.

А В С F 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 — 1 0 1 — 1 1 0 — 1 1 1 1
а) таблица истинности	б) карта Карно	в) доопределение карты Карно
Рис. 1.5 – Минимизация недоопределенной функции

1.3. Синтез и упрощение логических схем с помощью программы ewb

С помощью логического преобразователя можно синтезировать логические схемы на 8 входов.

В качестве примера синтезируем схему, логическая функция которой имеет вид .

Для выполнения синтеза в общем случае целесообразно соблюдать следующую последовательность действий.

Щелчком курсора мыши по иконке логического преобразователя непосредственно на линейке приборов раскрыть его лицевую панель.

Активизировать курсором клеммы-кнопки A, B и C, количество которых равно количеству входов синтезируемого устройства (А, В, С – переменные функции F).

Записать выражение логической функции на дополнительном дисплее, расположенном в нижней части лицевой панели, рисунок 1.6.

Рис. 1.6 – Вид логического преобразователя после активизации входов

и записи выражения логической функции

Получить выходную комбинацию таблицы истинности, для чего нажать кнопку . Выходная комбинация будет отображена в правой вертикальной колонке, рисунок 1.7.

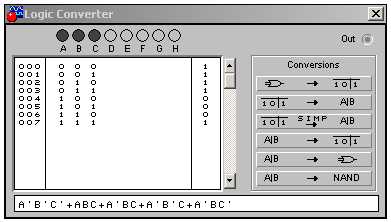
Рис. 1.7 – Вид логического преобразователя после получения выходной комбинации таблицы истинности

Нажав кнопку , упростить логическую функцию, рисунок 1.8.

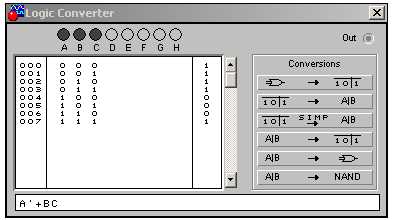
Рис. 1.8 – Выражение логической функции после упрощения

Получить логическую схему устройства, для чего нажать кнопку , рисунок 1.9.

Рис. 1.9 – Логическая схема устройства

Получить логическую схему устройства в базисе И-НЕ, для чего нажать кнопку , рисунок 1.10.

Рис. 1.10 – Логическая схема устройства в базисе И-НЕ

studfiles.net

Упрощение логических схем

Цель работы: Изучение способов упрощения логических функций, в том числе частично определенных (недоопределенных) функций. Приобретение практических навыков по разработке и расчету схем на базе логических элементов, в том числе на основе базовых логических элементов.

1. Теоретическая часть

1.1. Упрощение логических функций

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы пропорциональны числу операций и числу вхождений перемещений или их отрицаний. Логическая функция может быть упрощена с помощью аксиом и теорем алгебры логики. Для упрощения применяются правила, приведенные в таблице 1.1.

Таблица 1.1 – Правила вычисления

Наименование	Для умножения	Для сложения
Коммутативный закон	Х1Х2 = Х2Х1	Х1+Х2 = Х2+Х1
Ассоциативный закон	Х1(Х2Х3) = (Х1Х2)Х3	Х1+(Х2+Х3)=(Х1+Х2)+Х3
Дистрибутивный закон	Х1(Х2+Х3) = Х1Х2+Х1Х3
Правило повторения	ХХ = Х	Х+Х=Х
Правило отрицания
Правило двойного отрицания
Теоремы Де-Моргана:

Рассмотрим булево выражение:

.

Для реализации данного выражения необходимо 2 инвертора, 3 ЛЭ И и 1 ЛЭ ИЛИ.

Упростим данное логическое выражение:

.

Таким образом, все логическое выражение сведено к логической операции ИЛИ.

На практике для упрощения логических выражений, описывающих работу устройства, применяют карты Карно. Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте в виде клетки. Карта образуется путем такого расположения клеток, при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.

Карта Карно для 2-х переменных имеет вид, представленный на рисунке 1.1.а.

а)	б)	в)
Рис. 1.1 – Упрощение логического выражения с помощью карты Карно

Минимизируем исходное логическое выражение посредством применения карты Карно. Поставим 1 в карте Карно в тех клетках, которые соответствуют наборам функции, присутствующим в логическом выражении, рисунок 1.1.б.

Отыскание минимальной формы сводится к максимальному склеиванию по некоторому аргументу: по В – вертикаль и по А – горизонталь. Единицы, находящиеся в соседних клетках, объединим контурами (рисунок 1.1.в). Возможно объединение 2, 4, 8 и т.д. единиц, стоящих в соседних клетках. Кроме этого, карта Карно может быть свернута в горизонтальный или вертикальный цилиндры, или шар, что также позволяет объединить единицы, стоящие в соседних крайних клетках свернутых карт.

Нижний контур, даст аргумент А. Верхний контур – аргумент В

В результате значение функции будет также сведено к логической операции ИЛИ: F = А+В.

Рассмотрим пример построения карты Карно для трех переменных.

.

Карта Карно представлена на рисунке 1.2.

Рисунок 1.2 – Пример карты Карно для 3-х переменных

Рассмотрим пример построения карты Карно для четырех переменных, рисунок 1.3.

Рисунок 1.3 – Карта Карно для 4-х переменных

В рассмотренных примерах осуществлялась минимизация по 1, однако в некоторых случаях целесообразно использовать минимизацию по 0.

Пример такого случая представлен на рисунке 1.4. Минимизация по нулям показана штрихпунктирной линией. Для сравнения сплошной линией показана минимизация по единицам.

Рисунок 1.4 – Минимизация по 0

При минимизации по нулям получается отрицательная функция.

Последовательность преобразования отрицательной функции в положительную показана в таблице 1.2.

Таблица 1.2-Последовательность преобразования отрицательной функции в положительную

Шаг	Логическое выражение	Пояснения
		ЛЭ после минимизации по 0
1		С двух сторон ставится отрицание
2		Снимается двойное отрицание с левой стороны. Используется правило двойного отрицания. Снимается отрицание с правой стороны и применяется теоремы Де-Моргана.
3		Снимается двойное отрицание сигнала С. Используется правило двойного отрицания.

studfiles.net

Упрощение логических функций двух переменных методом карт карно

Н.Н. Моисеева

Государственное бюджетное образовательное учреждение «Школа № 1432»

УПРОЩЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ МЕТОДОМ КАРТ КАРНО

Аннотация

Предлагаемая авторская разработка может дополнить чебный материал при изучении темы «Основы математической логики» по предмету информатика, математика, а также в проектной и исследовательской деятельности обучающихся.

Актуальность данной работы состоит в понимании механизмов преобразования логических выражений, представления сложных логических функций (штрих Шеффера, стрелка Пирса, импликации и т.п.) через базовые логические функции И, ИЛИ, НЕ методом карт Карно.

Ключевые слова: логика, логические выражения, логические функции, инверсия, конъюнкция, дизъюнкция, методы минимизации, метод карт Карно.

Контактная информация

Моисеева Надежда Николаевна, учитель информатики и ИКТ, Государственное бюджетное образовательное учреждение «Школа № 1432», 119634 г. Москва ул. Шолохова д. 19, телефон 8(495)7327460, e-mail: [email protected]

N.N. Moiseevа

State educational institution «School № 1432»

SIMPLIFYING BOOLEAN FUNCTIONS OF TWO VARIABLES BY METHOD OF CARDS OF KARNO

Abstract

The proposed authoring can complement the learning material under the topic «foundations of mathematical logic» on the subject of computer science, mathematics, as well as in project and research activities of students.

The relevance of this work lies in understanding the mechanisms of transformation of logical expressions that represent complex logical functions (Sheffer’s stroke, arrow Pier, implications, etc.) using basic logic functions AND, OR, NOT by a method of cards of Carnot.

Keywords: logic, logical expression, logical functions, inverse, conjunction, disjunction, methods of minimization, a method of cards of Carnot.

Обучаем по-новому

В соответствии с требованиями ФГОС для развития потенциала одаренных и талантливых детей с участием самих обучающихся формируется индивидуальная траектория развития обучающегося. Предлагаемая авторская разработка может дополнить учебный материал при изучении темы «Основы математической логики» по предмету информатика, математика, а также в проектной и исследовательской деятельности обучающихся.

В настоящее время очевидна роль информатики в формировании современной научной картины мира, фундаментальный характер ее основных понятий, законов, всеобщность ее методологии.

Современные направления создания и использования информационной образовательной среды (ИОС) школы предоставляют множество новых возможностей в развитии авторских методик обучения.

Развитие ИКТ компетентности ребёнка — это приобретение опыта создания, преобразования, представления, хранения информационных объектов, умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.

Изучение основ логики имеет прикладное значение и используется для более полного представления о принципах действия современной компьютерной техники, а также при изучении программирования.

Почему надо научить ребят пониманию основ логики?

Развитие мышления школьников всегда было одной из задач обучения. Истина и логика взаимосвязаны, поэтому теоретическое и практическое значение логики невозможно переоценить. Научиться правильно, рассуждать, мыслить и познавать окружающий мир помогает одна из величайших наук – Логика. Наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью языка. Так как мышление оформляется на языке в виде рассуждения, то можно сказать, что логика — это наука о способах доказательств и опровержений.

Исторически логика изучалась как часть философии. Сейчас логика изучается как часть математики и информатики.

Предметом авторской разработки является представление логических функций двух переменных через набор базовых логических функций, практическая проверка тезиса о представимости любой логической функции через базовые.

Актуальность данной работы состоит в понимании механизмов преобразования логических выражений, представления сложных логических функций (штрих Шеффера, стрелка Пирса, импликации и т.п.) через базовые логические функции И, ИЛИ, НЕ. Приобретённые навыки позволяют глубже понять логические основы устройства компьютера и успешно освоить программирование.

В результате применения описанного метода упрощения (минимизации) можно проследить классификацию всех логических функций одной и двух переменных. Для каждой функции может быть получено их оптимальное представление через базовые функции И, ИЛИ, НЕ с помощью карт Карно.

Основоположники логики

«Воспитание нуждается в трех вещах: в даровании, науке, упражнении.»

Аристотель

Древнегреческий философ и учёный Аристотель является и основоположником логики. Познание у Аристотеля имеет своим предметом бытие. Основа опыта — в ощущениях, памяти и привычке. Любое знание начинается с ощущений: оно есть то, что способно принимать форму чувственно воспринимаемых предметов без их материи; разум же усматривает общее в единичном.

Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике, который сохраняет своё непреходящее значение и поныне. Он разработал теорию мышления и его формы, понятия, суждения и умозаключения.

В 1666 в Лейпциге Лейбниц пишет габилитационную работу по философии «О комбинаторном искусстве», в которой высказывается идея создания математической логики. Из божественного попечительства над миром философ выводит универсальную, неразрывную связь всего со всем. Одно тело не отделено от остальных. Оно – кирпичик в едином здании мира. «Я стою на том, что плохая голова, обладая вспомогательными преимуществами и упражняя их, может перещеголять самую лучшую, подобно тому, как ребенок может провести по линейке линию лучше, чем величайший мастер от руки».

Английский математик и логик. Буль был, обратившимся к логической проблематике. Идеи применения символического метода к логике впервые высказаны им в статье «Математический анализ логики».

Буль высказывал пожелание, чтобы о его взглядах судили по обширному трактату «Исследование законов мышления, на которых основываются математические теории логики и вероятностей». Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. 

Единицей Буль обозначал универсум мыслимых объектов, буквенными символами — выборки из него, связанные с обычными прилагательными и существительными. Буль показал, что символика такого рода подчиняется тем же законам, что и алгебраическая, из чего следовало, что их можно складывать, вычитать, умножать и даже делить. Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций. 

Аристотель, Джордж Буль и Лейбниц познакомили нас с наукой о формах, методах и законах интеллектуальной познавательной деятельности — с логикой.

Логические функции

В логике известны три базовые логические операции, выражаемые с помощью логических связок И, ИЛИ, НЕ (конъюнкция, дизъюнкция и отрицание).

Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

  Логический элемент — это устройство, реализующее ту или иную логическую функцию. Y=f(X1,X2,X3,…,Xn) — логическая функция, она может быть задана таблицей, которая называется таблицей истинности.

Логические функции одной переменной

Таблица истинности функции одной переменной Y=f(X) содержит всего 2 строки, а число функций одной переменной равно 4.

Функция константа 0, Y=0. Техническая реализация этой функции — соединение вывода Y с общей шиной с нулевым потенциалом. Таблица истинности функции константа 0 имеет вид:

 

Функция Y=f(X)=X — функция повторения. Техническая реализация этой функции — соединение между собой выводов X и Y.

Таблица истинности функции повторения имеет вид:

 

Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X). Техническая реализация этой функции — инвертор на любом транзисторе или логическом элементе, или транзисторный ключ.

Таблица истинности функции отрицания имеет вид:

 

Функция константа 1, Y=1. Техническая реализация этой функции — соединение вывода Y с источником питания.

Таблица истинности функции константа 1 имеет вид:

 

Важнейшей функцией одной переменной является отрицание НЕ, остальные функции являются тривиальными.

Логические функции двух переменных

Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4 строки, а число функций двух переменных равно 16.

Рассмотрим только несколько основных функций двух переменных.

Логическое ИЛИ (логическое сложение, дизъюнкция):

Y= X1 + X2 = X1VX2

Техническая реализация этой функции — два параллельно соединенных ключа:

 

Таблица истинности логического ИЛИ имеет вид:

 

Логический элемент ИЛИ обозначается на схемах следующим образом:

 

Логическое И (логическое умножение, конъюнкция, схема совпадений): Y = X1X2 = X1&X2

Техническая реализация этой функции — два последовательно соединенных ключа:

 

Таблица истинности логического И имеет вид:

 

Логический элемент И обозначается на схемах следующим образом:

 

Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)

Таблица истинности функции ИЛИ-НЕ имеет вид:

 

Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:

 

Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)

Таблица истинности функции И-НЕ имеет вид:

 

Логический элемент И-НЕ обозначается на схемах следующим образом:

 

Есть ещё три логические функции двух переменных, имеющие специальные названия: импликация, эквивалентность, неравнозначность (исключающее ИЛИ, сложение по модулю 2). Последние две функции являются взаимно обратными, также как, например, функция И и функция штрих Шеффера.

Число строк в таблице — это число возможных наборов значений аргументов. Оно равно 2n, где n — число переменных. Число различных функций n переменных равно 2^2n.

Представление логических функций через И, ИЛИ, НЕ

Теорема 1

Любая функция двух переменных может быть представлена в виде комбинации функций И, ИЛИ, НЕ.

Доказательство

Таблица истинности любой функции имеет вид:

Где Y0, Y1, Y2, Y3 принимают значения 0 или 1. Составим конъюнкцию (ИЛИ) из всех строк, где Yi равно 1. Каждый элемент конъюнкции это дизъюнкция (И) переменных, если Xi = 1 в соответствующей строке или их отрицание, если Xi = 0 в соответствующей строке. Очевидно, что данный элемент конъюнкции равен 1 только для этой строки и 0 для всех остальных.

Тогда, конъюнкция будет равна 1 только для Yi = 1 и 0 во всех остальных случаях. То есть данная конъюнкция будет равна исходной функции. Таким образом, исходная функция представляется через И, ИЛИ, НЕ, что и требовалось доказать.

Пример

Представим через И, ИЛИ, НЕ функцию эквивалентности. Таблица истинности функции имеет вид

Y = X1X2  X1X2

Через функции И, ИЛИ, НЕ логические функции могут быть представлены несколькими способами. Поэтому целесообразно минимизировать представление функций с использованием наименьшего количества базовых функций. Для этого служат карты Карно.

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 … XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 … XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

Упрощение представления функций

Карты Карно

Через функции И, ИЛИ, НЕ логические функции могут быть представлены несколькими способами. Поэтому целесообразно оптимизировать представление функций с использованием наименьшего количества базовых функций. Для минимизации функций алгебры логики был разработан ряд методов:

1. метод непосредственных преобразований логических функций;

2. метод минимизации логических функций при помощи карт Карно;

3. метод Квайна-Мак-Класки;

4. метод Блейка-Порецкого;

5. метод Петрика и другие.

Метод непосредственных преобразований логических функций с использованием законов логики обычно подробно разбирается в процессе изучения темы. Поэтому, остановимся более подробно на методе минимизации логических функций при помощи карт Карно.

Карта Карно – это графический способ минимизации (упрощения) логических функций и представляет собой операции попарного склеивание и элементарного поглощения. Карта Карно рассматривается как перестроенная соответствующим образом таблица истинности функции.

Карты Карно были изобретены в 1952 году Эдвардом В. Вейчем и усовершенствованы в 1953 году физиком Морисом Карно.

Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1 … XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1 … XN. Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности.

Принципы склейки:

• Склейку клеток карты Карно можно осуществлять по единицам

• Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.

• Область, которая подвергается склейке, должна содержать только единицы (нули).

• Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники. Все единицы (нули) должны попасть в какую-либо область.

• С точки зрения минимальности число областей должно быть как можно меньше.

• Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:

Минимизация логических функций двух переменных

1. Конъюнкция

X1 X2

1. Запрет по Х1

X1 X2

1. Повторение X1

X1

1. Запрет по Х2

X1 X2

1. Повторение X2

X2

1. Сложение по модулю 2

X1X2 или X2 X1

1. Дизъюнкция

X1 или X2

1. Стрелка Пирса

X1X2

Таким образом, соседние клетки карты Карно можно группировать для исключения переменной. Число группируемых клеток может быть и больше двух, но их число должно быть четным и они должны соприкасаться (являться соседними) друг с другом.

Допускается также иметь несколько групп перекрывающихся клеток, как в только что рассмотренном примере.

Группироваться могут также клетки первой и последней строк, первого и последнего столбцов, т. е. карту допускается сворачивать в цилиндр, как по вертикальной, так и по горизонтальной оси.

Рассмотрим несколько теорем, доказывающих что любая функция представима через И, ИЛИ, НЕ.

Представление логических функций через базовые функции

Функции И, ИЛИ, НЕ не являются единственным набором базовых функции. Существую ещё несколько наборов базовых функций, представляющих все другие функции.

Проверить является ли набор функций базовым можно на основе следующей теоремы.

Теорема 2

Для того, чтобы набор функций был базовым, то есть представлял все другие функции, достаточно чтобы через этот набор можно было представить функции И, ИЛИ, НЕ.

Доказательство

Любая функция представима через И, ИЛИ, НЕ. Заменим в этом представлении данные функции их эквивалентом через другой базовый набор. Тогда исходная функция представляется через данный базовый набор, что и требовалось доказать.

Представление логических функций через штрих Шеффера

Теорема 3

Через функцию штрих Шеффера Y = X1|X2 =  (X1X2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция штрих Шеффера была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =(Х11) = Х1|1

Конъюнкция Х1 Х2 = ((Х1 Х2)) = (X1|X2) = (X1|X2) |1

Дизъюнкция Х1Х2 = (Х1Х2) = Х1|Х2 = (Х1|1)|(Х2|1)

Теорема доказана.

Представление логических функций через стрелку Пирса

Теорема 4

Через функцию стрелка Пирса Y = X1X2 =  (X1X2) можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция стрелка Пирса была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =(Х10) = Х10

Конъюнкция Х1 Х2 = (Х1 Х2) = (X1X2)=(X10)(X20)

Дизъюнкция Х1Х2 = ((Х1Х2)) = (Х1Х2) = (Х1Х2)0

Теорема доказана.

Представление логических функций через импликацию

Теорема 5

Через функцию импликация Y = X1X2 =  X1X2 можно представить любую другую логическую функцию.

Доказательство

Согласно теореме 2 для того, чтобы функция импликации была базовой достаточно представить через неё функции И, ИЛИ, НЕ.

Отрицание Х1 =Х11 = Х11

Конъюнкция Х1 Х2 = (Х1 Х2) =  (X1X2)=(X1X2) 1

=( X1(X21) 1

Дизъюнкция Х1Х2 = (Х1)Х2 = (Х1) Х2 = (Х11)Х2

Теорема доказана.

Позитивный заключительный аккорд

Теория логических функций прошла долгую историю от Аристотеля до наших дней. В современном виде её сформулировал Джорж Буль.

Логические функции являются математической основой современных вычислительных устройств. Для реализации логических функций в вычислительных устройствах важно унифицировать и минимизировать их представление.

Таким образом, набор функций, через которые можно выразить любые другие функции, называется полным набором базовых функций, т.е. конъюнкция, дизъюнкция и отрицание является полным набором. Упрощение логических выражений можно произвести с помощью методов минимизации. Для несложных функций используются алгебраические преобразования. Для более сложных с числом переменных от 2 до 6 применяют карты Карно.

Понимание методов преобразования позволяют глубже понять логические основы устройства компьютера и успешно освоить программирование.

Список литературных и интернет-источников:

1. А.А. Ивин Логика, учебное пособие издание 2 Москва, Знание 1998

2. Государственные образовательные стандарты общего образования http://www.edu.ru/db/portal/obschee/

3. Д.А. Владимиров Булевы алгебры Москва, Наука 1969

4. Википедия свободная энциклопедия, Логика http://ru.wikipedia.org/

5. Высказывания, цитаты и афоризмы великих людей
   Источник: http://www.wisdoms.ru/pavt/p123.html

6. Н.Н. Моисеева Методические разработки, учебный сайт http://www.schools.keldysh.ru/sch2019/

7. Н.Н. Моисеева Минимизация логических функций двух переменных http://www.rusnauka.com/1_NIO_2014/Matemathics.htm

17

multiurok.ru