Окружность. Длина окружности. Касательная, дуга
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга. Расстояние от центра до любой точки окружности называется радиусом.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.


Общие определения
Радиус Для любой точки \( OL=R \). (Длина отрезка \( OL \) равняется радиусу окружности).
Хорда Отрезок, который соединяет две точки окружности, является ее хордой.
Диаметр Хорда, проходящая прямо через центр окружности, является диаметром этой окружности \( D=2R \)

Длина окружности Длина окружности вычисляется по формуле: \( C=2\pi R \)
Площадь круга Площадь круга: \( S=\pi R^{2} \)
Дуга окружностиДугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда \( CD \) стягивает две дуги: \( CMD \) и \( CLD \). Одинаковые хорды стягивают одинаковые дуги.
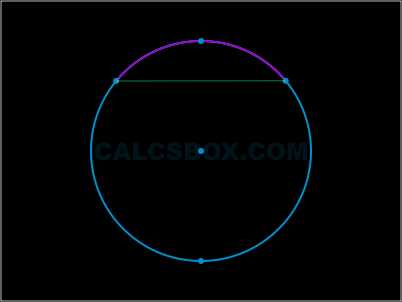
Центральный угол Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
- Используя градусную меру: \( CD = \dfrac{\pi R \alpha ^{\circ}}{180^{\circ}} \)
- Используя радианную меру: \( CD = \alpha R \)
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды \( AB \) и \( CD \) окружности имеют пересечение в точке \( N \), то произведения отрезков хорд, разделенные точкой \( N \), равны между собой.
\( AN\cdot NB = CN \cdot ND \)

Касательная к окружности
Касательная Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Секущая Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
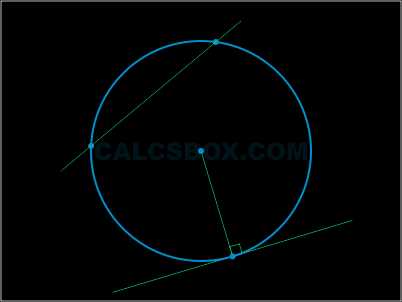
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
\( AC = CB \)
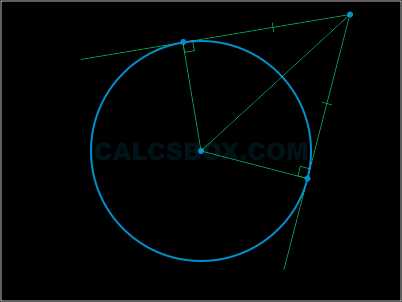
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
\( AC^{2} = CD \cdot BC \)

Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
\( AC \cdot BC = EC \cdot DC \)
Углы в окружности
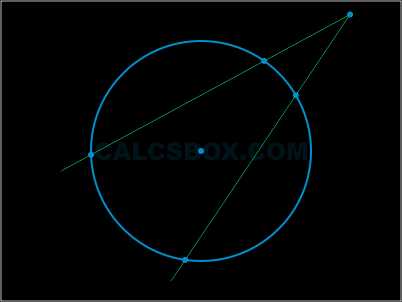
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
\( \angle COD = \cup CD = \alpha ^{\circ} \)
Вписанный угол Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
\( \angle AOB = 2 \angle ADB \)
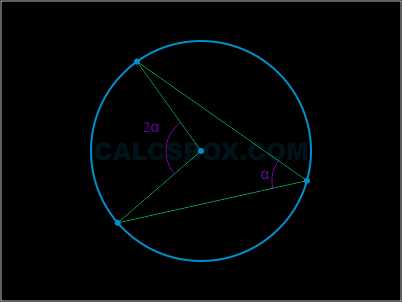
Опирающийся на диаметр, вписанный угол, прямой.
\( \angle CBD = \angle CED = \angle CAD = 90^ {\circ} \)
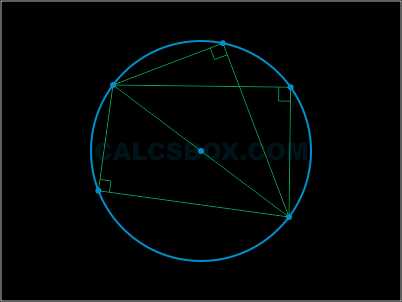
Вписанные углы, которые опираются на одну дугу, тождественны.
\( \angle ADB = \angle AEB = \angle AFB \)

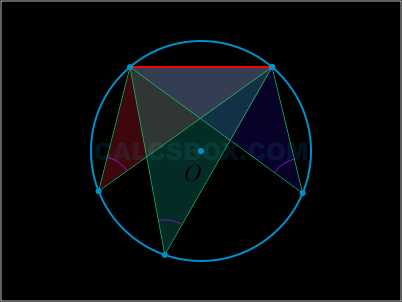
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется \( 180^ {\circ} \).
\( \angle ADB + \angle AKB = 180^ {\circ} \)
\( \angle ADB = \angle AEB = \angle AFB \)

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
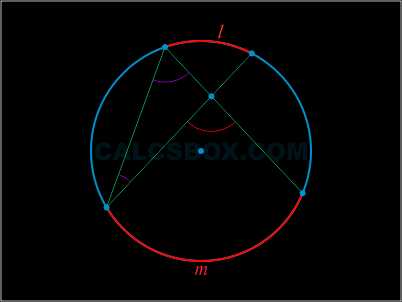
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\( \angle DMC = \angle ADM + \angle DAM = \dfrac{1}{2} \left ( \cup DmC + \cup AlB \right ) \)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\( \angle M = \angle CBD — \angle ACB = \dfrac{1}{2} \left ( \cup DmC — \cup AlB \right ) \)

Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
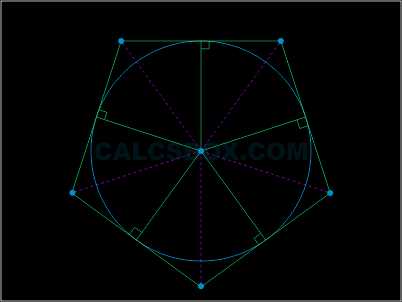
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
\( S = pr \),
где:
\( p \) — полупериметр многоугольника,
\( r \) — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
\( r = \dfrac{S}{p} \)
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
\( AB + DC = AD + BC \)
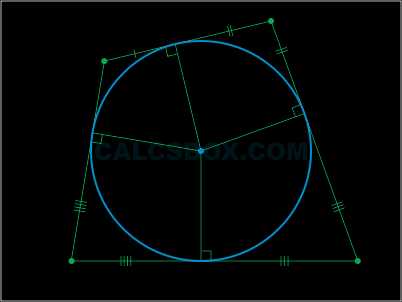
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
\( r = \dfrac{S}{p} \),
где \( p = \dfrac{a + b + c}{2} \)
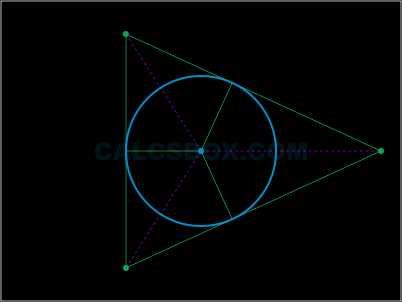
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна \( 180^{ \circ} \).
\( \angle A + \angle C = \angle B + \angle D = 180^ {\circ} \)

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
\( R = \dfrac{a}{2 \sin A} = \dfrac{b}{2 \sin B} = \dfrac{c}{2 \sin C} \)
\( R = \dfrac{abc}{4 S} \)
где:
\( a \), \( b \), \( c \) — длины сторон треугольника,
\( S \) — площадь треугольника.

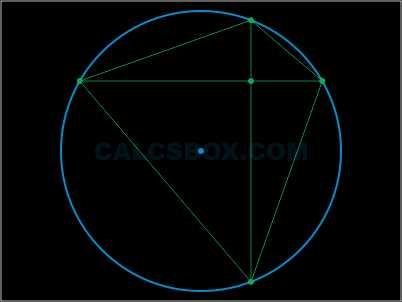
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
\( AC \cdot BD = AB \cdot CD + BC \cdot AD \)
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Окружность. Круг
Цели урока:
- Образовательная: формировать у уча щихся понятие об окружности и круге, как геометрических фигурах, познакомить с историей возникновения этих фигур, историей создания циркуля;
- Развивающая: развивать логическое мышление, наглядно-образное представление о математических понятиях;
- Воспитательная: продолжать формировать эстетическое отношение к предмету, графическую культуру.
“Из всех фигур прекраснейшая – круг”
Пифагор
Ход урока
1. Организационный момент.
2. Мотивация урока.
В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? – подумаете вы. Но это только на первый взгляд. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезли все колёса!
Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо.
Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму.
Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность.
Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания. Самым важным среди круглых тел был шар.
А теперь давайте поближе познакомимся с окружностью и кругом.
3. Актуализация опорных знаний.
На этом этапе урока ребятам сообщается о продолжении изучения геометрических фигур. Вспоминаются геометрические фигуры, изучаемые ранее (отрезок, прямая, угол, прямоугольник, квадрат и др.) и сообщается о том, что сегодня мы познакомимся с еще двумя. Приводятся и показываются примеры из жизни предметов, которые имеют форму круга (циферблат часов, чашка и т.д.). Обычно ребята называют эти фигуры, кто окружность, кто круг. Кто же из них прав? Чтобы выяснить эти вопросы мы обращаемся к геометрии. Что же в геометрии понимается под окружностью, а что под кругом.
4. Изучение нового материала.
1) Окружность – это множество точек плоскости, находящихся на одинаковом расстоянии от одной точки.
Окружность разбивает плоскость на 2 части.
Часть плоскости, находящаяся не внутри окружности вместе с этой окружностью, называется кругом.
У круга есть одна подруга
Известна всем ее наружность.
Она идет по краю круга
И называется…. Окружность.
2) Дается представление и определение окружности, центра, радиуса и диаметра, хорды окружности. Рассматривается формула связи радиуса и диаметра одной окружности. Сообщение исторических сведений
“радиус” (в переводе с латинского – луч) впервые встречается в “геометрии” французского ученого Рамуса, изданной в 1569 г, затем у Ф.Виета; термин “радиус” становится общепринятым лишь в конце XVII века.
“хорда” (от греческого “хорде” – струна) был введен в современном смысле европейскими учеными в XII-XIII веках.
Содержит ли диаметр в себе радиусы? Сколько?
D = 2r; r = d/2
3) Показывается, как строится окружность с помощью циркуля.
Конечно, опытные, тренированные люди весьма ловко одним росчерком изображают окружность. Рассказывают, что великий немецкий художник Альбрехт Дюрер одним движением руки мог столь точно нарисовать окружность, что последующая проверка при помощи циркуля не показывала никаких отклонений. Как же ему это удавалось? Я хочу познакомить вас с правилом, позволяющим сделать нужное изображение от руки.
Историческая справка.
Самый старый железный циркуль обнаружен во Франции при раскопках древнего кургана. Он пролежал в земле более 2-х тысяч лет. В пепле, засыпавшем греческий город Помпеи, археологи обнаружили очень много бронзовых циркулей. Циркуль всегда был незаменимым помощником архитекторов и строителей. Неслучайно на фасаде одного из самых древних и красивых храмов Грузии изображена рука архитектора, а позади неё циркуль.
В Древней Руси любили узор из мелких кружков. Стальной циркуль-резец для нанесения такого рисунка археологи нашли при раскопках в Новгороде. Есть в этом инструменте нечто такое, что заставляет относится к нему с уважением. Вот как описал знакомство с ним в детстве Ю. Олеина, автор знаменитой сказки “Три толстяка”: “В бархатном ложе лежит плотно сжав ноги, холодный сверкающий циркуль. У него тяжелая голова. Я намереваюсь поднять его. Он неожиданно раскрывается и производит укол в руку”.
4) Рассматривается взаимное расположение прямой и окружности.
Вводится понятие и свойство касательной к окружности.
5) Рассматривается взаимное расположение двух окружностей.
Понятие концентрической окружности.
6) Далее вводятся формулы для нахождения площади круга, зная радиус или диаметр круга.
5. Закрепление нового материала.
Решить № 506, 508(2), 509.
6. Самостоятельная работа.
Работа в парах с учебником.
Задача с.137.
7. Итоги урока. Рефлексия. Д/з.
Выучить п.17, вопросы с. 137, решить на 7 баллов №505, на 9 баллов №508(1), на 11 баллов №514.
Творческое задание: составить узор из окружностей. Оценивается отдельно.
А теперь продолжите предложения, которые вы видите на доске:
Сегодня я узнал…
Было интересно…
Я понял, что…
Теперь я могу…
Я научился…
У меня получилось…
Сегодня на уроке мы узнали, что такое окружность, круг, чем они отличаются. Познакомились с инструментом, — циркулем. Научились строить окружность с его помощью. Узнали что такое радиус, диаметр. В школе свойства окружности и круга изучаются до 11 класса, но первые представления у учащихся должны быть уже в 6 классе.
xn--j1ahfl.xn--p1ai
Окружность и круг
Окружность и круг являются геометрическими фигурами, которые связаны между собой. Окружность является граничной, ломаной линией (кривой) круга. Рассмотрим определение окружности несколько подробней. Окружность является замкнутой кривой с равноудаленными от центра точками. Стоит отметить, что центр окружности также является точкой. Для того, чтобы построить окружность, необходимо выбрать вышеупомянутую точку, которая будет служить центром, а затем провести циркулем замкнутую линию.
Если же мы соединим центр окружности с произвольной точкой, которая лежит на окружности, то получим отрезок, который называется радиусом. Причем, если мы меняем точки на окружности и проводим с центра несколько линий до разных точек окружности, не трудно догадаться, что отрезки (радиусы) будут одинаковыми. Если же мы соединяем две точки окружности одной линией, но при этом проводим данную линию через центр окружности, то мы получаем отрезок, который называется диаметром. Сделав нехитрые подсчеты и, даже просто взглянув на окружность, можно практически сразу сказать, что диаметр окружности равен двум радиусам.
Теперь поговорим о таком определении, как круг и выясним, чем же он отличается от окружности. Круг – это часть плоскости, которая лежит внутри окружности. Центр, диаметр и радиус окружности одновременно являются центром, диаметром и радиусом круга. Однако не забываем про то, что круг, в отличии от окружности, является частью плоскости, а значит имеет свою площадь. Как же измеряется данный параметр для круга? Все очень просто: площадь круга равна произведению радиуса, возведенному в квадрат и числу Пи. Также следует знать и то, что можно искать площадь не всего круга, а определенного сектора, который может образоваться в результате проведения из центра в две разные точки, которые лежат на окружности круга, прямых.
Окружность и круг | ||||||||||||||||||||||
Длина окружности | ||||||||||||||||||||||
| C = 2πr = πd | ||||||||||||||||||||||
Длина дуги, равной n° | ||||||||||||||||||||||
Площадь круга | ||||||||||||||||||||||
| ||||||||||||||||||||||
Свойства хорд, секущих и касательной | ||||||||||||||||||||||
| ||||||||||||||||||||||
Сегмент и сектор | ||||||||||||||||||||||
| ||||||||||||||||||||||
| ||||||||||||||||||||||
Площадь кругового кольца | ||||||||||||||||||||||
| ||||||||||||||||||||||
mateshka.ru
Окружность и круг
На этом уроке мы познакомимся с понятиями окружности и круга. Научимся чертить окружность и круг.
Чертить окружности вы научились ещё в младших классах. Давайте вспомним, как происходит этот процесс. Для того чтобы начертить окружность мы должны установить остриё циркуля в некоторой точке О. Далее будем вращать ножку с карандашом.
Определение
Карандаш начертит на плоскости листа линию, которая и называется окружностью. Точка, в которой устанавливалось остриё циркуля, или точка О, называется центром окружности.
Давайте соединим центр окружности, т.е. точку О, с любой понравившейся вам точкой на окружности. Обозначим эту точку, например, буквой А. Видим, у нас получился отрезок ОА.
Определение
Отрезок, соединяющий центр окружности с любой точкой на окружности, называется радиусом. Радиус обозначают маленькой латинской буквой r.
Отметим на этой окружности ещё несколько точек, например, В, С и D. И соединим их с центром окружности. Эти отрезки ОВ, ОС и OD также называют радиусами.
Все точки окружности равноудалены от её центра, т.е. удалены от центра на расстояние, равное длине радиуса.
Часто слово «длина» не произносят, а вместо «длина радиуса» говорят просто «радиус». Например, говорят: «Изображена окружность с радиусом, равным 3 см».
Теперь давайте соединим любые 2 точки на окружности, не проходящие через центр окружности, например, E и F. У нас получился отрезок EF.
Определение
Отрезок, концы которого лежат на окружности, называется хордой.
Хорда, проходящая через центр окружности, называется её диаметром.
Посмотрите внимательно на экран. На рисунке изображён отрезок АВ, он является диаметром окружности. По рисунку нетрудно заметить, что диаметр окружности равен двум её радиусам, т.е.
Диаметр обозначают маленькой латинской буквой d, тогда d = 2r.
Запомните, диаметр окружности в два раза длиннее радиуса.
Все диаметры окружности равны между собой.
Отметим на окружности 2 точки, например, M и N.
Определение
Эти 2 точки разделили окружность на 2 части, каждую из которых называют дугой.
На нашем рисунке они изображены линиями разного цвета.
Точки M и N называют концами дуг.
Окружность является замкнутой линией. Она разбивает плоскость на две части – внутреннюю и внешнюю.
Часть плоскости, находящаяся внутри окружности, вместе с этой окружностью называется кругом.
Окружность – это граница круга. Центром круга называется центр этой окружности. Радиусом круга называется радиус этой окружности. Диаметром круга называется диаметр этой окружности. Хордой круга называется хорда этой окружности.
Круг состоит из точек, удалённых от данной точки (его центра) на расстояние, меньшее или равное его радиусу.
Определение
Если в круге провести два его радиуса, например, ОА и ОВ, они выделят из круга его часть, которая называется сектором.
В нашем случае, получился сектор АОВ. Оставшаяся часть круга – также сектор.
Теперь давайте разберёмся с расположением точек, окружности и круга. Посмотрите внимательно на экран.
На нём изображена окружность с центром в точке О и точки А, В, С, D и E.
Точки А и Е лежат на окружности или ещё можно сказать принадлежат ей.
Точки В, С, D, O не принадлежат этой окружности.
Точки А, В, С, Е и О принадлежат кругу.
Точка D находится вне окружности или вне круга.
Итоги
Итак, сегодня на уроке мы познакомились с понятиями окружность, круг и их элементами. А также научились их чертить.
videouroki.net
Окружность и круг /qualihelpy
Окружностью называют множество всех точек плоскости, равноудаленных от некоторой данной точки, называемой центром окружности.
Отрезок, соединяющий центр окружности и любую точку окружности, называют радиусом окружности.
Хордой называют отрезок, соединяющий две точки окружности.
Если хорда перпендикулярна радиусу окружности, то точкой пересечения она делится пополам.
Например, на рисунке 8.83 , следовательно, .Хорду, проходящую через центр окружности, называют диаметром окружности. Диаметр состоит из двух радиусов.
Например, на рисунке 8.83 хорда – диаметр окружности и .Дугой окружности называют часть окружности, заключенную между двумя точками окружности. Если точки – концы диаметра окружности, то имеем две равные дуги, называемые полуокружностями.
Например, на рисунке 8.84 изображены дуги окружности: и т.д. Среди них две равные полуокружности . Дуги можно измерять в угловых единицах. Градусная мера полуокружности равна .Кругом называют часть плоскости, ограниченную окружностью, включая точки окружности.
Например, на рисунке 8.85 изображен круг.
Круговым сектором называют часть круга, ограниченную радиусами и дугой, на которую опираются радиусы.
Например, на рисунке 8.86 изображен круговой сектор .Круговым сегментом называют часть круга, отсекаемую хордой.
Например, на рисунке 8.87 изображен круговой сегмент .Свойство пересекающихся хорд: если через точку, лежащую внутри окружности, проведены две хорды, то произведения отрезков, на которые хорды делятся в точке пересечения, равны.
Например, на рисунке 8.88 .Касательной к окружности называют прямую, имеющую с окружностью только одну общую точку.
Например, на рисунке 8.89 из точки к окружности проведены касательные и .Если к окружности из одной точки провести две касательные, то окружность будет вписана в угол, образованный этими касательными. Центр окружности, вписанной в угол, расположен на биссектрисе угла (рис. 8.89).
Свойства касательных
1. Отрезки касательных, проведенных из одной точки к окружности, равны ( на рис. 8.89).2. Радиус окружности перпендикулярен касательной в точке касания ( на рис. 8.89).Свойство хорды и касательной: угол, образованный хордой и касательной, проходящей через конец хорды, измеряется половиной дуги, заключенной внутри его.
Например, на рисунке 8.90 – касательная к окружности, – хорда окружности, и .Секущей называют прямую, имеющую с окружностью две общие точки.
Например, на рисунке 8.91 – отрезок секущей, а – внешняя часть отрезка секущей.Свойство касательной и секущей: если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной равен произведению отрезка секущей и ее внешней части.
Например, на рисунке 8.91 .Свойство секущих к окружности: если из одной точки к окружности проведены секущие, то все произведения отрезков секущих и их внешних частей равны.
Например, на рисунке 8.92 .Угол называют центральным, если его вершина лежит в центре окружности, а стороны являются радиусами окружности. Центральный угол измеряется дугой, на которую он опирается.
Например, на рисунке 8.93 изображен центральный угол .Угол называют вписанным в окружность, если его вершина лежит на окружности, а стороны являются непересекающимися хордами этой окружности.
Например, на рисунке 8.94 изображен вписанный в окружность угол .Свойства вписанных в окружность углов
1. Вписанный в окружность угол равен половине соответствующего ему центрального угла.
Например, на рисунке 8.95.2. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 8.96).
3. Вписанные углы, опирающиеся на диаметр, прямые (рис. 8.97).
helpy.quali.me
Чем отличается окружность от круга
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Выводы TheDifference.ru
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
thedifference.ru
