Уравнение касательной к графику в точке функции онлайн – Уравнение касательной онлайн

Уравнение нормали — 19 Октября 2015 — Примеры решений задач

Определение . Нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.

Если существует конечная и отличная от нуля производная  f'(x₀)  то уравнение нормали к графику функции  y=f(x) в точке x₀ выражается следующим уравнением:

Пример 1. Написать уравнение  нормали к кривой y=3x-x² в точке x₀=2.

Решение.

1. Находим производную y’=3-2x

2. Находим значение производной в точке x₀=2:  f'(x₀)=f'(2)=3-2*2=-1

3. Находим значение функции в точке x₀=2:  f(x₀)=f(2)=3*2-2²=2

4. Подставляем найденные значения в уравнение нормали:

5. Получаем уравнение нормали:

y=x

Калькулятор уравнения нормали

Найти уравнение нормали онлайн можно с помощью данного калькулятора.

 

 

Пример 2. (Рассмотрим особый случай когда f'(x₀) равно нулю)

Написать уравнение нормали к кривой y=cos24x в точке x₀=π/2

Решение.

1. Находим производную y’=2cos4x*(-sin4x*4)=-4sin2x

2. Находим значение производной в точке x₀=π/2:

f'(x₀)=f'(π/2)=-4sin(2*π/2)=0, следовательно уравнение нормали в данном случае применить нельзя.

Воспользуемся определением нормали,сначала находим уравнение касательной, потом находим уравнение перпендикулярной прямой проходящей через данную точку.

 

www.reshim.su

Составить уравнение касательной

При составлении уравнения касательной к графику функции будем использовать следующий алгоритм ее составления:

1. Обозначим абсциссу точки касания через букву a.
2. Вычислим значение функции от а.
3. Найдем производную функции и найдем ее значение от а.
4. Подставим в общее уравнение касательной найденные значения:

   

Задача 1.
Составить уравнение касательной к графику функции  в точке А(3; 323).

Решение.
Точка А(3; 323) – точка касания. Это легко проверить, подставив ее координаты в заданную функцию:

   

Составим уравнение касательной:

1. a=3 – абсцисса точки касания.

2.    

      

      

      

Ответ. Уравнение касательной .

Задача 2.
Составить уравнения всех касательных к графику функции , которые проходят через точку .

Решение.
Точка  не является точкой касания, т.к. .

1. Обозначим абсциссу точки касания буквой а.
2. .
3. , .
4. ;

– уравнение касательной.
Поскольку касательная проходит через точку A(3; 17), значит, координаты этой точки однозначно удовлетворяют уравнению касательной:

   

   

   

   

   

При a=0,5 уравнение касательной имеет вид y=19,75–24x.
При a=6,5 уравнение касательной имеет вид y=481,75–156x.

Ответ. Касательные к графику функции , которые будут проходить через точку А(3; 17): y=19,75–24x и y=481,75–156x.

ru.solverbook.com

Уравнение касательной — Мои файлы — Каталог файлов

Вспомним геометрический смысл производной: если к графику функции  в точке  проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .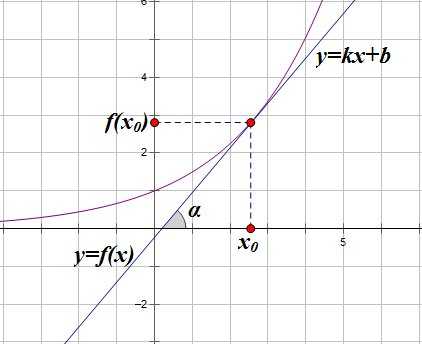

Возьмем на касательной произвольную точку  с координатами :

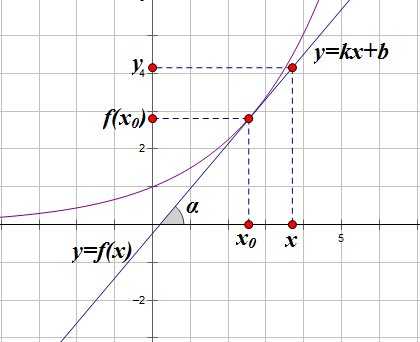
И рассмотрим прямоугольный треугольник :

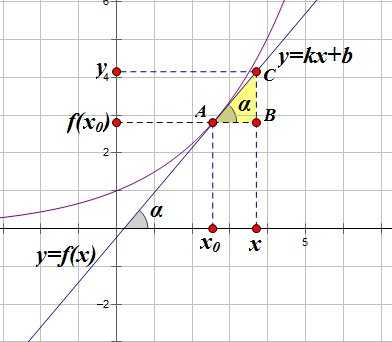
Это и есть уравнение касательной, проведенной к графику функции  в точке .

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти  и .

Есть три основных типа задач на составление уравнения касательной.

1. Дана точка касания  

2. Дан коэффициент наклона касательной, то есть значение производной функции  в точке .

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.

Рассмотрим каждый тип задач.

1. Написать уравнение касательной к графику функции   в точке .

а) Найдем значение функции в точке .

.

б) Найдем значение производной в точке . Сначала найдем производную функции 

Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим: 

Ответ: .

 

2. Найти абсциссы точек, в которых касательные к графику функции  параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси  равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции  в точках касания равно нулю.

а) Найдем производную функции .

б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :

Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5

 

3. Написать уравнения касательных к графику функции ,параллельных  прямой .

Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То естьмы знаем коэффициент наклона касательной, а, тем самым,значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция  и значение производной в точке касания.

а) Найдем точки, в которых производная функции  равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

Приравняем производную к числу -1.

 или 

 или 

б) Найдем уравнение касательной к графику функции  в точке .

Найдем значение функции в точке .

 (по условию)

Подставим эти значения в уравнение касательной:

.

б) Найдем уравнение касательной к графику функции  в точке .

Найдем значение функции в точке .

 (по условию).

Подставим эти значения в уравнение касательной:

.

Ответ: 

 

u4ilki.ucoz.ru